“Умножение и деление рациональных чисел”
1. Частное положительного и отрицательного чисел отрицательно, так ли это:
а) да +
б) нет
в) отчасти
2. На какое число надо умножить -4, чтобы получить -2:
а) 2
б) 0,5 +
в) -2
3. Произведение трех отрицательных чисел отрицательно, так ли это:
а) нет
б) отчасти
в) да +
4. При делении любых двух отрицательных чисел частное имеет знак:
а) “плюс” +
б) “минус”
в) делимого
5. При умножении отличного от нуля числа на -1 получается противоположное число, так ли это:
а) нет
б) отчасти
в) да +
6. Вычислите -13*(0,7):
а) -9,1
б) 9,1 +
в) -91
7. Частное двух отрицательных чисел равно частному их модулей, так ли это:
а) нет
б) отчасти
в) да +
8. Вычислите: (-12,8) : 4 :
а) -3,2 +
б) 3,2
в) -16,6
9. Найдите значение выражения 100 : (-0,1) • (-0,01):
а) -10
б) 0
в) 10 +
10. Могут ли дроби быть рациональными:
а) нет
б) да +
в) зависит от условия задачи
11. Укажите корень уравнения х • 14,2 =14, 2 : (-1):
Укажите корень уравнения х • 14,2 =14, 2 : (-1):
а) -1
б) 1
в) 14,2
12. Укажите неправильное правило умножения и деления:
а) -*-=+
б) +*-=+ +
в) +*+=+
13. Какой закон умножения выражает равенство (а – b) • c = a • c – b • c:
а) распределительный +
б) переместительный
в) сочетательный
14. Может ли быть положительное число рациональным:
а) нет
б) зависит от условия задачи
в) да +
15. Используя верное равенство 517 : 11 = 47, найдите значение выражения -51,7:4,7 :
а) -11 +
б) 11
в) -1,1
16. Может ли быть отрицательное число рациональным:
а) нет
б) да +
в) зависит от условия задачи
17. Укажите значение частного 30 : (-1,5):
а) 200
б) 20
в) -20 +
18. Может ли получаться остаток в процессе деления рациональных чисел:
а) не может
б) может, если выполняется деление с остатком +
в) иногда может
19. Выполните умножение -20 • (-21) • (-5):
а) 210
б) -2100
в) 2100 +
20. Если в числители дроби находится знак радикала, является ли она рациональной:
Если в числители дроби находится знак радикала, является ли она рациональной:
а) да
б) нет +
в) зависит от числа под знаком радикала
21. Укажите значение произведения 40 • (-1,2):
а) -48 +
б) -4,8
в) 48
22. Можно ли делить рациональные числа столбиком:
а) нет
б) да +
в) зависит от условия задачи
23. Известно, что a<0, b<0. Укажите выражение, значения которого отрицательны:
а) -a • (-b)
б) а : b
в) -a • b +
24. Какое число называется рациональным:
а) любое неотрицательное
б) любое число, которое не содержит в себе знак радикала +
в) любое положительное число
25. Известно, что a<0, b<0. Укажите выражение, значения которого отрицательны:
а) -a • (-b)
б) а : b
в) a : (-b) +
26. Вычислите: (-12,8) : (-4) :
а) -3,2
б) 3,2 +
в) -16,6
27. Известно, что a<0, b<0. Укажите выражение, значения которого положительны:
а) -a • (-b) +
б) -a • b
в) a : (-b)
28. Вычислите 13*(-0,7):
Вычислите 13*(-0,7):
а) 91
б) 9,1
в) -9,1 +
29. Известно, что a<0, b<0. Укажите выражение, значения которого положительны:
а) а : b +
б) a : (-b)
в) -a • b
30. При умножении любых двух чисел с разными знаками произведение имеет знак:
а) “плюс”
б) “минус” +
в) того множителя, модуль которого больше
Деление отрицательных чисел кратко Арифметика
Привет, мой друг, тебе интересно узнать все про деление отрицательных чисел, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое деление отрицательных чисел , настоятельно рекомендую прочитать все из категории Арифметика.
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если a и b положительные числа, то разделить число a на число b, значит найти такое число с, которое при умножении на b дает число a.
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число (- 15) на число 5 — значит, найти такое число, которое при умножении на число 5 дает число (- 15). Таким числом будет (- 3), так как
(- 3) • 5 = — 15
значит
(- 15) : 5 = — 3
Примеры деления рациональных чисел.
- 10 : 5 = 2, так как 2 • 5 = 10
- (- 4) : (- 2) = 2, так как 2 • (- 2) = — 4
- (- 18) : 3 = — 6, так как (- 6) • 3 = — 18
- 12 : (- 4) = — 3, так как (- 3) • (- 4) = 12
Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками — число отрицательное (примеры 3,4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
- модуль делимого разделить на модуль делителя;
- перед результатом поставить знак «+».

Примеры деления чисел с одинаковыми знаками:
- (- 9) : (- 3) = + 3
- 6 : 3 = 2
Чтобы разделить два числа с разными знаками, надо:
- модуль делимого разделить на модуль делителя;
- перед результатом поставить знак «-».
Примеры деления чисел с разными знаками:
- (- 5) : 2 = — 2,5
- 28 : (- 2) = — 14
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
| + : (+) = + | + : (-) = — |
| — : (-) = + | — : (+) = — |
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно . Об этом говорит сайт https://intellect.icu . Например, для вычисления дроби
Можно обратить внимание, что в числителе 2 знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
Частное от деления нуля на число, отличное от нуля, равно нулю.
0 : a = 0, a ≠ 0
Делить на ноль НЕЛЬЗЯ!
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
- а : 1 = a
- а : (- 1) = — a
- а : a = 1
, где а — любое рациональное число.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
- если a • b = с; a = с : b; b = с : a;
- если a : b = с; a = с • b; b = a : c
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.
Пример нахождения неизвестного.
x • (- 5) = 10
x = 10 : (- 5)
x = — 2
Знак «минус» в дробях
Разделим число (- 5) на 6 и число 5 на (- 6).
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, и запишем частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
- перед дробью;
- в числителе;
- в знаменателе.
При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.
Пример.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
См. также
- сложение отрицательных чисел ,
- умножение отрицательных чисел ,
- методы декомпозиции ячеек ,
Как ты считаеешь, будет ли теория про деление отрицательных чисел улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое деление отрицательных чисел и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но емко про деление отрицательных чиселЦелочисленное деление отрицательных чисел
27 сент. 2020 г. · 4 минуты чтения · питон разделение пол ·
Выложить на:
Может показаться удивительным, что существует разница в целочисленном делении между
Python и другие языки, такие как Swift, C++ и Java, когда дело доходит до отрицательных чисел.
Причина этого различия в том, что «Целочисленное деление» не является четко определенным
концепция и спецификация для каждого языка могут выбрать усечение в сторону нуля
или отрицательная бесконечность как определенный результат операции.
Гвидо ван Россум написал пост о причинах решения
в Python — почему целочисленное деление Python на 9 этаже0003
Деление и целочисленное деление
В следующем примере показано, что целочисленное деление двух чисел не дает одинакового абсолютного значения, когда одно из чисел отрицательно. Результаты показывают, что деление с плавающей запятой идентично, за исключением отрицательного знака, в то время как результаты целочисленного деления разные.
1 для i в диапазоне (1,12):
2 print(f"{11//i}, {-11//i}, {11/i:.2F} {-11/i:.2F}")
Сравнение целочисленного деления с положительными и отрицательными числами в Python
| и | 11 // я | -11 // я | 11/я | -11/я |
|---|---|---|---|---|
| 1 | 11 | -11 | 11. 00 00 | -11.00 |
| 2 | 5 | -6 | 5,50 | -5,50 |
| 3 | 3 | -4 | 3,67 | -3,67 |
| 4 | 2 | -3 | 2,75 | -2,75 |
| 5 | 2 | -3 | 2,20 | -2,20 |
| 6 | 1 | -2 | 1,83 | -1,83 |
| 7 | 1 | -2 | 1,57 | -1,57 |
| 8 | 1 | -2 | 1,38 | -1,38 |
| 9 | 1 | -2 | 1,22 | -1,22 |
| 10 | 1 | -2 | 1.10 | -1.10 |
| 11 | 1 | -1 | 1,00 | -1,00 |
Результат деления и целочисленного деления в Swift
Выполнение аналогичного кода в Swift дает разные результаты. Эти результаты соответствуют
для С++.
Эти результаты соответствуют
для С++.
1для я в 1...11{
2 print("\(i) : \(11/i), \(-11/i), \(11.0/Double(i)), \(-11.0/Double(i))")
3}
Сравнение целочисленного деления с положительными и отрицательными числами в Swift
| и | 11 // я | -11 // я | 11/я | -11/я |
|---|---|---|---|---|
| 1 | 11 | -11 | 11.00 | -11.00 |
| 2 | 5 | -5 | 5,50 | -5,50 |
| 3 | 3 | -3 | 3,67 | -3,67 |
| 4 | 2 | -2 | 2,75 | -2,75 |
| 5 | 2 | -2 | 2,20 | -2,20 |
| 6 | 1 | -1 | 1,83 | -1,83 |
| 7 | 1 | -1 | 1,57 | -1,57 |
| 8 | 1 | -1 | 1,38 | -1,38 |
| 9 | 1 | -1 | 1,22 | -1,22 |
| 10 | 1 | -1 | 1.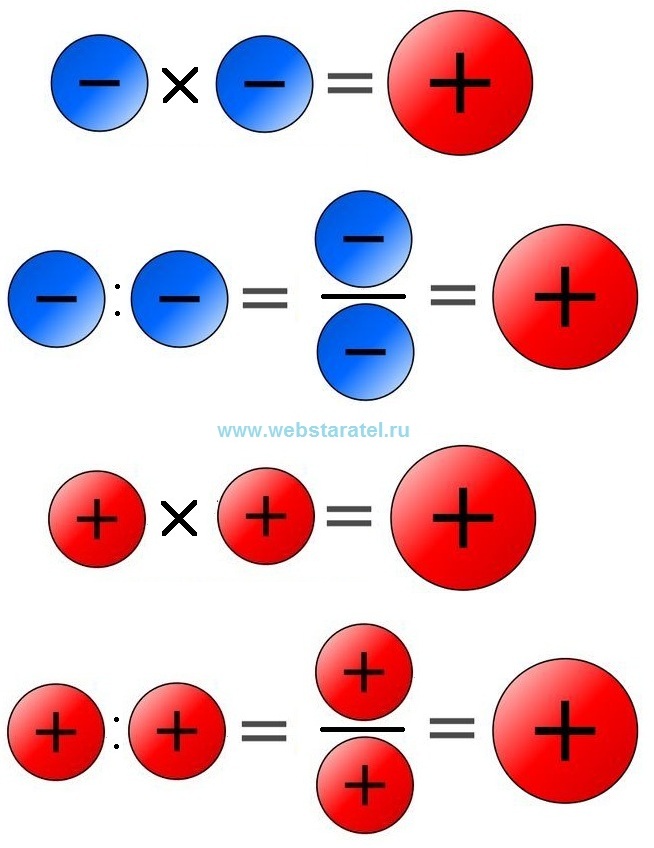 10 10 | -1.10 |
| 11 | 1 | -1 | 1,00 | -1,00 |
Этаж
Возьмем конкретный пример из приведенного выше, например, 11//4 , что приводит к значению
из 2,75 . При работе с положительными числами легко предположить, что
цифры после запятой отбрасываются, а возвращаемое целочисленное значение является числом
до десятичной точки. Это верно для положительных чисел, но то же предположение
для отрицательных чисел предполагает результат -2, что неверно для
Питон. Python использует math.floor для определения целочисленного результата, а
Ниже показано, что и положительный, и отрицательный результат составляют ±2,75, но положительный
целочисленный результат равен 2, а отрицательный целочисленный результат равен -3.
1 отпечаток(11//4) 2""" 32 4""" 5 6печать(11//-4) 7""" 8-3 9""" 10 11принт(11/4) 12""" 132,75 14""" 15 16принт(11/-4) 17""" 18-2,75 19"""
В Python math.floor усекается до отрицательной бесконечности
Прочие математические функции
Следует отметить, что преобразование двойного числа в целое число в Python усекает
к нулю. Округление двойного числа до math.round возвращает соответствующий
положительное или отрицательное ближайшее абсолютное целое число. math.trunc усекает
число к нулю, но math.floor этажа к отрицательной бесконечности.
1int(2.75), int(-2.75), int(2.15), int(-2.15) 2""" 3(2, -2, 2, -2) 4""" 5 6круг(2,75), круг(-2,75), круг(2,15), круг(-2,15) 7""" 8(3, -3, 2, -2) 9""" 10 11math.floor(2,75), math.floor(-2,75), math.floor(2,15), math.floor(-2,15) 12""" 13(2, -3, 2, -3) 14""" 15 16math.trunc(2,75), math.trunc(-2,75), math.trunc(2,15), math.trunc(-2,15) 17""" 18(2, -2, 2, -2) 19"""
Проиллюстрировать функции усечения и усечения в Python
Заключение
В Python деление целых чисел на отрицательные числа дает разные абсолютные значения. значений, чем эквивалентное целочисленное деление на положительные числа. Поведение согласуется с языком, и причиной является использование пола результат, а не усечение. Это может всплывать время от времени, когда перенос алгоритма с одного языка на другой и обнаружение расхождения. Если вы сомневаетесь, проверьте результаты целочисленного деления с отрицательным числа в языке или избегайте целочисленного деления при работе с отрицательными числами.
Модуль 2.3: Использование моделей для деления целых чисел
Модуль 2.3 — Использование моделей для деления целых чиселчто нам нужно знать использовать плитки алгебры для умножения целых чисел
— Правила знаков для умножения
— Значение слова «деление»
— Связь между умножением и делением
заметки для занятий
подробнее
давайте рассмотрим концепцию деления
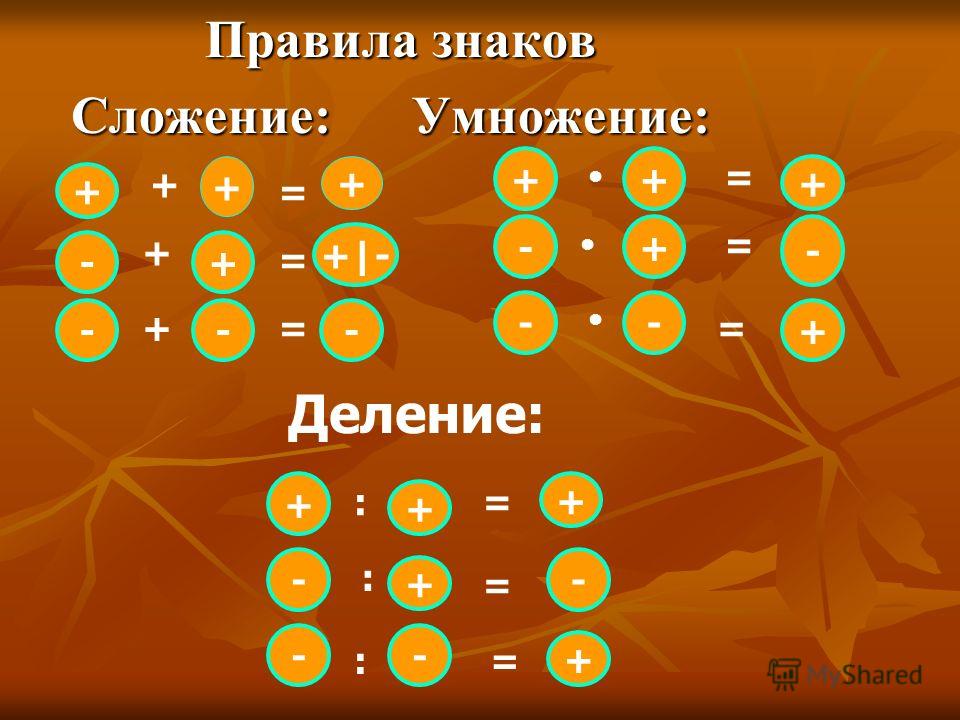
правило знаков для деления
Оказывается, правила знаков для деления точно такие же, как и для умножения!
Чтобы использовать числовые строки, убедитесь, что вы приняли во внимание следующее: — Делимое представляет собой «куда мы хотим пойти», а делитель — это «количество шагов». — Всегда начинать с нуля! — Дивиденды говорят вам, КАКИМ ПУТИ ВЫ БУДЕТЕ СТОЛКНУТЬСЯ. То есть, если вам нужно добраться до отрицательного числа, вы окажетесь лицом к отрицательной стороне числовой прямой. Если вам нужно добраться до положительного числа, вы окажетесь лицом к положительной стороне числовой прямой. — Если делитель ПОЛОЖИТЕЛЬНЫЙ, значит, вы шли ВПЕРЕД. Но если он отрицательный, это означает, что вы будете идти НАЗАД. Давайте сделаем несколько примеров: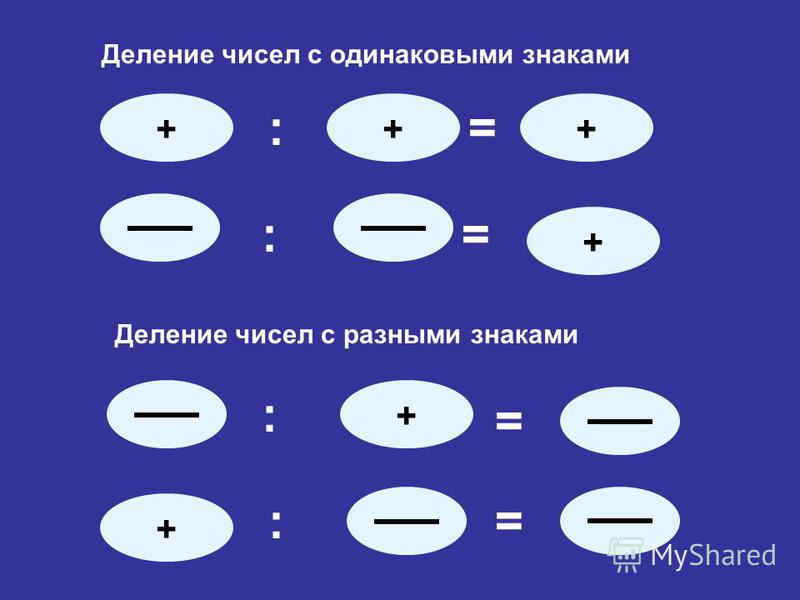
Пример: (+24) / (+6) ——-> мы хотим добраться до 24, делая группы из 6 шагов
Здесь:
-(+10) — это то, куда мы хотим попасть.
— Чтобы добраться до (+10), идите вперед. потому что вам нужно сделать 2 шага. То есть делитель положительный.
— Вы идете вперед, и, поскольку вы получаете +10, вы смотрите в сторону (+).
— Это означает, что ваш ответ (+).
— Мы сделали 5 шагов, поэтому наш ответ (+5).
Здесь:
— (-12) то, куда мы хотим добраться.
— Поскольку делитель отрицательный, это означает, что мы должны идти назад.
— Считаем до 6, идем задом. Но когда мы идем назад, мы оказываемся лицом к (+) стороне. Это означает, что наш ответ (+).
— Мы сделали 2 шага, поэтому наш ответ (+2).
Здесь:
— (-8) то, куда мы хотим добраться.
— Поскольку делитель положительный, это означает, что мы должны идти вперед. 900:10 — Считаем до 4, идем вперед. Когда мы идем вперед, мы оказываемся лицом к (-) стороне. Это означает, что наш ответ (-).
— Мы сделали 2 шага, поэтому наш ответ (-2).
Здесь:
— (+6) это то место, куда мы хотим попасть.
— Поскольку делитель отрицательный, это означает, что мы должны идти назад.
— Считаем на 2, идем задом. Но на этот раз, когда мы идем назад, мы оказываемся лицом к (-) стороне. Это означает, что наш ответ (-).
— Мы сделали 3 шага, поэтому наш ответ (-3).
Деление на положительные целые числа
Деление с отрицательными целыми числами
видео, которые могут помочь
youtube.com/embed/o1Q_1RuZCFI?wmode=opaque» frameborder=»0″ allowfullscreen=»»> рабочие листы
|
|
| ||||||||||||


 trunc(2,75), math.trunc(-2,75), math.trunc(2,15), math.trunc(-2,15)
17"""
18(2, -2, 2, -2)
19"""
trunc(2,75), math.trunc(-2,75), math.trunc(2,15), math.trunc(-2,15)
17"""
18(2, -2, 2, -2)
19"""
