Алгебра. Учебник для 6-8 классов
Алгебра. Учебник для 6-8 классов
ОглавлениеГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.  § 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений.  § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ.  КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.§ 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 82. Решение задач. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90.  (1/3)§ 130. Примеры графического решения уравнений и систем уравнений. |
Свойства степени с целым показателем / Рациональные выражения / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные выражения
- Свойства степени с целым показателем
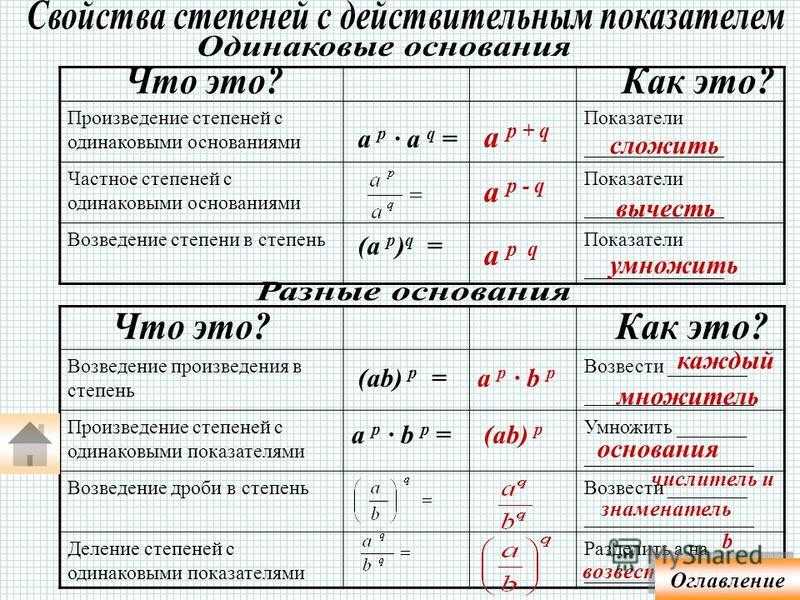
1) Для любого и любых целых и выполняются равенства:
- , то есть при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.
- , то есть при возведении степени в степень показатели перемножают, а основание оставляют прежним.
Равенство называют основным свойством степени.
2) Для любых и и любого целого выполняется равенство: , то есть при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают.
3) Для любого и любых целых и выполняется равенство: , то есть при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя, при этом учитываем то, что деление можно заменить дробью (делимое — числитель, делитель — знаменатель).
4) Для любых и и любого целого выполняется равенство: , то есть при возведении дроби в степень в эту степень возводят и числитель и знаменатель.
Примеры:
1) Представьте выражение в виде степени с основанием :
Решение:
2) Найдите значение выражения:
Решение:
3) Упростите выражение:
Решение:
4) Выполните вычисления и результат запишите в стандартном виде:
Решение:
Советуем посмотреть:
Рациональные дроби
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей.
Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Функция y=k/x и её график.
Рациональные выражения
Правило встречается в следующих упражнениях:
8 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 274, Мерзляк, Полонский, Якир, Учебник
Номер 275, Мерзляк, Полонский, Якир, Учебник
Номер 276, Мерзляк, Полонский, Якир, Учебник
Номер 278, Мерзляк, Полонский, Якир, Учебник
Номер 279, Мерзляк, Полонский, Якир, Учебник
Номер 280, Мерзляк, Полонский, Якир, Учебник
Номер 284, Мерзляк, Полонский, Якир, Учебник
Номер 291, Мерзляк, Полонский, Якир, Учебник
Номер 298, Мерзляк, Полонский, Якир, Учебник
Типы чисел Порядок операций
Сложение, вычитание, умножение, деление и возведение в степень — все это операции над действительными числами, т.
е. операции, которые вы делаете с действительными числами. Для сложных арифметических выражений важно выполнять операции в правильном порядке. Так что тактика «в каком порядке я хочу» не сработает для вас.
Этот правильный порядок задается волшебной фразой «Пожалуйста, извините, моя дорогая тетя Салли» (PEMDAS). О, бедная, дорогая тетя Салли; иногда она немного запутывается, и ей нужны аббревиатуры, чтобы напомнить ей, как решать ее любимые математические уравнения.
Буквы обозначают P арентезы, E xponents, M умножение и D ivision, A дополнение и S вычитание, в том порядке, в котором мы хотим их делать. Обратите внимание, что «Умножение и деление» и «Сложение и вычитание» сгруппированы вместе. Это потому, что умножение не обязательно должно быть выполнено перед делением — вам просто нужно завершить все ваши умножения и деления, прежде чем вы начнете сложение и вычитание.
Не расстраивайтесь, если вы не поняли этого сначала. Тетя Салли 40 лет пытается понять эту концепцию, но она все еще ускользает от нее.
Пример задачи
Сначала мы оцениваем значения в скобках. Мм, мы не можем упростить (4) больше, чем это уже есть, так что давайте перейдем к показателям степени.
Затем умножение и деление:
6 – 1
И, наконец, сложение и вычитание:
5
При сложении и вычитании мы работаем слева направо. Проверьте, на подошве какой из ваших туфель написана большая буква «L», если вы не уверены.
Пример задачи
Сколько будет 4–6–2?
У нас нет круглых скобок, показателей степени, умножения, деления или сложения, поэтому мы сразу переходим к вычитанию. Однако, как обычно, мы должны двигаться слева направо.
4 – 6 – 2 =
(4 – 6) – 2 =
-2 – 2 = -4
Обратите внимание, что если бы мы сначала вычли 6 – 2, мы получили бы совершенно другое (и неправильное) ответ:
4 – (6 – 2) =
4 – 4 = 0
Мы также работаем слева направо при оценке умножения и деления.
Пример задачи
Что такое 3 × 4 ÷ 2 ÷ 6?
Здесь у нас есть только умножение и деление, так что давайте прокручиваем слева направо.
3 × 4 ÷ 2 ÷ 6 =
12 ÷ 2 ÷ 6 =
6 ÷ 6 = 1
Если бы мы работали справа налево, мы бы получили другой ответ:
Один из способов отслеживать ваша работа состоит в том, чтобы разбить задачу на части, разделенные знаками сложения или вычитания. Каменный молоток или ступка и пестик должны помочь.
Пример задачи
Теперь вычислите каждую часть:
=
6 + 2 – 0 – 4
Затем соедините ответы по частям:
6 + 2 – 0 – 4 = 4
4 Пример задачи
Ой, какой зверь. Давайте разобьем его на более мелкие части, каждая из которых будет разделена знаком плюс или минус (поскольку сложение и вычитание идут последними).
=
3 + 6 × 16 – 6 × 1
Теперь займемся этим умножением.
3 + 6 × 16 – 6 × 1 =
3 + 96 – 6
И, наконец, качаем сложение и вычитание слева направо.
3 + 96 – 6 = 93
Хорошо, но, пожалуйста, извините, моя дорогая тетя Салли, это очень долгая вещь, которую нужно запомнить. И мы уже потратили последние 10 лет, пытаясь заблокировать ее. Здесь, в Shmoop, мы любим все упрощать («Shmoop» на самом деле является сокращением от «Shmoopalumpagus»).
Мы видели, что вычитание можно заменить добавлением отрицательного числа, а деление можно заменить умножением обратного числа. Так что все мы на самом деле нужно помнить, пожалуйста, извините мою тетю. Сначала сделайте то, что находится внутри скобок, затем возьмите все экспоненты, затем умножьте, затем добавьте. Только помните, что деление = умножение на обратное, а вычитание = прибавление минуса. Да, в любом случае, тебе придется кое-что вспомнить. Это алгебра.
Давайте разработаем последний пример.
Пример задачи
Итак, давайте начнем с того, что заключено в скобки: . Мы хотим превратить его во что-то более управляемое, прежде чем мы его исправим.
Нам также, вероятно, следует сменить радиостанцию. Что это, авангард-метал?
Довольно окольный путь, чтобы добраться до номера 1, но мы им воспользуемся.
Теперь, когда мы завершили все операции в скобках, мы ищем показатели степени. Если они сразу не представятся, громко свистнут и потрясут пакетом с угощением — прибегут.
В первой части уравнения у нас есть 1 2 , что, конечно же, равно 1. Затем мы ищем умножение. Поскольку его нет, остается только добавить -13. Вычитание такого несчастливого числа не может быть плохой вещью.
1 + (-13) = -12
Готово!
Что такое экспоненты?
Ключевые члены
o Экспонент
o База
o Порядок работы
Цели
Означение и конвертирование между повторными умножением и эксплуатативным представляющим. exponents
o Используйте порядок операций для правильной оценки нескольких операций в одном выражении
Умножение — это способ представления повторяющегося сложения.
Например, вместо сложения 5 + 5 + 5 + 5 + 5 + 5 мы можем просто умножить 5 на 6. Точно так же мы можем использовать альтернативное представление повторного умножения. Например, запись выражения 10 10 10 10 довольно громоздка (особенно если нам нужно умножить 10 еще несколько раз!). Вместо этого мы можем записать это повторяющееся умножение, используя показатель степени , — количество повторяющихся факторов. Показатель степени записывается в виде надстрочного индекса справа от умножаемого числа. Число, которое умножается (или «возводится в степень»), называется основанием . Таким образом, например,
Опять же, обратите внимание, что показатель степени — это число множителей в умножении; таким образом, показатель степени девяти будет означать, что умножение включает девять множителей основания. Ниже приведены некоторые дополнительные простые примеры показателей степени.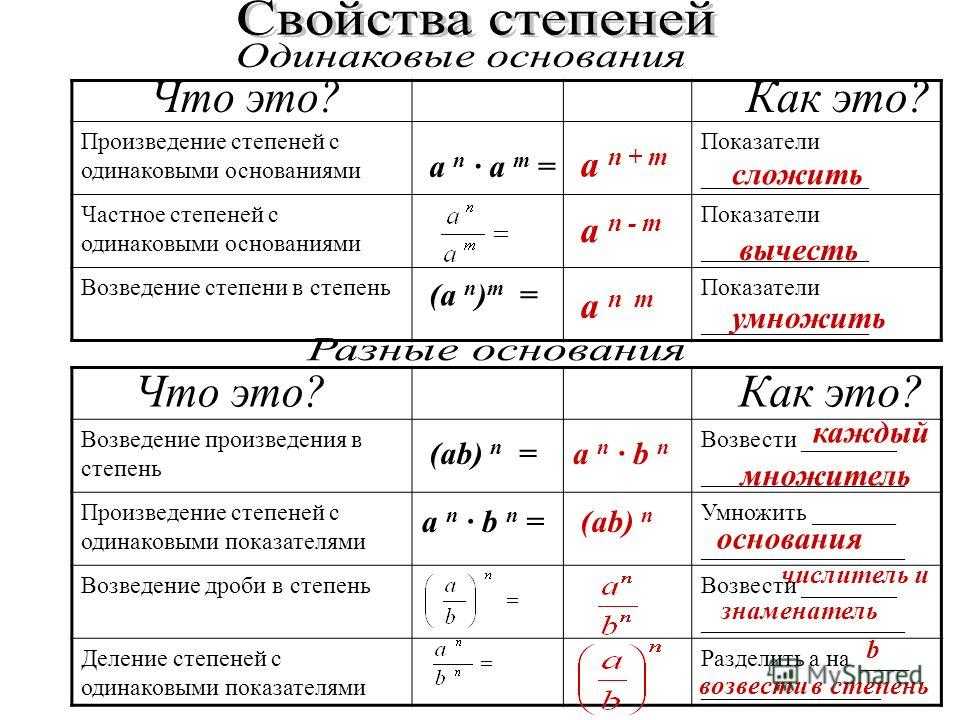
Язык из экспонентов
, возможно, больше, чем любая другая математическая операция. Хотя вы можете не использовать каждое из этих выражений, умение распознавать их полезно. Ниже приведен список некоторых способов выражения a b на английском языке. (И снова буквы используются здесь просто как заполнители для неуказанных чисел. Математическое выражение a b может быть 2 5 , 7 3 или любой другой комбинацией чисел основания и степени. Однако, независимо от их конкретных значений, a является основанием, а b — показателем степени. th power»
» a поднят до b (или b th )»
« a к
a в кубе» в случае b = 3.
В некоторых случаях один и тот же математик или ученый может даже использовать разные выражения для обозначения одного и того же показателя, все в зависимости от контекста и от потребности в краткости или ясности.
Подробнее об экспонентах
На основании того, что мы уже видели, работа с целыми показателями, большими или равными двум, достаточно проста. Но как насчет, например, показателей степени нуля или единицы? В случае основания a , возведенного в степень единицы, результатом будет просто a. Рассмотрим прогрессию, показанную ниже.
Возможно, наиболее неясным является случай 9.0021 и
, возведенные в нулевую степень. Следуя приведенному выше шаблону, количество множителей и будет равно нулю. В каждом случае мы можем умножить результат на единицу, ничего не меняя. Используя этот контекст, мы можем показать, что до нуля — это просто единица.
Хотите узнать больше? Почему бы не пройти онлайн-курс Pre-Algebra?
Обратите внимание, что значение a не указано, поэтому любое число, возведенное в нулевую степень, равно единице. Другие интересные случаи включают отрицательные показатели и дробные показатели.
Практическая задача : Оцените каждое из приведенных ниже экспоненциальных выражений.
а. б. c.
Решение : Показатель степени — это количество множителей основания. В случае, когда показатель степени равен нулю, ответ равен единице, а в случае, когда показатель степени равен единице, ответ является базовым значением.
а. б. c. d.
Практическая задача : Запишите каждое из следующих выражений в экспоненциальной форме.
а. б. c. 7 д.
Решение : Основанием экспоненциального представления является число, которое умножается, а показателем степени является количество факторов. Часть b использует букву ( c ) для обозначения неопределенного числа; однако с этой буквой можно обращаться так же, как с числом.
а. б. c. d.
Порядок операций
Прежде чем продолжить изучение показателей, мы должны рассмотреть порядок операций, который позволяет правильно интерпретировать ряд математических выражений. . Рассмотрим, например, следующее выражение.
Порядок, в котором мы выполняем перечисленные операции, определит ответ: не каждый порядок операций дает один и тот же результат! Мы можем проиллюстрировать это, выбрав два разных подхода: во-первых, мы будем выполнять операции в том порядке, в котором они перечислены, а во-вторых, мы будем выполнять операции умножения и деления (в указанном порядке), за которыми следуют операции сложения и вычитания.
(в порядке их перечисления).
Очевидно, что два результата отличаются. Таким образом, порядок операций был определен как соглашение, которое мы можем использовать для правильной интерпретации и выражения нескольких математических операций. Порядок операций приведен ниже.
1. Скобки: выполнять любые операции или серии операций в скобках
2. Показатель степени: оценка любых показателей степени
3. Умножение/деление: выполнение операций умножения и деления в указанном порядке
4. Сложение/вычитание: выполнение операций сложения и вычитания Один из способов запомнить этот порядок операций — запомнить мнемоническое слово PEMDAS. Поскольку выражение внутри набора круглых скобок само может содержать несколько операций или даже дополнительные круглые скобки, вы также должны оценивать это выражение в соответствии с порядком операций (для этого может потребоваться повторение первого шага несколько раз).
Второй шаг заключается в оценке любых показателей. Затем выполните операции умножения и деления в указанном порядке (слева направо). Наконец, выполните любые операции сложения и вычитания (в любом порядке). Рассмотрим пример.
Сначала мы должны оценить выражение во внешних скобках:
Обратите внимание, что эта экспрессия содержит другое выражение в руках; поэтому, чтобы правильно оценить его, мы должны еще раз применить первый шаг порядка операций.
Возвращаясь к исходному выражению, теперь мы должны вычислить показатели степени.
Далее мы ищем операции умножения и деления. В этом случае выражение содержит только один.
Теперь мы можем выполнять оставшиеся операции сложения и вычитания в любом порядке.
Практическая задача : Оцените каждое из следующих выражений.