Дифференциал функции ☑️ определение, виды, свойства, формула полного дифференциала функции, геометрический смысл, правило применения, примеры решения уравнений
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.
Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную
не равную нулю.
Применяя свойства предела функции, получают равенство
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
dx = Δx
Отсюда получается формула:
dy = f'(x)dx
Для второго порядка вводится обозначение d2y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,
Таблица производных
Примеры решения задач
Задача №1
Найти дифференциал функции
Решение.
Учитывая, что
записывается результат:
Задача №2
Вычислить значение дифференциала функции
при условии, что
Решение.
В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.
Если dx есть константа, то для высших порядков имеет место следующая формула:
Этот результат вытекает непосредственно из определения:
Задача №3
Найти d2y, если y = cos2x и x – независимая переменная.
Решение.
поэтому
Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,
Задача №4
Найти d2y, если y = x2 и x = t3 + 1, t – независимый аргумент.
Решение.
следовательно,
Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.
Учитывая, что
Δy ≈ dy
с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.
Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:
Задача №5
Вычислить приближённо arctg1,05.
Решение.
Пусть f(x) = arctg x. Тогда
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.
Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Дифференциал функции
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
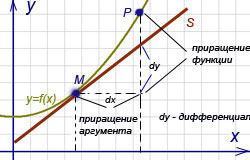
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
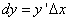
или
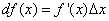
или же
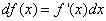
Геометрический смысл дифференциала. Дифференциал функции 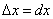 (см. рисунок).
(см. рисунок).
Дифференциал функции в точке x и обозначают
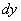
или
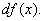
Следовательно,
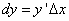 (1)
(1)
или
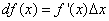 , (2)
, (2)
поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,
а 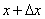 — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
— наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
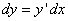 (3)
(3)
или
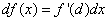 (4)
(4)
Пример 1. Найти дифференциалы функций:
1) 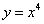 ;
;
2) 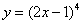
3) 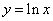 ;
;
4) 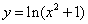 .
.
Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) 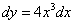 ;
;
2) 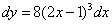 ;
;
3) 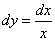 ;
;
4) 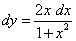 .
.
Найти дифференциалы самостоятельно, а затем посмотреть решения
Пример 2. Найти дифференциал функции
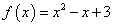
в точке x = 2,
1) выделив линейную часть;
2) по формуле.
Пример 3. Найти дифференциал функции
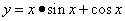
в точке x.
В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.
В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.
Дифференциал обладает свойствами, аналогичными свойствам производной:
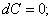
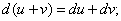 (6)
(6)
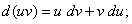 (7)
(7)
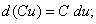 (8)
(8)
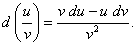 (9)
(9)
Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на 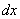 .
.
Одно из особеннейших свойств дифференциала — инвариантность формы дифференциала в случае сложных функций.
Установленное во втором параграфе приближенное равенство
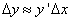
или
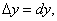 (10)
(10)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
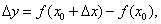
а
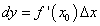
то
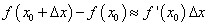
или
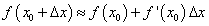 (11)
(11)
Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид
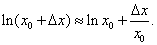
Положим
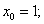
тогда
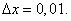
Следовательно,
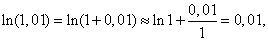
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 6. Пользуясь понятием дифференциала, вычислить приближенно
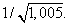
Решение. Число
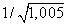 является одним из значений функции
является одним из значений функции
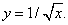
Так как производная этой функции
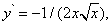
то формула (11) примет вид
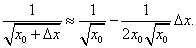
Полагая
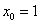
и
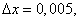
получаем
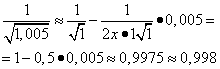
(табличное значение
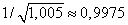 ).
).
Вычислить приближенно самостоятельно, а затем посмотреть решение
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность  приближенного числа
приближенного числа 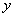 равна абсолютной величине разности между точным числом
равна абсолютной величине разности между точным числом 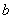 и его приближенным значением:
и его приближенным значением:
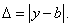 (12)
(12)
Относительной погрешностью 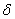 приближенного числа
приближенного числа 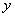 называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
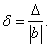 (13)
(13)
Если точное число неизвестно, то
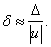 (14)
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина 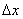 была достаточно малой по сравнению с
была достаточно малой по сравнению с 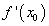 , так как чем меньше
, так как чем меньше 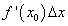 , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина
, тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина 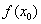 вычислялась просто.
вычислялась просто.
Пример 8. Пользуясь понятием дифференциала, вычислить приближенно 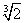 . Оценить точность полученного результата.
. Оценить точность полученного результата.
Решение. Рассмотрим функцию
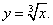
Её производная равна
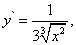
а формула (11) примет вид
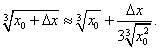
В данном случае было бы нерационально вычислять приближенно 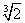 следующим образом:
следующим образом:
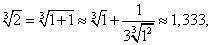
так как значение
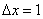
не является малым по сравнению со значением производной в точке
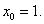
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
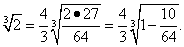
Теперь, полагая
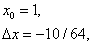
получим
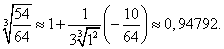
Умножая на 4/3, находим
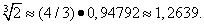
Принимая табличное значение корня
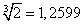
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
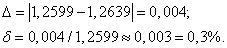

Весь блок «Производная»
Поделиться с друзьями
Дифференциал функции: основные понятия и определения
Пусть функция в точке имеет отличную от нуля производную
Тогда в некоторой окрестности этой точки отношение
где при Тому приращение функции можно представить в виде:
При этом величина является бесконечно малой более высокого порядка, чем и бесконечно малая поэтому величину называют главной частью приращения функции .
Замечание. Дифференциал называют также дифференциалом первого порядка.
Найдем дифференциал независимой переменной то есть дифференциал функции Так как получаем, что
то
То есть дифференциал независимой переменной равен ее приращению:
Тогда формула для дифференциала перепишется в виде:
Таким образом, дифференциал функции равен произведению производной указанной функции на дифференциал независимой переменной.
Геометрический и механический смыслы дифференциала функции
Геометрически дифференциал функции в точке равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная получает приращение .
Механический смысл дифференциала. Пусть материальная точка двигается по закону Дифференциал функции равен:
Для фиксированных значений и – это тот путь, который бы прошла материальная точка за время в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью
Стоит отметить, что фактический путь в случае неравномерного движения материальной точки, в отличии от дифференциала не является линейной функцией времени а поэтому отличается от пути Но все же, если время является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от до есть практически равномерным.
Основные формулы дифференциала
Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что а также соответствующие формулы для производных.
Рассмотрим две дифференцируемые функции и Тогда имеют место следующие равенства:
Теорема о производной обратной функции (Лекция №6)
ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y‘ из уравнения y=f(x), то можно:
- Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).
- Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x: .
- Выразить y‘ = y·j'(x) = f(x)·(lnx)’.
Примеры.
- y = xa – степенная функция с
произвольным показателем.
.
ПОКАЗАТЕЛЬНО-СТЕПЕННАЯ ФУНКЦИЯ И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ
Показательно-степенной функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.
Примеры.
- .
ТАБЛИЦА ПРОИЗВОДНЫХ
Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о производной сложной функции.
- .
- .
- .
- .
- .
а).
б) .
- .
- .
.
- .
- .
- .
- .
- .
- .
- .
- .
- .
Примеры.
- . Найти y’(–1).
ПОНЯТИЕ ДИФФЕРЕНЦИАЛА ФУНКЦИИ. СВЯЗЬ МЕЖДУ ДИФФЕРЕНЦИАЛОМ И ПРОИЗВОДНОЙ
Пусть функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в некоторой точке х0 Î [a; b] определяется равенством
.
Следовательно, по свойству предела
Умножая все члены полученного равенства на Δx, получим:
Δy = f ‘(x0)·Δx + a·Δx.
Итак, бесконечно малое приращение Δy дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f ‘(х0) ≠ 0) главная часть приращения, линейная относительно Δx, а второе – бесконечно малая величина более высокого порядка, чем Δx. Главную часть приращения функции, т.е. f ‘(х0)·Δx называют дифференциалом функции в точке х0 и обозначают через dy.
Таким образом, если функция y=f(x) имеет производную f ‘(x) в точке x, то произведение производной f ‘(x) на приращение Δx аргумента называют дифференциалом функции и обозначают:
Найдем дифференциал функции y= x. В этом случае y‘ = (x)’ = 1 и, следовательно, dy=dx=Δx. Таким образом, дифференциал dxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому формулу (1) мы можем записать так:
Но из этого соотношения следует, что . Следовательно, производную f ‘(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.
Справедливо и обратное утверждение.
Если для данного значения x приращение функции Δy = f(x+Δx) – f(x) можно представить в виде Δy = A·Δx + α, где α – бесконечно малая величина, удовлетворяющая условию , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f ‘(x)=А.
Действительно, имеем , и так как при Δx→0, то .
Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.
Примеры. Найти дифференциалы функций:
- .
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА
Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка
M1(x+Δx; y+Δy).
Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f ‘(x), а MN = Δx, то NT = f ‘(x)·Δx. Но по определению дифференциала dy=f ‘(x)·Δx, поэтому dy = NT.
Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ДИФФЕРЕНЦИАЛА
Ранее мы видели, что если u является независимой переменной, то дифференциал функции y=f ‘(u) имеет вид dy = f ‘(u)du.
Покажем, что эта форма сохраняется и в том случае, когда u является не независимой переменной, а функцией, т.е. найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=g(x) или y = f(g(x)). Тогда по правилу дифференцирования сложной функции:
.
Следовательно, по определению
, но g‘(x)dx= du, поэтому dy= f'(u)du.
Мы доказали следующую теорему.
Теорема. Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид dy=f'(u)du, какой он имел бы, если бы промежуточный аргумент u был независимой переменной.
Иначе говоря, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство дифференциала называется инвариантностью формы дифференциала.
Пример. . Найти dy.
Учитывая свойство инвариантности дифференциала, находим
.
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
Пусть нам известно значение функции y0=f(x0) и ее производной y0‘ = f ‘(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f‘(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f‘(x0)·Δx.
Откуда
Примеры.
- y = x2 – 2x. Найти
приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x изменяется от 3 до 3,01.
Имеем Δy≈dy=f‘(x)·Δx.
f‘(x)=2x – 2 ,f‘(3)=4, Δx=0,01.
Поэтому Δy ≈ 4·0,01 = 0,04.
- Вычислить
приближенно значение функции в точке x = 17.
Пусть x0= 16. Тогда Δx = x – x0= 17 – 16 = 1, ,
.
Таким образом, .
- Вычислить ln 0,99.
Будем рассматривать это значение как частное значение функции y=lnx при х=0,99.
Положим x0 = 1. Тогда Δx = – 0,01, f(x0)=0.
, f ‘(1)=1.Поэтому f(0,99) ≈ 0 – 0,01 = – 0,01.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Пусть функция y=f(x) дифференцируема на некотором отрезке [a; b]. Значение производной f‘(x), вообще говоря, зависит от x, т.е. производная f‘(x) представляет собой тоже функцию переменной x. Пусть эта функция также имеет производную. Дифференцируя ее, получим так называемую вторую производную от функции f(x).
Производная от первой производной называется производной второго порядка или второй производной от данной функции y=f(x) и обозначается y»или f»(x). Итак, y» = (y‘)’.
Например, если у = х5, то y‘= 5x4, а y»= 20x4.
Аналогично, в свою очередь, производную второго порядка тоже можно дифференцировать. Производная от второй производной называется производной третьего порядка или третьей производной и обозначается y»’или f»'(x).
Вообще, производной n-го порядка от функции f(x) называется производная (первая) от производной (n – 1)-го порядка и обозначается символом y(n) или f(n)(x): y(n) = (y(n-1))’.
Таким образом, для нахождения производной высшего порядка от данной функции последовательно находят все ее производные низших порядков.
Примеры.
- Найти производную четвертого порядка функции y= ln x.
.
- .
- Найти производную n-го порядка функции y = ekx.
y‘= k·ekx, y»= k2·ekx, y»’ = k3·ekx, …,y(n) =kn·ekx.
- Найти производную n-го
порядка функции y = sin x.
Имеем
Выясним механический смысл второй производной. (Механический смысл первой производной – скорость).
Пусть материальная точка движется прямолинейно по закону s=s(t), где s – путь, проходимый точкой за время t. Тогда скорость vэтого движения есть v= s'(t) = v(t), т.е. тоже некоторая функция времени.
В момент времени t скорость имеет значение v=v(t). Рассмотрим другой момент времени t+Δt. Ему соответствует значение скорости v1 = v(t+Δt). Следовательно, приращению времени Δt соответствует приращение скорости Δv= v1 – v = v(t + Δt) – v(t). Отношение называется средним ускорением за промежуток времени Δt.
Ускорением в данный момент времени t называется предел среднего ускорения при Δt→0:
.
Таким образом, ускорение прямолинейного движения точки есть производная скорости по времени. Но как мы уже видели, скорость есть производная пути s по времени t: v = s‘. Учитывая это, имеем:
a = v‘(t) = (s‘)’ = s»(t),
т.е. ускорение прямолинейного движения точки равно 2-й производной пути по времени
a = S»(t).
Дифференциал функции. Применение дифференциала к приближенным вычислениям
Задача 1
Вычислите приближенное значение функции в заданной точке .
Решение
Для нахождения приближенного значения функции в точке воспользуемся формулой:
Примем:
Находим производную:
Значение приращения функции :
Значение функции в точке :
Искомое приближенное значение:
Ответ:
Задача 2
Найти приближенно значение функции
при
Решение
Для нахождения приближенного значения функции в точке воспользуемся формулой:
Примем:
Производная:
Значение функции в точке :
Значение производной в точке :
Искомое приближенное значение:
Ответ: 0.587.
К оглавлению решебника по высшей математике 〉
Тема 9. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. Понятие дифференциала. — Студопедия
Понятие дифференциала.
Определение 9.1.Дифференциалом 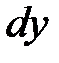 функции
функции 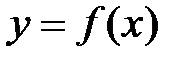 называется произведение производной этой функции на приращение независимого переменного, т.е
называется произведение производной этой функции на приращение независимого переменного, т.е
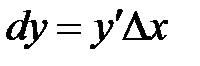 .
.
Поскольку дифференциал независимой переменной совпадает с ее приращением ( 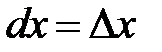 ), то
), то
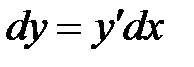 .
.
Таким образом, для того чтобы найти дифференциал функции, необходимо умножить производную этой функции на дифференциал ее независимой переменной.
Основные правила нахождения дифференциалов.
1) Дифференциал суммы (разности) двух дифференцируемых функций равен сумме (разности) дифференциалов этих функций:
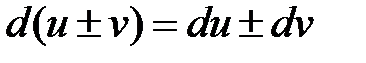 .
.
2) Дифференциал произведения двух дифференцируемых функций равен сумме произведений дифференциала первого сомножителя на второй и дифференциала второго сомножителя на первый:
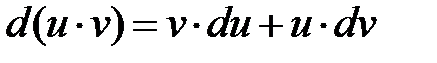 .
.
3) Дифференциал частного двух дифференцируемых функций может быть найден по формуле:
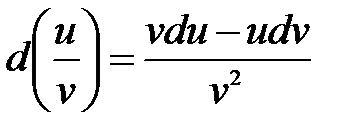 .
.
4) Постоянный множитель можно выносить за знак дифференциала:
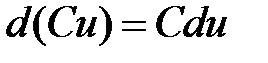 .
.
Пример 9.1. Найти дифференциал функции 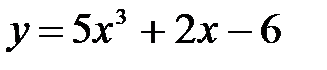
а) по определению;
б) используя правила нахождения дифференциала.
Решение:
а)Находим производную от заданной функции:
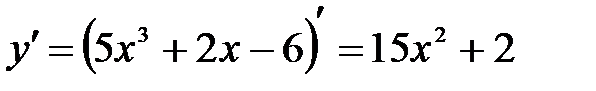 .
.
Тогда по определению дифференциала: 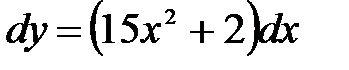 .
.
б) Находим непосредственно дифференциал, используя правила нахождения дифференциалов (1 и 4):
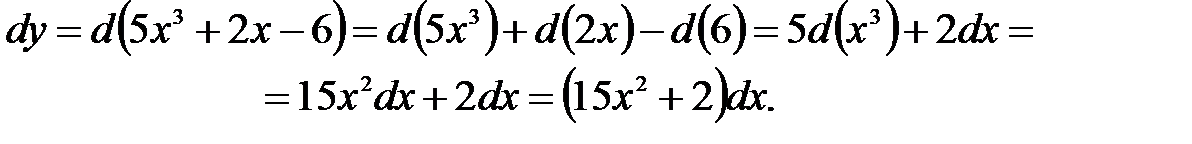 .
.
Решение типового варианта. Производная и дифференциал.
Пример 1.
Найти производные заданных функций
А) ;
Решение:
;
.
Б) ;
Решение:
Используем формулу .
.
В) ;
Решение:
Используем формулу .
.
Г) ;
Решение:
Используем формулу .
, где ;
.
Д) ;
Решение:
Используем формулу .
, где ;
.
Е) ;
Решение:
Пример 2.
Найти :
А) .
Решение:
Функция в примере задана неявно. Чтобы найти ее производную продифференцируем обе части равенства по X, полагая, что У есть функция от Х и обозначая производную У через :
.
Выразим из полученного равенства :
;
.
Б) .
Решение:
Аналогично предыдущему примеру:
;
;
.
В)
Решение:
Используем формулу .
.
Пример 3.
Найти :
А) ;
Решение:
;
Б) .
Решение:
Пример 4.
Найти дифференциал функции , если .
Решение:
Воспользуемся свойством логарифма частного для упрощения формулы:
.
Используем формулу .
;
Пример 5.
Составить уравнения касательной и нормали к кривой в точке с абсциссой .
Решение:
Найдем ординату точки касания:
.
Угловой коэффициент касательной равен значению производной в точке :
.
Подставляем значения и в уравнение касательной :
,
Получили уравнение касательной .
Подставляем значения и в уравнение нормали :
,
Получили уравнение нормали .
| < Предыдущая | Следующая > |
|---|
Дифференциалы
Производная функции часто может использоваться для аппроксимации определенных значений функции с удивительной степенью точности. Для этого необходимо ввести понятие дифференциала независимой переменной и зависимой переменной.Определение производной функции y = f (x) , как вы помните, равно

, который представляет наклон касательной к кривой в некоторой точке ( x, f (x) ).Если Δ x очень мало (Δ x ≠ 0), то наклон касательной примерно такой же, как наклон секущей линии через ( x, f (x) ). То есть

Дифференциал независимой переменной x записывается как dx и совпадает с изменением в x , Δ x . То есть

Дифференциал зависимой переменной y , записанный dy , определяется как

Вывод, который следует сделать из предыдущего обсуждения, состоит в том, что дифференциал y (dy ) приблизительно равен точному изменению y (Δ y ) при условии, что изменение x (Δ x = dx ) относительно невелик.Чем меньше изменение в x , тем ближе dy будет к Δ y , что позволит вам аппроксимировать значения функции, близкие к f (x) (рисунок).
Рисунок 1 Аппроксимация функции дифференциалами.
Пример 1: Найдите dy для y = x 3 + 5 x −1.

Пример 2: Используйте дифференциалы, чтобы аппроксимировать изменение площади квадрата, если длина его стороны увеличивается с 6 см до 6.23 см.
Пусть x = длина стороны квадрата. Площадь может быть выражена как функция x , где y = x 2 . Дифференциал dy —

Поскольку x увеличивается с 6 до 6,23, вы обнаруживаете, что Δ x = dx = 0,23 см; следовательно,

Площадь квадрата увеличится примерно на 2,76 см. 2 при увеличении длины стороны с 6 до 6.23. Обратите внимание, что точное увеличение площади (Δ y ) составляет 2,8129 см 2 .
Пример 3: Используйте дифференциалы, чтобы округлить значение  до ближайшей тысячной.
до ближайшей тысячной.
Поскольку функция, которую вы применяете, —  , выберите удобное значение x , которое является идеальным кубом и относительно близко к 26,55, а именно x = 27. Дифференциал dy равен
, выберите удобное значение x , которое является идеальным кубом и относительно близко к 26,55, а именно x = 27. Дифференциал dy равен

Потому что x уменьшается с 27 до 26.55, вы обнаружите, что Δ x = dx = −,45; следовательно,

, что означает, что  будет примерно на 1/60 меньше, чем
будет примерно на 1/60 меньше, чем  ; следовательно,
; следовательно,

с точностью до тысячных.
Обратите внимание, что значение  калькулятора — 2,983239874, которое округляется до того же ответа до ближайшей тысячной!
калькулятора — 2,983239874, которое округляется до того же ответа до ближайшей тысячной!
Дифференциальные уравнения — Введение
Дифференциальное уравнение — это уравнение с функцией и одной или несколькими производными:
Пример: уравнение с функцией y и ее производная dy dx
Решение
Мы решаем , когда обнаруживаем функцию y (или набор функций y).
Есть много «уловок» для решения дифференциальных уравнений (, если их можно решить!).
Но сначала: почему?
Почему полезны дифференциальные уравнения?
В нашем мире все меняется, и , описывающий, как они меняются, часто заканчивается дифференциальным уравнением:
Пример: кролики!
Чем больше у нас будет кроликов, тем больше у нас будет кроликов.
Тогда эти кролики вырастут и тоже родят детей! Население будет расти все быстрее и быстрее.
Важными частями этого являются:
- население N в любое время т
- темп роста р
- Скорость изменения населения дн дн
Думайте о dN dt как о «насколько изменяется население с изменением времени в любой момент времени».
Представим, что скорость роста r составляет 0,01 новых кроликов в неделю на каждого текущего кролика.
Когда популяция составляет 1000 , скорость изменения dN dt составляет 1000 × 0,01 = 10 новых кроликов в неделю.
Но это верно только в конкретное время и не включает тот факт, что население постоянно увеличивается. Чем больше популяция, тем больше у нас кроликов!
При населении 2000 мы получаем 2000 × 0.01 = 20 новых кроликов в неделю и т. Д.
Так что лучше сказать, что скорость изменения (в любой момент) — это скорость роста, умноженная на численность населения в этот момент:
dN dt = rN
И это дифференциальное уравнение , потому что оно имеет функцию N (t) и ее производную.
А какая мощная математика! В этом коротком уравнении говорится, что «скорость изменения численности населения с течением времени равна темпам роста, умноженным на численность населения».
Дифференциальные уравнения могут описывать, как изменяется население, как движется тепло, как вибрируют пружины, как распадается радиоактивный материал и многое другое. Это очень естественный способ описания многих вещей во Вселенной.
Что с ними делать?
Само по себе дифференциальное уравнение — прекрасный способ выразить что-либо, но его сложно использовать.
Итак, мы пытаемся решить их, превратив дифференциальное уравнение в более простое уравнение без дифференциальных битов, чтобы мы могли выполнять вычисления, строить графики, предсказывать будущее и так далее.
Пример: Сложные проценты
Деньги приносят проценты. Проценты могут рассчитываться в фиксированное время, например, ежегодно, ежемесячно и т. Д., И добавляться к исходной сумме.
Это называется сложным процентом.
Но когда он постоянно увеличивается на , тогда в любое время проценты добавляются пропорционально текущей стоимости ссуды (или инвестиций).
И по мере роста ссуды проценты по ней увеличиваются.
Используя t для времени, r для процентной ставки и V для текущей стоимости кредита:
dV dt = rV
И вот что интересно: это то же самое уравнение, которое мы получили с кроликами! Просто у него разные буквы.Итак, математика показывает нам, что эти две вещи ведут себя одинаково.
Решение
Дифференциальное уравнение хорошо говорит об этом, но его трудно использовать.
Но не волнуйтесь, это можно решить (с помощью специального метода, называемого разделением переменных), и в результате получится:
V = Pe rt
Где P — принципал (первоначальный заем), а e — число Эйлера.
Таким образом, непрерывно начисляемый заем в размере 1000 долларов США на 2 года с процентной ставкой 10% становится:
V = 1000 × e (2 × 0.1)
В = 1000 × 1,2 2140 …
V = 1221,40 $ (с точностью до цента)
Итак, дифференциальные уравнения хороши для описания вещей, но их нужно решать, чтобы они были полезными.
Другие примеры дифференциальных уравнений
Уравнение Ферхюльста
Пример: снова кролики!
Помните наше дифференциальное уравнение роста:
dN dt = rN
Что ж, этот рост не может продолжаться вечно, так как у них скоро закончится доступная еда.
Итак, давайте улучшим его, включив:
- максимальное население, которое может содержать еда тыс.
Парень по имени Ферхюльст во всем разобрался и получил это дифференциальное уравнение:
dN dt = rN (1 − N / k)
Уравнение Ферхюльста
Простое гармоническое движение
В физике простое гармоническое движение — это тип периодического движения, в котором восстанавливающая сила прямо пропорциональна смещению.Примером этого может служить груз на пружине.
Пример: пружина и вес
К пружине прикреплен груз:
- груз опускается под действием силы тяжести,
- при растяжении пружины ее натяжение увеличивается,
- вес сбавляет
- , затем натяжение пружины возвращает ее вверх,
- , затем он снова и снова падает вниз, вверх и вниз.
Опишите это математикой!
Гиря тянется вниз под действием силы тяжести, и мы знаем из Второго закона Ньютона, что сила равна массе, умноженной на ускорение:
F = m a
А ускорение — это вторая производная положения по времени, поэтому:
F = m d 2 x dt 2
Пружина подтягивает ее вверх в зависимости от того, насколько она растянута ( k — жесткость пружины, а x — степень ее растяжения): F = -kx
Две силы всегда равны:
м d 2 x dt 2 = −kx
У нас есть дифференциальное уравнение!
Имеет функцию x (t) и ее вторую производную г 2 x дт 2
Примечание: мы не включили «демпфирование» (замедление отскоков из-за трения), которое немного сложнее, но вы можете поиграть с ним здесь (нажмите play ):
Создание дифференциального уравнения является первым важным шагом.Но нам также нужно решить , чтобы узнать, как, например, пружина со временем подпрыгивает вверх и вниз.
Классифицируйте, прежде чем пытаться решить
Так как же решить ?
Это не всегда просто!
За годы мудрые люди разработали специальных методов для решения некоторых типов дифференциальных уравнений.
Итак, нам нужно знать , что это за тип дифференциального уравнения.
Это как путешествие: разные виды транспорта решили, как добраться до определенных мест. Это рядом, так что мы можем просто гулять? Есть дорога, по которой мы можем взять машину? Или это в другой галактике, и мы просто не можем туда добраться?
Итак, давайте сначала классифицируем дифференциальное уравнение .
Обычное или частичное
Первая основная группа:
- «Обычные дифференциальные уравнения» (ODE) содержат единственную независимую переменную (например, и )
- «Уравнения с частными производными» (PDE) имеют две или более независимых переменных.
Здесь мы изучаем обыкновенных дифференциальных уравнений !
Порядок и степень
Далее прорабатываем Порядок и Степень:
Заказать
Порядок — это старшая производная (первая производная? Вторая производная и т. Д.):
Пример:
dy dx + y 2 = 5x
Имеет только первую производную dy dx , как и «Первый Орден»
Пример:
d 2 y dx 2 + xy = sin (x)
Имеет вторую производную д 2 д dx 2 , как и «Заказ 2»
Пример:
d 3 y dx 3 + x dy dx + y = e x
Имеет третью производную д 3 д dx 3 который превосходит dy dx , как и «Заказ 3»
градусов
Степень — это показатель высшей производной.
Пример:
( dy dx ) 2 + y = 5x 2
Старшая производная — это просто dy / dx, и ее показатель степени равен 2, так что это «Вторая степень»
На самом деле это обыкновенное дифференциальное уравнение первого порядка второй степени
Пример:
d 3 y dx 3 + ( dy dx ) 2 + y = 5x 2
Старшая производная — это d 3 y / dx 3 , но у нее нет показателя степени (ну, на самом деле показатель степени 1, который не показан), так что это «Первая степень».
(Показатель 2 на dy / dx не учитывается, так как это не самая высокая производная).
Итак, это обыкновенное дифференциальное уравнение первой степени третьего порядка
Будьте осторожны, не путайте порядок со степенью. Некоторые люди используют порядок слов, когда имеют в виду степень!
Линейный
Это Линейное , когда переменная (и ее производные) не имеют показателя степени или другой функции.
Итак, нет y 2 , y 3 , √y, sin (y), ln (y) и т. Д. просто y (или любая другая переменная).
Более формально линейное дифференциальное уравнение имеет вид:
dy dx + P (x) y = Q (x)
Решение
Хорошо, мы классифицировали наше дифференциальное уравнение, следующий шаг — решение.
И у нас есть Руководство по решению дифференциальных уравнений, которое поможет вам.
,дифференциал функции | Примеры предложений
Словарь> Примеры дифференциала функциидифференциала функции еще нет в Кембриджском словаре. Ты можешь помочь!
В эпизоде показано использование линейной аппроксимации и дифференциала из и функции .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Схожим понятием является дифференциал из и функция .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Важно отметить, что в основе их понимания лежала формализация обратных свойств между интегралом и дифференциалом из и функцией .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Это приводит непосредственно к представлению, что дифференциал из функция в точке является линейным функционалом от приращения «x».ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Точнее, неточный дифференциал — это дифференциальная форма, которая не может быть выражена как дифференциал из функция .ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти примеры взяты из Cambridge English Corpus и из источников в Интернете.Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
дифференциала функции еще нет в Кембриджском словаре. Ты можешь помочь!
{{#сообщение}}{{message}}
{{/сообщение}} {{^ Сообщение}}Выберите часть речи и введите свое предложение в поле «Определение».
{{/сообщение}} Часть речиВыберите существительное, глагол и т. Д. имя прилагательное наречие восклицание существительное число префикс суффикс глагол
Определение
Отправить Отмена
,Дифференциальные уравнения — ступенчатые функции
Онлайн-заметки ПавлаНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Задачи практики и задания еще не написаны.Пока позволяет время, я работаю над ними, однако у меня нет того количества свободного времени, которое я имел раньше, поэтому пройдет некоторое время, прежде чем здесь что-нибудь появится.
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Обратное преобразование Лапласа
- Решение IVP с преобразованием Лапласа
- Разделы
- DE второго порядка
- Системы ДЭ
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Алгебра и триггерный обзор
- Распространенные математические ошибки
- Праймер комплексных чисел
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои студенты
- Notes Загрузки
- Полная книга
- Текущая глава
- Текущий раздел
- Practice Problems Загрузок
- Проблем пока не написано.
- Проблемы с назначением Загрузок
- Проблем пока не написано.
- Прочие товары
- Получить URL для загружаемых элементов
- Распечатать страницу в текущем виде (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- Алгебра
- Отборочные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- Полиномы
- Факторинговые многочлены
- Рациональные выражения
- Комплексные числа
- Решение уравнений и неравенств
- Решения и наборы решений
- Линейные уравнения
- Приложения линейных уравнений
- Уравнения с более чем одной переменной
- Квадратные уравнения — Часть I
- Квадратные уравнения — Часть II
- Квадратные уравнения: сводка
- Приложения квадратных уравнений
- Уравнения, сводимые к квадратичным в форме
- Уравнения с радикалами
- Линейные неравенства
- Полиномиальные неравенства
- Рациональные неравенства
- Уравнения абсолютных значений
- Неравенства абсолютных значений
- Графики и функции
- График
- Строки
- Круги
- Определение функции
- Графические функции
- Комбинирование функций
- Обратные функции
- Отборочные
