выборочная математическая статистика с примерами решения
Содержание:
- Примеры с решением
Разность называется отклонением случайной величины А от ее математического ожидания М(Х). Математическое ожидание отклонения равно нулю:
Дисперсией, или рассеянием, случайной величины X называется математическое ожидание квадрата ее отклонения:
Из определения и свойств математического ожидания следует, чтс дисперсия любой случайной величины неотрицательна, т.е.
Для вычисления дисперсии применяется формула
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
| Предмет теория вероятности |
Дисперсия случайной величины обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю:
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
5. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
Возможно вам будут полезны данные страницы:
Задачи на вероятность: примеры решения |
Формула вероятности: теория и примеры |
Математическое ожидание: пример решения |
Неравенство Чебышева |
Замечание.
Свойство 3 распространяется на п независимых случайных величин:
Дисперсия дискретной случайной величины с законом распределения
определяется формулой
или формулой
где
— другое обозначение для математического ожидания. Этим обозначением будем пользоваться и в дальнейшем, в зависимости от обстоятельств.
Если дискретная случайная величина принимает бесконечную по-следовательность-значений с законом распределения
то ее дисперсия определяется формулой
при условии, что этот ряд сходится.
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку определяется формулой
где р(х) — плотность распределения вероятностей этой величины, — ее математическое ожидание.
Дисперсию можно вычислять по формуле
Дисперсия непрерывной случайной величины X, все значения которой принадлежат отрезку , определяется формулой
если этот несобственный интеграл сходится.абсолютно.
Средним квадратическим отклонением, или стандартным отклонением, случайной величины X называется корень квадратный из ее дисперсии:
Это определение имеет смысл, поскольку выполнено условие (2.5.3).
Пример с решением
Пример 1.
Доказать формулы (2.5.1) и (2.5.4).
Решение:
Так как математическое ожидание М(Х) — постоянная величина, математическое ожидание постоянной равно этой постоянной, математическое ожидание разности случайных величин равно разности их математических ожиданий, то
равенство (2. 5.1) доказано.
5.1) доказано.
Учитывая свойства математического ожидания, получаем
равенство (2.5.4) доказано.
Пример 2.
Доказать равенства (2.5.5) — (2.5.8).
Решение:
Принимая во внимание определение дисперсии и тот факт, что математическое ожидание постоянной равно этой постоянной, получаем
Из определения дисперсии и свойств математического ожидания следует, что
Для доказательства формулы (2.5.8) воспользуемся формулой (2.5.4):
Равенство (2.5.8) следует из формул (2.5.6) и (2.5.7):
Пример 3.
Дискретная случайная величина X имеет закон распределения
Найти дисперсию и среднее квадратическое отклонение случайной величины X.
Решение:
По формуле (2.4.3) находим
Запишем закон распределения квадрата отклонения этой величины, т.е. величины
По формуле (2.5.10) получаем
В соответствии с формулой (2.5.16) находим среднее квадратическое отклонение
Замечание. :
:
Запишем закон распределения случайной величины
и найдем дисперсию случайной величины Xпо формуле (2.5.10):
Квадрат случайной величины X, т.е. X2 — это новая случайная величина, которая с теми же вероятностями, что и случайная величина X, принимает значения, равные квадратам ее значений.
Квадраты значений случайной величины X равны: ,, т.е. величина принимает значения Закон распределения случайной величины X2 можно записать в виде:
Вероятность 0,4 для значения получена по теореме сложения вероятностей, с которыми случайная величина X принимает значения -1 и 1. Аналогично получена вероятность 0,2 для значения
По формуле (2.4.3) находим
Следовательно, по формуле (2.5.4) имеем
Пример 5.
Симметричная монета подбрасывается 4 раза. Случайная величина X- «число выпадений герба при этих подбрасываниях». Найти числовые характеристики случайной величины
Решение:
Данная дискретная случайная величина X может принимать пять значений: .
Закон распределения случайной величины X можно задать таблицей Находим математическое ожидание
Закон распределения случайной величины имеет вид:
Вычислим дисперсию и среднее квадратическое отклонение :
Пример 6.
Найти дисперсию дискретной случайной величины X -числа очков, выпадающих при подбрасывании игрального кубика.
Решение:
Запишем сначала закон распределения этой случайной величины в виде таблицы
Найдем математические ожидания :
Дисперсию вычислим по формуле (2.5.4):
Пример 7.
Даны все возможные значения дискретной случайной величины а также известны Найти закон распределения случайной величины X
Решение:
Запишем законы распределения дискретных случайных величин X и X2.
где пока неизвестны, причем Используя условие, получаем систему двух уравнений с тремя неиз-вестными
Поскольку то система уравнений принимает вид
откуда . Поэтому
Поэтому
Итак, закон распределения случайной величины X определяется таблицей
Пример 8.
Дискретная случайная величина X может принимать только два значения , причем . Известны вероятность математическое ожидание и дисперсия Найти закон распределения дискретной случайной вели-чиньгЛ.
Решение:
Поскольку (см. формулу (2.1.2)) и то откуда . По формуле (2.5.12) находим
Решая систему уравнений
и учитывая условие получаем Следовательно,
Пример 9.
Найти числовые характеристики непрерывной случайной величины X, заданной плотностью распределения
Решение:
Сначала находим М(Х) по формуле (2.4.7):
В соответствии с формулой (2.5.13) найдем D(X) :
По формуле (2.5.16) находим
Пример 10.
Найти числовые характеристики непрерывной случайной величины X, заданной плотностью вероятностей
Решение:
С помощью формулы (2. 4.7) находим математическое ожидание:
4.7) находим математическое ожидание:
По формулам (2.5.13) и (2.5.16) соответственно получаем
Пример 11.
Случайная величина X задана функцией распределения
Найти числовые характеристики случайной величины
Решение:
Сначала найдем плотность распределения р(х) с помощью формулы (2.3.5). Так как , то
По формуле (2.4.7) вычисляем математическое ожидание:
В соответствии с формулами (2.5.13) и (2.5.16) находим дисперсию и среднее квадратическое отклонение:
Пример 12.
Независимые случайные величины имеют одинаковые распределения, для них
при Найти числовые характеристики среднего арифметического этих случайных величин, т.е. случайной величины
Решение:
С учетом формулы (2.4.13) и условия (I) находим
т.е. математическое ожидание среднего арифметического п независимых одинаково распределенных случайных величин равно математическому ожиданию каждой из этих величин.
Учитывая формулы (2.5.6), (2.5.9) и условие (I), получаем
т.е. дисперсия среднего арифметического п независимых одинаково распределенных случайных величин в л раз меньше дисперсии каждой из этих величин.
Учитывая определение и условие (I), находим
Таким образом, среднее квадратическое отклонение среднего арифметического n независимых одинаково распределенных случайных величин в раз меньше среднего квадратического отклонения каждой величины.
Решение задач по статистике: Правило сложения дисперсий
Решение задач по статистике: Правило сложения дисперсий
Количественный признакЗадача по статистике № 1
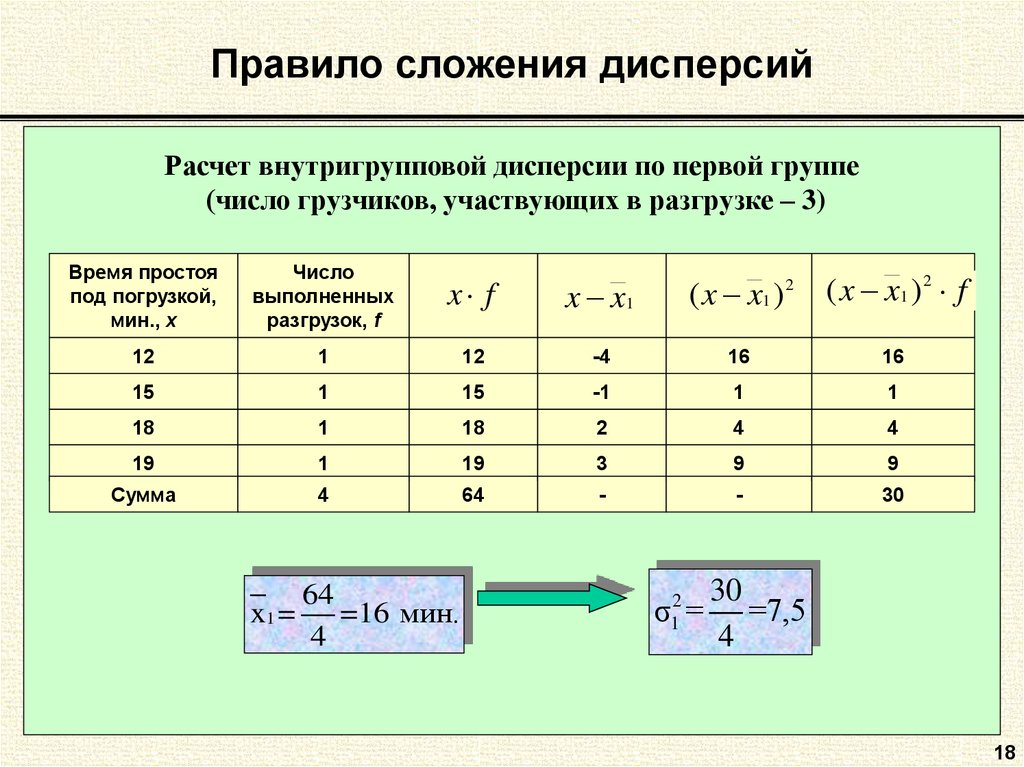
Определим групповые дисперсии, среднюю из групповых дисперсий,
межгрупповую дисперсию, общую дисперсию по данным табл.
Производительность труда двух бригад рабочих-токарей
Решение. Для расчета групповых дисперсий вычислим средние по каждой группе:
шт. ; шт.
; шт.
|
1-я бригада |
2-я бригада |
||||||
|
№ п/п |
Изготовлено деталей за час, шт. |
xi— |
(xi-)2 |
№
п/п |
Изготовлено деталей за час, шт. |
xi— |
(xi-)2 |
|
1 |
13 |
-2 |
4 |
7 |
18 |
-3 |
9 |
|
2 |
14 |
-1 |
1 |
8 |
19 |
|
4 |
|
3 |
15 |
0 |
0 |
9 |
22 |
1 |
1 |
|
4 |
17 |
2 |
4 |
10 |
20 |
-1 |
1 |
|
5 |
16 |
1 |
1 |
11 |
24 |
3 |
9 |
|
6 |
15 |
0 |
0 |
12 |
23 |
2 |
4 |
|
90 |
10 |
126 |
|
||||
Промежуточные расчеты дисперсий по группам представлены в табл. 7.4. Подставив полученные значения в формулу, получим:
7.4. Подставив полученные значения в формулу, получим:
Средняя из групповых дисперсий
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
шт.
Теперь определим межгрупповую дисперсию:
Таким образом, общая дисперсия по правилу сложения дисперсий
Проверим полученный результат, исчислив общую дисперсию обычным способом:
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением,
обозначается («эта») ирассчитывается по формуле . Для нашего примера эмпирическое корреляционное отношение — тесная связь на основе расчета между разбивкой на бригады и производительностью труда.
Измеряет какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Отношение факторной дисперсии к общей дисперсии результативного признака
Альтернативный признакЗадача № 2
Определить дисперсию альтернативного признака
|
Хозяйство |
Удельный вес всех дойных коров, pi= |
Всего коров в хозяйстве |
|
1 |
90 |
50 |
2 |
95 |
20 |
|
3 |
80 |
30 |
Решение
= p – среднее значение равно доле.
– общая средняя доля по хозяйствам
Межгрупповая дисперсия
–
обусловлена влиянием факторного признака – разбиения дойных коров по хозяйствам.
— внутригрупповая дисперсия по 1-му хозяйству
0.1=100%-90%
— внутригрупповая дисперсия по 2-му хозяйству
100%-95%
— внутригрупповая дисперсия по 3-му хозяйству
100%-80%
— дисперсия обусловленная влиянием результативного признака – удельный вес дойных коров
— общая дисперсия
Коэффициент детерминации:
Т.о. общая вариация на 97% обусловлена влиянием прочих неучтенных факторов, а разбивка на группы никак не зависит от количества дойных коров.
Дисперсия свойства, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор
В различных научных дисциплинах словосочетание «дисперсия это» характеризует мало схожие понятия. С латыни «dispersio» переводится как «рассеяние».
В физике, например, означает связь фазовой скорости волны с частотой. В химии описывает несмешиваемые субстанции. В биологии – многообразие признаков популяции.
В данной статье речь пойдет о математической трактовке. Рассматривается как одно из свойств случайных величин.
Содержание
- Что такое дисперсия в статистике
- Виды дисперсии дискретной случайной величины
- Общая дисперсия
- Межгрупповая дисперсия
- Внутригрупповая дисперсия
- Взаимосвязь
- Свойства дисперсии
- Показатели вариаций
- Пример расчета дисперсии
- Заключение
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:
При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.
В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.
Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
Или в несколько преобразованном виде:
Взвешенная дисперсия, для вариационного ряда:
где xi – значение из ряда;
fi – частота, количество повторений;
k – групп;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
Если вычислить среднюю величину от всех групповых,
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии
Опишем основные:
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
Усредненный стаж:
Дисперсия:
По альтернативной формуле:
Среднеквадратическое:
Коэффициент вариации:
youtube.com/embed/uK8MxzBGvEQ?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture»>Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Предыдущая
АлгебраПравило Лопиталя для вычисления пределов, примеры с подробным решением, доказательство
Следующая
АлгебраКоординаты вектора как найти длину отрезка по двум точкам, правило и формула нахождения в пространстве, свойства, задачи с решением, онлайн-калькулятор
ЭБ СПбПУ — Теория вероятностей и математическая статистика.
 Опорный конспект: учебное пособие
Опорный конспект: учебное пособие
|
Разрешенные действия: – Действие ‘Прочитать’ будет доступно, если вы выполните вход в систему или будете работать с сайтом на компьютере в другой сети Группа: Анонимные пользователи Сеть: Интернет |
Аннотация
В пособии приведены теоретические сведения и формулы по дисциплине «Теория вероятностей и математическая статистика». Теоретический материал снабжен большим количеством примеров. Предназначено для студентов всех форм обучения (очной, вечерней и заочной) при подготовке бакалавров и дипломированных специалистов.
Теоретический материал снабжен большим количеством примеров. Предназначено для студентов всех форм обучения (очной, вечерней и заочной) при подготовке бакалавров и дипломированных специалистов.
Права на использование объекта хранения
| Место доступа | Группа пользователей | Действие | ||||
|---|---|---|---|---|---|---|
| Локальная сеть ИБК СПбПУ | Все | |||||
| Внешние организации №2 | Все | |||||
| Внешние организации №1 | Все | |||||
| Интернет | Авторизованные пользователи | |||||
| Интернет | Анонимные пользователи |
Оглавление
- Министерство образования и науки Российской Федерации
- САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ
- А.
 М. ХАХИНА
М. ХАХИНА - ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- Учебное пособие
- Санкт-Петербург
- © Санкт-Петербургский государственный
- Испытания и события
- Виды случайных событий
- Классическое определение вероятности
- Основные формулы комбинаторики
- Относительная частота. Устойчивость относительной частоты
- Ограниченность классического определениявероятности. Статистическая вероятность
- Геометрические вероятности
- Теорема сложения вероятностей несовместных событий
- Противоположные события
- Принцип практической невозможности маловероятных событий
- Произведение событий
- Условная вероятность
- Теорема умножения вероятностей
- Независимые события. Теорема умножения для независимых событий
- Вероятность появления хотя бы одного события
- Теорема сложения вероятностей совместных событий
- Формула полной вероятности
- Вероятность гипотез.
 Формулы Бейеса
Формулы Бейеса - Формула Бернулли
- Вывод формулы Бернулли
- Локальная теорема Лапласа
- Интегральная теорема Лапласа
- Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
- Случайная величина
- Дискретные и непрерывные случайные величины
- Закон распределения вероятностей дискретной случайной величины
- Биномиальное распределение
- Распределение Пуассона
- Простейший поток событий
- Геометрическое распределение
- Гипергеометрическое распределение
- Числовые характеристики дискретных случайных величин
- Математическое ожидание дискретной случайной величины
- Вероятностный смысл математического ожидания
- Свойства математического ожидания
- Математическое ожидание числа появлений события в независимых испытаниях
- Целесообразность введения числовой характеристики рассеяния случайной величины
- Отклонение случайной величины от ее математического ожидания
- Дисперсия дискретной случайной величины
- Формула для вычисления дисперсии
- Свойства дисперсии
- Дисперсия числа появлений события в независимых испытаниях
- Среднее квадратическое отклонение
- Среднее квадратическое отклонение суммы взаимно независимых случайных величин
- Одинаково распределенные взаимно независимые случайные величины
- Начальные и центральные теоретические моменты
- Определение функции распределения
- Свойства функции распределения
- График функции распределения
- Вероятность попадания непрерывной случайной величины в заданный интервал
- Нахождение функции распределения по известной плотности распределения
- Свойства плотности распределения
- Вероятностный смысл плотности распределения
- Закон равномерного распределения вероятностей
- Числовые характеристики непрерывных случайных величин
- Нормальное распределение
- Нормальная кривая
- Влияние параметров нормального распределения на форму нормальной кривой
- Вероятность попадания в заданный интервал нормальной случайной величины
- Вычисление вероятности заданного отклонения
- Правило трех сигм
- Понятие о теореме Ляпунова.
 Формулировка центральной предельной теоремы
Формулировка центральной предельной теоремы - Оценка отклонения теоретического распределения от нормального.Асимметрия и эксцесс
- Функция одного случайного аргумента и ее распределение
- Математическое ожидание функции одного случайного аргумента
- Функция двух случайных аргументов.Распределение суммы независимых слагаемых.Устойчивость нормального распределения
- Распределение «хи квадрат»
- Распределение Стьюдента
- Распределение F Фишера — Снедекора
- Понятие о системе нескольких случайных величин
- Закон распределения вероятностей дискретной двумерной случайной величины
- Функция распределения двумерной случайной величины
- Свойства функции распределения двумерной случайной величины
- Вероятность попадания случайной точки в полуполосу
- Вероятность попадания случайной точки в прямоугольник
- Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)
- Нахождение функции распределения системы по известной плотности распределения
- Вероятностный смысл двумерной плотности вероятности
- Вероятность попадания случайной точки в произвольную область
- Свойства двумерной плотности вероятности
- Отыскание плотностей вероятности составляющих двумерной случайной величины
- Условные законы распределения составляющих системы дискретных случайных величин
- Условные законы распределения составляющих системы непрерывных случайных величин
- Условное математическое ожидание
- Зависимые и независимые случайные величины
- Числовые характеристики системы двух случайных величин.
 Корреляционный момент. Коэффициент корреляции
Корреляционный момент. Коэффициент корреляции - Коррелированность и зависимость случайных величин
- Нормальный закон распределения на плоскости
- Линейная регрессия. Прямые линии среднеквадратической регрессии
- Линейная корреляция. Нормальная корреляция
- Функция одного случайного аргумента
- Функции двух случайных аргументов
- Распределение функций нормальных случайных величин
- Распределение ,𝝌-𝟐. (хи-квадрат или Пирсона)
- Распределение Стьюдента
- Распределение Фишера—Снедекора
- Основные задачи
- Определение случайной функции
- Корреляционная теория случайных функций
- Математическое ожидание случайной функции
- Свойства математического ожидания случайной функции
- Дисперсия случайной функции
- Свойства дисперсии случайной функции
- Целесообразность введения корреляционной функции
- Корреляционная функция случайной функции
- Свойства корреляционной функции
- Нормированная корреляционная функция
- Взаимная корреляционная функция
- Свойства взаимной корреляционной функции
- Нормированная взаимная корреляционная функция
- Характеристики суммы случайных функций
- Производная случайной функции и ее характеристики
- Интеграл от случайной функции и его характеристики
- Комплексные случайные величины и их числовые характеристики
- Комплексные случайные функции и их характеристики
- Определение стационарной случайной функции
- Свойства корреляционной функциистационарной случайной функции
- Нормированная корреляционная функция стационарной случайной функции
- Стационарно связанные случайные функции
- Стационарно связанные случайные функции
- Корреляционная функция производной стационарной случайной функции
- Взаимная корреляционная функция стационарной случайной функции и ее производной
- Корреляционная функция интеграла от стационарной случайной функции
- Определение характеристик эргодических стационарных случайных функций на опытах
- Задачи математической статистики
- Краткая историческая справка
- Генеральная и выборочная совокупности
- Повторная и бесповторная выборки.
 Репрезентативная выборка
Репрезентативная выборка - Способы отбора
- Статистическое распределение выборки
- Эмпирическая функция распределения
- Полигон и гистограмма
- Статистические оценки параметровраспределения
- Несмещенные, эффективные и состоятельные оценки
- Генеральная средняя
- Выборочная средняя
- Оценка генеральной средней по выборочной средней. Устойчивость выборочных средних
- Групповая и общая средние
- Отклонение от общей средней и его свойство
- Генеральная дисперсия
- Выборочная дисперсия
- Формула для вычисления дисперсии
- Групповая, внутригрупповая, межгрупповая и общая дисперсии
- Сложение дисперсий
- Оценка генеральной дисперсии по исправленной выборочной
- Точность оценки, доверительная вероятность (надежность). Доверительный интервал
- Доверительные интервалы для оценки математического ожидания нормального распределения при известном о
- Доверительные интервалы для оценки математического ожидания нормального распределения при неизвестном о
- Оценка истинного значения измеряемой величины
- Доверительные интервалы для оценки среднего квадратического отклонения𝝈 нормального распределения
- Оценка точности измерений
- Оценка вероятности (биномиального распределения) по относительной частоте
- Точечная оценка
- Интервальная оценка.

- Метод моментов для точечной оценки параметров распределения
- Оценка одного параметра
- Оценка двух параметров
- Метод наибольшего правдоподобия
- Непрерывные случайные величины
- Другие характеристики вариационного ряда
Статистика использования
Python и статистический вывод: часть 4 / Хабр
Этот заключительный пост посвящен анализу дисперсии. Предыдущий пост см. здесь.
Анализ дисперсии
Анализ дисперсии (варианса), который в специальной литературе также обозначается как ANOVA от англ. ANalysis Of VAriance, — это ряд статистических методов, используемых для измерения статистической значимости расхождений между группами. Он был разработан чрезвычайно одаренным статистиком Рональдом Фишером, который также популяризировал процедуру проверки статистической значимости в своих исследовательских работах по биологическому тестированию.
Примечание. В предыдущей и этой серии постов для термина «variance» использовался принятый у нас термин «дисперсия» и в скобках местами указывался термин «варианс». Это не случайно. За рубежом существуют парные термины «variance» и «covariance», и они по идее должны переводиться с одним корнем, например, как «варианс» и «коварианс», однако на деле у нас парная связь разорвана, и они переводятся как совершенно разные «дисперсия» и «ковариация». Но это еще не все. «Dispersion» (статистическая дисперсия) за рубежом является отдельным родовым понятием разбросанности, т.е. степени, с которой распределение растягивается или сжимается, а мерами статистической дисперсии являются варианс, стандартное отклонение и межквартильный размах. Dispersion, как родовое понятие разбросанности, и variance, как одна из ее мер, измеряющая расстояние от среднего значения — это два разных понятия. Далее в тексте для variance везде будет использоваться общепринятый термин «дисперсия».
Однако данное расхождение в терминологии следует учитывать.
Наши тесты на основе z-статистики и t-статистики были сосредоточены на выборочных средних значениях как первостепенном механизме проведения разграничения между двумя выборками. В каждом случае мы искали расхождение в средних значениях, деленных на уровень расхождения, который мы могли обоснованно ожидать, и количественно выражали стандартной ошибкой.
Среднее значение не является единственным выборочным индикатором, который может указывать на расхождение между выборками. На самом деле, в качестве индикатора статистического расхождения можно также использовать выборочную дисперсию.
Длительности (сек), постранично и совмещенноВ целях иллюстрации того, как это могло бы работать, рассмотрим приведенную выше диаграмму. Каждая из трех групп слева может представлять выборки времени пребывания на конкретном веб-сайте с его собственным средним значением и стандартным отклонением. Если время пребывания для всех трех групп объединить в одну, то дисперсия будет больше средней дисперсии для групп, взятых отдельно.
Статистическая значимость на основе анализа дисперсии вытекает из соотношения двух дисперсий — дисперсии между исследуемыми группами и дисперсии внутри исследуемых групп. Если существует значимое межгрупповое расхождение, которое не отражено внутри групп, то эти группы помогают объяснить часть дисперсии между группами. И напротив, если внутригрупповая дисперсия идентична межгрупповой дисперсии, то группы статистически от друг друга неразличимы.
F-распределение
F-распределение параметризуется двумя степенями свободы — степенями свободы размера выборки и числа групп.
Первая степень свободы — это количество групп минус 1, и вторая степень свободы — размер выборки минус число групп. Если k представляет число групп, и n — объем выборки, то получаем:
Мы можем визуализировать разные F-распределения на графике при помощи функции библиотеки pandas plot:
def ex_2_Fisher(): '''Визуализация разных F-распределений на графике''' mu = 0 d1_values, d2_values = [4, 9, 49], [95, 90, 50] linestyles = ['-', '--', ':', '-.'] x = sp.linspace(0, 5, 101)[1:] ax = None for (d1, d2, ls) in zip(d1_values, d2_values, linestyles): dist = stats.f(d1, d2, mu) df = pd.DataFrame( {0:x, 1:dist.pdf(x)} ) ax = df.plot(0, 1, ls=ls, label=r'$d_1=%i,\ d_2=%i$' % (d1,d2), ax=ax) plt.xlabel('$x$\nF-статистика') plt.ylabel('Плотность вероятности \n$p(x|d_1, d_2)$') plt.show()
Кривые приведенного выше графика показывают разные F-распределения для выборки, состоящей из 100 точек, разбитых на 5, 10 и 50 групп.
F-статистика
Тестовая выборочная величина, которая представляет соотношение дисперсии внутри и между группами, называется F-статистикой. Чем ближе значение F-статистики к единице, тем более похожи обе дисперсии. F-статистика вычисляется очень просто следующим образом:
где S2b — это межгрупповая дисперсия, и S2w — внутригрупповая дисперсия.
По мере увеличения соотношения F межгрупповая дисперсия увеличивается по сравнению с внутригрупповой. Это означает, что это разбиение на группы хорошо справляется с задачей объяснения дисперсии, наблюдавшейся по всей выборке в целом. Там, где это соотношение превышает критический порог, мы можем сказать, что расхождение является статистически значимым.
F-тест всегда является односторонним, потому что любая дисперсия среди групп демонстрирует тенденцию увеличивать F. При этом F не может уменьшаться ниже нуля.
Внутригрупповая дисперсия для F-теста вычисляется как среднеквадратичное отклонение от среднего значения. Мы вычисляем ее как сумму квадратов отклонений от среднего значения, деленную на первую степень свободы. Например, если имеется k групп, каждая со средним значением x̅k, то мы можем вычислить внутригрупповую дисперсию следующим образом:
где SSW — это внутригрупповая сумма квадратов, и xjk — это значение j-ого элемента в группе .
Приведенная выше формула для вычисления SSW имеет грозный вид, но на деле довольно легко имплементируется на Python, как сумма квадратичных отклонений от среднего значения ssdev, делающая вычисление внутригрупповой суммы квадратов тривиальным:
def ssdev( xs ): '''Сумма квадратов отклонений между каждым элементом и средним по выборке''' mu = xs.mean() square_deviation = lambda x : (x - mu) ** 2 return sum( map(square_deviation, xs) )
Межгрупповая дисперсия для F-теста имеет похожую формулу:
где SST — это полная сумма квадратов отклонений, и SSW — значение, которое мы только что вычислили. Полная сумма квадратов является суммой квадратичных расхождений от «итогового» среднего значения, которую можно вычислить следующим образом:
Отсюда, SST — это попросту полная сумма квадратов без какого-либо разбиения на группы. На языке Python значения SST и SSW вычисляются элементарно, как будет показано ниже.
ssw = sum( groups.apply( lambda g: ssdev(g) ) ) # внутригрупповая сумма # квадратов отклонений sst = ssdev( df['dwell-time'] ) # полная сумма квадратов по всему набору ssb = sst – ssw # межгрупповая сумма квадратов отклонений
F-статистика вычисляется как отношение межгрупповой дисперсии к внутригрупповой. Объединив определенные ранее функции ssb и ssw и две степени свободы, мы можем вычислить F-статистика.
На языке Python F-статистика из групп и двух степеней свободы вычисляется следующим образом:
msb = ssb / df1 # усредненная межгрупповая msw = ssw / df2 # усредненная внутригрупповая f_stat = msb / msw
Имея возможность вычислить F-статистику из групп, мы теперь готовы использовать его в соответствующем F-тесте.
F-тест
Как и в случае со всеми проверками статистических гипотез, которые мы рассмотрели в этой серии постов, как только имеется выборочная величина (статистика) и распределение, нам попросту нужно подобрать значение уровня значимости и посмотреть, не превысили ли наши данные критическое для теста значение.
Библиотека scipy предлагает функцию stats.f.sf, но она измеряет дисперсию между и внутри всего двух групп. В целях выполнения F-теста на наших 20 разных группах, нам придется имплементировать для нее нашу собственную функцию. К счастью, мы уже проделали всю тяжелую работу в предыдущих разделах, вычислив надлежащую F-статистику. Мы можем выполнить F-тест, отыскав F-статистику в F-распределении, параметризованном правильными степенями свободы. В следующем ниже примере мы напишем функцию f_test, которая все это использует для выполнения теста на произвольном числе групп:
def f_test(groups): m, n = len(groups), sum(groups.count()) df1, df2 = m - 1, n - m ssw = sum( groups.apply(lambda g: ssdev(g)) ) sst = ssdev( df['dwell-time'] ) ssb = sst - ssw msb = ssb / df1 msw = ssw / df2 f_stat = msb / msw return stats.f.sf(f_stat, df1, df2) def ex_2_24(): '''Проверка вариантов дизайна веб-сайта на основе F-теста''' df = load_data('multiple-sites.tsv') groups = df.groupby('site')['dwell-time'] return f_test(groups)
0.014031745203658217
В последней строке приведенной выше функции мы преобразуем значение F-статистики в p-значение, пользуясь функцией scipy stats.f.sf, параметризованной правильными степенями свободы. P-значение является мерой всей модели, т.е. насколько хорошо разные веб-сайты объясняют дисперсию времени пребывания в целом. Нам остается только выбрать уровень значимости и выполнить проверку. Будем придерживаться 5%-ого уровня значимости.
Проверка возвращает p-значение, равное 0.014, т.е. значимый результат. Разные варианты веб-сайта действительно имеют разные дисперсии, которые нельзя просто объяснить одной лишь случайной ошибкой в выборке.
F-распределение со степенями свободы 19 и 980Для визуализации распределений всех вариантов дизайна веб-сайта на одном графике мы можем воспользоваться коробчатой диаграммой, разместив распределения для сопоставления рядом друг с другом:
def ex_2_25():
'''Визуализация распределений всех вариантов
дизайна веб-сайта на одной коробчатой диаграмме'''
df = load_data('multiple-sites. tsv')
df.boxplot(by='site', showmeans=True)
plt.xlabel('Номер дизайна веб-сайта')
plt.ylabel('Время пребывания, сек.')
plt.title('')
plt.suptitle('')
plt.show()
tsv')
df.boxplot(by='site', showmeans=True)
plt.xlabel('Номер дизайна веб-сайта')
plt.ylabel('Время пребывания, сек.')
plt.title('')
plt.suptitle('')
plt.show()В приведенном выше примере показана работа функции boxplot, которая вычисляет свертку на группах и сортирует группы по номеру варианта дизайна веб-сайта. Соответственно наш изначальный веб-сайт с номером 0, на графике расположен крайним слева.
Может создастся впечатление, что вариант дизайна веб-сайта с номером 10 имеет самое длительное время пребывания, поскольку его межквартильный размах простирается вверх выше других. Однако, если вы присмотритесь повнимательнее, то увидите, что его среднее значение меньше, чем у варианта дизайна с номером 6, имеющего среднее время пребывания более 144 сек.:
def ex_2_26():
'''T-проверка вариантов 0 и 10 дизайна веб-сайта'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
site_0 = groups. get_group(0)
site_10 = groups.get_group(10)
_, p_val = stats.ttest_ind(site_0, site_10, equal_var=False)
return p_val
get_group(0)
site_10 = groups.get_group(10)
_, p_val = stats.ttest_ind(site_0, site_10, equal_var=False)
return p_val0.0068811940138903786
Подтвердив статистически значимый эффект при помощи F-теста, теперь мы вправе утверждать, что вариант дизайна веб-сайта с номером 6 статистически отличается от изначального значения:
def ex_2_27():
'''t-тест вариантов 0 и 6 дизайна веб-сайта'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
site_0 = groups.get_group(0)
site_6 = groups.get_group(6)
_, p_val = stats.ttest_ind(site_0, site_6, equal_var=False)
return p_val0.005534181712508717
Наконец, у нас есть подтверждающие данные, из которых вытекает, что веб-сайт с номером 6 является подлинным улучшением существующего веб-сайта. В результате нашего анализа исполнительный директор AcmeContent санкционирует запуск обновленного дизайна веб-сайта. Веб-команда — в восторге!
Размер эффекта
В этой серии постов мы сосредоточили наше внимание на широко используемых в статистической науке методах проверки статистической значимости, которые обеспечивают обнаружение статистического расхождения, которое не может быть легко объяснено случайной изменчивостью. Мы должны всегда помнить, что выявление значимого эффекта — это не одно и то же, что и выявление большого эффекта. В случае очень больших выборок значимым будет считаться даже крошечное расхождение в выборочных средних. В целях более глубокого понимания того, является ли наше открытие значимым и важным, мы так же должны констатировать величину эффекта.
Мы должны всегда помнить, что выявление значимого эффекта — это не одно и то же, что и выявление большого эффекта. В случае очень больших выборок значимым будет считаться даже крошечное расхождение в выборочных средних. В целях более глубокого понимания того, является ли наше открытие значимым и важным, мы так же должны констатировать величину эффекта.
Интервальный индекс d Коэна
Индекс d Коэна — это поправка, которую применяется для того, чтобы увидеть, не является ли наблюдавшееся расхождение не просто статистически значимым, но и действительно большим. Как и поправка Бонферрони, она проста:
Здесь Sab — это объединенное стандартное отклонение (не объединенная стандартная ошибка) выборок. Она вычисляется аналогично вычислению объединенной стандартной ошибки:
def pooled_standard_deviation(a, b): '''Объединенное стандартное отклонение (не объединенная стандартная ошибка)''' return sp.sqrt( standard_deviation(a) ** 2 + standard_deviation(b) ** 2)
Так, для варианта под номером 6 дизайна нашего веб-сайта мы можем вычислить индекс d Коэна следующим образом:
def ex_2_28():
'''Вычисление интервального индекса d Коэна
для варианта дизайна веб-сайта под номером 6'''
df = load_data('multiple-sites. tsv')
groups = df.groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(6)
return (b.mean() - a.mean()) / pooled_standard_deviation(a, b)
tsv')
groups = df.groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(6)
return (b.mean() - a.mean()) / pooled_standard_deviation(a, b)0.38913648705499848
В отличие от p-значений, абсолютный порог для индекса d Коэна отсутствует. Считать ли эффект большим или нет частично зависит от контекста, однако этот индекс действительно предоставляет полезную, нормализованную меру величины эффекта. Значения выше 0.5, как правило, считаются большими, поэтому значение 0.38 — это умеренный эффект. Он определенно говорит о значительном увеличении времени пребывания на нашем веб-сайте и что усилия, потраченные на обновление веб-сайта, определенно не были бесполезными.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Резюме
В этой серии постов мы узнали о разнице между описательной и инференциальной статистикой, занимающейся методами статистического вывода. Мы еще раз убедились в важности нормального распределения и центральной предельной теоремы, и научились квантифицировать расхождение с популяциями, используя проверку статистических гипотез на основе z-теста, t-теста и F-теста.
Мы еще раз убедились в важности нормального распределения и центральной предельной теоремы, и научились квантифицировать расхождение с популяциями, используя проверку статистических гипотез на основе z-теста, t-теста и F-теста.
Мы узнали о том, каким именно образом методология инференциальной статистики анализирует непосредственно сами выборки, чтобы выдвигать утверждения о всей популяции в целом, из которой они были отобраны. Мы познакомились с целым рядом методов —интервалами уверенности, размножением выборок путем бутстрапирования и проверкой статистической значимости — которые помогают разглядеть глубинные параметры популяции. Симулируя многократные испытания, мы также получили представление о трудности проверки статистической значимости в условиях многократных сравнений и увидели, как F-тест помогает решать эту задачу и устанавливать равновесие между ошибками 1-го и 2-го рода.
Мы также коснулись терминологических болевых точек и выяснили некоторые нюансы смыслового дрейфа в отечественной статистике.
В следующей серии постов, если читатели пожелают, мы применим полученные знания о дисперсии и F-тесте к одиночным выборкам. Мы представим метод регрессионного анализа и воспользуемся им для обнаружения корреляции между переменными в выборке из спортсменов-олимпийцев.
Разбираем формулы среднеквадратического отклонения и дисперсии в Excel | Методы анализа
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Сморите пример расчета здесь: среднеквадратическое отклонние и дисперсия
Для этого временного ряда i=1, n=10, ,
Рассмотрим формулу среднего значения:
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. 2))/(n-1)
2))/(n-1)
=90/(10-1)=10
6. Среднеквадратическое отклонение равно = корень(10)=3,2
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Скачать файл с примером
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Скачать файл с примером
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.

- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Добавить комментарий
4.5.3 Расчет дисперсии и стандартного отклонения
Содержание
Текст начинается
Навигация по теме
- 4 Исследование данных
- 4.5 Меры рассеивания
- 4.5.1 Расчет диапазона и межквартильный диапазон
- 4.
 5.2 Визуализация графика прямоугольников и усов
5.2 Визуализация графика прямоугольников и усов - 4.5.3 Расчет дисперсии и стандартного отклонения
- 4.5 Меры рассеивания
В отличие от размаха и межквартильного размаха, дисперсия является мерой дисперсии, учитывающей разброс всех точек данных в наборе данных. Это мера дисперсии, которая используется чаще всего, наряду со стандартным отклонением, которое представляет собой просто квадратный корень из дисперсии. Дисперсия представляет собой среднеквадратичную разницу между каждой точкой данных и центром распределения, измеренным средним значением.
Пример 1. Расчет дисперсии и стандартного отклонения
Давайте посчитаем дисперсию следующего набора данных: 2, 7, 3, 12, 9.
Первым шагом является вычисление среднего значения. Сумма равна 33 и имеется 5 точек данных. Следовательно, среднее значение равно 33 ÷ 5 = 6,6. Затем вы берете каждое значение в наборе данных, вычитаете среднее значение и возводите в квадрат разницу. Например, для первого значения:
Например, для первого значения:
(2 — 6,6) 2 = 21,16
Квадраты разностей для всех значений складываются:
21,16 + 0,16 + 12,96 + 29,16 + 5,76 = 69,20
Сумма затем делится на количество точек данных:
69,20 ÷ 5 = 13,84
Дисперсия составляет 13,84. Чтобы получить стандартное отклонение, вы вычисляете квадратный корень из дисперсии, который равен 3,72.
Стандартное отклонение полезно при сравнении разброса двух отдельных наборов данных, которые имеют примерно одинаковое среднее значение. Набор данных с меньшим стандартным отклонением имеет более узкий разброс измерений вокруг среднего значения и, следовательно, обычно имеет сравнительно меньше высоких или низких значений. Элемент, выбранный случайным образом из набора данных с низким стандартным отклонением, имеет больше шансов быть близким к среднему значению, чем элемент из набора данных, стандартное отклонение которого выше. Однако на стандартное отклонение влияют экстремальные значения. Одно экстремальное значение может иметь большое влияние на стандартное отклонение.
Одно экстремальное значение может иметь большое влияние на стандартное отклонение.
Стандартное отклонение может быть трудно интерпретировать с точки зрения того, насколько большим оно должно быть, если учесть, что данные широко рассредоточены. Величина среднего значения набора данных влияет на интерпретацию его стандартного отклонения. Когда вы измеряете что-то в масштабе миллионов, наличие показателей, близких к среднему значению, не имеет такого же значения, как когда вы измеряете что-то в масштабе сотен. Например, показатель двух крупных компаний с разницей в годовом доходе в 10 000 долл. США считается довольно близким, а показатель двух людей с разницей в весе в 30 килограммов считается далеко отстоящим друг от друга. Вот почему в большинстве ситуаций полезно оценить размер стандартного отклонения по отношению к его среднему значению.
Помните о следующих свойствах при использовании стандартного отклонения:
- Стандартное отклонение чувствительно к экстремальным значениям.
 Одно очень экстремальное значение может увеличить стандартное отклонение и исказить дисперсию.
Одно очень экстремальное значение может увеличить стандартное отклонение и исказить дисперсию. - Для двух наборов данных с одинаковым средним значением большее стандартное отклонение имеет тот, в котором данные более разбросаны от центра.
- Стандартное отклонение равно 0, если все значения равны (потому что все значения равны среднему).
Причина, по которой стандартное отклонение так популярно в качестве меры дисперсии, заключается в его связи с нормальным распределением, которое описывает многие природные явления и чьи математические свойства интересны в случае больших наборов данных. Когда переменная подчиняется нормальному распределению, гистограмма имеет форму колокола и симметрична, а лучшими показателями центральной тенденции и дисперсии являются среднее значение и стандартное отклонение. Это очень полезное распределение вероятностей и относительно простое в использовании. Доверительные интервалы часто основаны на стандартном нормальном распределении.
Однако, когда:
- набор данных мал,
- распределение асимметрично, или
- набор данных включает экстремальные значения
лучше использовать межквартильный диапазон.
- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Свяжитесь с нами и сообщите, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Дисперсия | Стандартное отклонение
← предыдущее
следующее →
Рассмотрим две случайные величины $X$ и $Y$ со следующими PMF. $$ \label{eq:X-var}
\номер P_X(x) = \влево\{
\begin{массив}{л л}
0,5 & \quad \text{для} x=-100\\
0,5 & \quad \text{для} x=100\\
0 & \quad \text{иначе}
\end{массив} \right.
\hspace{10pt} (3.3)
$$
$$ \label{eq:X-var}
\номер P_X(x) = \влево\{
\begin{массив}{л л}
0,5 & \quad \text{для} x=-100\\
0,5 & \quad \text{для} x=100\\
0 & \quad \text{иначе}
\end{массив} \right.
\hspace{10pt} (3.3)
$$
$$ \label{eq:Y-var}
\номер P_Y(y) = \влево\{
\begin{массив}{л л}
1 & \quad \text{для} y=0\\
0 & \quad \text{иначе}
\end{массив} \right.
\hspace{20pt} (3.4)
$$
Обратите внимание, что $EX=EY=0$. Хотя обе случайные величины имеют одинаковое среднее значение, их распределение
совершенно другое. $Y$ всегда равно своему среднему значению $0$, а $X$ равно либо $100$, либо $-100$,
довольно далеко от своего среднего значения. Дисперсия является мерой того, насколько рассредоточено распределение
случайная величина есть. Здесь дисперсия $Y$ довольно мала, так как ее распределение сосредоточено в
единственное значение, в то время как дисперсия $X$ будет больше, поскольку его распределение более рассредоточено. 92$
часто велико, поэтому $X$ часто принимает значения, далекие от своего среднего значения. Это означает, что распределение очень
распространяться. С другой стороны, низкая дисперсия означает, что распределение сконцентрировано вокруг своего среднего значения.
Это означает, что распределение очень
распространяться. С другой стороны, низкая дисперсия означает, что распределение сконцентрировано вокруг своего среднего значения.
Обратите внимание, что если бы мы не возводили в квадрат разницу между $X$ и его средним значением, результат был бы равен $0$. То есть $$E[X-\mu_X]=EX-E[\mu_X]=\mu_X-\mu_X=0.$$ $X$ иногда ниже среднего, а иногда выше среднего. Таким образом, $X-\mu_X$ иногда отрицательный, а иногда и положительный, но в среднем он равен нулю. 92$. Чтобы решить эту проблему, мы определяем другую меру, называемую стандартным отклонением , обычно отображается как $\sigma_X$, что представляет собой просто квадратный корень из дисперсии.
Стандартное отклонение случайной величины $X$ определяется как $$\textrm{SD}(X)= \sigma_X= \sqrt {\textrm{Var}(X)}.$$
Стандартное отклонение $X$ имеет ту же единицу измерения, что и $X$. Для $X$ и $Y$, определенных в уравнениях 3.3 и 3.4, у нас есть
| $\sigma_X$ | $=\sqrt{10,000}= 100$ 92 \textrm{Var}(X)\\
\end{выравнивание} Из уравнения 3. Теорема Мы докажем эту теорему в главе 6, а пока посмотрим на пример, чтобы увидеть, как мы можем ее использовать. Пример Если $X \sim Binomial(n,p)$ найти Var$(X)$.
← предыдущая следующая → Печатная версия книги доступна на Amazon здесь. Поведенческая статистика в действииПоведенческая статистика в действии
Диапазон = высокая оценка низкая оценка
III. Среднее среднее отклонение Среднее среднее отклонение
IV. Отношение
Между генеральной совокупностью/выборкой и дисперсией/стандартным отклонением 90 120 (видео
Урок 5 IV) (Ютуб
версия) Отношение
Между генеральной совокупностью/выборкой и дисперсией/стандартным отклонением 90 120 (видео
Урок 5 IV) (Ютуб
версия)
В. Вариант Вариант
Дополнительные видеоролики о концепциях, которые могут помочь: Диапазон, Дисперсия, Стандартное отклонение Как рассчитать стандарт Отклонение и отклонение Что такое дисперсия в Статистика? В поисках стандарта Отклонение набора данных Стандартное отклонение Как рассчитать дисперсию за 4 простых шагаВ этой статье
Что такое дисперсия? Дисперсия — это параметр или статистика, которая измеряет, насколько разбросанные данные соотносятся со своим средним значением. Меры разброса, такие как дисперсия, важны в статистике, поскольку они дают вам дополнительную информацию о ваших данных. Вы не можете получить эту информацию, используя только меры центра, такие как:
Представьте, что есть два класса статистики, которые ведут два разных профессора. Оба профессора согласились стремиться к среднему баллу по классу 85 — букве B. Тем не менее, в одном классе разница оценок очень низкая. В другом классе разница оценок очень высока. 92s2 обозначает это.
Формула дисперсии Чтобы вычислить дисперсию, возьмите среднее квадратов отклонений, также называемых квадратами разностей, от среднего. Помните, что отклонение от среднего — это разница между конкретной точкой данных и средним значением. Когда использовать выборку или дисперсию генеральной совокупностиВ статистике под совокупностью понимается весь набор изучаемых объектов или событий. Выборка – это подмножество совокупности. В качестве примера представьте, что вы изучаете национальные выборы в Соединенных Штатах. Интересующая вас совокупность состоит из каждого избирателя, имеющего право голоса, в 50 штатах, но, поскольку вы не можете собрать данные обо всем населении, вы выбираете случайные выборки (подмножества) избирателей. Иногда у статистиков есть данные для всего населения, но в большинстве случаев у них есть только выборочные данные, из которых они делают статистические выводы о населении. Когда вы работаете с данными о населении и вычисляете дисперсию, используйте приведенную выше формулу дисперсии населения. Когда вы работаете с выборочными данными и хотите рассчитать дисперсию, используйте приведенную выше формулу выборочного стандартного отклонения. Как рассчитать дисперсию за 4 шагаВот пример того, как рассчитать дисперсию за 4 простых шага. Допустим, у вас есть следующие образцы данных о росте 10 игроков НБА, случайно выбранных из сезона 2021–22.
1. Find the Sample Mean Find the Sample MeanНайдите выборочное среднее xˉ\bar{x}xˉ ваших данных Чтобы найти дисперсию, вам нужно сначала узнать среднее арифметическое ваших данных. Чтобы найти среднее значение, сложите все значения в наборе данных и разделите на размер выборки nnn. Поскольку в этом наборе данных 10 человек, размер выборки равен n=10n=10n=10. xˉ=78+84+77+80+76+83+76+82+73+7510=78,4 дюйма\бар{x} =\frac{78 +84+77+80+76+83+76+82 +73+75}{10}= 78,4 \text{ дюйма}xˉ=1078+84+77+80+76+83+76+82+73+75=78,4 дюйма 92 = = 0,16 + 31,36 + 1,96 + 2,56 + 5,76 + 21,16 + 5,76 + 12,96 + 29,16 + 11,56 = 122,4 ∑ (xi−xˉ)2 = = 0,16 + 31,36 + 1,96 + 2,56 + 5,76 + 21,16 + 5,76 + 12,96+ 29,16+11,56=122,4 4. Найдите дисперсию путем деления суммы квадратов отклоненийНайдите дисперсию, разделив сумму квадратов отклонений на размер выборки минус один (nnn-1) Поскольку мы работаем с выборочными данными, мы делим сумму квадратов отклонений на nnn-1. Если бы вместо этого мы пытались найти дисперсию популяции, мы бы разделили ее на размер популяции NNN. ваш ответ! Дисперсия для этого набора данных составляет 13,6 дюйма в квадрате. Отклонение от стандартного отклоненияЕсли вы посмотрите на приведенный выше пример, вы заметите, что дисперсия измеряется в единицах, которые очень трудно интерпретировать. В примере мы хотели рассчитать дисперсию роста десяти игроков НБА. Мы измеряем высоту в дюймах, но мы измеряем разницу в дюймах в квадрате! При измерении дисперсии мы получаем единицу в квадрате, потому что в расчетах используем квадраты отклонений. Для этого есть веская причина. Чтобы измерить среднюю вариацию (или среднее отклонение), мы хотим убедиться, что отрицательные отклонения для точек данных, которые лежат ниже среднего, не компенсируют положительные отклонения для точек данных, которые лежат выше среднего. Недостатком этого является то, что в результате мы получаем квадратные единицы измерения. Чтобы избежать трудностей с интерпретацией дисперсии, вы часто будете использовать родственную меру разброса, называемую стандартным отклонением. Стандартное отклонение — это просто квадратный корень из дисперсии. Извлекая квадратный корень из дисперсии, мы возвращаем нашу меру в интерпретируемые единицы данных. В нашем примере NBA дисперсия составила 13,6 дюйма в квадрате, поэтому стандартное отклонение выборки будет равно 13,6≈\sqrt{13,6} \ приблизительно13,6≈ 3,69 дюйма. Поскольку мы измеряем стандартные отклонения в тех же единицах, что и данные, интерпретация становится намного проще. Стандартное отклонение в 3,69 дюйма говорит нам о том, что игрок НБА, случайно выбранный из нашей выборки, будет иметь рост на 3,69 дюйма выше или ниже среднего роста в 122,4 дюйма.
Вычисление дисперсии в Excel, Google Sheets, R и DesmosХотя важно знать, как рассчитать дисперсию вручную, вы, скорее всего, будете использовать такие программы, как Excel, R и Desmos, чтобы сделать расчет за вас! В таблицах Microsoft Excel или Google используйте формулу =VAR() для расчета дисперсии. В Desmos и R команда для дисперсии также является VAR(). Вы можете ввести свои данные прямо между скобками, поэтому, если ваши данные состоят из набора чисел {5, 7, 10, 15, 20}, вы должны ввести VAR (5, 7, 10, 15, 20). Если ваши данные хранятся как переменная, вы можете использовать команду var() с именем переменной в круглых скобках вместо списка точек данных. Для практики попробуйте рассчитать дисперсию из нашего примера NBA, используя одну или все эти программы для практики. Посмотрите, получите ли вы правильный ответ 13.6! Узнайте об отмеченных наградами курсах Outlier For-CreditOutlier (от соучредителя MasterClass) собрал лучших в мире преподавателей, дизайнеров игр и кинематографистов для создания будущего онлайн-колледжа. Ознакомьтесь с этими связанными курсами: Введение в статистикуИзучите курс Введение в статистику Как данные описывают наш мир. Обзор курса Введение в микроэкономикуЗнакомство с курсом Введение в микроэкономикуПочему маленькие решения имеют большое значение. Изучить курс Введение в макроэкономикуИзучить курс Введение в макроэкономикуКак деньги движут нашим миром. Изучить курс Введение в психологиюИзучить курс Введение в психологиюНаука о разуме. Изучить курс Население в сравнении с выборочной дисперсией и стандартным отклонениемС помощью калькулятора описательной статистики Excel можно легко рассчитать дисперсию генеральной совокупности или выборки и стандартное отклонение, а также асимметрию, эксцесс и другие показатели. Дисперсия и стандартное отклонение Определение и расчет Дисперсия и стандартное отклонение являются широко используемыми мерами разброса данных или, в финансах и инвестициях, мерами волатильности цен на активы. Дисперсия определяется и рассчитывается как среднеквадратичное отклонение от среднего значения. Стандартное отклонение рассчитывается как квадратный корень из дисперсии или, в полном определении, стандартное отклонение представляет собой квадратный корень из среднего квадратного отклонения от среднего. Эти определения могут показаться запутанными при первом знакомстве. Подробное объяснение того, как рассчитать обе меры, см. в разделе «Вычисление дисперсии и стандартного отклонения за 4 простых шага». В целом статистика выполняет две основные задачи. Его цель либо описать то, что уже произошло, либо уже существует ( описательная статистика ), или к оценка чего-то, что еще не произошло или до конца не известно ( выводная статистика ). Описательная статистика решает проблему эффективного анализа уже имеющихся данных. Логическая статистика (оценочная и прогнозирующая часть статистики) решает проблему нехватки всех данных. Из этих двух широких областей статистики статистика логического вывода гораздо интереснее и гораздо чаще используется в финансы и инвестиции . В конце концов, как инвесторы или спекулянты, нам часто приходится сталкиваться с проблемой, что мы хотим знать то, чего мы не знаем (например, вырастут или упадут акции XYZ завтра и насколько). Население по сравнению с выборкойОсновная задача статистического вывода (или оценки или прогнозирования) состоит в том, чтобы составить мнение о чем-то, используя только неполную выборку данных . В статистике очень важно различать популяция и выборка . Совокупность определяется как все члены (например, случаи, цены, годовые доходы) определенной группы. Популяция – это вся группа. Выборка — это часть совокупности , которая используется для описания характеристик (например, среднего значения или стандартного отклонения) всей совокупности. Население в сравнении с выборочной дисперсией и стандартным отклонениемПри расчете дисперсии и стандартного отклонения важно знать, рассчитываем ли мы их для всего населения, используя все данные, или мы вычисляем их, используя только выборку данных. В первом случае мы называем их дисперсией населения и стандартным отклонением населения . Во втором случае мы называем их выборочной дисперсией и выборочным стандартным отклонением . Пример 1. Дисперсия генеральной совокупности и стандартное отклонениеВопрос: Каково стандартное отклонение прошлогодней доходности 12 фондов, в которые я инвестировал? В этой задаче нет оценки или прогнозирования. Меня интересуют только 12 фондов, в которые я инвестировал, и меня не интересуют тысячи других фондов, существующих в мире. Моя популяция состоит только из этих 12 фондов. Я беру показатели каждого из 12 фондов за последний год, вычисляю среднее значение, затем отклонения от среднего, возвожу отклонения в квадрат, суммирую квадраты отклонений, делю на 12 (количество фондов) и получаю дисперсия. Тогда квадратный корень из дисперсии является стандартным отклонением. В этом случае, поскольку у меня есть данные по всему населению, я называю их 9.0007 дисперсия населения и стандартное отклонение населения . Пример 2: Выборочное отклонение и стандартное отклонениеВопрос: Каково стандартное отклонение доходности фондов акций за прошлый год в мире? По сравнению с расчетом стандартного отклонения конкретно указанных 12 фондов, теперь я хочу узнать стандартное отклонение доходности всех фондов акций в мире. Моя популяция теперь намного больше, чем в предыдущем примере. В отличие от предыдущего примера, теперь у меня нет всех доступных данных и мне придется оценить стандартное отклонение совокупности из выборки . Оценка стандартного отклонения совокупности от выборки Итак, как мне это сделать? Я попытаюсь собрать данные для некоторых фондов акций — эти фонды будут моей выборкой . Нет необходимости (и, вероятно, невозможно) собирать данные по всем фондам в мире (населению). Я должен только убедиться, что моя выборка достаточно велика. В то время как данных по 5 фондам, вероятно, будет недостаточно для оценки стандартного отклонения для всего населения, данных по 100 фондам может быть достаточно, и они все еще очень реалистичны. Взяв данные по этим 100 фондам, я рассчитываю дисперсию и стандартное отклонение так же, как в примере 1 для моих 12 фондов. Разница в расчетах: совокупность и выборочная дисперсияВ расчете дисперсии есть только одна маленькая разница, и она находится в самом конце. Как для генеральной совокупности, так и для выборочной дисперсии я вычисляю среднее значение, затем отклонения от среднего, а затем возношу все отклонения в квадрат. Суммирую все квадраты отклонений. До сих пор это было одинаково как для генеральной совокупности, так и для выборочной дисперсии. Когда я вычисляю дисперсию совокупности , я затем делю сумму квадратов отклонений от среднего на количество элементов в совокупности (в примере 1 я делил на 12). Когда я вычисляю дисперсию выборки , я делю ее на количество элементов в выборке минус один . В нашем примере 2 я делю на 99 (100 минус 1). В результате рассчитанная выборочная дисперсия (и, следовательно, стандартное отклонение) будет несколько выше, чем если бы мы использовали формулу дисперсии генеральной совокупности. Цель этой небольшой разницы — получить более точную и объективную оценку дисперсии генеральной совокупности (разделив на размер выборки, уменьшенный на единицу, мы компенсируем тот факт, что работаем только с выборкой, а не со всей совокупностью). ). В руководстве по расчету дисперсии и стандартного отклонения мы рассчитывали совокупность дисперсию и стандартное отклонение. Для выборки дисперсии и стандартного отклонения единственная разница заключается в шаге 4, где мы теперь делим на количество элементов минус один. ФормулыДисперсия генеральной совокупностиСтандартное отклонение генеральной совокупностиДисперсия выборкиСтандартное отклонение выборкиРасчет дисперсии и стандартного отклонения в Excel В Excel дисперсию и стандартное отклонение можно легко рассчитать с помощью встроенных функций: VAR. Вычисление дисперсии и стандартного отклонения в PythonВведениеДве тесно связанные статистические меры позволят нам получить представление о разбросе или дисперсии наших данных. Первая мера — это дисперсия , которая измеряет, насколько далеки от их среднего значения отдельные наблюдения в наших данных. Второе — стандартное отклонение , которое представляет собой квадратный корень из дисперсии и измеряет величину вариации или дисперсии набора данных. В этом уроке мы узнаем, как рассчитать дисперсию и стандартное отклонение в Python. Сначала мы напишем функцию Python для каждой меры, а позже узнаем, как использовать функцию Python 9. Обладая этими знаниями, мы сможем сначала взглянуть на наши наборы данных и получить представление об общем разбросе наших данных. Расчет дисперсииВ статистике дисперсия является мерой того, насколько отдельные (числовые) значения в наборе данных отличаются от среднего или среднего значения. Дисперсия часто используется для количественной оценки распространения или дисперсии. Разброс — это характеристика выборки или генеральной совокупности, которая описывает степень изменчивости в ней. Высокая дисперсия говорит нам о том, что значения в нашем наборе данных далеки от их среднего значения. Таким образом, наши данные будут иметь высокий уровень изменчивости. С другой стороны, низкая дисперсия говорит нам о том, что значения довольно близки к среднему. В этом случае данные будут иметь низкий уровень изменчивости. Чтобы вычислить дисперсию в наборе данных, нам сначала нужно найти разницу между каждым отдельным значением и средним значением. В этом уравнении x i обозначают отдельные значения или наблюдения в наборе данных. μ означает среднее значение этих значений. n — количество значений в наборе данных. Член x i — μ называется отклонением от среднего . Итак, дисперсия — это среднее квадратичных отклонений. Вот почему мы обозначили его как σ 2 . Допустим, у нас есть набор данных [3, 5, 2, 7, 1, 3]. Чтобы найти его дисперсию, нам нужно вычислить среднее значение, которое равно: 92 = 23,5 Чтобы найти дисперсию, нам просто нужно разделить этот результат на количество наблюдений следующим образом: $$ Вот и все. Дисперсия наших данных составляет 3,6667 . Например, если наблюдения в нашем наборе данных измеряются в фунтах, то дисперсия будет измеряться в квадратных фунтах. Таким образом, мы можем сказать, что наблюдения в среднем составляют 3,6667 квадратных фунтов далеко от среднего 3,5. К счастью, стандартное отклонение решает эту проблему, но это тема следующего раздела. Если мы применим концепцию дисперсии к набору данных, то мы сможем различить выборочную дисперсию и дисперсию генеральной совокупности . Дисперсия населения — это дисперсия, которую мы видели ранее, и мы можем рассчитать ее, используя данные всей совокупности и выражение для σ 2 92}} Это выражение очень похоже на выражение для вычисления σ 2 , но в этом случае x i представляет отдельные наблюдения в выборке, а X является средним значением образец. S 2 обычно используется для оценки дисперсии совокупности ( σ 2 ) с использованием выборки данных. Однако S 2 систематически занижает дисперсию генеральной совокупности. По этой причине он упоминается как 92}} Это очень похоже на предыдущее выражение. Это похоже на квадрат отклонения от среднего, но в данном случае мы делим на n — 1 вместо n . Это называется поправкой Бесселя. Поправка Бесселя показывает, что S 2 n-1 является наилучшей объективной оценкой дисперсии генеральной совокупности. Итак, на практике мы будем использовать это уравнение для оценки дисперсии совокупности с использованием выборки данных. Обратите внимание, что S 2 n-1 также известна как дисперсия с n — 1 степенями свободы. Теперь, когда мы научились вычислять дисперсию с помощью математического выражения, пришло время приступить к действию и вычислить дисперсию с помощью Python. Кодирование функции variance() в Python Чтобы вычислить дисперсию, мы напишем функцию Python с именем Вот возможная реализация для >>> def variance(data): ... # Количество наблюдений ... n = длина (данные) ... # Среднее значение данных ... среднее значение = сумма (данные) / n ... # Квадратные отклонения ... отклонения = [(x - среднее) ** 2 для x в данных] ... # Дисперсия ... дисперсия = сумма (отклонения) / n ... дисперсия возврата ... >>> дисперсия([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 5,76 Сначала мы вычисляем количество наблюдений ( Следующим шагом является вычисление квадратичных отклонений от среднего значения. Для этого мы используем Наконец, мы вычисляем дисперсию, суммируя отклонения и разделив их на количество наблюдений В этом случае Мы можем реорганизовать нашу функцию, чтобы сделать ее более лаконичной и эффективной. Вот пример: >>> дисперсия по определению (данные, ddof=0): . В этом случае мы удаляем некоторые промежуточные шаги и временные переменные, такие как Обратите внимание, что эта реализация принимает второй аргумент с именем Использование Python pvariance() и variance() Python включает стандартный модуль Вот как работает Python >>> статистика импорта >>>statistics.pvariance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 5.760000000000001 Нам просто нужно импортировать С другой стороны, мы можем использовать Python >>> статистика импорта >>>statistics.variance([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 6.4 Это выборочная дисперсия S 2 . Низкие значения стандартного отклонения говорят нам о том, что отдельные значения ближе к среднему. С другой стороны, высокие значения говорят нам о том, что отдельные наблюдения далеки от среднего значения данных. Значения, находящиеся в пределах одного стандартного отклонения от среднего, можно считать довольно типичными, тогда как значения, отличающиеся на три и более стандартных отклонения от среднего, можно считать гораздо более нетипичными. Они также известны как выбросы . В отличие от дисперсии, стандартное отклонение будет выражено в тех же единицах, что и исходные наблюдения. Таким образом, стандартное отклонение является более значимой и понятной статистикой. Если вернуться к нашему примеру, если наблюдения выражены в фунтах, то стандартное отклонение также будет выражено в фунтах. Кодирование функции stdev() в Python Чтобы вычислить стандартное отклонение набора данных, мы будем полагаться на нашу >>> import math >>> # Мы опираемся на нашу предыдущую реализацию для дисперсии >>> отклонение по определению (данные, ddof=0): ... n = длина (данные) ... среднее значение = сумма (данные) / n ... вернуть сумму ((x - среднее значение) ** 2 для x в данных) / (n - ddof) ... >>> деф stdev(данные): ... var = дисперсия (данные) ... std_dev = math.sqrt(var) ... вернуть std_dev >>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 2,4 Наша функция Если мы хотим использовать >>> def stdev(data, ddof=0): ... вернуть math.sqrt (дисперсия (данные, ddof)) >>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 2,4 >>> stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5], ddof=1) 2,5298221281347035 С этой новой реализацией мы можем использовать Использование pstdev() и stdev() Python Модуль статистики Python Вот как работают эти функции: >>> статистика импорта >>>statistics.pstdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 2.4000000000000004 >>>statistics.stdev([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 2,5298221281347035 Сначала нам нужно импортировать модуль Если у нас нет данных для всего населения, что является распространенным сценарием, мы можем использовать выборку данных и использовать |

 2(075.8)
2(075.8)
 М. ХАХИНА
М. ХАХИНА Формулы Бейеса
Формулы Бейеса Формулировка центральной предельной теоремы
Формулировка центральной предельной теоремы Корреляционный момент. Коэффициент корреляции
Корреляционный момент. Коэффициент корреляции Репрезентативная выборка
Репрезентативная выборка
 Однако данное расхождение в терминологии следует учитывать.
Однако данное расхождение в терминологии следует учитывать. ']
x = sp.linspace(0, 5, 101)[1:]
ax = None
for (d1, d2, ls) in zip(d1_values, d2_values, linestyles):
dist = stats.f(d1, d2, mu)
df = pd.DataFrame( {0:x, 1:dist.pdf(x)} )
ax = df.plot(0, 1, ls=ls,
label=r'$d_1=%i,\ d_2=%i$' % (d1,d2), ax=ax)
plt.xlabel('$x$\nF-статистика')
plt.ylabel('Плотность вероятности \n$p(x|d_1, d_2)$')
plt.show()
']
x = sp.linspace(0, 5, 101)[1:]
ax = None
for (d1, d2, ls) in zip(d1_values, d2_values, linestyles):
dist = stats.f(d1, d2, mu)
df = pd.DataFrame( {0:x, 1:dist.pdf(x)} )
ax = df.plot(0, 1, ls=ls,
label=r'$d_1=%i,\ d_2=%i$' % (d1,d2), ax=ax)
plt.xlabel('$x$\nF-статистика')
plt.ylabel('Плотность вероятности \n$p(x|d_1, d_2)$')
plt.show() f.sf(f_stat, df1, df2)
def ex_2_24():
'''Проверка вариантов дизайна веб-сайта на основе F-теста'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
return f_test(groups)
f.sf(f_stat, df1, df2)
def ex_2_24():
'''Проверка вариантов дизайна веб-сайта на основе F-теста'''
df = load_data('multiple-sites.tsv')
groups = df.groupby('site')['dwell-time']
return f_test(groups) tsv')
df.boxplot(by='site', showmeans=True)
plt.xlabel('Номер дизайна веб-сайта')
plt.ylabel('Время пребывания, сек.')
plt.title('')
plt.suptitle('')
plt.show()
tsv')
df.boxplot(by='site', showmeans=True)
plt.xlabel('Номер дизайна веб-сайта')
plt.ylabel('Время пребывания, сек.')
plt.title('')
plt.suptitle('')
plt.show() get_group(0)
site_10 = groups.get_group(10)
_, p_val = stats.ttest_ind(site_0, site_10, equal_var=False)
return p_val
get_group(0)
site_10 = groups.get_group(10)
_, p_val = stats.ttest_ind(site_0, site_10, equal_var=False)
return p_val tsv')
groups = df.groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(6)
return (b.mean() - a.mean()) / pooled_standard_deviation(a, b)
tsv')
groups = df.groupby('site')['dwell-time']
a = groups.get_group(0)
b = groups.get_group(6)
return (b.mean() - a.mean()) / pooled_standard_deviation(a, b)
 5.2 Визуализация графика прямоугольников и усов
5.2 Визуализация графика прямоугольников и усов Одно очень экстремальное значение может увеличить стандартное отклонение и исказить дисперсию.
Одно очень экстремальное значение может увеличить стандартное отклонение и исказить дисперсию. 6 мы заключаем, что для стандартного отклонения $\textrm{SD}(aX+b)=|a|\textrm{SD}(X)$. Мы
упомянул, что дисперсия НЕ является линейной операцией. Но есть очень важный случай, когда
дисперсия ведет себя как линейная операция, и это когда мы смотрим на сумму независимых случайных величин.
6 мы заключаем, что для стандартного отклонения $\textrm{SD}(aX+b)=|a|\textrm{SD}(X)$. Мы
упомянул, что дисперсия НЕ является линейной операцией. Но есть очень важный случай, когда
дисперсия ведет себя как линейная операция, и это когда мы смотрим на сумму независимых случайных величин. Моррисетт, доктор философии
Моррисетт, доктор философии
 Пожалуйста, обратите внимание на различия между
два, но знай, что ты будешь ТОЛЬКО использовать образцы формул для домашних заданий и экзаменов.
Пожалуйста, обратите внимание на различия между
два, но знай, что ты будешь ТОЛЬКО использовать образцы формул для домашних заданий и экзаменов. Исходные данные
Коллекция:
Исходные данные
Коллекция: 
 Обратите внимание, как
как невычислительная формула, так и вычислительная формула пришли к
точно такой же ответ. Вы можете использовать тот, который вам удобнее, чтобы
решать задачи на дисперсию на экзамене.
Обратите внимание, как
как невычислительная формула, так и вычислительная формула пришли к
точно такой же ответ. Вы можете использовать тот, который вам удобнее, чтобы
решать задачи на дисперсию на экзамене.
 673
673 5
5 23
23  Так же, как мы сделали с мерами центрального
тенденции и дисперсии, мы можем рассчитать стандартное отклонение для необработанные данные и сгруппированных частотных данных. Мы также можем рассчитать стандартное отклонение
как для населения , так и для выборки и есть два разных
формулы, которые вы можете использовать, невычислительная формула и расчетная формула . Все эти формулы рассчитываются в
точно так же, как решение дисперсии, за исключением того, что, как только вы нашли
дисперсии, вы просто берете квадратный корень из этого значения, чтобы определить стандарт
отклонение.
Так же, как мы сделали с мерами центрального
тенденции и дисперсии, мы можем рассчитать стандартное отклонение для необработанные данные и сгруппированных частотных данных. Мы также можем рассчитать стандартное отклонение
как для населения , так и для выборки и есть два разных
формулы, которые вы можете использовать, невычислительная формула и расчетная формула . Все эти формулы рассчитываются в
точно так же, как решение дисперсии, за исключением того, что, как только вы нашли
дисперсии, вы просто берете квадратный корень из этого значения, чтобы определить стандарт
отклонение.
 ОСТОРОЖНО : помните это маленькое x равно (СРЕДНЯЯ ТОЧКА — X бар )
ОСТОРОЖНО : помните это маленькое x равно (СРЕДНЯЯ ТОЧКА — X бар )  Мы рассчитываем дисперсию как среднее квадратов отклонений от среднего.
Мы рассчитываем дисперсию как среднее квадратов отклонений от среднего.

 92}{n-1}=\frac{122,4}{9}= 13,6 \text{дюймы в квадрате}s2=n−1∑(xi−xˉ)2=9122,4=13,6 дюймы в квадрате
92}{n-1}=\frac{122,4}{9}= 13,6 \text{дюймы в квадрате}s2=n−1∑(xi−xˉ)2=9122,4=13,6 дюймы в квадрате
 Ваши данные должны быть заключены в круглые скобки, поэтому, если у вас есть десять точек данных в ячейках с A1 по A10; формула будет =VAR(A1:A10).
Ваши данные должны быть заключены в круглые скобки, поэтому, если у вас есть десять точек данных в ячейках с A1 по A10; формула будет =VAR(A1:A10).

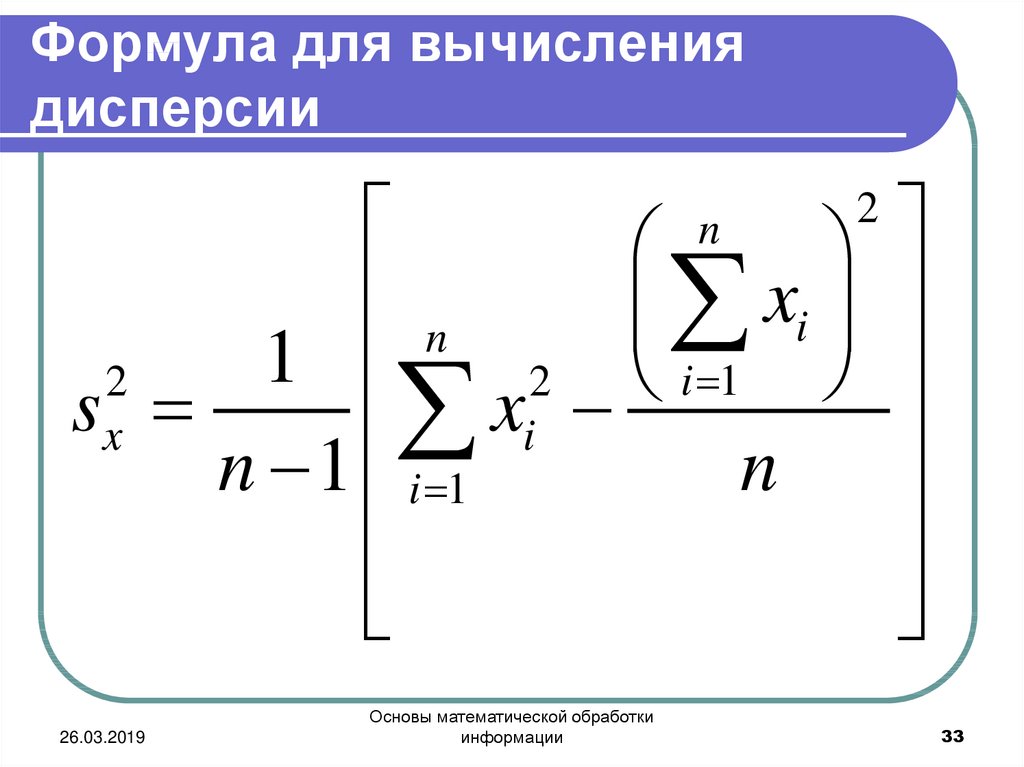
 Размер выборки может быть меньше 1%, 10% или 60% населения, но это никогда не все население.
Размер выборки может быть меньше 1%, 10% или 60% населения, но это никогда не все население.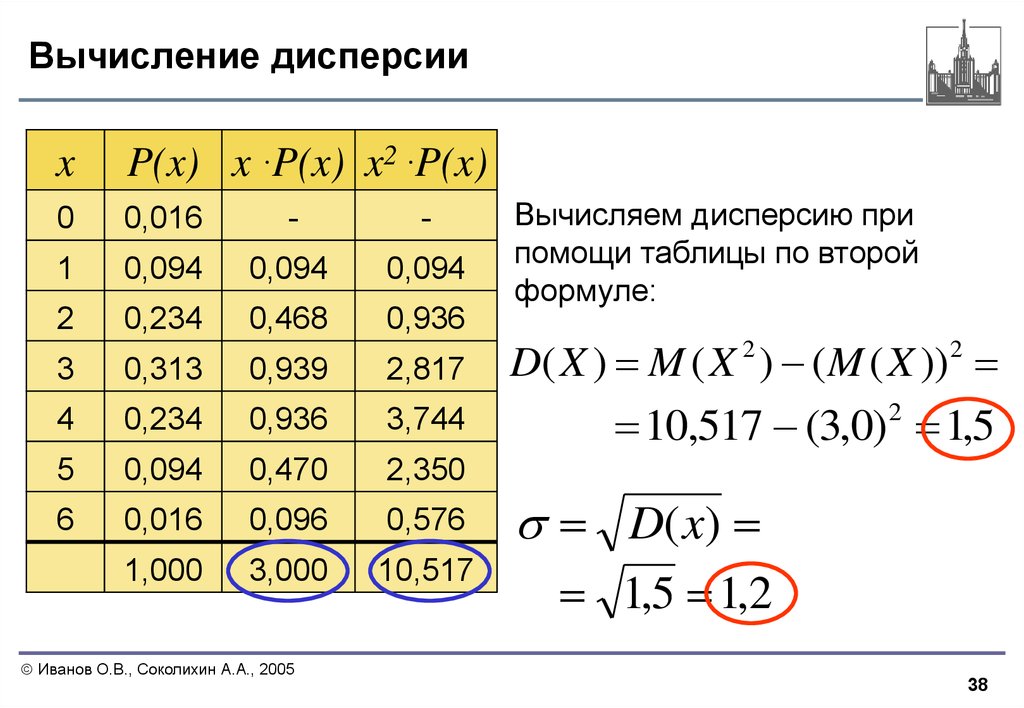 У меня есть все доступные данные , так как очень легко найти данные об эффективности этих 12 фондов.
У меня есть все доступные данные , так как очень легко найти данные об эффективности этих 12 фондов. В мире существуют тысячи фондов акций. Некоторых из них, вероятно, нет в Bloomberg, у них нет веб-сайта и они не публикуют свои результаты. Короче говоря, у меня нет шансов получить данные по всем фондам. И даже если бы я мог, это заняло бы много времени и стоило больших денег, чтобы получить все данные.
В мире существуют тысячи фондов акций. Некоторых из них, вероятно, нет в Bloomberg, у них нет веб-сайта и они не публикуют свои результаты. Короче говоря, у меня нет шансов получить данные по всем фондам. И даже если бы я мог, это заняло бы много времени и стоило больших денег, чтобы получить все данные.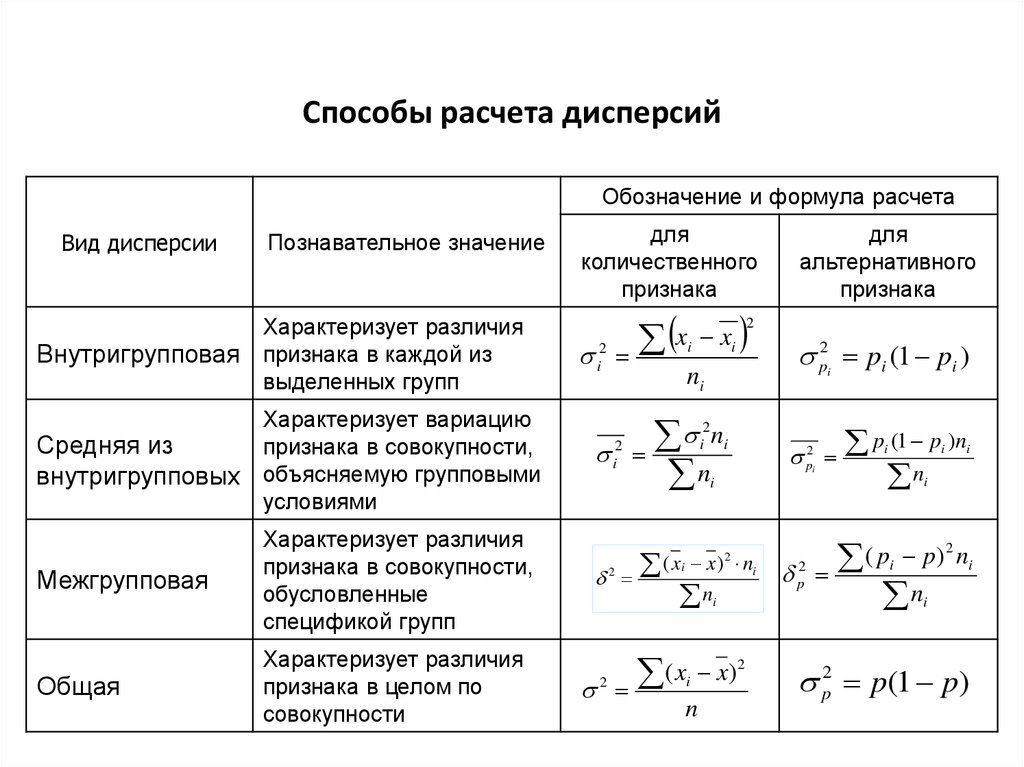

 P, VAR.S, СТАНДОТКЛОН.P и СТАНДОТКЛОН.С (конечно, вы также можете рассчитать их напрямую, используя приведенные выше формулы, если тебе нравится). Вы можете увидеть, как вычисление работает на практике (а также вычисление асимметрии, эксцесса и других показателей) в калькуляторе описательной статистики Excel.
P, VAR.S, СТАНДОТКЛОН.P и СТАНДОТКЛОН.С (конечно, вы также можете рассчитать их напрямую, используя приведенные выше формулы, если тебе нравится). Вы можете увидеть, как вычисление работает на практике (а также вычисление асимметрии, эксцесса и других показателей) в калькуляторе описательной статистики Excel. Модуль статистики 2291 для быстрого выполнения той же задачи.
Модуль статистики 2291 для быстрого выполнения той же задачи. Дисперсия представляет собой среднее значение квадратов этих разностей. Мы можем выразить дисперсию следующим математическим выражением: 92}}
Дисперсия представляет собой среднее значение квадратов этих разностей. Мы можем выразить дисперсию следующим математическим выражением: 92}}  Дисперсию трудно понять и интерпретировать, особенно насколько странными являются ее единицы.
Дисперсию трудно понять и интерпретировать, особенно насколько странными являются ее единицы.


 .. n = длина (данные)
... среднее значение = сумма (данные) / n
... вернуть сумму ((x - среднее значение) ** 2 для x в данных) / (n - ddof)
...
>>> дисперсия([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5,76
>>> дисперсия([4, 8, 6, 5, 3, 2, 8, 9, 2, 5], ddof=1)
6.4
.. n = длина (данные)
... среднее значение = сумма (данные) / n
... вернуть сумму ((x - среднее значение) ** 2 для x в данных) / (n - ddof)
...
>>> дисперсия([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5,76
>>> дисперсия([4, 8, 6, 5, 3, 2, 8, 9, 2, 5], ddof=1)
6.4
 В этом случае
В этом случае  Таким образом, результатом использования Python
Таким образом, результатом использования Python  92_{n-1}}
92_{n-1}}  Для этого мы полагаемся на нашу предыдущую функцию
Для этого мы полагаемся на нашу предыдущую функцию