Дисперсия случайной величины: Дисперсия случайной величины, дисперсия что это такое

Теория вероятностей

Теория вероятностей

Вентцель Е.С. Теория вероятностей: Учеб. для вузов. — 6-е изд. стер. — М.: Высш. шк., 1999.— 576 c. Книга представляет собой один из наиболее известных учебников по теории вероятностей и предназначена для лиц, знакомых с высшей математикой и интересующихся техническими приложениями теории вероятностей. Она представляет также интерес для всех тех, кто применяет теорию вероятностей в своей практической деятельности. В книге уделено большое внимание различным приложениям теории вероятностей (теории вероятностных процессов, теории информации, теории массового обслуживания и др.). Оглавление Глава 1. Введение ПРЕДИСЛОВИЕ 1. 1. Предмет теории вероятностей Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2.4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5. 4. Плотность распределения 5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5.9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8. Системы случайных величин 8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений. Общая запись нормального закона для системы произвольного числа случайных величин Глава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10.3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин. Композиция законов распределения 12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13.1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14. 3. Доверительный интервал. Доверительная вероятность 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15. 7.2. Производная от случайной функции 15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17. 7. Эргодическое свойство стационарных случайных функций 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19. 3. Поток событий. Простейший поток и его свойства 19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19.6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона

Дисперсия случайной величины — Энциклопедия по экономике

Дисперсия .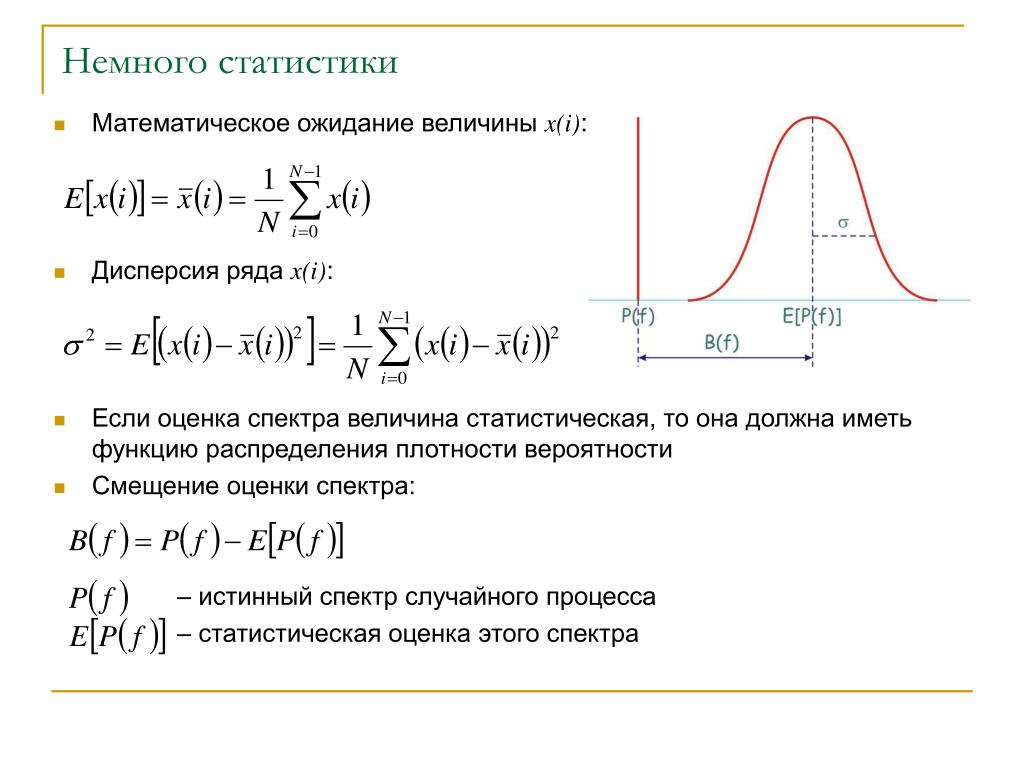 случайной величины 153  [c.391]

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от математического ожидания. При заданном законе распределения дисперсия дискретной случайной величины определяется как  [c.121]

Для дисперсии случайной величины X используется также обозначение Var(X).)  [c.27]

Свойства дисперсии случайной величины  [c.28]

Пример 2.4. Найти математическое ожидание и дисперсию случайной величины Z= Х- 5Y+ 7, если даны М(Х) = 3, M(Y) = 2, ДА) = 1,5и D(Y) = 1 и известно, что А и Y— независимые случайные величины.  [c.28]

При каком значении параметра С эта функция является плотностью распределения некоторой случайной величины Найти математическое ожидание и дисперсию случайной величины X.  [c.49]

При фиксированном f увеличение дисперсий случайных величин a(-.-( j) и bj(линейное неравенство и 2 aj.-Xj bj, имеющее структуру, аналогичную структуре основного  [c.93]

Здесь вместо математического ожидания и дисперсии случайной величины взяты ее статистические моменты. Назовем закон распределения случайной величины Я, заданной плотностью /(Я) теоретическим. Зная, закон распределения, можно найти теоретические вероятности попадания в каждый из ин-  [c.197]

Дисперсию случайной величины у = f + e в произвольной точке х можно выразить следующим образом  [c.121]

Дисперсия случайной величины у = f + е в произвольной точке t вычисляется по формуле  [c.147]

Дисперсия случайной величины, являющейся линейной комбинацией коррелированных случайных величин равна  [c.163]

Дисперсия случайной величины  [c.133]

Стандартной для расчета волатильности считается трехмесячная выборка однодневных изменений цен. Наиболее простой алгоритм оценки о следующий. После расчета среднего значения доход-ностей вычисляют отклонения от среднего хг = г — и дисперсию случайной величины г  [c.199]

D(TJ = X) — условная дисперсия случайной величины т], вычисленная при условии, что значение другой случайной величины зафиксировано на уровне X GOV( , л) » Ё[( — Е )(Л — ЕЛ) — ковариация случайных величин  [c. 456]

Статистические методы управления качеством. Распределение частоты среднего значения и дисперсии случайных величин. Термины и общие методы расчетов  [c.34]

Дисперсия погрешности на основании свойств дисперсий случайных величин  [c.73]

Большинство величин в производственных процессах и отношениях случайно, т.е. их значение невозможно предсказать абсолютно точно, но подчинено определенным законам. В связи с этим приходится иметь дело с понятиями случайной величины и ее законом распределения вероятностей, основными числовыми характеристиками распределения (математическое ожидание или среднее значение случайной величины, дисперсия случайной величины или среднее квадратическое отклонение, коэффициент вариации).  [c.249]

Из этого определения следует, что дисперсия случайной величины X вычисляется по формуле  [c.193]

Наряду с дисперсией случайной величины, в качестве характеристики рассеивания случайной величины используется среднее квадратическое отклонение, которое равно положительному значению корня квадратного из дисперсий.  [c.16]

Дисперсия случайной величины X, имеющей показательное распределение, равна  [c.32]

Дисперсия случайной величины X, имеющей равномерное распределение на участке [а, Ь], вычисляется по формуле  [c.34]

Двойственная задача 238 Двойственные оценки 247 Дисперсия случайной величины  [c.424]

Для практического расчета дисперсии случайных величин часто бывает удобно использовать следующую формулу  [c.263]

Отсюда дисперсия случайной величины а(т, ) определяется формулой  [c.191]

Распределение Пуассона зависит от одного параметра а. Для случайной величины распределенной по закону Пуассона M[X]=D[X]=a, где М — математическое ожидание, D — дисперсия случайной величины X.  [c.152]

Напомним, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений я, а на число степеней свободы (degress of freedom) я — т, равное разности между числом независимых наблюдений случайной величины п и числом связей, ограничивающих свободу их изменения, т. е. число т уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (3.26) стоит число степеней свободы п — 2, так как две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений (3.5).  [c.62]

Здесь ац и я,у (о>) — соответственно, детерминированный и случайный коэффициенты матрицы условий bjubi(u>) -детерминированная испуганная компоненты вектора ограничений шел — случайный параметр 5″,- и в»,у — математическое ожидание случайных величин и,- (и>) и а,у (о>) у/ — вероятность выполнения г -го условия Ф»1 (7г-) — обратная функция нормального распределения о — — дисперсия случайной величины в,у (и ) f — дисперсия случайной величины 1ц (ш) лу — интенсивность /-го способа производства.  [c.18]

КОЭФФИЦИЕНТ ВАРИАЦИИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [variation oeffi ient] — мера относительного разброса случайной величины показывает, какую долю среднего значения этой величины составляет ее средний разброс. Вычисляется по формуле квадратный корень из дисперсии случайной величины (стандартное отклонение), деленный на ее математическое ожидание  [c. 157]

Определенные соотношениями (1.8) и (1.8 ) соответственно теоретический и выборочный коэффициенты корреляции могут быть формально вычислены для любой двумерной системы наблюдений они являются измерителями степени тесно- ты линейной статистической связи между анализируемыми признаками. Однако только в случае совместной нормальной рас-пределенности исследуемых случайных величин и ц коэффициент корреляции г имеет четкий смысл как характеристика степени тесноты связи между ними. В частности, в этом, случае соотношение г — 1 подтверждает чисто функциональную линейную зависимость между исследуемыми величинами, а уравнение г = 0 свидетельствует об их полной взаимной независимости. Кроме того, коэффициент корреляции вместе со средними и дисперсиями случайных величин и TJ составляет те пять параметров, которые дают исчерпывающие сведения о стохастической зависимости исследуемых величин, так как однозначно определяют их двумерный закон распределения (см. [14, с. 171, формула (6.9)]).  [c. 63]

Ол—безусловная дисперсия случайной величины т , а а%/х) —УсРеД» ненная по различным значениям X случайной величины величина условной дисперсии О(л  [c.456]

Для вычислений вероятностей Р(у = у ) ряда распределения Пуассона удобно использовать функцию ПУАССОН(х среднее …) пакета Mi rosoft Ex el. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны между собой ШУ = Dy = а. График вероятностного ряда распределения Пуассона для среднего значения а=1,7 представлен на рис. 7.5.  [c.250]

3.7: Дисперсия дискретных случайных величин

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4373

• Кристин Кутер
• Колледж Святой Марии
92],\notag$$
, где \(\mu\) обозначает ожидаемое значение \(X\). Стандартное отклонение для \(X\) равно
$$\sigma = \text{SD}(X) = \sqrt{\text{Var}(X)}.\notag$$

Проще говоря, дисперсия случайной величины — это среднее квадратов отклонений случайной величины от ее среднего значения (ожидаемого значения). Обратите внимание, что дисперсия случайной величины будет равна числу с квадратами единиц, но стандартное отклонение будет иметь те же единицы измерения, что и случайная величина. Таким образом, стандартное отклонение легче интерпретировать, поэтому мы уделяем особое внимание его определению.

Дисперсия и стандартное отклонение дают нам меру разброса случайных величин. Стандартное отклонение интерпретируется как мера того, насколько «разбросаны» возможные значения \(X\) относительно среднего значения \(X\), \(\mu = \text{E}[X] \).

Пример \(\PageIndex{1}\)

Рассмотрим две случайные величины \(X_1\) и \(X_2\), функции вероятностной массы которых представлены гистограммами на рисунке 1 ниже. Обратите внимание, что \(X_1\) и \(X_2\) имеют одно и то же среднее значение. Однако, глядя на гистограммы, мы видим, что возможные значения \(X_2\) более «разбросаны» от среднего значения, что указывает на то, что дисперсия (и стандартное отклонение) \(X_2\) больше.

Рисунок 1: Гистограммы для случайных величин \(X_1\) и \(X_2\), обе с одинаковым математическим ожиданием и разной дисперсией.

---

Теорема 3.6.1 на самом деле говорит нам, как вычислить дисперсию, поскольку она получается путем нахождения ожидаемого значения функции , примененной к случайной величине. Во-первых, если \(X\) является дискретной случайной величиной с возможными значениями \(x_1, x_2, \ldots, x_i, \ldots\) и функцией массы вероятности \(p(x)\), то дисперсия \ (X\) определяется как 92 = 1,5 — 1 = 0,5 \\
\Стрелка вправо\ \text{SD}(X) &= \sqrt{\text{Var}(X)} = \sqrt{0,5} \приблизительно 0,707
\end{align* }

---

Упражнение \(\PageIndex{1}\)

Рассмотрим контекст примера 3. 6.2, где мы определили случайную величину \(X\) как наш выигрыш в одной игре, включающей подбрасывание ярмарки монета трижды. Мы обнаружили, что \(\text{E}[X] = 1,25\). Теперь найдите дисперсию и стандартное отклонение \(X\).

Ответить

92 = 1,1875 \\
\стрелка вправо \text{SD}(X) &= \sqrt{1,1875} \приблизительно 1,0897
\end{align*}

Учитывая, что дисперсия случайной величины определяется как ожидаемое значение в квадрате отклонений от среднего значения, дисперсия не является линейной, как ожидаемое значение. Однако у нас есть следующее полезное свойство дисперсии.

Теорема \(\PageIndex{2}\)

Пусть \(X\) — случайная величина, а \(a, b\) — константы. Тогда верно следующее: 92\text{Var}(X)
\end{align*}

Теорема 3.7.2 легко следует из небольшой алгебраической модификации. Обратите внимание, что «\(+\ b\)» исчезает в формуле. Для этого есть интуитивная причина. А именно, «\(+\ b\)» соответствует сдвигу по горизонтали вероятностной массы функция для случайной величины. Такое преобразование этой функции не повлияет на спред , т. е. дисперсия не изменится.

Как и в случае ожидаемых значений, для многих распространенных распределений вероятностей дисперсия задается параметром или функцией параметров распределения.

Разница для дискретных распределений

Распределение	Разница
Бернулли(\(р\))	\(р(1-р)\)
биномиальный(\(п, р\))	\(нп(1-р)\)
гипергеометрический(\(N, n, m\))	\(\frac{n(m/N)(1 — m/N)(N-n)}{N-1}\) 92}\)
Пуассон(\(\лямбда\))	\(\лямбда\)

---

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Кристин Кутер

   Показать оглавление

   да

2. Теги

   На этой странице нет тегов.

Объяснение урока: Дисперсия дискретных случайных величин

В этом объяснении мы узнаем, как рассчитать дисперсию дискретных случайных величин.

Чтобы найти дисперсию дискретной случайной величины, полезно вспомним, что такое дискретная случайная величина .

Определение: Дискретная случайная величина

Дискретная случайная величина — это переменная, которая может принимать только счетное количество числовых значений. Значение, которое принимает переменная, равно определяется результатом случайного явления или эксперимента. Такая переменная часто обозначается заглавной 𝑋 со значением, которое переменная принимает обозначение в нижнем регистре 𝑥.

Чтобы представить дискретную случайную величину , мы можем использовать вероятность функция распределения . Это функция, отображающая значения дискретного случайной переменной к связанным с ними вероятностям.

Определение: Функция распределения вероятностей

Функция распределения вероятностей — это функция, которая генерирует вероятности значения 𝑓(𝑥) учитывая результат значения 𝑥 и должен удерживать следующие свойства:

• 𝑓(𝑥)=1 для всех значений 𝑥 может принимать случайная величина,
• каждое значение 𝑓(𝑥) должно лежать в интервале [0,1].

Мы можем представить функцию распределения вероятностей многими способами, включая таблица в виде 𝑃(𝑋=𝑥)=𝑝 или в виде формулы, связывающей 𝑥 и 𝑓(𝑥).

Определение: дисперсия дискретной случайной величины

дисперсия дискретной случайной величины 𝑋 является мерой степени которых значения переменной отличаются от ожидаемого значения 𝜇. Мы обозначаем это как Вар(𝑋)=𝜎, где 𝜎 — стандартное отклонение распределения.

Это можно найти по следующей формуле: Вар(𝑋)=𝐸(𝑋−𝜇), где 𝜇=𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥)) ожидаемое значение 𝑋 и 𝑥 представляет все значения 𝑋 может принимать.

Формулу дисперсии 𝑋 можно расширить, чтобы получить VarsinceVar(𝑋)=𝐸(𝑋−𝜇)=𝐸𝑋−2𝑋𝜇+𝜇=𝐸𝑋−2𝑋×𝐸(𝑋)+𝐸(𝑋)(𝜇=𝐸(𝑋))= 𝑋−𝐸[2𝑋×𝐸(𝑋)]+𝐸𝐸(𝑋)=𝐸𝑋−2𝐸(𝑋)×𝐸(𝑋)+𝐸(𝑋)(𝐸[𝐸(𝑋)]=𝐸 (𝑋))=𝐸𝑋−2𝐸(𝑋)+𝐸(𝑋)(𝑋)=𝐸𝑋−𝐸(𝑋), где 𝐸𝑋=𝑥×𝑃(𝑋=𝑥) и 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥)).

При расчете дисперсии дискретной случайной величины проще использовать форму Var(𝑋)=𝐸𝑋−𝐸(𝑋); однако, в следующем примере мы будем использовать и эту версию, и форму Var(𝑋)=𝐸(𝑋−𝜇), чтобы продемонстрировать, как их применять.

Пример 1. Нахождение дисперсии дискретной случайной величины по таблице

Функция в данной таблице является функцией вероятности дискретная случайная величина 𝑋. Найдите дисперсию 𝑋. При необходимости дайте ответ с точностью до двух знаков после запятой.

𝑥	3	5	7	8
𝑓(𝑥)	2𝐴	5𝐴	5𝐴	𝐴

Answer

Во-первых, нам нужно найти значение 𝐴 в таблице. Напомним, что для дискретная случайная величина, 𝑓(𝑥)=1. Поэтому мы можем использовать этот факт, чтобы найти значение 𝐴: 2𝐴+5𝐴+5𝐴+𝐴=110𝐴+3𝐴−1=0(5𝐴−1)(2𝐴+1)=0∴5𝐴−1=02𝐴+1=05𝐴=12𝐴=−1𝐴=15𝐴=−12. ужас

Поскольку каждое значение 𝑓(𝑥) должно лежать в интервал [0,1], мы нужно проверить, какое значение или значения 𝐴 являются допустимыми решениями.

Если 𝐴=15, то подставив в выражение для 𝑓(𝑥) получаем следующее.

𝑥	3	. 15=525=15	15

Мы видим, что каждое значение 𝑓(𝑥) лежит в интервале [0,1]; поэтому, 𝐴=15 является допустимым решением.

Если 𝐴=−12, то подставив в выражение для 𝑓(𝑥) получаем следующее.

𝑥	3	.	5×−12=54	−12

Мы видим, что хотя бы одно из значений 𝑓(𝑥) делает не лежать в интервале [0,1]; поэтому, 𝐴=−12 не является допустимым решением.

Обратите внимание, что в этом случае ни одно из значений не попало в интервал [0,1], но если хотя бы одно значение находится вне этого интервала, то оно не может быть допустимая функция распределения вероятностей.

Теперь найдем дисперсию по формуле Var(𝑋)=𝐸𝑋−𝐸(𝑋), где 𝐸𝑋=𝑥×𝑃(𝑋=𝑥) и 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥)). Поэтому мы используем значения в таблице для расчета Var(𝑋). Обратите внимание, что 𝑃(𝑋=𝑥) относится к значению 𝑓(𝑥), соответствующее значению 𝑥.

𝑥	3	5	7	8
𝑓(𝑥)	25	15	15	15

To calculate Var(𝑋) in этом случае полезно сначала вычислить 𝐸(𝑋) и 𝐸𝑋 отдельно.

Для 𝐸(𝑋), 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥))=3×25+5×15+7×15+8×15=65+55+75+85=265.

Для 𝐸 𝑋, 𝐸𝑋=𝑥×𝑃(𝑋=𝑥)=9×25+25×15+49×15+64×15=185+255+495+645=1565. 

Затем подставляем 𝐸(𝑋) и 𝐸𝑋 в формула: Var(𝑋)=𝐸𝑋−𝐸(𝑋)=1565−265=1565−67625=4,16.

Итак, дисперсия составляет 4,16 с точностью до 2 знаков после запятой.

В нашем предыдущем примере мы продемонстрировали, как найти дисперсию с помощью формула Var(𝑋)=𝐸𝑋−𝐸(𝑋). Теперь мы увидим, как с помощью альтернативной формы Var(𝑋)=𝐸(𝑋−𝜇) даст нам такой же результат.

Мы будем использовать значение 𝐸(𝑋)=265 которые мы вычислили ранее, а затем вычислить 𝑋−𝜇 и его квадрат для каждого значения 𝑥. Полезно добавлять строки в стол для этого.

𝑥	3	5	7	8
𝑓(𝑥)	25	15	15	15
𝑋−𝜇	3−265= −115	5−265=−15	7−265=95	8−265=145
(𝑋−𝜇)	12125	125	8125	19625

Затем мы вычисляем 𝐸(𝑋−𝜇), дисперсию, отмечая, что 𝑃(𝑋=𝑥) относится к значению 𝑓(𝑥) в таблице: Var(𝑋)=𝐸(𝑋−𝜇)=(𝑋−𝜇)×𝑃(𝑋=𝑥)=12125×25+125×15+8125×15+19625×15=242125+1125+81125+196125=4,16. 

Таким образом, дисперсия равна 4,16 с точностью до 2 знаков после запятой.

Обратите внимание, что хотя и подход в примере, и подход здесь действительны, подход в примере является рекомендуемым, поскольку меньше возможностей сделать арифметические ошибки.

В следующем примере функция распределения вероятностей представлена ​​в виде 𝑃(𝑋=𝑥)=𝑝 для дискретной случайной величины 𝑋. Снова, требуется найти дисперсию; однако на этот раз мы использовать только формулу Вар(𝑋)=𝐸𝑋−𝐸(𝑋) сделать это.

Пример 2. Нахождение дисперсии дискретной случайной величины

Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения 2, 3, 5 и 8. Учитывая, что 𝑃(𝑋=2)=124, 𝑃(𝑋=3)=512, 𝑃(𝑋=5)=38, и 𝑃(𝑋=8)=16, найдите дисперсию 𝑋. Дайте ответ с точностью до двух знаков после запятой.

Ответ

Чтобы вычислить дисперсию дискретной случайной величины, мы можем использовать формулу Var(𝑋)=𝐸𝑋−𝐸(𝑋). 

Полезно вычислить 𝐸(𝑋) и 𝐸𝑋 сначала отдельно при вычислении Var(𝑋).

Для 𝐸(𝑋), 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥))=2×124+3×512+5×38+8×16=224+1512+158+86=10924.

Для 𝐸𝑋, 𝐸𝑋=𝑥×𝑃(𝑋=𝑥)=2×124+3×512+5×38+8×16=424+4512+758+646=57524.

Затем подставляем 𝐸(𝑋) и 𝐸𝑋 в формулу: Varcorrectto2decimalplaces(𝑋)=𝐸𝑋−𝐸(𝑋)=57524−10924=1919576=3,33.

Итак, дисперсия составляет 3,33 с точностью до 2 знаков после запятой.

В следующем примере мы найдем дисперсию 𝑋 при заданной вероятности функция распределения в виде 𝑓(𝑥). Подход аналогичен к тому, когда 𝑓(𝑥) представлено в таблице или в форме 𝑃(𝑋=𝑥)=𝑝, за исключением того, что нам нужно сгенерировать значения 𝑓(𝑥), оценивая функцию для заданных значений 𝑥.

Пример 3. Нахождение дисперсии дискретной случайной величины

Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения −2, −1, 𝑀 и 2. Учитывая, что 𝑋 имеет функция распределения вероятностей 𝑓(𝑥)=𝑥+416, найдите дисперсию 𝑋.

Ответ

Во-первых, поскольку у нас есть неизвестное значение 𝑀, нам нужно вычислить его. Мы знаем, что для любой функции распределения вероятностей 𝑓(𝑥)=1, поэтому мы можем использовать это, чтобы определить неизвестное значение 𝑀.

Чтобы найти выражение для 𝑓(𝑥), нам нужно подставить значения −2, −1, 𝑀 и 2 вместо 𝑥 в 𝑓(𝑥).

Когда 𝑥=−2, 𝑓(−2)=−2+416=216.

Когда 𝑥=−1, 𝑓(−1)=−1+416=316.

Когда 𝑥=𝑀, 𝑓(𝑀)=𝑀+416.

Когда 𝑥=2, 𝑓(2)=2+416=616.

Итак, чтобы найти 𝑀, составим уравнение, используя 𝑓(𝑥)=1 и решить для 𝑀: 𝑓(𝑥)=𝑓(−2)+𝑓(−1)+𝑓(𝑀)+𝑓(2)=1216+316+𝑀+416+616=12+3+𝑀+4+616=1𝑀+ 1516=1𝑀+15=16𝑀=1.

Далее мы вычисляем 𝑓(𝑀), используя 𝑀=1: 𝑓(1)=1+416=516.

Теперь, когда мы нашли 𝑀=1 и соответствующее значение 𝑓(𝑀), мы можем вычислить дисперсию 𝑋. Мы будем использовать формулу Вар(𝑋)=𝐸𝑋−𝐸(𝑋) сделать это. Обратите внимание, что 𝑃(𝑋=𝑥) относится к значению 𝑓(𝑥), соответствующее значению 𝑥.

Полезно вычислить 𝐸(𝑋) и 𝐸𝑋 сначала отдельно при вычислении Var(𝑋).

Для 𝐸(𝑋), 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥))=−2×216+−1×316+1×516+2×616=−416−316+516+1216=1016=58.

Для 𝐸𝑋, 𝐸𝑋=𝑥×𝑃(𝑋=𝑥)=(−2)×216+(−1)×316+1×516+2×616=816+316+516+2416=4016=52 .

Наконец, подставляем 𝐸(𝑋) и 𝐸𝑋 в формулу: Var(𝑋)=𝐸𝑋−𝐸(𝑋)=52−58=13564.

Итак, дисперсия равна 13564.

В следующем примере мы найдем дисперсию дискретной случайной величины в виде функции распределения вероятностей, где коэффициент функция неизвестна.

Пример 4. Нахождение дисперсии дискретной случайной величины

Пусть 𝑋 обозначает дискретную случайную величину, которая может принимать значения 3, 4 и 5. Учитывая, что 𝑓(𝑥)=𝑎𝑥12, найдите дисперсию из 𝑋. При необходимости дайте ответ с точностью до двух знаков после запятой. места.

Ответ

Сначала нам нужно найти неизвестный коэффициент вероятности функция распределения 𝑓(𝑥). чтобы сделать это, мы используем тот факт, что для 𝑓(𝑥) быть допустимая функция распределения вероятностей, тогда 𝑓(𝑥)=1.

Чтобы найти 𝑓(𝑥), мы должны сначала найти 𝑓(𝑥) для каждого значения 𝑋, который в данном случае принимает значения 3, 4 и 5.

Для 𝑥=3, 𝑓(3)=𝑎×312=3𝑎12.

Для 𝑥=4, 𝑓(4)=𝑎×412=4𝑎12.

Для 𝑥=5, 𝑓(5)=𝑎×512=5𝑎12.

Чтобы найти 𝑎, подставим в формулу 𝑓(𝑥)=1: 𝑓(𝑥)=𝑓(3)+𝑓(4)+𝑓(5)=13𝑎12+4𝑎12+5𝑎12=112𝑎12=1𝑎=1.

Далее, поскольку мы нашли значение 𝑎, мы можем определить функция распределения вероятностей 𝑓(𝑥) на заменив 𝑎: 𝑓(𝑥)=1×𝑥12=𝑥12.

Итак, для каждого значения 𝑥=3,4 и 5 имеем следующее: 𝑓(3)=312, 𝑓(4)=412, 𝑓(5)=512.

Теперь мы можем найти дисперсию дискретной случайной величины. Делаем это по формуле Var(𝑋)=𝐸𝑋−𝐸(𝑋). Обратите внимание, что 𝑃(𝑋=𝑥) относится к значению 𝑓(𝑥) соответствует значению 𝑥.

Полезно вычислить 𝐸(𝑋) и 𝐸𝑋 сначала отдельно при расчете Вар(𝑋).

Для 𝐸(𝑋), 𝐸(𝑋)=(𝑥×𝑃(𝑋=𝑥))=3×312+4×412+5×512=912+1612+2512=5012=256.

Для 𝐸𝑋, 𝐸𝑋=𝑥×𝑃(𝑋=𝑥)=3×312+4×412+5×512=2712+6412+12512=21612=18.

Наконец, подставляем 𝐸(𝑋) и 𝐸𝑋 в формулу: Varcorrectto2decimalplaces(𝑋)=𝐸𝑋−𝐸(𝑋)=18−256=0,64.

Таким образом, дисперсия составляет 0,64 с точностью до 2 знаков после запятой.

В этом объяснителе мы научились находить дисперсию дискретного случайной величиной, а также решать задачи на нахождение дисперсии, где неизвестны в функции распределения вероятностей.

No related posts.