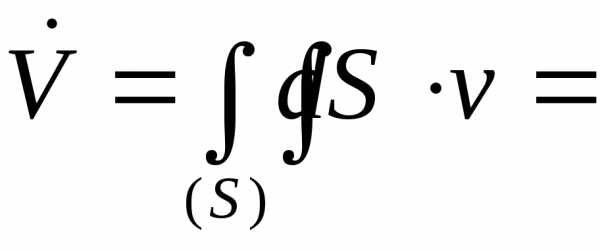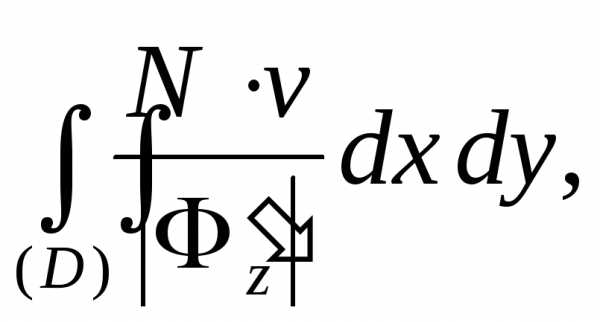Теорема о градиенте, дивергенции, роторе
Теорема.
Если область  ограничена поверхностью
ограничена поверхностью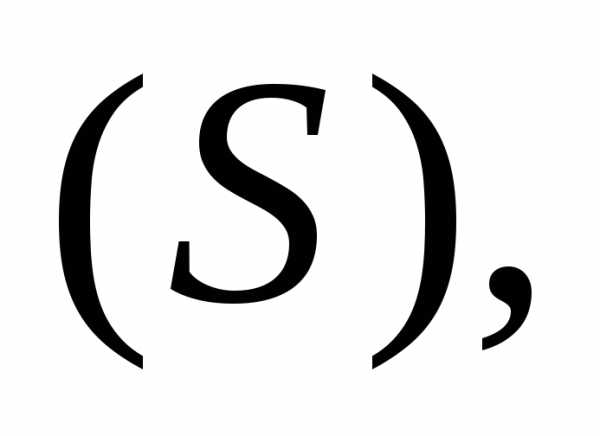 то
то
(П.4.1)
(П.4.2)
(П.4.3)
Формально эти равенства получаются сразу из определений (П.3.1)-(П.3.3). Равенство (П.4.2) называется формулой Остроградского-Гаусса.
Строгое доказательство этих формул опирается на тот факт, что поверхностные интегралы в правых частях изменяют свой знак при изменении ориентации поверхности.
5. Градиент, дивергенция и ротор в декартовых координатах
В декартовой системе координат градиент, дивергенция и ротор определяются по формулам |
(П.5.2) |
где скаляр (скалярная функция, скалярное поле), вектор (векторная функция, векторное поле) ( |
В
П.3 мы выяснили, что формулы
(П.3.1)-(П.3.3) не зависят от формы замкнутой
поверхности  ограничивающей фигуру
ограничивающей фигуру 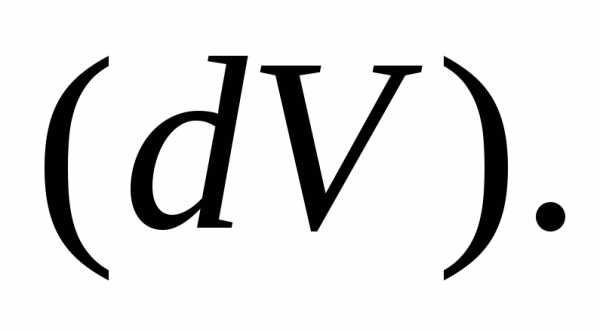
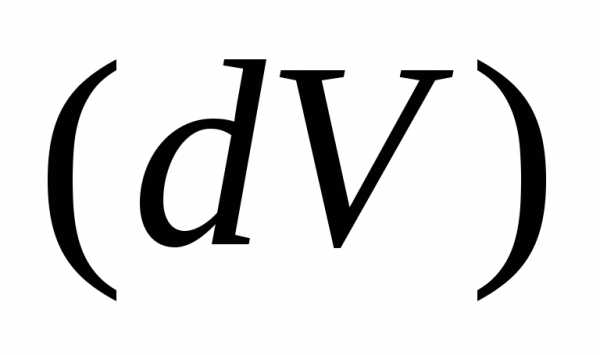 – бесконечно малый параллелепипед со
сторонами
– бесконечно малый параллелепипед со
сторонами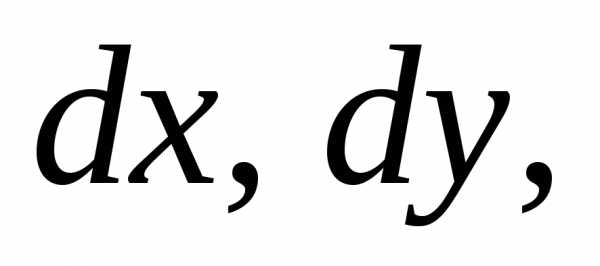
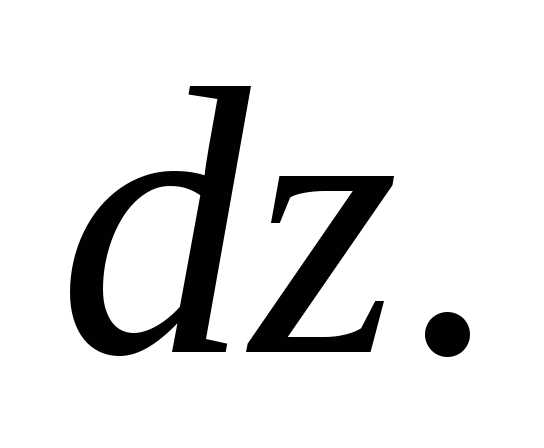 Его объём
Направим
координатные оси вдоль рёбер (рис. 5.1).
Его объём
Направим
координатные оси вдоль рёбер (рис. 5.1). Д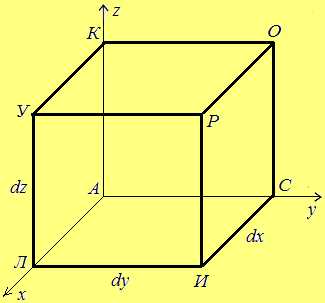 окажем
формулу (П.5.1).
окажем
формулу (П.5.1).
(П.3.1) 
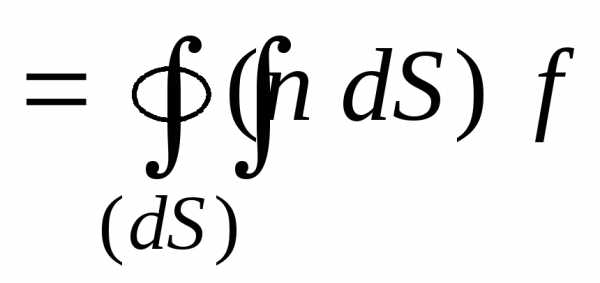 =Поверхность
=Поверхность 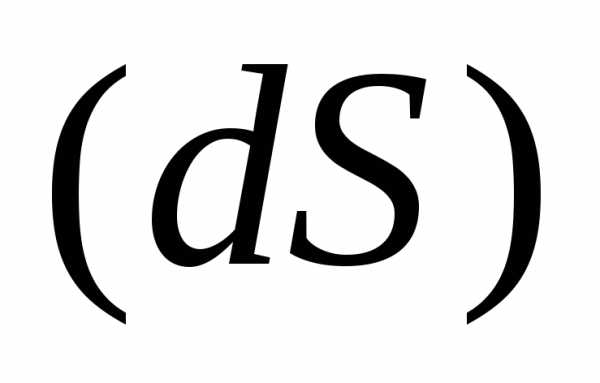 состоит из шести граней=
состоит из шести граней=
=На грани (ЛИРУЛ) имеем внеш-
ний
вектор  на противополож-
Рис.
5.1
на противополож-
Рис.
5.1
ной
грани (АСОКА)
будет 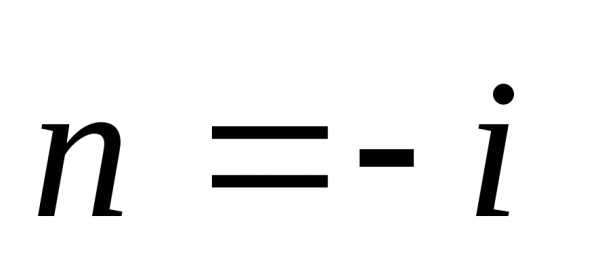
=Грань
(ЛИРУЛ)
мала, поэтому в пределах этой грани
функция  не успевает измениться. Значит, на нейАналогично, на грани (АСОКА)
будет
И т.д.=
не успевает измениться. Значит, на нейАналогично, на грани (АСОКА)
будет
И т.д.=
=Площадь
грани
(ЛИРУЛ)
равна  и равна площади грани (АСОКА).
И т.д.=
и равна площади грани (АСОКА).
И т.д.=
=При
перемещении от точки А к Л изменяется лишь координата 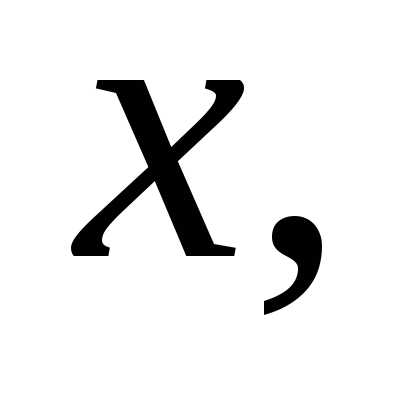 поэтому
поэтому

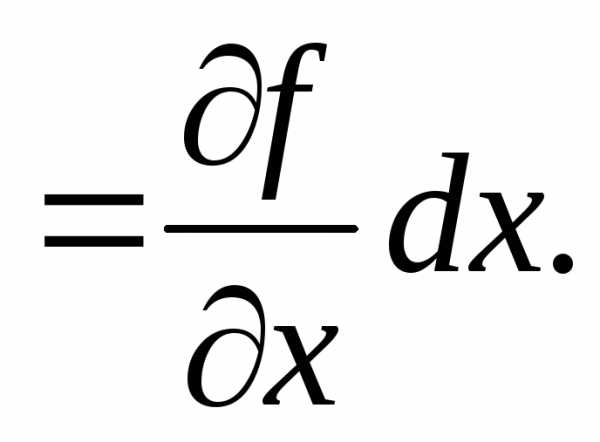 И
т.д.=
И
т.д.=
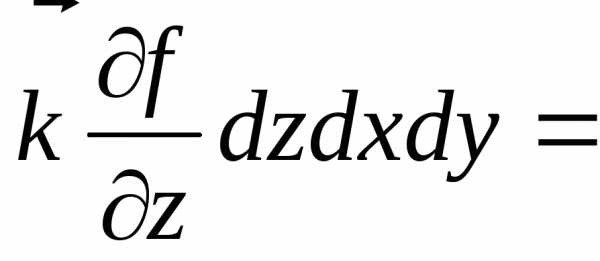
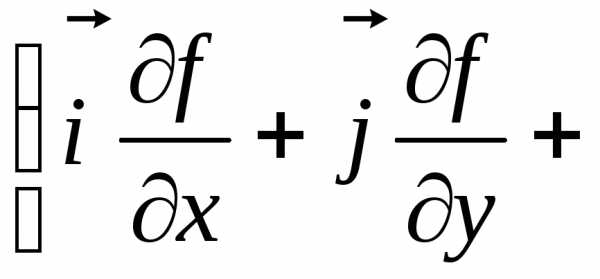
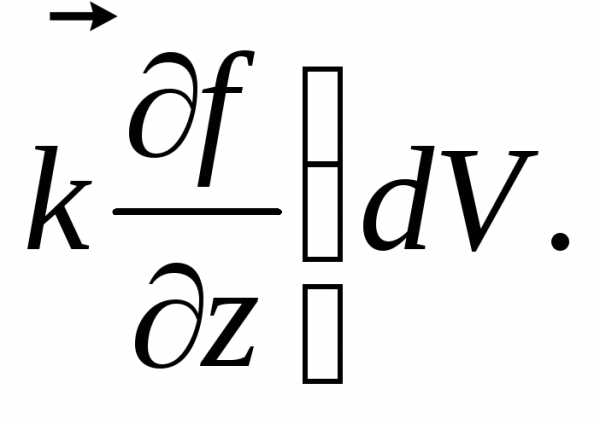
Полученное
равенство 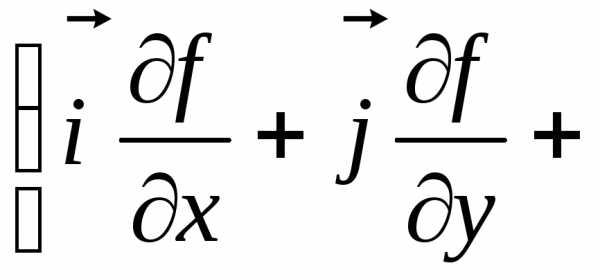
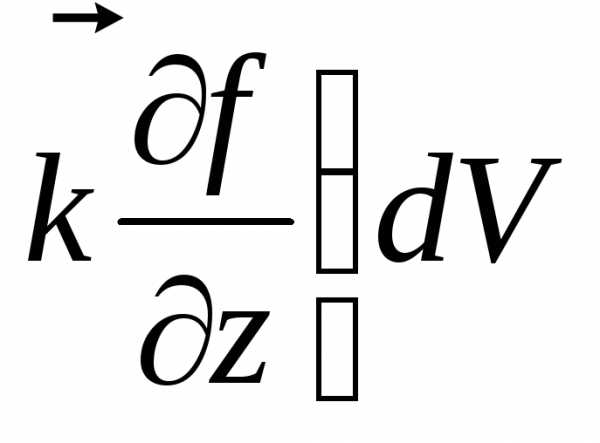 даёт
нам формулу (П.5.1).
даёт
нам формулу (П.5.1).
Остальные две формулы можно вывести таким же путём, но мы поступим иначе. Выпишем полученные равенства
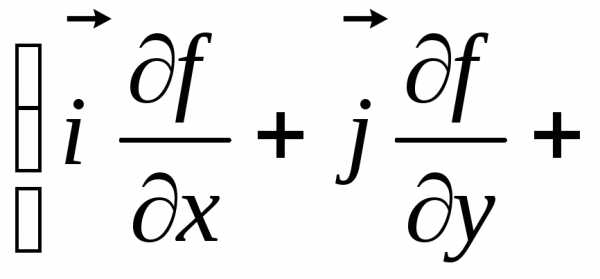
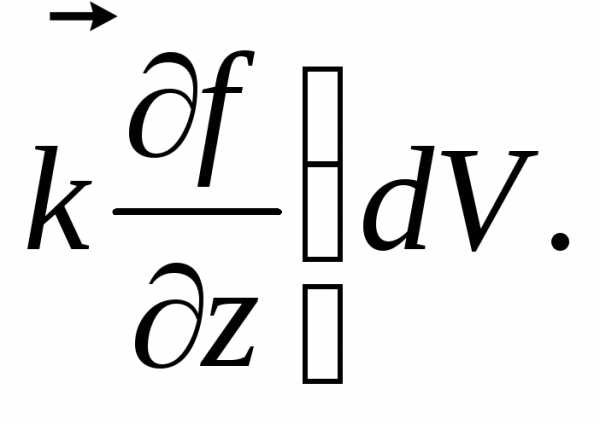 (а)
(а)
Заметим,
что в (а) вектор  заменяется
в правой части на векторы
заменяется
в правой части на векторы 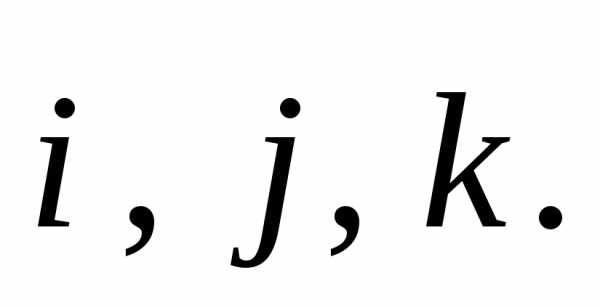
Посмотрим на определение дивергенции:
В
отличие от выражения (а) здесь присутствует
вектор 
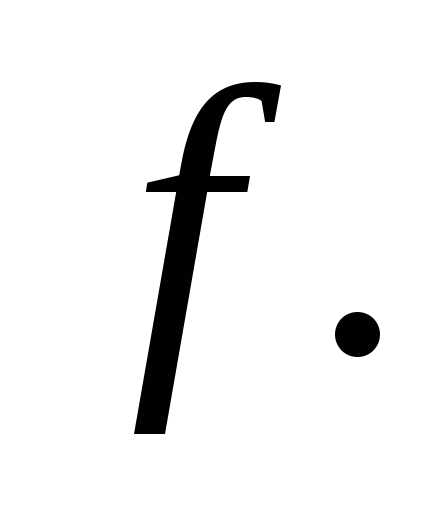 Поэтому
в (а) заменим
Поэтому
в (а) заменим  на
на  и
обычное умножение заменим на скалярное,
обозначаемое точкой. Будем иметь
и
обычное умножение заменим на скалярное,
обозначаемое точкой. Будем иметьотсюда
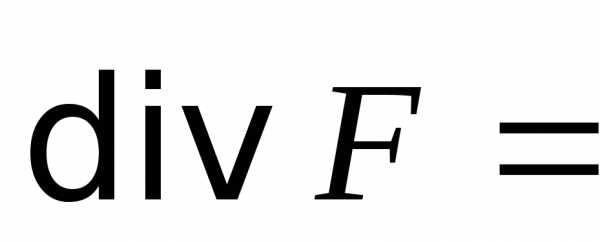
Но аналогично, 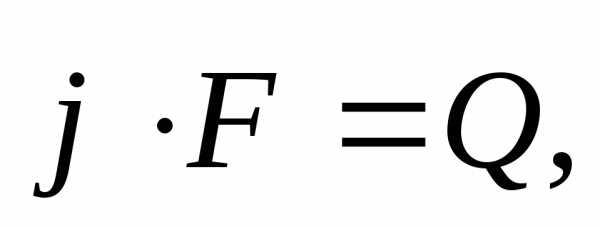
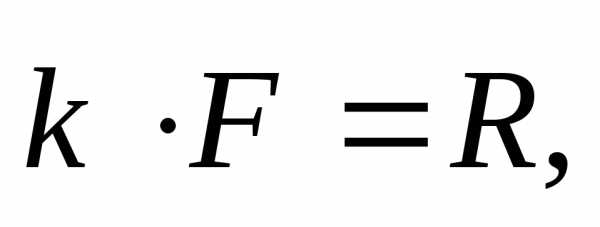 поэтому
поэтому
Получилась формула (П.5.2). Наконец, посмотрим на определение ротора:
В
отличие от выражения (а) здесь присутствует
вектор  (вместо
(вместо 
отсюда

6. Оператор Гамильтона
Введём специальный символ
(6.1)
называемый оператором Гамильтона, или оператором набла2.
Оператор  преобразует, переводит величину в другую
величину, Он обладает свойствами и
вектора, и производной. Применение
оператора
преобразует, переводит величину в другую
величину, Он обладает свойствами и
вектора, и производной. Применение
оператора к какой-либо величине назовём «умножением»
оператора
к какой-либо величине назовём «умножением»
оператора на эту величину.
на эту величину.
1.
«Умножение»  на числовую функциюдаст градиент этой функции:
на числовую функциюдаст градиент этой функции:
(6.2)
■
2. Скалярное
«умножение»  на векторную функциюдаст её дивергенцию:
на векторную функциюдаст её дивергенцию:
(6.3)
■
3. Векторное
«умножение»  на векторную функциюдаст её ротор:
на векторную функциюдаст её ротор:
(6.4)
■
7. Вычисление расхода через произвольную поверхность
Расход
жидкости, или поток поля скоростей  сквозь
поверхность
сквозь
поверхность  вы можете найти по формуле
вы можете найти по формуле
|
в
которой
– уравнение поверхности,–
нормальный вектор поверхности, 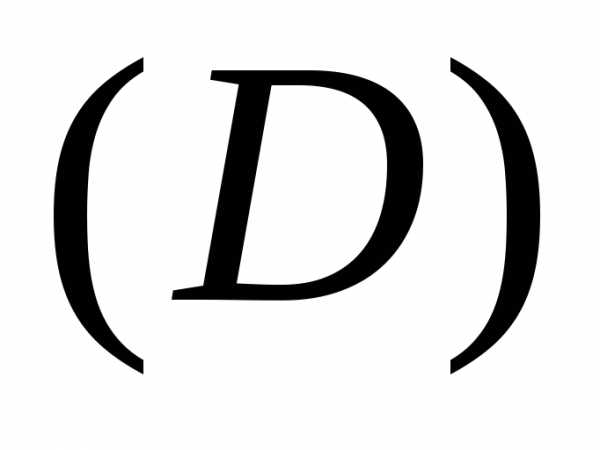 –
проекция поверхности на плоскость
–
проекция поверхности на плоскость 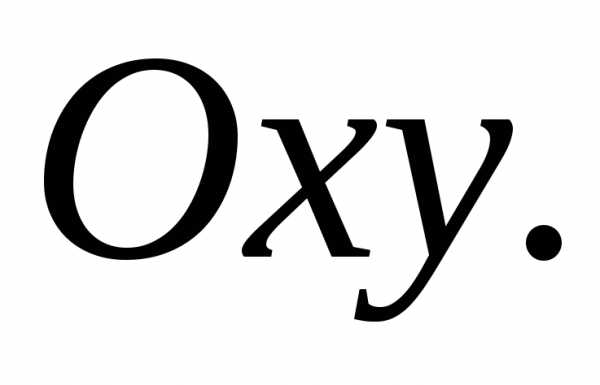
Если
поверхность  замкнутая, то расход можно найти по
формуле Остроградского-Гаусса:
замкнутая, то расход можно найти по
формуле Остроградского-Гаусса:
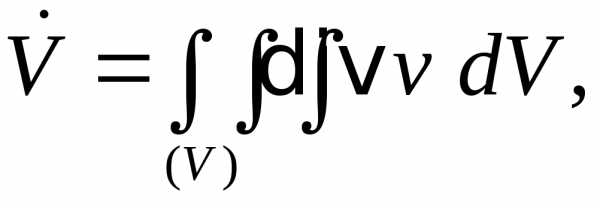
где 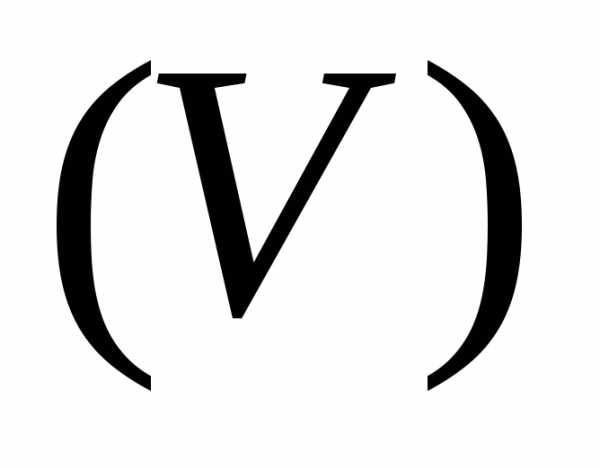 –
область внутри
–
область внутри 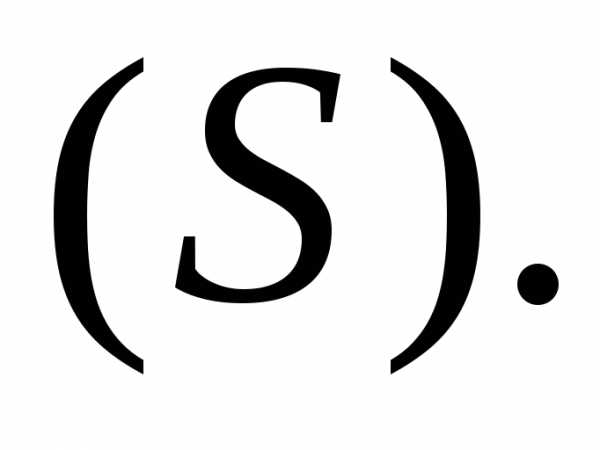
studfiles.net
Градиент, дивергенция, ротор
Брянск 2011
Составители: Баранова И.М., зав. кафедрой математики,
Алексеева Г.Д., доцент кафедры математики,
Гущин Г.В., доцент кафедры математики,
Часова Н.А., доцент кафедры математики,
Муравьев А.Н., доцент кафедры математики
Рецензент: Евтюхов К.Н. – к., ф.- м.н., профессор кафедры физики
Рассмотрены УМК МТФ
Протокол № от
ВВЕДЕНИЕ
Многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных.
В настоящих методических указаниях рассматриваются вопросы:
— основные понятия;
— частные производные;
— дифференциал функции;
— применение дифференциала к приближенным вычислениям;
— производная по направлению, градиент;
— экстремум функции нескольких переменных;
— наибольшее и наименьшее значения функции;
— условный экстремум, метод множителей Лагранжа;
— понятие об эмпирических формулах, метод наименьших квадратов.
Сведения из теории изложены лишь конспективно. Опущены строгие доказательства, однако практические вопросы рассмотрены довольно подробно, что необходимо для выполнения расчетно-графической работы.
1. Функции нескольких переменных, основные понятия
1) Если каждой точке М из некоторого множества точек евклидова пространства ставится в соответствие по известному закону некоторое число , то говорят, что на множестве задана функция или .
Если множество принадлежит или евклидовой прямой, или евклидовой плоскости, говорят о функциях одной, двух, трех, …, n переменных.
Пример 1.1 Площадь прямоугольника со сторонами, длины которых равны и , выражается формулой .
Пример 1.2. Объем прямоугольного параллелепипеда с ребрами, длины которых равны выражается формулой .
Пример 1.3. Величина силы притяжения двух материальных точек, имеющих массы и занимающих соответственно положение и , согласно закону Ньютона равна
, где .
Следовательно, есть функция от шести переменных
2) Всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т.е. придать постоянные значения.
Например, пусть мы имеем функцию трех переменных .
Если положить то мы получим функцию от двух переменных , если зафиксировать переменную то получим функцию одной переменной . Таким образом, в разных вопросах по желанию, функцию можно рассматривать как функцию одной, двух или трех переменных.
3) Геометрическим изображением (графиком) функции двух переменных является, вообще говоря, поверхность в пространстве .
Линией уровня функции называется множество всех точек плоскости , для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение где – некоторая постоянная. Поверхностью уровня функции определяется уравнением где .
Пример 1.4. Соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или давлением, получим соответственно изотермы и изобары, являющиеся важными исходными данными для прогноза погоды.
4) Пусть задана функция двух переменных . Если зафиксировать переменную и дать переменной приращение , то разность называется частным приращением функции по переменной . Аналогично, зафиксировав переменную и дав приращение переменной , получим частное приращение функции по : . Придавая приращение сразу двум переменным и , можно получить полное приращение функции .
Пример 1.5. Найти полное приращение функции , где изменяется от 2 до 2,2 и от 1 до 0,9; ; ; , ;
.
5) Частной производной функции от нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремится к нулю.
Таким образом, по определению, для функций двух переменных ; .
Пример 1.6. Пусть , тогда ; .
6) Функция называется дифференцируемой в данной точке если ее полное приращение в этой точке может быть представлено в виде где А, В – некоторые не зависящие от и числа, а и – бесконечно малые при .
Полным дифференциалом функции называется главная линейная часть полного приращения этой функции .
Если функция дифференцируема в точке , то и . Тогда , или
Пример 1.7. Найти дифференциал функции .
, , .
7) Частными производные второго порядка для функции называются: .
Продолжая таким путем дальше, можно определить частные производные третьего порядка, четвертого, …. Справедливо следующее утверждение: если все входящие в вычисления частные производные непрерывны, то смешанные частные производные не зависят от последовательности дифференцирования, т.е. в случае непрерывности, например .
Пример 1.8. Пусть , тогда: ; ; ; ; .
Градиент, дивергенция, ротор
Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М.
Если каждой точке М некоторой области V поставлен в соответствие определенный вектор , то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций: P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. Вектор в этом случае записывается в виде
а функции P(x,y,z), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля называется скаляр
Ротором (вихрем) векторного поля называется вектор
Все рассмотренные величины полей: grad u, div и rot вычисляются с помощью частного дифференцирования скалярного поля u и компонентов P, Q, R векторного поля . Таким образом, мы имеем дело с дифференциальными операциями первого порядка. Наряду с ними можно рассмотреть дифференциальные операции второго порядка: grad div , rot rot и div grad u. Рассмотрим последнюю операцию:
Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
pdnr.ru
34. Дивергенция и ротор векторного поля
Ранее нами было получено выражение для теоремы Остроградского–Гаусса для электростатического поля в дифференциальной форме (3.23):
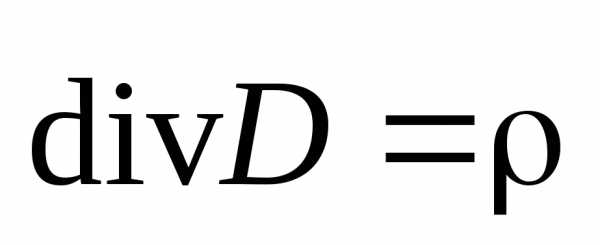 ,
(8.6)
,
(8.6)
следовательно, дивергенция поля характеризует плотность источников данного поля.
Согласно
теореме Остроградского–Гаусса в
интегральном виде,  .
Таким образом,.
Следовательно,поток
векторного поля через произвольную
замкнутую поверхность равен объемному
интегралу от дивергенции этого поля по
объему, ограниченному поверхностью.
В этом и заключается математический
смысл теоремы Остроградского,
сформулированной им для любого векторного
поля.
.
Таким образом,.
Следовательно,поток
векторного поля через произвольную
замкнутую поверхность равен объемному
интегралу от дивергенции этого поля по
объему, ограниченному поверхностью.
В этом и заключается математический
смысл теоремы Остроградского,
сформулированной им для любого векторного
поля.
Если
учесть, что 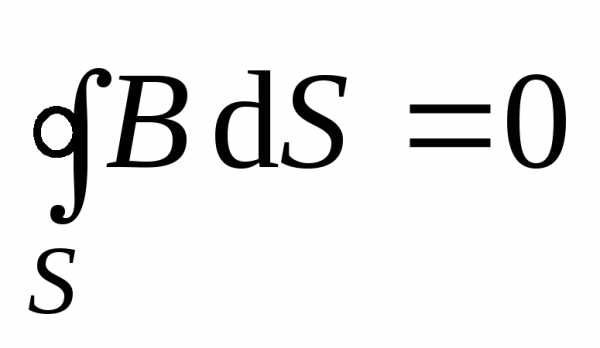 ,
то отсюда будет следовать, что
,
то отсюда будет следовать, что
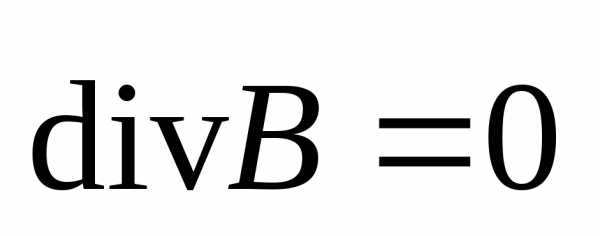 .
(8.7)
.
(8.7)
Таким образом, мы получили запись третьего и четвертого уравнений Максвелла в дифференциальной форме.
Чтобы
записать в дифференциальной форме
первое и второе уравнения Максвелла,
введем понятие ротора векторного поля. Для произвольного
вихревого поля, определяемого в каждой
точке вектором  ,
ротором (вихрем)
поля называется вектор, равный
максимальному пределу отношения
циркуляции поля по произвольному
замкнутому контуру к площади поверхности,
ограниченной контуром, при стремлении
последней к нулю (рис. 8.4). При этом ротор
направлен в сторону единичной нормали
к этой поверхности, согласуясь с
направлением вектора
,
ротором (вихрем)
поля называется вектор, равный
максимальному пределу отношения
циркуляции поля по произвольному
замкнутому контуру к площади поверхности,
ограниченной контуром, при стремлении
последней к нулю (рис. 8.4). При этом ротор
направлен в сторону единичной нормали
к этой поверхности, согласуясь с
направлением вектора  по правилу правого винта. Математически
это записывается так:
по правилу правого винта. Математически
это записывается так:
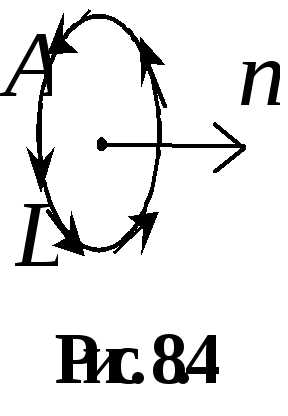
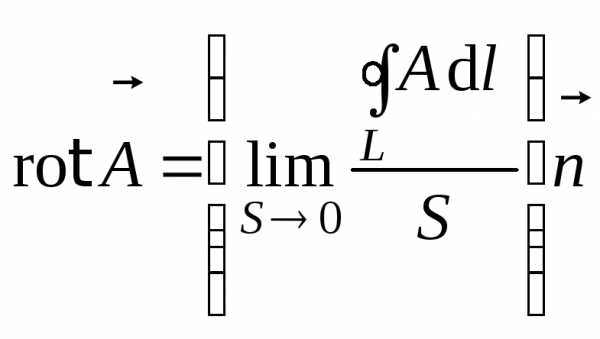 .
(8.8)
.
(8.8)Поскольку
величина предела в (8.8) зависит от
ориентации контура, выбираемого в
пространстве, то ротор поля по своему
физическому смыслу определяет ориентацию
векторов  в пространстве, степень их “закрученности”
по замкнутым линиям (для электрического
и магнитного полей ими выступают силовые
линии и линии индукции). Вспомним, что
для электростатического поля справедливо
(1.11),
то.
Следовательно, отличие ротора векторного
поля от нуля указывает на вихревой
характер поля, т.е. на замкнутость его
силовых линий.
в пространстве, степень их “закрученности”
по замкнутым линиям (для электрического
и магнитного полей ими выступают силовые
линии и линии индукции). Вспомним, что
для электростатического поля справедливо
(1.11),
то.
Следовательно, отличие ротора векторного
поля от нуля указывает на вихревой
характер поля, т.е. на замкнутость его
силовых линий.
Рассмотрим второе уравнение Максвелла из системы (8.5):
.
Если подставить это выражение в определение ротора (8.8), то получим
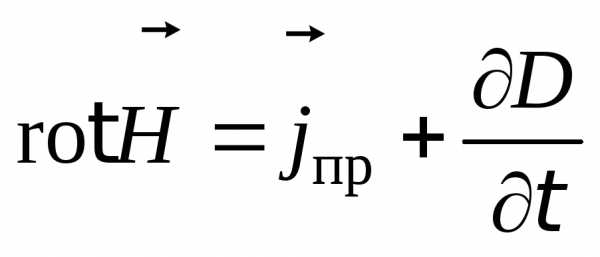 .
(8.9)
.
(8.9)
Выражение
(8.9) представляет собой второе уравнение
Максвелла в дифференциальной форме.
Помножим обе части этого соотношения
скалярно на  :
:
.
Теперь проинтегрируем в пределах площадки S:
.
Согласно второму уравнению Максвелла, правая часть полученного выражения равна циркуляции напряженности магнитного поля по контуру, ограничивающему площадку, поэтому
.
Получившееся уравнение справедливо для любого вихревого векторного поля, что было доказано английским математиком и физиком Дж. Г. Стоксом в 1854 г.: циркуляция вихревого поля по произвольному замкнутому контуру равна потоку ротора поля через поверхность, ограниченную контуром (теорема Стокса).
Если теперь рассмотреть первое уравнение из системы (8.5), согласно которому
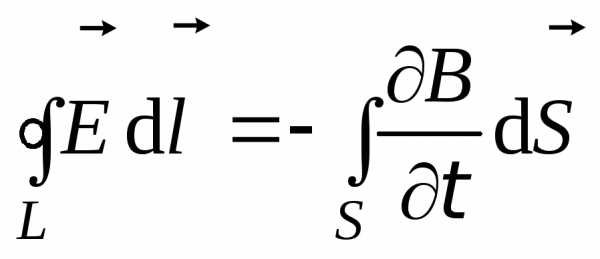 ,
,
то,
согласно теореме Стокса получим, что 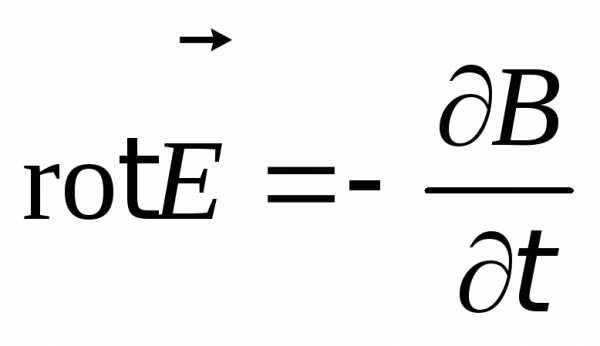 (8.10)
(8.10)
.
 то
и есть запись первого уравнения Максвелла
в дифференциальной форме.
то
и есть запись первого уравнения Максвелла
в дифференциальной форме.В дифференциальной форме записи системы уравнений Максвелла используются понятия дивергенции и ротора векторного поля. Напомним, что, согласно (3.23), .
Получим
теперь выражения для расчета ротора
векторного поля  .
.
Поскольку, согласно (8.8), ротор – это вектор, то для его нахождения определим компоненты разложения этого вектора в некоторой системе координат: (8.11)
.
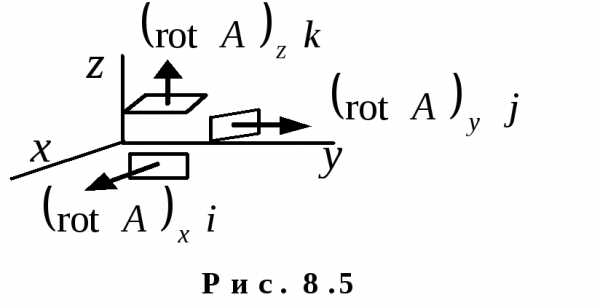
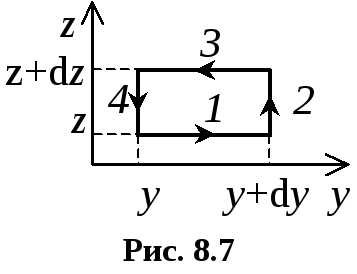
Каждое из этих слагаемых – вектор, направленный по соответствующей координатной оси. Т.к. ротор направлен по нормали к площадке, то это означает, что соответствующие площадки для определения компонент ротора должны быть сориентированы перпендикулярно координатным осям (рис. 8.5). Важно только помнить, что площадки, изображенные на рис. 8.5, проходят через одну точку пространства, в которой и ищется ротор поля (рис. 8.6).
Определим
первую компоненту ротора из (8.11). Для
этого необходимо рассмотреть ту площадку
из трех, изображенных на рис. 8.5, которая
перпендикулярна оси Ох.
Эта площадка расположена в плоскости zOy (рис. 8.7). Поскольку вектор  на этом рисунке смотрит “на нас”, то
направление обхода контура, ограничивающего
на этом рисунке смотрит “на нас”, то
направление обхода контура, ограничивающего
площадку,
должно быть выбрано против часовой
стрелки. Тогда циркуляция вектора  по выбранному контуру определится так:
по выбранному контуру определится так:
,
где
каждое из слагаемых представляет
циркуляцию вектора  по соответствующему элементу контура
(они обозначены на рис. 8.7) цифрами.
Преобразуем полученное соотношение:
по соответствующему элементу контура
(они обозначены на рис. 8.7) цифрами.
Преобразуем полученное соотношение:
.
Для
получения соответствующей компоненты
ротора, согласно (8.8), необходимо поделить
это выражение на площадь площадки, т.е.
на  :
:
.
Аналогично
можно получить, что
,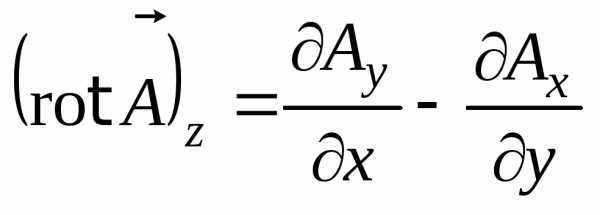 .
.
В окончательном виде запишем
. (8.12)
Оказывается, что это можно короче записать, используя понятие определителя матрицы:
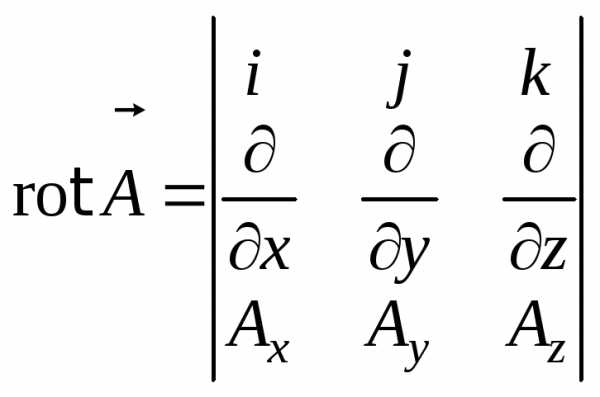 .
(8.13)
.
(8.13)
Итак, соотношения (3.23) и (8.12) или (8.13) позволяют найти дивергенцию и ротор исследуемых векторных полей.
studfiles.net
ПОВЕРХНОСТНЫЕ ГРАДИЕНТ, ДИВЕРГЕНЦИЯ И РОТОР
Транскрипт
1 Серия «Естественные и физико-математические науки» 5/14 УДК И П Попов ПОВЕРХНОСТНЫЕ ГРАДИЕНТ, ДИВЕРГЕНЦИЯ И РОТОР Вводится понятие о слагаемых векторных произведений, которыми являются первая, или ортоположительная часть и вторая, или ортоотрицательная часть; дальнейшим развитием этого понятия является представление о сопряженных векторах, векторном дифференциальном поверхностном операторе, поверхностном градиенте, производной по поверхности, поверхностных дивергенции и роторе Рассматриваются поверхностные функции, их поверхностное дифференцирование и интегрирование Показаны особенности поверхностных функций, для которых все слагаемые являются функциями не менее чем двух переменных, кроме того, поверхностные функции имеют смешанные частные производные второго порядка, при этом, по крайней мере, одна из смешанных частных производных второго порядка от любого слагаемого не обращается в нуль Доказывается теорема о восстановлении поверхностной функции по ее поверхностному градиенту Вводится понятие о линейной комбинации координат и ее делении на вектор, нулевом и мнимом нулевом векторных операторах, псевдовекторах и комбинированных векторах Приведен ряд разложений с использованием введенных операций Ключевые слова: вектор, оператор, поверхностный, координаты Введение Работа посвящена рассмотрению ряда операций на пространстве гладких функций и векторных полей в R В качестве исходного пункта могут выступать нулевые величины Их можно условно разделить на две категории К первой категории относятся величины, содержимое которых «пусто» Ко второй состоящие из величин, сумма которых равна нулю К последней категории относится векторное произведение оператора Гамильтона (набла) на самого себя При этом использование взаимно противоположных компонентов этого произведения создает определенные перспективы, в частности, развития элементов поверхностного векторного анализа К таким элементам могут быть отнесены векторный дифференциальный поверхностный оператор, поверхностный градиент, производная по произвольной поверхности, поверхностные дивергенция и ротор, являющиеся аналогами соответствующих величин первого порядка [1, ] Названные операции относятся к поверхностному дифференцированию, которое можно рассматривать в качестве обратной задачи к поверхностному интегрированию Перечисленные операции могут использоваться для получения разложений ряда векторных представлений второго порядка, часть которых имеет аналоги первого порядка В ряде случаев для этого придется прибегнуть к специальным методам, таким, как сопряжение векторов, использование линейной комбинации координат, ее деление на вектор, введение нулевого и мнимого нулевого векторных операторов, псевдовекторов и комбинированных векторов 159
2 Вестник ПсковГУ 1 Слагаемые векторных произведений Для векторов G и H имеет место операция векторного произведения G H G H G H i G H G H j G H G H k y y y y Его можно представить в виде: G H G H i G H j G H k G H i G H j G H k y y y y Определение 11 Операция G H G H i G H j G H k I : y y является первой, или ортоположительной частью векторного произведения векторных полей G Gi Gyj Gk и H Hi H yj Hk Определение 1 Операция G H H G G H i G H j G H k II : I y y 16 G H является второй, или ортоотрицательной частью векторного произведения Очевидно, что G H G I H H I G G I H G II H Все вышесказанное справедливо и для ротора Определение 1 Операция M M M y rot IM : I M i j k y является первой, или ортоположительной частью ротора rotm векторного поля M M i M j M k y Определение 14 Операция M y M M rot IIM : II M i j k y является второй, или ортоотрицательной частью ротора rotm Очевидно, что rotm rot IM rot IIM или M I M II M Сопряженные векторы Определение 1 Операция G H: GI H HI G GI H GII H является сопряженным векторным произведением векторных полей G и H Определение Операция rot M : rot IM rot IIM или M I M II M является сопряженным ротором векторного поля M Определение Оператор : I II i j k y y является векторным дифференциальным поверхностным оператором
3 Серия «Естественные и физико-математические науки» 5/14 Поверхностный градиент и производная по поверхности Определение 1 Вектор W W W grad W : W i j k (1) y y является поверхностным градиентом функции W По аналогии с производной по направлению вычисляется производная по поверхности dw W W W : grad W n cos cos cos () d y y Здесь n icos jcos k cos поле единичных нормалей поверхности дифференцирования Теорема 1 Производная функции W(, y, ) (скалярного поля) по некоторой поверхности равна проекции поверхностного градиента на единичный вектор нормали к этой поверхности (в соответствующей точке) dw grad W cosgrad W, n d Справедливость этой теоремы непосредственно вытекает из () Следствие Поверхностный градиент скалярного поля равен по величине производной поля по поверхности, для которой эта производная (в соответствующей точке) является максимальной, и совпадает по направлению с единичным вектором нормали к этой поверхности d W W W W ma grad W d y y Пусть для функции U(, y, ), все слагаемые которой являются функциями не менее чем двух переменных, имеющей смешанные частные производные второго порядка, по крайней мере, одна из смешанных частных производных второго порядка от любого слагаемого не обращается в нуль Для единообразия терминологии такая функция может быть названа поверхностной Теорема Поверхностная функция U(, y, ) может быть восстановлена по ее поверхностному градиенту G в соответствии с формулой: U G dyd G dd G ddy V y P (, y, ) P ( y, ) Q (, y, ) Q (, ) R (, y, ) R (, y) V При этом V P1 Q1 R1, а интегралы понимаются как повторные неопределенные с нулевыми аддитивными составляющими Доказательство G G U y G () y y 161
4 U можно искать в виде: При этом Вестник ПсковГУ y U G dyd G dd G ddy f (, y, ) Gdyd P1 (, y, ) P ( y, ), Gydd Q1 (, y, ) Q (, ), Gddy R1 (, y, ) R (, y), G y y P1 Gdyd, G Q y y y y 1 Gydd, G R1 Gddy y y Тогда f (, y, ) V При этом С учетом () P1 Q1 R1 V (, y, ) U Gdyd Gydd Gddy f (, y, ) y y G Q1 Q (, ) R1 R (, y) V G y Аналогично, U G y U y G Теорема доказана Замечание 1 Равенство нулю аддитивных составляющих повторных неопределенных интегралов вытекает из того, что в поверхностных функциях соответствующих слагаемых нет Замечание Поверхностная функция может быть восстановлена по ее поверхностному градиенту и с помощью поверхностного интеграла, однако это решение может оказаться более громоздким из-за необходимости определения поверхности интегрирования Кроме того, при поверхностном интегрировании могут появляться константы и функции одной переменной, вследствие чего возникает необходимость прибегать к их отбрасыванию, т е к произволу 1 grad U sin y i y y j k, y U y sin y y sin y y y y y y Пример 4 Поверхностная дивергенция и поверхностный ротор В (1) имеет место произведение вектора на скаляр W Могут быть рассмотрены скалярное и векторное произведения на вектор M 16
5 Серия «Естественные и физико-математические науки» 5/14 Определение 41 Операция M M y M div M : M y y является поверхностной дивергенцией векторного поля M Определение 4 Операция M M y M M M y M rot M : M i j k y y y y является поверхностным ротором векторного поля M Определение 4 Операция M M M y rot,im : I M i j k y y является первой, или ортоположительной частью поверхностного ротора rot M Определение 44 Операция M y M M rot,iim : II M i j k y y является второй, или ортоотрицательной частью поверхностного ротора rot M rot M rot,i M rot,iim, или M I M II M Определение 45 Операция rot M : rot M rot M или M : M M,I,II 16 I является сопряженным поверхностным ротором векторного поля M 5 Некоторые формулы V W V W ( const, const) E F E F E F E F y y y i j k y y y I i j k, y y II i j k y y II
6 Вестник ПсковГУ W W (, y, ) div grad W W y y V W V W F F i F j F k y W W W divgrad W W divgradw y V W V W F F i F j F k VW V W V W W V W V y W W W W W W W i j k y y y W rotgrad W W rot gradw F F F F Fy F y F F y y y divrot F F div rot F F 164 F F y F y F F i y y y F F F F y j F F y F F y k y y y F F F F F F F F F F F F F F F F F F F F F F F F F F F F graddiv grad div grad div rotrot rot rot rot rot rot grad W W div rot F F
7 Серия «Естественные и физико-математические науки» 5/14 VW W V V W V W W W W W F F ( ) F ( F ) Известные методы не позволяют получить аналогичные формулы для выра- F G, F G, ( G ) WF, ( WF ), ( F G ), ( G ) F, VW Для их получения, а также для решения других задач существующий ар- жений сенал средств операций с векторами может быть расширен за счет введения в рассмотрение линейной комбинации координат и ее деления на вектор, нулевого и мнимого нулевого векторных дифференциальных операторов, псевдовекторов и комбинированных векторов 6 Линейная комбинация координат В результате операций над векторными функциями, например, скалярного произведения, взятия дивергенции и т п появляются скалярные функции вида y W W W W (61) Такая функция является линейной комбинацией координат Ее особенностью является то, что подобные, входящие в состав слагаемых W, W, W, не приведены Пример 61 W F G ( y i y j yk) ( i yj k ) y y y линейная комбинация координат, а W y y линейной комбинацией координат не является Здесь и далее волнистой чертой помечена операция, результатом которой является сумма с неприведенными слагаемыми Может быть введена операция деления линейной комбинации координат на вектор С 1 y y WС G Gy G G Gy G F W W W W W W W G i j G i j k k (6) Действительно, F G W W, FyGy Wy, FG W, F, G F y y y Wy W, F, G G W W y W G Gy G W С G i G j y G k i j k W, в отличие от W, содержит информацию, достаточную для восстановления одного из векторов-сомножителей при известном другом F G FG FyGy FG F FG ygy FG i j k F G G i G j G k G G G y y 165
8 Вестник ПсковГУ Пример 6 См данные примера 61 y y y y y y F y y y i yj k i y j k i j k Линейную комбинацию координат можно делить на любой вектор, а не только на один из сомножителей, которые ее образовали F G FG FyGy FG F FG ygy FG i j k H H i H j H k H H H y y Пример 6 y y F y y i y j y k i yj k,5 y i yj yk,5 y y y Замечание В общем виде линейная комбинация координат имеет вид W W W W, y где,, постоянные коэффициенты Последнее выражение может быть получено из (61) следующим образом: W W i j k i j k W Wy W W Wy W i j k i j k 7 Нулевой векторный оператор Может быть рассмотрена следующая задача Имеются две линейные комбинации координат W С и V С Найти формулы, связывающие W С и V С с выражениями и W V W V W V W V W V W V y y y y Для решения этих и подобных задач может быть введен нулевой векторный оператор i j k i j k y Некоторые свойства U Ui Uj Uk Эта величина может рассматриваться в качестве нулевого градиента G функции U G gradu U F F F F F y Эта величина может рассматриваться в качестве нулевой дивергенции векторного поля F divf F F F F i F F j F F k y y 166
9 Серия «Естественные и физико-математические науки» 5/14 Эта величина может рассматриваться в качестве нулевого ротора векторного поля F rot F F ( F) div (rot F ) Из (6) WС 1 W Wy W W i Wyj Wk W W W, 1 F F, 1 y y, 1 ( ) y, 1 ( ) 1 i j k, y 1 ( ) y i y y j y k i j k y y 1 ( ) i j k y y I II Возвращаясь к задаче, приведенной в начале параграфа, 1 1 WV WyVy WV W V, 1 1 WVy WyV WV W I V Таким образом, применение нулевого векторного оператора позволяет решать подобные задачи Представление полного дифференциала функции с помощью векторных операторов
10 Вестник ПсковГУ W W W 1 dw d dy d ( W ) ( d1 ) y Здесь d 1 полный дифференциал элементарной симметрической функции 1 y С помощью нулевого векторного оператора можно, например, преобразовать вектор в линейную комбинацию координат, выполнить некие операции, а затем результат преобразовать обратно в вектор И наоборот, сначала линейную комбинацию координат преобразовать в вектор, выполнить векторные операции, а результат преобразовать в линейную комбинацию координат 8 Мнимый нулевой векторный оператор Может быть рассмотрена следующая задача Имеются линейная комбинация координат W и вектор F Найти формулу, связывающую W и F с выражением С F W i F W j F W k Для решения подобных задач может быть введен мнимый y y нулевой векторный оператор { } i { } { } { } j k i j k y Его главное отличие от оператора заключается в том, что псевдоорты (мнимые орты) { i }, { j }, { k } с ортами i, j, k не взаимодействуют, а взаимодействуют только с псевдоортами Поэтому правила применения оператора { } по отношению к векторам такие же, как и оператора в отношении линейных комбинаций координат Некоторые свойства { } { } U U{ i} U{ j} U{ k } Эта величина может рассматриваться в качестве мнимого нулевого градиента { G } функции U { G } {grad U} { } U W 1 { } W Wy W W{ i} Wy{ j} W{ k } { } 1 { } { } W W, 1 { } { } { } { } F 1 { } F Fi{ i} Fy j{ j} Fk { k }, { } 1 { } { } F F 1 F Fy F F Fy F { } { } F k j { i} i k { j} j i { k } 1 { } i{ i} j{ j} k{ k }, y y 168 С
11 Серия «Естественные и физико-математические науки» 5/14 1 { } { } 1 { } { } { } { } { } y k j i y i y k j j y i k 1 { } i{ i} j{ j} k{ k }, y 1 { } { } 1 { } { } k j{ i} i k { j} j i { k } y y 1 { } { i} { j} { k }, y 1 { } ({ } ) 1 { } ({ } ) { i} { j} { k } y y 1 1 { } { } k j { i} i k { j} j i { k } y y 1 { } { } { } W, { } { } I II { } { } { } { } { } Возвращаясь к задаче, приведенной в начале параграфа, 1 1 FW yi FyW j FWk { } { } F I { } W Таким образом, применение мнимого нулевого векторного оператора позволяет решать подобные задачи Другими словами, применение { } позволяет сохранить орты исходного вектора 9 Псевдовекторы и комбинированные векторы Применение мнимого векторного оператора приводит к появлению псевдовекторов В частности, { i}, { j}, { k } являются псевдоортами Определение 91 Псевдовектор это скаляр, в котором содержится информация о включенном в него векторе Псевдовектор может быть обозначен следующим образом: { P} P A A A P i Py j P k P P Из представленных выше выражений значительная часть является комбинированными векторами, т е сочетаниями векторов и псевдовекторов 169
12 Вестник ПсковГУ Комбинированный вектор может быть обозначен следующим образом: {P} P F B F B P F Нижний индекс содержит информацию о направлении вектора, верхний индекс информацию о направлении псевдовектора При выполнении операций с комбинированными векторами орты взаимодействуют с ортами, а псевдоорты с псевдоортами Орты и псевдоорты между собой не взаимодействуют При умножении комбинированного вектора на другой комбинированный вектор могут использоваться следующие четыре формы записи операций умножения: «{ }», «{ }», «{ }», «{ }» Действие знака произведения, расположенного в скобках, распространяется на псевдовекторные составляющие комбинированных векторов, а расположенного за скобками на векторные Пример W { i} j W { j} k W { k} i {} V { i} k V { j} i V { k} j W V i W V j W V k y y y y При перемножении псевдовектора и комбинированного вектора нет необходимости размещения знака произведения в скобки Очевидно, что знак произведения или в этом случае распространяется на псевдовекторные составляющие Величина div { F} { } { F } F Fy F, может рассматриваться в качестве мнимой нулевой дивергенции мнимого векторного поля {F} Она совпадает с нулевой дивергенцией векторного поля F Величина rot { F} { } { F} F F { i} F F { j} F F { k }, 17 y y может рассматриваться в качестве мнимого нулевого ротора мнимого векторного поля {F} { } ({ } { F}) div {(rot { F })} С помощью мнимого нулевого векторного оператора можно преобразовать вектор в комбинированный вектор, выполнить некие операции, а затем результат преобразовать обратно в вектор И наоборот, сначала комбинированный вектор преобразовать в вектор, выполнить векторные операции, а результат преобразовать в комбинированный вектор 1 Некоторые формулы (продолжение) F G F G G F G F F G F G G F I I I I II I I II F G G F I I
13 Серия «Естественные и физико-математические науки» 5/14 I II F G G ( F) F ( G ) ( F) ( G ) 1 1 ( II F) ( I G) ( ) ( ) F G ( G ) WF F( G W ) W ( G ) F 1 1 { } ( W ) { } ( ) ( W ) G F G II ( F ) При этом { } ( W ) { } ( ) ( W ) ( ) G F G F ( W) G II ( F) G I ( W ) II ( F) G II ( W ) II ( F ) 1 1 ( WF) W F W F { } W { } { } F ( F) W W ( F ) I I II II ( F G) ( G ) F G( F) ( F ) G F( G ) F G G F { } { } { } { } ( F) ( G) ( F) ( G ) I I II II 1 1 II G F G F ( G ) F { } G { } F G F 1 1 II VW ( V ) W ( W ) V 4( V ) ( W ) 1 1 V W W V V W Без применения «расщепления» векторных произведений на слагаемые, сопряжения векторов, использования линейной комбинации координат, ее деления на вектор, введения нулевого и мнимого нулевого векторных операторов, псевдовекторов и комбинированных векторов получить представленные выше разложения было бы невозможно Замечание Несмотря на то, что в некоторых приведенных разложениях использован мнимый оператор { }, разложения сами по себе являются «чистыми» скалярами или векторами Литература 1 Попов И П О некоторых аспектах магнитоэлектрического взаимодействия // Вестник Челябинского государственного университета Физика 9 Вып 5 4 (16) С 4 9 Попов И П О пространственной конфигурации вихревого электрического поля // Вестник Курганского государственного университета Естественные науки 9 Вып 1 (15) С
14 Вестник ПсковГУ I Popov URFAE GRADIENT, DIVERGENE AND ROTOR We introduce the notion of the terms of vector products, which are the first ( orthopositive) part and the second (orthonegative) part; further development of this concept is the notion of conjugate vectors, vector differential operator on the surface, the surface gradient, the derivative on the surface, the surface divergence and rotor urface functions, their surface differentiation and integration are considered The features of surface functions for which all terms are functions of at least two variables, are shown; in addition, surface functions have mied partial derivatives of the second order, while at least one of the mied partial derivatives of second order of any term does not vanish The theorem on the restoration of surface features on its surface gradient is proved The notion of a linear combination of coordinates and its division into a vector, ero and ero imaginary vector operators, pseudo and combined vectors are introduced A number of epansions using these operations are presented Key words: vector, operator, surface, coordinates 17
docplayer.ru
34. Дивергенция и ротор векторного поля
Ранее нами было получено выражение для теоремы Остроградского–Гаусса для электростатического поля в дифференциальной форме (3.23):
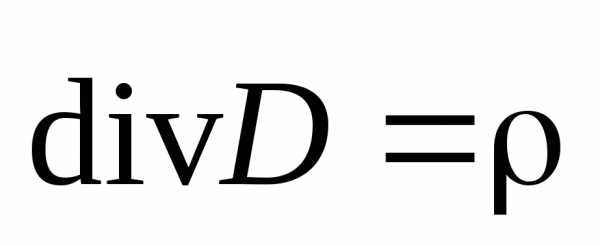 ,
(8.6)
,
(8.6)
следовательно, дивергенция поля характеризует плотность источников данного поля.
Согласно
теореме Остроградского–Гаусса в
интегральном виде,  .
Таким образом,.
Следовательно,поток
векторного поля через произвольную
замкнутую поверхность равен объемному
интегралу от дивергенции этого поля по
объему, ограниченному поверхностью.
В этом и заключается математический
смысл теоремы Остроградского,
сформулированной им для любого векторного
поля.
.
Таким образом,.
Следовательно,поток
векторного поля через произвольную
замкнутую поверхность равен объемному
интегралу от дивергенции этого поля по
объему, ограниченному поверхностью.
В этом и заключается математический
смысл теоремы Остроградского,
сформулированной им для любого векторного
поля.
Если
учесть, что  ,
то отсюда будет следовать, что
,
то отсюда будет следовать, что
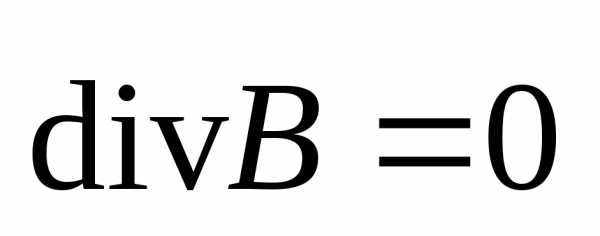 .
(8.7)
.
(8.7)
Таким образом, мы получили запись третьего и четвертого уравнений Максвелла в дифференциальной форме.
Чтобы
записать в дифференциальной форме
первое и второе уравнения Максвелла,
введем понятие ротора векторного поля. Для произвольного
вихревого поля, определяемого в каждой
точке вектором  ,
ротором (вихрем)
поля называется вектор, равный
максимальному пределу отношения
циркуляции поля по произвольному
замкнутому контуру к площади поверхности,
ограниченной контуром, при стремлении
последней к нулю (рис. 8.4). При этом ротор
направлен в сторону единичной нормали
к этой поверхности, согласуясь с
направлением вектора
,
ротором (вихрем)
поля называется вектор, равный
максимальному пределу отношения
циркуляции поля по произвольному
замкнутому контуру к площади поверхности,
ограниченной контуром, при стремлении
последней к нулю (рис. 8.4). При этом ротор
направлен в сторону единичной нормали
к этой поверхности, согласуясь с
направлением вектора  по правилу правого винта. Математически
это записывается так:
по правилу правого винта. Математически
это записывается так:
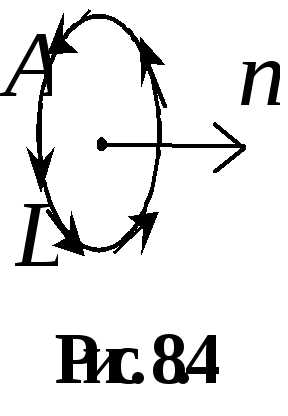
 .
(8.8)
.
(8.8)Поскольку
величина предела в (8.8) зависит от
ориентации контура, выбираемого в
пространстве, то ротор поля по своему
физическому смыслу определяет ориентацию
векторов  в пространстве, степень их “закрученности”
по замкнутым линиям (для электрического
и магнитного полей ими выступают силовые
линии и линии индукции). Вспомним, что
для электростатического поля справедливо
(1.11),
то.
Следовательно, отличие ротора векторного
поля от нуля указывает на вихревой
характер поля, т.е. на замкнутость его
силовых линий.
в пространстве, степень их “закрученности”
по замкнутым линиям (для электрического
и магнитного полей ими выступают силовые
линии и линии индукции). Вспомним, что
для электростатического поля справедливо
(1.11),
то.
Следовательно, отличие ротора векторного
поля от нуля указывает на вихревой
характер поля, т.е. на замкнутость его
силовых линий.
Рассмотрим второе уравнение Максвелла из системы (8.5):
.
Если подставить это выражение в определение ротора (8.8), то получим
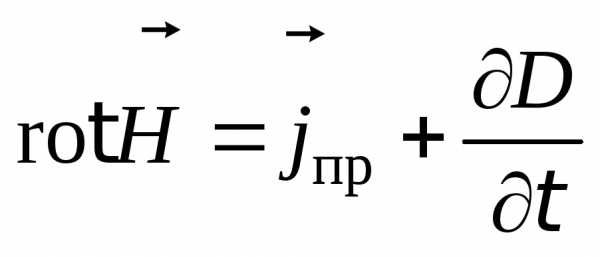 .
(8.9)
.
(8.9)
Выражение
(8.9) представляет собой второе уравнение
Максвелла в дифференциальной форме.
Помножим обе части этого соотношения
скалярно на  :
:
.
Теперь проинтегрируем в пределах площадки S:
.
Согласно второму уравнению Максвелла, правая часть полученного выражения равна циркуляции напряженности магнитного поля по контуру, ограничивающему площадку, поэтому
.
Получившееся уравнение справедливо для любого вихревого векторного поля, что было доказано английским математиком и физиком Дж. Г. Стоксом в 1854 г.: циркуляция вихревого поля по произвольному замкнутому контуру равна потоку ротора поля через поверхность, ограниченную контуром (теорема Стокса).
Если теперь рассмотреть первое уравнение из системы (8.5), согласно которому
 ,
,
то, согласно теореме Стокса получим, что
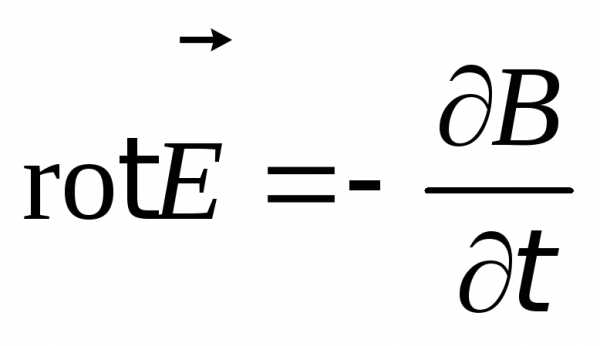 .
(8.10)
.
(8.10)
Это и есть запись первого уравнения Максвелла в дифференциальной форме.
В дифференциальной форме записи системы уравнений Максвелла используются понятия дивергенции и ротора векторного поля. Напомним, что, согласно (3.23),
.
Получим
теперь выражения для расчета ротора
векторного поля  .
.
Поскольку, согласно (8.8), ротор – это вектор, то для его нахождения определим компоненты разложения этого вектора в некоторой системе координат:
. (8.11)
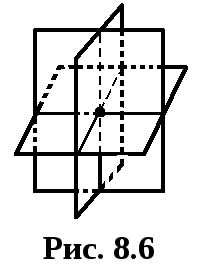
Каждое из этих слагаемых – вектор, направленный по соответствующей координатной оси. Т.к. ротор направлен по нормали к площадке, то это означает, что соответствующие площадки для определения компонент ротора должны быть сориентированы перпендикулярно координатным осям (рис. 8.5). Важно только помнить, что площадки, изображенные на рис. 8.5, проходят через одну точку пространства, в которой и ищется ротор поля (рис. 8.6).
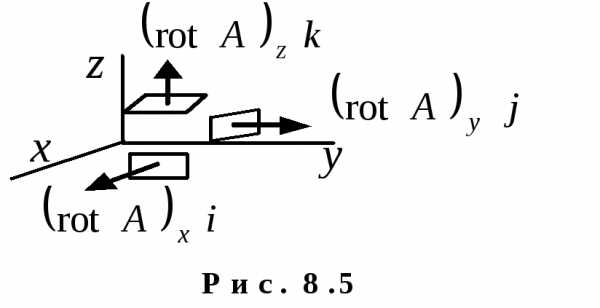
 на этом рисунке смотрит “на нас”, то
направление обхода контура, ограничивающего
на этом рисунке смотрит “на нас”, то
направление обхода контура, ограничивающего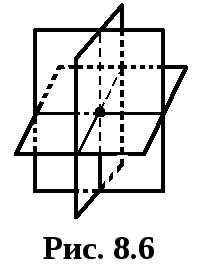
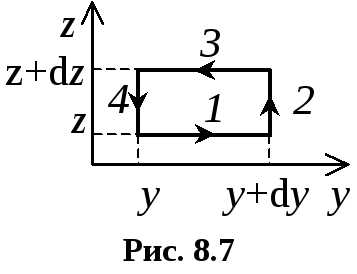 площадку,
должно быть выбрано против часовой
стрелки. Тогда циркуляция вектора
площадку,
должно быть выбрано против часовой
стрелки. Тогда циркуляция вектора  по выбранному контуру определится так:
по выбранному контуру определится так:,
где
каждое из слагаемых представляет
циркуляцию вектора  по соответствующему элементу контура
(они обозначены на рис. 8.7) цифрами.
Преобразуем полученное соотношение:
по соответствующему элементу контура
(они обозначены на рис. 8.7) цифрами.
Преобразуем полученное соотношение:
.
Для
получения соответствующей компоненты
ротора, согласно (8.8), необходимо поделить
это выражение на площадь площадки, т.е.
на  :
:
.
Аналогично можно получить, что
, 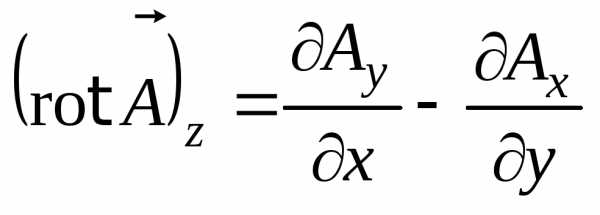 .
.
В окончательном виде запишем
. (8.12)
Оказывается, что это можно короче записать, используя понятие определителя матрицы:
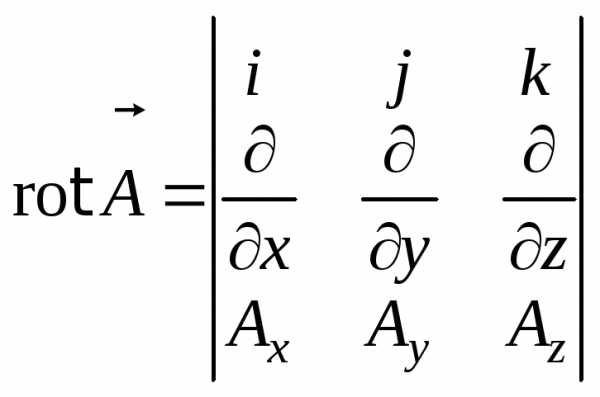 .
(8.13)
.
(8.13)
Итак, соотношения (3.23) и (8.12) или (8.13) позволяют найти дивергенцию и ротор исследуемых векторных полей.
studfiles.net
/sci/ — Ротор, дивергенция и градиент
>>407373>Однако про водичку что-то не особо понял.
Формулируй вопросы точнее, а там разберёмся.
>диффуры
Нам интересно описание процессов, происходящих вокруг нас. Практически всегда мы хотим описать динамику явлений — другими словами, что-то меняется. Меняется положение частичек воды (со временем), меняется количество хищников и жертв (со временем), меняется вероятность обнаружения электрона (со временем), меняется цена опционов (c ценой акций), меняется экономический рост (с капиталом), и многое, многое другое. Можно погуглить, скажем, уравнения Навье-Стокса и Эйлера, Блэка-Шоулза и Солоу-Свана, Фоккера-Планка и Ньютона.
Наверное, первое диф. ур-ие, с которым встречается большинство — уравнение Ньютона. Тем не менее, оно не самое «удачное» для ознакомления, т.к. оно эффективно второго порядка.
Я рекомендую погуглить, или найти любой свежий американский учебник для колледжей\инженеров по обыкновенным диф. уравнениям, и ознакомиться по выбранному источнику с моделью Лотки-Вольтерры. По моему опыту, именно на этом уравнении у людей «щёлкает» идея диф. ур-ий.
Пример попроще — рост популяции без ограничений. Скажем, мы ничего сугубо технического не знаем про рост населения Земли. Обозначим текущее (в момент времени t) население за P(t). Нам бы хотелось смоделировать P(t), какой у неё может быть вид? Конечно, сначала нужно посмотреть на имеющиеся данные, и вид кривой натолкнёт нас на мысли, но пока это проигнорируем.
Давайте рассмотрим изменение за небольшой промежуток времени. Т.е. мы рассматриваем P(t+dt), где dt — мало. Как же, приблизительно, изменится P(t) до P(t+dt)? Обозначим для краткости это за dP.
Логично предположить, что чем больше людей, тем больше прирост, верно? Скажем, тысяча человек за 1 месяц изменится на 5-10 человек, а миллион — на несколько тысяч. В общем случае это говорит лишь о том, что dP является какой-то возрастающей функций от P.
Например, dP = aP + bP^2 +cP^3.
Но самый простой вариант, конечно — линейный, т.е. dP = aP. Это значит, что у нас было P(t) человек, но за dt оно выросло на aP до числа P(t)+aP. Здесь a — какая-то константа. Почему выбираем линейную модель? Во-первых, это самый простой и удобный вариант, и городить сущности без теоретической на то основы часто не приносит ощутимой пользы. Во-вторых, представим себе график численности населения. Приблизим его поближе к точке (t, P(t)). Приблизим ещё. И ещё. И ещё! Он будет практически неотличим от прямой, и это есть важная мотивация производной вообще. Прямая -> линейность при очень-очень малых изменениях.
Что если мы возьмём другой dT, отличный от dt, но тоже маленький? Линейность останется, но коэффициент «а» придётся выбрать другой, т.е.
dP1 (за dt) = aP
dP2 (за dT) = AP
Легче просто ввести один коэффициент k для «единичного» изменения, и тогда можно это переписать в виде
dP1 = k.dt.P
dP2 = k.dT.P
Отсюда естественно получается dP/dt = kP — самая простая модель роста численности; решение — экспоненциальная функция.
Если есть «нативное» понимание производной как роста, то можно было сократить пост, но на всякий случай я расписал подробней.
2ch.hk
Градиент, дивергенция, ротор. Если каждой точке М пространства или некоторой его области V поставлена в
Градиент, дивергенция, ротор. Если каждой точке М пространства или некоторой его области V поставлена вЕсли каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М.
Если каждой точке М некоторой области V поставлен в соответствие определенный вектор , то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций: P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. Вектор в этом случае записывается в виде
а функции P(x,y,z), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля называется скаляр
Ротором (вихрем) векторного поля называется вектор
Все рассмотренные величины полей: grad u, div и rot вычисляются с помощью частного дифференцирования скалярного поля u и компонентов P, Q, R векторного поля . Таким образом, мы имеем дело с дифференциальными операциями первого порядка. Наряду с ними можно рассмотреть дифференциальные операции второго порядка: grad div , rot rot и div grad u. Рассмотрим последнюю операцию:
Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
Дата добавления: 2015-07-16; просмотров: 94 | Нарушение авторских прав
mybiblioteka.su — 2015-2019 год. (0.009 сек.)
mybiblioteka.su

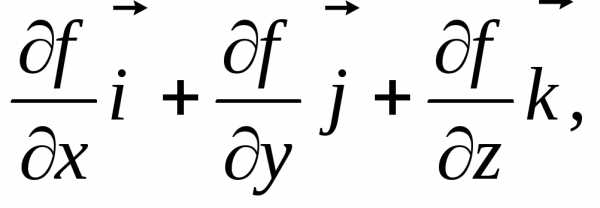 (П.5.1)
(П.5.1)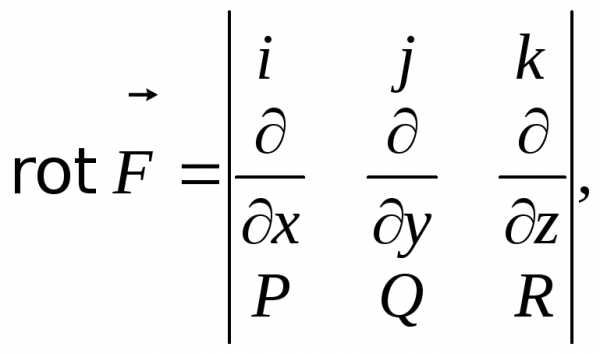 (П.5.3)
(П.5.3)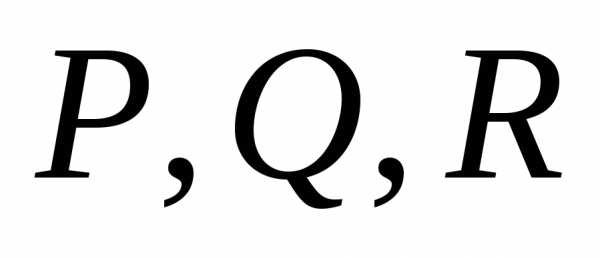 – функции
от
– функции
от 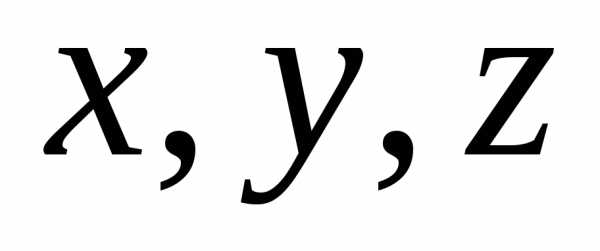 ).
).