Длина дуги сектора круга формула: Площадь кругового сектора, теория в ЕГЭ по математике

Площадь сектора круга

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-01-17

Площадь сектора круга и площадь сегмента учить не нужно! Дорогие друзья! Вы, наверное, не раз просматривали справочник с математическими формулами, и, наверняка, возникала мысль: «Да разве возможно их все выучить?». Скажу вам, что возможно, но зачем? Зачем забивать голову массой формул, постоянно повторять их, ужасаться тому, что какую-то забыл и снова повторять? Не надо!

На самом деле достаточно запомнить треть всех формул, базовых формул или ещё меньше. Далее вы поймёте о чём идёт речь. Все остальные формулы можно быстро вывести, зная основу, применяя логику, и запомнив принципы, которым нужно следовать.

Приведу пример, существует 32 формулы приведения, учить их – это бессмысленное занятие. Как быстро вспомнить любую из них — изложено в статье «Формулы приведения», посмотрите.

В этой статье мы рассмотрим, как быстро восстановить в памяти формулы площади сектора круга, площади его сегмента, длину дуги окружности. Именно эти формулы понадобятся для решения ряда по планиметрии,  которые разберем в следующей статье. Итак, «базовые» формулы, их нужно выучить и знать!

Площади круга (формула):

Формула длины окружности:

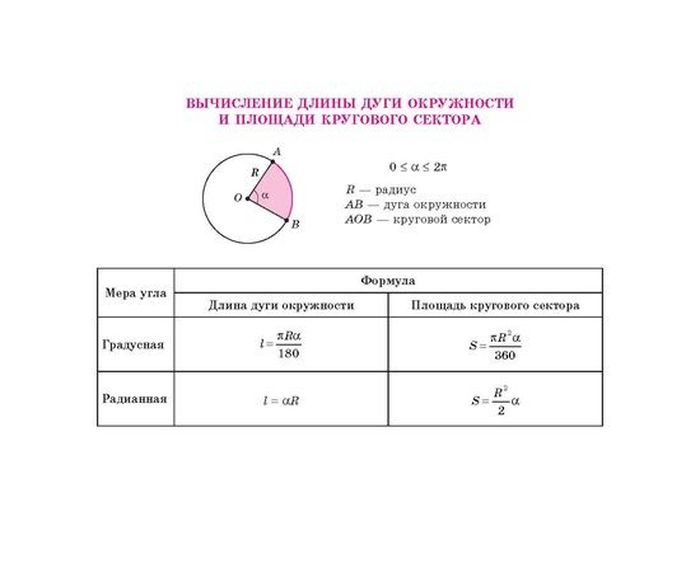
Изобразим сектор, соответствующий определённому центральному углу n:

Рассуждаем логически: если площадь круга равна S=ПR², то площадь соответствующая сектору в один градус будет равна 1/360  от площади круга (мы знаем, что вся окружность — это  угол в 360 градусов), то есть

Далее понятно, что площадь сектора, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой площади круга и центрального угла n (соответствующего сектору), то есть

Вот вам и формула площади  сектора.

Или можно выстроить рассуждение следующим образом:

Сектор в 1 градус — это 1/360 часть круга, соответственно сектор в n градусов — это n/360 часть круга. То есть площадь сектора будет равна произведению площади круга и этой части:

Далее найдём площадь сегмента.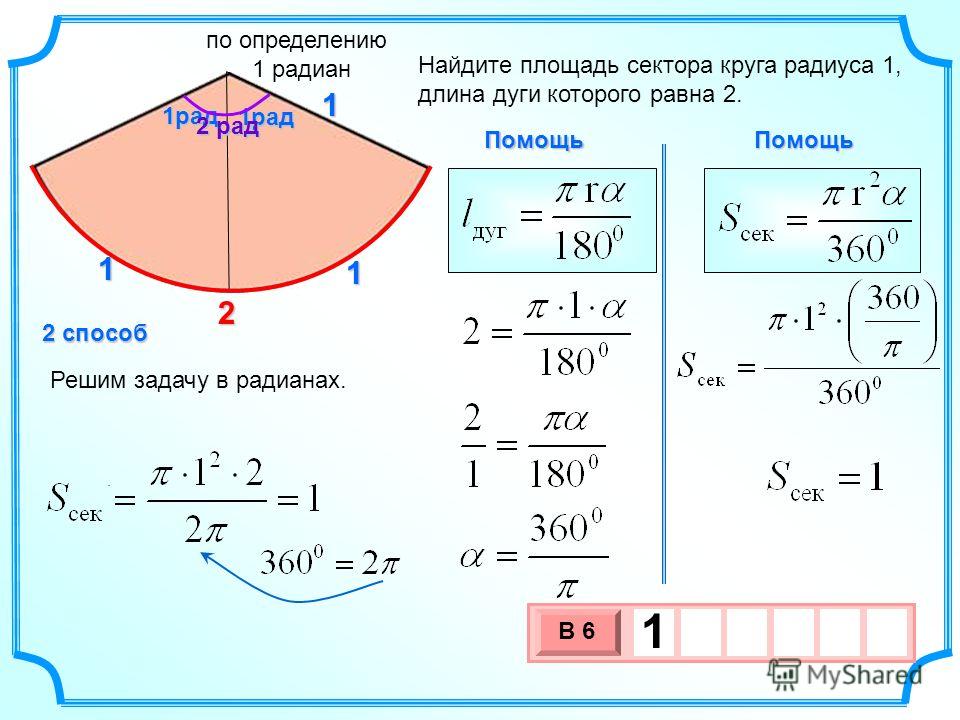

Всё просто. Необходимо из площади сектора вычесть площадь треугольника (он обозначен жёлтым цветом). Площадь треугольника, как мы знаем, равна половине произведения соседних сторон на синус угла между ними (эту формулу нужно знать, она не сложная). В данном случае это:

Значит,

Вот вам и площадь сегмента!

Площадь сегмента, где центральный угол больше 180 градусов находится просто:

Из площади круга вычитаем площадь полученного нами сегмента:

Угол  360 – n градусов это угол, который соответствует изображённому сектору (жёлтый цвет):

То есть, другими словами, к его площади мы прибавляем площадь треугольника и получаем площадь оговоренного сегмента.

Аналогичным образом определяем длину дуги окружности. Как уже сказано, длина окружности равна:

Значит, длина дуги окружности соответствующая одному  градусу будет равна одной тристашестидесятой от 2πR, то есть

Далее понятно, что длина дуги, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой длины окружности и соответствующему  углу, то есть

Получили длину дуги окружности. Конечно, данную информацию учителя дают ученикам, и ничего такого секретного вы не узнали. Но, уверен, статья принесёт вам пользу. 

Повторюсь, что самое главное — знать формулы площади круга и длины окружности, а далее работает только логика.

Предлагаю посмотреть дополнительный урок Дмирия Тарасова на эту тему. Рассматриваются формулы длины дуги окружности и площади сектора, где центральный угол задан в радианной мере.

 

 

На этом всё. Успехов Вам!!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Формулы Теория | Как запомнитьОкружность КругФормулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.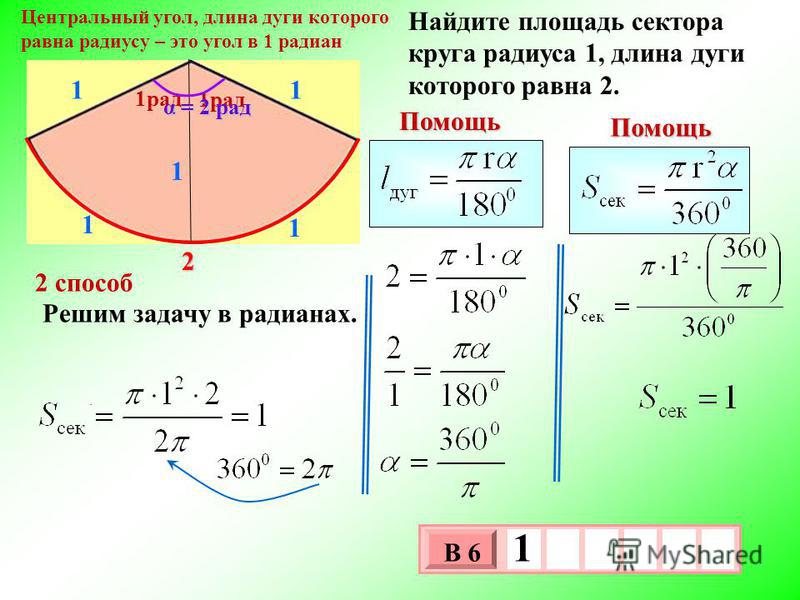

формула вычисления через длину дуги

Определение кругового сектора

Пусть имеется окружность радиусом R. Из центра проведем два радиуса под углом α друг к другу, при этом радиусы будет стягивать дуга длиной L.

Определение 

Полученная поверхность, ограниченная радиусами окружности и образованной этими радиусами дугой, называется круговым сектором.

Угол α — центральный угол.

Важно знать, что круговой сектор представляет собой развертку боковой поверхности конуса. При этом образующая конуса соответствует радиусу сектора, длина основания конуса — длине дуги сектора.

Формулы площади кругового сектора

Площадь кругового сектора выражается через центральный угол дуги. Как известно, угол может быть задан в радианной мере или в градусной.

Обозначим:

• центральный угол, выраженный в угловых градусах — α;
• длину дуги —L;
• радиус — R.

Тогда выражение для вычисления площади кругового сектора через радиус и длину дуги будет иметь вид:

Формула 1

S=R·L2

Из курса геометрии (8-9 классы) известно следующее выражение для нахождения длины дуги сектора круга:

Формула 2

L=αрад·R

где αрад — центральный угол, Рад.

Узнаем, как найти площадь сектора через центральный угол, заданный в радианах. Для этого подставим в выражение для L в формулу площади.

Формула 3

S=R·L2=R·αрад·R2=αрад·R22

Теперь переведем угол в радианах в градусы и приведем соответствующую формулу для расчета площади.

Формула 4

S=αрад·R22=R2·α·π2·180°=παR2360°

Примеры решения задач

Пример 1

Вычислить площадь кругового сектора, если его радиус 15 м, а центральный угол равен 2 Рад.

Решение.

Воспользуемся формулой: S=αрад·R22

Подставим известные значения и найдем площадь.

S=2·1522=225 м2

Ответ: 225м2.

Пример 2

Дана окружность с центром O и радиусом 10 см. Через окружность проведена хорда MN так, что в результате получился правильный треугольник MON. Найти площадь заштрихованной фигуры.

Решение.

Искомую площадь будем искать как разность площади сектора, заданного радиусами и дугой MN, и площади треугольника MON. Поскольку треугольник правильный, все его стороны равны радиусу, а каждый из углов равен 60°.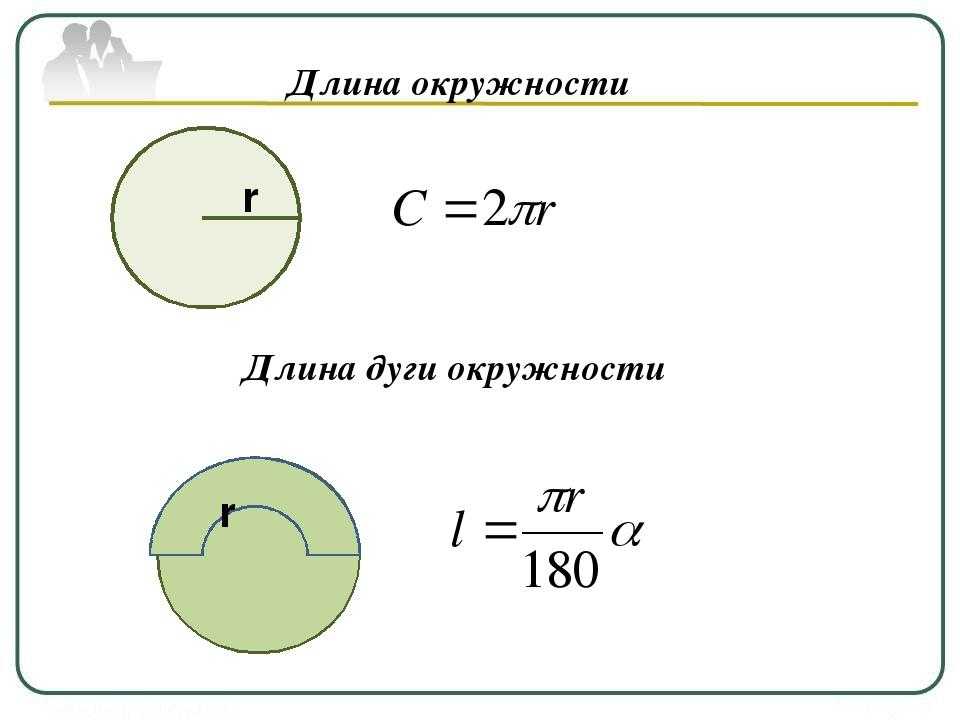

Узнаем, чему равна площадь кругового сектора. Для этого воспользуемся формулой для угла в градусной мере.

Sсектора=παR2360°=3.14·60°·102360°=52.3 см2

Теперь найдем площадь треугольника MON.

SMON=OM2·34=R2·34=100·34=43.3 см2

Найдем площадь искомой поверхности

S=Sсектора-SMON=52.3-43.3=9 см2

Ответ: 9см2.

Пример 3

Известен радиус кругового сектора R и длина его дуги L. Определить, чему равна высота конуса, полученного из заданного сектора.

Решение.

Круговой сектор есть развертка боковой поверхности конуса. Сделаем рисунок, на котором покажем конус в продольном разрезе. Получим равнобедренный треугольник. Обозначим его MNK, а высоту — NH.

Высоту MH найдем как катет прямоугольного треугольника MNH. Образующая конуса MN равна радиусу кругового сектора, то есть MN=NK=R. Сторона MH равна радиусу основания конуса — R_{конуса}. Радиус основания вычислим через длину.

Lконуса=2πRконуса⇒Rконуса=Lконуса2π

НоLконуса=L,тогдаRконуса=L2π.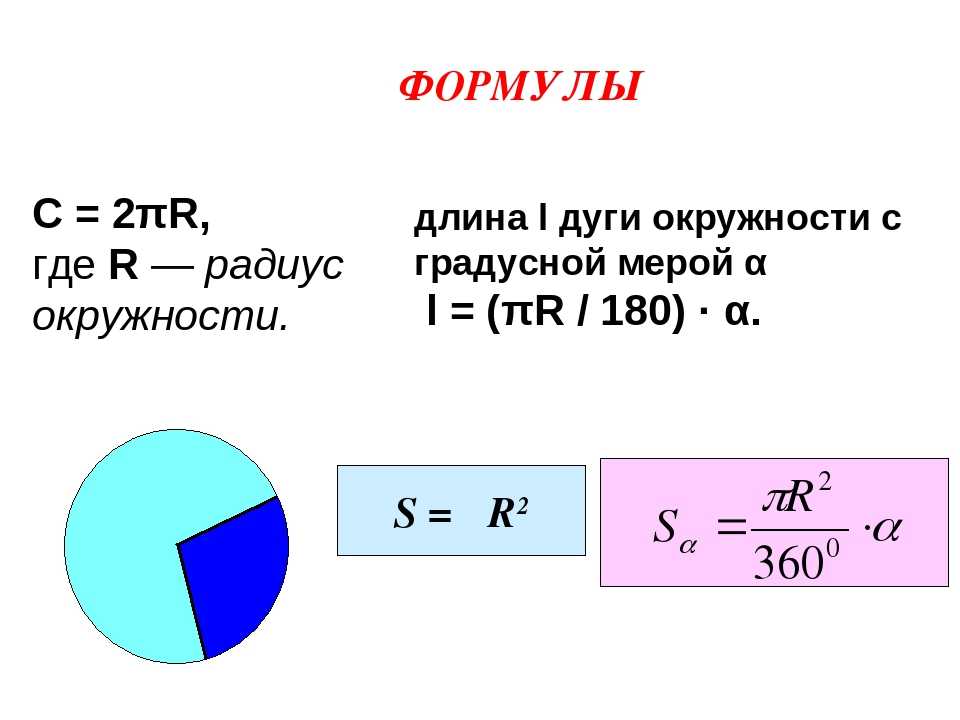

Теперь по теореме Пифагора вычислим NH.

NH=MN2-Nh3=R2-Rконуса2=R2-L2π2

Ответ: R2-L2π2.

Площадь сектора круга

, написанного

Малкольм МакКинси

11 января 2023

Проверка по фактам

Пол Маззала

Сектор круга

тыквенный пирог, круглый торт ко дню рождения или круглая пицца, вы удаляете сектор. Сектор  образован центральным углом, образованным двумя радиусами, и включает область внутри круга от этой центральной точки до самого круга. Часть окружности круга, ограниченная радиусами  дуга , является частью сектора.

Дуги окружности

Острые центральные углы всегда будут давать малых дуг  и малых секторов. Когда центральный угол, образованный двумя радиусами, равен 90° , сектор называется квадрантом (поскольку весь круг состоит из четырех квадрантов или четвертей).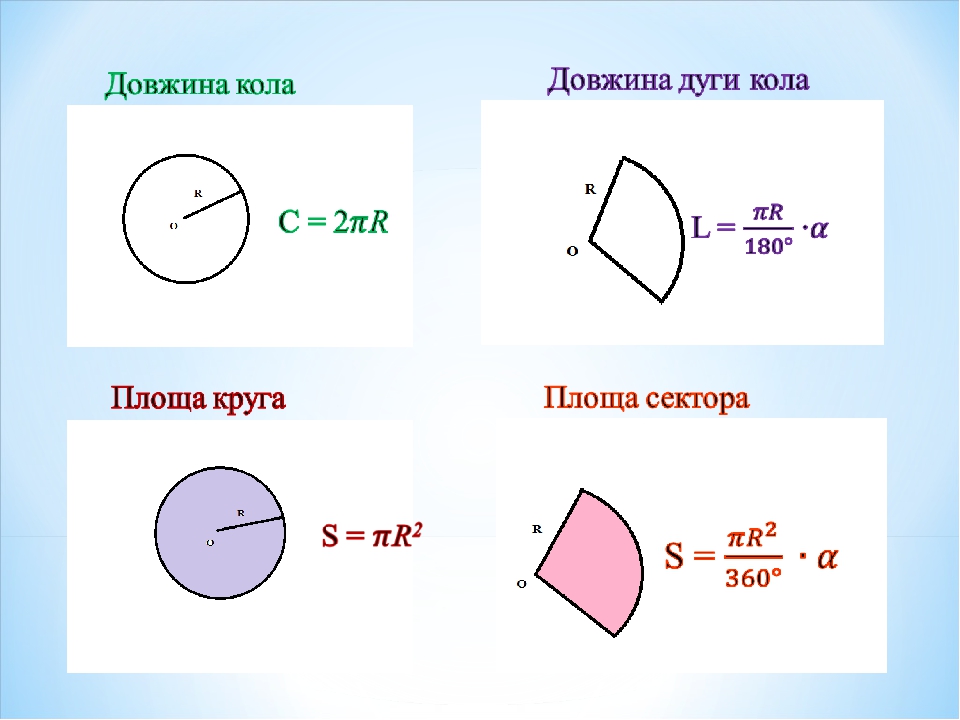 Когда два радиуса образуют 180° или половину круга, сектор называется полуокружностью и имеет большую дугу .

В отличие от треугольников, границы секторов а не  установлены отрезками. Правда, у вас есть два радиуса, образующих центральный угол, но часть окружности, которая составляет третью «сторону», изогнута, поэтому найти площадь сектора немного сложнее, чем найти площадь треугольника. Расстояние вдоль этой изогнутой «стороны» равно длине дуги .

Как найти площадь сектора

Вы не можете найти площадь сектора, если не знаете радиус окружности. Однако будьте осторожны; Вы можете найти радиус, если у вас есть диаметр или окружность. Возможно, вам придется сделать небольшую предварительную математику, чтобы получить радиус.

Найдите радиус круга

, учитывая диаметр, D , из круга, радиус, R , IS:

. радиус,  r , равен:

Зная радиус, вы получаете длины двух частей сектора. Вам нужно только знать длину дуги или центральный угол в градусах или радианах.

Площадь сектора по формуле

Центральный угол позволяет узнать, какую часть или процент от всего круга составляет ваш сектор. Квадрант имеет центральный угол 90° и составляет одну четвертую часть всей окружности. 45°  центральный угол составляет одну восьмую окружности.

Это простые дроби, но что, если ваш центральный угол 9-дюймового тыквенного пирога равен, скажем, 31° ?

Формула для нахождения площади сектора

Эта формула поможет вам найти площадь,  A , сектора, если известен центральный угол в градусах, № и радиус, r , круга:

Для тыквенного пирога вставьте 318 90 9 дюймов :

Площадь сектора в радианах

Если вместо центрального угла в градусах вам дается радиан , вы используете еще более простую формулу.

Чтобы найти площадь A сектора с центральным углом θ\thetaθ радиан и радиусом 9{2}(2θ​)×r2.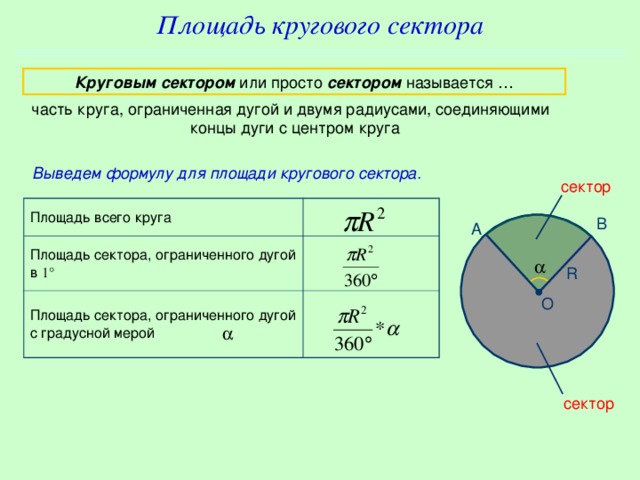

Площадь сектора круга примеры

У вас есть личная форма для пиццы диаметром из 30 см . Вы разрезали его на шесть равных частей, так что центральный угол каждой части равен 60° . Какова площадь в квадратных сантиметрах каждого куска?

Сначала попробуйте сами, прежде чем смотреть вперед!

Вы не забыли взять половину диаметра  , чтобы найти радиус?

Пример площади сектора в радианах

Предположим, у вас есть сектор с центральным углом 0,8 радиана и радиусом 1,3 метра . Ваша формула:

Попробуйте сами, прежде чем смотреть вперед!

Длина дуги и площадь сектора

Вы также можете найти площадь сектора по его радиусу и длине дуги. Формула для площади A круга с радиусом r и длиной дуги L :

Вот трехъярусный торт ко дню рождения высотой 6 дюймов и диаметром 10 дюймов .

Длина дуги и площадь сектора

Вы разрезаете его на 16 ровные части; если пренебречь объемом торта вместо , сколько квадратных дюймов верхней части торта получит каждый человек?

Каждый срез имеет заданную длину дуги 1,963 дюйма . Радиус равен  5 дюймов , поэтому:

Поскольку торт имеет объем, вы также можете вычислить его: V=(π×52×6×22,5°)360°=29{3}V=360°(π×52×6×22,5°)​=29,452 дюйма3 или кубических дюймов.

Калькулятор длины дуги и площади сектора окружности

Калькулятор длины дуги и площади сектора окружности Введите то, что вы знаете ниже
  

---

Как работает калькулятор длины дуги и площади сектора круга?

Вычисляет длину дуги окружности и площадь сектора окружности
Этот калькулятор имеет 2 входа.

Какая 1 формула используется для расчета длины дуги и площади сектора круга?

1. s = rθ
   A = ½r ² θ

Дополнительные математические формулы см. в нашем досье формул

Какие 4 понятия рассматриваются в калькуляторе длины дуги и площади сектора круга?

дуга

часть границы окружности или кривой

длина дуги и площадь сектора окружности

окружность

совокупность всех точек на плоскости, находящихся на фиксированном фиксированная точка

сектор

круговая часть круга, состоящая из дуги вместе с двумя ее радиусами
(θ/360°) * πr ² , где θ измеряется в градусах.

No related posts.