Додавання дробів калькулятор: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком

Онлайн-калькулятор для ділення в стовпчик десяткових дробів

Ділити десяткові дроби в стовпчик трохи складніше, ніж цілі числа через плаваючою точки, ще задачу ускладнює потреба поділу залишку. Тому якщо ви хочете спростити цей процес або перевірити свій результат, можна скористатися онлайн-калькулятором, який не тільки виведе відповідь, але і покаже всю процедуру вирішення.

Читайте також: Конвертери величин онлайн

зміст

• Ділимо в стовпчик десяткові дроби за допомогою онлайн-калькулятора
  • Спосіб 1: OnlineMSchool
  • Спосіб 2: Rytex

Відповідних під цю мету онлайн-сервісів існує велика кількість, проте практично всі вони мало чим відрізняються один від одного. Сьогодні ми підготували для вас два різних варіанти обчислення, а ви, ознайомившись з інструкціями, виберіть той, який буде найбільш підходящим.

Спосіб 1: OnlineMSchool

Сайт OnlineMSchool був розроблений для вивчення математики. Зараз на ньому присутні не тільки безліч корисної інформації, уроків і завдань, а й вбудовані калькулятори, один з яких ми сьогодні задіємо. Розподіл в стовпчик десяткових дробів в ньому відбувається так:

Перейти на сайт OnlineMSchool

1. Відкрийте головну сторінку сайту OnlineMSchool і перейдіть в розділ «Калькулятори».
2. Внизу ви знайдете сервіси для теорії чисел. Виберіть там «Розподіл в стовпчик» або «Розподіл в стовпчик із залишком».
3. В першу чергу зверніть увагу на інструкцію з використання, представлену у відповідній вкладці. Рекомендуємо з нею ознайомитися.
4. Тепер поверніться в «Калькулятор». Тут вам слід ще раз переконатися, що обрана правильна операція. Якщо немає, змініть її, скориставшись спливаючим меню.
5. Введіть два числа, використовуючи точку для позначення цілої частини дробу, а також відзначте галочкою пункт, якщо необхідно ділити залишок.
6. Для отримання рішення клацніть лівою кнопкою миші на знак одно.
7. Вам буде надана відповідь, де докладно розписано кожен крок отримання кінцевого числа. Ознайомтеся з ним і можете переходити до наступних обчислень.

Перед тим як ділити залишок, уважно вивчіть умову задачі. Часто цього робити не потрібно, інакше відповідь можуть зарахувати неправильним.

Всього за сім простих кроків ми змогли поділити десяткові дроби в стовпчик за допомогою невеликого інструменту на сайті OnlineMSchool.

Спосіб 2: Rytex

Онлайн-сервіс Rytex також допомагає у вивченні математики, надаючи приклади і теорію. Однак сьогодні нас цікавить присутній в ньому калькулятор, перехід до роботи з якими здійснюється наступним чином:

Перейти на сайт Rytex

1. Скористайтеся посиланням вище, щоб перейти на головну сторінку Rytex. На ній клікніть по напису «Онлайн калькулятори».
2. Опустіться в самий низ вкладки і на панелі зліва знайдете «Розподіл стовпчиком».
3. Перед початком виконання основного процесу прочитайте правила використання інструменту.
4. Тепер у відповідних полях введіть перше і друге число, а потім вкажіть, чи потрібно ділити залишок, зазначивши галочкою необхідний пункт.
5. Для отримання рішення натисніть на кнопку «Вивести результат».
6. Тепер ви можете дізнатися, як було отримано підсумкове число. Підніміться вище по вкладці, щоб перейти до введення нових значень для подальшої роботи з прикладами.

Як бачите, розглянуті нами сервіси практично не відрізняються між собою, хіба що тільки зовнішнім виглядом. Тому можна зробити висновок — немає різниці, який веб-ресурс використовувати, все калькулятори вважають правильно і надають розгорнуту відповідь за вашим прикладом.

Читайте також:
Додавання систем числення онлайн
Переклад з вісімковій в десяткову онлайн
Переклад з десяткової в шістнадцяткову систему онлайн

1.2: Математичні операції — LibreTexts

1. Last updated

2. Save as PDF

Page ID

103263

• Kelly Brooks
• Eastern Gateway Community College

Додавання цілих і десяткових чисел

Додавання чисел з однаковими знаками

• Додайте абсолютні значення чисел і призначте загальний знак результату
• ПРИМІТКА: Коли знаки обидва позитивні, додайте значення

Приклад:\(23+18\)

Загальний знак — +, тому відповідь буде позитивною, тепер ми додаємо цифри, щоб отримати

\[23+18=41\]

Приклад:\(-17+(-31)\)

Загальний знак -, тому відповідь буде негативним, тепер складаємо абсолютні значення чисел для отримання:

\[-17+\left( -31\right) =\]

Спочатку обчислюємо суму абсолютних значень:

\[\left|-17\right|+\left|-31\right|=\ 17+31=48\]

Далі призначте результату загальний знак, тому остаточна відповідь буде: -48.

\[-17+\left(-31\right)=-48\]

Додавання чисел з протилежними знаками

• Візьміть абсолютне значення кожного числа
• Відніміть меншу кількість від більшого числа
• Призначте знак результату на основі знака числа з більшим абсолютним значенням
• ПРИМІТКА: Знак більшого абсолютного значення виграє. З практикою ці кроки почнуть відчувати себе безшовно.

Приклад:\(21+(-13)\)

Спочатку обчислимо абсолютне значення кожного числа:

\[\left|21\right|=21 \text{ and } \left|-13\right|=13\]

Далі відніміть меншу кількість з більшого числа:

\[21-13=8\]

Далі призначають знак числа, абсолютне значення якого було більше, в цьому випадку знак 21 є ознакою остаточної відповіді (позитивної), звідси

\[21+\left(-13\right)=8\]

Науковий калькулятор натискань клавіш:

Приклад:\(28+(-54)\)

Спочатку обчислимо абсолютне значення кожного числа:

\(\left|28\right|=28\)і\(\left|-54\right|=54\)

Далі відніміть меншу кількість з більшого числа:

\[54-28=26\]

Далі призначають знак числа, абсолютне значення якого було більше, в цьому випадку знак -54 є ознакою остаточної відповіді (негативної), звідси

\[28+\left(-54\right)=-26\]

Short-cut: Тепер, коли ми пройшли формальний процес додавання цілих чисел, давайте отримаємо загальне уявлення про процес:

• Якщо знаки однакові, об’єднайте цифри і збережіть знак
• Якщо ознаки різні, не враховуючи ознаки, відніміть меншу кількість з більшого числа, потім збережіть знак більшого числа

Приклад:\(13+(-29)\)

Оскільки 29 більше 13, віднімаємо 13 з 29, щоб отримати 16, і використовуємо знак 29, який є негативним: -16

Приклад:\(-28+(-54)\)

Так як знаки однакові, відповідь буде мати той же знак (негативний), тепер об’єднайте цифри 28 + 54 = 82, тому остаточний відповідь -82

Аналогічно з десятковими числами:

Приклад:\(-2. 34+\left(-5.4\right)=\)

Так як знаки однакові, складаємо цифри: 2,34 + 5,4 = 7,74 і тримаємо загальний знак (негативний), щоб отримати — 7,74

Віднімання цілих і десяткових чисел

При відніманні цілого або десяткового числа додаємо протилежне числу після віднімання.

Приклад:\(15-7=\)

У цьому випадку ми можемо виконувати регулярне віднімання, однак ми також можемо застосувати правило віднімання додавання протилежного для отримання:

\[15+\left(-7\right)=8\]

оскільки 15 більше 7, віднімаємо і зберігаємо знак більшого числа, яке є позитивним

Приклад:\(3-12=\)

Пам’ятаючи додати протилежне 12, отримуємо

\[3+\left(-12\right)=-9\]

Оскільки знаки різні і 12 більше 3, віднімаємо,\(12 -3\) щоб отримати 9, але використовуємо знак 12, який є негативним, щоб отримати -9

Аналогічно з десятковими значеннями:

Приклад:\(8.23-(-1.2)=\)

Спочатку додаємо протилежне -1.2:\(8.23+1.2=\)

Далі ми поєднуємо числа, оскільки вони мають однакові знаки для отримання:

\[8. 23-\left(-1.2\right)=8.23+1.2=9.43\]

Множення та ділення цілих і десяткових чисел

Для множення або поділу цілих і десяткових чисел використовуємо множення чисел і використовуємо такі правила для знака:

• Якщо два числа мають однакові ознаки, результат позитивний
• Якщо два числа мають різні (протилежні) знаки, результат негативний

Приклади:

1. \(\left(3\right)\left(-7\right)=\ -21\)
2. \(\left(-15\right)\left(-10\right)=150\)
3. \(\left(-5.2\right)\left(2\right)=-10.4\)
4. \(\left(2\right)\left(7\right)=14\)
5. \(\left(-25\right)\div \left(-5\right)=5\)
6. \(\left(-12.8\right)\div \left(4\right)=-3.2\)
7. \(\left(250\right)\div \left(-10\right)=-25\)
8. \(\left(48\right)\div \left(6\right)=8\)

Додавання, віднімання, множення та ділення цілих і десяткових чисел за допомогою наукового калькулятора

Існує багато типів наукових калькуляторів, доступних на роздрібному ринку, на наших персональних комп’ютерах і навіть на наших персональних пристроях, таких як мобільні телефони та планшети.

В результаті давайте спочатку розмежовуємо два типи наукових калькуляторів: калькулятор дисплея та калькулятор без відображення. Деякі приклади калькуляторів відображення: TI30XIIS, TI-36X Pro, TI-30XS Multiview та Casio FX-350es PLUS. Деякі приклади калькуляторів, що не відображаються, — це TI-30xA, більшість калькуляторів стільникових телефонів та більшість калькуляторів на персональних комп’ютерах.

Для наших цілей ми визначимо, чи є калькулятор калькулятором «Відображення» або «непоказним» калькулятором, виконавши наступне:

Введіть 2 + 3 на калькуляторі.

• Якщо на вашому екрані відображається весь вираз 2 + 3, то у вас є калькулятор «Відображення».
• Якщо на екрані відображається тільки 3 після набору 2 + 3, то у вас є «непоказний» калькулятор.

На дисплеї калькуляторів ми зазвичай можемо ввести проблему так, як вона написана. На калькуляторі, що не відображається, ми зазвичай повинні вводити задачу в зворотному порядку операцій (див. розділ 2 для отримання додаткової інформації).

Давайте повернемося до деяких наших попередніх прикладів і розрахуємо їх на науковому калькуляторі. Для негативних чисел обов’язково використовуйте негативний символ (-), який зазвичай знаходиться внизу клавіатури на калькуляторі TI, а не символ віднімання, -, який зазвичай знаходиться в правій частині клавіатури. Кожен калькулятор відрізняється, тому вам, можливо, доведеться поекспериментувати з калькулятором, щоб визначити процес.

Для обчислення -17+ (-31) використовуйте наступну послідовність натискань клавіш для отримання -48:

Дисплей калькулятор:	Калькулятор без відображення:
(-) 17 + (-) 31 ВВЕСТИ	17 (-) + 31 (-) =
Введіть негативний знак перед числом	Введіть від’ємне число після знака

Для обчислення 8.23- (-1.2) = використовуйте наступну послідовність натискань клавіш, щоб отримати 9.43:

Дисплей калькулятор	Калькулятор без відображення:
8.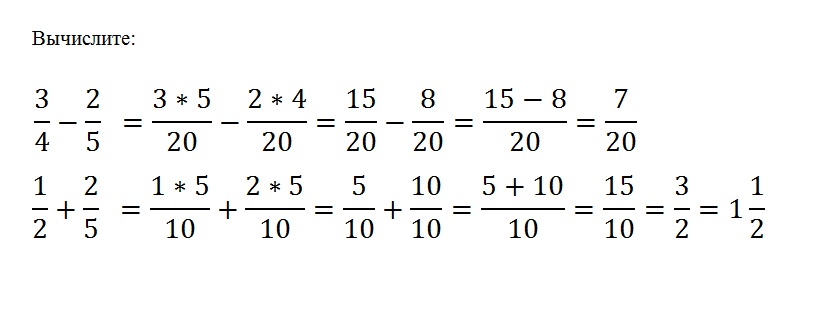 23 — (-) 1.2 ВВЕСТИ	8.23 — 1.2 (-) =
Використовуйте клавішу віднімання, а потім введіть негативний знак перед числом	Використовуйте клавішу віднімання, а потім введіть негативний знак після числа

Для обчислення (-15) (-10) = використовуйте наступну послідовність натискань клавіш, щоб отримати 150:

Дисплей калькулятор	Калькулятор без відображення:
(-) 15 Х (-) 10 ВВЕДІТЬ	15 (-) Х 10 (-) =
Введіть негативний знак перед числом	Введіть негативний знак після числа

Для обчислення (250)\(\div\) (-10) = використовуйте наступну послідовність натискань клавіш для отримання -25:

Дисплей калькулятор	Калькулятор без відображення:
250\(\div\) (-) 10 ВВЕСТИ	250\(\div\) 10 (-) =
Введіть негативний знак перед числом	Введіть негативний знак після числа

Дроби

Дроби — це дійсні числа, які вказують на частину цілого. Дріб складається з чисельника і знаменника. Знаменник являє собою кількість рівних частин предмета, а чисельник — частину цих рівних частин. Наприклад, якщо труба розділена на 4 рівні частини, ¼ представлятиме 1 з 4 частин, 2/4 представлятиме 2 з 4 частин, ¾ представлятиме 3 з 4 частин, а 4/4 = 1 представлятиме всі 4 частини або всю трубу. Так само 0/4 представлятиме 0 з 4 частин або нічого, отже, 0/4 = 0.

Прямокутник внизу ділимо на дві рівні частини. Отже, 1 з шматків з 2 штук представлятиме 1/2.

Коло, показане нижче, ділиться на 8 рівних частин. 1 частина представляла б 1/8. 2 частини представляли б 2/8, що зменшилося б до ¼ з кількох причин:

1. якби ми повинні були затінювати 2 з 8 штук, що б також представляти 1 з 4 рівних частин і
2. 2/8 можна зменшити, розділивши як чисельник (2), так і знаменник (8) на одне і те ж число, яке в даному випадку дорівнювало б 2, отже:\(\frac{2}{8}=\frac{2\div 2}{8\div 2}=\frac{1}{4}\)

«Бар» у дробі також являє собою поділ, тому ¼ також означало б\(1\div 4\). Це можна трактувати як ціле, розділене на 4 рівні частини або 1 з 4 рівних частин.

Дроби мають безліч застосувань. Дроби також можуть бути використані для представлення одиниць, таких як милі на годину або\(\frac{miles}{hour}\). Дроби також можуть бути використані для позначення коефіцієнтів і пропорцій; ми побачимо використання дробів у цих додатках в більш пізній одиниці.

Множення та ділення дробів

Щоб помножити дроби:

Множимо чисельники і множимо знаменники.

Щоб спростити, зменшіть, діливши подібні множники (числа, які діляться на інші числа).

Приклади:

1. \(\frac{2}{3}\cdot \frac{5}{7}\)

а Множимо чисельники і множимо знаменники.

\[\frac{2}{3}\cdot \frac{5}{7}=\frac{10}{21}\nonumber \]

Оскільки 10 і 21 не мають якихось загальних факторів, це спрощений або скорочений відповідь.

2. \(\frac{22}{63}\cdot \frac{9}{24}\)

а Множимо чисельники і множимо знаменники.

\[\frac{22}{63}\cdot \frac{9}{24}=\frac{108}{1512}\nonumber \]

b. спростити, зменшивши дріб (розділити чисельник і знаменник на однакові числа (и))

\[\frac{108}{1512}=\frac{108\div 12}{1512\div 12}=\frac{9}{126}=\frac{9\div 9}{126\div 9}=\frac{1}{14}\nonumber \]

Ще один варіант цієї проблеми — зменшити перед множенням:

\[\frac{12}{63}\cdot \frac{9}{24}\nonumber \]

а Зменшити чисельники і знаменники, розділивши кожен на одне і те ж число

\[\frac{12\div 12}{63\div 9}\cdot \frac{9\div 9}{24\div 12}=\frac{1}{7}\cdot \frac{1}{2}\nonumber \]

b. множити чисельники і знаменники (помножити прямо поперек)

\[\frac{1}{7}\cdot \frac{1}{2}=\frac{1}{14}\nonumber \]

3. \(\frac{24}{72}\cdot \frac{18}{30}\)

Так як числа в дробах великі, давайте спочатку зменшимо, потім множимо.

Визначте числа, які діляться як на чисельник, так і на знаменник:

9 ділиться на 18 і 72; 6 ділиться на 24 і 30 АБО 6 ділиться на 18 і 30; 24 ділиться на 24 і 72

\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 6}{72\div 9}\cdot \frac{18\div 9}{30\div 6}=\frac{4}{8}\cdot \frac{2}{5}=\frac{4\div 4}{8\div 4}\cdot \frac{2}{5}=\frac{1}{2}\cdot \frac{2}{5}=\frac{1}{2\div 2}\cdot \frac{2\div 2}{5}=\frac{1}{5} \nonumber \]

АБО

\[\frac{24}{72}\cdot \frac{18}{31}=\frac{24\div 24}{72\div 24}\cdot \frac{18\div 6}{30\div 6}=\frac{1}{3}\cdot \frac{3}{5}=\frac{1}{3\div 3}\cdot \frac{3\div 3}{5}=\frac{1}{5} \nonumber \]

Для поділу дробів: Інвертуйте другий дріб і змініть операцію на множення і продовжуйте, як описано вище.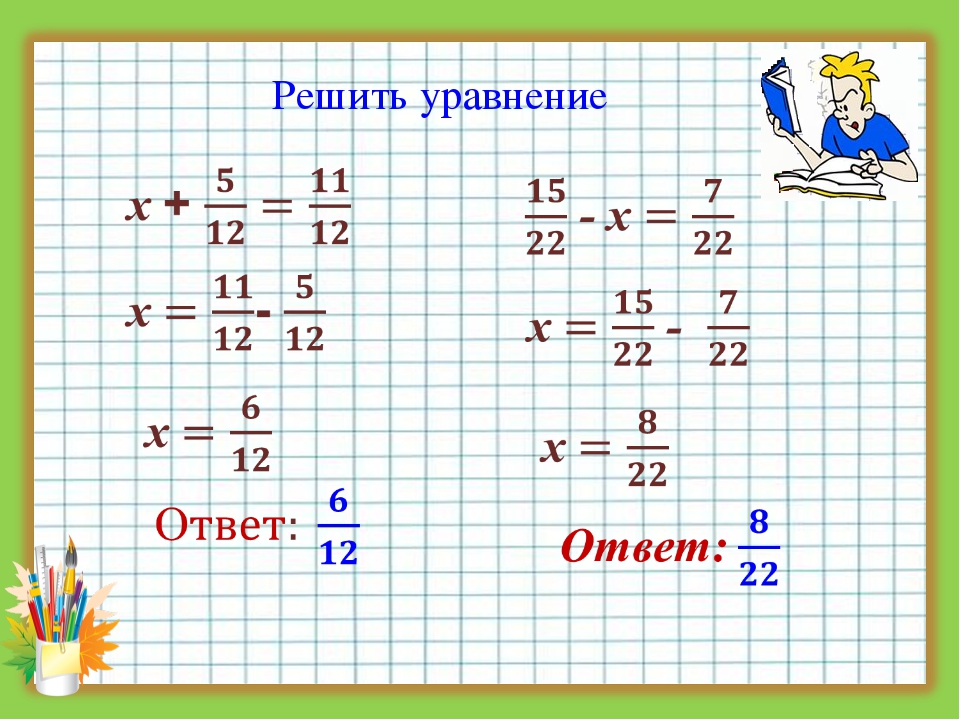

Приклад:\(\frac{3}{5}\div \frac{9}{10}\)

\[\frac{3}{5}\div \frac{9}{10}= \frac{3}{5}\cdot \frac{10}{9}=\frac{30}{45}=\frac{2}{3}\nonumber \]

Приклад:\(\frac{15}{7}\div \frac{25}{21}\)

\[\frac{15}{7}\div \frac{25}{21}=\frac{15}{7}\cdot \frac{21}{25}=\frac{3}{1}\cdot \frac{3}{5}=\frac{9}{5}\nonumber \]

Додавання та віднімання дробів

З подібними знаменниками

Для додавання або віднімання дробів дроби повинні мати однаковий знаменник:

Крок 1: Переконайтеся, що дроби схожі на дроби (дроби з однаковим знаменником).

Крок 2: Додайте або відніміть чисельники і збережіть той самий знаменник.

Приклади:

1. \(\frac{2}{7}+\frac{3}{7}=\frac{2+3}{7}=\frac{5}{7}\)
2. \(\frac{14}{17}-\frac{5}{17}=\frac{14-5}{17}=\frac{9}{17}\)

З відмінними знаменниками

Крок 1: Перепишіть несхожі дроби (дроби з різними знаменниками) як подібні дроби (дроби з однаковим знаменником) з найменш загальним кратним як їх новий знаменник. Цей новий знаменник називається найменш загальним знаменником (РК).

Щоб визначити найменший спільний знаменник (РК), знайдіть найменший спільний кратний знаменників, іншими словами, знайдіть найменше число, на яке поділяють обидва знаменника

Перепишіть несхожі дроби як подібні дроби, множивши чисельник і знаменник кожного дробу на число, яке робить знаменник кожного найменш спільним знаменником.

Крок 2: Додайте або відніміть чисельники і збережіть загальний знаменник.

Приклади:

1. \(\frac{2}{3}+\frac{1}{9}=\)

Спочатку знайдіть найменше число, на яке поділяться і 3, і 9, в цьому випадку це буде 9, тому 9 — це РК-дисплей.

Отже, нам потрібно помножити перший дріб на 3/3, щоб створити 9 в знаменнику:

\[\frac{3}{3}\cdot \frac{2}{3}+\frac{1}{9}=\frac{6}{9}+\frac{1}{9}=\frac{7}{9}\nonumber \]

2. \(\frac{3}{7}+\frac{1}{4}=\)

Найменший спільний знаменник = 28 (так як 28 — це найменше число, яке можна розділити як на 7, так і на 4)

Далі помножте чисельник і знаменник 3/7 на 4/4, щоб створити знаменник 28 і помножте чисельник і знаменник ¼ на 7/7, щоб створити знаменник 28, нарешті, додайте чисельники і збережіть загальний знаменник.

\[\frac{4}{4}\cdot \frac{3}{7}+\frac{1}{4}\cdot \frac{7}{7}=\frac{12}{28}+\frac{7}{28}=\frac{19}{28}\nonumber \]

ПРИМІТКА: Ми додаємо, віднімаємо, множимо та ділимо від’ємні дроби аналогічно тому, як ми додавали, віднімали, множили та ділили від’ємні числа в Розділі ___.

Відсотки

Відсоток визначається як сума на основі 100. Якщо розділити слово на два слова, то маємо «per» і «cent». Per означає ділити на і цент означає 100, отже, розділити на 100 або з 100.

Приклад: 54% означає 54 з 100

Ми будемо використовувати відсотки для обчислення значень в одиниці ____.

Перетворення між різними типами чисел (дроби, десяткові та відсотки)

Щоб перетворити з дробу в десятковий, розділіть чисельник на знаменник.

Щоб перетворити з десяткового числа в дріб, визначте місце останньої цифри після десяткової, запишіть дріб як всі цифри після десяткового числа над останнім знаком десяткової.

Приклад: 0.547 являє собою 547 тисячних, оскільки остання цифра після десяткового числа знаходиться в тисячному місці, у нас 547/1000.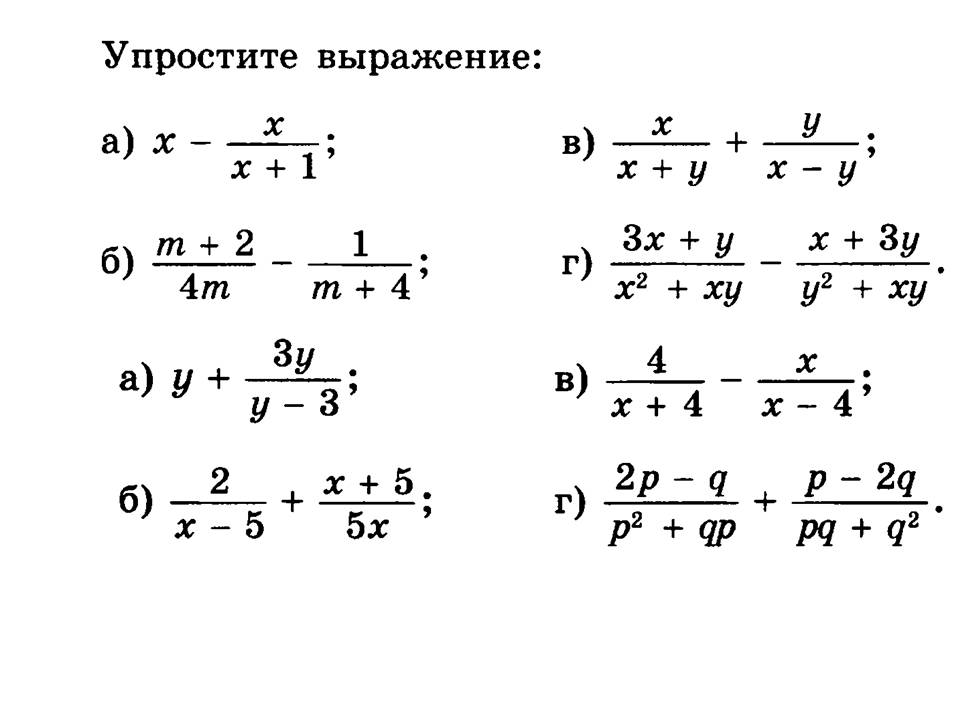

Перетворення з дробу в відсоток

Варіант 1: Перетворіть дріб у десятковий, а потім перетворіть десятковий у відсоток

Варіант 2: Використовуйте пропорцію, щоб написати дріб зі знаменником 100, тоді використовуючи визначення відсотка, відсоток буде заснований на чисельнику дробу зі знаменником 100. Ми вивчимо цей варіант більше в Unit ___, коли дізнаємося про пропорції.

Щоб перетворити з десяткового числа в відсоток, помножте десяткове число на 100 або перемістіть десятковий розряд на дві одиниці вправо.

Щоб перетворити з відсотка в десяткове число, розділіть число відсотків на 100 або перемістіть десятковий розряд на дві одиниці вліво.

1. Back to top

• Was this article helpful?

1. Article type

   Section or Page

   License

   CC BY

   License Version

   4. 0

   Show Page TOC

   No on Page

2. Tags

   1. authorname:kbrooks
   2. source[translate]-workforce-20031

Калькулятор дробей

– умножение, деление, сложение и вычитание

На этой странице находится калькулятор дробей . Введите две дроби и выберите, нужно ли складывать, вычитать, умножать или делить дроби. Мы выполним ваш выбор математики и позволим инструменту вернуть вам простейшую форму дроби.

Арифметический калькулятор дробей

Что такое дроби?

Дроби — это два числа, выраженные как часть целого. Они состоят из верхнего числа (числителя) и нижнего числа (знаменателя) и подразумевают 9.0003 отдел .

дробь\ form=\frac{числитель}{знаменатель}

Арифметика дробей

Для четырех основных арифметических функций – сложение , вычитание , деление и мульти пликация – основные правила, которым нужно следовать при работе с дробями. Я расскажу вам о каждом и покажу пример.

Сложение дробей

Чтобы сложить две дроби:

1. Сначала приведите обе дроби к общему основанию, умножив верхнее и нижнее число на одно и то же число, чтобы получить основание. (Можно найти наименьший общий знаменатель или лениво перемножить все знаменатели вместе).
2. Сложите два числителя и поместите результат в новый числитель.
3. Сложите два знаменателя и поместите результат в новый знаменатель.
4. (Необязательно) Найдите сокращенную или простейшую форму дроби.

Пример сложения дробей

Сложим две дроби: 3/9 и 1/7.

\frac{3}{9}+\frac{1}{7}\ общий\ знаменатель\ = 21\\~\\\frac{3}{9}=\frac{1}{3}*\ frac{7}{7}=\frac{7}{21}\\~\\\frac{1}{7}*\frac{3}{3}=\frac{3}{21}\\~ \\\frac{7}{21}+\frac{3}{21}=\frac{10}{21}

Вычитание дробей

Чтобы вычесть две дроби:

1. Сначала приведите обе дроби к общему основанию. Затем вам нужно умножить верхние и нижние числа на одно и то же число, чтобы получить основание. (Либо найдите наименьший общий знаменатель, либо просто перемножьте знаменатели).
2. Вычесть второй числитель из первого, поместив результат в новый числитель.
3. Вычтите второй знаменатель из первого, поместив результат в новый знаменатель.
4. (Необязательно) Найдите сокращенную или простейшую форму дроби.

Пример Вычитание дроби

Давайте вычтем дробь 1/7 из 6/21.

\frac{6}{21}-\frac{1}{7}\ общий\ знаменатель\ = 21\\~\\\frac{1}{7}*\frac{3}{3}=\ frac{3}{21}\\~\\\frac{6}{21}-\frac{3}{21}=\frac{3}{21}\\~\\(уменьшенный)=\frac{ 1}{7}

Умножение дробей

Умножение двух дробей проще всего запомнить — просто умножьте числитель и знаменатель на:

1. Умножьте первый числитель на второй и подставьте его в новый числитель.
2. Умножьте первый знаменатель на второй и подставьте в новый знаменатель.
3. (Необязательно) Найдите сокращенную или простейшую форму дроби.

Пример умножения дробей

Давайте умножим дроби 3/9 и 1/7.

\frac{3}{9}*\frac{1}{7}=\frac{3}{63}\\~\\(сокращенный)=\frac{1}{21}

Деление дробей

Деление дробей также относительно просто. Мы добавляем один шаг к умножению и инвертируем или «переворачиваем» вторую дробь.

1. Перепишите вторую дробь так, чтобы она была обратной, или поместите знаменатель над числителем.
2. Умножьте первый числитель на новый числитель переписанного второго и подставьте его в третий числитель.
3. Умножьте первый знаменатель на новый знаменатель переписанного второго и подставьте его в третий знаменатель.
4. (Необязательно) Найдите сокращенную или простейшую форму дроби.

Пример дроби

Разделим дробь 1/7 на 1/3. 9{-1}=\\~\\\разрыв{1}{7}*\разрыв{3}{1} =\frac{3}{7}

Как пользоваться калькулятором дробей

Вы можете использовать калькулятор дробей, не запоминая все эти арифметические функции!

В поле Первая дробь введите числитель первой дроби. В поле Дробь вторая введите числитель и знаменатель второй дроби.

В меню Операция выберите, какую функцию выполнять – хотите ли вы сложить (+), вычесть (-), умножить (*) или разделить (÷) дроби? Выберите свои предпочтения в меню. Затем нажмите Кнопка Выполнить дробную арифметику .

Автоматически упрощенный ответ будет указан в поле Результат .

Связанные инструменты дробей

• Поделиться
• Твитнуть
• LinkedIn
• Электронная почта
• Печать

Калькулятор дробей | iCalculator™

Используйте этот математический онлайн-калькулятор, чтобы складывать и вычитать дроби.

Калькулятор дробей

	+-

★ 90 169 ★ ★ ★ ★ [ 1143 Голоса ]

Что такое дроби?

С математической точки зрения, дробь — это числовая величина, которая не является целым числом: 1/2, 1/4, 3/8 и т. д.

Как мне считать дроби?

В следующих примерах показано, как выполнять математические действия с дробями.

Как складывать дроби

Хитрость при сложении дробей заключается в том, чтобы следить за числом под чертой, это число называется Знаменатель . Когда знаменатель обеих дробей один и тот же, сложение дроби простое. Вы просто добавляете числа над строкой (это число называется числителем ).

Расчет дробей Пример 1: 1⁄3 + 1⁄3 = 2⁄3 Легко, а?

Теперь сложение дробей становится немного (но только немного) более сложным, когда знаменатели (число внизу, под чертой) дробей, которые вы складываете, не совпадают. Существует простое правило при сложении дробей, номиналы всегда должны быть одинаковыми, математически это называется Общий знаменатель , так как все знаменатели имеют одинаковое «общее» значение.

Итак, вы пытаетесь сложить дробь и вам нужен общий знаменатель, как его получить? Если вы работаете с двумя дробями, вы можете найти общий знаменатель, просто перемножив знаменатели:

Пример расчета дроби 2a: 2⁄5 + 3⁄4 наши два знаменателя равны 5 и 4.

Пример расчета дроби 2b: 5 x 4 = 20 Умножаем их: 20 — наш Общий знаменатель.

Получилось? Большой. Теперь, чтобы сделать наши исходные дроби эквивалентными дробям .

Эквивалентная дробь — это дробь одного и того же значения, записанная в другом формате, например, 1/2 совпадает с 2/4 и 5/10.

Чтобы сделать наши дроби эквивалентными, мы должны выполнить то же действие с верхним числом (числителем), что и с нижним числом (знаменателем) умножьте 3 на 5, как мы ранее умножали 4 на 5.

Пример расчета дроби 2d: 15/20 — эквивалент дроби 3/4.

Затем мы повторяем упражнение для другой нашей дроби

Пример расчета дроби 2e: 4 x 2 = 8 Умножаем 2 на 4, как ранее умножали 5 на 4.

Пример расчета дроби 2f: 8⁄2 0 является эквивалентной долей 2/5.

Отлично, теперь нам нужно сложить две дроби с общими знаменателями, так как мы превратили их в эквивалентные дроби, которые легче складывать.

Пример расчета дробей 2g: 8/20 + 15/20 = 23/20.

Наша дробь в этом случае больше единицы (23 части головоломки из 20 частей), поэтому мы можем записать дробь как 1 3/20

Как вычитать дроби

Хитрость с вычитанием дробей заключается в том, чтобы следить за число под чертой, это число называется Знаменатель . Когда знаменатель обеих дробей один и тот же, вычитание дроби выполняется просто. Вы просто добавляете числа над строкой (это число называется 9).0114 Числитель ).

Расчет дроби Пример 1: 2⁄3 — 1⁄3 = 1⁄3 Легко, а?

Теперь вычитание дробей становится немного (но только немного) сложнее, когда знаменатели (число внизу, под чертой) дробей, которые вы вычитаете, не совпадают. Существует простое правило при вычитании дробей: номиналы всегда должны быть одинаковыми, в математических терминах это называется общим знаменателем , поскольку все знаменатели имеют одинаковое «общее» значение.

Итак, вы пытаетесь сложить дробь и вам нужен общий знаменатель, как его получить? Если вы работаете с двумя дробями, вы можете найти общий знаменатель, просто перемножив знаменатели:

Пример расчета дроби 2a: 4/5 + 3/4 наши два знаменателя равны 5 и 4.

Пример расчета дроби 2b: 5 x 4 = 20 Умножаем их: 20 — наш Общий знаменатель.

Получилось? Большой. Теперь, чтобы сделать наши исходные дроби Эквивалентные дроби .

Эквивалентная дробь — это дробь одного и того же значения, записанная в другом формате, например, 1/2 совпадает с 2/4 и 5/10.

Чтобы сделать наши дроби эквивалентными, мы должны выполнить то же действие с верхним числом (числителем), что и с нижним числом (знаменателем) умножьте 3 на 5, как мы ранее умножали 4 на 5.

Пример вычисления дроби 2d: 15/20 — эквивалентная доля 3/4.

Затем мы повторяем упражнение для другой нашей дроби

Пример вычисления дроби 2e: 4 x 4 = 16 Мы умножаем 4 на 4, как ранее умножали 5 на 4.

No related posts.