Решение задач по теме раздела. Продолжение 2 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Соотношения между сторонами и углами треугольника. Раздел 3. Скалярное произведение векторов
Урок: Решение задач по теме раздела. Продолжение 2
1. Тема урока, введение
Тема урока: «Решение задач по теме раздела. Продолжение 2». Здесь мы кратко повторим теорию и решим задачи на скалярное произведение векторов. В число задач включены доказательства некоторых известных теорем с помощью векторов.
2. Напоминание основных формул, связанных со скалярным произведением векторов
Разложение вектора по двум неколлинеарным векторам и .
пара чисел x, y – единственна.
и по правилу параллелограмма
Разложение вектора по двум неколлинеарным векторам можно использовать в решении задач следующим образом:
1.
выбрать удобную пару неколлинеарных векторов и ;
2. выразить через них искомые (или иные промежуточные) векторы;
3. использовать формулы и получить ответ.
Основные формулы:
Основные формулы в координатах.
;
3. Решение задач на скалярное произведение векторов
Задача 1. Доказать, что диагонали ромба перпендикулярны.
Дано: ABCD – ромб.
Доказать:
Доказательство:
Пусть
тогда
Умножим скалярно эти равенства:
и
Задача 2. В
Найти длину медианы AM.
Решение:
1. Пусть , тогда
2.
Ответ:
Задача 3. Доказать, что в параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.
Дано: ABCD – параллелограмм.
Доказать:
Доказательство:
Пусть , тогда
Переходя к длинам отрезков
Задача 4.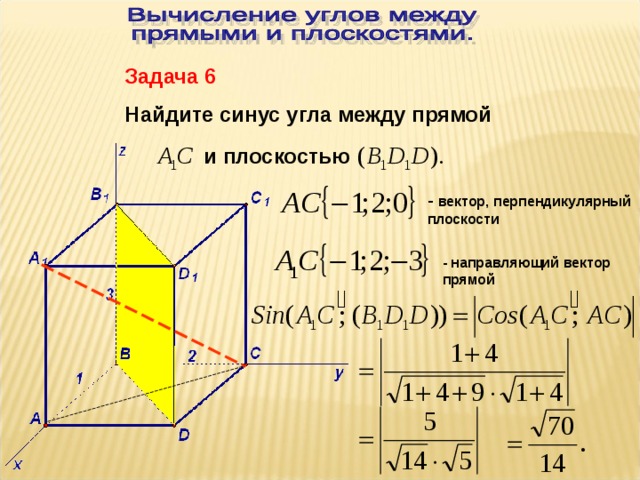
Доказать перпендикулярность векторов:
1. и ;
2. и .
Доказательство.
1.
2.
Задача 5. При каком значении t перпендикулярны векторы:
1. и ;
2. и
Решение.
1.
Ответ: при
2.
Ответ: при
Задача 6. Дано:
Доказать: ABCD – прямоугольник.
Доказательство. Чтобы доказать, что ABCD – прямоугольник, нужно доказать, что ABCD – параллелограмм и .
1.
ABCD – параллелограмм;
2. ABCD – прямоугольник.
Задача 7.
Дано:
Найти: Значение x, при котором векторы и перпендикулярны.
Решение:
1.
2.
Ответ:
4. Заключение
Итак, мы повторили теорию и решили серию задач на скалярное произведение векторов.
На следующем уроке мы рассмотрим правильные многоугольники.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия. Уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л. С. и др. Геометрия 7–9 классы. №№1052, 1053, 1069.
36. Теорема о скалярном произведении векторов. Следствие о перпендикулярных векторах (без доказательства).
Определение. Два вектора называются
перпендикулярными, если угол между ними
равен 90o.
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними.
Скалярное произведение векторов и обозначается так:.
Теорема. Скалярное произведение векторов {x1; y1; z1} и {x2; y2; z2} выражается формулой
= x1x2+ y1y2+ z1z2
Следствие 1. Ненулевые векторы {x1; y1; z1} и {x2; y2; z2} перпендикулярны тогда и только тогда, когда x1x2+ y1y2+ z1z2 = 0.
Следствие 2. Косинус угла между ненулевыми векторами {x1; y1; z1} и {x2; y2; z2} выражается формулой
37. Доказать формулу Герона.
Формула Герона выражает площадь треугольника через длины трех его сторон.
Теорема (формула Герона). Площадь треугольника со сторонами a, b, c и полупериметром p равна выражению:
Доказательство. Пусть O — центр вписанной в треугольник ABC окружности, r — ее радиус
.
Соединив центр O с вершинами
A, B и C,
получим треугольники AOC,
BOC и AOB с
высотами, равными r.
Согласно свойству площадей:
пл. треугольника ABC=пл. треугольника AOC+пл. треугольника AOB+пл. треугольника BOC=
= 1/2 b . r+1/2 c . r+1/2 a . r=r/2 (a+b+c)=p . r.
Выражая r через стороны треугольника a, b и с, получаем
Тогда ,
что и требовалось доказать.
38. Определение синуса, косинуса и тангенса для любого угла 0° до 180° (без доказательства).
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Гипотенуза прямоугольного треугольника
— это сторона, лежащая напротив прямого
угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
39. Доказать теорему об отрезках пересекающихся хорд.
Хорда — отрезок, соединяющий две точки, лежащие на окружности.
Теорема об отрезках хорд. Если две хорды одной окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство.
Проведём BC и AD.
по двум углам (опираются на одну дугу) и (вертикальные) => =>.
Задача геометрических доказательств с векторами
Задача геометрических доказательств с векторами
Решение
Начнем с определения общего прямоугольника с помощью неизвестных векторов. Затем мы используем эти векторы, чтобы найти выражения для диагоналей.
Затем мы запишем, что означает перпендикулярность этих векторов.- Начните геометрическое доказательство, пометив важные точки
Сначала задаем прямоугольник с векторами. Помещаем нижний левый угол в начало координат. Пусть верхний левый и нижний правый углы заданы векторами $\mathbf{a}$ и $\mathbf{b}$.
- Геометрический вид сложения векторов
При сложении векторов правый верхний угол равен $\mathbf{a} + \mathbf{b}$.
Поскольку нам дана информация о диагоналях прямоугольника, мы выражаем их в виде векторов.
- Вычитание дает вектор между двумя точками
Вектор, идущий из $\mathbf{a}$ в $\mathbf{b}$, равен $\mathbf{b} — \mathbf{a}$.
Аналогично, вектор, идущий от $\mathbf{0}$ к $\mathbf{a} + \mathbf{b}$, равен $\mathbf{a} + \mathbf{b}$.
Напомним, что
- Скалярное произведение перпендикулярных векторов равно нулю
Если два вектора перпендикулярны, их скалярное произведение равно нулю.
Следовательно, $$(\mathbf{b}-\mathbf{a}) \cdot (\mathbf{a} + \mathbf{b}) = 0$$
- Алгебра скалярных произведений
Поскольку скалярное произведение является дистрибутивным, мы расширим это уравнение до \begin{align}
\mathbf{b} \cdot \mathbf{a} + \mathbf{b} \cdot \mathbf{b} — \mathbf{a} \cdot \mathbf{a} — \mathbf{a} \cdot \mathbf{b} &= 0.\\
\end{выравнивание}- Алгебра скалярных произведений
Поскольку $\mathbf{a}\cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a}$, мы можем упростить это уравнение до $$\mathbf{b} \cdot \mathbf{b} = \mathbf{a} \cdot \mathbf{a}.
$$Напоминая, что
- Скалярное произведение и длина вектора
Отсюда $ \left | \mathbf{b} \право | = \ влево | \mathbf{a} \right |$, что доказывает, что прямоугольник является квадратом.
Затем мы запишем, что означает перпендикулярность этих векторов.
$$Похожие темы
- Многомерное исчисление
(147 задач)
- Векторы
(55 задач)
- Добавление вектора
(10 задач)
Сумма двух векторов — это вектор, полученный путем совмещения хвоста одного вектора с началом другого:
(6 задач)
- Вычитание векторов
(20 задач)
Вектор из $\bfx$ в $\bfy$ задается как $\bfy — \bfx$.
(14 задач)
92.$
(7 задач)
- Добавление вектора
- Алгебра скалярных произведений
$$\begin{align}
\mathbf{x} \cdot ( \mathbf{y} + \mathbf{z}) &= \mathbf{x} \cdot \mathbf{y} + \ mathbf{x} \cdot \mathbf{z}\\
(\mathbf{w} + \mathbf{x})\cdot(\mathbf{y} + \mathbf{z}) &= \mathbf{w}\ cdot \mathbf{y} + \mathbf{w}\cdot \mathbf{z} + \mathbf{x} \cdot \mathbf{y} + \mathbf{x} \cdot \mathbf{z}\\
\mathbf {x}\cdot \mathbf{y} &= \mathbf{y}\cdot \mathbf{x}
\end{align}$$(6 задач)
- Геометрические доказательства с векторами
(6 задач)
Начните геометрическое доказательство, пометив важные точки как можно меньшим числом переменных.
(5 задач)
- Векторы
страница не найдена — Williams College
| ’62 Центр Театра и Танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий/помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр изучения карьеры, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Служба поддержки инвалидов, Парески | 597-4672 | |
| Приемная, Уэстон Холл | 597-2211 | 597-4052 факс |
| Позитивные действия, Хопкинс-холл | 597-4376 | |
| Африканские исследования, Голландия | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art/Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотостудия, Spencer Studio Art | 597-2030 | |
| Студия печати, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео/фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Голландия | 597-2391 | 597-3028 факс |
| Астрономия/астрофизика, Физика Томпсона | 597-2482 | 597-3200 факс |
| Отделение легкой атлетики, физического воспитания, отдыха, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочная пристань, озеро Онота | 443-9851 | |
| Вагоны | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Хоккейная площадка Ice Line, Lansing Chapman | 597-2433 | |
| Очные занятия, Спортивный центр Чендлера | 597-3321 | |
| Физкультура | 597-2141 | |
| Влажная линия бассейна, Спортивный центр Чендлера | 597-2419 | |
| Информация о спорте, Хопкинс-холл | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Корты для сквоша | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Биология Томпсона | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Томпсон Биология | 597-2126 | 597-3495 факс |
| Безопасность и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа/Системы сигнализации | 597-4970/4033 | |
| Служба сопровождения, Хопкинс-холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Распределительный щит | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
Центр экологических исследований, выпуск 1966 г. |