Алгоритм Форда-Фалкерсона / Хабр
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.
Исходный графКак работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
Отправлять определенное количество потока из текущей вершины в соседние.

Возвращать определенное количество потока из соседних вершин в текущую.
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.

Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
Начальная остаточная сетьОстаточная сеть после 1-ой итерацииРёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .
Остаточная сеть после 1-ой итерации Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Источники
Паша и Алгосы
Инструмент для работы с графами
Задача о максимальном потоке | это… Что такое Задача о максимальном потоке?
Максимальный поток в транспортной сети. Числа обозначают потоки и пропускные способности.
Числа обозначают потоки и пропускные способности.
В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сумма потоков из истока, или, что то же самое, сумма потоков в сток максимальна.
Задача о максимальном потоке является частным случаем более трудных задач, как например задача о циркуляции.
Содержание
|
История
После вступления США во Вторую мировую войну в 1941 году математик Джордж Бернард Данциг поступил на работу в отдел статистического управления Военно-воздушных сил США в Вашингтоне. С 1941 по 1946 годы он возглавлял подразделение анализа военных действий (Combat Analysis Branch), где работал над различными математическими проблемами.[1][2] Впоследствии c использованием работы Данцига задача о максимальном потоке была впервые решена в ходе подготовки воздушного моста во время блокады Западного Берлина, происходившей в 1948—1949 году.[3][4][5]
С 1941 по 1946 годы он возглавлял подразделение анализа военных действий (Combat Analysis Branch), где работал над различными математическими проблемами.[1][2] Впоследствии c использованием работы Данцига задача о максимальном потоке была впервые решена в ходе подготовки воздушного моста во время блокады Западного Берлина, происходившей в 1948—1949 году.[3][4][5]
В 1951 году Джордж Данциг впервые сформулировал задачу в общем виде.[6]
В 1955 году, Лестер Форд и Делберт Фалкерсон (англ. Delbert Ray Fulkerson) впервые построили алгоритм, специально предназначенный для решения этой задачи. Их алгоритм получил название алгоритм Форда-Фалкерсона.[7][8]
В дальнейшем решение задачи много раз улучшалось.
В 2010 году исследователи Джонатан Кёлнер (Jonathan Kelner) и Александер Мондры (Aleksander Mądry) из МТИ вместе со своими коллегами Дэниелем Спилманом (en:Daniel Spielman) из Йельского университета и Шень-Хуа Тенем (en:Shang-Hua Teng) из Южно-Калифорнийского университета продемонстрировали очередное улучшение алгоритма, впервые за 10 лет. [3][9][10]
[3][9][10]
Определение
- Величиной потока (value of flow) называется сумма потоков из источника . В статье «Транспортная сеть» доказано, что она равна сумме потоков в сток .
Задача о максимальном потоке заключается в нахождении потока такого, что величина потока максимальна.
Решения
Следующая таблица перечисляет некоторые алгоритмы решения задачи.
| Метод | Сложность | Описание |
|---|---|---|
| Линейное программирование | Зависит от конкретного алгоритма. Для симплекс-метода экспоненциальна. | Представить задачу о максимальном потоке как задачу линейного программирования. Переменными являются потоки по рёбрам, а ограничениями — сохранение потока и ограничение пропускной способности. |
| Алгоритм Форда-Фалкерсона | Зависит от алгоритма поиска увеличивающего пути.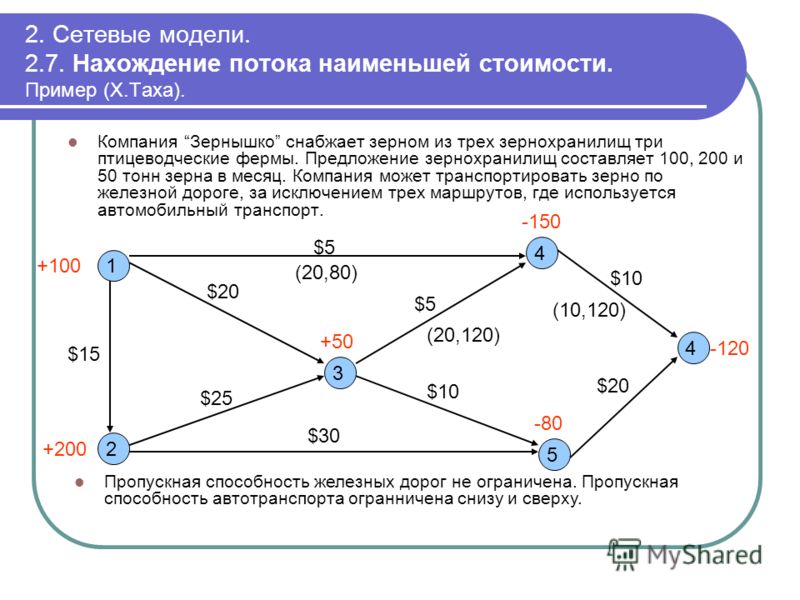 Требует O(max| f |) таких поисков. | Найти любой увеличивающий путь. Увеличить поток по всем его рёбрам на минимальную из их остаточных пропускных способностей. Повторять, пока увеличивающий путь есть. Алгоритм работает только для целых пропускных способностей. В противном случае, он может работать бесконечно долго, не сходясь к правильному ответу. |
| Алгоритм Эдмондса-Карпа | O(VE²) | Выполняем алгоритм Форда-Фалкерсона, каждый раз выбирая кратчайший увеличивающий путь (находится поиском в ширину). |
| Алгоритм Диница | O(V²E) для единичных пропускных способностей с использованием динамических деревьев Слетора и Тарьяна[11] | Усовершенствование алгоритма Эдмондса-Карпа (но хронологически был найден раньше). На каждой итерации, используя поиск в ширину, определяем расстояния от источника до всех вершин в остаточной сети. Строим граф, содержащий только такие рёбра остаточной сети, на которых это расстояние растёт на 1. |
| Алгоритм проталкивания предпотока | O(V²E) | Вместо потока оперирует с предпотоком. Отличие в том, что для любой вершины u, кроме источника и стока, сумма входящих в неё потоков для потока должна быть строго нулевой (условие сохранения потока), а для предпотока — неотрицательной. Эта сумма называется избыточным потоком в вершину, а вершина с положительным избыточным потоком называется переполненной. Кроме того, для каждой вершины алгоритм сохраняет дополнительную характеристику, высоту, являющуюся целым неотрицательным числом. Алгоритм использует две операции: проталкивание, когда поток по ребру, идущему из более высокой в более низкую вершину, увеличивается на максимально возможную величину, и подъём, когда переполненная вершина, проталкивание из которой невозможно из-за недостаточной высоты, поднимается. Проталкивание возможно, когда ребро принадлежит остаточной сети, ведёт из более высокой вершины в более низкую, и исходная вершина переполнена. Подъём возможен, когда поднимаемая вершина переполнена, но ни одна из вершин, в которые из неё ведут рёбра остаточной сети, не ниже её. Он совершается до высоты на 1 большей, чем минимальная из высот этих вершин. Изначально высота источника V, по всем рёбрам, исходящим из источника, течёт максимально возможный поток, а остальные высоты и потоки нулевые. Операци проталкивания и подъёма выполняются до тех пор, пока это возможно. Алгоритм использует две операции: проталкивание, когда поток по ребру, идущему из более высокой в более низкую вершину, увеличивается на максимально возможную величину, и подъём, когда переполненная вершина, проталкивание из которой невозможно из-за недостаточной высоты, поднимается. Проталкивание возможно, когда ребро принадлежит остаточной сети, ведёт из более высокой вершины в более низкую, и исходная вершина переполнена. Подъём возможен, когда поднимаемая вершина переполнена, но ни одна из вершин, в которые из неё ведут рёбра остаточной сети, не ниже её. Он совершается до высоты на 1 большей, чем минимальная из высот этих вершин. Изначально высота источника V, по всем рёбрам, исходящим из источника, течёт максимально возможный поток, а остальные высоты и потоки нулевые. Операци проталкивания и подъёма выполняются до тех пор, пока это возможно. |
| Алгоритм «поднять в начало» | O(V³) O(VE log(V²/E)) с использованием динамических деревьев | Вариант предыдущего алгоритма, специальным образом определяющий порядок операций проталкивания и подъёма. |
| Алгоритм двоичного блокирующего потока * |
Для более подробного списка, см. * и Список алгоритмов нахождения максимального потока.
Теорема о целом потоке
Если пропускные способности целые, максимальная величина потока тоже целая.
Теорема следует, например, из теоремы Форда—Фалкерсона.
Обобщения, сводящиеся к исходной задаче
Некоторые обобщения задачи о максимальном потоке легко сводятся к исходной задаче.
Произвольное число источников и/или стоков
Если источников больше одного, добавляем новую вершину S, которую делаем единственным источником. Добавляем рёбра с бесконечной пропускной способностью от S к каждому из старых источников.
Аналогично, если стоков больше одного, добавляем новую вершину T, которую делаем единственным стоком. Добавляем рёбра с бесконечной пропускной способностью от каждого из старых стоков к T.
Неориентированные рёбра
Каждое неориентированное ребро (u, v) заменяем на пару ориентированных рёбер (u, v) и (v, u).
Ограничение пропускной способности вершин
Каждую вершину v с ограниченной пропускной способностью расщепляем на две вершины vin и vout. Все рёбра, до расщепления входящие в v, теперь входят в vin. Все рёбра, до расщепления исходящие из v, теперь исходят из vout. Добавляем ребро (vin,vout) с пропускной способностью .
См. также
- Поток минимальной стоимости
- Транспортная сеть
Примечания
- ↑ Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. George Dantzig (англ.) в архиве MacTutor.
- ↑ Cottle, Richard; Johnson, Ellis; Wets, Roger, «George B. Dantzig (1914—2005)», Notices of the American Mathematical Society, v.54, no.3, March 2007. Cf. p.348
- ↑ 1 2 Hardesty, Larry, «First improvement of fundamental algorithm in 10 years», MIT News Office, September 27, 2010
- ↑ Borndörfer, Ralf; Grötschel, Martin; Löbel, Andreas, «Alcuin’s Transportation Problems and Integer Programing», Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Germany, November 1995.
 Cf. p.3
Cf. p.3 - ↑ Powell, Stewart M., «The Berlin Airlift», Air Force Magazine, June 1998.
- ↑ Dantzig, G.B., «Application of the Simplex Method to a Transportation Problem», in T.C. Koopman (ed.): Activity Analysis and Production and Allocation, New York, (1951) 359—373.
- ↑ Ford, L.R., Jr.; Fulkerson, D.R., «Maximal Flow through a Network», Canadian Journal of Mathematics (1956), pp.399-404.
- ↑ Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
- ↑ Kelner, Jonathan, «Electrical Flows, Laplacian Systems and Faster Approximation of Maximum Flow in Undirected Graphs», talk at CSAIL, MIT, Tuesday, September 28 2010
- ↑ Electrical Flows, Laplacian Systems, and Faster Approximation of Maximum Flow in Undirected Graphs, by Paul Cristiano et al., October 19, 2010.
- ↑ Алгоритм Диница
Литература
- Schrijver, Alexander, «On the history of the transportation and maximum flow problems», Mathematical Programming 91 (2002) 437—445
- Кормен, Т.
 , Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4. Глава 26. Максимальный поток.
, Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4. Глава 26. Максимальный поток. - ↑ Andrew V. Goldberg and S. Rao (1998). «Beyond the flow decomposition barrier». J. Assoc. Comput. Mach. 45: 753–782. DOI:10.1145/290179.290181.
- ↑ Andrew V. Goldberg and Robert E. Tarjan (1988). «A new approach to the maximum-flow problem». Journal of the ACM (ACM Press) 35 (4): 921–940. DOI:10.1145/48014.61051. ISSN 0004-5411.
- ↑ Joseph Cheriyan and Kurt Mehlhorn (1999). «An analysis of the highest-level selection rule in the preflow-push max-flow algorithm». Information Processing Letters 69 (5): 239–242. DOI:10.1016/S0020-0190(99)00019-8.
- ↑ Daniel D. Sleator and Robert E.

- ↑ Daniel D. Sleator and Robert E. Tarjan (1985). «Self-adjusting binary search trees». Journal of the ACM (ACM Press) 32 (3): 652–686. DOI:10.1145/3828.3835. ISSN 0004-5411.
- Eugene Lawler 4. Network Flows // Combinatorial Optimization: Networks and Matroids. — Dover, 2001. — P. 109–177. — ISBN 0486414531
Учебные пособия и примечания по максимальному расходу | Алгоритмы
В теории графов сеть потоков определяется как ориентированный граф, включающий источник ( $$S$$ ) и сток ( $$T$$ ) и несколько других узлов, соединенных ребрами. Каждое ребро имеет индивидуальную пропускную способность, которая является максимальным пределом потока, который может позволить ребро.
Поток в сети должен соответствовать следующим условиям:
- Для любого узла, не являющегося источником и неприемником, входной поток равен выходному потоку.

- Для любого ребра ($$E_i$$) в сети $$ 0 \le flow(E_i) \le Capacity(E_i) $$.
- Общий исходящий поток из узла-источника равен общему потоку к узлу-приемнику.
- Чистый поток на ребрах следует косой симметрии, т. е. $$F(u,v) = -F(v,u)$$, где $$F(u,v)$$ — это поток из узла u в узел v. Это приводит к выводу, где вы должны суммировать все потоки между двумя узлами (в любом направлении), чтобы изначально найти чистый поток между узлами.
Максимальный поток:
Определяется как максимальный объем потока, который сеть может пропускать от источника к приемнику. Существует несколько алгоритмов решения задачи о максимальном потоке. Двумя основными алгоритмами для решения такого рода проблем являются алгоритм Форда-Фалкерсона и алгоритм Диника. Они объясняются ниже.
Алгоритм Форда-Фалкерсона:
Он был разработан Л. Р. Фордом-младшим и Д. Р. Фулкерсоном в 1956 году. Псевдокод для этого алгоритма приведен ниже,
Требуемые входные данные: сетевой граф $$G$$, исходный узел $ $S$$ и стоковой узел $$T$$.
функция: FordFulkerson (график G, узел S, узел T):
Инициализировать поток на всех ребрах до 0
в то время как (существует увеличивающий путь (P) между S и T в графе остаточной сети):
Увеличение потока между S и T по пути P
Обновить график остаточной сети
возвращаться
Увеличивающий путь — это простой путь от истока к приемнику, который не включает циклов и проходит только через положительные взвешенные ребра. Остаточный сетевой граф показывает, насколько больше потока разрешено на каждом ребре в сетевом графе. Если не существует увеличивающих путей из $$S$$ в $$T$$, то поток максимален. Результатом, т. е. максимальным потоком, будет общий поток, исходящий из узла-источника, который также равен общему потоку, поступающему в узел-приемник.
Демонстрация работы алгоритма Форда-Фалкерсона показана ниже с помощью диаграмм.
Реализация:
- Увеличивающий путь в остаточном графе можно найти с помощью DFS или BFS.

- Обновление остаточного графа включает в себя следующие шаги: (обратитесь к диаграммам для лучшего понимания)
- Для каждого ребра на увеличивающемся пути значение минимальной пропускной способности пути вычитается из всех ребер этого пути.
- Ребро равного количества добавляется к ребрам в обратном направлении для каждого последующего узла на увеличивающемся пути.
Сложность алгоритма Форда-Фалкерсона не может быть точно рассчитана, так как все зависит от пути от источника к приемнику. Например, при рассмотрении сети, показанной ниже, если каждый раз выбирается путь $$S-A-B-T$$ и $$S-B-A-T$$ попеременно, то это может занять очень много времени. Вместо этого, если выбран путь только $$S-A-T$$ и $$S-B-T$$, также будет генерироваться максимальный поток.
Алгоритм Диника
В 1970 г. Ю. А. Диниц разработал более быстрый алгоритм расчета максимального потока по сетям. Он включает в себя построение графов уровней и остаточных графов, а также нахождение увеличивающих путей наряду с блокирующим потоком.
Уровневый граф — это граф, в котором значением каждого узла является его кратчайшее расстояние от источника.
Блокирующий поток включает поиск нового пути от узла узкого места.
Остаточный граф и увеличивающие пути обсуждались ранее.
Ниже приведен псевдокод алгоритма Диника.
Требуемые входные данные: граф сети G, узел-источник S и узел-приемник T.
Функция: DinicMaxFlow(График G,Узел S,Узел T):
Инициализировать поток на всех ребрах до 0, F = 0
Построить график уровня
while (существует увеличивающий путь в графе уровней):
найти блокирующий поток f в графе уровней
Ф = Ф + Ф
График уровня обновления
вернуть F
Обновление графа уровня включает удаление ребер с полной пропускной способностью. Удаление узлов, которые не являются стоковыми и являются тупиковыми. Демонстрация работы алгоритма Диника показана ниже с помощью диаграмм.
Предоставил: Vinay Kumar
Введение в проблему максимального расхода — GeeksforGeeks
Улучшить статью
Сохранить статью
- Уровень сложности: Hard
- Последнее обновление: 23 ноя, 2022
Улучшить статью
Сохранить статью
Проблемы с максимальным потоком связаны с поиском допустимого потока через сеть потока с одним источником и одним стоком, который является максимальным. Давайте возьмем изображение, чтобы объяснить, что хочет сказать приведенное выше определение. Каждое ребро помечено вместимостью, максимальным количеством вещей, которые оно может нести. Цель состоит в том, чтобы выяснить, сколько материала можно переместить из вершины s (источник) в вершину t (приемник). . максимально возможный расход: 23 Ниже приведены различные подходы к решению проблемы: 1. Подход на основе жадного алгоритма (может не дать оптимального или правильного результата) Жадный подход к задаче о максимальном потоке состоит в том, чтобы начать с полностью нулевого потока и жадно создавать потоки со все более высокой ценностью. Естественный способ перейти от одного к другому — направить больше потока по некоторому пути от s к t. Как работает жадный подход для нахождения максимального потока:
Давайте возьмем изображение, чтобы объяснить, что хочет сказать приведенное выше определение. Каждое ребро помечено вместимостью, максимальным количеством вещей, которые оно может нести. Цель состоит в том, чтобы выяснить, сколько материала можно переместить из вершины s (источник) в вершину t (приемник). . максимально возможный расход: 23 Ниже приведены различные подходы к решению проблемы: 1. Подход на основе жадного алгоритма (может не дать оптимального или правильного результата) Жадный подход к задаче о максимальном потоке состоит в том, чтобы начать с полностью нулевого потока и жадно создавать потоки со все более высокой ценностью. Естественный способ перейти от одного к другому — направить больше потока по некоторому пути от s к t. Как работает жадный подход для нахождения максимального потока:
E количество ребер
ф(д) поток края
C(e) емкость края
1) Инициализировать: max_flow = 0
f(e) = 0 для каждого ребра 'e' в E
2) Повторить поиск s-t пути P, пока он существует. а) Найдите, существует ли путь из s в t, используя BFS
или ДФС. Путь существует, если f(e) < C(e) для
каждое ребро e на пути.
б) Если путь не найден, вернуть max_flow.
c) В противном случае найдите минимальное значение ребра для пути P
// Наш поток ограничен наименьшим оставшимся
// край пропускной способности на пути P.
(i) поток = min(C(e)-f(e)) для пути P]
max_flow += поток
(ii) Для всех ребер e потока приращений пути
f(e) += поток
3) Вернуть max_flow
а) Найдите, существует ли путь из s в t, используя BFS
или ДФС. Путь существует, если f(e) < C(e) для
каждое ребро e на пути.
б) Если путь не найден, вернуть max_flow.
c) В противном случае найдите минимальное значение ребра для пути P
// Наш поток ограничен наименьшим оставшимся
// край пропускной способности на пути P.
(i) поток = min(C(e)-f(e)) для пути P]
max_flow += поток
(ii) Для всех ребер e потока приращений пути
f(e) += поток
3) Вернуть max_flow Обратите внимание, что при поиске пути нужно просто определить, существует ли путь s-t в подграфе ребер e с f(e) < C(e). Это легко сделать за линейное время с помощью BFS или DFS. Существует путь от источника (ов) к приемнику (t) [ s -> 1 -> 2 -> t] с максимальным потоком 3 единицы (путь показан синим цветом). После удаления всех бесполезных ребер из графика это выглядит так. Для выше На графике нет пути от источника к стоку, поэтому максимальный поток: 3 единицы. Но максимальный поток составляет 5 единиц. Чтобы решить эту проблему, мы используем остаточный график.
Но максимальный поток составляет 5 единиц. Чтобы решить эту проблему, мы используем остаточный график.
2. Остаточные графики
Идея состоит в том, чтобы расширить наивный жадный алгоритм, разрешив операции «отмены». Например, из точки, где этот алгоритм застревает на изображении выше, мы хотели бы направить еще две единицы потока вдоль края (s, 2), затем назад по краю (1, 2), отменив 2 из 3 единицы, которые мы проложили на предыдущей итерации, и, наконец, вдоль ребра (1,t) обратного ребра: (f(e)) и прямого ребра: (C(e) – f(e)) Нам нужен способ формального указания допустимые операции «отмены». Это мотивирует следующее простое, но важное определение остаточной сети. Идея состоит в том, что, имея граф G и поток f в нем, мы формируем новую сеть потоков G f , имеющее то же множество вершин G и имеющее по два ребра для каждого ребра G. Ребро e = (1,2) графа G, несущее поток f(e) и имеющее пропускную способность C(e) (для приведенных выше image ) порождает «передний край» G f с пропускной способностью C(e)-f(e) (оставшаяся комната) и «обратный край» (2,1) G f с пропускной способностью f(e ) (объем ранее перенаправленного потока, который можно отменить).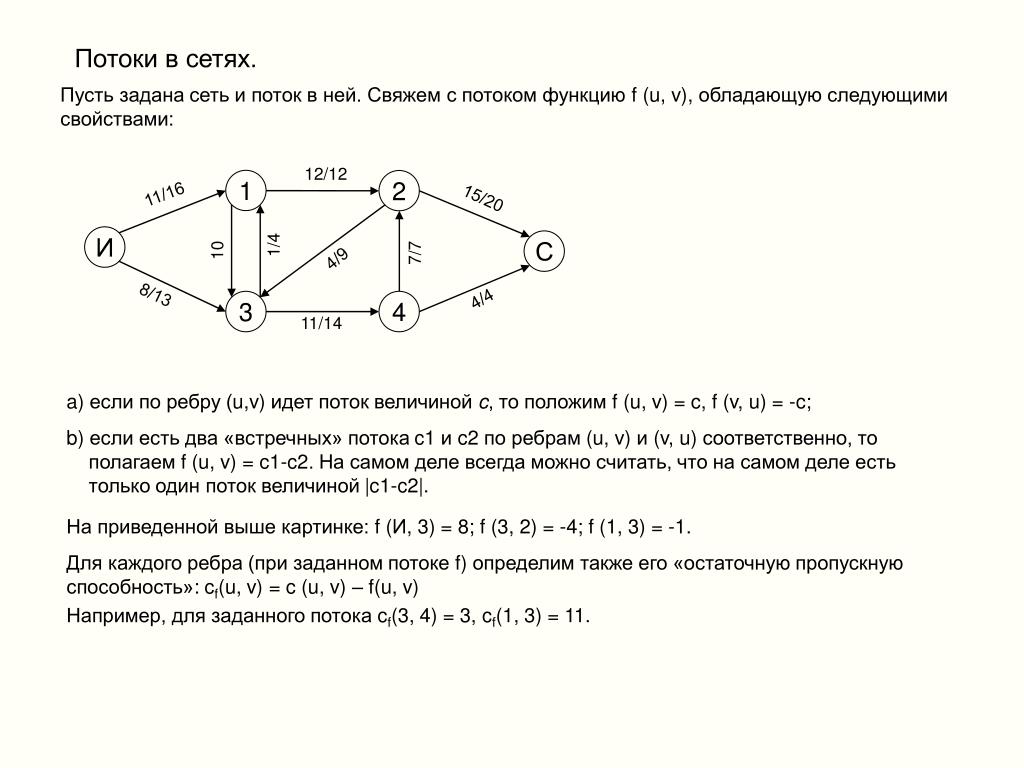



 Cf. p.3
Cf. p.3 , Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4. Глава 26. Максимальный поток.
, Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4. Глава 26. Максимальный поток.


 а) Найдите, существует ли путь из s в t, используя BFS
или ДФС. Путь существует, если f(e) < C(e) для
каждое ребро e на пути.
б) Если путь не найден, вернуть max_flow.
c) В противном случае найдите минимальное значение ребра для пути P
// Наш поток ограничен наименьшим оставшимся
// край пропускной способности на пути P.
(i) поток = min(C(e)-f(e)) для пути P]
max_flow += поток
(ii) Для всех ребер e потока приращений пути
f(e) += поток
3) Вернуть max_flow
а) Найдите, существует ли путь из s в t, используя BFS
или ДФС. Путь существует, если f(e) < C(e) для
каждое ребро e на пути.
б) Если путь не найден, вернуть max_flow.
c) В противном случае найдите минимальное значение ребра для пути P
// Наш поток ограничен наименьшим оставшимся
// край пропускной способности на пути P.
(i) поток = min(C(e)-f(e)) для пути P]
max_flow += поток
(ii) Для всех ребер e потока приращений пути
f(e) += поток
3) Вернуть max_flow