Событие называется достоверным, — КиберПедия
А. если вероятность его близка к единице;
В. если при заданном комплексе факторов оно может произойти;
+ С. если при заданном комплексе факторов оно обязательно произойдет;
D. если вероятность события не зависит от причин, условий, испытаний.
12. Событие, которое при заданном комплексе факторов не может осуществиться называется:
А. несовместным;
В. независимым;
+ С. невозможным;
D. противоположным.
События называются несовместными, если
А. в данном опыте они могут появиться все вместе;
В. сумма вероятностей их равна единице;
С. хотя бы одно из них не может появиться одновременно с другим;
+ D. в одном и том же опыте появление одного из них исключает появление других событий.
Несколько событий в данном опыте называются равновозможными,
А. если при заданном комплексе факторов они произойдут;
В. если есть основание считать, что ни одно из этих событий не является более возможным чем другое и появление одного из них исключает появление другого.
если есть основание считать, что ни одно из этих событий не является более возможным чем другое и появление одного из них исключает появление другого.
+ С. если есть основание считать, что ни одно из этих событий не является более возможным чем другое.
Два события называются противоположными
А. если они равновозможные и в сумме составляют достоверное событие;
+ В. если они несовместны и в сумме составляют достоверное событие;
С. если сумма вероятностей их равна единице;
D. если они взаимно исключают друг друга.
Суммой, (объединением) нескольких случайных событий называется
А. событие, состоящее в появлении любого из этих событий;
В. событие, состоящее в появлении всех указанных событий;
+ С. событие, состоящее в появлении хотя бы одного из этих событий;
D. событие, состоящее в появлении одного из этих событий.
Произведением, совмещением, нескольких событий называется
А. событие, состоящее в осуществлении любого из этих событий;
событие, состоящее в осуществлении любого из этих событий;
В. событие, состоящее в появлении хотя бы одного из этих событий;
С. событие, состоящее в последовательном появлении всех этих событий;
+D. событие, состоящее в осуществлении одновременно всех этих событий.
Вероятность совместного наступления двух независимых событий определяется как
A. сумма их вероятностей;
B. разность их вероятностей;
+ C. произведение их вероятностей;
D. среднее значение их вероятностей.
Вероятность наступления одного из нескольких несовместных случайных событий (все равно какого) определяется как
+ A. сумма их вероятностей;
B. разность их вероятностей;
C. произведение их вероятностей;
D. среднее значение их вероятностей.
Значение вероятности случайного события
А. лежит в интервале от -1 до +1;
+ В. лежит в интервале от 0 до 1;
С. положительное число.
Может ли относительная частота наступления случайного события в серии экспериментов оказаться больше, чем его вероятность?
+ А. да, может;
да, может;
В. нет, не может;
С. может в результате ошибки экспериментатора.
Перестает ли событие быть случайным, если оно уже происходило?
+ А. да;
В. нет;
С. нужна дополнительная информация.
23. Случайным событием является:
A. лечение пациента прошло эффективно;
+ B. на прием к врачу пришло 3 пациента;
C. положительный исход операции;
D. артериальное давление человека равно 165/110 мм.рт.ст.
24. Из определений относительной частоты и вероятности случайного события следует:
A. относительная частота равна вероятности случайного события;
B. относительная частота приблизительно равна вероятности случайного события при небольшом числе испытаний;
+ C. относительная частота приблизительно равна вероятности случайного события при большом числе испытаний;
D. верного ответа нет.
25. Теорема сложения формулируется для:
A. достоверных событий;
+ B. несовместимых событий;
несовместимых событий;
C. независимых событий;
D. невозможных событий.
26. Не является случайным событие:
A. рождение девочки;
+ B. закат солнца;
C. температура тела человека равна 38,2С;
D. положительный исход операции.
27. Испытание — это…
+ A. процесс многократно повторяющийся;
B. результат процесса многократно повторяющегося;
C. верного ответа нет.
28. Теорема умножения формулируется для:
A. несовместимых событий;
+B. независимых событий;
C. достоверных событий;
D. невозможных событий.
Случайное событие, это такое событие
A. причины, которого неизвестны;
B. если условия, в которых оно происходит, различны;
C. закономерности, которого не поддаются наблюдению;
+ D. событие, которое при совокупности одних и тех же условий может произойти, а может не произойти.
|
Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными. 1) Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз. 2) Невозможным называют событие, которое в результате испытания заведомо не произойдёт. Пример невозможного события: в условиях земного тяготения подброшенная монета трах-тибидох улетит вверх. 3) И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно  Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д.
Подчёркнутый критерий случайности очень важен – так, карточный шулер может очень ловко имитировать случайность и давать выигрывать клиенту, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт. Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости. События (любые) обозначают большими латинскими буквами либо теми же буквами с подстрочными индексами, например: . При этом стараются избегать буквы , которая зарезервирована под другие нужды. Запишем следующие случайные события: – в результате броска монеты выпадет «орёл»; Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них). Важной характеристикой случайных событий является их равновозможность. Два или бОльшее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другое. Например: – выпадение орла или решки при броске монеты; При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт. Могут ли быть те же события НЕ равновозможными? Легко. Так, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Если кто-то ловко спрятал в рукаве туза треф, то становится менее возможным, что оппоненту будет сдана трефа, и, главное, менее возможно, что будет сдан туз. 1.2.2. Совместные и несовместные события. Полная группа событий 1.1. Понятие теории вероятностей | Оглавление | Полную и свежую версию этой книги в pdf-формате, Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно! С наилучшими пожеланиями, Александр Емелин |
Терминология вероятности | Введение в статистику
Результаты обучения
- Понимание и использование терминологии вероятности
Вероятность — это мера, связанная с тем, насколько мы уверены в результатах определенного эксперимента или действия. Эксперимент — это запланированная операция, проводимая в контролируемых условиях. Если результат не предопределен заранее, то говорят, что эксперимент является случайным экспериментом . Подбрасывание одной честной монеты дважды является примером эксперимента.
Результат эксперимента называется результатом . выборочное пространство эксперимента представляет собой набор всех возможных результатов. Существует три способа представления выборочного пространства: составить список возможных результатов, создать древовидную диаграмму или создать диаграмму Венна. Заглавная буква [латекс]S[/латекс] используется для обозначения пространства выборки. Например, если вы подбрасываете одну честную монету, [латекс]S[/латекс] = {[латекс]Н[/латекс], [латекс]Т[/латекс]}, где [латекс]Н[/латекс] = решка и [latex]T[/latex] = решка — результат.
Событие – это любая комбинация исходов. Буквы верхнего регистра, такие как [латекс]А[/латекс] и [латекс]В[/латекс], обозначают события. Например, если эксперимент заключается в подбрасывании одной честной монеты, событие [latex]A[/latex] может получить не более одного орла. Вероятность события [latex]A[/latex] записывается как [latex]P[/latex]([latex]A[/latex]).
Вероятность любого исхода — это долгосрочная относительная частота этого исхода. Вероятности от нуля до единицы включительно
Равновероятный означает, что каждый результат эксперимента имеет равную вероятность. Например, если вы подбрасываете , шестигранный кубик, каждая грань ([латекс]1, 2, 3, 4, 5, \текст{или}\,6[/латекс]) с высокой вероятностью выпадет как и любое другое лицо.
Чтобы вычислить вероятность события [latex]A[/latex], когда все исходы в пространстве выборки равновероятны , подсчитайте количество исходов для события [latex]A[/latex] и разделите на общее количество результатов в пространстве выборки. Например, если вы подбрасываете чистую монету и чистую монету, пространство выборки равно {[latex]HH[/latex], [latex]TH[/latex], [latex]HT[/latex], [latex]TT. [/latex]} где [latex]T[/latex] = хвосты и [latex]H[/latex] = головы. Пространство выборки имеет четыре результата. [latex]A[/latex] = получить одну голову. Этому условию удовлетворяют два исхода {[латекс]HT[/латекс], [латекс]TH[/латекс]}, поэтому [латекс]\displaystyle{P}{({A})}=\frac{{2 }}{{4}}={0,5}[/латекс].
Предположим, вы бросили один правильный шестигранный кубик с числами {[latex]1, 2, 3, 4, 5, 6[/latex]} на его гранях. Пусть событие [latex]E[/latex] = выпадение числа, которое не меньше пяти. Есть два исхода {[latex]5, 6[/latex]}. [latex]\displaystyle{P}{({E})}=\frac{{2}}{{6}}[/latex] по мере увеличения количества повторений.
Эта важная характеристика вероятностных экспериментов известна как закон больших чисел , который гласит, что по мере увеличения числа повторений эксперимента относительная частота, полученная в эксперименте, стремится стать все ближе и ближе к теоретической вероятности. Несмотря на то, что результаты не происходят в соответствии с какой-либо установленной закономерностью или порядком, в целом наблюдаемая в долгосрочной перспективе относительная частота будет приближаться к теоретической вероятности. (Слово эмпирический часто используется вместо слова наблюдаемое.)
В этом видео приведены дополнительные примеры основных вероятностей.
Важно понимать, что во многих ситуациях исходы неравновероятны. Монета или игральная кость могут быть несправедливыми или предвзятыми . Два профессора математики в Европе попросили своих студентов-статистиков протестировать бельгийскую монету в один евро и обнаружили, что в [latex]250[/latex] испытаниях решка выпадала [latex]56[/latex]% времени, а решка — решка. [латекс]44[/латекс]% времени. Данные, кажется, показывают, что монета не является честной монетой; больше повторений было бы полезно, чтобы сделать более точный вывод о такой предвзятости. Некоторые кости могут быть необъективными. Посмотрите на кости в игре, которая есть у вас дома; пятна на каждом лице обычно представляют собой небольшие отверстия, вырезанные, а затем окрашенные, чтобы сделать пятна видимыми.
Событие «ИЛИ»
Исход находится в событии [латекс]А[/латекс] ИЛИ [латекс]В[/латекс], если исход находится в [латекс]А[/латекс] или в [латекс ]B[/latex] или находится как в [latex]A[/latex], так и в [latex]B[/latex]. Например, пусть [латекс]А[/латекс] = {[латекс]1, 2, 3, 4, 5[/латекс]} и [латекс]В[/латекс] = {[латекс]4, 5, 6 , 7, 8[/латекс]}. [латекс]А[/латекс] ИЛИ [латекс]В[/латекс] = {[латекс]1, 2, 3, 4, 5, 6, 7, 8[/латекс]}. Обратите внимание, что [латекс]4[/латекс] и [латекс]5[/латекс] НЕ указаны дважды.
[латекс]А[/латекс] ИЛИ [латекс]В[/латекс] = {[латекс]1, 2, 3, 4, 5, 6, 7, 8[/латекс]}. Обратите внимание, что [латекс]4[/латекс] и [латекс]5[/латекс] НЕ указаны дважды.
Событие «И»
Исход находится в событии [латекс]А[/латекс] И [латекс]В[/латекс], если исход находится как в [латекс]А[/латекс], так и в [латекс]В [/латекс] в то же время. Например, пусть [латекс]А[/латекс] и [латекс]В[/латекс] равны {[латекс]1, 2, 3, 4, 5[/латекс]} и {[латекс]4, 5, 6 , 7, 8[/latex]} соответственно. Тогда [латекс]А[/латекс] И [латекс]В[/латекс] = {[латекс]4, 5[/латекс]}.
Дополнение события [latex]A[/latex] обозначается как [latex]A'[/latex] (читается как «[latex]A[/latex] простое число»). [latex]A'[/latex] состоит из всех исходов, равных НЕ в [латекс]А[/латекс]. Обратите внимание, что [латекс]P[/латекс]([латекс]А[/латекс]) + [латекс]П[/латекс]([латекс]А'[/латекс]) = [латекс]1[/латекс]. Например, пусть [латекс]S[/латекс] = {[латекс]1, 2, 3, 4, 5, 6[/латекс]} и пусть [латекс]А[/латекс] = {[латекс]1, 2, 3, 4[/латекс]}. Тогда [латекс]А’={5, 6}[/латекс]. [латекс]P(A) = \frac{{4}}{{6}}[/latex] и [латекс]P(A’) = \frac{{2}}{{6}}[/latex] , и [латекс]P(A) +P(A’) =\frac{{4}}{{6}}+\frac{{2}}{{6}}={1}[/latex].
Тогда [латекс]А’={5, 6}[/латекс]. [латекс]P(A) = \frac{{4}}{{6}}[/latex] и [латекс]P(A’) = \frac{{2}}{{6}}[/latex] , и [латекс]P(A) +P(A’) =\frac{{4}}{{6}}+\frac{{2}}{{6}}={1}[/latex].
условная вероятность из [латекс]А[/латекс] для данного [латекс]В[/латекс] записывается как [латекс]Р[/латекс]([латекс]А[/латекс]|[латекс]В[/латекс]). [latex]P[/latex]([latex]A[/latex]|[latex]B[/latex]) — это вероятность того, что произойдет событие [latex]A[/latex] при условии, что событие [latex]B [/latex] уже произошло. Условное выражение уменьшает размер выборки. Мы вычисляем вероятность [latex]A[/latex] из сокращенного пространства выборки [latex]B[/latex]. Формула для вычисления [латекс]P[/латекс]([латекс]А[/латекс]|[латекс]В[/латекс]): [латекс]\displaystyle{P}{({A}{|}{B })}=\frac{{{P}{({A}\text{ AND } {B})}}}{{{P}{({B})}}}[/latex], где [латекс] P[/latex]([latex]B[/latex]) больше нуля.
Например, предположим, что мы подбрасываем один правильный шестигранный кубик. Пример пространства
Пример пространства
[латекс]S[/латекс] = {[латекс]1, 2, 3, 4, 5, 6[/латекс]}. Пусть [латекс]А[/латекс] = лицо равно [латекс]2[/латекс] или [латекс]3[/латекс] и [латекс]В[/латекс] = лицо четное ([латекс]2, 4, 6[/латекс]). Чтобы рассчитать [латекс]P[/латекс]([латекс]А[/латекс]|[латекс]В[/латекс]), мы подсчитываем количество исходов [латекс]2[/латекс] или [латекс]3[ /latex] в пространстве примеров [latex]B[/latex] = {[latex]2, 4, 6[/latex]}. Затем мы делим это на количество результатов [latex]B[/latex] (а не [latex]S[/latex]).
Мы получаем тот же результат, используя формулу. Помните, что [latex]S[/latex] имеет шесть исходов.
[латекс]\displaystyle{P}{({A}{|}{B})}=\frac{{{P}{({A}\text{ AND } {B})}}}{{ {P}{({B})}}}=\frac{{\frac{{\text{количество исходов, равных 2 или 3 и даже } {S}}}{{6}}}}{ {\ frac {{\ text {количество четных результатов в } {S}}} {{6}}}} = \ frac {{\ frac {{1}} {{6}}}} {{ \frac{{3}}{{6}}}}=\frac{{1}}{{3}}[/latex]
Понимание терминологии и символов
и понять, что это за события. Понимание формулировки — первый очень важный шаг в решении вероятностных задач. При необходимости перечитайте задачу несколько раз. Четко определите интересующее вас событие. Определить, имеется ли в формулировке условие, указывающее на то, что вероятность является условной; тщательно определить условие, если таковое имеется.
Понимание формулировки — первый очень важный шаг в решении вероятностных задач. При необходимости перечитайте задачу несколько раз. Четко определите интересующее вас событие. Определить, имеется ли в формулировке условие, указывающее на то, что вероятность является условной; тщательно определить условие, если таковое имеется.
Пример
Пример пространства [latex]S[/latex] – это целые числа, начинающиеся с единицы и менее [latex]20[/latex].
- [латекс]S[/латекс] = _____________________________ Пусть событие [латекс]А[/латекс] = четные числа, а событие [латекс]В[/латекс] = числа больше, чем [латекс]13[/латекс].
- [латекс]A[/латекс] = _____________________, [латекс]B[/латекс] = ___________________________
- [латекс]P[/латекс]([латекс]A[/латекс]) = _____________, [латекс]P[/латекс]([латекс]B[/латекс]) = ________________
- [латекс]A[/латекс] И [латекс]B[/латекс] = ____________________, [латекс]A[/латекс] ИЛИ [латекс]B[/латекс] = ________________
- [латекс]P[/латекс]([латекс]A[/латекс] И [латекс]B[/латекс]) = _________, [латекс]P[/латекс]([латекс]A[/латекс] ИЛИ [ латекс]В[/латекс]) = _____________
- [латекс]A'[/латекс] = _____________, [латекс]P[/латекс]([латекс]A'[/латекс]) = _____________
- [латекс]P[/латекс]([латекс]A[/латекс]) + [латекс]P[/латекс]([латекс]A'[/латекс]) = ____________
- [латекс]P[/латекс]([латекс]A[/латекс]|[латекс]B[/латекс]) = ___________, [латекс]P[/латекс]([латекс]B[/латекс]|[ латекс]А[/латекс]) = _____________; вероятности равны?
Показать решение
Попробуйте
Образец пространства [latex]S[/latex] представляет собой упорядоченные пары двух целых чисел, первое от одного до трех, а второе от одного до четырех (Пример: ([latex]1, 4 [/латекс])).
- [латекс]S[/латекс] = _____________________________Пусть событие [латекс]А[/латекс] = сумма четная, а событие [латекс]В[/латекс] = первое число простое.
- [латекс]А[/латекс] = _____________________, [латекс]В[/латекс] = ___________________________
- [латекс]P[/латекс]([латекс]A[/латекс]) = _____________, [латекс]P[/латекс]([латекс]B[/латекс]) = ________________
- [латекс]A[/латекс] И [латекс]B[/латекс] = ____________________, [латекс]A[/латекс] ИЛИ [латекс]B[/латекс] = ________________
- [латекс]P[/латекс]([латекс]A[/латекс] И [латекс]B[/латекс]) = _________, [латекс]P[/латекс]([латекс]A[/латекс] ИЛИ [ латекс]В[/латекс]) = _____________
- [латекс]B'[/латекс] = _____________, [латекс]P[/латекс]([латекс]B'[/латекс]) = _____________
- [латекс]P[/латекс]([латекс]A[/латекс]) + [латекс]P[/латекс]([латекс]A[/латекс]) = ____________
- [латекс]P[/латекс]([латекс]A[/латекс]|[латекс]B[/латекс]) = ___________, [латекс]P[/латекс]([латекс]B[/латекс]|[ латекс]А[/латекс]) = _____________; вероятности равны?
Показать решение
Пример
Брошена ровная шестигранная игральная кость. Опишите выборочное пространство [latex]S[/latex], идентифицируйте каждое из следующих событий с подмножеством [latex]S[/latex] и вычислите его вероятность (результатом является количество отображаемых точек).
Опишите выборочное пространство [latex]S[/latex], идентифицируйте каждое из следующих событий с подмножеством [latex]S[/latex] и вычислите его вероятность (результатом является количество отображаемых точек).
- Событие [латекс]Т[/латекс] = результат равен двум.
- Событие [latex]A[/latex] = результатом является четное число.
- Событие [latex]B[/latex] = результат меньше четырех.
- Дополнение [latex]A[/latex].
- [латекс]A[/латекс] ДАННЫЙ [латекс]B[/латекс]
- [латекс]B[/латекс] ДАННЫЙ [латекс]A[/латекс]
- [латекс]A[/латекс] И [латекс]B[/латекс]
- [латекс]A[/латекс] ИЛИ [латекс]B[/латекс]
- [латекс]A[/латекс] ИЛИ [латекс]B'[/латекс]
- Событие [latex]N[/latex] = результатом является простое число.
- Событие [latex]I[/latex] = результат семь.
Показать решение
Попробуйте
В таблице описано распределение случайной выборки [latex]S[/latex] из [latex]100[/latex] индивидуумов, сгруппированных по полу и правшам или левшам.
| Правша | Левша | |
|---|---|---|
| Самцы | [латекс]43[/латекс] | [латекс]9[/латекс] |
| Женщины | [латекс]44[/латекс] | [латекс]4[/латекс] |
Обозначим события [latex]M[/latex] = субъект мужского пола, [latex]F[/latex] = субъект женского пола, [latex]R[/latex] = субъект прав- handed, [latex]L[/latex] = субъект левша. Вычислить следующие вероятности:
- [латекс]P[/латекс]([латекс]М[/латекс])
- [латекс]P[/латекс]([латекс]F[/латекс])
- [латекс]P[/латекс]([латекс]R[/латекс])
- [латекс]P[/латекс]([латекс]L[/латекс])
- [латекс]P[/латекс]([латекс]M[/латекс] И [латекс]R[/латекс])
- [латекс]P[/латекс]([латекс]F[/латекс] И [латекс]L[/латекс])
- [латекс]P[/латекс]([латекс]M[/латекс] ИЛИ [латекс]F[/латекс])
- [латекс]P[/латекс]([латекс]M[/латекс] ИЛИ [латекс]R[/латекс])
- [латекс]P[/латекс]([латекс]F[/латекс] ИЛИ [латекс]L[/латекс])
- [латекс]P[/латекс]([латекс]M'[/латекс])
- [латекс]P[/латекс]([латекс]R[/латекс]|[латекс]M[/латекс])
- [латекс]P[/латекс]([латекс]F[/латекс]|[латекс]L[/латекс])
- [латекс]P[/латекс]([латекс]L[/латекс]|[латекс]F[/латекс])
Показать решение
Ссылки
«Список стран по континентам». Worldatlas, 2013. Доступно на сайте http://www.worldatlas.com/cntycont.htm (по состоянию на 2 мая 2013 г.).
Worldatlas, 2013. Доступно на сайте http://www.worldatlas.com/cntycont.htm (по состоянию на 2 мая 2013 г.).
Обзор концепции
В этом модуле мы изучили основную терминологию вероятности. Множество всех возможных исходов эксперимента называется пространством выборки. События представляют собой подмножества выборочного пространства, и им присваивается вероятность, представляющая собой число от нуля до единицы включительно.
Formula Review
[latex]A[/latex] и [latex]B[/latex] являются событиями
[latex]P[/latex]([latex]S[/latex]) = [latex]1 [/latex] где [latex]S[/latex] — пространство выборки 0 ≤ [latex]P[/latex]([latex]A[/latex]) ≤ [latex]1[/latex]
[latex ]P[/латекс]([латекс]А[/латекс]|[латекс]В[/латекс])=[латекс]\displaystyle\frac{{{P}{({A}\text{ AND } {B })}}}{{{P}{({B})}}}[/latex]
Вероятность: типы событий
Жизнь полна случайностей!
Чтобы быть умными и успешными, вам нужно «почувствовать» их.
Бросание монеты, бросок игральной кости и розыгрыш лотереи — все это примеры случайных событий.
События
«Событие» может быть одним или несколькими исходами.
Примеры:
Событие может быть одним исходом:
- Выпадение решки при подбрасывании монеты является событием
- Выпадение «5» — это событие.
Событие может включать несколько исходов:
- Выбор «Короля» из колоды карт (любого из 4 Королей) также является событием
- Выпадение «четного числа» (2, 4 или 6) является событием
События могут быть:
- Независимый (каждое событие не зависит от других событий),
- Зависимый (также называемый «условным», когда событие зависит от других событий)
- Взаимоисключающий (события не могут происходить одновременно)
Давайте рассмотрим каждый из этих типов.
Независимые события
События могут быть «независимыми», что означает, что каждое событие не зависит от других событий.
Это важная идея! Монета не «знает», что раньше она выпадала орлом… каждый бросок монеты — это совершенная изолированная вещь.
Пример: Вы подбрасываете монету три раза, и каждый раз выпадает «орел»… какова вероятность того, что при следующем подбрасывании тоже выпадет «орел»?
Вероятность равна 1/2 или 50%,
как и при ЛЮБОМ ДРУГОМ подбрасывании монеты.
То, что он сделал в прошлом, не повлияет на текущий бросок!
Некоторые люди думают, что «решка уже настала», но на самом деле действительно следующий бросок монеты совершенно не зависит от любых предыдущих бросков.
Высказывание «Выпадение решки» или «Еще одна попытка, моя удача неизбежна» называется Заблуждение игрока
Узнайте больше на независимых мероприятиях.
Зависимые события
Но некоторые события могут быть «зависимыми». .. это значит, что на них могут влиять предыдущие события .
.. это значит, что на них могут влиять предыдущие события .
Пример: Вытягивание 2 карт из колоды
После взятия одной карты из колоды доступно на карт меньше , поэтому вероятности меняются!
Давайте посмотрим на шансы получить короля.
Для 1-й карты шанс вытянуть короля 4 из 52
А для 2-й карты:
- Если 1-я карта была королем, то 2-я карта на меньше, чем , вероятно, будет королем, поскольку только 3 из 51 оставшейся карты являются королями.
- Если 1-я карта была , а не королем, то 2-я карта немного больше , вероятно, будет королем, поскольку 4 из 51 оставшейся карты являются королями.
Это потому, что мы удаляем карты из колоды.
Замена: Когда кладем каждую карту обратно после его розыгрыша шансы не меняются, так как события независимы .
Без замены: шансы изменятся, а события зависят .
Вы можете узнать больше в Зависимые события: условная вероятность
Древовидные диаграммы
Когда у нас есть зависимые события, это помогает сделать «древовидную диаграмму»
Пример: игра в футбол
Вы собираетесь играть в футбол, и вам нравится быть вратарем, но это зависит от того, кто сегодня тренер:
- с тренером Сэмом ваша вероятность стать вратарем равна 0,5
- с тренером Алексом ваша вероятность быть вратарем равна 0,3
Сэм тренирует чаще … примерно в 6 из каждых 10 игр (вероятность 0,6 ).
Давайте построим древовидную диаграмму!
Начните с тренеров. Мы знаем, что для Сэма 0,6, поэтому для Алекса должно быть 0,4 (вероятности должны складываться до 1):
Затем заполните ветки для Сэма (0,5 Да и 0,5 Нет), а затем для Алекса (0,3 Да и 0,7 Нет):
Теперь все аккуратно разложено, можно вычислить вероятности (подробнее читайте в Дереве диаграммы).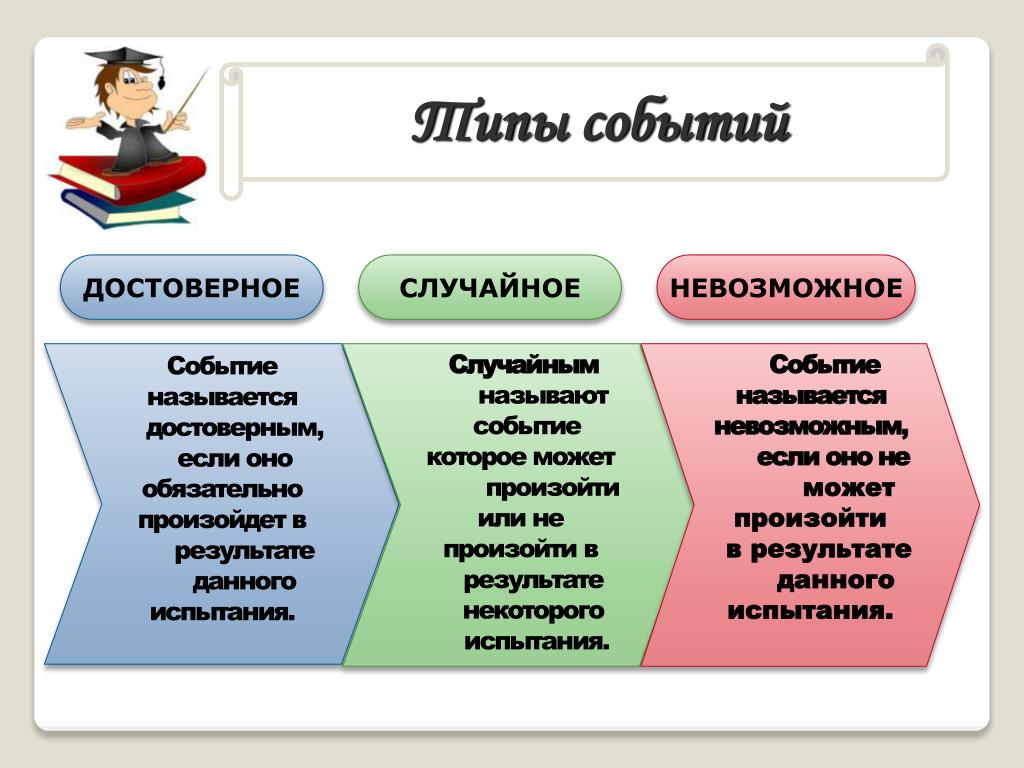

 Виды событий
Виды событий

