Дроби что такое и как их решать: дроби как их решать — ответ на Uchi.ru

Виды дробей и основные понятия, формулы и примеры решений

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Определение

Дробью или обыкновенной дробью называется число, состоящее из одной или нескольких равных частей (долей) единицы.

Подробнее об обыкновенных дробях по ссылке →

Обыкновенные дроби записываются с помощью двух натуральных чисел и горизонтальной (называется винкулум) или наклонной (солидус) черты, которую называют чертой дроби.

Например. 1/3, $\frac{1}{3}$ (читается: одна третья).

Определение

Число, которое стоит над чертой дроби, называется числителем, а число, записанное под чертой дроби — знаменателем.

Например. 1/3, У дроби $\frac{15}{17}$ (пятнадцать семнадцатых) число 15 является числителем, 17 — знаменателем.

Определение

Если числитель дроби меньше, чем ее знаменатель, то дробь называется

правильной.

Дробь, числитель которой либо равен, либо больше знаменателя, называется неправильной.

Подробнее о правильных и неправильных дробях по ссылке →

Например. Дробь $\frac{3}{4}$ (три четвертых) является правильной, так как числитель этой дроби — 3 — меньше, чем знаменатель, который равен 4: 3

Определение

Сумму натурального числа и правильной дроби обычно записывают без знака плюс. Такие дроби называются смешанными. Натуральное число называют целой частью смешанного числа, а правильную дробь — дробной частью смешанного числа.

Подробнее о смешанных дробях по ссылке →

Например. $7 \frac{4}{5}=7+\frac{4}{5}$ (семь целых четыре пятых). 7 — целая часть, $\frac{4}{5}$ — дробная.

Определение

Если числитель и знаменатель дроби нельзя сократить на одно и тоже число, отличное от 1, то дробь называется

несократимой; иначе — сократимой.

Например. Дробь $\frac{3}{5}$ (три пятых) является несократимой, так 3 и 5 являются взаимно простыми числами, то есть их нельзя поделить на одно и тоже число. Дробь $\frac{3}{9}$ (три девятых) сократимая, так как числитель и знаменатель делится на 3.

Определение

Если знаменателем дроби являются числа 10, 100, 1000 и т.п., то такая дробь называется десятичной.

Подробнее о десятичных дробях по ссылке →

Например. $\frac{3}{10}, \frac{17}{1000}, \frac{7}{100}$

Для удобства записи такие дроби записывают без знаменателя, целую часть от дробной отделяют запятой.

Например. $\frac{3}{10}=0,3, \frac{17}{1000}=0,017,7 \frac{7}{100}=7,07$

Определение

Составной дробью

называется выражение, которое содержит несколько черт дроби.

Например. $\frac{\frac{1}{2}}{\frac{2}{3}}, \frac{3 / 4}{6 / 7}$

Читать следующую тему: обыкновенные дроби.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Виды дробей

Виды дробей

Навигация по странице:

В математике часто применяются следующие виды дробей:
• Обыкновенная дробь
  • Правильная дробь
  • Неправильная дробь
• Смешанная дробь (смешаное число)
• Десятичная дробь

Обыкновенная дробь

Определение.

Обыкновенная дробь или простая дробь — запись рационального числа в виде отношения двух чисел

mn

. Делимое m называется числителем дроби, а делитель n — знаменателем дроби.

Правильная дробь

Определение.

Правильной дробью называется дробь, у которой числитель меньше знаменателя.

7	,	5	— правильные дроби.
9		6

Неправильная дробь

Определение.

Неправильной дробью называется дробь, у которой числитель больше или равен знаменателю.

9	,	3	— неправильные дроби.
7		3

Смешанная дробь (смешаное число)

Всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби.

Определение.

Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

3	2	= 3 +	2	=	21	+	2	=	23
	7		7		7		7		7

Десятичная дробь

Определение.

Десятичная дробь дробь со знаменателем 10ⁿ, где n — натуральное число.

Десятичная дробь имеет следующую форму записи: сначала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть, количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.

3.2609	= 3 +	2	+	6	+	0	+	9	= 3 +	2609
		10		100		1000		10000		10000

Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби

Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь

Онлайн калькуляторы дробей

Онлайн упражнения с дробями

Основные дроби Solve It Strips® · Inspired Elementary

4,00 $

Всего страниц: 29

Размер файла: 36 МБ

Количество

Основные фракции Solve It Strips®

Категории: Математика, МАТЕМАТИКА — Индивидуальные наборы Solve It Strips® Теги: 2-й, 3-й, Деятельность, Фракции, Домашняя школа, Математика, Математические центры, Карточки с заданиями

• Описание
• Отзывы (0)

СЭКОНОМЬТЕ БОЛЬШЕ И ПОЛУЧИТЕ НАБОР ПОЛОС SOLVE IT!

Полоски Solve It Strips — это ВЕСЕЛОЕ, практическое, БЕЗ ПОДГОТОВКИ дополнительное задание по математике, которое поддерживает интерес учащихся! Их можно использовать в качестве математического центра, занятия для первоклассников, с математической группой под руководством родителей или в качестве мини-оценки.

Полоски Solve It также делают забавную домашнюю тренировку!

Этот набор полосок Solve It посвящен основным дробям. Есть три полосы для дробей в составе целого, две полосы для названий слов дробей, две полосы для отсутствующих дробей из целого, три полосы для дробей в составе группы, одна полоса для эквивалентных дробей, одна полоса для дробей на числовая строка и три полоски, представляющие собой смешанный обзор предыдущих умений.

Ученикам предлагается использовать свои математические способности в уме, чтобы найти дробь на каждой полоске. Учащиеся начинают с полоски «Начало» и решают дробь на этой полоске. Это приведет их ко второй полоске и так далее, пока учащиеся не получат решение для полоски «ФИНИШ». Включены три варианта обложки, а также простые инструкции по хранению полосок Solve It Strips. Также предоставляется ключ ответа для легкой проверки и забавная страница трекера Solve It Strip для учащихся, чтобы отмечать их успехи!

См. ФАЙЛ ПРЕДВАРИТЕЛЬНОГО ПРОСМОТРА для примера в действии.

Это такой ВЕСЕЛЫЙ и ЛЕГКИЙ математический центр, который будет работать ВЕСЬ ГОД! СЭКОНОМЬТЕ БОЛЬШУЮ И ПОЛУЧИТЕ ПОЛНЫЙ НАБОР! или соберите свой собственный комплект вместе с отдельными наборами, указанными ниже:

Полоски Solve It: отделочные узоры
Полоски Solve It: суммы и разности до 10
Полоски Solve It: суммы и разности до 20
Полоски Solve It: подсчет монет
Solve It Полоски: пропущенные числа до 10

Реши полоски: пропущенные числа до 20
Решаем полоски: присваиваем значение 100
Решаем полоски: присваиваем значение 1000
Решаем полоски: пропускаем счет
Решаем полоски: давайте умножим!
Решайте полоски: давайте разделим!
Полоски Solve It: давайте умножим и разделим!
Полоски Solve It: расскажи время!
Решайте полоски: прошедшее время и многое другое!
Полоски Solve It: посчитайте и раскрасьте до 20
Полоски Solve It: давайте округлим!
Решайте полоски: сложение и вычитание двузначных чисел БЕЗ ПЕРЕГРУППИРОВКИ!
Решаем полоски: основные дроби!
Полоски Solve It: Числа до 100
Полоски Solve It: Уравнения баланса

*** Напоминаем, что этот продукт предназначен ТОЛЬКО ДЛЯ ОДНОГО ПОЛЬЗОВАТЕЛЯ. Это означает, что копирование или совместное использование любой части этого продукта с другим учителем, классом, школой, отделом, районом и т. д. строго запрещено. У вас есть возможность приобрести несколько лицензий (со скидкой) для каждого дополнительного человека/класса, с которым вы хотите поделиться этим продуктом. Спасибо за уважение к моему труду!

© Все права защищены. Эрин Лейн. www.Inspired Elementary.com

Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставить отзыв.

Три способа их решения – Доктора математики

Поскольку мы только что рассмотрели сложное рациональное неравенство, давайте рассмотрим более простые рациональные уравнения , сначала линейное уравнение с дробями, а затем действительно рациональные уравнения, в которых переменная( s) появляются в знаменателе. Эта дискуссия касалась распространенной путаницы, которую я наблюдал у студентов.

Проблема

Вопрос пришел от Fairooz в 2017 году:

 Умножение верха и низа против умножения слева и справа
Всем привет.  Это довольно простой вопрос, поэтому я, вероятно, упускаю здесь очень простую концепцию.
Учитывая x/2 + y/5 = 1, мы обычно получаем общий знаменатель 10, верно? Чего я не понимаю, так это того, что когда мы умножаем первый знаменатель на 5, а второй знаменатель на 2 и делаем то же самое с числителями, почему мы также не умножаем 1 на 10?
   5х/10 + 2у/10 = 10
 
  Разве мы не должны умножать все  в уравнении, если мы сделали это с одним из членов? 

Файруза научили решать $$\frac{x}{2} + \frac{y}{5} = 1$$, переписав это как $$\frac{5x}{10} + \frac{2y {10} = 1,$$, умножая числитель и знаменатель каждой дроби, чтобы получить общий знаменатель 10. Он задается вопросом, почему правая часть осталась неизменной. В конце концов, что бы вы ни делали с одной стороной, вы должны делать и с другой, верно?

Объединение дробей сначала

Я ответил:

 Вы путаете две процедуры (как это делают многие студенты), не сосредотачиваясь на том, ЧТО вы на самом деле делаете, и ПОЧЕМУ вы делаете то, что делаете. 
Есть два основных способа обработки такого уравнения.
  Один из подходов  - это то, что вы предлагаете, чтобы  изменить каждый член, чтобы использовать общий знаменатель   . Вы переписали x/2 как 5x/10, а y/5 как 2y/10, ЧТОБЫ МОЖНО ИХ ДОБАВИТЬ. Обратите внимание, что вы не умножили левую часть на 10; вы только что изменили знаменатели, умножив верхнюю и нижнюю части каждой дроби. Каждый термин по-прежнему имеет ОДИНАКОВОЕ ЗНАЧЕНИЕ. Следовательно, вы также не можете изменить значение на другой стороне; он также должен сохранить то же значение, 1. 

Он не умножил левую часть на 10, а просто переписал ее как эквивалентное выражение , оставив значение без изменений. Следующим шагом будет сложение дробей: $$\frac{5x + 2y}{10} = 1.$$

 Если вы ДЕЙСТВИТЕЛЬНО хотите изменить правую часть,  сделать то же самое, что и , значит просто написать это , тоже со знаменателем 10:
   5х/10 + 2г/10 = 10/10
Это было бы правильно и, может быть, даже полезно.  Обе стороны по-прежнему имеют одинаковое значение, но теперь их можно комбинировать:
    (5х + 2г)/10 = 10/10
Отсюда можно пойти несколькими путями; нужно просто умножить обе части на 10, сократив знаменатели:
         5х + 2у = 10
(Нам действительно не нужно было писать 10/10, да и я редко; умножение на 10 все равно меняет 1 на 10. Я сделал это только для того, чтобы показать, что вы  мог бы сделать  с правой стороны, если бы вы чувствовали себя обязанным.) 

Когда мы говорим о том, чтобы «делать одно и то же с обеими сторонами», мы имеем в виду, что применяет некоторую операцию к значению на каждой стороне (например, умножение обоих стороны на 10). Нет необходимости переписывать обе части уравнения одинаково, так как это не меняет их значений. Важно то, что значения должны оставаться равными (при любом значении переменной).

Заметьте, кстати, что цель нам не сказали. Если бы это было уравнение только с одной переменной, мы, вероятно, пытались бы найти решение для этой переменной.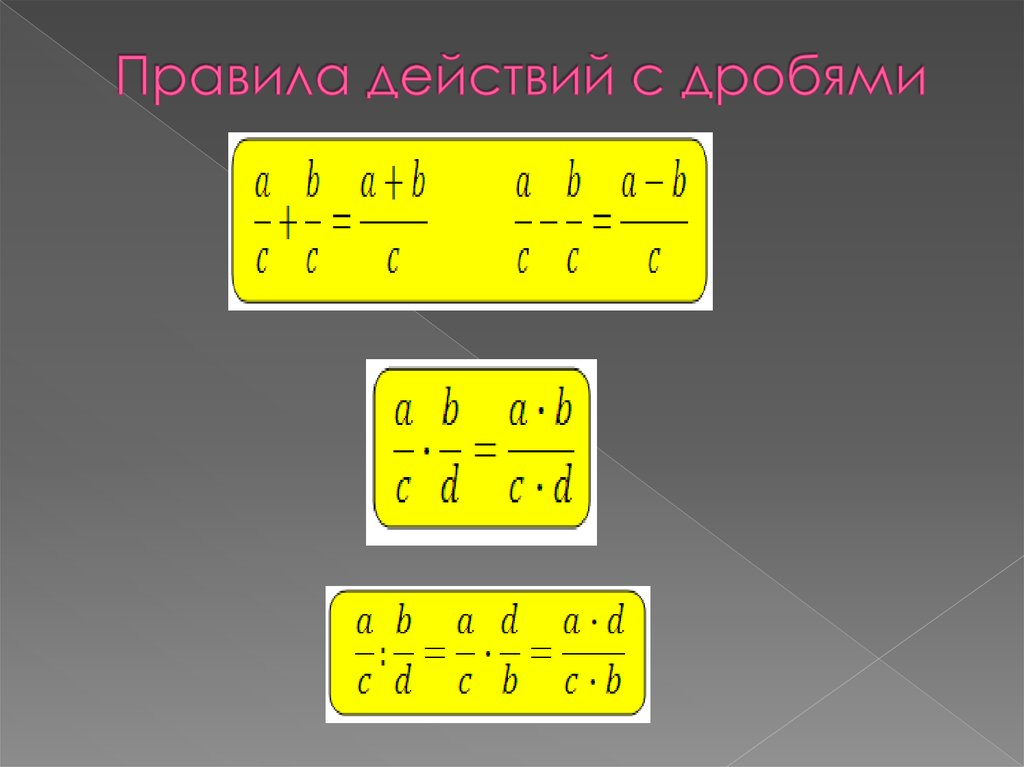 Здесь, вероятно, цель состоит в том, чтобы переписать уравнение в какой-то конкретной форме (такой форме наклон-пересечение, что означает решение для y ), чтобы изобразить это на графике.

Сначала очистить дроби

  Другой основной метод  состоит в УМНОЖЕНИИ обеих сторон на 10, что  ОЧИСТКА Дробей  . Здесь мы больше не пытаемся сохранить значения одинаковыми (что требовало умножения и числителя, и знаменателя на одно и то же число), а работаем со всем уравнением, сохраняя его эквивалентность , умножая обе части на одно и то же число .
А у нас другая цель: не просто сделать возможным добавление членов, а полностью исключить дроби. Поэтому мы не ставим 10 в знаменателе. Наша цель состоит в том, чтобы иметь возможность сократить знаменатели с 10.
Это выглядит так (записывая больше шагов, чем мы обычно делаем, когда мы знакомы с этим):
     10(х/2 + у/5) = 10(1)
   10*х/2 + 10*у/5 = 10
           5х + 2у = 10
Это тот же результат, который мы получили раньше, без необходимости так много делать с дробями.  Отсюда, конечно, вы можете просто найти y как обычно, без дробей, чтобы все усложнить. 

В обычном печатном виде работа выглядит так:

$$10\cdot\frac{x}{2} + 10\cdot\frac{y}{5} = 10\cdot1$$

$$5x + 2y = 10$$

Это тот же результат, что и раньше, но полученный быстрее и без добавления дробей. Теперь мы можем делать все, что запланировали, с более простым уравнением. Если мы находим y , мы можем вычесть 5 x и затем разделить на 2:

$$2y = 10 – 5x$$

$$y = \frac{10 – 5x}{2} = \frac{10}{2} – \frac{5x}{2} = 5 – \frac{5}{2}x$$

Я обнаружил, что многие ученики, обученные одному из этих способов, путают его с другим, в результате чего получается неверный гибридный результат. Первый способ заставляет их немедленно столкнуться с фракциями, а второй пытается устранить фракции как можно скорее. Оба фокусируются на дробях как на главной особенности уравнения.

Просто сделай это!

Но есть третий способ , который в книгах часто не указывается: вместо того, чтобы упрощать вещи, чтобы избежать дробей, мы могли бы просто стиснуть зубы и делать ту же работу, что и без дробей:

 Теперь вам не нужно ничего этого делать.  Вы можете просто делать всю обычную работу, сохраняя дроби. Это просто немного более подвержено ошибкам для некоторых студентов:
   х/2 + у/5 = 1
         у/5 = 1 - х/2
       5*у/5 = 5(1 - х/2)
           у = 5 - 5x/2
И мы закончили! В этом случае очистка дробей на самом деле не так уж полезна. Обычно мы преподаем его только потому, что  очень многие ученики боятся дробей  и  чаще делают ошибки,  манипулируя ими.
Надеюсь, это поможет. Ключ не в том, чтобы просто механически умножать на что-то, потому что вы делали это в других задачах, а в том, чтобы обращать внимание на то, что вы делаете.  Если умножить одну сторону  на что-то, то непременно -- как ты сказал --  умножь и другую сторону тоже на  . Но , если вы измените только форму  с одной стороны, то сделайте только то, что с другой стороны,  не изменит свое значение . И не думайте, что вы умножаетесь, если это не так. 

Опять же, вот такая работа:

$$\frac{x}{2} + \frac{y}{5} = 1$$

$$\frac{y}{5} = 1 – \frac{x}{2}$$

$$5\cdot\frac{y}{5} = 5\cdot1 – 5\cdot\frac{x}{2}$$

$$y = 5 – \frac{5}{2}x$$

Другие примеры

Очевидно, Файруз только что привел простой пример для иллюстрации проблемы, а теперь дал нам «настоящую» задачу:

 Ааа, понял.  Спасибо.
Только поясню этот метод другим вопросом -- главным, который меня и смутил в первую очередь...
Учитывая y = (c - bc)/(b + 1) + c
Мы знаем, что c эквивалентно c/1. Раньше, когда я думал об умножении знаменателя и числителя на (b + 1), я считал, что должен сделать это и с левой частью (y). Теперь я знаю до  оставить y как есть  , верно?
Последний вопрос. Скажем, мне дано Y/1 = 2/X + 3. Буду ли я умножать 3 (=3/1) на X (и числитель, и знаменатель), а затем также умножать Y/1 на X (числитель и знаменатель) так что у них всех  общий знаменатель  ? 

Оба этих примера являются рациональными уравнениями с переменными в знаменателе; но до сих пор неясно, какова цель, так как у обоих слева и .

Упрощение решения

Первая задача — это уравнение, которое уже решено для y . Я ответил, что оставлю и как есть:

 Верно. Слева ничего делать не нужно. У тебя уже есть y один, так что ты совсем не хочешь его менять.  То, что вы делаете справа, НЕ умножается; там ваша цель просто упростить   :
   у = (с - ВС)/(Ь + 1) + с
   y = (c - bc)/(b + 1) + c(b + 1)/(b + 1)
   y = (c - bc)/(b + 1) + (bc + c)/(b + 1)
   y = (c - bc + bc + c)/(b + 1)
   у = (2с)/(б + 1)
В этом случае вам не нужно умножать на LCD (b + 1), потому что это заставит вас изменить левую сторону. Но вы могли бы сделать это, если бы вам не нравились дроби:
          у = (с - ВС)/(Ь + 1) + с
   y(b + 1) = (c - bc) + c(b + 1)
   y(b + 1) = c - bc + bc + c
   у (б + 1) = 2с
          у = (2с)/(б + 1) 

На самом деле нет никакой необходимости переписывать правую часть вообще, чтобы сделать это правильным решением задачи, которая должна быть решена для y . Но это оказалось значительным упрощением, так что стоило бы сделать это как часть более крупной проблемы. Здесь снова работа по первому способу (сочетание дробей):

$$y = \frac{c – bc}{b + 1} + c$$

$$y = \frac{c – bc} {b + 1} + \frac{c(b + 1)}{b + 1} = \frac{c – bc}{b + 1} + \frac{bc + c}{b + 1} = \frac {c – bc + bc + c}{b + 1} = \frac{2c}{b + 1}$$

А вот и второй способ (очистка дробей):

$$y = \frac{c – bc}{b + 1} + c$$

$$y(b + 1) = \frac{c – bc}{b + 1}(b + 1) + c(b + 1)$$

$$y(b + 1) = c – bc + bc + c$$

$$y(b + 1) = 2c$$

$$y = \frac{2c}{b + 1}$$

Обратите внимание, что я не сводил глаз с цели, найти y , поэтому я не распределял левая сторона. По сути, я «нерешал», а затем решал, потому что с нерешенной формой было легче работать.

Снова упрощая

Как насчет второго вопроса, о приведении общего знаменателя к уравнению \(\displaystyle\frac{y}{1} = \frac{2}{x} + 3\)? Это действительно та же проблема, что и другая, поскольку левая сторона на самом деле просто y .

 Нет, я бы не стал этого делать; здесь нет причин переписывать левую часть. Так как y там один, вам нужно только  упростить правую часть  .
я бы сделал так:
   у = 2/х + 3
   у = 2/х + 3х/х
   у = (2 + 3х)/х 

Здесь я просто упростил:

$$y = \frac{2}{x} + 3 = \frac{2}{x} + \frac{3x}{x} = \frac{2 + 3x}{ x}$$

Нет необходимости работать со всем уравнением.

 Если бы я хотел, чтобы  избегал дробей  , я мог бы изменить левую часть. Поскольку x — единственный знаменатель, который у вас есть (это не 1), я бы умножил всю левую часть и всю правую часть на x, то есть умножил бы каждый член:
    у = 2/х + 3
   ху = 2/х*х + 3х
   ху = 2 + 3х
Тогда я мог бы найти у, разделив на х:
    у = (2 + 3х)/х
Здесь это уже было решено; но я временно "отменил" его, чтобы избежать рискованной работы. 
Теперь, если бы целью этих задач было найти х, а не у, все изменилось бы!
Помните, держите цель в уме, а не слепо следуйте какой-то рутине. 

Здесь у нас было:

$$y = \frac{2}{x} + 3$$

$$xy = \frac{2}{x}\cdot x + 3x$$

$$xy = 2 + 3x$$

$$y = \frac{2 + 3x}{x}$$

Файруз был доволен:

 Я понял. Спасибо. 

Решение для

x

Давайте посмотрим на последнее, что я сказал, что все изменит: мы попробуем решить $$y = \frac{2}{x} + 3$$ для x в терминах из и в этот раз. Теперь мы решаем настоящее, полноценное рациональное уравнение. попробую несколько способов.

Сначала очищаем дроби

Второй метод, о котором я говорил выше, — это то, что, по моему опыту, в учебниках обычно преподают как «самый» способ решения рационального уравнения.

Чтобы получить x из знаменателя (что мы должны сделать в конечном итоге, независимо от того, какой метод мы используем), я бы умножил каждое слагаемое (обе части) на x :

$$y = \frac {2}{x} + 3$$

$$xy = \frac{2}{x}\cdot x + 3x$$

$$xy = 2 + 3x$$

Теперь я хочу решить для x , поэтому я получаю все элементы, содержащие x , на одной стороне, а затем выношу их на множители:

$$xy – 3x= 2$$

$$x(y – 3)= 2$$

$$x = \frac{2}{y – 3}$$

Шаг факторизации (эквивалентный объединению одинаковых терминов) – это то, что учащиеся чаще всего пропускают, когда впервые сталкиваются с такой задачей!

Сначала объединим дроби

На этот раз я сначала объединим члены в правой части; многие студенты рефлекторно делают это, когда сталкиваются с дробями (они были приучены упрощать любое выражение, которое они видят), поэтому вместо того, чтобы запрещать это, я говорю им, как это делать правильно , если они обнаружат, что делают это. (Иногда, действительно, этот метод требует меньше написания, так что это совсем неплохой метод.)

Мы хотим только упростить:

$$y = \frac{2}{x} + 3 = \frac{2}{x} + \frac{3x}{x} = \frac{2 + 3x}{x}$$

Теперь нам еще нужно получить x из знаменателя путем умножения обе стороны:

$$xy = x\cdot\frac{2 + 3x}{x}$$

$$xy = 2 + 3x$$

Последние шаги будут такими же, как и раньше.

Просто сделай это

Как и в приведенных выше примерах, у нас нет , чтобы сосредоточиться на дробях, хотя рациональное уравнение состоит исключительно из дробей. Для кого-то это будет сюрпризом! Я могу просто проигнорировать тот факт, что x находится внизу, и решить, как будто это не так, просто выделив член, вычитая 3:

$$y = \frac{2}{x} + 3$$

$$y – 3= \frac{2}{x}$$

Теперь у меня одна дробь в правой части, и мне не нужно x , чтобы остаться в знаменателе. Что я могу сделать? Я могу просто взять обратное число с каждой стороны! Этому не часто учат в явном виде как одной из «вещей, которые вы можете делать с обеими сторонами», но если два значения равны, очевидно, что их обратные значения тоже равны:

$$\frac{1}{y – 3} = \frac{x}{2}$$

Теперь нам просто нужно умножить на 2:

$$\frac{2}{y – 3} = x$$

Выберите способ, который соответствует вашему мнению Лучший!

Математика — это набор инструментов, и какой инструмент вы используете в данный момент, зависит от того, что, по вашему мнению, нужно сделать.