Два последних уравнения точно не относятся к дробно-рациональным, несмотря на то, что они состоят из дробей. Но самое важное, что в знаменателе нет переменной (буквы). А вот в дробно-рациональном уравнении в знаменателе всегда есть переменная.
Итак, после того, как вы верно определили, какое именно епред вами уранвение, начнем его решать. Первое, что нужно сделать, обозначается тремя большими буквами, О.Д.З. Что же означают эти буквы? Область Допустимых Значений. Что это означает в науке математике, сейчас объяснять не буду, наша цель научиться решать уравнения, а не повторить тему «Алгебраические дроби». А вот для нашей цели это означает следующее: мы берем знаменатель или знаменатели наших дробей, выписываем их отдельно и отмечаем, что они не равны нулю.
Дальше используем определение дроби равной нулю. Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. То, что знаменатель не равен нулю, мы указали в ОДЗ, укажем, что числитель равен нулю. \((x-2)(x+2)=0\). И решим это уравнение. Оно состоит из двух множителей x-2 иx+2. Помним, что произведение двух множителей равно нулю, когда один из множителей равен нулю.
Значит: x+2=0 или x-2=0
Из первого уравнения получаем x=-2 , из второго x=2 . Переносим число, и знак меняем.
На последнем этапе проверяем ОДЗ: x+1≠0
Подставляем вместо x числа 2 и -2.
Получаем 2+1≠0. Выполняется? Да! Значит x=2 — наш корень. Проверяем следующий: -2+1≠0. Выполняется. Да. Значит и x=-2, тоже наш корень. Итак, ответ: 2 и -2.
Последнее уравнение решим без пояснений. Алгоритм тот же:
1. ОДЗ
2.
2≠0\) Выполняется!
\(-3+2≠0 \) Выполняется! Следовательно, x=-3 решение нашего уравнения.
Уверена, что ваше решение сошлось с образцом.
Напоследок хочу сказать, что мы рассмотрели только один способ решения дробно-рациональных уравнений. Надеюсь, что этот способ не показался вам сложным. Успехов в учебе!
Дробно рациональное уравнение приведя. Решение дробно-рациональных уравнений. Как решаются дробно-рациональные уравнения
Дробным уравнением называется уравнение, в котором хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное. Например, дробным уравнением является уравнение .
Решать дробные уравнения удобно в следующем порядке:
- найти общий знаменатель дробей, входящих в уравнение, если каждая дробь имеет смысл,
- заменить данное уравнение целым, умножив обе его часть на общий знаменатель,
- решить получившееся целое уравнение,
- исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решить дробное уравнение:
Решение. Воспользуемся основным свойством дроби с представим левую и правую части этого уравнения в виде дробей с одинаковым знаменателем:
.
Эти дроби равны при тех и только тех значениях, при которых равны их числители, а знаменатель отличен от нуля. Если знаменатель равен нулю, то дроби, а следовательно, и уравнение не имеет смысла.
Таким образом, чтобы найти корни данного уравнения, нужно решить уравнение
Упростив уравнение (раскрыв скобки и приведя подобные члены), получим квадратное уравнение
.
При решении квадратного уравнения получаем его корни:
.
Найденные корни не обращают знаменатель в нуль, поэтому они являются корнями исходного дробного уравнения.
Пример 2. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное дробное уравнение. Общий знаменатель —
Заменим исходное уравнение целым. Для этого умножим обе его части на
общий знаменатель.
Получим:
Выполним необходимые преобразования в полученном уравнении и придём к квадратному уравнению
Решенив квадратное уравнение , получаем его корни:
Если x = -3 , то найденный на первом шаге знаменатель обращается в нуль:
,
то же самое, если x = 3 .
Следовательно, числа -3 и 3 не являются корнями исходного уравнения, а, поскольку никакие другие корни не найдены, данное уравнение не имеет решения.
Пример 3. Решить дробное уравнение:
.
Решение. Найдём общий знаменатель дробей, входящих в данное уравнение. Для этого знаменатели дробей разложим на множители:
.
Общий знаменатель — выражение
Заменим исходное уравнение целым, умножив обе его части на общий знаменатель. Получим:
Выполнив преобразования, придём к квадратному уравнению
.
Решенив квадратное уравнение , получаем его корни:
.
Ни один из корней не обращает общий знаменатель в нуль.
Следовательно,
числа -4 и 9 — корни данного уравнения.
Пример 4. Решить дробное уравнение:
.
Решение. Введём новую переменную, обозначив . Получим уравнение с переменной y .
§ 1 Целое и дробное рациональные уравнение
В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение. Рассмотрим решение рациональных уравнений.
Рациональным уравнением называют уравнение, в котором левая и правая части являются рациональными выражениями.
Рациональные выражения бывают:
Дробные.
Целое выражение составлено из чисел, переменных, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.
Например:
В дробных выражениях есть деление на переменную или выражение с переменной. Например:
Дробное выражение не при всех значениях входящих в него переменных имеет смысл. Например, выражение
при х = -9 не имеет смысла, так как при х = -9 знаменатель обращается в нуль.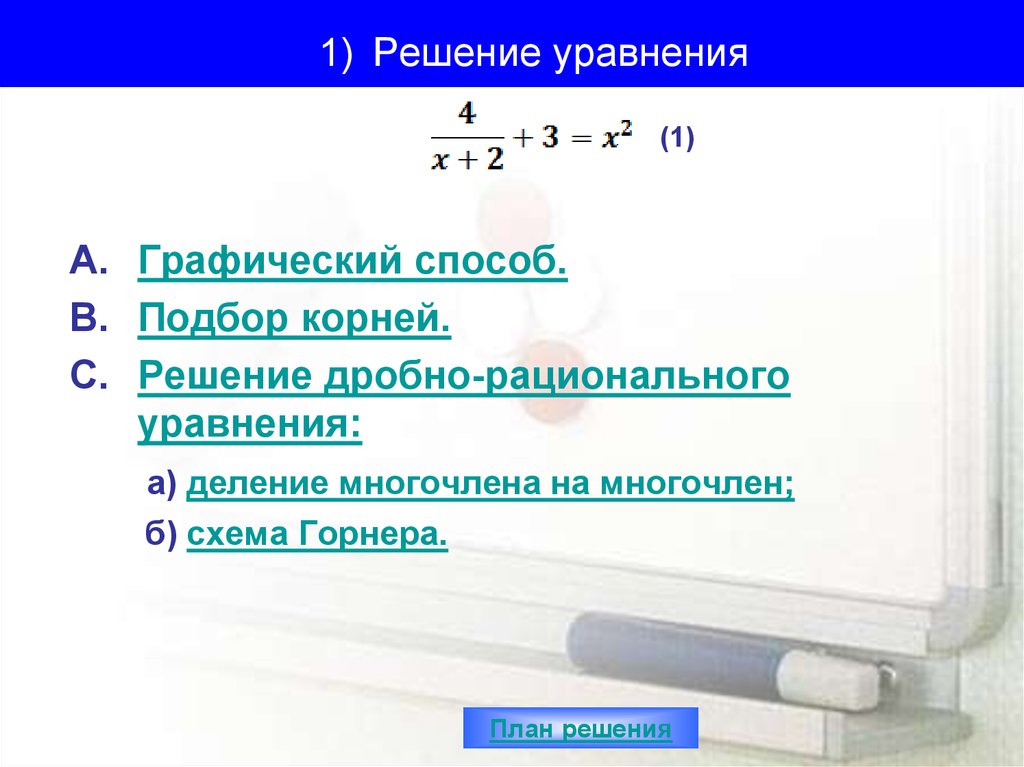
Значит, рациональное уравнение может быть целым и дробным.
Целое рациональное уравнение — это рациональное уравнение, в котором левая и правая части — целые выражения.
Например:
Дробное рациональное уравнение — это рациональное уравнение, в котором или левая, или правая части — дробные выражения.
Например:
§ 2 Решение целого рационального уравнения
Рассмотрим решение целого рационального уравнения.
Например:
Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него дробей.
Для этого:
1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6;
2. найдем дополнительный множитель для каждой дроби. Для этого общий знаменатель 6 делим на каждый знаменатель
дополнительный множитель для дроби
дополнительный множитель для дроби
3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение
которое равносильно данному уравнению
Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.
Приведем подобные члены многочлена и получим
Видим, что уравнение линейное.
Решив его, найдем, что х = 0,5.
§ 3 Решение дробного рационального уравнения
Рассмотрим решение дробного рационального уравнения.
Например:
1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него рациональных дробей.
Найдем общий знаменатель для знаменателей х + 7 и х — 1.
Он равен их произведению (х + 7)(х — 1).
2.Найдем дополнительный множитель для каждой рациональной дроби.
Для этого общий знаменатель (х + 7)(х — 1) делим на каждый знаменатель. Дополнительный множитель для дроби
равен х — 1,
дополнительный множитель для дроби
равен х+7.
3.Умножим числители дробей на соответствующие им дополнительные множители.
Получим уравнение (2х — 1)(х — 1) = (3х + 4)(х + 7), которое равносильно данному уравнению
4.Слева и справа умножим двучлен на двучлен и получим следующее уравнение
5.
Правую часть перенесем налево, изменив знак каждого слагаемого при переносе на противоположный:
6.Приведем подобные члены многочлена:
7.Можно обе части разделить на -1. Получим квадратное уравнение:
8.Решив его, найдем корни
Так как в уравнении
левая и правая части — дробные выражения, а в дробных выражениях при некоторых значениях переменных знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.
При х = -27 общий знаменатель (х + 7)(х — 1) не обращается в нуль, при х = -1 общий знаменатель также не равен нулю.
Следовательно, оба корня -27 и -1 являются корнями уравнения.
При решении дробного рационального уравнения лучше сразу указать область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.
Рассмотрим еще один пример решения дробного рационального уравнения.
Например, решим уравнение
Знаменатель дроби правой части уравнения разложим на множители
Получим уравнение
Найдем общий знаменатель для знаменателей (х — 5), х, х(х — 5).
Им будет выражение х(х — 5).
теперь найдем область допустимых значений уравнения
Для этого общий знаменатель приравняем к нулю х(х — 5) = 0.
Получим уравнение, решив которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.
Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.
Теперь можно найти дополнительные множители.
Дополнительным множителем для рациональной дроби
дополнительным множителем для дроби
будет (х — 5),
а дополнительный множитель дроби
Числители умножим на соответствующие дополнительные множители.
Получим уравнение х(х — 3) + 1(х — 5) = 1(х + 5).
Раскроем скобки слева и справа, х2 — 3х + х — 5 = х + 5.
Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:
Х2 — 3х + х — 5 — х — 5 = 0
И после приведения подобных членов получим квадратное уравнение х2 — 3х — 10 = 0. Решив его, найдем корни х1 = -2; х2 = 5.
Но мы уже выяснили, что при х = 5 общий знаменатель х(х — 5) обращается в нуль.
Следовательно, корнем нашего уравнения
будет х = -2.
§ 4 Краткие итоги урока
Важно запомнить:
При решении дробных рациональных уравнений надо поступить следующим образом:
1.Найти общий знаменатель дробей входящих в уравнение. При этом если знаменатели дробей можно разложить на множители, то разложить их на множители и затем найти общий знаменатель.
2.Умножить обе части уравнения на общий знаменатель: найти дополнительные множители, умножить числители на дополнительные множители.
3.Решить получившееся целое уравнение.
4.Исключить из его корней те, которые обращают в нуль общий знаменатель.
Список использованной литературы:
- Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б. / Под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. — М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. — М.: Мнемозина.
- Рурукин А. Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. -Волгоград: Учитель, 2005.
Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.«Рациональные уравнения с многочленами» — одна из самых часто встречающихся тем в тестовых заданиях ЕГЭ по математике. По этой причине их повторению стоит уделить особое внимание. Многие ученики сталкиваются с проблемой нахождения дискриминанта, перенесения показателей из правой части в левую и приведения уравнения к общему знаменателю, из-за чего выполнение подобных заданий вызывает трудности. Решение рациональных уравнений при подготовке к ЕГЭ на нашем сайте поможет вам быстро справляться с задачами любой сложности и сдать тестирование на отлично.
Выбирайте образовательный портал «Школково» для успешной подготовки к единому экзамену по математике!
Чтобы знать правила вычисления неизвестных и легко получать правильные результаты, воспользуйтесь нашим онлайн-сервисом.
Портал «Школково» — это единственная в своем роде площадка, где собраны необходимые для подготовки к ЕГЭ материалы. Наши преподаватели систематизировали и изложили в понятной форме все математические правила. Кроме того, мы предлагаем школьникам попробовать силы в решении типовых рациональных уравнений, база которых постоянно обновляется и дополняется.
Для более результативной подготовки к тестированию рекомендуем следовать нашему особому методу и начать с повторения правил и решения простых задач, постепенно переходя к более сложным. Таким образом, выпускник сможет выделить для себя самые трудные темы и сделать акцент на их изучении.
Начните подготовку к итоговому тестированию со «Школково» уже сегодня, и результат не заставит себя ждать! Выберите самый легкий пример из предложенных. Если вы быстро справились с выражением, переходите к более сложной задаче. Так вы сможете подтянуть свои знания вплоть до решения заданий ЕГЭ по математике профильного уровня.
Обучение доступно не только выпускникам из Москвы, но и школьникам из других городов.
Уделяйте пару часов в день занятиям на нашем портале, например, и совсем скоро вы сможете справиться с уравнениями любой сложности!
Мы уже научились решать квадратные уравнения. Теперь распространим изученные методы на рациональные уравнения.
Что такое рациональное выражение? Мы уже сталкивались с этим понятием. Рациональными выражениями называются выражения, составленные из чисел, переменных, их степеней и знаков математических действий.
Соответственно, рациональными уравнениями называются уравнения вида: , где — рациональные выражения.
Раньше мы рассматривали только те рациональные уравнения, которые сводятся к линейным. Теперь рассмотрим и те рациональные уравнения, которые сводятся и к квадратным.
Пример 1
Решить уравнение: .
Решение:
Дробь равна 0 тогда и только тогда, когда ее числитель равен 0, а знаменатель не равен 0.
Получаем следующую систему:
Первое уравнение системы — это квадратное уравнение.
Прежде чем его решать, поделим все его коэффициенты на 3. Получим:
Получаем два корня: ; .
Поскольку 2 никогда не равно 0, то необходимо, чтобы выполнялись два условия: . Поскольку ни один из полученных выше корней уравнения не совпадает с недопустимыми значениями переменной, которые получились при решении второго неравенства, они оба являются решениями данного уравнения.
Ответ: .
Итак, давайте сформулируем алгоритм решения рациональных уравнений:
1. Перенести все слагаемые в левую часть, чтобы в правой части получился 0.
2. Преобразовать и упростить левую часть, привести все дроби к общему знаменателю.
3. Полученную дробь приравнять к 0, по следующему алгоритму: .
4. Записать те корни, которые получились в первом уравнении и удовлетворяют второму неравенству, в ответ.
Давайте рассмотрим еще один пример.
Пример 2
Решить уравнение: .
Решение
В самом начале перенесем все слагаемые в левую сторону, чтобы справа остался 0.
Получаем:
Теперь приведем левую часть уравнения к общему знаменателю:
Данное уравнение эквивалентно системе:
Первое уравнение системы — это квадратное уравнение.
Коэффициенты данного уравнения: . Вычисляем дискриминант:
Получаем два корня: ; .
Теперь решим второе неравенство: произведение множителей не равно 0 тогда и только тогда, когда ни один из множителей не равен 0.
Необходимо, чтобы выполнялись два условия: . Получаем, что из двух корней первого уравнения подходит только один — 3.
Ответ: .
На этом уроке мы вспомнили, что такое рациональное выражение, а также научились решать рациональные уравнения, которые сводятся к квадратным уравнениям.
На следующем уроке мы рассмотрим рациональные уравнения как модели реальных ситуаций, а также рассмотрим задачи на движение.
Список литературы
- Башмаков М.И. Алгебра, 8 класс. — М.: Просвещение, 2004.
- Дорофеев Г. В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра, 8 класс. Учебник для общеобразовательных учреждений. — М.: Просвещение, 2006.
В., Суворова С.Б., Бунимович Е.А. и др. Алгебра, 8. 5-е изд. — М.: Просвещение, 2010.- Фестиваль педагогических идей «Открытый урок» ().
- School.xvatit.com ().
- Rudocs.exdat.com ().
Домашнее задание
Сегодня мы разберемся, как решать дробные рациональные уравнения.
Посмотрим: из уравнений
(1) 2х + 5 = 3(8 – х),
(3)
(4)
дробными рациональными уравнениями являются только (2) и (4), а (1) и (3) это целые уравнения.
Предлагаю решить уравнение (4), а затем сформулировать правило.
Поскольку уравнение дробное, то надо найти общий знаменатель. В этом уравнении это выражение 6(х – 12)(х – 6). Затем мы умножаем обе части уравнения на общий знаменатель:
После сокращения получаем целое уравнение:
6(х – 6) 2 – 6(х – 12) 2 = 5(х – 12)(х – 6).
Решив это уравнение надо обязательно проверить не обращают ли полученные корни в нуль знаменатели дробей в исходном уравнении.
Раскрываем скобки:
6х 2 – 72х + 216 – 6х 2 + 144х – 864 = 5х 2 – 90х + 360, упрощаем уравнение: 5х 2 – 162х + 1008 = 0.
Находим корни уравнения
D = 6084, √D = 78,
х 1 = (162 – 78)/10= 84/10 = 8,4 и х 2 = (162 + 78)/10 = 240/10 = 24.
При х = 8,4 и 24 общий знаменатель 6(х – 12)(х – 6) ≠ 0, значит эти числа являются корнями уравнения (4).
Ответ: 8,4; 24.
Решив предложенное уравнение, приходим к следующим положениям :
1) Находим общий знаменатель.
2) Умножаем обе части уравнения на общий знаменатель.
3) Решаем полученное целое уравнение.
4) Проверяем, какие из корней обращают общий знаменатель в нуль и исключаем их из решения.
Посмотрим теперь на примере, как работают полученные положения.
Решить уравнение:
1) Общий знаменатель: х 2 – 1
2) Умножаем обе части уравнения на общий знаменатель, получаем целое уравнение: 6 – 2(х + 1) = 2(х 2 – 1) – (х + 4)(х – 1)
3) Решаем уравнение: 6 – 2х – 2 = 2х 2 – 2 – х 2 – 4х + х + 4
х 2 – х – 2 = 0
х 1 = — 1 и х 2 = 2
4) При х = -1, общий знаменатель х 2 – 1 = 0.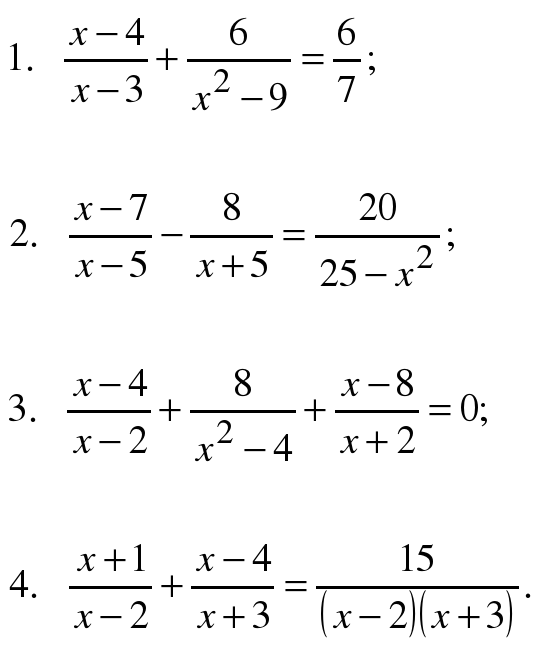
Число -1 корнем не является.
При х = 2, общий знаменатель х 2 – 1 ≠ 0. Число 2 – корень уравнения.
Ответ : 2.
Как видите, наши положения работают. Не бойтесь, у вас все получится! Самое главное правильно найдите общий знаменатель и аккуратно выполните преобразования . Надеемся, что при решение дробных рациональных уравнений у вас всегда будут получаться правильные ответы. Если у вас остались вопросы или вы хотите попрактиковаться в решении подобных уравнений, записывайтесь на уроки к автору этой статьи, репетитору й.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
4.7 Решение уравнений с дробями — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли дробь решением уравнения
- Решите уравнения с дробями, используя свойства сложения, вычитания и деления равенства
- Решите уравнения, используя свойство умножения равенства
- Переведите предложения в уравнения и решите
Приготовься 4.
17Прежде чем начать, пройдите этот тест на готовность. Если вы пропустили проблему, вернитесь к указанному разделу и просмотрите материал.
Вычислить x+4x+4, когда x=−3x=−3
Если вы пропустили эту проблему, просмотрите пример 3.23.
Приготовься 4.18
Решите: 2y−3=9,2y−3=9.
Если вы пропустили эту проблему, просмотрите пример 3.61.
Приготовься 4.19
Решите: y−3=−9y−3=−9
Если вы пропустили эту задачу, просмотрите пример 4.28.
Определить, является ли дробь решением уравнения
Как мы видели в разделе «Решение уравнений со свойствами равенства на вычитание и сложение» и «Решение уравнений с использованием целых чисел»; Свойство деления равенства, решение уравнения — это значение, которое дает истинное утверждение при замене переменной в уравнении. В этих разделах мы нашли целые числа и целые решения уравнений. Теперь, когда мы поработали с дробями, мы готовы найти решения уравнений в виде дробей.
Шаги, которые мы предпринимаем, чтобы определить, является ли число решением уравнения, одинаковы, независимо от того, является ли решение целым числом, целым числом или дробью.
Как
Определить, является ли число решением уравнения.
- Шаг 1. Подставьте число вместо переменной в уравнении.
- Шаг 2. Упростите выражения в обеих частях уравнения.
- Шаг 3. Определить, верно ли полученное уравнение. Если это правда, число является решением. Если это не так, число не является решением.
Пример 4,95
Определите, является ли каждое из следующих решений решением x-310=12.x-310=12.
- ⓐx=1x=1
- ⓑх=45х=45
- ⓒx=−45x=−45
Решение
| ⓐ | |
Переход на дроби с ЖК-дисплеем 10. | |
| Вычесть. |
Поскольку x=1x=1 не дает истинного уравнения, 11 не является решением уравнения.
| ⓑ | |
| Вычесть. |
Поскольку x=45x=45 дает истинное уравнение, 4545 является решением уравнения x−310=12.x−310=12.
| ⓒ | |
| Вычесть. |
Поскольку x=−45x=−45 не приводит к истинному уравнению, −45−45 не является решением уравнения.
Попытайся 4.189
Определите, является ли каждое число решением данного уравнения.
х-23=16х-23=16:
- ⓐx=1x=1
- ⓑх=56х=56
- ⓒx=-56x=-56
Попытайся 4.190
Определите, является ли каждое число решением данного уравнения.
г-14=38г-14=38:
- ⓐy=1y=1
- ⓑу=-58у=-58
- ⓒy=58y=58
Решите уравнения с дробями, используя свойства сложения, вычитания и деления равенства
В Решать уравнения со свойствами вычитания и сложения равенства и Решать уравнения, используя целые числа; Свойство деления равенства, мы решали уравнения, используя свойства равенства сложения, вычитания и деления. Мы будем использовать эти же свойства для решения уравнений с дробями.
Сложение, вычитание и деление свойств равенства
Для любых чисел a,b,a,b и c,c,
| , если a=b,a=b, то a+c=b+c.a+c=b+c. | Дополнительное свойство равенства |
если a=b,a=b, то a-c=b-c. a-c=b-c. | Свойство равенства вычитания |
| если a=b,a=b, то ac=bc,c≠0.ac=bc,c≠0. | Раздел имущества равенства |
Таблица 4,3
Другими словами, когда вы прибавляете или вычитаете одну и ту же величину из обеих частей уравнения или делите обе части на одну и ту же величину, вы все равно получаете равенство.
Пример 4,96
Решите: у+916=516.у+916=516.
Решение
| Вычтите | 6 с каждой стороны, чтобы отменить сложение. | ||
| Упростите каждую часть уравнения. | |||
| Упростите дробь. | |||
| Чек: | |||
| Замените y=-14y=-14. | |||
Переписать как дроби с ЖК-дисплеем. | |||
| Доп. | |||
Поскольку y=−14y=−14, получается y+916=516y+916=516 верное утверждение, мы знаем, что нашли решение этого уравнения.
Попытайся 4.191
Решите: y+1112=512.y+1112=512.
Попытайся 4.192
Решите: y+815=415.y+815=415.
Мы использовали свойство равенства вычитания в примере 4.96. Теперь воспользуемся дополнительным свойством равенства.
Пример 4,97
Решите: a−59=−89.a−59=−89.
Решение
| Добавьте 5959 с каждой стороны, чтобы отменить вычитание. | ||
| Упростите каждую часть уравнения. | ||
Упростите дробь. | ||
| Чек: | ||
| Замените a=−13a=−13. | ||
| Переход к общему знаменателю. | ||
| Вычесть. | ||
Поскольку a=−13a=−13 делает уравнение верным, мы знаем, что a=−13a=−13 является решением уравнения.
Попытайся 4.193
Решите: a−35=−85.a−35=−85.
Попытайся 4.194
Решите: n−37=−97.n−37=−97.
Может показаться, что в следующем примере нет дроби, но давайте посмотрим, что произойдет, когда мы решим его.
Пример 4,98
Решите: 10q=44.10q=44.
Решение
| 10q=4410q=44 | ||
Разделите обе части на 10, чтобы отменить умножение. | 10q10=441010q10=4410 | |
| Упрощение. | q=225q=225 | |
| Чек: | ||
| Подставьте q=225q=225 в исходное уравнение. | 10(225)=?4410(225)=?44 | |
| Упрощение. | 102(225)=?44102(225)=?44 | |
| Умножить. | 44=44✓44=44✓ | |
Решением уравнения была дробь 225,225. Оставляем как неправильную дробь.
Попытайся 4.195
Решите: 12u=-76.12u=-76.
Попытайся 4.196
Решить: 8m=92,8м=92.
Решение уравнений с дробями с использованием свойства умножения равенства
Рассмотрим уравнение x4=3.x4=3. Мы хотим знать, какое число, деленное на 44, дает 3,3. Итак, чтобы «отменить» деление, нам нужно будет умножить на 4,4. Свойство умножения на равенство позволит нам сделать это.
Это свойство говорит о том, что если мы начнем с двух равных величин и умножим их на одно и то же число, результаты будут равны.
Свойство равенства умножения
Для любых чисел a,b,a,b и c,c,
ifa=b,thenac=bc.ifa=b,thenac=bc.
Если обе части уравнения умножить на одну и ту же величину, получится равенство.
Давайте воспользуемся свойством умножения равенства, чтобы решить уравнение x7=−9.x7=−9.
Пример 4,99
Решите: x7=-9.x7=-9.
Решение
| Используйте свойство равенства умножения, чтобы умножить обе части на 77. Это изолирует переменную. | ||
| Умножение. | ||
Упрощение. | ||
| Уравнение верно. | ||
Попытайся 4.197
Решите: f5=−25.f5=−25.
Попытайся 4.198
Решите: h9=-27.h9=-27.
Пример 4.100
Решите: p−8=−40.p−8=−40.
Решение
Здесь pp делится на −8,−8. Мы должны умножить на −8−8, чтобы выделить pp.
| Умножить обе части на −8−8 | ||
| Умножение. | ||
| Упрощение. | ||
| Чек: | ||
Замените p=320p=320. | ||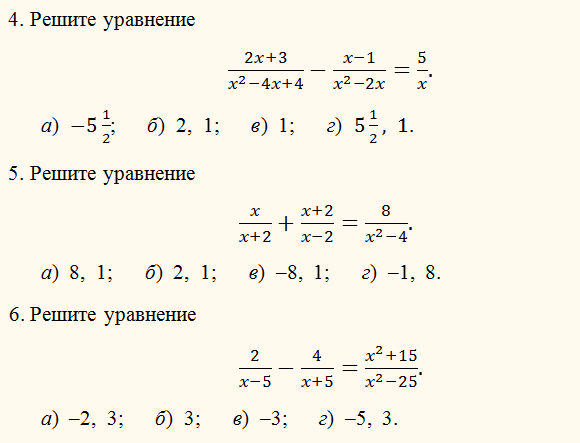
| Уравнение верно. | ||
Попытайся 4.199
Решите: c−7=−35.c−7=−35.
Попытайся 4.200
Решите: x−11=−12.x−11=−12.
Решение уравнений с коэффициентом −1−1
Посмотрите на уравнение −y=15.−y=15. Похоже, что yy уже изолирован? Но перед y,y стоит знак минус, поэтому он не изолирован.
Существует три различных способа выделения переменной в уравнении этого типа. Мы покажем все три способа в примере 4.101.
Пример 4.101
Решите: −y=15.−y=15.
Решение
Один из способов решить уравнение — переписать −y−y как −1y,−1y, а затем использовать свойство равенства деления, чтобы выделить y.y.
Перепишите -y-y как -1y-1y. | |
| Разделите обе части на −1. | |
| Упростите каждую сторону. |
Другой способ решить это уравнение — умножить обе части уравнения на −1,−1.
| Умножьте обе части на −1. | |
| Упростите каждую сторону. |
Третий способ решить уравнение — прочитать -y-y как «противоположное yy». Какое число имеет противоположность 1515? Противоположность 1515 – –15,–15. Таким образом, y=−15.y=−15.
Для всех трех методов мы изолировали yy и решили уравнение.
Чек:
| Замените y=-15y=-15. | |
| Упрощение. Уравнение верное. |
Попытайся 4.
201Решите: −y=48.−y=48.
Попытайся 4.202
Решите: −c=−23.−c=−23.
Решение уравнений с коэффициентом дроби
Когда у нас есть уравнение с дробным коэффициентом, мы можем использовать свойство равенства умножения, чтобы сделать коэффициент равным 1,1.
Например, в уравнении:
34x=2434x=24
Коэффициент xx равен 34,34. Чтобы найти x,x, нам нужно, чтобы его коэффициент был равен 1,1. Поскольку произведение числа и его обратного числа равно 1,1, наша стратегия здесь будет состоять в том, чтобы изолировать xx путем умножения на обратное число 34,34. Мы сделаем это в примере 4.102.
Пример 4.102
Решите: 34x=24,34x=24.
Решение
Умножьте обе части на обратную величину коэффициента. | ||
| Упрощение. | ||
| Умножение. | ||
| Чек: | ||
| Замените x=32x=32. | ||
| Перепишите число 3232 в виде дроби. | ||
| Умножить. Уравнение верное. | ||
Обратите внимание, что в уравнении 34x=24,34x=24 мы могли бы разделить обе части на 3434, чтобы получить xx отдельно. Деление — это то же самое, что и умножение на обратное, поэтому мы получим тот же результат. Но большинство людей согласны с тем, что умножать на обратное проще.
Попытайся 4.203
Решите: 25n=14,25n=14.
Попытайся 4.204
Решите: 56y=15,56y=15.
Пример 4.103
Решите: −38w=72.−38w=72.
Решение
Коэффициент представляет собой отрицательную дробь.
Помните, что число и его обратная величина имеют один и тот же знак, поэтому обратная величина коэффициента также должна быть отрицательной.
| Умножьте обе части на обратную величину −38−38. | ||
| Упрощение; обратные умножаются на единицу. | ||
| Умножение. | ||
| Чек: | ||
| Пусть w=−192w=−192. | ||
| Умножить. Это проверяет. | ||
Попытайся 4.205
Решите: −47a=52.−47a=52.
Попытайся 4.206
Решите: −79w=84.−79w=84.
Перевести предложения в уравнения и решить
Теперь мы рассмотрели все четыре свойства равенства — вычитание, сложение, деление и умножение.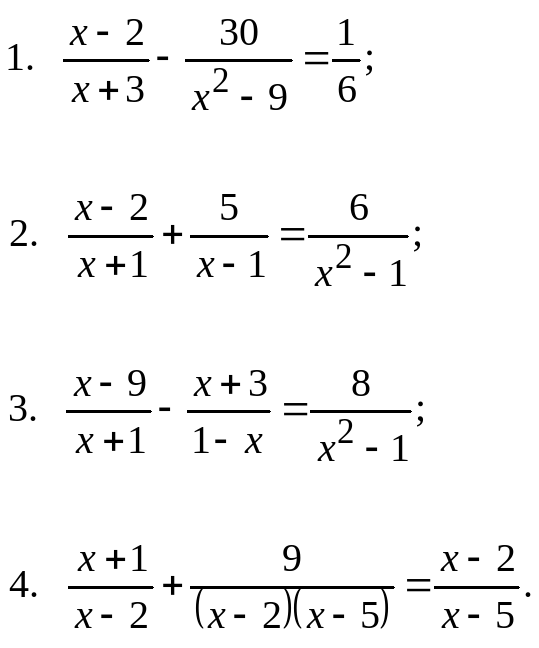
Мы перечислим их все вместе здесь для удобства.
| Свойство равенства вычитания: Для любых действительных чисел a, b, a, b и c, c, , если a=b,a=b, то a-c=b-c.a-c=b-c. | Аддитивное свойство равенства: Для любых действительных чисел a, b, a, b и c, c, , если a=b,a=b, то a+c=b+c.a+c=b +с. |
| Свойство равенства деления: Для любых чисел a, b, a, b и c, c, где c≠0c≠0 , если a=b,a=b, то ac=bcac=bc | Свойство равенства умножения: Для любых действительных чисел a, b, a, b и cc , если a=b,a=b, то ac=bcac=bc |
Когда вы складываете, вычитаете, умножаете или делите одну и ту же величину из обеих частей уравнения, вы все равно получаете равенство.
В следующих нескольких примерах мы будем переводить предложения в уравнения, а затем решать уравнения. Может быть полезно просмотреть таблицу перевода в разделе Вычислить, упростить и перевести выражения.
Пример 4.104
Переведите и решите: nn разделить на 66 равно −24,−24.
Решение
| Перевести. | ||
| Умножьте обе стороны на 66. | ||
| Упрощение. | ||
| Чек: | Разделенное на 66 -144-144 равно -24-24? | |
| Перевести. | ||
| Упрощение. Это проверяет. | ||
Попытайся 4.207
Переведите и решите: nn разделить на 77 равно −21,−21.
Попытайся 4.208
Переведите и решите: nn разделить на 88 равно −56,−56.
Пример 4.105
Переведите и решите: Частное qq и −5−5 равно 70,70.
Решение
| Перевести. | ||
| Умножьте обе части на −5−5. | ||
| Упрощение. | ||
| Чек: | Является ли частное −350−350 и −5−5 равным 7070? | |
| Перевести. | ||
| Упрощение. Это проверяет. | ||
Попытайся 4.209
Переведите и решите: Частное qq и −8−8 равно 72,72.
Попытайся 4.210
Переведите и решите: Частное pp и −9−9 равно 81,81.
Пример 4.
106Переведите и решите: Две трети ff равно 18,18.
Решение
| Перевод. | ||
| Умножьте обе стороны на 3232. | ||
| Упрощение. | ||
| Чек: | Две трети от 2727 равны 1818? | |
| Перевести. | ||
| Упрощение. Это проверяет. | ||
Попытайся 4.211
Переведите и решите: Две пятых от ff равно 16,16.
Попытайся 4.212
Переведите и решите: Три четверти ff равно 21,21.
Пример 4.107
Переведите и решите: Частное мм и 5656 равно 34,34.
Решение
Частное мм и 5656 равно 3434. | ||
| Перевести. | m56=34m56=34 | |
| Умножьте обе стороны на 5656, чтобы получить мм. | 56(m56)=56(34)56(m56)=56(34) | |
| Упрощение. | m=5·36·4m=5·36·4 | |
| Удалить общие множители и умножить. | м=58м=58 | |
| Проверка: | ||
| Является ли частное 5858 и 5656 равным 3434? | 5856=?345856=?34 | |
| Переписать как деление. | 58÷56=?3458÷56=?34 | |
| Умножьте первую дробь на обратную вторую. | 58·65=?3458·65=?34 | |
| Упростить. | 34=34✓34=34✓ | |
Наше решение проверяет.
Попытайся 4.213
Переведи и реши. Частное nn и 2323 равно 512,512.
Попытайся 4.214
Переведи и реши Частное cc и 3838 равно 49,49.
Пример 4.108
Переведите и решите: Сумма трех восьмых и xx равна трем с половиной.
Решение
| Перевести. | |
| Используйте свойство равенства вычитания, чтобы вычесть 3838 из обеих сторон. | |
| Объедините одинаковые термины в левой части. | |
| Преобразовать смешанное число в неправильную дробь. | |
| Преобразование в эквивалентные дроби с ЖК-дисплеем, равным 8. | |
| Вычесть. | |
| Запишите как смешанное число. |
Мы запишем ответ как смешанное число, потому что в исходной задаче использовалось смешанное число.
Проверить:
Является ли сумма трех восьмых и 318318 равной трем с половиной?
| 38+318=?31238+318=?312 | |
Доп. | 348=?312348=?312 |
| Упрощение. | 312=312✓312=312✓ |
Проверка решения.
Попытайся 4.215
Переведите и решите: Сумма пяти восьмых и xx равна одной четвертой.
Попытайся 4.216
Переведите и решите: Разница между одной и тремя четвертыми и xx составляет пять шестых.
Раздел 4.7 Упражнения
Практика делает совершенным
Определите, является ли дробь решением уравнения
В следующих упражнениях определите, является ли каждое число решением данного уравнения.
498.
х-25=110х-25=110:
- ⓐx=1x=1
- ⓑх=12х=12
- ⓒx=−12x=−12
499.
г-13=512г-13=512:
- ⓐy=1y=1
- ⓑу=34у=34
- ⓒу=-34у=-34
500.
ч+34=25ч+34=25:
- ⓐ ч=1ч=1
- ⓑ В=720В=720
- ⓒ ч=-720ч=-720
501.
к+25=56к+25=56:
- ⓐk=1k=1
- ⓑк=1330к=1330
- ⓒk=-1330k=-1330
Решайте уравнения с дробями, используя свойства сложения, вычитания и деления равенства
В следующих упражнениях решите.
502.
у+13=43у+13=43
503.
м+38=78м+38=78
504.
f+910=25f+910=25
505.
ч+56=16ч+56=16
506.
а-58=-78а-58=-78
507.
с-14=-54с-14=-54
508.
х-(-320)=-1120x-(-320)=-1120
509.
z-(-512)=-712z-(-512)=-712
510.
n−16=34n−16=34
511.
р-310=58р-310=58
512.
с+(-12)=-89с+(-12)=-89
513.
k+(−13)=−45k+(−13)=−45
514.
5j=175j=17
515.
7к=187к=18
516.
−4w=26−4w=26
517.
−9v=33−9v=33
Решение уравнений с дробями с использованием свойства умножения равенства
В следующих упражнениях решите.
518.
f4=−20f4=−20
519.
b3=-9b3=-9
520.
у7=-21у7=-21
521.
x8=-32×8=-32
522.
р-5=-40р-5=-40
523.
q−4=−40q−4=−40
524.
r−12=−6r−12=−6
525.
с-15=-3с-15=-3
526.
−x=23−x=23
527.
−y=42−y=42
528.
−h=−512−h=−512
529.
−k=−1720−k=−1720
530.
45n=2045n=20
531.
310р=30310р=30
532.
38q=-4838q=-48
533.
52м=-4052м=-40
534.
−29a=16−29a=16
535.
−37b=9−37b=9
536.
−611u=−24−611u=−24
537.
−512v=−15−512v=−15
Смешанная практика
В следующих упражнениях решите.
538.
3x=03x=0
539.
8у=08у=0
540.
4f=454f=45
541.
7г=797г=79
542.
р+23=112р+23=112
543.
д+56=112д+56=112
544.
78м=11078м=110
545.
14n=71014n=710
546.
−25=x+34−25=x+34
547.
−23=y+38−23=y+38
548.
1120=-f1120=-f
549.
815=-d815=-d
Превратите предложения в уравнения и решите
В следующих упражнениях переведите в алгебраическое уравнение и решите.
550.
nn разделить на восемь равно −16,−16.
551.
nn разделить на шесть равно −24,−24.
552.
мм разделить на −9−9 равно −7,−7.
553.
мм разделить на −7−7 равно −8,−8.
554.
Частное ff и −3−3 равно −18,−18.
555.
Частное ff и −4−4 равно −20,−20.
556.
Частное gg и двенадцать равно 8,8.
557.
Частное gg и девять равно 14,14.
558.
Три четверти qq равно 12,12.
559.
Две пятых от qq составляет 20,20.
560.
Семь десятых pp составляют −63,−63.
561.
Четыре девятых части составляет −28,−28.
562.
мм разделить на 44 равно минус 6,6.
563.
Частное чч и 22 равно 43,43.
564.
Три четверти zz равно 15,15.
565.
Частное аа и 2323 равно 34,34.
566.
Сумма пяти шестых и xx равна 12,12.
567.
Сумма трех четвертых и xx равна 18,18.
568.
Разница между yy и одной четвертой составляет −18,−18.
569.
Разница yy и одной трети составляет −16,−16.
Математика на каждый день
570.
Покупки Тереза купила пару туфель на распродаже за 48 долларов 48 долларов. Цена продажи составила 2323 от обычной цены. Найдите обычную цену обуви, решив уравнение 23p=4823p=48
571.
Игровой домик Стол в детском игровом домике размером 3535 от взрослого стола. Стол для игрового домика имеет высоту 1818 дюймов. Найдите высоту стола для взрослых, решив уравнение 35h=18,35h=18.
Письменные упражнения
572.
Пример 4.100 описывает три метода решения уравнения −y=15.−y=15. Какой метод вы предпочитаете? Почему?
573.
Ричард считает, что решение уравнения 34x=2434x=24 равно 16,16. Объясните, почему Ричард ошибается.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?
3.4 Решение уравнений с дробями или десятичными коэффициентами – средний уровень алгебры II
К концу этого раздела вы сможете:
- Решать уравнения с дробными коэффициентами
- Решение уравнений с десятичными коэффициентами
Давайте воспользуемся представленной ранее общей стратегией решения линейных уравнений, чтобы решить уравнение .
The next line says, “Change the constants to equivalent fractions with the LCD,” and shows one-eighth x equals one-fourth minus two-fourths. The next line says, “Subtract,” and shows one-eighth x equals negative one-fourth. The next line says, “Multiply both sides by the reciprocal of one-eighth,” and shows a red 8 over 1 times one-eighth x equals a red 8 over 1 times negative one-fourth. The next line says, “Divide,” and shows 12x over a red 12 equals 4.8 over a red 12. The last line says, “Simplify,” and shows x equals negative 2.» data-label=»»> Этот метод работал нормально, но многие ученики не чувствуют себя уверенно, когда видят все эти дроби.
Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.
Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель числа 9.0464 все дроби в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется очисткой уравнения дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.
Решить: .
Решение
The next line says, “Solve using the General Strategy for Solving Linear Equations,” and shows x plus 4 minus a red 4 equals 2 minus a red 4. The last step says, “Check. Let x equal negative 2.” Beside that is the original equation followed by one-eighth times a red negative 2 plus one-half, equal sign with a question mark, one-fourth. Below that is negative 2 over 8 plus one-half, equal sign with a question mark, one-fourth. Below that is negative 2 over 8 plus 4 over 8, equal sign with a question mark, one-fourth. Below that is 2 over 8, equal sign with a question mark, one-fourth. The last line says one-fourth equals one-fourth.» data-label=»»>
Решить: .
Показать ответРешить: .
Показать ответy = 3
Обратите внимание на (рисунок), что после того, как мы очистили уравнение дробей, оно стало таким же, как те, которые мы решали ранее в этой главе. Мы изменили задачу на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.
- Найдите наименьший общий знаменатель всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
- Решите, используя общую стратегию решения линейных уравнений.
Решить: .
Решение
Мы хотим очистить дроби, умножив обе части уравнения на LCD всех дробей в уравнении.
The next line says, “Multiply both sides of the equation by 12,” and shows a red 12 times each side of the original equation. The next line says, “Distribute,” and shows 12 times 7 equals 12 times one-half x plus 12 times three-fourths x minus 12 times two-thirds x. The next line says, “Simplify — and notice, no more fractions!” Beside that is 84 equals 6x plus 9x minus 8x. The next line says, “Combine like terms,” and shows 84 equals 7x. The next line says, “Divide by 7,” and shows 84 over a red 7 equals 7x over a red 7. The next line says, “Simplify,” and shows 12 equals x. The last step says, “Check: Let x equal 12.” Beside that is the original equation. Below that is 7 followed by an equal sign with a question mark, then one-half times a red 12 plus three-fourths times a red 12 minus two-thirds times a red 12. Bellow that is 7 followed by an equal sign with a question mark, then 6 plus 9 minus 8. The last line says 7 equals 7, followed by a check mark.» data-label=»»>
Решить: .
Показать ответv = 40
Решить: .
Показать ответu = −12
В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.
Решить: .
Решение
The next step says, “Distribute,” and shows 6x plus 6 times one-third equals 6 times one-sixth x minus 6 times one-half. The next step says, “Simplify — no more fractions!” and shows 6x plus 2 equals x minus 3. The next line says, “Subtract x from both sides,” and shows 6x minus a red x plus 2 equals x minus a red x minus 3. The next line says, “Simplify,” and shows 5x plus 2 equals negative 3. The next line says, “Subtract 2 from both sides,” and shows 5x plus 2 minus a red 2 equals negative 3 minus a red 2. The next line says, “Simplify,” and shows 5x equals negative 5. The next line says, “Divide by 5,” and shows 5x over a red 5 equals negative 5 over a red 5. The next line says, “Simplify,” and shows x equals negative 1. The next line says, “Check,” and shows the original equation. The following line says, “Substitute x equals negative 1.” Beside that is a red negative 1 plus one-third followed by an equal sign with a question mark, then one-sixth times a red negative 1 minus one-half.
Below that is negative 1 plus one-third followed by an equal sign with a question mark, then negative one-sixth minus one-half. Below that is negative 3 over 3 plus 1 over 3 followed by an equal sign with a question mark, then negative 1 over 6 minus 3 over 6. Below that is negative 2 over 3 followed by an equal sign with a question mark, then negative 4 over 6. The last line says negative 2 over 3 equals negative 2 over 3.» data-label=»»>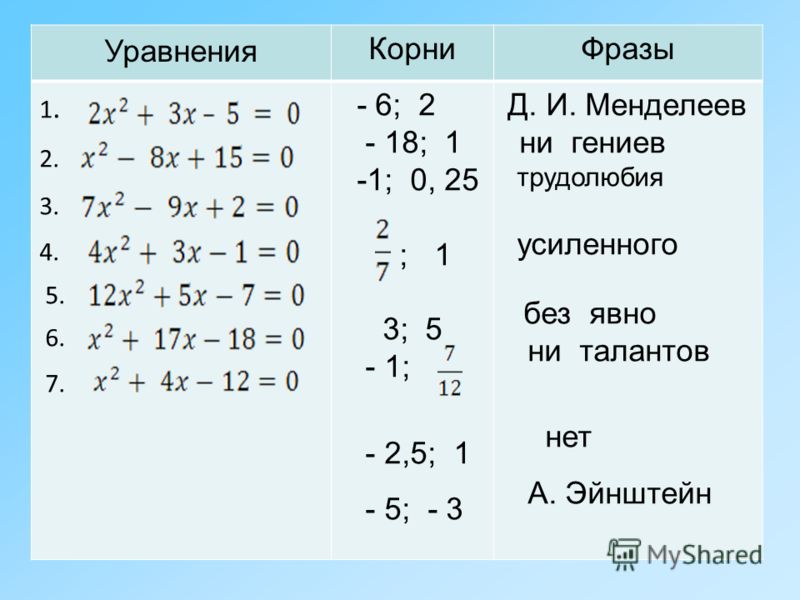
Решить: .
Показать ответa = −2
Решить: .
Показать ответc = −2
На (рис.) мы начнем с использования свойства Distribution. Этот шаг сразу очистит дроби!
Решить: .
Раствор
Below that is 1 followed by an equal sign with a question mark, then one-half times parentheses 4 times a red 0 plus 2. Below that is 1 followed by an equal sign with a question mark, then one-half times 2. Below that is a 1 followed by an equal sign with a question mark, then 2 over 2. The last line says 1 equals 1.» data-label=»»>Решить: .
Показать ответp = −4
Решить: .
Показать ответq = 2
Много раз, даже после распределения, все еще будут дроби.
Решить: .
Решение
The next line says, “Simplify,” and shows y equals 9. The last step says, “Check. Substitute: 9 for y,” and shows the original equation. Below that is one-half times parentheses red 9 minus 5, equal sign with a question mark, one-fourth times parentheses red 9 minus 1. Below that is one-half times 4, equal sign with a question mark, one-fourth times 8, then 2 equals 2 followed by a check mark.» data-label=»»>Решить: .
Показать ответn = 2
Решить: .
м = −1
В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем задачи, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей. Например, и . Итак, когда у нас есть уравнение с десятичными дробями, мы можем использовать тот же процесс, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.
Решить: .
Решение
Единственным десятичным знаком в уравнении является . Так как , LCD есть . Мы можем умножить обе части на, чтобы очистить десятичную дробь.
The next line says, “Add 50 to get all constants to the right,” and shows 8x minus 50 plus a red 50 equals 70 plus a red 50. The next line says, “Simplify,” and shows 8x equals 120. The next line says, “Divide both sides by 8,” and shows 8x over a red 8 equals 120 over a red 8. The next line says, “Simplify,” and shows x equals 15. The last step says, “Check. Let x equal 15.” Beside that is 0.8 times a red 15 minus 5 equals 7, then 12 minus 5 equals 7, then 7 equals 7.» data-label=»»>
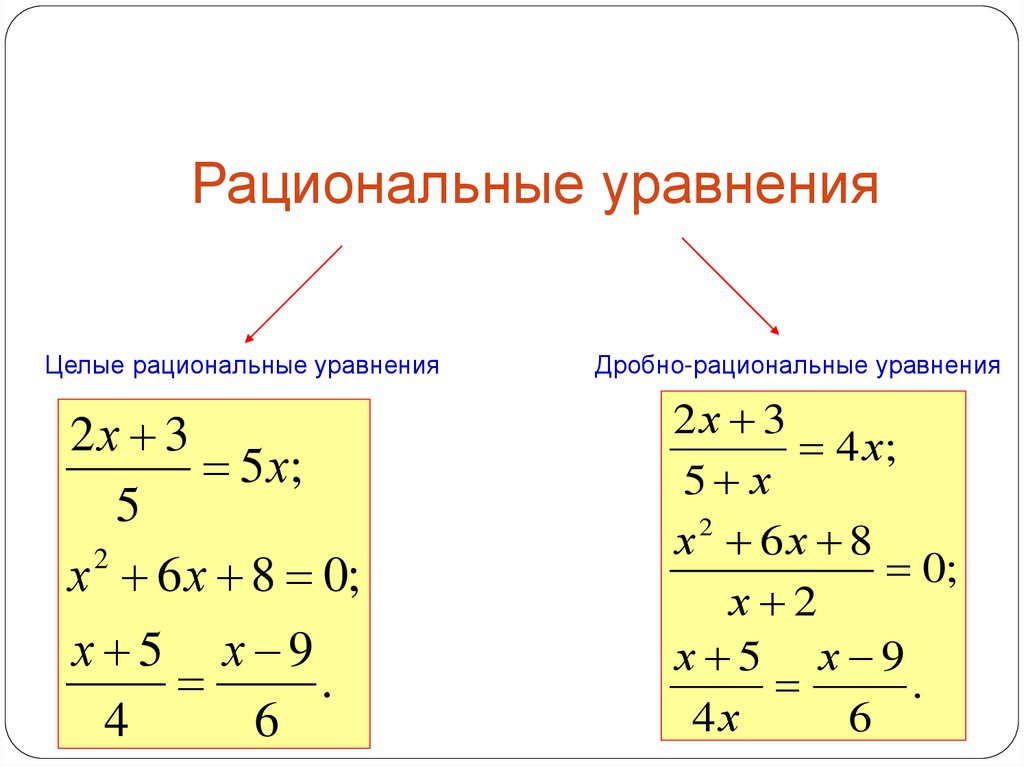
Решить: .
Показать ответx = 20
Решить: .
Показать ответx = 10
Решить: .
Решение
Посмотрите на десятичные дроби и придумайте эквивалентные дроби.
Обратите внимание, ЖК-дисплей.
Путем умножения на ЖК-дисплее мы очистим десятичные дроби.
The next line says, “Simplify,” and shows 2 equals 19x minus 150. The next line says, “Collect the constants to the left,” and shows 2 plus a red 150 equals 19x minus 150 plus a red 150. The next line says, “Simplify,” and shows 152 equals 19x. The next line says, “Divide by 19,” and shows 152 over a red 19 equals 19x over a red 19. The next line says, “Simplify,” and shows 8 equals x. The last line says, “Check: Let x equal 8,” and shows 0.06 times a red 8 plus 0.02 equals 0.25 times a red 8 minus 1.5. Below that is 0.48 plus 0.02 equals 2.00 minus 1.5. The last line says 0.50 equals 0.50.» data-label=»»>
Решить: .
Показать ответч = 12
Решить: .
Показать ответk = −1
В следующем примере используется уравнение, типичное для тех, которые мы увидим в приложении к деньгам в следующей главе. Обратите внимание, что мы сначала распределим десятичную дробь, прежде чем очистим все десятичные дроби в уравнении.
Решить: .
Раствор
30x plus 0.15 equals a red 100 times 2.85. The next line says, “Distribute,” and shows 30x plus 15 equals 285. The next line says, “Subtract 15 from both sides,” and shows 30x plus 15 minus a red 15 equals 285 minus a red 15. The next line says, “Simplify,” and shows 30x equals 270. The next line says, “Divide by 30,” and shows 30x over a red 30 equals 270 over a red 30. The next line says “Simplify” and shows x equals 9. The next line says, “Check,” and shows the original equation. Below that is “Let x equal 9” and 0.25 times a red 9 plus 0.05 times parentheses red 9 plus 3, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.05 times 12, equal sign with a question mark, 2.85. Below that is 2.25 plus 0.60 followed by an equal sign with a question mark, then 2.85. The last line shows 2.85 equals 2.85.» data-label=»»>
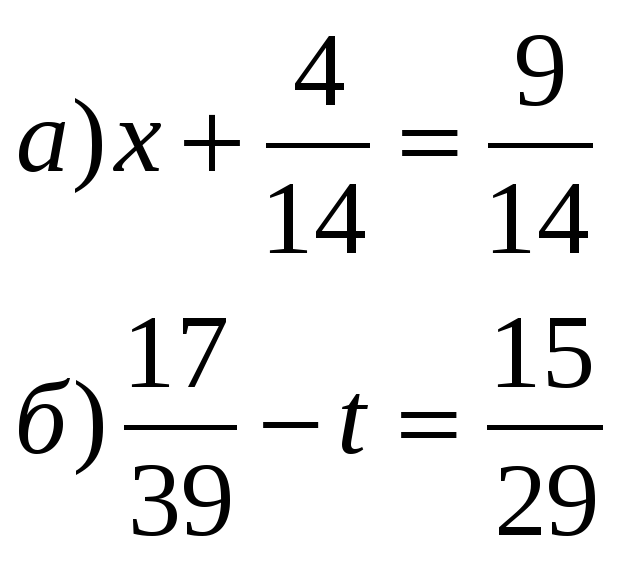
Решить: .
Показать ответn = 9
Решить: .
Показать ответd = 16
- Решайте уравнения с дробными коэффициентами, очищая дроби.
- Найдите наименьший общий знаменатель всех дробей в уравнении.
- Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает дроби.
- Решите, используя общую стратегию решения линейных уравнений.
Решение уравнений с дробными коэффициентами
В следующих упражнениях решите уравнение, очистив дроби.
| 1. | 2. |
| 3. | 4. |
| 5. | 6. |
| 7. | 8. |
| 9. | 10. |
| 11. | 12. |
| 13. | 14. |
| 15. | 16. |
| 17. | 18. |
| 19. | 20. |
| 21. | 22. |
| 23. | 24. |
Решение уравнений с десятичными коэффициентами
В следующих упражнениях решите уравнение, удалив десятичные дроби.
| 25. | 26. |
| 27. | 28. |
| 29. | 30. |
| 31. | 32. |
| 33. | 34. |
| 35. | 36. |
| 37. | 38. |
39. | 40. |
Математика на каждый день
| Монеты 41 . У Тейлора есть десять центов. Количество копеек больше, чем количество десятицентовиков. Решите уравнение для , количество десятицентовиков. | Марки 42. Трэвис накупил марок и марок. Количество марок было меньше количества марок. Решите уравнение для , чтобы найти количество марок, купленных Трэвисом. |
Письменные упражнения
| 43. Объясните, как найти наименьший общий знаменатель . | 44. Если в уравнении несколько дробей, как умножение обеих частей на ЖК облегчает решение? |
| 45. Если в уравнении дроби есть только с одной стороны, то зачем обе части уравнения умножать на LCD? | 46. Что такое LCD в уравнении? Откуда вы знаете? |
1. |