(2 в минус 1 степени минус 3 в минус 1 степени×6)в минус … -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
Заяц за 2 ч пробегает 14 км, а сокол за 3 ч пролетает 210 км. Во сколько раз сокол движется быстрее зайца? На сколько километ¬ров в час скорость зайца меньше скорости сокола?…
Номер 56 3,4 решите поже…
В саду было 128 деревьев. 3/8 деревьев это яблони, 2/4 груши, а остальные деревья – сливы. Сколько слив было в саду?…
Помогите решить уравнения!!СРОЧНО ОЧЕНЬ…
(2 в минус 1 степени минус 3 в минус 1 степени×6) в минус 1 степени=.
Помогите пожалуйста
30 баллов…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский языкХимия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Как выбрать солнцезащитные очки? — Полезная информация «Оптик Центр»
Солнцезащитные очки
Во все времена люди старались защитить свои глаза от прямого воздействия солнечных лучей: в Китае лицо закрывали широкополыми шляпами, в Японии надевали на глаза тканевые повязки с прорезями, в которые вставляли слюду, а в Индии их покрывали шелковыми полосками, пропитанными смолой. Настоящие солнцезащитные очки появились 200 лет назад, и предназначались они для солдат армии Наполеона.
Настоящие солнцезащитные очки появились 200 лет назад, и предназначались они для солдат армии Наполеона.
Зачем нужны солнцезащитные очки?
Основное предназначение очков от солнца — защищать глаза от прямого попадания на них солнечных лучей.
В чем опасность такого воздействия?
Солнечный свет состоит из совокупности ультрафиолетовых и инфракрасных лучей разной длины. И, если инфракрасные лучи в основном рассеиваются в атмосферной влаге, то ультрафиолетовые лучи длиной от 280 до 380 нанометров доходят до земли, их поглощает хрусталик, который защищая сетчатку, сам при этом страдает:
- С годами белки хрусталика начинают терять свою естественную структуру и начинают мутнеть, что приводит к развитию катаракты.
- Также теряется способность хрусталика фокусироваться на близких предметах, снижается его эластичность, что приводит к развитию дальнозоркости.
Мы расскажем вам, на какие технические характеристики солнцезащитной оптики обратить внимание, чтобы вы смогли выбрать те очки, которые уберегут глаза от воздействия ультрафиолета.
Стекло или пластик?
Несмотря на то, что линзы из стекла вообще не пропускают ультрафиолетовые лучи, 95 % современных производителей отдают предпочтение специальному пластику:
- Очки с пластиковыми линзами легкие.
- Они не травмоопасные, что особенно важно, если выбирать модели для детей и водителей.
Будьте внимательны! Из какого бы материала вы ни выбрали солнцезащитные очки (стекла или пластика), их основная задача — защита от ультрафиолетовых лучей, и будут ли очки надежно уберегать глаза, никак не зависит от цвета линз.
Темные линзы или светлые?
Линзы могут быть и темными, и прозрачными, но поглощать ультрафиолетовые лучи они будут одинаково хорошо только в том случае, если сверху их покроют специальным фильтром от ультрафиолета.
Производители качественных солнцезащитных очков тщательно следят за этим, и обязательно указывают на степень защиты от ультрафиолета в маркировке.
Если вы на дужках очков или в документах к ним видите знак «UV400», это говорит о том, что перед вами качественные солнцезащитные очки.
Цифра 400 в маркировке выбрана неслучайно. Она означает, что ультрафиолетовые волны, длина которых измеряется в нанометрах и равна 400 единицам, не проникнут через защитное напыление. В дешевых очках линзы только окрашиваются, затемняются, а не покрываются специальным фильтром.
Зрачок под темными линзами расширяется, ультрафиолетовые лучи легко проникают под затемненные линзы, поглощаются хрусталиком, что очень опасно для зрения.
Обязательно обращайте внимание на то, защитят ли вас очки от ультрафиолета, а лишь затем выбирайте степень светопропускания линз — их затененность. Об этом тоже расскажет специальная маркировка, как правило на дужке таких очков может находиться следующая надпись: «Cat. 3» или «Filter cat. 3».
Классификация очков по степени светопропускания
- Очки с 0 степенью светопропускания почти прозрачные.

- Очки с 1 и 2 степенью светопропускания пропускают от 43 до 80% и от 18 до 43% света соответственно. Их рекомендуют носить при слабом и среднем освещении солнцем.
- Очки с 3 степенью светопропускания следует выбирать для ношения при очень ярком солнце.
Выбор будет зависеть от того, где и когда вы собираетесь носить солнцезащитные очки:
- Для наших широт в жаркий летний период оптимальным выбором будут очки с 2-3 степенью светопропускания.
- Для весенней поры и раннего летнего утра идеально подойдут очки 1-2 степени светопропускания.
- Если вы решили покорять горы, то выбирайте самые темные очки 4 категории.
Еще раз акцентируем ваше внимание, что степень затененности линз никак не влияет на их свойства защиты от воздействия ультрафиолета.
Цвет и размер линз
Линзы не всех цветов и форм будут комфортными для глаз.
- Так, наши специалисты советуют остановить свой выбор на очках с коричневыми, зелеными или серыми оттенками линз, которые считаются наиболее приятными для глаз, а к выбору моделей с цветными линзами следует относиться крайне осторожно.
- Водителям рекомендуется выбирать очки с градиентными линзами, которые сверху затемнены сильнее, чем снизу.
- Обратите внимание на размер линз. Они должны быть большими. Выбирать очки с узкими стеклами не рекомендуется. Весь смысл защиты от ультрафиолета в этом случае пропадает, потому что линзы небольших размеров пропускают лучи через незакрытые участки и ограничивают поле зрения.
- Очки должны удобно сидеть на лице, прилегать к нему, но при этом не сдавливать виски и не давить в переносицу. Это может вызвать головную боль и утомление.

Вопрос качества
Информацию о качестве используемых материалов можно всегда узнать на ярлыке, в котором указывается, из чего изготовлены линзы, а также из маркировки на оправе или из паспорта к товару.
-
Аббревиатуры 89/686/ЕЕС, ANSI Z80.3, AS 1067, EN 1836 означают, что очки качественные, и материалы, которые использовались для их изготовления, соответствуют мировым стандартам безопасности.
Также проверить качество линз можно, обратившись к специалистам салона «Очки и Мода» на ул. Васенко, 4, где с помощью оптического прибора — спектрофотометра или калориметра — вы сможете убедиться в безопасности выбранных вами солнцезащитных очков.
Лучше не носить очки вообще, чем ходить в моделях низкого качества. Лишь пользование очками с защитой от ультрафиолета убережет ваши глаза. Это первое и главное, на что вы должны обращать внимание при выборе качественного товара.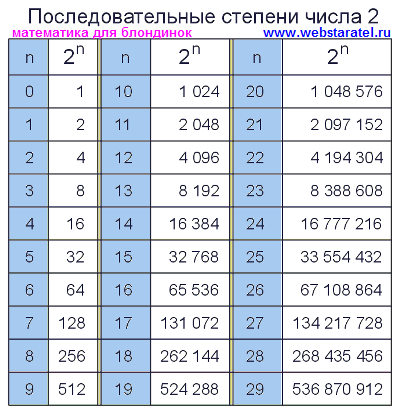 Насколько очки будут при этом темными, и какую будут иметь форму — это уже дело вкуса.
Насколько очки будут при этом темными, и какую будут иметь форму — это уже дело вкуса.
Смотрите также:
ФРК (фоторефракционная кератэктомия)
Статистика свидетельствует, что более 300 миллионов человек во всем мире испытывают проблемы со зрением. Особое предпочтение офтальмологи отдают фоторефракционной кератэктомии.
Советы по сохранению зрения у детей
Познавая незнакомый мир вокруг себя, дети полагаются на все свои сенсорные системы: каждый звук и каждое прикосновение несут информацию о ранее неведомом. 80% сенсорной информации ребенку приносит зрение, а потому здоровые глаза являются фундаментом, как для умственного, так и для физического развития.
Вернуться к списку
Степени двойки минус один / Полезные заметки
http://tvtropes.org/pmwiki/pmwiki.php/usefulnotes/powersoftwominusone
СледующийПерейти к
Видеоигры — не что иное, как компьютерные программы, и они ограничены системами, на которых они работают. Одним особенно строгим ограничением является тот факт, что компьютеры не могут обрабатывать числа произвольного размера с какой-либо эффективностью. Поскольку эффективность обычно очень важна для видеоигр, это накладывает жесткие ограничения на диапазон значений, с которыми они могут работать. Поскольку компьютеры работают в двоичном формате, этот размер должен быть определенным количеством бит (двоичные цифры — ноль или единица). Числа, хранящиеся в памяти компьютера, называются 9.0008 переменные .
Одним особенно строгим ограничением является тот факт, что компьютеры не могут обрабатывать числа произвольного размера с какой-либо эффективностью. Поскольку эффективность обычно очень важна для видеоигр, это накладывает жесткие ограничения на диапазон значений, с которыми они могут работать. Поскольку компьютеры работают в двоичном формате, этот размер должен быть определенным количеством бит (двоичные цифры — ноль или единица). Числа, хранящиеся в памяти компьютера, называются 9.0008 переменные .
Компьютеры также имеют ограничение на максимальный размер переменной. Это не жесткое ограничение, но использование больших чисел значительно замедляет вычисления. Всякий раз, когда вы слышите о «количестве битов» игровой консоли (например, Nintendo Entertainment System является «8-битной»), они имеют в виду именно это. NES имеет 8-битную шину данных; он может перемещать только 8 бит данных за раз. Если он должен двигаться дальше, он должен сделать это более чем за один цикл (и если ему нужно выполнить математические операции с ними, он должен нести Единицу). С технической точки зрения это называется «размером слова».
С технической точки зрения это называется «размером слова».
В новых видеоиграх многие вещи — скажем, количество предметов в гиперпространственном арсенале игрока — ограничены разумными пределами, потому что переменная, фактически используемая для хранения этого значения, имеет решительно и разумных пределов. Однако в прежние времена было обычным делом позволять самому компьютеру ограничивать эти значения, потому что пределы были намного ниже — 8-битный компьютер, такой как NES, имеет «предел» 255.
Максимальное значение, которое вы можете сохранить в переменной или регистре, определяется количеством используемых битов. Это 2 в степени количества битов минус 1, потому что мы считаем с нуля. Вот удобная таблица.
- 8 бит может содержать значение до 255. Atari 2600 и 7800, Nintendo Entertainment System, Sega Master System и ранние домашние компьютеры были 8-битными.
- 12-битный может содержать значение до 4095.
 Некоторые игры для NES, такие как Final Fantasy и Rygar , использовали хаки для получения таких больших значений.
Некоторые игры для NES, такие как Final Fantasy и Rygar , использовали хаки для получения таких больших значений. - 16 бит может содержать значение до 65 535. Super Nintendo Entertainment System и Sega Genesis являются 16-битными, как и ПК, выпущенные в середине 19-го века.80-х и несколько японских игровых компьютеров.
- 32 бита может содержать значение до 4 294 967 295. Sega Saturn и Dreamcast, Sony PlayStation, Microsoft Xbox и Wii — все 32-битные. Так же как и настольные ПК, выпущенные с 1987 по 2007 год, как и большинство смартфонов, выпущенных до 2018 года. Большинство устройств никогда не достигнет этого предела, но есть несколько основных исключений, которые сделали переход на 64-разрядную версию необходимостью, например проблема Y2K38. (в котором количество секунд, прошедших с 1970 достигнет этого количества, вызывая проблемы в системах, использующих Unix Time) и ограниченный пул адресов IPv4.
- 64 бита может содержать значение до 18 446 744 073 709 551 615.
 примечание Около 18,4 квинтиллиона Nintendo 64, GameCube, примечание Хотя с некоторыми 32-разрядными компонентами Sony PlayStation 2 и современные настольные ПК являются 64-разрядными, 64-разрядные операционные системы стали довольно распространенным явлением в 2010 г. (по крайней мере, , на новых компьютерах).
примечание Около 18,4 квинтиллиона Nintendo 64, GameCube, примечание Хотя с некоторыми 32-разрядными компонентами Sony PlayStation 2 и современные настольные ПК являются 64-разрядными, 64-разрядные операционные системы стали довольно распространенным явлением в 2010 г. (по крайней мере, , на новых компьютерах). - 128 бит может содержать значение до 340 282 366 920 938 463 463 374 607 431 768 211 455. примечание 340.2 Undecillion Компьютеры обычно не имеют 128-битных регистров общего назначения, но Cell PS3, ЦП Xbox 360 и современные ЦП x64 (используемые как на ПК, так и на Mac) имеют 128-битные векторные регистры (вмещающие 4 регистра). 32-битные значения). Они используются для векторной математики.
Обратите внимание, что в дополнение к вышеперечисленному самые последние процессоры имеют дополнительные «векторные» процессоры для параллельного выполнения нескольких вычислений; до сих пор они имели ширину до 256 бит. Кроме того, вычисления с плавающей запятой часто выполняются с разными размерами.
Кроме того, вычисления с плавающей запятой часто выполняются с разными размерами.
Так что же произойдет, если вы попытаетесь сохранить большее число? Допустим, вы пытались добавить единицу к 16-битной переменной, для которой уже установлено значение 65 535. Это будет «обертывание» — добавление единицы к 65 535 даст вам ноль. Добавление двух даст вам один. И так далее. То же самое и в другую сторону — вычитание единицы из нуля дает 65 535. Когда это происходит, это называется «переносом», если ожидается, или «переполнением», если нет. Это источник многих хороших плохих ошибок; большинство из них являются случаем недосмотра программиста, поскольку всякий раз, когда это происходит, срабатывает флаг «переполнения» в ЦП. Также см. Кап.
Однако на этом история не заканчивается. Все эти значения предполагают, что переменная не имеет знака, то есть она не может содержать отрицательное число. Числа со знаком по существу жертвуют одним битом, чтобы иметь возможность хранить как положительные , так и отрицательные числа. Нуль считается первым «положительным» числом, тогда как отрицательные числа начинаются с -1, что делает отрицательный предел выше (абсолютно говоря). Это эффективно уменьшает наполовину максимальное число, которое может содержать значение, для представления отрицательных чисел. Вот некоторые пересмотренные таблицы:
Нуль считается первым «положительным» числом, тогда как отрицательные числа начинаются с -1, что делает отрицательный предел выше (абсолютно говоря). Это эффективно уменьшает наполовину максимальное число, которое может содержать значение, для представления отрицательных чисел. Вот некоторые пересмотренные таблицы:
- 8 бит может содержать значение от -128 до 127.
- 12 бит может содержать значение от -2048 до 2047.
- 16 бит может содержать значение от -32 768 до 32 767.
- 32 бита может содержать значение от -2 147 483 648 до 2 147 483 647.
И так далее.
Следует отметить, что, хотя процессоры могут работать с переменными различных размеров, обычно это не обязательно; 64-битный процессор все еще может работать с 8-битными значениями. Таким образом, предел любого заданного значения может варьироваться в зависимости от фактического размера переменной, используемой для его хранения. Меньшие переменные часто используются для уменьшения памяти, необходимой для игры. Если это действительно необходимо, в большинстве систем также есть способы представления чисел гораздо больше , чем аппаратный размер слова, потенциально с миллионами цифр, но это редко требуется в видеоиграх (и также значительно медленнее).
Меньшие переменные часто используются для уменьшения памяти, необходимой для игры. Если это действительно необходимо, в большинстве систем также есть способы представления чисел гораздо больше , чем аппаратный размер слова, потенциально с миллионами цифр, но это редко требуется в видеоиграх (и также значительно медленнее).
Это объясняет сами числа. Но что заставляет их появляться в играх? Есть несколько причин, по которым эти цифры появляются:
- В качестве колпачка. Программирование для старых систем действительно действительно сложно; эти системы были относительно хороши в обработке графики, но очень плохи в вычислениях, поэтому каждый сэкономленный цикл процессора имел большое значение. примечание Atari пострадала сильнее всего: у нее не было видеопамяти , поэтому программистам приходилось создавать картинку путем своевременных манипуляций с графическими регистрами вывода, но поскольку у нее также не было линий прерывания в ЦП, это было возможно только тщательная синхронизация самой программы и вставка команд графического вывода в нужные места.
 Если вы ограничиваете значение до фактического предела вашей переменной, вы можете применить ограничение с помощью теста «выполнялось ли переполнение предыдущей инструкции», который обычно быстрее, чем тест «X больше, чем Y» (последний часто включает скрытое вычитание, даже на новых процессорах).
Если вы ограничиваете значение до фактического предела вашей переменной, вы можете применить ограничение с помощью теста «выполнялось ли переполнение предыдущей инструкции», который обычно быстрее, чем тест «X больше, чем Y» (последний часто включает скрытое вычитание, даже на новых процессорах).- Обратите внимание, что многие игры содержат ошибки из-за того, что , а не проверяет переполнение после добавления. То есть шапка есть, потому что как только шапку пересекаешь, что-то ломается или ведет себя странно.
- Чтобы использовать смены. Компьютеры могут умножать и делить на степени двойки, используя операции сдвига влево и вправо. Сдвиги намного, намного быстрее, чем умножение или деление, но работают только для степеней двойки.
- Программисты в первые дни нашли способы обойти это. Хотите умножить на 9? Сдвиньте влево три раза и добавьте исходное число. Этот прием расширен и используется некоторыми современными процессорами.

- Это может иметь неприятные последствия для современных процессоров, так как умножение занимает несколько циклов, но сдвиги могут представлять опасность для данных и вызывать остановку циклов. Будем надеяться, что процессор будет реализовывать выполнение вне очереди.
- Программисты в первые дни нашли способы обойти это. Хотите умножить на 9? Сдвиньте влево три раза и добавьте исходное число. Этот прием расширен и используется некоторыми современными процессорами.
- Ошибки. Многие вызовы функций используют -1 в качестве кода ошибки. Если это значение не проверяется, а затем сохраняется в переменной без знака, оно становится максимальным числом, которое может содержать переменная (из-за того, как работает подпись «дополнение до двух».)
- Разделить на ноль. В качестве конкретного примера вышеизложенного некоторые старые системы возвращали бы наибольшее число, которое может содержать переменная в результате деления на ноль (представьте, что это «бесконечность»). Это гораздо более желательно, чем вылет, когда на кону стоит файл сохранения игрока.
- При делении на ноль для чисел с плавающей запятой поведение определяется IEEE 754 (стандартом обработки чисел с плавающей запятой).
 Иногда это усугубляет ситуацию, если скрывает ошибку — вместо явного сбоя на этапе тестирования у вас есть потенциально поврежденный файл сохранения.
Иногда это усугубляет ситуацию, если скрывает ошибку — вместо явного сбоя на этапе тестирования у вас есть потенциально поврежденный файл сохранения.
- При делении на ноль для чисел с плавающей запятой поведение определяется IEEE 754 (стандартом обработки чисел с плавающей запятой).
- Для центровки. Для большинства целей данные в памяти должны быть выровнены по размеру. Например, однобайтовое (8-битное) значение может храниться по любому адресу, а четырехбайтное значение должно храниться на некоторых платформах по адресу, кратному четырем. Когда разработчики игр размечали память, используемую игрой, они помнили об этом требовании выравнивания. Скажем, данный блок памяти используется для хранения инвентаря игрока, и каждый элемент в инвентаре представляет собой один байт. Имеет смысл дать игроку степень двух элементов, поскольку любое значение, хранящееся после него, будет иметь то же выравнивание, что и начало блока.
- Считывание данных для чего-то, для чего они не предназначены. Очень частым источником хороших плохих ошибок в старые времена было то, что данные загружались как нечто, чем они на самом деле не были.
 Например, предположим, что в коде что-то идет не так, и игра начинает считывать данные карты, как если бы это были данные атаки. Но данные карты сильно отличаются от данных атаки. Возможно, игра использует значение FFFF (65535 в шестнадцатеричном формате) для обозначения конца карты. Это обычное значение для этой цели (на жаргоне программирования оно называется «терминальное значение»), потому что это 9-е значение.0008 последнее значение может хранить два байта, поэтому его легко запомнить. (Один FF сам по себе может использоваться, скажем, для конца комнаты или конца сценария, который выполняется на этой карте.) Однако, если код начинает считываться на карте как данные атаки, эти значения могут закончиться в любом месте. Например, если FFFF считать уроном от атаки, атака нанесет 65535 урона (конечно, возможно, с ограничением до 9999).
Например, предположим, что в коде что-то идет не так, и игра начинает считывать данные карты, как если бы это были данные атаки. Но данные карты сильно отличаются от данных атаки. Возможно, игра использует значение FFFF (65535 в шестнадцатеричном формате) для обозначения конца карты. Это обычное значение для этой цели (на жаргоне программирования оно называется «терминальное значение»), потому что это 9-е значение.0008 последнее значение может хранить два байта, поэтому его легко запомнить. (Один FF сам по себе может использоваться, скажем, для конца комнаты или конца сценария, который выполняется на этой карте.) Однако, если код начинает считываться на карте как данные атаки, эти значения могут закончиться в любом месте. Например, если FFFF считать уроном от атаки, атака нанесет 65535 урона (конечно, возможно, с ограничением до 9999). - Поскольку у программистов эти числа запечатлены в голове, для программиста с достаточно двоичным мышлением «256» (двоичный код 100000000) является скорее круглым числом, чем «300».
 Поэтому они появляются без всякой причины.
Поэтому они появляются без всякой причины.- Это часть обоснования всей концепции «магических чисел» в технике. Когда вы делаете что-то, вам все равно нужно определиться с некоторыми свойствами (например, размером доски или высотой потолка), так почему бы не использовать те, которые кто-то уже использовал раньше? А потом случается, что одинаковые размеры обеспечивают совместимость и интероперабельность, это становится самоусиливающимся соглашением, и все мы в итоге получаем 2×4s примечание Размерный пиломатериал, используемый в США и Канаде. Они названы в честь толщины профиля пиломатериала в дюймах. Следует отметить, что 2×4 на самом деле 1½×3½. Разве стандарты не забавны? Та же логика применима и к программированию. 90 или 1.
До сих пор все было о целых числах. Если вы хотите сохранить дробный компонент, у вас есть два варианта:
- Фиксированная точка. Это означает, что вы, по сути, берете свое число и ставите десятичную точку в определенном месте этого числа.
 Точка никогда не перемещается. С другой стороны, с ними очень быстро работать. Обратите внимание, что число по-прежнему двоичное, поэтому речь идет о половинах и четвертях и т. д., а не о десятых и сотых долях и т. д., которые используются в десятичных дробях.
Точка никогда не перемещается. С другой стороны, с ними очень быстро работать. Обратите внимание, что число по-прежнему двоичное, поэтому речь идет о половинах и четвертях и т. д., а не о десятых и сотых долях и т. д., которые используются в десятичных дробях. - С плавающей запятой. Это работает как научная нотация; один бит используется для хранения знака, некоторое количество битов (называемых мантиссом) используется для хранения числа справа от десятичной точки, а оставшиеся биты (называемые показателем степени), как и ожидалось, используются для хранения степени 2 умножить на. (Мы используем 2 вместо 10, потому что, опять же, компьютеры работают в двоичном формате.) Следует отметить, что это сильное упрощение — если у вас есть десять минут, чтобы убить и как Super Mario 64 , спидраннер pannenkoek2012 здесь подробнее.
Конечно, также возможно просто хранить рациональное число в виде дроби, сохраняя два целых числа, что позволяет избежать различных арифметических ошибок, встречающихся в числах с фиксированной и плавающей запятой, но такое представление редко используется за пределами строгого математического программирования, так как оно не только менее эффективно использует память (эквивалентные дроби могут иметь разные числители и знаменатели), но и медленнее вычисляет сложение, поскольку знаменатели должны быть одинаковыми.
 Математические ошибки, присущие числам с фиксированной и плавающей запятой, являются причиной многих спорадических ошибок в современных играх, поскольку они вызывают необработанные пограничные случаи в физических симуляциях.
Математические ошибки, присущие числам с фиксированной и плавающей запятой, являются причиной многих спорадических ошибок в современных играх, поскольку они вызывают необработанные пограничные случаи в физических симуляциях.Таблица отрицательных степеней двойки
Вот таблица первых 64 отрицательных степеней двойки (от 2 -1 до 2 -64 ), показанная в десятичных дробях:
173988342285156259 n 2 нет -1 0,5 -2 0,25 -3 0,125 -4 0,0625 -5 0,03125 -6 0,015625 -7 0,0078125 -8 0,003 -9 0,001953125 -10 0,0009765625 -11 0,00048828125 -12 0,000244140625 -13 0,0001220703125 -14 0,00006103515625 -15 0,000030517578125 -16 0,00001525878 -17 0,00000762939453125 -18 0,000003814697265625 -19 0,000001 86328125 -20 0,00000095367431640625 -21 0,000000476837158203125 -22 0,0000002384185791015625 -23 0,00000011920928955078125 -24 0,0000000596046447753 -25 0,0000000298023223876953125 -26 0,000000014119384765625 -27 0,000000007450580596923828125 -28 0,0000000037252 4619140625 -29 0,00000000186264514923095703125 -30 0,000000000931322574615478515625 -31 0,0000000004656612873077392578125 -32 0,000000000232830643653869628 -33 0,000000000116415321826934814453125 -34 0,0000000000582076609134674072265625 -35 0,00000000002910383045673370361328125 -36 0,000000000014551915228366851806640625 -37 0,000000000007275957614183425 03125 -38 0,00000000000363797880709171295166015625 -39 0,000000000001818989403545856475830078125 -40 0,000000000000 -41 0.  00000000000045474735088646411895751953125
00000000000045474735088646411895751953125-42 0.000000000000227373675443232059478759765625 -43 0.0000000000001136868377216160297393798828125 -44 0,00000000000005684341886080801486968994140625 -45 0,000000000000028421709430404007434844970703125 -46 0.0000000000000142108547152020037174224853515625 -47 0,00000000000000710542735760100185871124267578125 -48 0.0000000000000035527136788005009293556213378 -49 0.0000000000000017763568394002504646778106689453125 -50 0,0000000000000000888178419700125232338 447265625-51 0,000000000000000444089209850062616169452667236328125 -52 0.0000000000000002220446049250313080847263336181640625 -53 0,00000000000000011102230246251565404236316680 3125-54 0,000000000000000055511151231257827021181583404541015625 -55 0,0000000000000000277555756156289135105 7022705078125 -56 0.  000000000000000013877787807814456755295395851135253
000000000000000013877787807814456755295395851135253-57 0.000000000000000006938893 -58 0.0000000000000000034694469519536141888238489627838134765625 -59 0.000000000000000001734723475976807094411924481391 -60 0,0000000000000000000867361737988403547205962240695953369140625 -61 0.0000000000000000004336808689942017736029811203479766845703125 -62 0,0000000000000000002168404344971008868014 -63 0,000000000000000000108420217248550443400745280086994171142578125 -64 0.00000000000000000005421010862427522170037264004349708557128 (ознакомьтесь с разделом «Образцы последних цифр положительных степеней числа пять», чтобы узнать о закономерностях последних цифр).



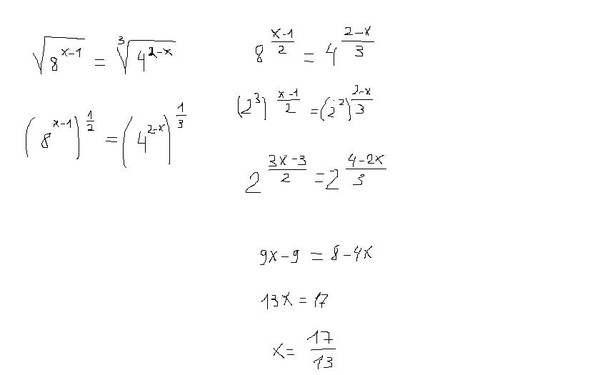
 Некоторые игры для NES, такие как Final Fantasy и Rygar , использовали хаки для получения таких больших значений.
Некоторые игры для NES, такие как Final Fantasy и Rygar , использовали хаки для получения таких больших значений. примечание Около 18,4 квинтиллиона Nintendo 64, GameCube, примечание Хотя с некоторыми 32-разрядными компонентами Sony PlayStation 2 и современные настольные ПК являются 64-разрядными, 64-разрядные операционные системы стали довольно распространенным явлением в 2010 г. (по крайней мере, , на новых компьютерах).
примечание Около 18,4 квинтиллиона Nintendo 64, GameCube, примечание Хотя с некоторыми 32-разрядными компонентами Sony PlayStation 2 и современные настольные ПК являются 64-разрядными, 64-разрядные операционные системы стали довольно распространенным явлением в 2010 г. (по крайней мере, , на новых компьютерах).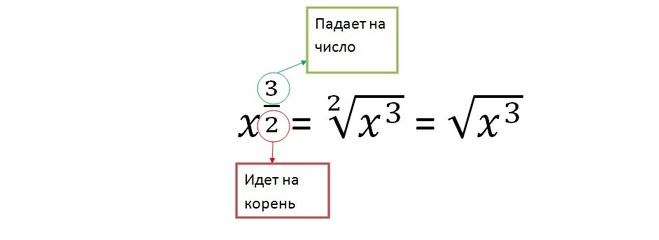 Если вы ограничиваете значение до фактического предела вашей переменной, вы можете применить ограничение с помощью теста «выполнялось ли переполнение предыдущей инструкции», который обычно быстрее, чем тест «X больше, чем Y» (последний часто включает скрытое вычитание, даже на новых процессорах).
Если вы ограничиваете значение до фактического предела вашей переменной, вы можете применить ограничение с помощью теста «выполнялось ли переполнение предыдущей инструкции», который обычно быстрее, чем тест «X больше, чем Y» (последний часто включает скрытое вычитание, даже на новых процессорах).
 Иногда это усугубляет ситуацию, если скрывает ошибку — вместо явного сбоя на этапе тестирования у вас есть потенциально поврежденный файл сохранения.
Иногда это усугубляет ситуацию, если скрывает ошибку — вместо явного сбоя на этапе тестирования у вас есть потенциально поврежденный файл сохранения. Например, предположим, что в коде что-то идет не так, и игра начинает считывать данные карты, как если бы это были данные атаки. Но данные карты сильно отличаются от данных атаки. Возможно, игра использует значение FFFF (65535 в шестнадцатеричном формате) для обозначения конца карты. Это обычное значение для этой цели (на жаргоне программирования оно называется «терминальное значение»), потому что это 9-е значение.0008 последнее значение может хранить два байта, поэтому его легко запомнить. (Один FF сам по себе может использоваться, скажем, для конца комнаты или конца сценария, который выполняется на этой карте.) Однако, если код начинает считываться на карте как данные атаки, эти значения могут закончиться в любом месте. Например, если FFFF считать уроном от атаки, атака нанесет 65535 урона (конечно, возможно, с ограничением до 9999).
Например, предположим, что в коде что-то идет не так, и игра начинает считывать данные карты, как если бы это были данные атаки. Но данные карты сильно отличаются от данных атаки. Возможно, игра использует значение FFFF (65535 в шестнадцатеричном формате) для обозначения конца карты. Это обычное значение для этой цели (на жаргоне программирования оно называется «терминальное значение»), потому что это 9-е значение.0008 последнее значение может хранить два байта, поэтому его легко запомнить. (Один FF сам по себе может использоваться, скажем, для конца комнаты или конца сценария, который выполняется на этой карте.) Однако, если код начинает считываться на карте как данные атаки, эти значения могут закончиться в любом месте. Например, если FFFF считать уроном от атаки, атака нанесет 65535 урона (конечно, возможно, с ограничением до 9999).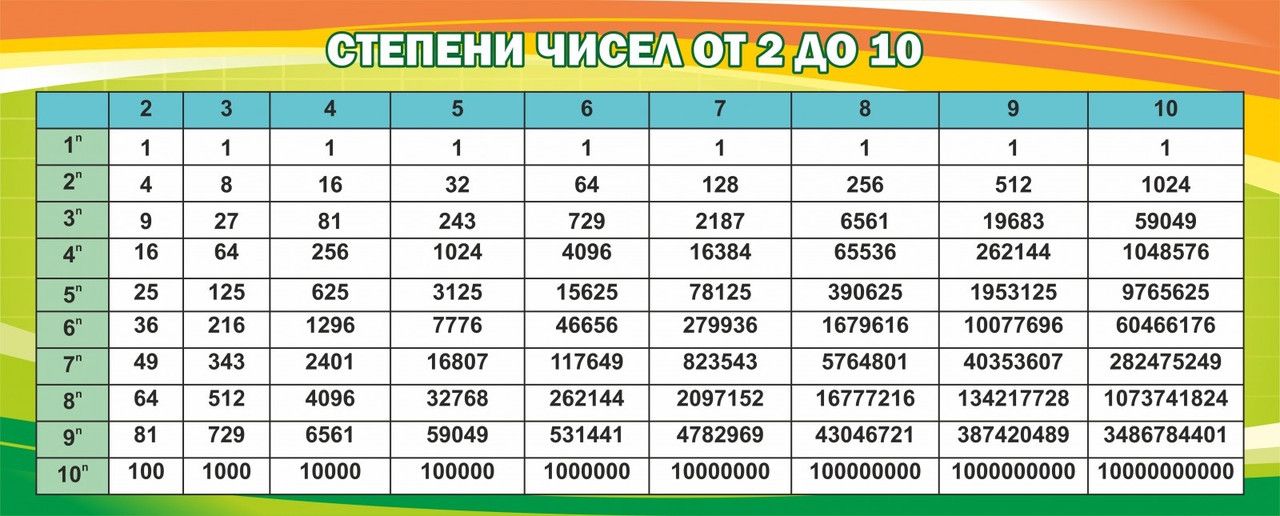 Поэтому они появляются без всякой причины.
Поэтому они появляются без всякой причины. Точка никогда не перемещается. С другой стороны, с ними очень быстро работать. Обратите внимание, что число по-прежнему двоичное, поэтому речь идет о половинах и четвертях и т. д., а не о десятых и сотых долях и т. д., которые используются в десятичных дробях.
Точка никогда не перемещается. С другой стороны, с ними очень быстро работать. Обратите внимание, что число по-прежнему двоичное, поэтому речь идет о половинах и четвертях и т. д., а не о десятых и сотых долях и т. д., которые используются в десятичных дробях. Математические ошибки, присущие числам с фиксированной и плавающей запятой, являются причиной многих спорадических ошибок в современных играх, поскольку они вызывают необработанные пограничные случаи в физических симуляциях.
Математические ошибки, присущие числам с фиксированной и плавающей запятой, являются причиной многих спорадических ошибок в современных играх, поскольку они вызывают необработанные пограничные случаи в физических симуляциях. 00000000000045474735088646411895751953125
00000000000045474735088646411895751953125 000000000000000013877787807814456755295395851135253
000000000000000013877787807814456755295395851135253