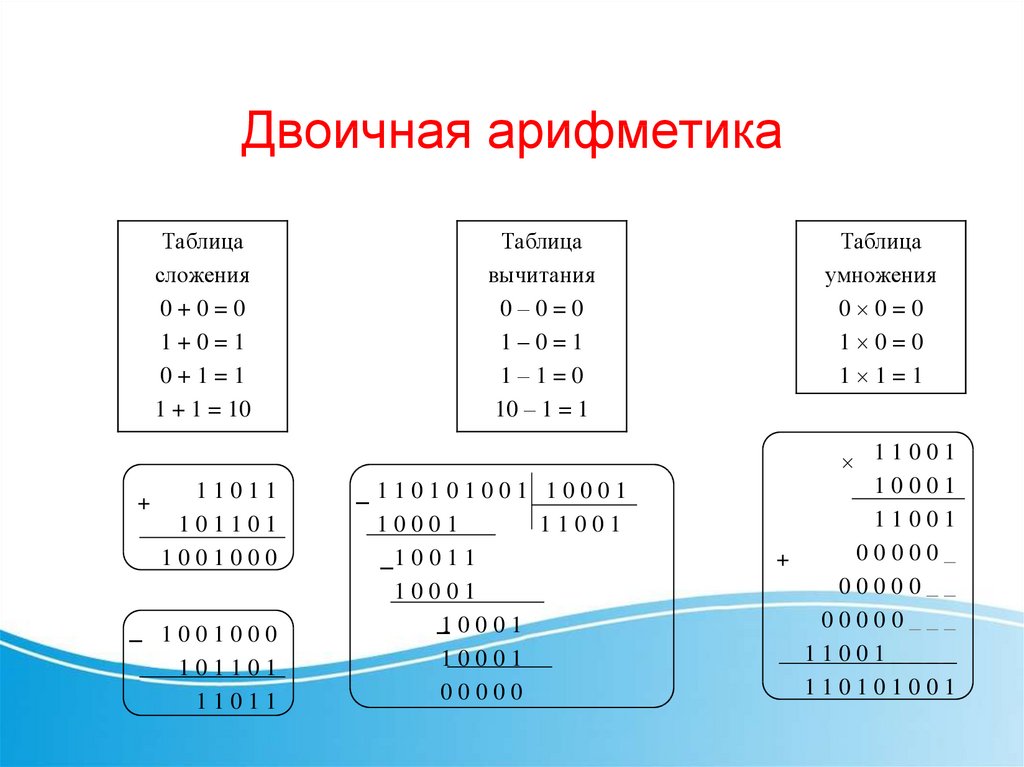
Как разделить двоичные числа
Мы уже рассмотрели три действия и думаю уже понятно, что в общем-то действия над двоичными числами мало отличаются от действий над десятичными числами. Разница появляется только в том, что цифр две а не десять, но это только упрощает арифметические операции. Так же обстоит дело и с делением, но для лучшего понимания алгоритм деления разберём более подробно. Пусть нам необходимо разделить два десятичных числа, например разделить на 7.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Системы счисления.
Арифметические действия в двоичной системе счисления
Деление в двоичной системе счисления - Системы счисления. Арифметические действия в двоичной системе счисления
- Арифметические операции в двоичной системе
- Пример деления двоичных чисел методом без восстановления остатка
- Двоичный калькулятор онлайн
- Двоичная целочисленная арифметика
- 1.15 Деление двоичных чисел
- Деление на два
- Двоичная система счисления. Бит и байт. Сегментация памяти.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Сложение,вычитание, умножение и деление в двоичной системе счисления
youtube.com/embed/_64mBE0JBG4″ frameborder=»0″ allowfullscreen=»»/>Системы счисления. Арифметические действия в двоичной системе счисления
В этой статье: Деление в столбик Дополнения 10 Источники. Двоичные числа можно делить в столбик, чтобы лучше понять сам процесс или написать простую компьютерную программу. Также можно применить метод дополнений, который довольно редко используется в программировании. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек а. Категории: Математика.
Как делить двоичные числа Информация об авторе 10 Источники. Количество источников, использованных в этой статье: Вы найдете их список внизу страницы. Метод 1. Разделите в столбик два десятичных числа. Если вы прекрасно делите в столбик, перейдите к следующему шагу, чтобы узнать, как делить двоичные числа.
Делимое делится на делитель и получается частное.
Сравните делитель с первой цифрой делимого. Если делитель больше этой цифры, сравните делитель с двумя цифрами делимого и так далее, пока делитель не станет меньше рассматриваемого числа. Напишите первую цифру частного под делителем. Умножьте и вычтите, чтобы найти остаток. Запишите 16 под 17, а затем вычтите 17 — 16, чтобы найти остаток 1.
Повторите сравнение. Окончательный ответ: Разделите в столбик два двоичных числа. Здесь — делимое, а 11 — делитель. Оставьте достаточно места для вычислений. В случае с двоичными числами сделать это проще, чем с десятичными: либо число не делится на делитель и записываем 0, либо делится и записываем 1.
Напишите 0 как первую цифру частного под делителем. Продолжайте сравнивать числа с делителем, пока не получите 1. В нашем примере: Сравните делитель с двумя цифрами делимого. Напишите 0 как вторую цифру частного. Сравните делитель с тремя цифрами делимого. Напишите 1 как третью цифру частного. Вычислите остаток. Умножьте найденную цифру 1 на делитель 11 и запишите полученный результат под делимым а именно под соответствующими разрядами.
Обратите внимание, что при умножении 1 на делитель всегда получается делитель. Запишите делитель под делимым. В нашем примере запишите 11 под первыми тремя цифрами делимого. Вычтите — 11, чтобы получить остаток Если вы не помните, как вычитать двоичные числа, прочитайте эту статью.
Повторите описанные действия, пока не решите задачу. Добавьте следующую цифру делимого к остатку, чтобы получить Остатка нет, поэтому задача решена. Ответ: или просто Добавьте десятичную запятую если нужно. Иногда результат не является целым числом. Повторите этот процесс до тех пор, пока не получите результат нужной точности, а затем округлите ответ.
Чтобы округлить полученный результат, избавьтесь от последнего 0, или, если последняя цифра 1, отбросьте ее и добавьте 1 к новой последней цифре. В программировании следуйте одному из стандартных алгоритмов округления, чтобы избежать ошибок при преобразовании между двоичными и десятичными числами. Метод 2.
Уясните основные принципы. Чтобы разделить два числа как десятичные, так и двоичные , можно вычесть делитель из делимого, а затем последовательно вычитать делитель из остатков, пока не получится отрицательное число; при этом нужно считать, сколько вычитаний было выполнено.
Отрицательное число, поэтому дальше вычитать не нужно.
Ответ: 3 с остатком 5. Обратите внимание, что этот метод не вычисляет дробную часть ответа. Уясните основы метода дополнений. Изложенный выше метод можно применить к двоичным числам, а можно использовать более эффективный способ, который позволит сэкономить время при программировании деления двоичных чисел.
Такой способ называется методом дополнений. Например, вычтите — оба числа должны иметь одинаковое количество цифр : Найдите дополнение ко второму числу. Для этого вычтите каждую цифру этого числа из 1. В двоичной системе просто замените 1 на 0, а 0 на 1. Этот процесс называется дополнением до двух и позволяет заменить вычитание операцией сложения. Полученный результат прибавьте к первому числу. Объедините два метода, которые описаны выше. Первый метод — это метод последовательного вычитания, а второй — метод дополнения до двух.
Эти методы можно объединить в один, чтобы с его помощью делить числа процесс объединения методов описывается далее.
Вычтите делитель из делимого, заменив вычитание сложением с помощью дополнения до двух. Прибавьте 1 к частному. В компьютерной программе это строка, где частное увеличивается на единицу. На бумаге сделайте заметку, чтобы не запутаться.
Вы успешно вычли один раз, поэтому на данный момент частное равно 1. Повторите описанный процесс. Для этого вычтите делитель из остатка. Остаток — это результат последнего вычисления. Операцию вычитания замените сложением: к остатку прибавляйте дополненный до двух делитель, а затем избавляйтесь от первый цифры результата. После каждого вычитания к частному прибавляйте 1.
Частное является окончательным результатом операции деления. Остаток является конечным результатом операции вычитания; в нашем примере это 0 остатка нет. Советы Игнорируйте знаковый разряд в двоичных числах со знаком, за исключением случаев, когда нужно понять, получен положительный или отрицательный результат.
Метод дополнения до двух не применяется, если числа состоят из разного количества цифр.
Дополнительные статьи. Информация о статье wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. Была ли эта статья полезной? Да Нет. Can you please put wikiHow on the whitelist for your ad blocker? Learn how. Куки помогают сделать WikiHow лучше.
Продолжая использовать наш сайт, вы соглашаетесь с нашими куки правилами. Наугад Написать статью.
Деление в двоичной системе счисления
Click here to read about Mrs. Двоичная система счисления является основной системой представления информации в памяти компьютера. Таблица сложения. Таблица вычитания.
Двоичная система счисления — это позиционная система счисления с Пример: Для перевода десятичного числа в двоичное надо разделить его на 2.
Системы счисления.
Арифметические действия в двоичной системе счисленияДвоичная система счисления проще десятичной. Однако двоичное изображение числа требует большего для многоразрядного числа примерно в 3,3 раза числа разрядов, чем его десятичное представление. Тем не менее применение двоичной системы создает большие удобства для проектирования ЭВМ, так как для представления в машине разряда двоичного числа может быть использован любой простой элемент, имеющий всего два устойчивых состояния. Также достоинством двоичной системы счисления является простота двоичной арифметики. Как и в десятичной, в двоичной системе счисления для отделения целой части от дробной используется точка. Значение веса разрядов справа от точки равно основанию двоичной системы 2 , возведенному в отрицательную степень. Каждая позиция, занятая двоичной цифрой, называется битом. Бит является наименьшей единицей информации в ЭВМ. Наименьшим значащим битом МЗР называют самый младший двоичный разряд, а самым старшим двоичным разрядом — наибольший значащий бит СЗР.
Арифметические операции в двоичной системе
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера. Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.
Компьютерные сети Системное программное обеспечение Информационные технологии Программирование. Все о программировании Обучение Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации Главная Тексты статей Добавить статьи Контакты Арифметические операции в двоичной системе.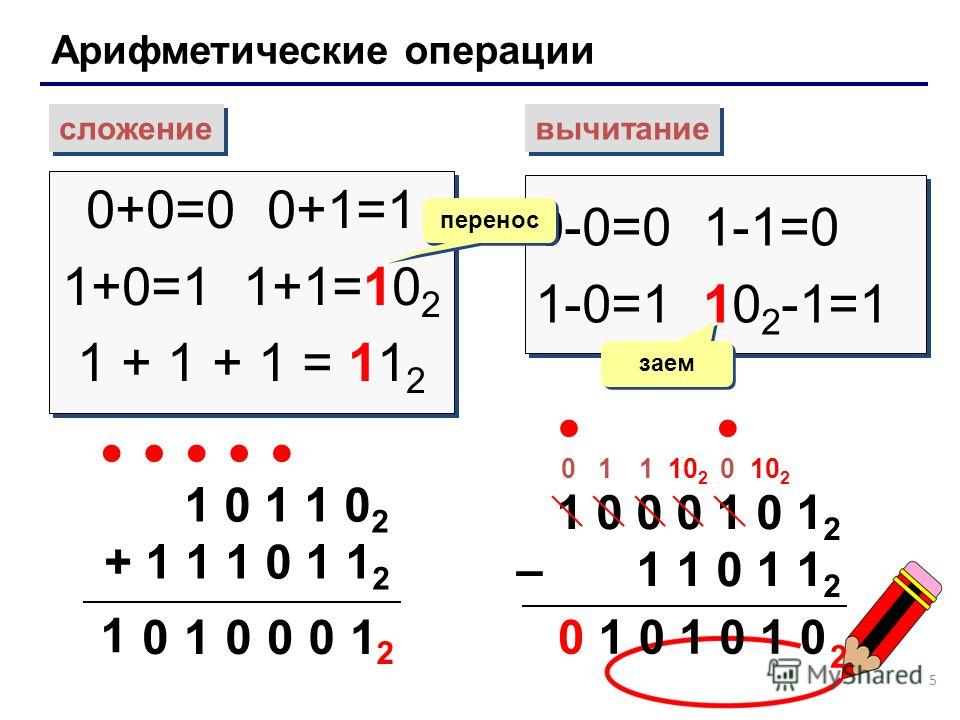
Пример деления двоичных чисел методом без восстановления остатка
В той системе счета, которой мы пользуемся каждый день, десять цифр — от нуля до девяти. Поэтому она называется десятичной. Однако в технических расчетах, особенно тех, которые имеют отношение к компьютерам, используются и другие системы , в частности, двоичная и шестнадцатеричная. Поэтому нужно уметь переводить числа из одной системы счисления в другую. Двоичная система — самая простая.
Двоичный калькулятор онлайн
Устройство управления руководит прохождением и обработкой информации в системе, память хранит эту информацию для дальнейшего использования, арифметическое устройство выполняет арифметические и логические операции над ней, периферийные устройства преобразуют ее из внешней формы представления во внутреннюю и наоборот. В этом разделе мы рассмотрим двоичную и шестнадцатеричную системы счисления, которые лежат в основе внутреннего представления информации, а затем перейдем к обсуждению двоичной целочисленной арифметики, одной из арифметик, применяющихся в современных ЭВМ.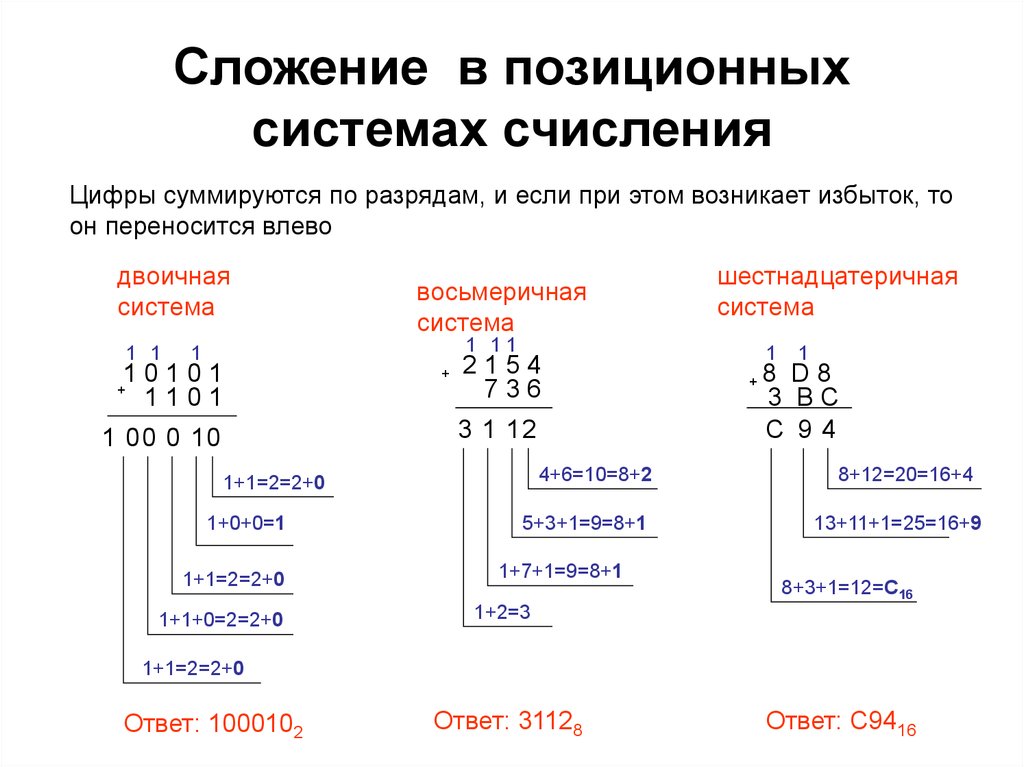
Двоичная система счисления. Наша десятичная система счисления является позиционной в том смысле, что величина числа зависит от порядка цифр в нем. Например, число На самом деле, когда мы пишем Положение цифры относительно десятичной точки определяет степень числа 10, на которую эта цифра будет умножена при вычислении суммы.
Арифметические действия в двоичной системе счисления . В частном смело пишем первую 1, т.к. число в двоичной системе не может начинаться с 0.
Двоичная целочисленная арифметика
Войдите , пожалуйста. Хабр Geektimes Тостер Мой круг Фрилансим. Мегапосты: Криминальный квест HR-истории Путешествия гика. Войти Регистрация.
1.15 Деление двоичных чисел
ВИДЕО ПО ТЕМЕ: Просто о двоичной системе счисления и двоичном коде. #1
Сдвинем делитель B влево так, чтобы позиция старшей значащей единицы, в нем, совпала с позицией старшей значащей единицы в делимом A.
Количество необходимых для этого сдвигов запомним в числе k В нашем случае старшая значащая единица в делимом A расположена в 7-м разряде, a в делителе B — в 4-м разряде. Сдвинутый делитель выглядит следующим образом :. В регистр результата записываем «0» если остаток отрицательный и единицу в противном случае. Помним, что отрицательному числу соответствует наличие единицы в м разряде и наоборот. При этом крайний правый младший разряд заполняется нулем, а знаковый разряд й в процессе сдвига не участвует.
Разделы: Информатика.
Деление на два
В этой статье: Деление в столбик Дополнения 10 Источники. Двоичные числа можно делить в столбик, чтобы лучше понять сам процесс или написать простую компьютерную программу. Также можно применить метод дополнений, который довольно редко используется в программировании. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 25 человек а. Категории: Математика. Как делить двоичные числа Информация об авторе 10 Источники.
Двоичная система счисления. Бит и байт. Сегментация памяти.
Деление в двоичной системе Помогите пожалуйста поделить на , желательно с алгоритмом Помогите решить. Просьба расписать по действиям.
Перевод из одной системы счисления в другую
- Системы счисления: основные сведения
- Двоичная система счисления
- Восьмеричная и шестнадцатеричная системы счисления
- Двоично-десятичная система счисления
- Перевод чисел из одной системы счисления в другую
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число X в позиционной системе с основанием s может быть представлено в виде полинома:
где s — база системы счисления, — цифры,
допустимые в данной системе счисления .
Последовательность
образует целую часть X, а последовательность
— дробную часть X.
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только
две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент
с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.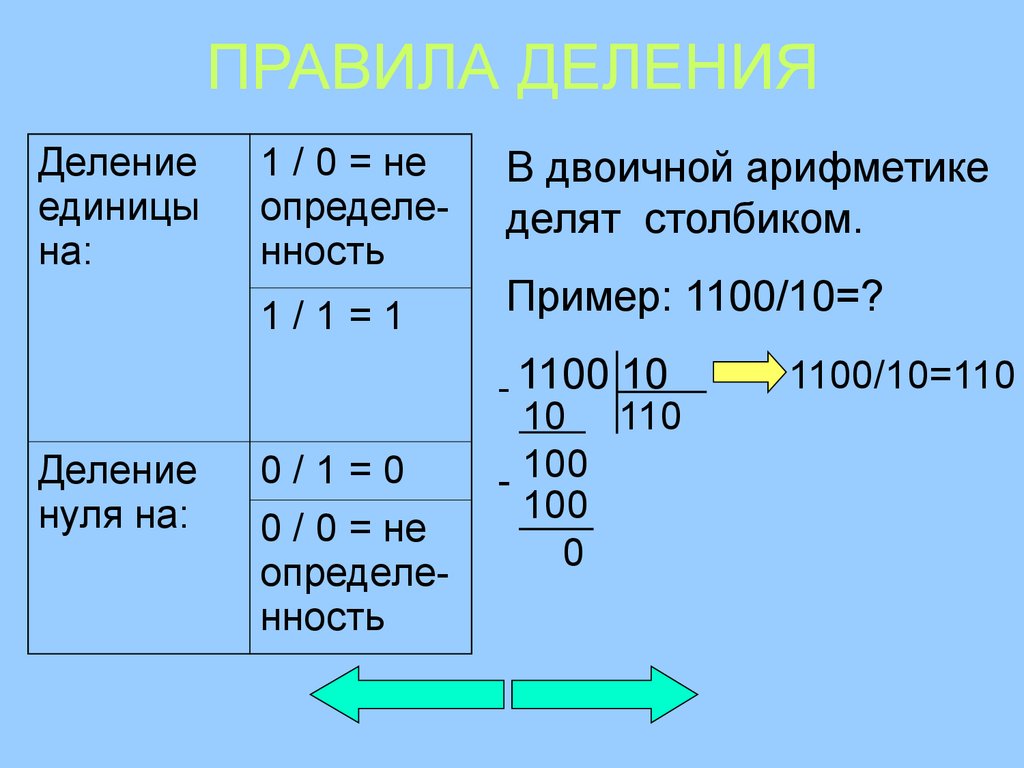
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления представляет собой целую степень двойки: — для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см.
таблицу).
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h. Удобно различать два случая.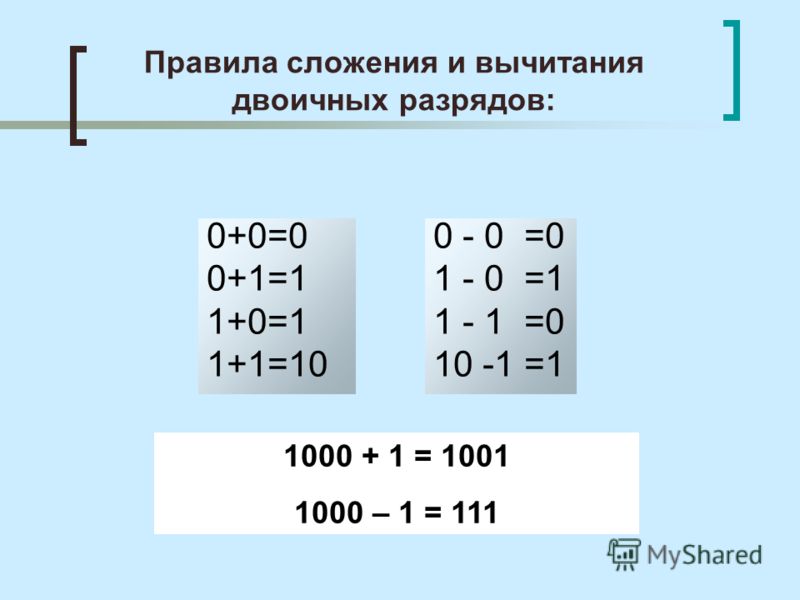
В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае () удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе.
Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:
.
Для нахождения значений разделим этот многочлен на h:
.
Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:
.
Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.
Пример 1.
Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.
Решение:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Перевод правильных дробей
Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра может быть найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения. Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т.
к. не всегда можно представить дробь
по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется .
Пример 2.
Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
Ответ:
** В восьмеричную систему:
Ответ:
*** В шестнадцатеричную систему:
Ответ: так как , то
Поделиться с друзьями
ДВОИЧНЫЙ КАЛЬКУЛЯТОР ВЫЧИТАНИЯ С ШАГАМИ
Ввод положительных двоичных чисел.
1001101111001
ШАГИ РЕШЕНИЯ
⟲ Повтор
1001101111001220124s Place101
Последний шаг:
2 4 разряд s:
Вычтите числа в разряде 2 4 s.
1 – 0 = 1
Запишите 1 на место 2 4 s.
Все шаги:
2 0 разряд:
Вычтите числа в разряде 2 0 .
1 – 0 = 1
Запишите 1 на место 2 0 s.
2 1 s место:
0 < 1
Занять 1 из 2 2 место.
2 2 s место:
Мы не можем перегруппироваться с 0 .
2 3 s place:
Borrow 1 from 1
1 – 1 = 0
2 2 s place:
Add 2 на место 2 2 с.
0 + 2 = 2
2 2 s place:
Borrow 1 from 2
2 – 1 = 1
2 1 s place:
Add 2 to the 2 1 место.
0 + 2 = 2
2 1 разряд:
Вычесть числа в разряде 2 2 .
2 – 1 = 1
Запишите 1 на место 2 1 s.
2 2 разряд s:
Вычтите числа в разряде 2 2 s.
1 – 1 = 0
Запишите 0 на место 2 2 s.
2 3 разряд s:
Вычтите числа в разряде 2 3 s.
0 – 0 = 0
Запишите 0 на место 2 3 с.
2 4 разряд s:
Вычтите числа в разряде 2 4 s.
1 – 0 = 1
Запишите 1 на место 2 4 s.
Скачать решение
Скопировано в буфер обмена
Скопировать текст
© MadforMath
Посмотреть решение
ДВОИЧНОЕ ВЫЧИТАНИЕ Выполните следующие действия при двоичном вычитании.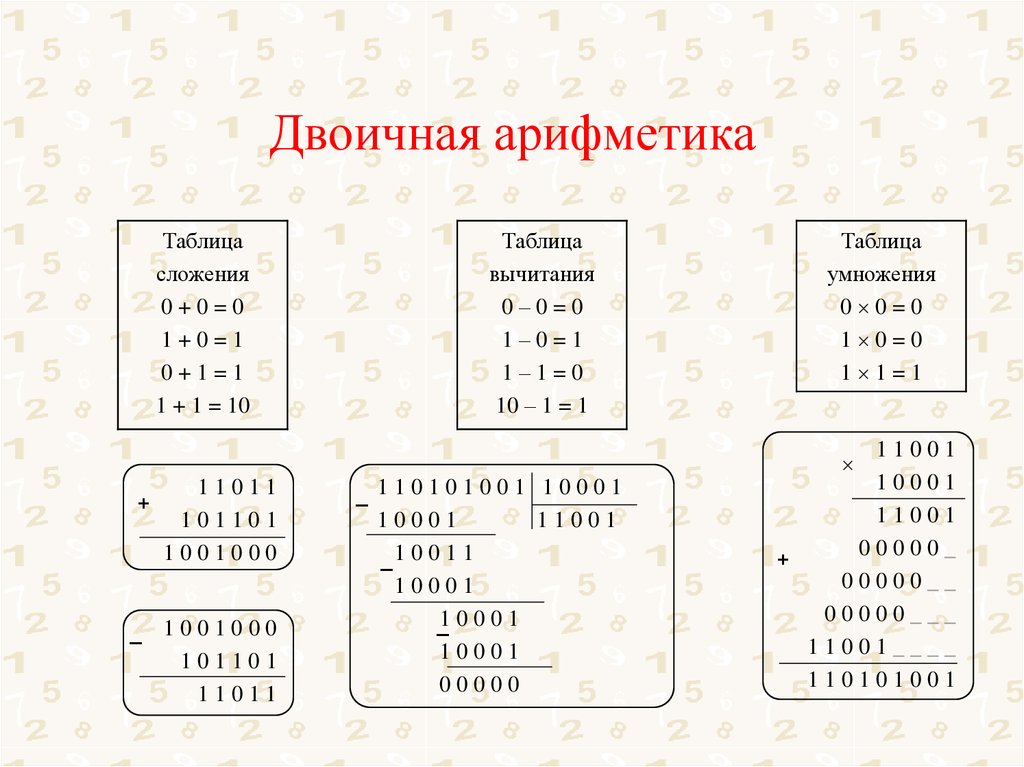
Напишите числа так, чтобы одинаковые места совпадали в одном столбце.
Начинайте вычитать числа с самой правой цифры и каждый раз сдвигайте на одну цифру влево.
В любой цифре, если число сверху больше или равно числу снизу, выполните вычитание и запишите результат на то же место.
Если число сверху меньше, чем число снизу, двигайтесь влево, пока сверху не будет достигнуто ненулевое число.
Занять 1 из первого ненулевого числа и уменьшить его на 1.
Добавьте 2 к одной цифре справа и перейдите к этой цифре.
Продолжайте перегруппировывать и прибавлять 2 к младшей цифре, пока не будет достигнута цифра, которую нужно вычесть.
Выполните вычитание и переместитесь на одну цифру влево.
Калькулятор двоичного вычитания,
- Вычисляет вычитание введенных чисел (целых или десятичных) и
- Иллюстрирует этапы решения с помощью анимации.
Калькулятор двоичного вычитания можно использовать двумя способами.
- ПОЛЬЗОВАТЕЛЬСКИЕ ВВОДЫ
Вы можете ввести два положительных двоичных числа в поля ввода и нажать кнопку « ВЫЧИСЛИТЬ ». Результат и пояснения появляются под калькулятором
- СЛУЧАЙНЫЕ ВВОДЫ
Вы можете нажать на ЗНАЧОК УМЕР рядом с полями ввода. Если вы используете это свойство, два случайных числа генерируются и автоматически вводятся в калькулятор. Вы можете увидеть результат и пояснения под калькулятором. Вы можете создавать свои собственные примеры и практиковаться в использовании этого свойства.
- ОЧИСТКА ПОЛЯ ВВОДА
Чтобы найти разницу некоторых других чисел, вы можете очистить поле ввода, нажав кнопку ОЧИСТИТЬ под полем ввода.
- КОПИРОВАНИЕ И ЗАГРУЗКА РЕШЕНИЯ
Сгенерированное решение можно скопировать, щелкнув ссылку «Копировать текст», которая находится под панелью решения.
Решение можно загрузить даже в виде файла изображения с расширением .jpg, если щелкнуть ссылку «Загрузить решение» в нижней части панели решений. Вы можете поделиться загруженный файл изображения.
КАЛЬКУЛЯТОР НЕСКОЛЬКИХ ДВОИЧНЫХ СЛОЖЕНИЙ С ШАГАМИ
Ввод положительных двоичных чисел.
0111011111101000111221
ШАГИ РЕШЕНИЯ
⟲ Повтор
0111011111125s Место:110=11201110202011
Последний шаг:
2 5 Место:
1 = 1 10
Преобразовать 1 10 в двоичный код.
1 10 = 1 2
Запишите 1 на место 2 5 с.
Все шаги:
2 0 S Плейс:
0 + 1 + 1 = 2 10
1 = 2 10 CONTER 2 = 2 10 .2 10 = 10 2
Запишите 0 на место 2 0 с. Перенесите 1 на место 2 1 с.
2 1 S Place:
1 + 1 + 0 + 1 = 3 10
Конвертируйте 3 10 в Binal.
3 10 = 11 2
Запишите 1 в разряд 2 1 . Перенесите 1 на место 2 2 с.
2 2 s место:
1 + 1 + 1 + 1 = 4 10 32 Преобразовать 4 10 в двоичный формат. 4 10 = 100 2 Запишите 0 в разряд 2 2 . Перенесите 10 2 = 2 10 на место 2 3 . 2 3 s разряд: 2 + 1 + 1 = 4 10 3 1 в двоичном виде 4 10 = 100 2 Запишите 0 в разряд 2 3 . Нести 10 2 = 2 10 на место 2 4 . 2 4 s разряд: 2 = 2 10 Преобразовать 2 10 в двоичное число. 2 10 = 10 2 Запишите 0 в разряд 2 4 . Перенесите 1 на место 2 5 s. 2 5 S-место: 1 = 1 10 Преобразовать 1 10 в двоичное число. 1 10 = 1 2 Запишите 1 в разряд 2 5 с. Скачать решение Скопировано в буфер обмена Копировать текст © Madformath См. Решение
Добавляйте числа справа налево, цифра за цифрой.
Для каждой цифры проверить, больше ли результат 1 или нет. В любом случае, записывайте единицы результата под числами в тот же столбец.
Если результат больше 1, удалить цифру единиц и перенести остальные на следующую цифру.
ЧТО ТАКОЕ МНОЖЕСТВЕННЫЙ ДВОИЧНЫЙ (ОСНОВА 2) КАЛЬКУЛЯТОР СЛОЖЕНИЯ?Калькулятор множественного двоичного сложения,
- Вычисляет сложение не более 10 двоичных чисел, разделенных запятыми, пробелами или символами новой строки,
- Иллюстрирует этапы решения анимацией.
Калькулятор множественного двоичного сложения можно использовать двумя способами.
- ПОЛЬЗОВАТЕЛЬСКИЕ ВВОДЫ
Вы можете ввести от 2 до 10 положительных двоичных чисел (целых или дробных), разделенных запятыми, пробелами или символами новой строки, в поле ввода и нажать кнопку « ВЫЧИСЛИТЬ ».
Результат и
пояснения появляются под калькулятором - СЛУЧАЙНЫЕ ВВОДЫ
Вы можете нажать на УМРИ ЗНАЧОК рядом с полем ввода. Если вы используете это свойство, несколько случайных чисел генерируются и автоматически вводятся в калькулятор. Вы можете увидеть результат и пояснения под калькулятором. Вы можете создавать свои собственные примеры и практиковаться в использовании этого свойства.
- ОЧИСТКА ПОЛЯ ВВОДА
Чтобы найти сумму некоторых других чисел, вы можете очистить поле ввода, нажав кнопку ОЧИСТИТЬ под полем ввода.
- КОПИРОВАНИЕ И ЗАГРУЗКА РЕШЕНИЯ
Сгенерированное решение можно скопировать, щелкнув ссылку «Копировать текст», которая находится под панелью решения.
Решение можно загрузить даже в виде файла изображения с расширением .jpg, если щелкнуть ссылку «Загрузить решение» в нижней части панели решений.
