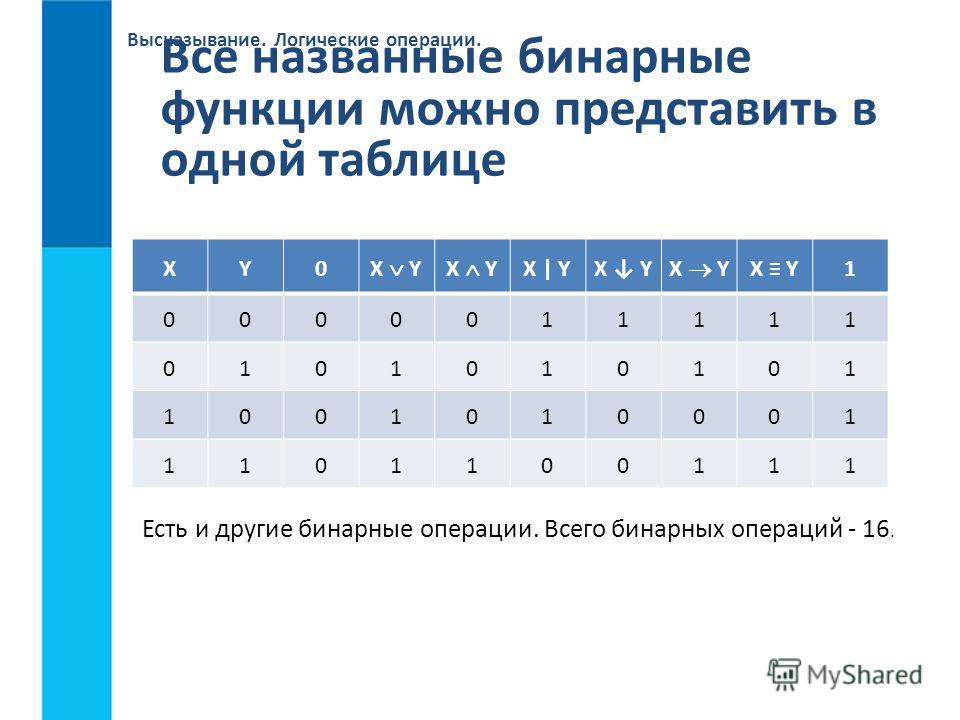
3. Основы математической логики
n-мерный булевый куб
Множество всех двоичных слов (обозначаемое как ), содержитэлементов-слов, т.е..
Алгебра Жегалкина
Алгебра , образованная множествомвместе с операциями конъюнкции (), суммы по модулю 2 () и константами 0 и 1.
Алгебра логики
Двухэлементная булева алгебра , где носитель алгебры, и в которой множество операций дополнено двумя бинарными операциями: импликациейи эквивалентностью.
Булева алгебра (двухэлементная)
Алгебраическая структура , гдеи операцияесть конъюнкция,есть дизъюнкция, «» есть отрицание.
Булева функция
Функция вида , аргументыи значениякоторой принадлежат множеству.
Булевы константы
Значения
0 и 1 из множества .
Булевы переменные
Переменные, которые могут принимать значения только из множества .
Булевый базис
Базис, состоящий из отрицания, дизъюнкции и конъюнкции.
Булевый набор
Совокупность конкретных значений аргументов булевой функции.
Двоичное слово (-слово)
Совокупность конкретных значений аргументов булевой функции.
Двойственная функция
Функция называетсядвойственной к функции , если.
Дизъюнктивная нормальная форма (ДНФ)
Формула, представленная в виде дизъюнкции элементарных конъюнкций.
Дизъюнктивное поглощение
, где некоторая элементарная конъюнкция переменных; булева переменная.
Дизъюнктивное ядро булевой функции
Такое
множество её простых импликант, которое
образует покрытие
,
но после удаления импликанты теряет
это свойство, то есть перестает быть
полной системой импликант.
Длина полинома Жегалкина
Количество попарно различных элементарных конъюнкций в полиноме Жегалкина.
Единичный элемент (единица)
Элемент 1 из множества .
Закон ассоциативности (сочетательный закон)
; .
Законы де Моргана
; .
Закон дистрибутивности (распределительный закон)
; .
Закон идемпотентности
Закон инволюции (двойного отрицания)
.
Закон исключенного третьего
.
Закон коммутативности (переместительный закон)
; .
Закон поглощения (элиминации)
; .
Закон противоречия
.
Закон тождества (свойство констант)
; ;;.
Замкнутый класс булевых функций
Класс (множество) называется замкнутым классом, если (где некоторое подмножество функций из ).
Замыкание множества булевых функций
Множество , состоящее из функций, представимых в виде формул через функции множества(где некоторое подмножество функций из ).
Импликанта
Импликантой некоторой функции называется функция, такая, что на всех интерпретациях, на которыхравна единице,тоже равна единице.
Имплицента
Импликантой некоторой функции называется функция, такая, что на всех интерпретациях, на которыхравна нулю,тоже равна нулю.
Инверсия
Функция
,
равная 1, когда аргумент принимает
значение 0, и равная 0 при аргументе 1.
Индекс (коэффициент) простоты
Коэффициент, характеризующий «сложность» ДНФ (КНФ).
Интерпретация булевой функции
Для булевой функции конкретное (индивидуальное) значение булевого набора.
Инфисная запись формул
Запись формул, при которой знаки функций стоят между аргументами.
Классы Поста
−класс функций, сохраняющих 0; − класс функций, сохраняющих 1;− класс самодвойственных функций;− класс монотонных функций;− класс линейных функций.
Конституента единицы
Булева функция аргументов, которая принимает значение, равное 1, только на одной интерпретации (наборе).
То же, что и минтерм -го ранга
Конституента нуля
Булева
функция
аргументов, которая принимает значение,
равное 0, только на одной интерпретации
(наборе).
То же, что и макстерм -го ранга
Конъюнктивная нормальная форма (КНФ)
Формула, представленная в виде конъюнкции элементарных дизъюнкций.
Конъюнктивное поглощение
, где некоторая элементарная дизъюнкция переменных; булева переменная.
Кортеж
Совокупность конкретных значений аргументов булевой функции.
Линейная функция
Булева функция, которая представляется в алгебре Жегалкина каноническим многочленом (полиномом Жегалкина), не содержащем конъюнкций переменных:, где коэффициенты, принимающие значение 0 или 1.
Логические переменные
То же, что и булевы переменные.
Логическая функция
То же, что и булева функция.
Макстерм -го ранга
Член
конъюнктивной нормальной формы,
представляющий собой элементарную
конъюнкцию
букв.
Макстерм -го ранга
То же, что и конституента нуля.
Минимальная ДНФ (МДНФ) булевой функции
Одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) ДНФ.
Минимальная КНФ (МКНФ) булевой функции
Одна из её тупиковых КНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) КНФ.
Минимально полный базис
Система функций называется минимально полным базисом, если удаление из неё любой функции превращает эту систему в неполную.
Минтерм -го ранга
Член дизъюнктивной нормальной формы, представляющий собой элементарную конъюнкцию букв.
Минтерм -го ранга
То
же, что и конституента
единицы.
Монотонная функция
Функция называетсямонотонной, если для любых двух наборов и, находящихся в отношении предшествования (нестрогого порядка), имеет место и неравенство.
Неполное дизъюнктивное склеивание
, где некоторая элементарная конъюнкция переменных; булева переменная.
Неполное конъюнктивное склеивание
, где некоторая элементарная дизъюнкция переменных; булева переменная.
Несократимая полная система булевых функций,
Полная система булевых функций, из которой нельзя исключить ни одной булевой функции без потери свойств полноты.
Номер интерпретации (кортежа)
Десятичный эквивалент двоичного представления интерпретации.
Нулевой элемент (нуль)
Элемент
0 из множества .
Область определения булевой функции
Множество слов длины , которые представляют собой всевозможные наборы издвоичных цифр и их общее количество равно.
Ослаблено функционально полная система
Система функций из, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
То же, что и функционально полная система булевых функций в слабом смысле.
Отрицание
Функция , равная 1, когда аргумент принимает значение 0, и равная 0 при аргументе 1.
Переключательная функция
То же, что и булева функция.
Покрытие функции
Множество
,
состоящее из импликант функции,
если каждое единичное значение функциипокрывается единицей хотя бы одной
импликанты из множества.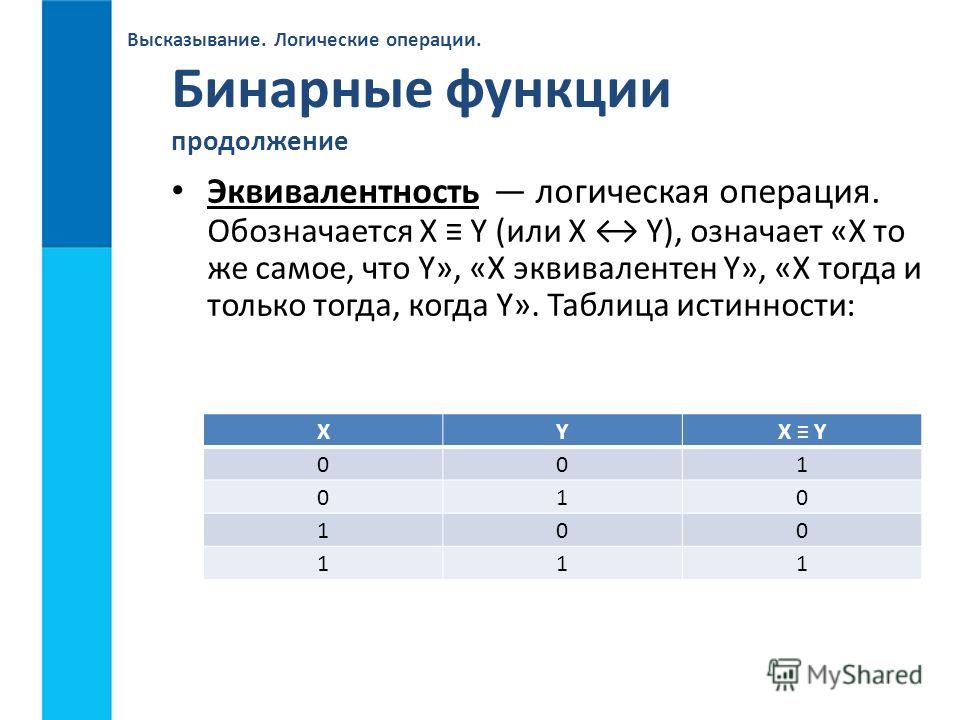
Полином Жегалкина
Конечная сумма по модулю 2 попарно различных элементарных конъюнкций над множеством переменных .
Полная система импликант функции
То же, что и покрытие функции.
Полная система имплицент функции
Множество , состоящее из имплицент функции, если каждое единичное значение функциипокрывается нулем хотя бы одной имплиценты из множества.
Полное дизъюнктивное склеивание
, где некоторая элементарная конъюнкция переменных; булева переменная.
Полное конъюнктивное склеивание
, где некоторая элементарная дизъюнкция переменных; булева переменная.
Полностью определенная функция
Функция,
зависящая от
аргументов, является полностью
определенной, если указаны её значения
для всех наборов (кортежей, слов) значений
элементов.
Принцип двойственности
Указывает правило получения двойственных формул в булевой алгебре.
Простая импликанта функции
Такая конъюнкция-импликанта, что никакая её собственная часть не является импликантой данной функции.
Простая имплицента функции
Такая дизъюнкция-имплицента, что никакая её собственная часть не является имплицентой данной функции.
Равносильные формулы
Формулы, представляющие одну и ту же функцию.
Ранг элементарной конъюнкции
Количество переменных, входящих в элементарную конъюнкцию.
Самодвойственная функция
Функция, двойственная сама себе, т.е. .
Собственной частью конъюнкции
Всякая
элементарная конъюнкция
,
входящая в состав элементарной конъюнкциии содержащая меньше переменных, чем
конъюнкция.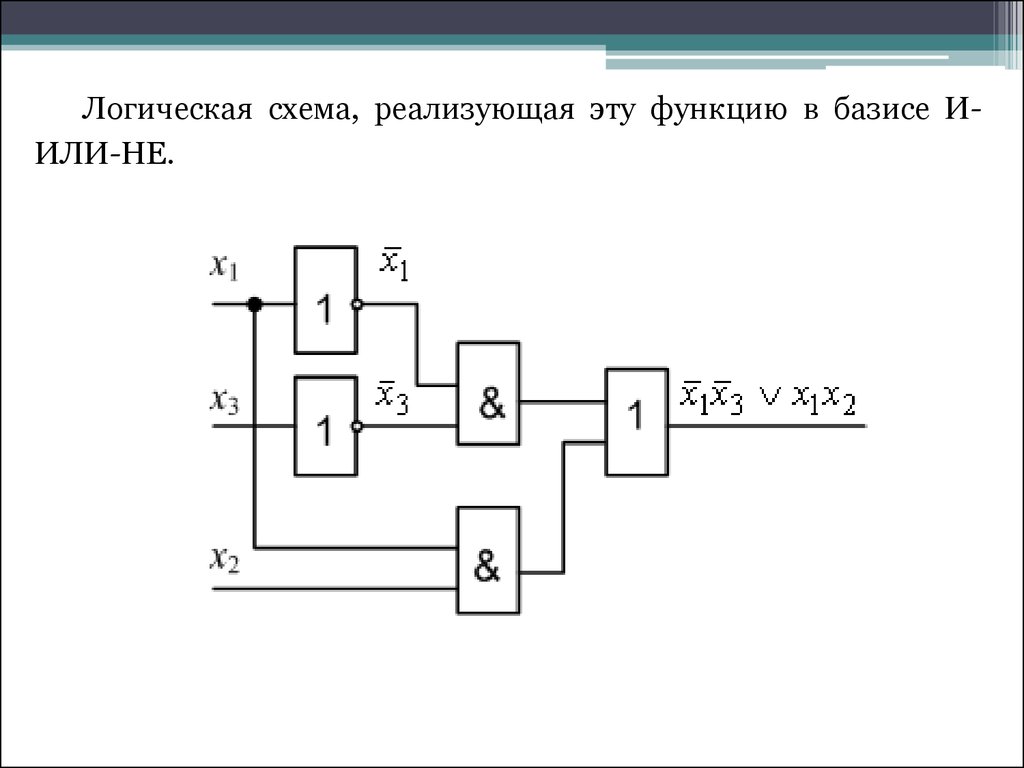
Совершенная дизъюнктивная нормальная форма (СДНФ) булевой функции
Формула, представленная в виде дизъюнкции конституент единицы булевой функции.
Совершенная конъюнктивная нормальная форма (СКНФ) булевой функции
Формула, представленная в виде конъюнкции конституент нуля булевой функции.
Сокращенная дизъюнктивная нормальная форма (ДНФ)
Дизъюнкция всех простых импликант функции.
Сокращенная конъюнктивная нормальная форма КНФ
Конъюнкция всех простых имплицент функции.
Суперпозиция
Прием получения новых функций путем подстановки значений одних функций вместо значений аргументов других функций.
Таблица истинности
Таблица, в которых
каждой интерпретации (то есть набору
аргументов) функции поставлено в
соответствие её значение.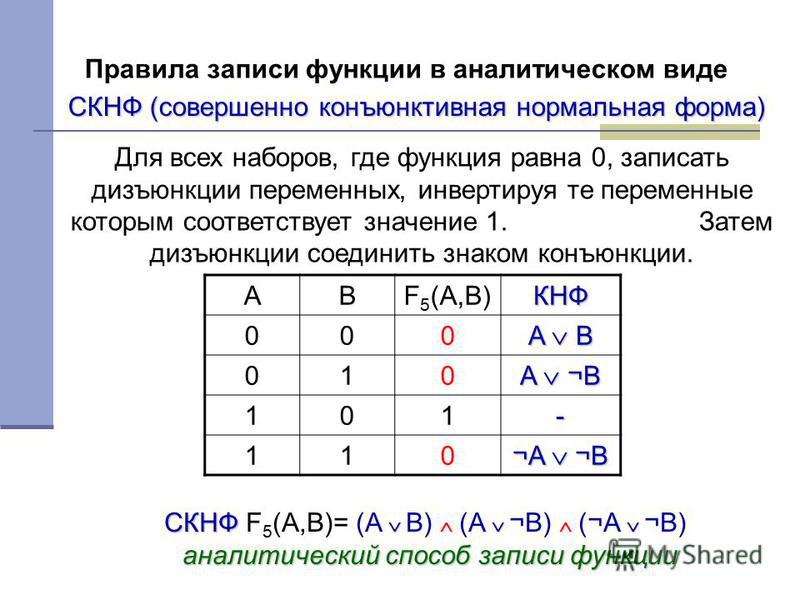
Таблица соответствия
То же, что и таблица истинности.
Тупиковая дизъюнктивная нормальная форма (ДНФ) булевой функции
ДНФ булевой функции, состоящая только из простых импликант.
Тупиковая дизъюнктивная нормальная форма (КНФ) булевой функции
КНФ булевой функции, состоящая только из простых имплицент.
Формула
Выражение, содержащее булевы функции и их суперпозиции.
Формула, реализующая (представляющая) функцию
Формула, которая задает булеву функцию.
Функционально полная система булевых функций
Система
функций
из(где− множество всех возможных булевых
функций, зависящих от любого числа
переменных), в которой любая булева
функция может быть записана в виде
формулы через функции этой системы (в
виде суперпозиции функций из этой
системы).
Функционально полная система булевых функций в слабом смысле
Система функций из, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
То же, что и ослаблено функционально полная система.
Функция, сохраняющая единицу (1)
Булева функция , которая на единичном наборе равна 1, т.е..
Функция, сохраняющая ноль (0)
Булева функция , которая на нулевой наборе равна 0, т.е..
Эквивалентные формулы
Формулы, представляющие одну и ту же функцию (то же, что и равносильные формулы).
Элементарная дизъюнкция
Дизъюнкция любого
числа булевых переменных, взятых с
отрицанием или без него, в которой каждая
переменная встречается не более одного
раза.
Элементарная конъюнкция
Конъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза.
Прикладная теория цифровых автоматов
Прикладная теория цифровых автоматов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ИНФОРМАЦИОННЫЕ ОСНОВЫ ЦИФРОВЫХ АВТОМАТОВ 1.1. ПОНЯТИЕ ИНФОРМАЦИИ 1.2. КОЛИЧЕСТВО ИНФОРМАЦИИ И ЭНТРОПИЯ 1.3. ДИСКРЕТИЗАЦИЯ ИНФОРМАЦИИ 1.4. АЛФАВИТНОЕ ПРЕДСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ ИНФОРМАЦИИ Глава 2. СИСТЕМЫ СЧИСЛЕНИЯ И ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ В ЭВМ 2.1. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.2. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.3. КОДИРОВАННЫЕ ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.4. СИСТЕМЫ СЧИСЛЕНИЯ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 2.5. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ С НЕПОСТОЯННЫМИ ВЕСАМИ РАЗРЯДОВ 2.6. СИМВОЛИЧЕСКИЕ СИСТЕМЫ СЧИСЛЕНИЯ 2.7. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ 2.8. ВЫБОР СИСТЕМЫ СЧИСЛЕНИЯ ДЛЯ ПРИМЕНЕНИЯ ЭВМ 2.9. ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ 2.10. ПРЕДСТАВЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ В ЭВМ 2.11. ТОЧНОСТЬ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЭВМ Глава 3. 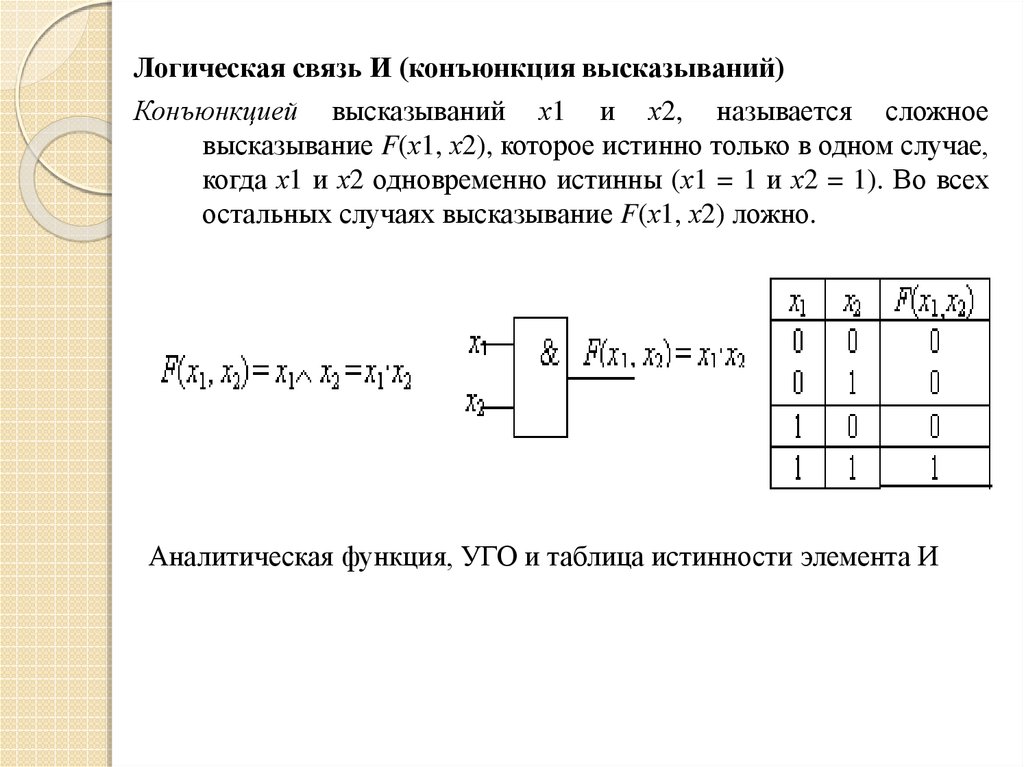 ВЫПОЛНЕНИЕ ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ И СДВИГА В ЭВМ ВЫПОЛНЕНИЕ ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ И СДВИГА В ЭВМ3.2. ОПЕРАЦИЯ АЛГЕБРАИЧЕСКОГО СЛОЖЕНИЯ В ЭВМ 3.3. ОПЕРАЦИЯ СДВИГА 3.4. СЛОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 3.5. ОКРУГЛЕНИЕ ЧИСЕЛ В ЭВМ Особенности округления чисел, заданных инверсными кодами Погрешности выполнения арифметических операций 3.6. ТОЧНОСТЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ В МАШИНЕ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 3.7. ВЫЧИСЛЕНИЯ С ДВОЙНОЙ ТОЧНОСТЬЮ Глава 4. ВЫПОЛНЕНИЕ ОПЕРАЦИИ УМНОЖЕНИЯ И ДЕЛЕНИЯ В ЭВМ 4.2. УМНОЖЕНИЕ, ВЫПОЛНЯЕМОЕ МЕТОДОМ НАКОПЛЕНИЯ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ 4.3. СРАВНЕНИЕ СХЕМ УМНОЖЕНИЯ МЕТОДОМ НАКОПЛЕНИЯ 4.4. МЕТОДЫ УСКОРЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ Матричный метод умножения Быстрое умножение чисел большой разрядности 4.5. УМНОЖЕНИЕ ЧИСЕЛ, ЗАДАННЫХ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.6. УМНОЖЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.7. ОСОБЕННОСТИ ВЫПОЛНЕНИЯ ОПЕРАЦИИ УМНОЖЕНИЯ В СОВРЕМЕННЫХ ЭВМ 4.8. ДЕЛЕНИЕ ЧИСЕЛ С ВОССТАНОВЛЕНИЕМ ОСТАТКОВ 4.9. ДЕЛЕНИЕ БЕЗ ВОССТАНОВЛЕНИЯ ОСТАТКОВ 4.  10. МАШИННЫЕ СХЕМЫ ДЕЛЕНИЯ 10. МАШИННЫЕ СХЕМЫ ДЕЛЕНИЯ4.11. ДЕЛЕНИЕ ЧИСЕЛ В ДОПОЛНИТЕЛЬНОМ КОДЕ 4.12. СПОСОБЫ УСКОРЕННОГО ДЕЛЕНИЯ 4.13. ДЕЛЕНИЕ ЧИСЕЛ В МАШИНАХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ 4.14. ДЕЛЕНИЕ ЧИСЕЛ В ЭВМ СОВРЕМЕННЫХ МОДЕЛЕЙ Глава 5. НЕОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ 5.1. ОПЕРАЦИЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ 5.2. ВЫЧИСЛЕНИЕ СУММ ПАРНЫХ ПРОИЗВЕДЕНИИ 5.3. АРИФМЕТИКА КОМПЛЕКСНЫХ ЧИСЕЛ 5.4. МЕТОДЫ ВЫЧИСЛЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ Глава 6. ДВОИЧНО-ДЕСЯТИЧНАЯ АРИФМЕТИКА 6.2. СЛОЖЕНИЕ ЧИСЕЛ В ИНВЕРСНЫХ Д-КОДАХ 6.3. СДВИГ Д-КОДОВ 6.4. УМНОЖЕНИЕ ЧИСЕЛ В Д-КОДАХ 6.5. ДЕЛЕНИЕ ЧИСЕЛ В Д-КОДАХ 6.6. ПЕРЕВОД ЧИСЕЛ В Д-КОДАХ Глава 7. ВЫПОЛНЕНИЕ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ В СИСТЕМАХ СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ 7.2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В МИНУС-ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ 7.3. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ Глава 8. КОНТРОЛЬ ВЫПОЛНЕНИЯ ОПЕРАЦИИ 8.2. ВЫБОР МОДУЛЯ ДЛЯ КОНТРОЛЯ 8.8. КОНТРОЛЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙ 8.4. КОНТРОЛЬ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ Глава 9.  БУЛЕВЫ ФУНКЦИИ БУЛЕВЫ ФУНКЦИИ9.2. АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БУЛЕВЫХ ФУНКЦИИ 9.3. ФУНКЦИОНАЛЬНО ПОЛНЫЕ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ 9.4. МИНИМИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ 9.5. МИНИМИЗАЦИЯ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ 9.6. АБСОЛЮТНО МИНИМАЛЬНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ БУЛЕВЫХ ФУНКЦИЙ 9.7. МНОГОЗНАЧНЫЕ ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ Глава 10. АБСТРАКТНЫЕ ЦИФРОВЫЕ АВТОМАТЫ 10.2. ДЕКОМПОЗИЦИЯ АБСТРАКТНЫХ АВТОМАТОВ Глава 11. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ 11.2. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ В БУЛЕВОМ И МОНОФУНКЦИОНАЛЬНОМ БАЗИСАХ 11.3. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ С УЧЕТОМ КОЭФФИЦИЕНТОВ ОБЪЕДИНЕНИЯ ПО ВХОДУ И ВЫХОДУ 11.4. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ДЕШИФРАТОРАХ И МУЛЬТИПЛЕКСОРАХ 11.5. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЗУ 11.6. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ПЛМ 11.7. АСИМПТОТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ПЕРЕКЛЮЧАТЕЛЬНЫХ СХЕМ Глава 12. ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ АВТОМАТОВ С ПАМЯТЬЮ 12.1. КАНОНИЧЕСКИЙ МЕТОД СТРУКТУРНОГО СИНТЕЗА АВТОМАТОВ С ПАМЯТЬЮ 12.  2. ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ ФУНКЦИОНИРОВАНИЯ ЦИФРОВЫХ АВТОМАТОВ 2. ОБЕСПЕЧЕНИЕ УСТОЙЧИВОСТИ ФУНКЦИОНИРОВАНИЯ ЦИФРОВЫХ АВТОМАТОВ12.8. СТРУКТУРНЫЙ СИНТЕЗ ЭКОНОМИЧНЫХ СХЕМ АВТОМАТОВ С ПАМЯТЬЮ 12.4. МИКРОПРОГРАММНЫЕ АВТОМАТЫ Глава 13. ЭЛЕМЕНТЫ ТЕОРИИ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ 13.2 ЛИНЕЙНЫЕ ГРУППОВЫЕ КОДЫ 13.3. ЦИКЛИЧЕСКИЕ КОДЫ Глава 14. КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ 14.2. ОБЩИЕ МЕТОДЫ ФУНКЦИОНАЛЬНОГО КОНТРОЛЯ ЦИФРОВЫХ АВТОМАТОВ 14.3. ФУНКЦИОНАЛЬНЫЙ КОНТРОЛЬ ЦИФРОВЫХ АВТОМАТОВ ПРИ ИСПОЛЬЗОВАНИИ ЛИНЕЙНЫХ ГРУППОВЫХ КОДОВ 14.4. ЭЛЕМЕНТЫ ТЕОРИИ САМОПРОВЕРЯЕМЫХ ЦИФРОВЫХ АВТОМАТОВ 14.5. ТЕСТОВЫЙ КОНТРОЛЬ 14.6. САМОДИАГНОСТИРУЕМЫЕ ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ |
Бинарные булевы логические функции — Нейронный дамп
Три прочеловеческих закона робототехники
Адвент-календарь LEGO Star Wars на 2017 год #75184
октябрь 12 2017
Логические функции , иногда также называемые функциями переключения, представляют собой функции, которые принимают в качестве входных данных ноль или более логических значений (1 или 0, истина или ложь и т. д.) и выводят одно логическое значение. Количество входов функции называется арностью функции и обозначается как 9.0013 к . Каждая k -арная функция может быть записана как пропозициональная формула, предложение в пропозициональной логике. Бинарная булева функция, булева функция с двумя аргументами, может быть описана одной из шестнадцати канонических формул.
д.) и выводят одно логическое значение. Количество входов функции называется арностью функции и обозначается как 9.0013 к . Каждая k -арная функция может быть записана как пропозициональная формула, предложение в пропозициональной логике. Бинарная булева функция, булева функция с двумя аргументами, может быть описана одной из шестнадцати канонических формул.
Рассмотрим функцию, которая имеет два входа с двоичным значением и выводит двоичное значение. Два входа, каждый из которых может принимать одно из двух значений, 0 или 1, означают, что существуют возможные комбинации входных значений.
| х | г |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
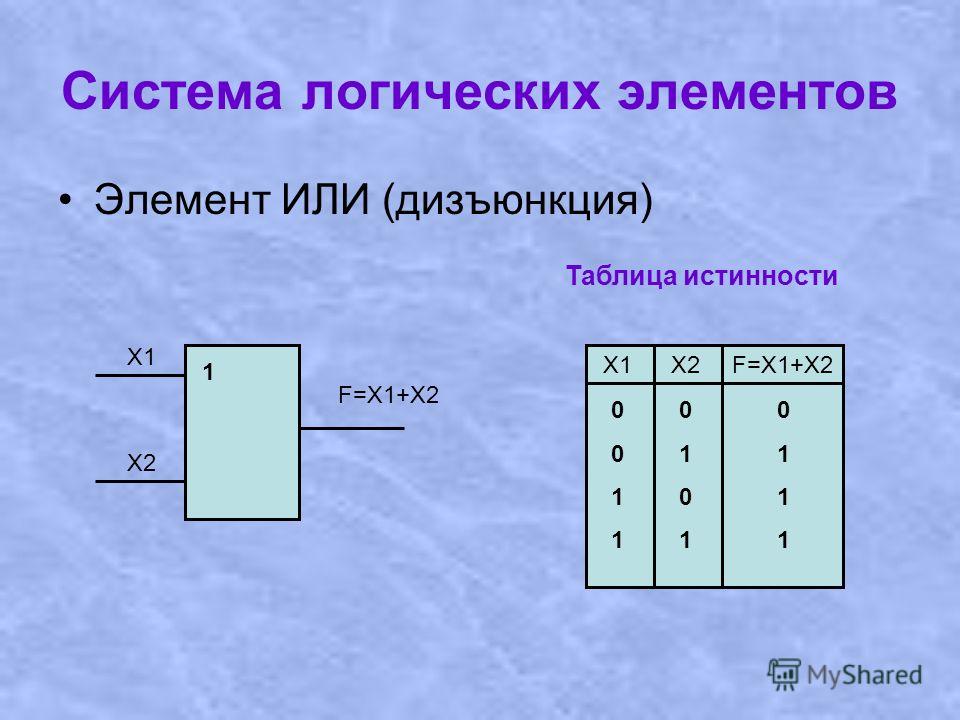
Распространенным способом иллюстрации бинарных булевых функций является таблица истинности , таблица, которая перечисляет все возможные входные комбинации и их выходные данные.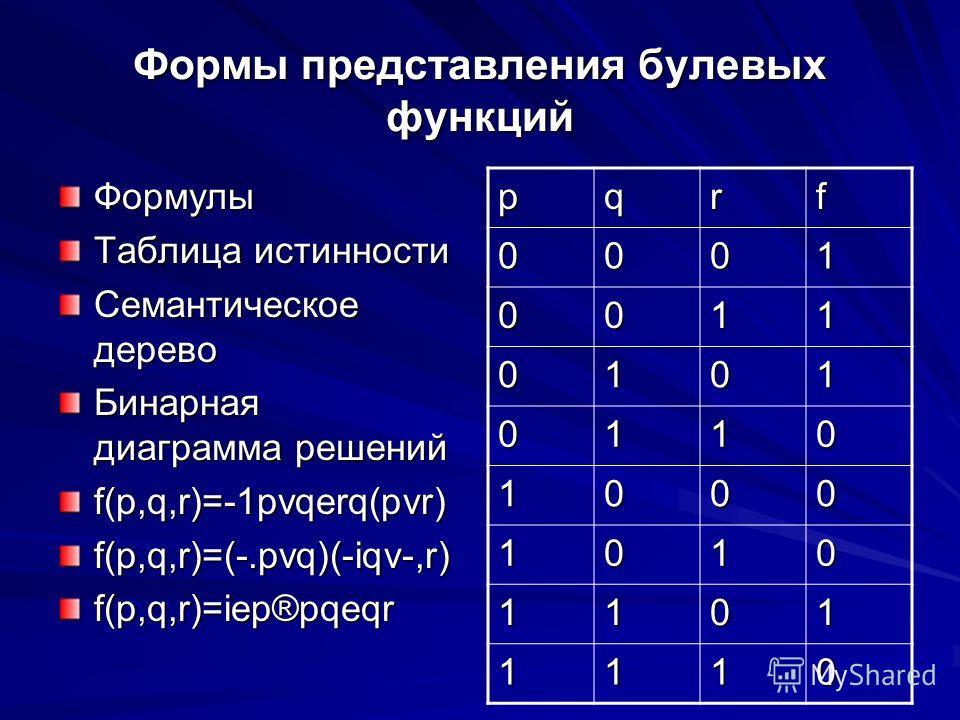 Например, таблица истинности для функции, применяющей булев оператор А , обозначаемый символом пропозициональной логики ∧, на два входа имеет вид:
Например, таблица истинности для функции, применяющей булев оператор А , обозначаемый символом пропозициональной логики ∧, на два входа имеет вид:
| х | г | х ∧ у |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Другие функции будут иметь разные выходные значения в последнем столбце для соответствующих входов. Учитывая, что имеется 4 возможных выходных значения, по одному для каждой из входных комбинаций, это означает, что существует , или 16, возможных комбинаций выходных значений, т. е. для пары двоичных входов существует ровно 16 возможных булевых функций, которые могут применяться к ним. Их называют канонических функций , потому что любую бинарную булеву функцию можно привести к одной из этих 16 форм.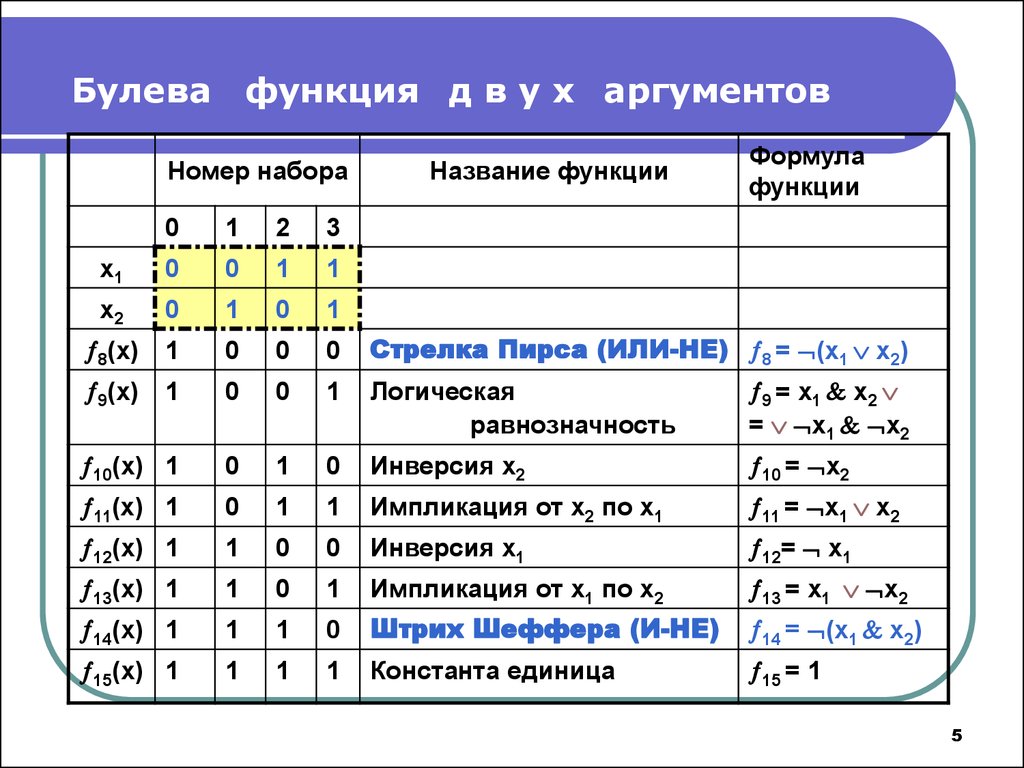 В общем, для k входов есть канонические булевы функции.
В общем, для k входов есть канонические булевы функции.
В таблице ниже перечислены 16 канонических двоичных логических функций:
| х, у | |||||
|---|---|---|---|---|---|
| Логическая функция | Предложение | 0, 0 | 0, 1 | 1, 0 | 1, 1 |
| Константа 0 | 0 | 0 | 0 | 0 | 0 |
| И | х ∧ у | 0 | 0 | 0 | 1 |
| х И не у | х ∧ ¬y | 0 | 0 | 1 | 0 |
| х | х | 0 | 0 | 1 | 1 |
| Не х А у | ¬х ∧ у | 0 | 1 | 0 | 0 |
| у | и | 0 | 1 | 0 | 1 |
| Хор | (х ∧ ¬у) ∨ (¬х ∧ у) | 0 | 1 | 1 | 0 |
| Или | х ∨ у | 0 | 1 | 1 | 1 |
| Нор | ¬(х ∨ у) | 1 | 0 | 0 | 0 |
| Эквивалент | (х ∧ у) ∨ (¬х ∧ ¬у) | 1 | 0 | 0 | 1 |
| Нет у | ¬й | 1 | 0 | 1 | 0 |
| y Подразумевается x (если y, то x) | г ⇒ х ⇔ х ∨ ¬y | 1 | 0 | 1 | 1 |
| Не х | ¬х | 1 | 1 | 0 | 0 |
| x Подразумевается y (если x, то y) | х ⇒ у ⇔ ¬х ∨ у | 1 | 1 | 0 | 1 |
| Нанд | ¬(х ∨ у) | 1 | 1 | 1 | 0 |
| Константа 1 | 1 | 1 | 1 | 1 | 1 |
Две из вышеперечисленных функций, Nor и Nand, очень особенные, поскольку любая из них может использоваться для определения остальных пятнадцати функций.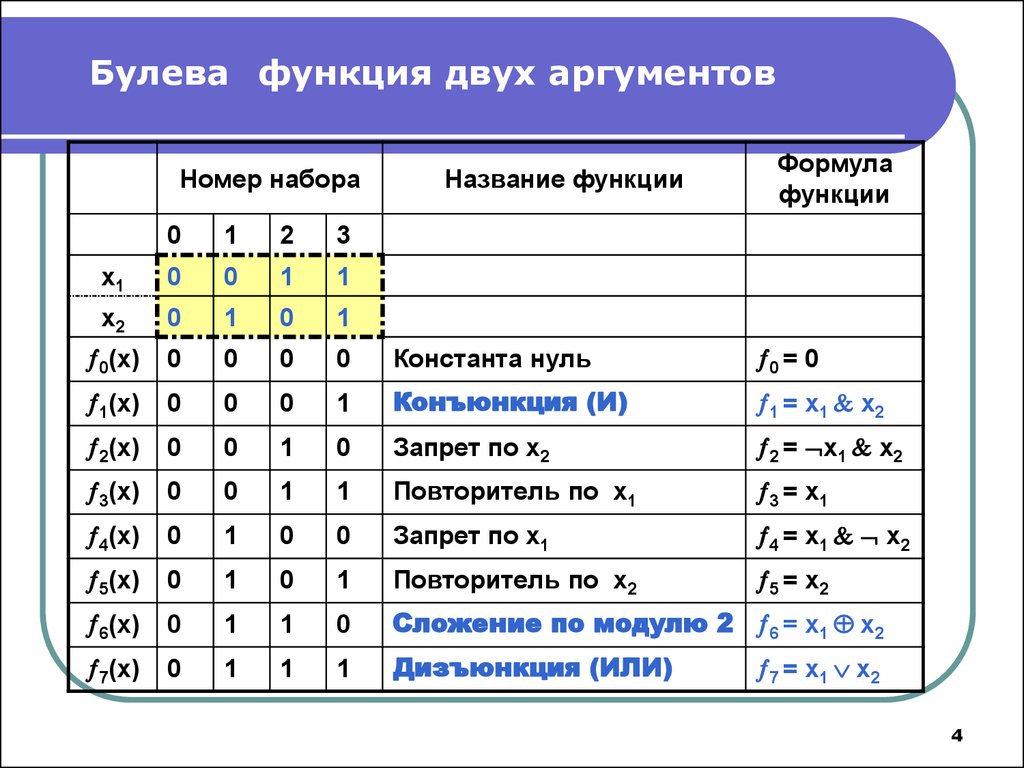 Впрочем, это история для другого поста.
Впрочем, это история для другого поста.
- и, арность, бинарные, логические, логические функции, канонические, функции, логика, nand, nor, or, пропозициональные формулы, пропозициональная логика, xor
Двоичное представление данных; логическая логика — CS 111, Бостонский университет
Старая версия
Это сайт CS 111, который появился 10 мая 2018 года.
Эта лабораторная работа не является обязательной.
Лаборатории не проводятся в течение недели с 19 февраля из-за
выходных, но мы публикуем эту дополнительную лабораторную работу, чтобы вы могли
собственной — для дополнительной практики и/или помощи в работе над
проблемные наборы.
- Задача 0: представление целых чисел; двоичная арифметика
- Задача 1: таблицы истинности для логических выражений
- Задача 2: рекурсивная обработка двоичных чисел
- Задача 3: оценка и создание принципиальных схем
Задача 0: представление целых чисел; двоичная арифметика
На лекции вы видели, как мы можем представлять числа по основанию два. (двоичный) и десятичный (десятичный). Например, мы можем представить
десятичное число 21 как 10101 в двоичном формате и десятичное число 7 как 111
в двоичном формате.
(двоичный) и десятичный (десятичный). Например, мы можем представить
десятичное число 21 как 10101 в двоичном формате и десятичное число 7 как 111
в двоичном формате.
Выполните следующие упражнения. Запишите свои решения в текстовом файле с именем lab4task0.txt .
- Преобразование десятичного числа 44 в двоичное.
- Преобразование десятичного числа 35 в двоичное.
- Преобразование двоичного числа 100111 в десятичное.
- Преобразование двоичного числа 10000 в десятичное.
Теперь займемся арифметикой двоичных чисел.
- Сложите двоичные числа 10110 и 1101.
- Перемножьте двоичные числа 10110 и 1101.
Задача 1: таблицы истинности для логических выражений
Напомним, что мы можем представить логическое выражение в виде таблицы истинности с помощью перечисление всех возможных комбинаций переменных в выражении. Другими словами, если логическое выражение имеет 92 = 4 рядов:
| х | г | х и у |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Аналогично, чтобы представить формулу x или y или z (три переменные),
таблица истинности имеет 93 = 8 рядов:
| х | г | г | x или y или z |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Создайте таблицу истинности для следующего логического выражения: (x или y) и z . Строки таблицы истинности должны «покрывать» все возможные
комбинации истинных и ложных значений переменных. Положите вашу
ответ в текстовом файле с именем
Строки таблицы истинности должны «покрывать» все возможные
комбинации истинных и ложных значений переменных. Положите вашу
ответ в текстовом файле с именем lab4task1.txt .
Задача 2: рекурсивная обработка двоичных чисел
В наборе задач 4 вы будете писать рекурсивные функции, которые манипулировать двоичными числами, представленными в виде строк.
побитовое ИЛИ двух двоичных чисел формируется путем рассмотрения биты в числах справа налево. При этом каждая пара соответствующие биты объединяются вместе для получения соответствующего бита за результат.
Например, чтобы получить побитовое ИЛИ 10100 и 00101 , мы бы
начните с того, что выровняйте два числа следующим образом:
10100 00101 -----
Затем мы объединим ИЛИ каждую пару/столбец битов справа налево.
Например, самый правый столбец дает нам (0 ИЛИ 1) , что равно 1 :
10100
00101
-----
1
Следующая пара/столбец битов дает нам (0 ИЛИ 0) , что равно 0 :
10100 00101 ----- 01
Продолжая в том же духе, получим:
10100 00101 ----- 10101
Таким образом, побитовое ИЛИ 10100 и 00101 равно 10101 .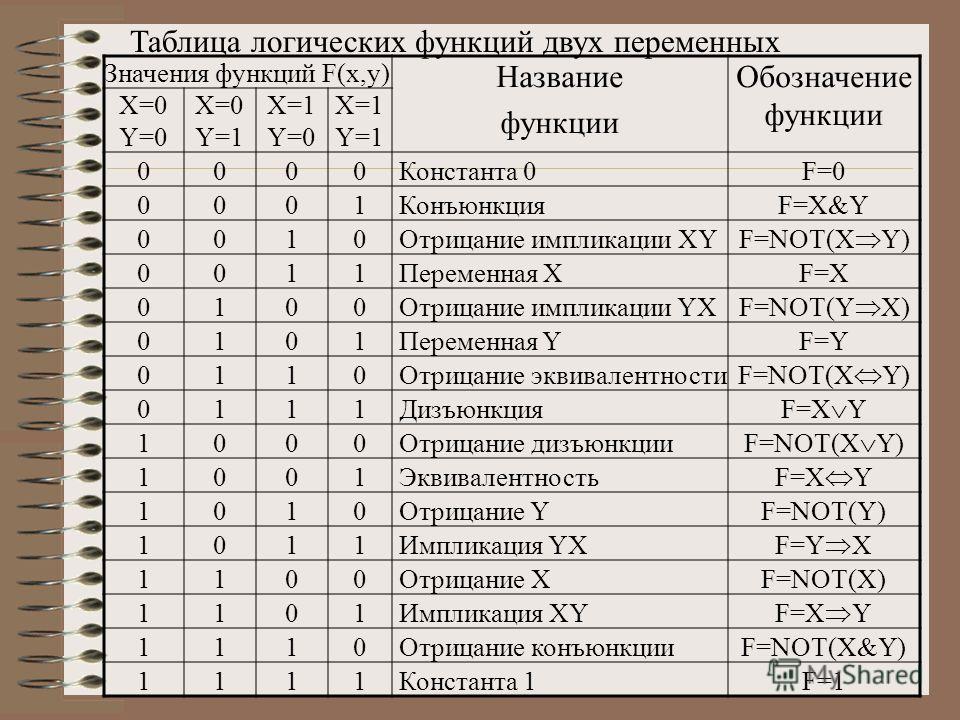
Если одно число имеет больше битов, чем другое, лишние биты эффективно ORed с 0, и, таким образом, они не меняются в результате. Например:
10101010 11000 -------- 10111010
В IDLE используйте пункт меню File -> New Window , чтобы открыть новый редактор
окно для вашего кода и сохраните его под именем lab4task2.py .
Обязательно укажите расширение .py .
Напишите функцию с именем bitwise_or(b1, b2) , которая принимает на вход два
строки b1 и b2 , представляющие двоичные числа. Функция должна использовать рекурсию для вычисления побитового ИЛИ двух чисел, и вернуть результат в виде строки. Например:
>>> bitwise_or('10100', '00101')
«10101»
>>> bitwise_or('10101010', '11000')
'10111010`
Примечания/советы:
Базовые случаи: Поскольку функция будет вызываться рекурсивно на все меньших и меньших струнах вы в конце концов опуститесь в пустую строку для одного или обоих входов.

Если оба входа являются пустой строкой, функция должен вернуть пустую строку.
Если только один из входов является пустой строкой, функция должна возвращать строку, представляющую результат операции ИЛИ другой вход с 0s.
Например:
>>> побитовое_ИЛИ('', '') '' >>> побитовое_или('101', '') «101» >>> побитовое_или('', '11010') «11010»Вы должны использовать рекурсию для ИЛИ остальных битов в двух числа. Когда вы это сделаете, убедитесь, что вы в конечном итоге рассматриваете биты справа налево, а не слева направо.
Как обычно, мы рекомендуем сделать рекурсивный вызов в начале рекурсивного случая и сохранение возвращаемого значения в переменной. Затем вы можете использовать эту переменную для создания значения, которое ты вернешься.
Вам нужно будет использовать условное выполнение (
if-elif-else), чтобы решить, что вернуть, на основе битов, которые объединяются по ИЛИ текущим вызовом функции.