Двоичный логарифм: основные свойства и примеры решения логарифмических задач / Skillbox Media

Содержание

Двоичный логарифм | это… Что такое Двоичный логарифм?

График двоичного логарифма

Двоичный логарифм — логарифм по основанию 2. Другими словами, двоичный логарифм числа есть решение уравнения

Двоичный логарифм числа существует, если Он обозначается (согласно ISO 31-11), или . Примеры:

Содержание

1 Алгебраические свойства
2 Функция двоичного логарифма
3 Применение
- 3.1 Теория информации
- 3.2 Сложность рекурсивных алгоритмов
- 3.3 Другие применения
4 См. также
5 Литература
6 Ссылки
7 Примечания

Алгебраические свойства

В нижеследующей таблице предполагается, что все значения положительны^[1]:

	Формула	Пример
Произведение
Частное от деления
Степень
Корень

Существует очевидное обобщение приведенных формул на случай, когда допускаются отрицательные переменные, например:

Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:

Связь двоичного, натурального и десятичного логарифмов:

Функция двоичного логарифма

Если рассматривать логарифмируемое число как переменную, мы получим функцию двоичного логарифма: . Она определена при всех . Область значений: . График этой кривой часто называется логарифмикой^[2].

Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:

Ось ординат является левой вертикальной асимптотой, поскольку:

Применение

Теория информации

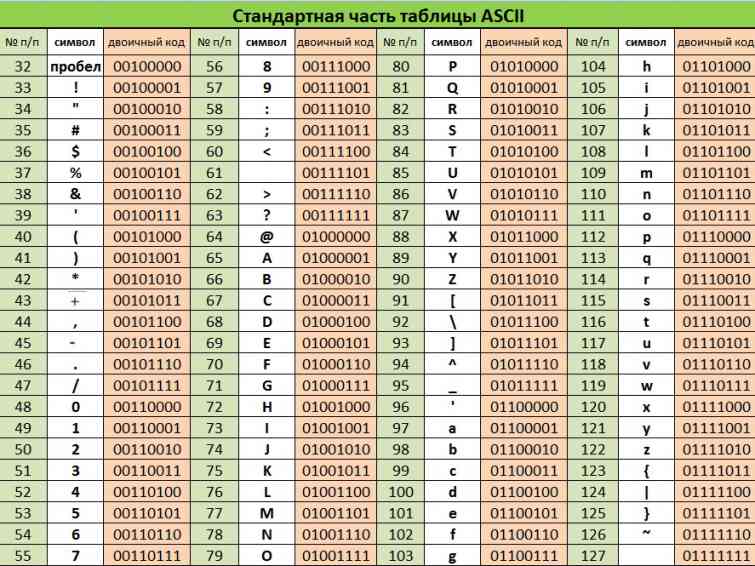
Двоичный логарифм натурального числа позволяет определить число цифр во внутреннем компьютерном (битовом) представлении этого числа:

(скобки обозначают целую часть числа)

Информационная энтропия — мера количества информации, также основана на двоичном логарифме

Сложность рекурсивных алгоритмов

Оценка асимптотической сложности рекурсивных алгоритмов, основанных на принципе «разделяй и властвуй»^[3] — таких, как быстрая сортировка, быстрое преобразование Фурье, двоичный поиск и т. п.

Другие применения

Число кругов игры по олимпийской системе равно двоичному логарифму от числа участников соревнований.

В теории музыки, чтобы решить вопрос о том, на сколько частей делить октаву, требуется отыскать рациональное приближение для Если разложить это число в непрерывную дробь, то третья подходящая дробь (7/12) позволяет обосновать классическое деление октавы на 12 полутонов^[4].

См. также

Бит
Десятичный логарифм.
Натуральный логарифм.

Литература

Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6
Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.

Ссылки

Таблица двоичных логарифмов целых чисел от 1 до 100.

Примечания

↑ Выгодский М. Я. Справочник по элементарной математике, 1978, с. 187.
↑ Логарифмическая функция. 2
Можно ли использовать логарифмы для преобразования чисел в двоичные?
спросил 7 лет, 5 месяцев назад
Изменено 7 лет, 5 месяцев назад
Просмотрено 5к раз
Я новичок в CS, и я нахожу способ деления нахождения двоичного числа болезненным. Можно ли использовать журнал, чтобы быстро найти 24, например, в двоичном формате?
- двоичный
- логарифмический
1
Если вы хотите использовать логарифмы, вы можете .
Определить log ₂ ( b ) как log( b ) / log(2) или ln( b ) / ln(2) (они одинаковы).
Повторите следующее:

Рабочий пример: преобразование 2835 в двоичный код
- log ₂ (2835) = 11,47. . => н = 11
  Двоичное представление имеет 1 в позиции 2 ¹¹.
- 2835 — (2 ¹¹ = 2048) = 787
  log ₂ (787) = 9,62… => n = 9
  В двоичном представлении 1 стоит на позиции 2 ⁹.
- 787 — (2 ⁹ = 512) = 275
  log ₂ (275) = 8,10… => n = 8
  Двоичное представление имеет 1 в 2 ⁸ позиция.
- 275 — (2 ⁸ = 256) = 19
  log ₂ (19) = 4,25… => n = 4
  В двоичном представлении 1 стоит на позиции 2 ⁴.
- 19 — (2 ⁴ = 16) = 3
  
  log ₂ (3) = 1,58.. => n = 1
  В двоичном представлении 1 стоит на позиции 2 ¹.
- 3 — (2 ^{1 911 10 9 8 7 6 5 4 3 2 1 0
  двоичный 1 0 1 1 0 0 0 1 0 0 1 1}
  , поэтому двоичное представление 2835 равно 101100010011 .
  3
  С точки зрения CS, двоичный код довольно прост, потому что обычно вам нужно всего лишь дойти до 255. Или до 15, если вы используете HEX-нотацию. Чем больше вы его используете, тем легче становится.
  Как я делаю это на лету, так это запоминая все 2 степени до 128, включая 1. (Наличие 1 вместо 1.4xxx, возможно, означает, что вы не можете использовать журналы).
```
 128,64,32,16,8,4,2,1
 
```
  Затем я использую правило, согласно которому, если число больше, чем каждая степень в порядке убывания, это «1», и я вычитаю его, иначе это «0».
  
  Итак 163
```
 163 >= 128 = '1' R 35
35 !>= 64 = '0'
35 >= 32 = '1' R 3
3 !>= 16 = '0'
3 !>= 8 = '0'
3 !>= 4 = '0'
3 >= 2 = '1' R 1
1 >= 1 = '1' R 0
163 = 10100011.
 
```
  Возможно, это не самый элегантный метод, но когда вам просто нужно преобразовать что-то специальное, думать об этом как о сравнении и вычитании может быть проще, чем о делении.
  Да, вам нужно перебрать 0 -> мощность, которая больше, чем вам нужно, а затем взять остаток и сделать то же самое, что тоже является проблемой.
  Я бы посоветовал вам попробовать рекурсивный подход к разделению под названием «Разделяй и властвуй».
  http://web.stanford.edu/class/archive/cs/cs161/cs161.1138/lectures/05/Small05.pdf
  Но опять же, поскольку вам нужно двоичное представление, я думаю, если вы не используете готовые утилиты , подход деления самый простой ИМХО.
  
  Зарегистрируйтесь или войдите в систему
  Зарегистрируйтесь с помощью Google
  Зарегистрироваться через Facebook
  Зарегистрируйтесь, используя адрес электронной почты и пароль
  Опубликовать как гость
  Электронная почта
  Обязательно, но не отображается
  Опубликовать как гость
  Электронная почта
  Требуется, но не отображается
  9{k+1} \rfloor = 0⌊n/2k+1⌋=0.
  Мы видим, что kkk — это позиция самого левого бита или, что то же самое, что для представления числа nnn требуется k+1k + 1k+1 бит, но не меньше.
  На потолочной/напольной стойке также указано
  ⌊…⌊⌊n/2⌋/2⌋…/2⌋=⌊n2⋅2⋯2⌋,\lfloor \ldots \lfloor \lfloor n/2 \rfloor /2 \rfloor \ldots /2 \rfloor = \left\lfloor \frac{n}{2 \cdot 2 \cdots 2} \right\rfloor, ⌊…⌊⌊n/2⌋/2⌋…/2⌋=⌊2⋅2⋯2n⌋,
  , что означает, что мы можем многократно делить целое число на два, пока не достигнем нуля. Если быть точнее:
```
 шаблон  
 без знака floor_log2(T v) { 
 без знака r = -1; 
 в то время как (v) { v >>= 1; р++; } 
 вернуть р; 
 } 
```
  Преимущество этого алгоритма в том, что он работает для всех (положительных) целочисленных типов при условии, что определен побитовый сдвиг вправо >> или целочисленное деление на два. Плохо то, что это не очень быстро.
  
  Наблюдение, которое может привести к ускорению алгоритмов, заключается в том, что, как упоминалось выше, ⌊log⁡2n⌋\lfloor \log_2 n \rfloor⌊log2n⌋ — это позиция самого левого бита. Сначала обратимся к числам с множественной точностью. Предположим, что положительное целое число nnn представлено, как в предыдущем посте, как 9.pb=2p для некоторого ppp, как это обычно бывает, имеем:
  ⌊log⁡2n⌋=(d−1)p+⌊log⁡2nd−1⌋.\lfloor \log_2 n \rfloor = (d-1 ) p + \lfloor \log_2 n_{d-1} \rfloor. ⌊log2n⌋=(d−1)p+⌊log2nd−1⌋.
  Таким образом, задача вычисления целочисленного двоичного логарифма для целого числа кратной точности указанного типа сводится к нахождению целочисленного двоичного логарифма одной разрядной цифры ppp.
  Теперь рассмотрим положительное целое число, представленное 16-битным словом. Поскольку нас интересует крайний левый бит, мы можем искать его, используя своего рода метод бинарного поиска. Сначала мы делаем побитовое и с маской (1111111100000000)2(1111111100000000)_2(1111111100000000)2, чтобы увидеть, находится ли крайний левый бит в верхней или нижней части слова. Если оно находится среди младших 8 бит, мы просто вычисляем результат для этого 8-битного числа; если он находится среди старших 8 бит, мы вычисляем результат для старших 8 бит и добавляем 8.
  Таким образом, мы свели задачу нахождения целочисленного двоичного логарифма 16-битного числа к нахождению той же функции 8-битного числа. Этот принцип можно использовать рекурсивно, пока мы не рассмотрим только 1 бит:
```
 без знака floor_log2(uint16_t v) { 
 static const uint16_t единиц = -1; 
 без знака г = 0; 
 if (v & (ones << 8)) { v >>= 8; р += 8; } 
 if (v & (ones << 4)) { v >>= 4; г += 4; } 
  if (v & (ones << 2)) { v >>= 2; г += 2; } 
 if (v & (ones << 1)) { v >>= 1; р += 1; } 
 вернуть р; 
 } 
```
  (Обратите внимание, что эта функция возвращает 0, если аргумент равен 0. Типы uint8_t , uint16_t и т. д. определены в stdint.h и cstdint .)
  Если мы посмотрим на небольшие числа, скажем, на 8-битные целые числа, мы можем добиться большего успеха с помощью простого поиска в таблице. Например:
```
 const short floor_log2_table[256] = {
 -1, 0, 1,1, 2,2,2,2, 3,3,3,3,3,3,3,3, 4,4 ,4,4,4,4,4,4,4,4,4,4,4,4,4,4, 
 5,5,5,5,5,5,5,5,5,5, 5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5, 
 6,6,6 ,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6 ,6,6,6,6, 
 6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6, 6,6,6,6,6,6,6,6,6,6,6,6, 
 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7 ,7,7,7,7,7,7,7, 
 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7, 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7, 
 7,7,7,7,7,7,7,7,7,7 ,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7, 
 7,7, 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7,7, 7,7,7,7,7};  без знака floor_log2 (uint8_t v) { 
 return floor_log2_table [v]; 
 } 
 
```
  Для больших чисел мы можем комбинировать бинарный поиск и поиск по таблице.
  No related posts.