Математика. Ее содержание, методы и значение. Том 1
Математика. Ее содержание, методы и значение. Том 1
ОглавлениеПРЕДИСЛОВИЕГлава I. ОБЩИЙ ВЗГЛЯД НА МАТЕМАТИКУ § 1. ОСОБЕННОСТИ МАТЕМАТИКИ § 2. АРИФМЕТИКА § 3. ГЕОМЕТРИЯ § 4. АРИФМЕТИКА И ГЕОМЕТРИЯ § 5. ЭПОХА ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ § 6. МАТЕМАТИКА ПЕРЕМЕННЫХ ВЕЛИЧИН § 7. СОВРЕМЕННАЯ МАТЕМАТИКА § 8. СУЩНОСТЬ МАТЕМАТИКИ § 9. ЗАКОНОМЕРНОСТИ РАЗВИТИЯ МАТЕМАТИКИ Глава II. АНАЛИЗ § 2. ФУНКЦИЯ Графики функций. § 3. ПРЕДЕЛ § 4 НЕПРЕРЫВНЫЕ ФУНКЦИИ § 5. ПРОИЗВОДНАЯ Примеры вычисления производных. § 6. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Производная суммы. Производная произведения. Производная частного. Производная обратной функции. Таблица производных. Нахождение производной функции от функции. § 7. МАКСИМУМ И МИНИМУМ. ИССЛЕДОВАНИЕ ГРАФИКОВ ФУНКЦИЙ Отыскание наибольших и наименьших значений функции. Производные высших порядков. Смысл второй производной. Выпуклость и вогнутость. Признаки максимумов и минимумов.  Исследование графиков функций.§ 8. ПРИРАЩЕНИЕ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ Теорема о среднем и примеры ее применения. § 9. ФОРМУЛА ТЕЙЛОРА Формула Тейлора. Ряд Тейлора. § 10. ИНТЕГРАЛ Определенный интеграл. Связь дифференциального и интегрального исчисления. § 11. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. ТЕХНИКА ИНТЕГРИРОВАНИЯ § 12. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Неявное задание функции. Геометрическое изображение. Частные производные и дифференциал. Дифференцирование неявных функций. Задачи на максимум и минимум. Формула Тейлора. Относительный максимум и минимум. § 13. ОБОБЩЕНИЯ ПОНЯТИЯ ИНТЕГРАЛА Формула Остроградского. § 16. РЯДЫ Сходимость ряда. Ряды функций. Равномерно сходящиеся ряды. Степенные ряды. Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ § 2. ДВЕ ОСНОВНЫЕ ИДЕИ ДЕКАРТА Идея сопоставления уравнениям с двумя неизвестными линий на плоскости. Основные задачи, решаемые аналитической геометрией, и определение аналитической геометрии.  2.§ 6. ОБЩАЯ ТЕОРИЯ ДИАМЕТРОВ НЬЮТОНА § 7. ЭЛЛИПС, ГИПЕРБОЛА И ПАРАБОЛА Уравнение эллипса и его фокальное свойство. Законы движения планет. Эллипс инерции. Гипербола и ее фокальное свойство. Парабола и ее директрисса. Свойство касательной к параболе. Директриссы эллипса и гиперболы. Конические сечения. Парабола как график пропорциональности квадрату и гипербола как график обратной пропорциональности. § 8. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ 2-Й СТЕПЕНИ К КАНОНИЧЕСКОМУ ВИДУ Формулы преобразования координат. Приведение любого уравнения 2-й степени к одному из 9 канонических видов. § 9. ЗАДАНИЕ СИЛ, СКОРОСТЕЙ И УСКОРЕНИЙ ТРОЙКАМИ ЧИСЕЛ. ТЕОРИЯ ВЕКТОРОВ Арифметизация сил, скоростей и ускорений, введенная Лагранжей. Алгебра векторов. Скалярное произведение и его свойства. § 10. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ. УРАВНЕНИЕ ПОВЕРХНОСТИ В ПРОСТРАНСТВЕ И УРАВНЕНИЯ ЛИНИИ Уравнение плоскости и уравнения прямой. Общее уравнение 2-й степени с тремя переменными и 17 его канонических видов.  Эллипсоид. Гиперболоиды и конус 2-го порядка. Параболоиды. § 11. ПРЕОБРАЗОВАНИЯ АФФИННЫЕ И ОРТОГОНАЛЬНЫЕ Эллипс как результат «сжатия» окружности. Пример решения более сложной задачи. Важнейшие применения аффинных преобразований Ортогональные преобразования. § 12. ТЕОРИЯ ИНВАРИАНТОВ § 13. ПРОЕКТИВНАЯ ГЕОМЕТРИЯ Применение основной теоремы плоской перспективы в аэрофотосъемке. Проективная плоскость. Проективные отображения; основная теорема. Проективная геометрия. Запись проективных преобразований формулами. § 14. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА Проективные преобразования круга в себя. ЗАКЛЮЧЕНИЕ Глава IV. АЛГЕБРА (ТЕОРИЯ АЛГЕБРАИЧЕСКОГО УРАВНЕНИЯ) § 2. АЛГЕБРАИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЯ Разложение многочлена на множители и формулы Виета. Теорема о симметрических многочленах. Работы Лагранжа. Открытие Абеля. Теория Галуа. Приложение теории Галуа к вопросу о разрешимости геометрической задачи циркулем и линейкой.  Две основные нерешенные задачи, связанные с теорией Галуа. § 3. ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ Теория комплексных чисел. Поверхность модуля многочлена. О возрастании модуля многочлена при удалении от начала. Существование минимумов поверхности M. Лемма Даламбера. § 4. ИССЛЕДОВАНИЕ РАСПОЛОЖЕНИЯ КОРНЕЙ МНОГОЧЛЕНА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ Простые и кратные корни многочлена. Теорема Ролля и некоторые ее следствия. Правило знаков Декарта. Теорема Штурма. Задача Гурвица. § 5. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ КОРНЕЙ |
12.04. Исследование функции с помощью второй производной
Исследование функции с помощью второй производной
Вторая производная функции, если она существует, может быть так же эффективно использована для исследования на экстремум, определения промежутков выпуклости и вогнутости ее графика, отыскания точек перегиба.
ТЕОРЕМА 1 (ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА).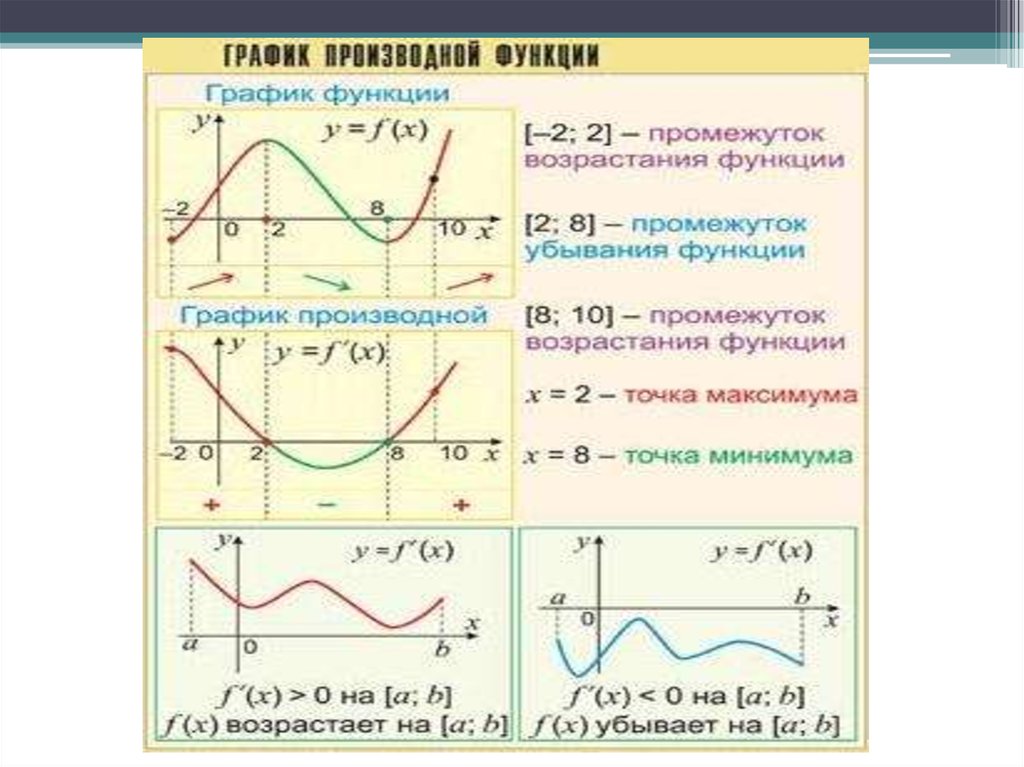
Если для функции в точке производная
ДОКАЗАТЕЛЬСТВО.
Пусть в точке с выполняется равенство
И имеет место неравенство
Будучи непрерывной, вторая производная сохраняет свой знак при х, Близких к с. Поэтому для этих x
Но вторая производная функции есть производная от первой производной
|
Рис. 11.17. Возможное взаимное расположение графиков функций , И в окрестности точки Максимума. |
|
Это условие является достаточным признаком для существования экстремума, но не является необходимым. |
Следовательно, есть функция убывающая. По условию теоремы, . Это означает, что левее точки с Положительна, а правее – отрицательна. Переходя к самой функции , можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций , И в окрестности точки с.
Данная теорема может оказаться удобной, когда знак определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда не существует.
Сформулируем без доказательства некоторое обобщение данной теоремы для случая, когда функция имеет производные порядка .
ТЕОРЕМА 2. Если функция в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем то при четном (n+1) функция имеет максимум, если и минимум, если .
Рассмотрим примеры.
Исследуем на экстремум функцию
Находим первую производную:
И приравниваем ее к нулю:
.
Получаем, что x = 0 – Точка, подозрительная на экстремум.
Следовательно, в этой точке функция имеет максимум:
Рассмотрим теперь функцию
Ее первая производная
Также обращается в нуль при .
Легко обнаружить, что , так как
Однако по теореме 2 имеем:
Следовательно, функция при Экстремума не имеет.
Отсутствие экстремума у данной функции легко установить и без применения производной.
Действительно, так как функция всюду возрастает, то функция
Убывает для , то есть экстремум отсутствует. Этот пример еще раз показывает, что при исследовании функций полезно использовать разнообразные приемы.
Применим теперь вторую производную к исследованию на выпуклость и вогнутость графика функции.
Выше, в главе 3, мы определили эти понятия, связывая расположение кривой с расположением хорды, соединяющей две близкие точки этой кривой. Возможен и иной способ описания выпуклости и вогнутости кривой.
Будем называть график функции в точке вогнутым (выпуклым), если в окрестности точки М он расположен выше (ниже) касательной к кривой в этой точке (рис. 11.18).
|
Рис. 11.18. Расположение кривой по отношению А) расположение касательной к вогнутой кривой; Б) расположение касательной к выпуклой кривой. |
ТЕОРЕМА 3. Если функция в интервале имеет положительную (отрицательную) вторую производную, то кривая на этом интервале вогнута (выпукла).
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольную точку с в интервале и покажем, что при точки графика функции, соответствующие значениям аргумента х, близлежащим к с, будут располагаться выше точек касательной к кривой , Проведенной в точке (рис. 11.18). Уравнение касательной имеет вид:
Где – Ордината ее произвольной точки.
Найдем разность ординат кривой и касательной к ней при одном и том же значении х, близком к с :
Здесь мы применили теорему Лагранжа к разности ,
К разности , рассматриваемой на отрезке , снова применим теорему Лагранжа. Получим:
Где .
Если , то поэтому
,
И при условии, что , имеем
При
И так как , то
Таким образом, любая точка кривой Лежит выше касательной, что и требовалось доказать.
Аналогично доказывается выпуклость графика при
Точка графика функции называется Точкой перегиба, если при переходе через нее кривая меняет свою выпуклость на вогнутость, или же наоборот. Последующие теоремы определяют критерии существования перегиба.
ТЕОРЕМА 4 (НЕОБХОДИМОЕ УСЛОВИЕ ПЕРЕГИБА). Если функция имеет в окрестности внутренней точки c области определения вторую непрерывную производную и точка , лежащая на графике функции, является точкой перегиба, то
ДОКАЗАТЕЛЬСТВО.
|
Может ли точка экстремума совпадать с точкой перегиба? |
Предположим противное:
|
Можно ли утверждать, что между двумя точками экстремума функции лежит хотя бы одна точка перегиба? |
В силу непрерывности найдется окрестность точки С, в которой сохраняет знак, то есть график функции будет либо выпуклым, либо вогнутым, а потому точка не может быть точкой перегиба.
Полученное противоречие доказывает утверждение теоремы
|
Можно ли утверждать, что между двумя точками перегиба лежит хотя бы одна точка экстремума? |
.
|
Графиком функции на отрезке является выпуклая кривая, причем . Может ли она иметь экстремум на этом промежутке? |
Данная теорема позволяет отнести к точкам, где следует ожидать перегиб графика функции , те точки ее области определения, в которых Однако множество точек, подозрительных на перегиб, может быть расширено за счет тех, в которых обращается в бесконечность или вовсе не существует. На рис. 11.19 указаны возможные случаи перегиба графика функции.
Укажем достаточные условия перегиба графика функции.
|
Рис. 11.19. Возможные случаи перегиба графика Функции . |
ТЕОРЕМА 5 (ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА). Если при переходе через точку c, подозрительную на перегиб графика функции , вторая производная меняет знак, то точка графика есть точка перегиба.
ДОКАЗАТЕЛЬСТВО.
Из условия теоремы следует, что левее точки – кривая выпуклая (вогнутая), а правее ее – вогнутая (выпуклая). Значит, – точка перегиба.
Приведем без доказательства еще два признака перегиба графика функции.
ТЕОРЕМА 6. Если функция такова, что в точке с , а и конечна, то ее график в точке имеет перегиб.
Следующая теорема является более общей.
ТЕОРЕМА 7. Если функция в некоторой окрестности точки с имеет производную до (N+1)-го порядка, непрерывную в самой точке С, причем а , то при нечетном (n+1) График функции в точке будет иметь перегиб.
Рассмотрим примеры.
Найдем точки перегиба функции .
Выше получено:
.
Условие приводит нас к уравнению
|
Можно ли с помощью второй производной исследовать функцию на монотонность? |
Которое имеет решения:
|
Какая из производных несет большую информацию о свойствах функции – первая или вторая? |
Исследуем эти точки, подозрительные на перегиб. Очевидно, что
для
|
Есть ли функции, у которых: А) вторая производная изменяется, как и сама функция; Б) функция не совпадает с первой производной, но первая и вторая ее производные совпадают между собой? |
И ;
для
,
|
Дана функция, являющаяся второй производной некоторой функции. |
Укажите функции, имеющие такую же вторую производную.Следовательно, для и кривая вогнута; для кривая выпукла, а точки графика и являются точками перегиба.
Данная функциональная зависимость встречается часто в теории вероятностей. Она известна под названием кривой Гаусса. Ее график изображен на рис. 11.20.
|
Рис. 11.20. График функции . |
Вернемся теперь еще раз к функции .
Ее вторая производная имеет вид:
Условие
Приводит нас к уравнению
Которое имеет корни
Являющиеся абсциссами точек графика данной функции, подозрительных на перегиб.
Теорема 7 позволяет достаточно просто их исследовать. Имеем:
Следовательно, точка является точкой перегиба графика кривой .
А потому и точка также является точкой перегиба. График данной функции схематично изображен на рис. 11.21.
|
Рис. 11.21. График функции . |
| < Предыдущая | Следующая > |
|---|
AC Вторая производная
Мотивирующие вопросы
Как производная функции говорит нам, возрастает или убывает функция на интервале?
Что мы можем узнать, взяв производную от производной ( второй производной) функции \(f\text{?}\)
Что значит сказать, что функция вогнута вверх или вогнута вниз? Как эти характеристики связаны с некоторыми свойствами производной функции?
В каких единицах измеряется вторая производная? Как они помогают нам понять скорость изменения скорости изменения?
Для данной дифференцируемой функции \(y= f(x)\text{,}\) мы знаем, что ее производная \(y = f'(x)\text{,}\) является родственной функцией, выход которой \(x=a\) сообщает нам наклон касательной к \(y = f(x)\) в точке \((a,f(a))\text{.
}\) То есть высоты на графике производной сообщают нам значения наклонов на графике исходной функции.
В точке, где \(f'(x)\) положительно, наклон касательной к \(f\) положителен. Следовательно, на интервале, где \(f'(x)\) положительно, функция \(f\) возрастает (или возрастает). Точно так же, если \(f'(x)\) отрицательно на интервале, график \(f\) убывает (или падает).
Производная от \(f\) говорит нам не только о том, возрастает или убывает функция \(f\) на интервале, но также о том, как функция \(f\) возрастает или убывает. Посмотрите на две касательные линии, показанные на рисунке 1.6.1. Мы видим, что вблизи точки \(A\) значение \(f'(x)\) положительно и относительно близко к нулю, а вблизи этой точки график медленно растет. Напротив, вблизи точки \(B\text{,}\) производная отрицательна и относительно велика по модулю, а \(f\) быстро убывает вблизи \(B\text{.}\)
Рисунок 1.6.1. Две касательные линии на графике.Помимо вопроса о том, является ли значение производной функции положительным или отрицательным, а также большим или малым, мы также можем спросить: «Как изменяется производная?»
Поскольку производная \(y = f'(x)\text{,}\) сама по себе является функцией, мы можем взять ее производную — производную от производной — и спросить: «Что говорит производная от производной нам о том, как ведет себя исходная функция?» Начнем с исследования движущегося объекта.
Предварительный просмотр 1.6.1.
Положение автомобиля, движущегося по прямой дороге в момент времени \(t\) в минутах, определяется функцией \(y = s(t)\), изображенной на рисунке 1.6.2. Функция положения автомобиля измеряется в тысячах футов. Например, точка \((2,4)\) на графике указывает на то, что за 2 минуты автомобиль проехал 4000 футов.
Рисунок 1.6.2. График \(y = s(t)\text{,}\) положения автомобиля (измеряемого в тысячах футов от его начального местоположения) в момент времени \(t\) в минутах.Обыденным языком опишите поведение автомобиля на указанном интервале времени. В частности, следует тщательно обсудить, что происходит на каждом из временных интервалов \([0,1]\text{,}\) \([1,2]\text{,}\) \([2,3 ]\text{,}\) \([3,4]\text{,}\) и \([4,5]\text{,}\) плюс общий комментарий о том, что машина делает на интервале \([0,12]\текст{.}\)
На левых осях, представленных на рисунке 1.6.3, нарисуйте аккуратный и точный график \(y = s'(t)\text{.
}\)Что означает функция \(y = s'(t)\) в контексте данной задачи? Что мы можем сказать о поведении автомобиля, когда \(s'(t)\) положительно? когда \(s'(t)\) равно нулю? когда \(s'(t)\) отрицательно?
Переименуйте функцию, которую вы нарисовали в (b), так, чтобы она называлась \(y = v(t)\text{.}\) Опишите поведение \(v\) словами, используя такие фразы, как «\(v\) возрастает на интервале \(\ldots\)» и «\(v\) постоянно на интервале \(\ldots\text{.}\)»
Нарисуйте график функции \(y = v'(t)\) на правой оси, представленной на рисунке 1.6.3. Напишите хотя бы одно предложение, чтобы объяснить, как поведение \(v'(t)\) связано с графиком \(y=v(t)\text{.}\)
}\)Подраздел 1.6.1 Увеличение или уменьшение
До сих пор мы интуитивно использовали слова , увеличивающие , и , уменьшающие , для описания графика функции. Здесь мы определим эти термины более формально.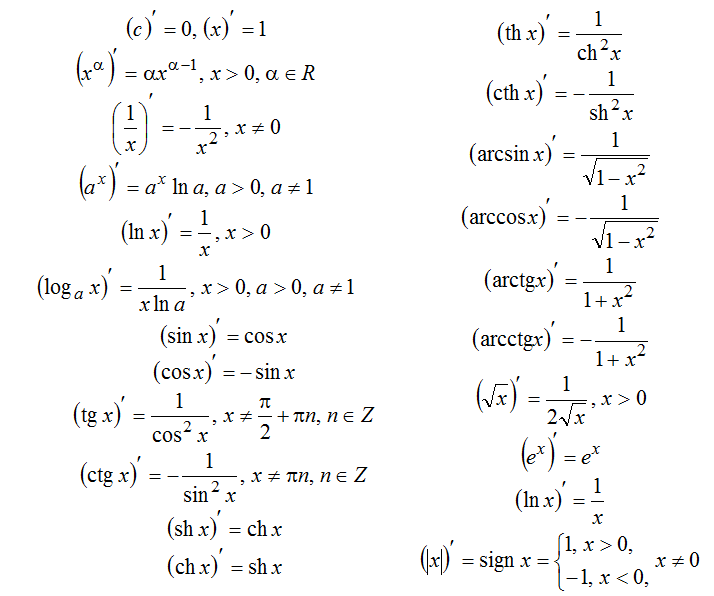
Определение 1.6.4.
Для данной функции \(f(x)\), определенной на интервале \((a,b)\text{,}\), мы говорим, что \(f\) возрастает на \((a,b)\ ) при условии, что для всех \(x\text{,}\) \(y\) в интервале \((a,b)\text{,}\) if \(x \lt y\text{,} \) тогда \(f(x) \lt f(y)\text{.}\) Аналогично, мы говорим, что \(f\) убывает на \((a,b)\) при условии, что для всех \(x\text{,}\) \(y\) в интервале \((a,b)\text{,}\) если \(x \lt y\text{,}\), то \(f (x) \gt f(y)\text{.}\)
Проще говоря, возрастающая функция — это функция, возрастающая по мере движения слева направо по графику, а убывающая функция — функция, уменьшающаяся по мере увеличения входного значения. Если у функции есть производная, то знак производной говорит нам, является ли функция возрастающей или убывающей.
Пусть \(f\) — функция, дифференцируемая на отрезке \((a,b)\text{.}\) Можно показать, что если \(f'(x) > 0\) для каждый \(x\) такой, что \(a \lt x \lt b\text{,}\), то \(f\) возрастает на \((a,b)\text{;}\) аналогично, если \(f'(x) \lt 0\) на \((a,b)\text{,}\), то \(f\) убывает на \((a,b)\text{.
}\)
Например, функция, изображенная на рис. 1.6.5, возрастает на всем интервале \(-2 \lt x \lt 0\text{,}\) и убывает на интервале \(0 \lt x \lt 2\ text{.}\) Обратите внимание, что значение \(x = 0\) не включено ни в один из интервалов, поскольку в этом месте функция меняется с возрастающей на убывающую.
Рисунок 1.6.5. Функция, убывающая на промежутках \(-3 \lt x \lt -2\) и \(0 \lt x \lt 2\) и возрастающая на \(-2 \lt x \lt 0\) и \ (2 \lt x \lt 3\text{.}\)Подраздел 1.6.2 Вторая производная
Теперь мы привыкли исследовать поведение функции, исследуя ее производную. Производная функции \(f\) — это новая функция, заданная правилом
\begin{уравнение*} f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}\text{.} \end{уравнение*}
Поскольку \(f’\) сама по себе является функцией, для нас вполне возможно рассмотреть производную производной, которая является новой функцией \(y = [f'(x)]’\text{.}\ ) Назовем полученную функцию вторую производную от \(y = f(x)\text{,}\) и обозначим вторую производную через \(y = f»(x)\text{.
}\). Следовательно, иногда мы будем называть \(f’\) «первая производная» от \(f\text{,}\), а не просто «производная» от \(f\text{.}\)
Определение 1.6.6.
Вторая производная определяется предельным определением производной первой производной. То есть
\begin{уравнение*} f»(x) = \lim_{h \to 0} \frac{f'(x+h)-f'(x)}{h}\text{.} \end{уравнение*}
Смысл функции производной сохраняется, поэтому при вычислении \(y = f»(x)\text{,}\) эта новая функция измеряет наклоны касательных к кривой \(y = f'( x)\text{,}\), а также мгновенную скорость изменения \(y = f'(x)\text{.}\) Другими словами, точно так же, как первая производная измеряет скорость, с которой исходная функция изменяется, вторая производная измеряет скорость изменения первой производной. Вторая производная поможет нам понять, как меняется сама скорость изменения исходной функции.
Подраздел 1.6.3 Вогнутость
В дополнение к вопросу о том, возрастает или убывает функция, естественно также спросить о том, как функция возрастает или убывает.
Есть три основных поведения, которые возрастающая функция может демонстрировать на интервале, как показано на рисунке 1.6.7: функция может возрастать все быстрее, она может увеличиваться с той же скоростью или она может увеличиваться медленно. вниз. По сути, мы начинаем думать о том, как изгибается конкретная кривая, с естественным сравнением с линиями, которые вообще не изгибаются. Более того, мы хотим понять, как изгиб графика функции связан с поведением, характеризуемым первой производной функции.
На самой левой кривой на рисунке 1.6.7 нарисуйте последовательность касательных линий к кривой. По мере того, как мы движемся слева направо, наклон этих касательных линий будет увеличиваться. Следовательно, скорость изменения изображенной функции увеличивается, и это объясняет, почему мы говорим, что эта функция увеличивается с возрастающей скоростью .
Для крайнего правого графика на рисунке 1.6.7 обратите внимание, что по мере увеличения \(x\) функция увеличивается, но наклоны касательных линий уменьшаются. Эта функция увеличивается с убывающей скоростью .
Аналогичные варианты относятся к уменьшению функции. Здесь мы должны быть особенно осторожны с нашим языком, потому что убывающие функции предполагают отрицательный наклон. Отрицательные числа представляют интересное противоречие между обычным языком и математическим языком. Например, может возникнуть соблазн сказать, что «\(-100\) больше, чем \(-2\текст{.}\)». Но мы должны помнить, что «больше чем» описывает, как числа лежат на числовой прямой: \(x \gt y\) при условии, что \(x\) лежит справа от \(y\text{.}\). Конечно, \(-100\) меньше, чем \(-2\text{ .}\) Неформально может быть полезно сказать, что «\(-100\) более отрицательно, чем \(-2\text{.}\)». Когда значения функции отрицательны, и эти значения становятся более отрицательными по мере вход увеличивается, функция должна быть убывающей.
Теперь рассмотрим три графика, показанные на рисунке 1.6.8. Ясно, что средний график изображает функцию, уменьшающуюся с постоянной скоростью. Теперь на первой кривой нарисуйте последовательность касательных линий. Мы видим, что наклоны этих линий становятся все менее и менее отрицательными по мере нашего движения слева направо. Это означает, что значения первой производной, хотя и отрицательные, увеличиваются, поэтому мы говорим, что самая левая кривая равна 9.0011 уменьшается с возрастающей скоростью .
Остается рассмотреть только крайнюю правую кривую на рис. 1.6.8. Для этой функции наклоны касательных линий отрицательны на всем изображенном интервале, но по мере движения слева направо наклоны становятся все более и более отрицательными. Следовательно, наклон кривой уменьшается, и мы говорим, что функция убывает с убывающей скоростью .
Теперь мы вводим понятие вогнутости , которое обеспечивает более простой язык для описания этих поведений.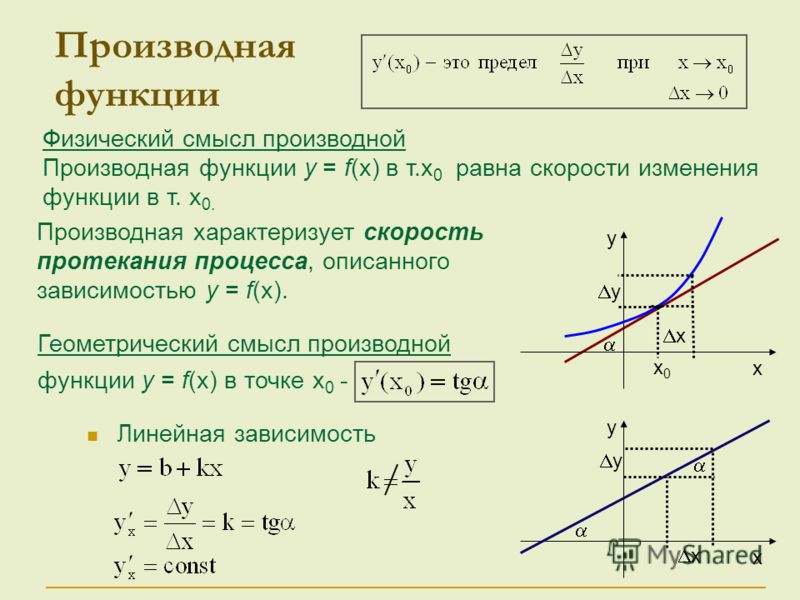
x\text{,}\), мы говорим, что кривая 9{x}\text{,}\) мы говорим, что функция вогнута вниз . Вогнутость связана как с первой, так и со второй производной функции.
На рис. 1.6.9 мы видим две функции и последовательность касательных линий к каждой из них. На левом графике, где функция вогнута, обратите внимание, что касательные линии всегда лежат ниже самой кривой, а наклоны касательных линий увеличиваются по мере движения слева направо. Другими словами, функция \(f\) является вогнутой на показанном интервале, потому что ее производная \(f’\text{,}\) возрастает на этом интервале. Аналогично, на правом графике на рисунке 1.6.9, где показанная функция вогнута вниз, мы видим, что касательные линии всегда лежат выше кривой, а наклоны касательных линий уменьшаются по мере нашего движения слева направо. Тот факт, что его производная \(f’\text{,}\) убывает, делает \(f\) вогнутой вниз на интервале.
Рисунок 1.6.9. Слева — вогнутая вверх функция; справа, вогнутый вниз. Мы формулируем эти самые последние наблюдения формально, поскольку определения терминов вогнуты вверх, и вогнуты вниз 9.
0012 .
Определение 1.6.10.
Пусть \(f\) — дифференцируемая функция на отрезке \((a,b)\text{.}\). Тогда \(f\) вогнута вверх на \((a,b)\), если и только если \(f’\) возрастает на \((a,b)\text{;}\) \(f\) вогнут вниз на \((a,b)\) тогда и только тогда, когда \(f’\) убывает на \((a,b)\text{.}\)
Мероприятие 1.6.2.
Положение автомобиля, движущегося по прямой дороге в момент времени \(t\) в минутах, определяется функцией \(y = s(t)\), изображенной на рисунке 1.6.11. Функция положения автомобиля измеряется в тысячах футов. Помните, что вы работали с этой функцией и рисовали графики \(y = v(t) = s'(t)\) и \(y = v'(t)\) в предварительном просмотре 1.6.1.
Рисунок 1.6.11. График \(y = s(t)\text{,}\) положения автомобиля (измеряемого в тысячах футов от его начального местоположения) в момент времени \(t\) в минутах.На каких интервалах функция положения \(y = s(t)\) возрастает? уменьшается? Почему?
На каких интервалах функция скорости \(y = v(t) = s'(t)\) возрастает? уменьшается? ни один? Почему?
Ускорение определяется как мгновенная скорость изменения скорости, поскольку ускорение объекта измеряет скорость изменения скорости объекта.
Скажем, функция ускорения автомобиля называется \(a(t)\text{.}\) Как \(a(t)\) вычисляется из \(v(t)\text{?}\) Как \( a(t)\) вычисляется из \(s(t)\text{?}\) Объясните.Что вы можете сказать о \(s»\) всякий раз, когда \(s’\) возрастает? Почему?
Используя только слова возрастающее , убывающее , постоянное , вогнутое вверх , вогнутое вниз и линейное , завершите следующие предложения. Для функции положения \(s\) со скоростью \(v\) и ускорением \(a\text{,}\)
на интервале, где \(v\) положительно, \(s\) равно .
на интервале, где \(v\) отрицательно, \(s\) равно .
на интервале, где \(v\) равно нулю, \(s\) равно .
на интервале, где \(a\) положителен, \(v\) равен .
на интервале, где \(a\) отрицательно, \(v\) равно .
на интервале, где \(a\) равно нулю, \(v\) равно .
на интервале, где \(a\) положителен, \(s\) равен .
на интервале, где \(a\) отрицательно, \(s\) равно .
на интервале, где \(a\) равно нулю, \(s\) равно .
Скажем, функция ускорения автомобиля называется \(a(t)\text{.}\) Как \(a(t)\) вычисляется из \(v(t)\text{?}\) Как \( a(t)\) вычисляется из \(s(t)\text{?}\) Объясните.
Изучение контекста положения, скорости и ускорения — отличный способ понять, как функция, ее первая и вторая производные связаны друг с другом. В упражнении 1.6.2 мы можем заменить \(s\text{,}\) \(v\text{,}\) и \(a\) на произвольную функцию \(f\) и ее производные \(f ‘\) и \(f»\text{,}\) и, по существу, все те же самые наблюдения. В частности, обратите внимание, что следующие условия эквивалентны: на интервале, где график \(f\) вогнут вверх, \(f’\) возрастает, а \(f»\) положителен. Точно так же на интервале, где график \(f\) вогнут вниз, \(f’\) убывает, а \(f»\) отрицательна.
Мероприятие 1.6.3.
Картофель помещают в печь, измеряют температуру картофеля \(F\) (в градусах по Фаренгейту) в различные моменты времени и записывают в следующую таблицу. Время \(t\) измеряется в минутах. В упражнении 1.
5.2 мы вычислили приближения к \(F'(30)\) и \(F'(60)\), используя центральные разности. Эти значения представлены во второй таблице ниже вместе с несколькими другими, рассчитанными таким же образом.
Таблица 1.6.12. Выберите значения \(F(t)\text{.}\)
| \(т\) | \(Ф(т)\) |
| \(0\) | \(70\) |
| \(15\) | \(180.5\) |
| \(30\) | \(251\) |
| \(45\) | \(296\) |
| \(60\) | \(324,5\) |
| \(75\) | \(342,8\) |
| \(90\) | \(354,5\) |
Таблица 1.6.13. Выберите значения \(F'(t)\text{.}\)
| \(т\) | \(Ф'(т)\) |
| \(0\) | нет данных |
| \(15\) | \(6.03\) |
| \(30\) | \(3,85\) |
| \(45\) | \(2,45\) |
| \(60\) | \(1,56\) |
| \(75\) | \(1. 00\) |
| \(90\) | нет данных |
В каких единицах выражены значения \(F'(t)\text{?}\)
Используйте центральную разность для оценки значения \(F»(30)\text{.}\)
Что означает значение \(F»(30)\), которое вы вычислили в (b), в зависимости от температуры картофеля? Напишите несколько аккуратных предложений, в которых с соответствующими единицами обсуждаются значения \(F(30)\text{,}\) \(F'(30)\text{,}\) и \(F»(30) \text{,}\) и объясните общее поведение температуры картофеля в этот момент времени.
В целом температура картофеля увеличивается с возрастающей скоростью, с постоянной скоростью или с убывающей скоростью? Почему?
Мероприятие 1.6.4.
Это упражнение основано на нашем опыте и понимании того, как набросать график \(f’\) по графику \(f\text{.}\)
На рисунке 1.6.14, учитывая соответствующие графики двух разных функций \(f\text{,}\), нарисуйте соответствующий график \(f’\) на первых осях ниже, а затем нарисуйте \(f» \) на втором наборе осей.
Кроме того, для каждого напишите несколько аккуратных предложений в духе предложений из упражнения 1.6.2, которые связывают поведение \(f\text{,}\) \(f’\text{,}\) и \(f »\text{.}\) Например, напишите что-то вроде
\(f’\) находится на интервале , что связано с тем, что \(f\) находится на том же интервале , а \(f»\) находится на интервале.
, но, конечно, с заполненными пробелами. Всюду рассматривайте масштаб сетки для графика \(f\) как \(1 \times 1\text{,}\) и примите горизонтальный масштаб сетки для графика \(f’\) идентичен графику для \(f\text{.}\) Если вам нужно настроить вертикальный масштаб по осям для графика \(f’\) или \(f »\text{,}\) вы должны пометить это соответствующим образом.
Рисунок 1.6.14. Две заданные функции \(f\text{,}\) с осями для построения графиков \(f’\) и \(f»\) ниже.Подраздел 1.6.4 Резюме
Дифференцируемая функция \(f\) возрастает на отрезке, если ее первая производная положительна, и убывает, когда ее первая производная отрицательна.
Взяв производную от производной функции \(f\text{,}\), мы получим вторую производную, \(f»\text{.}\) Вторая производная измеряет мгновенную скорость изменения первой производной. Знак второй производной говорит нам, увеличивается или уменьшается наклон касательной к \(f\). 9х\текст{.}\)
Единицы второй производной — это «единицы выпуска на единицу ввода на единицу ввода». Они говорят нам, как значение производной функции изменяется в ответ на изменения входных данных. Другими словами, вторая производная сообщает нам скорость изменения скорости изменения исходной функции.
Упражнения 1.6.5 Упражнения
1. Сравнение значений \(f, f’, f»\).
Рассмотрим функцию \(f(x)\), показанную ниже.
Для этой функции следующие ненулевые величины положительны или отрицательны?
\(f(3)\) равно
положительный
отрицательный
\(f'(3)\) равно
положительный
отрицательный
\(f»(3)\) равно
положительный
отрицательный
(Поскольку это задача с несколькими вариантами ответов, она не покажет, какие части задачи верны, а какие нет, когда вы отправляете ее.
)
2. Знаки величин \(f, f’, f»\).
Ровно в двух отмеченных точках на рисунке ниже, который показывает функцию \(f\text{,}\), производная \(f’\) равна нулю; вторая производная \(f»\) не равна нулю ни в одной из отмеченных точек. Выберите правильные знаки для каждого из \(f\text{,}\) \(f’\) и \(f»\) в каждой отмеченной точке.
| Точка | А | Б | С | Д | Е |
| \(ж\) |
|
|
|
|
|
| \(ж’\) |
|
|
|
|
|
| \(ж»\) |
|
|
|
|
|
3.
Ускорение от скорости.Предположим, что разгоняющийся автомобиль разгоняется с 0 до 64,1 миль в час за пять секунд. Его скорость указана в следующей таблице в пересчете из миль в час в футы в секунду, так что все измерения времени даны в секундах. (Примечание: 1 миля в час равна 22/15 футам/сек.) Найдите среднее ускорение автомобиля в течение первых двух секунд.
| \(т\) (с) | 0 | 1 | 2 | 3 | 4 | 5 |
| \(v(t)\) (фут/с) | 0,00 | 32,05 | 55,55 | 72,64 | 85,45 | 94.00 |
среднее ускорение за первую секунду =
среднее ускорение за вторую секунду =
4. Скорость изменения стоимости акций.
Пусть \(P(t)\) представляет собой цену акции корпорации в момент времени \(t\text{.}\) Что каждое из следующих утверждений говорит нам о знаках первого и второго производные от \(P(t)\text{?}\)
(a) Цена акции падает все медленнее и медленнее.
Первая производная \(P(t)\) равна
положительная
ноль
отрицательный
Вторая производная \(P(t)\) равна
положительная
ноль
отрицательный
(b) Цена акции близка к минимуму.
Первая производная \(P(t)\) равна
положительная
ноль
отрицательный
Вторая производная \(P(t)\) равна
положительная
ноль
отрицательный
5. Интерпретация графика \(f’\).
График \(f’\) (, а не \(f\)) приведен ниже.
(Обратите внимание, что это график \(f’\text{,}\), а не график \(f\text{.}\))
При каком из отмеченных значений \(x\)
A. \(f(x)\) наибольшее? \(x =\)
B. \(f(x)\) наименьшее? \(x =\)
C.
\(f'(x)\) наибольшее? \(x =\)
D. \(f'(x)\) наименьшее? \(x =\)
E. \(f»(x)\) наибольшее? \(x =\)
F. \(f»(x)\) наименьшее? \(х =\)
6.
Предположим, что \(y = f(x)\) — дважды дифференцируемая функция такая, что \(f»\) непрерывна, для которой известна следующая информация: \(f(2) = -3\text{ ,}\) \(f'(2) = 1,5\текст{,}\) \(f»(2) = -0,25\текст{.}\)
Является ли \(f\) возрастающим или убывающим вблизи \(x = 2\text{?}\) Является ли \(f\) вогнутым вверх или вогнутым вниз вблизи \(x = 2\text{?}\)
Ожидаете ли вы, что \(f(2.1)\) будет больше, чем \(-3\text{,}\), равно \(-3\text{,}\) или меньше, чем \(-3\text {?}\) Почему?
Ожидаете ли вы, что \(f'(2.1)\) будет больше, чем \(1.5\text{,}\), равно \(1.5\text{,}\) или меньше, чем \(1.5\text{? }\) Почему?
Нарисуйте график \(y = f(x)\) вблизи \((2,f(2))\) и включите график касательной.
7.
Для некоторой функции \(y = g(x)\text{,}\) ее производная задается функцией, изображенной на рисунке 1.6.15.
Рисунок 1.6.15. График \(y = g'(x)\text{.}\)Каков приблизительный наклон касательной к \(y = g(x)\) в точке \((2, г(2))\текст{?}\)
Сколько вещественных решений может быть у уравнения \(g(x) = 0\text{?}\) Обоснуйте свой вывод полностью и тщательно, объяснив, что вы знаете о том, как график \(g\) должен вести себя на основе заданного графика \(g’\text{.}\)
Сколько раз на интервале \(-3 \lt x \lt 3\text{,}\) изменяется вогнутость \(g\)? Почему?
Используйте предоставленный график для оценки значения \(g»(2)\text{.}\)
8.
Высота банджи-джампера \(h\) (в футах) в момент времени \(t\) (в секундах) частично указана в таблице:
| \(т\) | \(0.0\) | \(0,5\) | \(1.0\) | \(1,5\) | \(2. 0\) | \(2,5\) | \(3.0\) | \(3,5\) | \(4.0\) | \(4,5\) | \(5.0\) |
| \(ч(т)\) | \(200\) | \(184.2\) | \(159.9\) | \(131.9\) | \(104.7\) | \(81.8\) | \(65,5\) | \(56.8\) | \(55,5\) | \(60.4\) | \(69.8\) |
| \(т\) | \(5,5\) | \(6.0\) | \(6,5\) | \(7.0\) | \(7,5\) | \(8.0\) | \(8,5\) | \(9.0\) | \(9,5\) | \(10.0\) |
| \(ч(т)\) | \(81.6\) | \(93,7\) | \(104.4\) | \(112.6\) | \(117.7\) | \(119.4\) | \(118.2\) | \(114.8\) | \(110.0\) | \(104.7\) |
Используйте полученные данные для оценки \(h'(4.5)\text{,}\) \(h'(5)\text{,}\) и \(h'(5.
5)\text{.} \) В какой момент времени банджи-джампер поднимается быстрее всего?Используйте данные и вашу работу в (а) для оценки \(h»(5)\text{.}\)
Какое физическое свойство банджи-джампера измеряет значение \(h»(5)\)? Каковы его единицы?
Исходя из данных, на каких примерных интервалах времени функция \(y = h(t)\) вогнута вниз? Что происходит со скоростью банджи-джампера в эти промежутки времени?
5)\text{.} \) В какой момент времени банджи-джампер поднимается быстрее всего?9.
Для каждой последующей подсказки нарисуйте возможный график функции на интервале \(-3 \lt x \lt 3\), который удовлетворяет указанным свойствам.
\(y = f(x)\) такое, что \(f\) возрастает на \(-3 \lt x \lt 3\text{,}\) вогнуто вверх на \(-3 \lt x \lt 0\text{,}\) и вогнут вниз на \(0 \lt x \lt 3\text{.}\)
\(y = g(x)\) такое, что \(g\) возрастает на \(-3 \lt x \lt 3\text{,}\) вогнуто вниз на \(-3 \lt x \ lt 0\text{,}\) и вогнут на \(0 \lt x \lt 3\text{.}\)
\(y = h(x)\) такое, что \(h\) убывает на \(-3 \lt x \lt 3\text{,}\) вогнуто вверх на \(-3 \lt x \ lt -1\text{,}\) не вогнут вверх и не вогнут вниз на \(-1 \lt x \lt 1\text{,}\) и не вогнут вниз на \(1 \lt x \lt 3\text{ .
}\)\(y = p(x)\) такое, что \(p\) убывает и вогнуто вниз на \(-3 \lt x \lt 0\) и возрастает и вогнуто вниз на \(0 \lt x \lt 3\текст{.}\)
}\)4.2 Применение второй производной – методы исчисления 1
Вторая производная и вогнутость
Вторая производная функции предоставляет информацию о том, как изменяется первая производная, и приводит к выводам относительно вогнутости графика.
Графически функция вогнута вверх , если ее график искривлен отверстием вверх (a на рисунке). Точно так же функция является вогнутой вниз , если ее график открывается вниз (б) на рис. 4.10).
Рисунок 4.10Подробное описание: Левый график обозначен как (a) и показан вогнутой вверх кривой. Правый график обозначен как (b) и показывает вогнутую кривую вниз.
На этом рисунке показана вогнутость функции в нескольких точках. Обратите внимание, что функция может быть вогнутой независимо от того, возрастает она или убывает.
Важно понимать разницу между возрастающими/убывающими характеристиками и вогнутостью графика.
В качестве примера этой разницы обратите внимание на левую часть рисунка 3.4, которая помечена как «вогнутая вверх»: эта часть графика сначала уменьшается, а затем увеличивается, несмотря на то, что этот участок графика вогнут вверх.
Рисунок 4.11Подробное описание: левая часть графика помечена как вогнутая вверх, центральная часть графика помечена как вогнутая вниз, а правая часть графика помечена как вогнутая вверх.
Например, Эпидемия: Предположим, началась эпидемия, и вы, как член конгресса, должны решить, эффективно ли текущие методы борются с распространением болезни или нужны более радикальные меры и больше денег. На приведенном ниже рисунке f(x) — это количество людей, больных этим заболеванием в момент времени x, и показаны две разные ситуации. Как в (а), так и в (б) количество людей с болезнью f (сейчас) и скорость, с которой заболевают новые люди, f’ (сейчас), одинаковы.
Разница в этих двух ситуациях заключается в вогнутости f, и эта разница вогнутости может сильно повлиять на ваше решение.
Подробное описание: Левая часть графика обозначена как (a) и показывает вогнутый вниз график с соответствующей касательной линией. Правая часть графика помечена как (b) и показывает вогнутый график с соответствующей касательной линией.
На (а) f вогнута вниз в «сейчас», наклоны уменьшаются, и кажется, что она сходит на нет. Мы можем сказать, что «f увеличивается с убывающей скоростью». Похоже, что нынешние методы начинают брать эпидемию под контроль.
В (b) f вогнута вверх, наклоны увеличиваются, и похоже, что она будет расти все быстрее и быстрее. Похоже, эпидемия все еще вышла из-под контроля.
Различия между графиками связаны с тем, увеличивается или уменьшается производная. Производная функции f — это функция, которая дает информацию о наклоне f. Производная говорит нам, увеличивается или уменьшается исходная функция.
Поскольку [latex]f ‘[/latex] — это функция, мы можем взять ее производную. Эта вторая производная также дает нам информацию о нашей исходной функции f. Вторая производная дает нам математический способ сказать, как изогнут график функции. Вторая производная говорит нам, является ли исходная функция вогнутой вверх или вниз. 92}.[/latex] Читается вслух как «вторая производная от f».
Если [latex]f ‘ ‘(x)[/latex] положителен на интервале, график [latex]y = f (x)[/latex] будет вогнутым вверх по на этом интервале. Мы можем сказать, что f увеличивается (или уменьшается) с возрастающей скоростью.
Если [latex]f ‘ ‘(x)[/latex] отрицательно на интервале, график [latex]y = f (x)[/latex] будет вогнутым вверх по на этом интервале.
Можно сказать, что f увеличивается (или уменьшается) с убывающей скоростью.
Точки перегиба
Определение
Точка перегиба – это точка на графике функции, в которой вогнутость функции изменяется с вогнутой вверх на нижнюю или с вогнутой вниз на верхнюю.
Пример 1
Какие из отмеченных точек на графике ниже являются точками перегиба?
Рисунок 4.13 Подробное описание: изменение вогнутости в точках b и g. В точках a и h график вогнут вверх с обеих сторон. В точках c и f график вогнут вниз с обеих сторон. В точке e граф вогнут вниз с обеих сторон.
Вогнутость меняется в точках b и g. В точках a и h график вогнут с обеих сторон, поэтому вогнутость не меняется. В точках c и f график вогнут вниз с обеих сторон. В точке e, хотя график там выглядит странно, график вогнут вниз с обеих сторон — вогнутость не меняется.
Точки перегиба возникают при изменении вогнутости. Поскольку мы знаем связь между вогнутостью функции и знаком ее второй производной, мы можем использовать это для нахождения точек перегиба.
Рабочее определение
Точка перегиба — это точка на графике, в которой вторая производная меняет знак.
Чтобы вторая производная менял знак, она должна быть либо равна нулю, либо быть неопределенной.
Таким образом, чтобы найти точки перегиба функции, нам нужно только проверить точки, в которых [latex]f »(x)[/latex] равен 0 или не определен.
Обратите внимание, что недостаточно, чтобы вторая производная была равна нулю или была неопределенной. Нам еще нужно проверить, что знак [latex]f’’[/latex] меняет знак. Функции в следующем примере иллюстрируют, что может произойти. 9{–\frac53}[/латекс] . [latex]h»[/latex] не определен, если [latex]x = 0,[/latex], но [latex]h »(\;отрицательное \;число) > 0[/latex] и [latex] ч »(\;положительное \;число)
Пример 3
Нарисуйте график функции с [латекс]f(2) = 3, f ‘(2) = 1,[/латекс] и точкой перегиба в [латекс](2,3) .[/latex]
Здесь показаны два возможных решения.
Подробное описание: На каждом графике показана касательная, пересекающая график в точке (2, 3). Крайний левый график вогнут вниз, затем переключается на вогнутость вверх в точке (2, 3). Крайний правый график вогнут вверх, затем переключается на вогнутость вниз в точке (2, 3).