Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Решить неопределенный интеграл
Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте.
Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу.
Ответы
| |||||||||||
03.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Группа богословов преподаёт в религиозном образовательном учреждении дисциплину, связанную с обоснованием вероучения. Они не только ссылаются на
Сколько существует прямоугольников со сторонами, параллельными осям координат, таких что круг радиуса дробь 1/2 с центром (12;19) попадает
Маша сложила нить пополам, получившуюся двойную нить снова сложила пополам, а затем еще раз пополам.
После этого она разрезала в некотором месте
Решено
Помогите, пожалуйста!!! Очень важно!!! 1)В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 9 раз больше, чем с зеленым. Найдите
Найдите площадь прямоугольного треугольника с гипотенузой 4 и углом 15
Пользуйтесь нашим приложением
Найти неопределенный интеграл dx x 3 1. Решение неопределённых интегралов. Вводная к интегралам
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел.
Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции.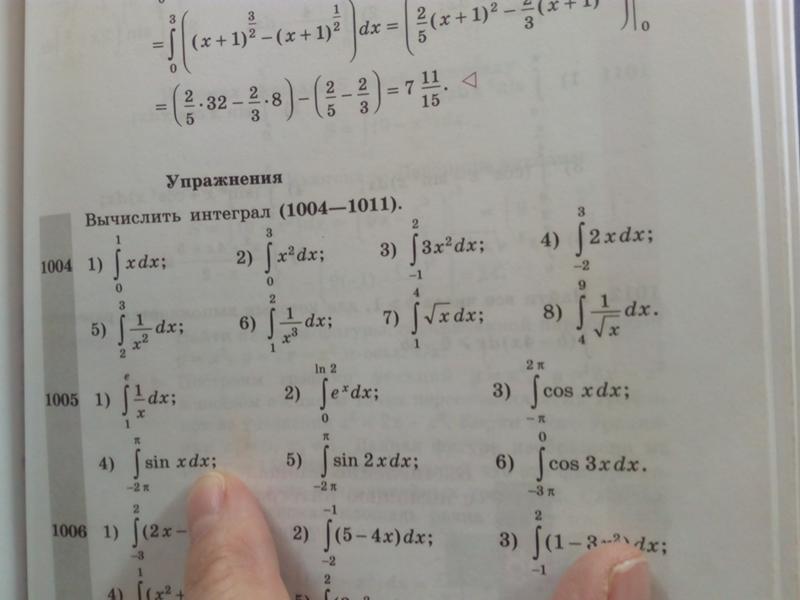
Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Решить неопределенный интеграл
Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания.
Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Интеграция по частям
Интеграция по частям
Вывод интегрирования по частям
Вспомним правило произведения:
(uv)’ = u’ v + uv’
или
uv’ = (uv)’ — u’ v
Объединяя обе стороны, мы получаем
ув’ дх
= (ув.
)’
дх — и’
в дх
= uv — u’ в дх.
Теорема: интегрирование по частям Пусть ты и v — дифференцируемые функции, то |
Примеры
Интегрировать
Раствор
Мы используем интеграцию по частям. Обратите внимание, что нам нужно использовать подстановку, чтобы найти интеграл e x .
| и = х | dv= e 3x dx |
| ду = дх | v = 1/3 e 3x |
Отсюда имеем
Упражнение
Оценка
x ln x dx
Двойное интегрирование по частям
Пример
Оценка
x 2 e x dx
Используем интегрирование по частям
| и = х 2 | дв = е х дх |
| ду = 2x dx | v = е х |
У нас есть
x 2 e x — 2xe x dx = x 2 e x — 2xe x dx
Мы никуда не ушли? Теперь мы теперь используем интегрирование по частям во второй раз найти этот интеграл
| и = х | дв = е х дх |
| ду = дх | v = е х |
Получаем
x 2 e x — 2xe x + 2e x dx
= x 2 e x — 2xe x + 2e x + C
Другое по частям
Иногда нет очевидной пары u и
дв.
Здесь мы
проявите творческий подход.
Пример:
Найти
ln х дх
Что мы должны позволить U и DV быть? Пытаться
| и = ln х | дв = дх |
| du = 1/x dx | v = х |
Получаем
х lnx — дх = x lnx — x + C
Когда использовать интеграцию по частям
- Когда u-подстановка не работает
- При наличии комбинации двух типов функций, таких как экспоненциальная и полиномиальные, полиномиальные и логарифмические и т. д.
- С пер. Икс.
- Когда ничего не помогает.
Вычисление определенного интеграла
Мы можем использовать интегрирование по частям для вычисления определенных интегралов.
Мы только
должны помнить, что все термины получают ограничения.
Пример
Оценить
Раствор
Использование интегрирование по частям
| и = ln х | дв = х 2 дх |
| du = 1/x dx | v = 1/3 x 3 |
Мы получить
Применение: Текущая стоимость
Ваш патент приносит вам годовой доход в размере 3000 т долларов, где t – количество лет, прошедших с момента начинается патент. Срок действия патента истекает через 20 годы. Компания предложила вам приобрести патент. Как много ли вы должны просить за это? Предположим, что уровень инфляции 5%.
Этот вопрос представляет собой проблему приведенной стоимости. Так как есть инфляция,
ваш более поздний заработок будет стоить меньше, чем заработок в этом году.
формула для определения этого дается
Формула текущей стоимости Если с(т) постоянный годовой доход за t 1 лет с уровнем инфляции r, то текущая стоимость может быть найдена с помощью |
Для наш пример, у нас есть
c(t) = 2000 t r = 0,05 t 1 = 20
Мы интегрировать
Использование интегрирование по частям и обратите внимание, что с заменой
u = -0,05t du = -0,05 dt 90 909
или
-20du = dt
мы получить
так что
| и = 2000т | дв = е -0,05т дт |
| ду = 2000 dt | v = -20e -0,05t |
Это дает нам
Мы
уже нашли первообразную для этого последнего интеграла.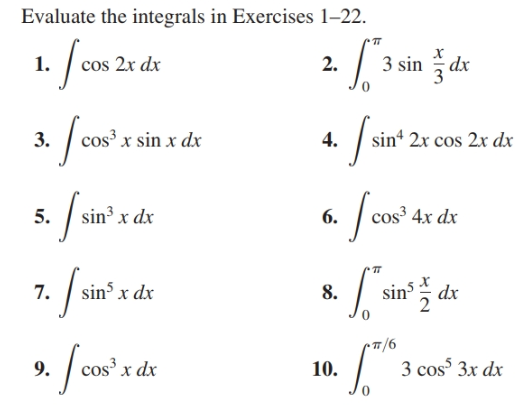
У нас есть
Вы стоит просить $211,393.
Назад на домашнюю страницу Math 116
Назад к математике Дом Департамента
электронная почта Вопросы и предложения
Исчисление II. Несобственные интегралы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-8: Несобственные интегралы
В этом разделе нам нужно рассмотреть пару различных видов интегралов. Оба они являются примерами интегралов, которые называются несобственными интегралами.
Начнем с первого вида несобственных интегралов, которые мы собираемся рассмотреть.
Бесконечный интервал
В этом виде интеграла один или оба предела интегрирования равны бесконечности. В этих случаях говорят, что интервал интегрирования превышает бесконечный интервал.
Давайте рассмотрим пример, который также покажет нам, как мы будем работать с этими интегралами. 9т = 1 — \фракция{1}{т}\]
Теперь мы можем получить площадь под \(f\left( x \right)\) на \(\left[ {1,\,\infty } \right)\), просто взяв предел \({ A_t}\) при стремлении \(t\) к бесконечности.
\[A = \mathop {\lim }\limits_{t \to \infty} {A_{\,t}} = \mathop {\lim }\limits_{t \to \infty} \left( {1 — \ frac{1}{t}} \right) = 1\]
Вот так мы и будем делать сам интеграл.
t\\ & = \mathop {\lim }\limits_{t \to \infty} \left( {1 — \frac{1}{t}} \right) = 1\end{align*}\]
Итак, вот как мы будем поступать с этими типами интегралов в целом. Мы заменим бесконечность переменной (обычно \(t\)), сделаем интеграл, а затем возьмем предел результата, когда \(t\) стремится к бесконечности.
Кстати, обратите внимание, что площадь под кривой на бесконечном интервале не равна бесконечности, как мы могли предположить. На самом деле, это было удивительно мало. Конечно, так будет не всегда, но достаточно важно отметить, что не все области на бесконечном интервале дадут бесконечные области.
Давайте теперь разберемся с некоторыми определениями. Мы будем называть эти интегралы сходящимися , если соответствующий предел существует и является конечным числом (, т.е. это не плюс или минус бесконечность), и расходящимся , если связанный предел либо не существует, либо равен (плюс или минус) бесконечности.
2}}}\,dx}}\]
9t \\ & = \ mathop {\ lim} \ limit_ {t \ to \ infty} \ left ({\ cos 2 — \ cos t} \ right) \ end {align *} \]
Этот предел не существует, поэтому интеграл расходится.
В большинстве примеров класса Calculus II, которые работают с бесконечными интервалами, предел либо существует, либо бесконечен. Однако есть пределы, которых не существует, как показал предыдущий пример, так что не забывайте о них.
Разрывное интегральное число
Теперь нам нужно рассмотреть второй тип несобственных интегралов, который мы рассмотрим в этом разделе. Это интегралы, имеющие разрывные подынтегральные выражения. Процесс здесь в основном такой же, с одним небольшим отличием. Вот общие случаи, которые мы рассмотрим для этих интегралов. 9{{\,b}}{{е\влево( х \вправо)\,dx}}\]
Где \(c\) — любое число. Опять же, это требует, чтобы ОБА интеграла были сходящимися, чтобы этот интеграл также был сходящимся.
Обратите внимание, что ограничения в этих случаях действительно должны быть правосторонними или левосторонними.
2}}}\,dx}}\]
Показать решение
Это интеграл по бесконечному интервалу, который также содержит разрывную подынтегральную функцию. Чтобы сделать этот интеграл, нам нужно разделить его на два интеграла, чтобы каждый интеграл содержал только одну точку разрыва. Важно помнить, что все процессы, с которыми мы работаем в этом разделе, поэтому каждый интеграл содержит только одну проблемную точку.
Мы можем разделить его где угодно, но выбрать значение, которое будет удобно для целей оценки. 9+ }} \left( { — 1 + \frac{1}{t}} \right)\\ & = \infty \end{align*}\]
Итак, первый интеграл расходится, а значит, расходится и весь интеграл.
Интегрирование x – формула, определение, примеры
Интегрирование x относится к процессу определения значения интеграла x с использованием различных методов интегрирования. Интегрирование можно определить как процесс нахождения первообразной функции.
Есть два основных метода найти интегрирование x. Это степенное правило и интегрирование по частям.
В этой статье мы вычислим определенный и неопределенный интеграл от x, найдем интегрирование x с помощью различных методов, а также изучим различные сопутствующие примеры.
| 1. | Чему равен интеграл от х? |
| 2. | Интеграция формулы x |
| 3. | Интеграция x с помощью Power Rule |
| 4. | Интеграция x с использованием интеграции по частям |
| 5. | Определенный интеграл от x |
| 6. | Часто задаваемые вопросы по интеграции x |
Что такое интегрирование x?
Интегрирование x относится к процессу нахождения первообразной x. Другими словами, интегрирование x — это то же самое, что нахождение первообразной x. Общая форма интегрирования задается как ∫f(x) dx.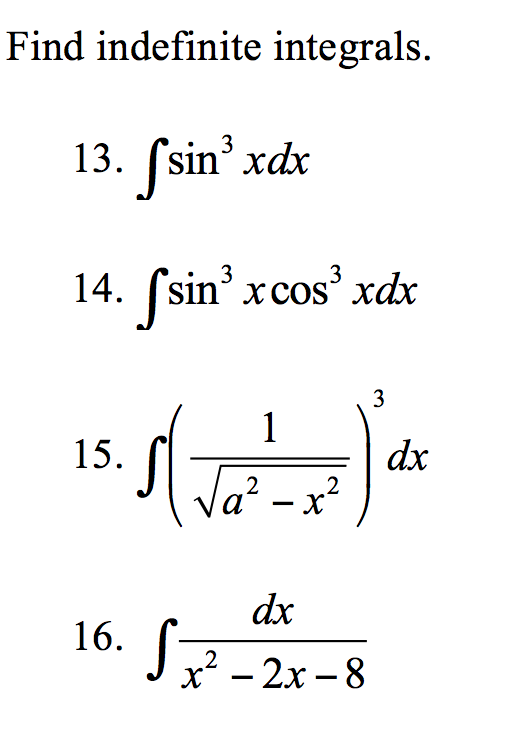
Здесь «∫» обозначает знак интегрирования. f(x) обозначает интегрируемую функцию, а dx используется для обозначения переменной, по которой интегрируется функция. Таким образом, интегрирование x представляется следующим образом: 9{2}}{2}\) + C. где C обозначает постоянную интегрирования. Интегралы используются для представления семейства кривых, что подразумевает, что значение интеграла не будет уникальным. Именно поэтому требуется постоянная интегрирования. Он используется, чтобы показать, что интегралы семейства кривых отличаются на постоянное число.
Интеграция x с использованием расширенного правила
Самый простой способ найти интеграл от x — использовать правило степени. Это правило гласит, что интеграл от x, возведенный в степень n, будет равен x, возведенному в степень n + 1, деленному на n + 1. Формула для степенного правила интегрирования дается следующим образом: 9{2}}{2}\) + номер телефона
Интеграция x с использованием интеграции по частям
Когда две функции представлены в виде произведения, то для вычисления значения интеграла используется интегрирование по частям.
{n+1}}{n+1} + C\), где n = 1,9{3+1}}{3+1} + C\) = x 4 / 4 + C
Что такое производная и интеграл от x?
Используя правило степени дифференцирования, производная от x будет равна 1. Интеграл от x равен (x 2 / 2) + C
Что обозначает C в интеграле от x?
C обозначает постоянную интегрирования в интеграле от x. Он используется, чтобы показать, что различные интегралы семейства кривых отличаются друг от друга на константу.
4.7: Определенные интегралы подстановкой.
- Последнее обновление
- Сохранить как PDF
- ID страницы
- 10314
Эта страница является черновиком и находится в активной разработке.
Замена для определенных интегралов
Замена может использоваться и для определенных интегралов.
Однако использование подстановки для вычисления определенного интеграла требует изменения пределов интегрирования. Если мы меняем переменные в подынтегральном выражении, то меняются и пределы интегрирования. 93)\,дх.\]
- Подсказка
Используйте процесс из примера для решения проблемы.
- Ответить
\(\dfrac{2}{3π}≈0,2122\)
Подстановка может быть только одним из методов, необходимых для вычисления определенного интеграла. Все свойства и правила интегрирования применяются независимо друг от друга, и, возможно, потребуется переписать тригонометрические функции с использованием тригонометрического тождества, прежде чем мы сможем применить подстановку. Кроме того, у нас есть возможность заменить исходное выражение для u после того, как мы найдем первообразную, что означает, что нам не нужно менять пределы интегрирования. Эти два подхода показаны в примере.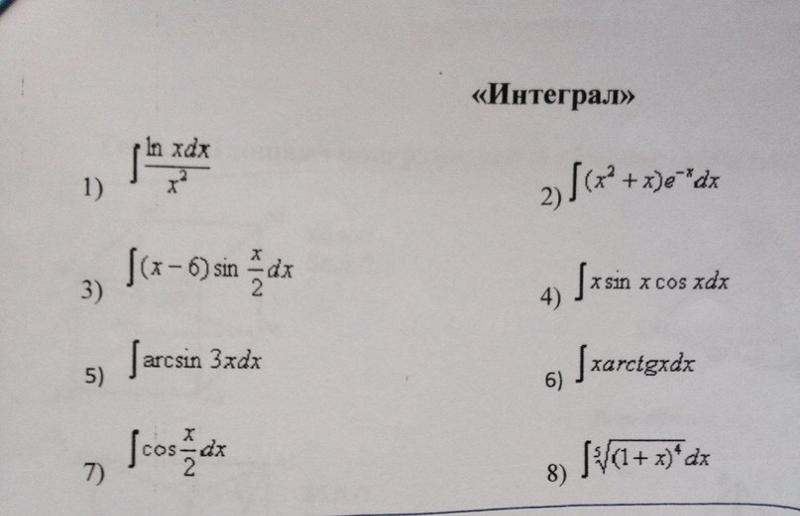
92}\).
- Подсказка
Для решения проблемы следуйте процедурам из примера.
- Ответить
\[ \dfrac{π}{8}\]
Как упоминалось в начале этого раздела, экспоненциальные функции используются во многих реальных приложениях. Число e часто ассоциируется с составным или ускоряющимся ростом, как мы видели в предыдущих разделах о производной. Хотя производная представляет собой скорость изменения или скорость роста, интеграл представляет собой общее изменение или общий рост. Давайте рассмотрим пример, в котором интеграция экспоненциальной функции решает обычное бизнес-приложение.
Функция «цена-спрос» сообщает нам о соотношении между объемом спроса на продукт и ценой на него. Как правило, цена снижается по мере увеличения объема спроса. Функция предельной цены-спроса является производной от функции цены-спроса и говорит нам, как быстро меняется цена при данном уровне производства.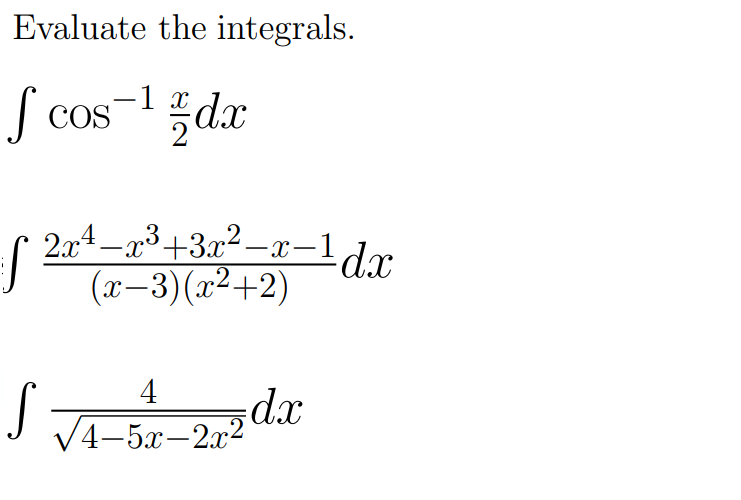
2}\ ,дх.\] 92_1=[\ln 2−\ln 1]=\ln 2\]
Ключевые понятия
- Подстановка — это метод, упрощающий интегрирование функций, являющихся результатом производной цепного правила. Термин «подстановка» относится к изменению переменных или замене переменных u и du на соответствующие выражения в подынтегральном выражении.
- При подстановке определенного интеграла приходится также менять пределы интегрирования.
Ключевые уравнения
- 9{g(b)}_{g(a)}f(u)du\)
Глоссарий
- замена переменных
- замена переменной, такой как u , на выражение в подынтегральном выражении
- интеграция путем замены
- метод интеграции, который позволяет интегрировать функции, являющиеся результатом производной цепочки правил
Авторы и авторство
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Лицензия
- CC BY-NC-SA
- Показать страницу Оглавление
- да
- Этап
- Проект
- Теги
- расчетный график:да
- юпитер: питон
Нижние и верхние индексы — оборотная сторона, онлайн-редактор LaTeX
Содержание
- 1 Введение
- 2 Более подробные примеры
- 3 Операторы, использующие нижние и верхние индексы
- 4 Открыть все фрагменты кода на обороте
- 5 Справочник
- 5.
- 5.
