Решение интегралов методом замены переменной
Метод замены переменной
С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.
Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.
Основная формула замены переменной
Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .
Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .
Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .
Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .
На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.
Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .
Важное замечание
В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое либо выражение.
И более того, в качестве переменной интегрирования может быть какое либо выражение.
В качестве примера рассмотрим табличный интеграл
.
Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.
В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.
В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.
Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;
.
Примеры интегрирования заменой переменной
1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда
.
Здесь мы применили подстановку t = sin x .
2) Вычислим интеграл
.
Замечаем, что . Тогда
Тогда
.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .
3) Проинтегрируем
.
Замечаем, что . Тогда
. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .
Линейные подстановки
Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.
Примеры интегрирования линейными подстановками
B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.
.
C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.
.
D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.
.
Интегрируем, применяя метод замены переменной .
.
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов . Опубликовано: 06-09-2015
Суть метода замены переменной
Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.
Вводится новая переменная, назовём её t . Например,
- в интеграле можем ввести новую переменную ;
- в интеграле можем ввести новую переменную ;
- в интеграле можем ввести новую переменную .
Далее dx определеяем как дифференциал по переменной t . После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x , находим данный интеграл окончательно.
Заменив обратно t на функцию от x , находим данный интеграл окончательно.
Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.
Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула
(1)
Формула (1) называется формулой замены переменной в неопределённом интеграле.
Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.
Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим.
Пример 1. Найти неопределённый интеграл методом замены переменной:
Решение. Производим замену x − 1 = t ; тогда x = t + 1 . Отсюда dx = dt . По формуле (1)
Возвращаясь к переменной x , окончательно получаем
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.
Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть

Пример 2. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим . Отсюда
.
По формуле (1)
.
Возвращаясь к переменной x, окончательно получаем
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Если трудно уследить, куда в процессе решения примера 2 делись и , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.
Пример 3. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим , откуда и .
Тогда , в свою очередь .
Заменяем переменную и получаем:
,
где степени при t складываются. Продолжаем преобразования и получаем:
Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:
Пример 4. Найти неопределённый интеграл методом замены переменной:
.
Пример 5. Найти неопределённый интеграл методом замены переменной:
.
Пример 6. Найти неопределённый интеграл методом замены переменной:
.
Пример 7. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим , откуда , , .
Тогда
(не забываем о правиле дифференцирования сложной функции).
Заменяем переменную и получаем:
.
Возвращаясь к переменной х, получаем ответ:
.
Проверить решение задач на неопределённый интеграл можно на
Пример 8. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим , откуда , .
Заменяем переменную и получаем:
Подставляя вместо t его выражение через x получаем ответ:
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Кому лишь смутно понятно или совсем не понятно, как преобразуются выражения в примере 5, пожалуйста, повторите из курса элементарной (школьной) математики действия с корнями, степенями и дробями!
И если вы ещё не открыли в новых окнах пособия Действия со степенями и корнями и Действия с дробями, то сделайте это сейчас!
Пример 9. Найти неопределённый интеграл методом замены переменной:
.
Решение. Положим , тогда
Заменяем переменную и получаем:
Решение с переменной t получено с использованием формулы 21 из таблицы интегралов.
Подставляя вместо t его выражение через x получаем ответ:
.
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ int f(x) dx $, сделаем замену $ x=phi(t) $. 5 x cos x dx =frac<1><6>sin x + C $$
5 x cos x dx =frac<1><6>sin x + C $$
| Пример 3 |
| Найти интеграл с помощью замены переменной: $$ int frac<cos sqrt><sqrt> dx $$ |
| Решение |
Интегрирование по частям и методом замены переменной
ПрактическАЯ РАБОТА№ 8
Тема: Техника интегрирования. Интегрирование методом замены переменной. Интегрирование по частям.
Цели:
Оснащение занятия: конспект лекций.
Критерии оценок
оценка «5» ставится за верное выполнение всех заданий работы
оценка «4» ставится за выполнение задания 1 и верное решение любых восьми примеров из задания 2.
оценка «3» ставится за выполнение задания 1 и верное решение любых шести примеров из задания 2.
Порядок выполнения работы
Задание 1.
— Ознакомиться с лекциями № 10 и № 11
— Выписать тетрадь примеры на применение метода замены переменной и метода интегрирования по частям при вычислении неопределенного интеграла
Задание 2.
Решить примеры для самостоятельного решения
Лекция 10.
Тема «Неопределенный интеграл. Метод замены переменной»
В основе интегрирования методом замены переменной лежит свойство инвариантности формул интегрирования, которое заключается в следующем: если,
то ,
где u(x) – произвольная дифференцируемая функция от х.
Замена переменной в неопределенном интеграле производится с помощью подстановок следующих двух типов:
1) х = (t), где t – новая переменная, а (t) – непрерывно дифференцируемая функция. В этом случае формула замены переменной такова:
(1)
Функцию (t) стараются выбирать таким образом, чтобы правая часть формулы (1) приобрела более удобный для интегрирования вид;
2) t = (x), где t – новая переменная. В этом случае формула замены переменной имеет вид:
Примеры.
1.
Решение. Данный интеграл окажется табличным, если под знаком дифференциала будет находиться аргумент 3х подынтегральной функции . Так как d(3x) = 3dx, то
=
Следовательно, подстановка 3х = t приводит рассматриваемый интеграл к табличному: = = = -cost + C
Возвращаясь к старой переменной х, окончательно получим
= -cos3х + C
2.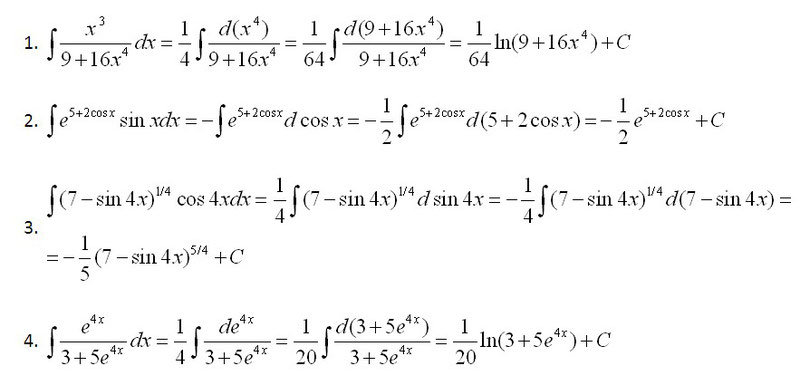
Решение. Так как d() = 3х2dx, то
Полагая = t, получим
+ C = + C.
3.
Решение. Поскольку d(sinx) = cosx, имеем
Поэтому, используя подстановку t = , приходим к табличному интегралу:
= = =
4.
Из соотношения d( получаем
=
Воспользовавшись подстановкой t = , приходим к табличному интегралу:
= = arcsin
5.
Решение. Здесь используем подстановку . Отсюда х = t3, dx = 3t2dt и, следовательно по формуле (1) находим
= = 3sin t + C
Возвращаясь к старой переменной х, получим
= 3sin + C
6.
Применим подстановку x = . Тогда dx = — , = , t =
Тогда dx = — , = , t =
По формуле (1) находим
= — = — = — ln + C
Возвращаясь к старой переменной х, получим
— ln + C = — ln + C = -ln + x
Примеры для самостоятельного решения
Вычислите интегралы, используя метод замены переменной:
1.
2.
3.
4.
5.
6.
Лекция 11.
Тема «Неопределенный интеграл. Интегрирование по частям».
Интегрированием по частям называется нахождение интеграла по формуле (1)
где и — непрерывно дифференцируемые функции от х. С помощью формулы (1) отыскание интеграласводится к нахождению другого интеграла, её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом в качестве берется функция, которая при дифференцировании упрощается, а в качестве — та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Так при нахождении интегралов вида
за следует принять многочлен, а за — соответственно выражения, ; при отыскании интегралов вида
за принимаются соответственно функции , а за — выражение .
Примеры.
1.
. Положим = lnx, = , откуда
du = , v =
Тогда по формуле (1) находим
= lnx( = — + = — — + С
2.
Решение. Полагая = = найдем du =,
v = =
Следовательно,
= =
3.
Решение. Пусть = , = du =, v =
По формуле (1) находим
= — (
К последнему интегралу снова применим формулу интегрирования по частям.
Положим =, = du =, v = и, следовательно, — =
Подставляя найденное выражение в соотношение (, получим
= (
4.
Положим = = , откуда du = , v =
Используя формулу (1), находим
=
= — х +
5.
Решение. Пусть = ; тогда du = — v = —
Согласно формуле (1) имеем
I = = = — . (
К последнему интегралу снова применяем интегрирование по частям. Полагая = , находим du = — v = и, следовательно, =
Подставляя полученное выражение в соотношение (приходим к уравнению с неизвестным интегралом I:
I = = — — – I,
Из которого находим
I = — (
Примеры для самостоятельного решения
Вычислите интегралы, используя метод интегрирования по частям:
1.
2.
3.
4.
5.
Контроль знаний обучающихся:
Требования к оформлению практической работы:
Задание должно быть выполнено в тетради для практических работ
Работу сдать после занятия
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда. Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 6Следующая ⇒ Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле. Пример 5 Найти неопределенный интеграл. В качестве примера я взял интеграл, который мы рассматривали в самом начале урока. Как мы уже говорили, для решения интеграла нам приглянулась табличная формула , и всё дело хотелось бы свести к ней. Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой. Итак: Действие следующее. После того, как мы подобрали замену, в данном примере, , нам нужно найти дифференциал . Так как , то После разборок с дифференциалом окончательный результат рекомендую переписать максимально коротко: В итоге:
Чистовое оформление рассмотренного примера должно выглядеть примерно так: “ Проведем замену:
Значок не несет никакого математического смысла, он обозначает, что мы прервали решение для промежуточных объяснений. Также всем рекомендую использовать математический знак вместо фразы «из этого следует это». И коротко, и удобно. При оформлении примера в тетради надстрочную пометку обратной замены лучше выполнять простым карандашом. Внимание! В следующих примерах нахождение дифференциала расписываться подробно не будет. А теперь самое время вспомнить первый способ решения: В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче. Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала. Пример 6 Найти неопределенный интеграл. Проведем замену: (другую замену здесь трудно придумать) Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.
Другое дело, что такое решение очевидно далеко не для всех студентов. Пример 7 Найти неопределенный интеграл. Выполнить проверку. Пример 8 Найти неопределенный интеграл. Замена: Готово. Пример 9 Найти неопределенный интеграл. Пример 10 Найти неопределенный интеграл. Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде. Настало время рассказать об основной предпосылке использования метода замены переменной: в подынтегральном выражении должна находиться некоторая функцияи её производная : (функции , могут быть и не в произведении) В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных. В рассматриваемом примере замечаем, что степень числителя на единицу меньше степени знаменателя. В таблице производных находим формулу , которая как раз понижает степень на единицу. А, значит, если обозначить за знаменатель, то велики шансы, что числитель превратится во что-нибудь хорошее. Замена: Кстати, здесь не так сложно подвести функцию под знак дифференциала: Следует отметить, что для дробей вроде , такой фокус уже не пройдет (точнее говоря, применить нужно будет не только прием замены). Интегрировать некоторые дроби можно научиться на уроке Интегрирование некоторых дробей. Вот еще пара типовых примеров для самостоятельного решения из той же оперы: Пример 11 Найти неопределенный интеграл. Пример 12 Найти неопределенный интеграл. Решения в конце урока. Пример 13 Найти неопределенный интеграл. Смотрим в таблицу производных и находим наш арккосинус: . У нас в подынтегральном выражении находится арккосинус и нечто похожее на его производную. Общее правило: В данном случае: . Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения . В этом примере нахождение я распишу подробно поскольку – сложная функция.
Таким образом: Вот здесь подвести функцию под знак дифференциала уже не так-то просто. Пример 14 Найти неопределенный интеграл. Пример для самостоятельного решения. Ответ совсем близко. Внимательные читатели заметили, что я рассмотрел мало примеров с тригонометрическими функциями. И это не случайно, поскольку под интегралы от тригонометрических функций отведён отдельный урок. Более того, на указанном уроке даны некоторые полезные ориентиры для замены переменной, что особенно актуально для чайников, которым не всегда и не сразу понятно, какую именно замену нужно проводить в том или ином интеграле. Также некоторые типы замен можно посмотреть в статье Определенный интеграл. Примеры решений. Более опытные студенты могут ознакомиться с типовой заменой в интегралах с иррациональными функциями. Замена при интегрировании корней является специфической, и её техника выполнения отличается от той, которую мы рассмотрели на этом уроке. Желаю успехов! Пример 3:Решение: Пример 4:Решение: Пример 7:Решение: Пример 9:Решение: Пример 11:Решение: Пример 12:Решение: Пример 14:Решение: Интегрирование по частям.
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статьюНеопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статьюМетод замены переменной в неопределенном интеграле)либо интеграл как раз на метод интегрирования по частям. Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений. Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы: . Зато есть такая: – формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче). И сразу список в студию. По частям берутся интегралы следующих видов: 1) , , – логарифм, логарифм, умноженный на какой-нибудь многочлен. 2) , – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». 3) , , – тригонометрические функции, умноженные на какой-нибудь многочлен. 4) , – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен. Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов Пример 1 Найти неопределенный интеграл. Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем: Прерываем решение на промежуточные объяснения. Используем формулу интегрирования по частям: ⇐ Предыдущая123456Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
1. Математика ППИ
Лекция 11.Неопределённый интеграл, его свойства .
Непосредственное интегрирование. Метод
замены переменной в неопределенном
интеграле. Интегрирование функций,
содержащих квадратный трехчлен
2. Математика ППИ
Лекция 11.Неопределённый интеграл . Методы
интегрирования: замена переменной.

3. Цели и задачи:
Дать понятие первообразной инеопределенного интеграла.
Изучить основные свойства
интеграла.
4. Цели и задачи:
Изучить основные методыинтегрирования:
интегрирование методом замены
переменной, по частям.
5. Вопросы лекции
1. Первообразная инеопределенный интеграл.
2. Основные свойства
неопределённого интегра.
3.Интегрирование
разложением, внесением под
знак дифференциала.
4. Метод замены переменной в
неопределенном интеграле.
Интегрирование функций,
содержащих квадратный
трехчлен.
6. ЛИТЕРАТУРА
[1] Н.С. Пискунов. Дифференциальноеи интегральное исчисления. Т 1.
Москва: Интеграл-Пресс, 2004. с. 340375;
[3] Б.П. Демидович, В.А. Кудрявцев.
Краткий курс высшей математики.
Москва: Издательство АСТ, 2004.. с.
229-275;
Интеграл (от лат. integer — целый), одно
из важнейших понятий математики. Оно
возникло в связи с потребностью, с одной
стороны, отыскивать функции по их
производным.

Например, находить функцию,
выражающую путь, пройденный
движущейся точкой, по скорости этой
точки.
А с другой — измерять площади, объёмы,
длины дуг, работу сил за определённый
промежуток времени и т. п. В
соответствии с этим различают
неопределённые и определённые
интегралы, вычисление которых является
задачей интегрального исчисления.
Немецкий учёный Г. Лейбниц
одновременно с английским учёным
И. Ньютоном и независимо от него
открыл основные принципы
дифференциального и
интегрального исчислений в 80-х
годах XVII века.
Теория приобрела силу после того,
как Лейбницем и Ньютоном было
доказано, что дифференцирование и
интегрирование –
взаимно обратные
операции.
Исаак Ньютон
(1643 – 1727)
Работы Коши и Вейерштрасса
подвели итог многовековому
развитию интегрального
исчисления.
Огюстен Луи Коши
(1789 – 1857)
Карл Теодор Вильгельм
Вейерштрасс (1815 -1897 )
Работы Коши и Вейерштрасса
подвели итог многовековому
развитию интегрального
исчисления.
Огюстен Луи Коши
(1789 – 1857)
Карл Теодор Вильгельм
Вейерштрасс (1815 -1897 )
14. Учебный вопрос.
Первообразная инеопределенный интеграл.
15. Первообразная и неопределённый интеграл.
Определение. Функция F(x) называетсяпервообразной для функции f(x) на отрезке
[a; b] если во всех точках этого отрезка
выполняется равенство F’(x)=f(x).
Пример. Найти первообразную от функции
f x x
2
Из определения первообразной следует, что
x3 . Действительно,
F ( x)
3
x3 1 3
1
F ‘( x) ‘ x ‘ 3x 2 x 2
3
3 3
Замечание. Задача отыскания функции по заданной
производной этой функции решается, например, в
инерциальных системах счисления пути самолёта. В
них с помощью акселерометров определяются
ускорения движения самолёта. По ускорениям
вычисляются скорости, а по скоростям – пройденный
самолётом путь с указанием его текущих координат.
Замечание. Легко видеть, что если для данной
функции f(x) существует первообразная, то эта
первообразная не является единственной.

Пример.
Рассмотрим функцию
f ( x) x 2 и найдём её первообразные.
Решение. Первообразные
1 3
F1 ( x) x
3
1 3
F2 ( x) x 1
3
1 3
F3 ( x) x 1
3
Теорема. Если F(x)
– первообразная
для функции f(x), то любая
первообразная для f(x) имеет вид
Ф(x)=F(x)+C, где C=const.
Доказательство. В силу определения
первообразной : F’(x)=f(x). Пусть Ф(x) – другая
первообразная, тогда Ф’(x)=f(x). Рассмотрим
функцию
.
Найдём
‘( x) F ( x) ( x) ‘ F ‘( x) ‘( x)
f ( x) f ( x) 0
Таким образом, производная равная нулю. Такое
возможно лишь если
, ( x) C
Следовательно, ( x) F ( x) ( x) C
F ( x ) ( x ) C
откуда
▲
Определение. Совокупность всех
первообразных F ( x) ( x) C для функции
f(x) на некотором интервале называется
неопределённым интегралом от функции
f(x) на этом интервале и обозначается
f x dx F x С
где — знак интеграла,
f x dx — подынтегральное выражение,
— подынтегральная функция.

Пример. cos( x)dx sin( x) C
Проверим результат:
sin x С
cos x
Отыскание всех первообразных для данной
функции или одной из них называется
интегрированием.
Интегрирование – есть действие, обратное
дифференцированию. С геометрической точки
зрения неопределённый интеграл представляет
совокупность (семейство) интегральных
кривых .
Естественно возникает вопрос: для всякой ли
функции f ( x )существуют первообразные, а значит
и неопределённый интеграл?
На этот вопрос отвечает теорема
существования неопределённого интеграла, которую
мы примем без доказательства.
Теорема. Если функция f ( x ) непрерывна на
некотором интервале, то для неё на этом
интервале существует первообразная, то
есть неопределённый интеграл.
23. УЧЕБНЫЙ ВОПРОС,
Основные свойстванеопределённого интеграла.
24. Основные свойства неопределённого интеграла.
1. Производная от неопределённогоинтеграла равна подынтегральной
функции: если F x f x ,
то
f x dx F x С f x
2.
 Дифференциал от неопределённого
Дифференциал от неопределённогоинтеграла равен подынтегральному
выражению, то есть
d
f x dx f x dx
3. Неопределённый интеграл от
дифференциала некоторой функции равен
этой функции, плюс произвольная
постоянная
d F x F x С
Справедливость последующего равенства
легко проверить дифференцированием
(дифференциалы от обеих частей равенства
равны
d F x
4. Неопределённый интеграл от
алгебраической суммы функций равен
алгебраической сумме интегралов от
слагаемых
(
f
(
x
)
g
(
x
))
dx
f ( x)dx g ( x)dx
5. Числовой множитель можно выносить
за знак неопределенного интеграла:
C
f
(
x
)
dx
C
f
(
x
)
dx
.
6. Свойство инвариантности (постоянства) формул
интегрирования.
Всякая формула интегрирования сохраняет
свой вид при подстановке вместо
независимой переменной любой
дифференцируемой функции,
т.е., если
f x dx F x С ,
то
f u du F u С
Доказательство.

Возьмём функцию
F u F x ;
для её дифференциала в силу теоремы об
инвариантности вида первого
дифференциала имеем:
d F u F u du f u du
отсюда
f u du
d F u F u С
▲
1
f (kx b)dx F (kx b) C
k
а. F(x) =Сх+С1
1.f(x) = хn
б. F(x) =
2.f(x) = C
в. F(x) =tg x+С
3.f(x)=sinx
1
4.f(x) = cos 2 x
г. F(x) = sin x+С
д. F(x) = сtg x+С
5.f(x) =cosx
6.f(x)=
x n 1
С
n 1
1
2
sin x
е. F(x) = — cos x+С
32. Таблица основных интегралов (через u(x)!)
1. u dxu
1
C , где 1
1
du
2.
u ln u C
3.
sin u dx cos u C
4.
cos u dx sin u C
5.
dx
cos2 u tg u C
6.
dx
sin 2 u ctgu C
7.
tgudu
ln
cos
u
C
8.
ctgudu
ln
sin
u
C
9.
e
du
e
C
u
u
u
a
10. a du
C
ln a
u
du
1
u
11.
arctg
C
2
2
a u a
a
du
1
a u
a2 u 2 2a ln a u C
dx
u
13.

a 2 u 2 arcsin a C
12.
14.
dx
u a
2
ln u u a C
2
2
2
15.
16.
du
u
ln
tg
C
sin u
2
du
u
cos u ln tg 2 4 C
Замечание. Таблица основных интегралов
в силу свойства инвариантности формул
интегрирования оказывается
справедливой независимо от того,
является ли переменная интегрирования
независимой переменной или любой
дифференцируемой функцией от неё.
Пример.
5
1
sin(5 x)dx sin(5 x) 5 dx sin(5 x) 5 d 5 x
5x t
1
1
sin(5 x)d 5 x
sin tdt
d (5 x) dt 5
5
1
1
cos t C cos 5 x C
5
5
Пример
4
3
(
x
3 х ) dx
cos 2 x
39. Найти интегралы для функций:
1) f(x) =10х2) f(x) =3 х²
3) f(x) = sinх+5
4) f(x) = 5cosx
5) f(x) = 6х²
6) f(x) = 3-2х
40. Верно ли что:
а)в)
x
dx
5
x
C
5
4
3
x
dx
x
C
2
г)
б)
3
x
dx
6
x
C
2
3
41.
 УЧЕБНЫЙ ВОПРОСИнтегрирование
УЧЕБНЫЙ ВОПРОСИнтегрированиеразложением, внесением
под знак дифференциала.
Непосредственное интегрирование вычисление интеграла с помощью
• его свойств,
• тождественных преобразований
подынтегральной функции,
• таблицы основных интегралов.
Использование при этом свойства
линейности неопределённого интеграла
называется методом разложения
вычисления интеграла.
Таблица основных интегралов в силу
.
свойства инвариантности формул
интегрирования оказывается
справедливой независимо от того,
является ли переменная
интегрирования независимой
переменной или дифференцируемой
функцией.
Например,
dx
1 5dx
1 d 5x
1
sin 2 5x 5 sin 2 5x 5 sin 2 5x 5 ctg5x C
Найти интеграл
2 x xe 4
dx
.
x
3
x
Решение:
2 x xe 4
2 x 4
dx
2
x
e
dx
x
x
3
x
dx 2 3 x
2 x dx e dx 4 x e 4ln x C.
x 3
2
x
Интегрирование внесением
под знак дифференциала.

Известно, что дифференциал функции
равен произведению производной этой
функции и дифференциала её аргумента:
x dx d x
Переход в этом равенстве слева
направо называют подведением
множителя x под знак
дифференциала.
46. Таблица дифференциалов
Пусть требуется найти интеграл видаf x x dx.
Подводя в этом интеграле множитель
x под знак дифференциала, а затем
используя свойство инвариантности
формул интегрирования, получим
x dx f x d x F x C ,
f
x
если
f
x
dx
F
x
C
.
Метод интегрирования введением под
знак дифференциала используется для
интегрирования сложных функций:
• аргумент сложной функции записывается
под знак дифференциала;
• затем необходимо разделить
подынтегральное выражение на
производную этого аргумента.
Пример. Найти интеграл
dx
2 x 3
5
2 x 3 dx
5
dx
2 x 3
5
2 x 3
.
d 2 x 3
2
5
1
5
2 x 3 d 2 x 3 .

2
Здесь подынтегральное выражение
разделено на 2, так как d 2x 3 2dx,
d 2 x 3
dx
.
2
Теперь используем свойство
инвариантности и применим формулу 1
таблицы относительно переменной
интегрирования 2х – 3.
dx
1 2 x 3
1
2 x 3 5 2 4 C C 8 2 x 3 4 .
4
Таким образом,
1
f
аx
b
dx
F
(
ax
b
)
C
,
где
F
(
x
)
f
(
x
a
Примеры.
1. F(x) =Сх+С1
1.f(x) = хn
2. F(x) =
2.f(x) = C
x n 1
С
n 1
3. F(x) = tg x+С
3.f(x)=sinx
1
4. F(x) = sin x+С
5.f(x) =cosx
5. F(x) = сtg x+С
4.f(x) = cos 2 x
6.f(x)=
1
2
sin x
6. F(x) = — cos x+С
53. УЧЕБНЫЙ ВОПРОС
Метод замены переменной внеопределенном интеграле.
Интегрирование функций,
содержащих квадратный трехчлен.
Замена переменной или подстановка.
Метод заключается во введении новой
переменной интегрирования.
При этом интеграл приводится к
новому интегралу, который является
табличным или к нему сводящимся (в
случае «удачной» подстановки).
Общих методов подбора подстановок
не существует.
Введём в интеграле f x dx новую
переменную t, положив x=φ(t), где φ(t) –
непрерывная, дифференцируемая
функция. Тогда dx=φ’(t) dt и справедливо
равенство
f x dx f t t dt
Это формула замены переменной
или метода подстановки. После этого
получим новый интеграл, который
проще приводится к табличному.
Доказательство.
Находим производную от левой части
равенства
.
f x dx
x
f x
Правую часть равенства будем
дифференцировать по x как сложную
функцию, где t – промежуточный аргумент,
при этом dx
и по правилу
dt
t
дифференцирования обратной функции
dt
1
dx t
Таким образом, имеем
dt
f
t
t
dt
f
t
t
dt
x
t dx
.
1
f t t
f t f x
t
Следовательно, производные по х от
правой и левой частей равенства равны,
что и требовалось доказать.
 ▲
▲Замечание 1. После интегрирования
в правой части равенства вместо t
необходимо подставить его выражение
через x на основании равенства x=φ(t).
Замечание 2. При замене
переменной функцию x=φ(t) надо
подбирать так, чтобы новый интеграл
стал проще.
Замечание 3. При интегрировании
иногда целесообразно подбирать
замену переменной не в виде x=φ(t), а в
виде t=ψ(x).
61. Интегрирование функций, содержащих квадратный трехчлен.
64. Задание на самостоятельную работу
[1] Н.С. Пискунов. Дифференциальное иинтегральное исчисления. Т 1. Москва: ИнтегралПресс, 2004, с. 340-375.
[3] Б.П. Демидович, В.А. Кудрявцев. Краткий
курс высшей математики. Москва: Издательство
АСТ, 2004, с. 229-250.
Выучить таблицу основных интегралов.
65. Математика ППИ
Лекция 12.Метод интегрирования по частям в
неопределенном интеграле. Интегрирование
тригонометрических функций
66. Вопросы лекции
1. Интегрирование по частям внеопределенном интеграле.

2. Интегрирование
тригонометрических функций.
УЧЕБНЫЙ ВОПРОС
Интегрирование по частям.
Одной из причин сложности операции
интегрирования является отсутствие
формулы интегрирования произведения
функций.
Есть метод интегрирования
произведения некоторых классов
функций, который называется методом
интегрирования по частям.
Выведем формулу интегрирования по
частям.
Пусть u=u(x) и v=v(x) –
дифференцируемые функции и
d u v udv vdu
Отсюда, интегрируя последнее
равенство, получаем:
u v udv vdu
или
udv
u
vdu
формулой интегрирования по частям.
Успех формулы интегрирования по
частям зависит от умения правильно разбить
подынтегральное выражение на множители u
и dv.
Как правило, за u выбирается функция,
которая при дифференцировании
упрощается.
Иногда необходимо применять
интегрирование по частям последовательно
несколько раз.
Укажем некоторые часто встречающиеся
интегралы, которые вычисляются методом
интегрирования по частям.

I. Интегралы вида:
P x ln xdx, P x log xdx, P x arcsin x dx, P x arccos xdx,
P x arctg xdx, P x arcctg xdx,
a
где P(x) – многочлен.
Во всех случаях за u при
интегрировании по частям применяют
функцию, являющуюся множителем
после P(x).
kx
P
x
e
dx,
kx
P
x
a
dx,
P x sin kx dx, P x cos kxdx,
Решение.
(опечатка
в du)
v
75. Контрольные вопросы:
1. В чем заключается метод непосредственногоинтегрирования ?
2. В чем заключается метод интегрирования
заменой?
3. В чем заключается метод интегрирования по
частям?
Метод замены переменной (способ подстановки). — МегаЛекции
Найти заданный неопределённый интеграл непосредственным интегрированием удаётся далеко не всегда, а иногда это сопряжено с большими трудностями. В таких случаях применяют другие способы интегрирования.
Одним из наиболее эффективных методов является способ подстановки или замены переменной интегрирования.
Сущность этого метода заключается в том, что путём введения новой переменной интегрирования удаётся свести заданный интеграл к новому интегралу, который сравнительно лёгко берётся непосредственно.
Алгоритм метода:
Пусть дан интеграл , который не является табличным.
1. Записываем уравнение замены
,
где — некоторая функция.
2. Находим дифференциал этой функции
.
3. Выражаем
.
4. Подставим и в данный интеграл:
.
Если замена выполнена правильно, то
будет табличным.
5. Находим
.
6. Чтобы получить окончательный ответ, вместо переменной подставляем выражение :
.
Пример 1. Найти .
Решение. Сделаем подстановку , тогда . Следовательно,
.
Пример 2. Найти .
Решение. Сделаем подстановку , тогда , следовательно,
.
Пример 3. Найти
Решение. Сделаем подстановку , тогда , следовательно,
.
Пример 4. Найти .
Решение. Сделаем подстановку , тогда , получаем
.
Пример 5. Найти .
Решение. Подстановка , тогда , получим
.
Пример 6. Найти .
Решение. Сделаем подстановку , тогда , следовательно,
.
Пример 7. Найти .
Решение. Сделаем подстановку , тогда , следовательно,
.
Пример 8. Найти .
Решение. Сделаем подстановку , тогда , получим
Пример 9. Найти .
Решение. Преобразуем подынтегральную функцию
= . Сделаем замену , тогда
, получим
= .
Пример 10. Найти .
Решение. Замена , тогда , получаем
.
Пример 11. Найти .
Решение. Сделаем замену , тогда получаем
.
Часто при нахождении неопределённых интегралов используются следующая теорема:
,
на основании которой может быть составлена следующая таблица интегралов от сложных функций, промежуточным аргументом которых является линейная функция:
Пользуясь данной таблицей можно в некоторых случаях, не применяя метод замены переменной, сразу получать конечный результат.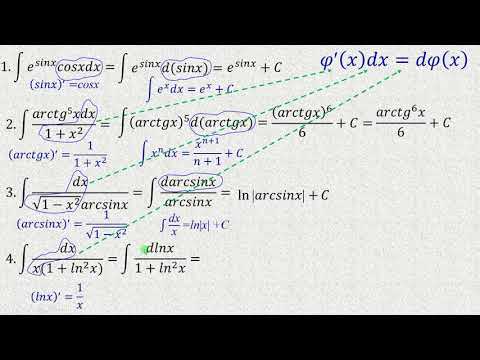
Упражнения.
Найти неопределённые интегралы методом замены переменной
№1 №2
№3 №4
№5 №6
№7 №8
№9 №10
№11. №12.
№13. №14.
№15. №16.
№17. №18.
№19. №20
№21. №22.
№ 23. №24.
№25 №26
№27. №28.
№29. №30
№31. №32
№33. №34.
Интегрирование по частям.
Интегрирование по частям – это, практически, формула интегрирования произведения двух функций.
Хорошо известна формула дифференциала произведения двух функций:
Проинтегрировав обе части данного равенства, получим:
,
т.к.
,
то
,
откуда
.
Последняя формула называется формулой интегрирования по частям.
Формула интегрирования по частям сводит нахождение интеграла к отысканию другого интеграла ; её применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо подобен ему.
При этом в качестве берётся функция, которую проще продифференцировать, а в качестве берётся та часть подынтегрального выражения, которую проще проинтегрировать. Иногда формулу интегрирования по частям приходиться использовать несколько раз.
При применении формулы интегрирования по частям интегралы можно разбить на 3 основные группы:
1. В интегралах вида
,
где — многочлен переменной , — число, полагают
2. В интегралах вида
полагают
3. В интегралах вида
за принимают любую функцию, за соответственно оставшуюся часть подынтегрального выражения.
Пример 1. Найти .
Решение. Данный интеграл относится к первой группе, поэтому
.
Пример 2. Найти .
Решение. Данный интеграл относится ко второй группе, поэтому положим
Тогда по формуле интегрирования по частям находим:
.
Пример 3. Найти .
Данный интеграл относится к первой группе, поэтому , по формуле интегрирования по частям имеем
.
Пример 4. Найти .
Решение. Интеграл относится к первой группе, поэтому , , тогда имеем
.
К последнему интегралу снова применим формулу интегрирования по частям, положив , тогда получим
.
Исходный интеграл равен
.
Пример5. Найти .
Решение. Данный интеграл относится ко второй группе, поэтому . По формуле интегрирования по частям получим
= .
Пример 6. Найти .
Решение. Данный интеграл относится к третьей группе, поэтому выбор и в данном случае произволен. Пусть , , тогда по формуле интегрирования по частям получим
.
Для второго интеграла применим ещё раз формулу интегрирования по частям:
,
тогда
.
Подставляя полученное выражение в соотношение для исходного интеграла, получим
.
Перенесём интеграл из правой части в левую, получим
Упражнения
Найти неопределённый интеграл методом интегрирования по частям:
№1. №2.
№2.
№3. №4.
№5. №6.
№7. №8
№9. №10.
Воспользуйтесь поиском по сайту:
Замена переменных в кратных интегралах · Исчисление
Замена переменных в нескольких интегралах · Исчисление- Определить образ области при заданном преобразовании переменных.
- Вычислить якобиан заданного преобразования.
- Вычислите двойной интеграл с помощью замены переменных.
- Вычислите тройной интеграл с помощью замены переменных.
Вызов из правила подстановки метода интегрирования подстановкой. При вычислении интеграла, такого как ∫23x(x2−4)5dx,
подставляем u=g(x)=x2−4.
Тогда du=2xdx
или xdx=12du
и пределы меняются на u=g(2)=22−4=0
и u=g(3)=9−4=5.
Таким образом, интеграл становится ∫0512u5du
, и этот интеграл гораздо проще вычислить.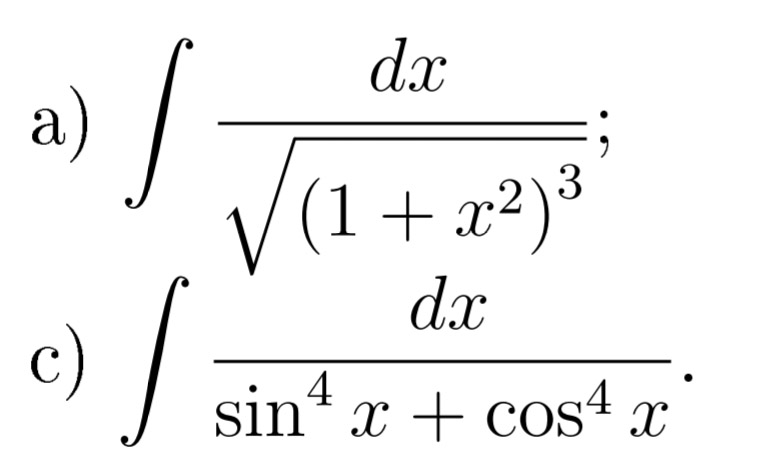 Другими словами, при решении задач интегрирования мы делаем соответствующие замены, чтобы получить интеграл, который становится намного проще исходного интеграла.
Другими словами, при решении задач интегрирования мы делаем соответствующие замены, чтобы получить интеграл, который становится намного проще исходного интеграла.
Мы также использовали эту идею, когда преобразовывали двойные интегралы в прямоугольных координатах в полярные координаты и тройные интегралы в прямоугольных координатах в цилиндрические или сферические координаты, чтобы упростить вычисления. В общем,
∫abf(x)dx=∫cdf(g(u))g′(u)du,
Где x=g(u),dx=g′(u)du,
и и=с
и u=d
удовлетворить c=g(a)
и d=g(b).
Аналогичный результат получается в двойных интегралах, когда мы заменяем x=f(r,θ)=rcosθ,
y=g(r,θ)=rsinθ,и dA=dxdy=rdrdθ.
Тогда мы получим
∬Rf(x,y)dA=∬Sf(rcosθ,rsinθ)rdrdθ
где домен R
заменен на домен S
в полярных координатах. Как правило, функция, которую мы используем для изменения переменных, чтобы упростить интеграцию, называется преобразование или отображение.
Планарные преобразования
A плоскостное преобразование T
— функция, преобразующая область G
в одной плоскости в область R
в другой плоскости заменой переменных. Оба G
и Р
являются подмножествами R2.
Например, [ссылка] показывает регион G
в уф-плоскости
преобразован в регион R
в плоскости xy
заменой переменных x=g(u,v)
и у=ч(и,в),
или иногда мы пишем x=x(u,v)
и y=y(u,v).
Обычно мы будем предполагать, что каждая из этих функций имеет непрерывные первые частные производные, что означает gu,gv,hu,
и хв
существуют и также являются непрерывными. Необходимость этого требования скоро станет очевидной.
Определение
Преобразование T:G→R,
определенное как T(u,v)=(x,y),
называется преобразованием «один к одному» , если никакие две точки не сопоставляются с одной и той же точкой изображения.
Чтобы показать, что Т
— взаимно однозначное преобразование, мы предполагаем, что T(u1,v1)=T(u2,v2)
и покажем, что как следствие получаем (u1,v1)=(u2,v2).
Если преобразование T
взаимно однозначно в домене G,
, то обратное T−1
существует с доменом R
такое, что T−1∘T
и T∘T−1
— это функции тождества.
[ссылка] показывает отображение T(u,v)=(x,y)
где х
и у
связаны с тобой
и v
по уравнениям x=g(u,v)
и y=h(u,v).
Регион Г
— это домен T
и регион R
это диапазон Т,
, также известный как изображение G
под преобразование Т.
Определение того, как работает трансформация
Предположим, что преобразование T
определено как T(r,θ)=(x,y)
, где x=rcosθ,y=rsinθ.
Найти образ полярного прямоугольника G={(r,θ)\|0 в плоскости rθ в область R в xy-плоскость. Покажите, что T является взаимно однозначным преобразованием в G , и найдите T−1(x,y). Поскольку r изменяется от 0 до 1 в плоскости rθ, мы имеем круговой диск с радиусом от 0 до 1 в плоскости xy. Поскольку θ изменяется от 0 до π/2 в плоскости rθ, мы получаем четверть окружности радиусом 1 в первом квадранте плоскости xy ([ссылка] ). Следовательно, R является четвертью окружности, ограниченной x2+y2=1 в первом квадранте. Чтобы показать, что T является взаимно однозначным преобразованием, предположим T(r1,θ1)=T(r2,θ2) и покажем, как следствие, что (r1,θ1)=( г2, θ2). В этом случае имеем T(r1,θ1)=T(r2,θ2),(x1,y1)=(x1,y1),(r1cosθ1,r1sinθ1)=(r2cosθ2,r2sinθ2),r1cosθ1=r2cosθ2 ,r1sinθ1=r2sinθ2. Разделив, получим r1cosθ1r1sinθ1=r2cosθ2r2sinθ2cosθ1sinθ1=cosθ2sinθ2tanθ1=tanθ2θ1=θ2 , так как функция тангенса является однозначной функцией в интервале 0≤2θ. Также, поскольку 0 имеем r1=r2,θ1=θ2. Следовательно, (r1,θ1)=(r2,θ2) и T является взаимно однозначным преобразованием из G в R. Чтобы найти T−1(x,y) , найдите r,θ через x,y. Мы уже знаем, что r2=x2+y2 и tanθ=yx. Таким образом, T−1(x,y)=(r,θ) определяется как r=x2+y2 и θ=tan−1(yx). Поиск изображения под
T Пусть преобразование T определяется формулой T(u,v)=(x,y) , где x=u2−v2 и y=uv. Найти изображение треугольника в uv-плоскости с вершинами (0,0),(0,1), и (1,1). Треугольник и его изображение показаны в [ссылка]. Чтобы понять, как трансформируются стороны треугольника, назовем сторону, соединяющую (0,0) и (0,1) , сторону A, стороной, соединяющей (0,0) и (1, 1) сторона B, и сторона, соединяющая (1,1) и (0,1) сторона C. Для стороны A:u=0,0≤v≤1 преобразуется в x=−v2,y=0 , так что это сторона A’ , которая соединяет (−1,0) и (0,0). Для стороны B:u=v,0≤u≤1 преобразуется в x=0,y=u2 , так что это сторона B′ , которая соединяет (0,0) и (0 ,1). Для стороны C:0≤u≤1,v=1 преобразуется в x=u2−1,y=u (отсюда x=y2−1) так что это сторона C′ что составляет верхнюю половину параболической дуги, соединяющей (−1,0) и (0,1). Все точки всей области треугольника в uv-плоскости отображаются внутри параболической области в xy-плоскости. Пусть преобразование T определено как T(u,v)=(x,y) , где x=u+v,y=3v. Найти изображение прямоугольника G={(u,v):0≤u≤1,0≤v≤2} из uv-плоскости после преобразования в область R в xy -самолет. Покажите, что T является взаимно однозначным преобразованием, и найдите T−1(x,y). T−1(x,y)=(u,v) , где u=3x−y3 и v=y3 Подсказка Выполните шаги [ссылка]. Напомним, что в начале этого раздела мы упоминали, что каждая из составляющих функций должна иметь непрерывные первые частные производные, а это означает, что gu,gv,hu, и хв существуют и также являются непрерывными. Преобразование, обладающее этим свойством, называется C1 (здесь C означает непрерывный). Пусть T(u,v)=(g(u,v),h(u,v)), , где х=g(u,v) и у=ч(и,в), быть один к одному C1 трансформация. Мы хотим посмотреть, как он трансформирует небольшую прямоугольную область S, ед. по Δv шт, в уф-плоскости (см. следующий рисунок). Так как x=g(u,v) и у=ч(и,в), у нас есть вектор положения r(u,v)=g(u,v)i+h(u,v)j изображения точки (u,v). Предположим, что (u0,v0) — это координата точки в левом нижнем углу, которая соответствует (x0,y0)=T(u0,v0). Строка v=v0 отображает кривую изображения с помощью векторной функции r(u,v0), и касательный вектор в точке (x0,y0) к кривой изображения ru=gu(u0,v0)i+hu(u0,v0)j=∂x∂ui+∂y∂uj. Аналогично строка u=u0 отображает кривую изображения с помощью векторной функции r(u0,v), и касательный вектор в точке (x0,y0) к кривой изображения rv=gv(u0,v0)i+hv(u0,v0)j=∂x∂vi+∂y∂vj. Обратите внимание, что ru=limΔu→0r(u0+Δu,v0)−r(u0,v0)Δusor(u0+Δu,v0)−r(u0,v0)≈Δuru. Аналогично, rv=limΔv→0r(u0,v0+Δv)−r(u0,v0)Δvsor(u0,v0+Δv)−r(u0,v0)≈Δvrv. Это позволяет нам оценить площадь ΔA изображения R путем нахождения площади параллелограмма, образованного сторонами Δvrv и Δуру. Путем перекрестного произведения этих двух векторов путем добавления k -й компонент как 0, площадь ΔA изображения R (см. В форме определителя перекрестное произведение равно ru×rv=\|ijk∂x∂u∂y∂u0∂x∂v∂y∂v0\|=\|∂x∂u∂y∂u∂x∂v∂y∂v\|k=( ∂x∂u∂y∂v−∂x∂v∂y∂u)k. Поскольку \|k\|=1, имеем ΔA≈\|ru×rv\|ΔuΔv=(∂x∂u∂y∂v−∂x∂v∂y∂u)ΔuΔv. Определение Якобиан преобразования C1 T(u,v)=(g(u,v),h(u,v)) обозначается J(u,v) и определяется определителем 2×2 J(u,v)=\|∂(x,y)∂(u,v)\|= \|∂x∂u∂y∂u∂x∂v∂y∂v\|=(∂x∂u∂y∂v−∂x∂v∂y∂u). Используя определение, мы имеем ΔA≈J(u,v)ΔuΔv=\|∂(x,y)∂(u,v)\|ΔuΔv. Обратите внимание, что якобиан часто обозначается просто J(u,v)=∂(x,y)∂(u,v). Обратите внимание, что \|∂x∂u∂y∂u∂x∂v∂y∂v\|=(∂x∂u∂y∂v−∂x∂v∂y∂u)=\|∂x∂u∂x ∂v∂y∂u∂y∂v\|. Отсюда обозначение J(u,v)=∂(x,y)∂(u,v) предполагает, что мы можем записать определитель Якоби с частями x в первой строке и части у во втором ряду. Нахождение якобиана Нахождение якобиана преобразования, приведенного в [ссылка]. Преобразование в примере T(r,θ)=(rcosθ,rsinθ) , где x=rcosθ и y=rsinθ. Таким образом, якобиан равен J(r,θ)=∂(x,y)∂(r,θ)=\|∂x∂r∂x∂θ∂y∂r∂y∂θ\|=\ |cosθ−rsinθsinθrcosθ\|=rcos2θ+rsin2θ=r(cos2θ+sin2θ)=r. Нахождение якобиана Нахождение якобиана преобразования, приведенного в [ссылка]. Преобразование в примере T(u,v)=(u2−v2,uv) , где x=u2−v2 и y=uv. Таким образом, якобиан равен J(u,v)=∂(x,y)∂(u,v)=\|∂x∂u∂x∂v∂y∂u∂y∂v\|=\ |2uv−2vu\|=2u2+2v2. Найдите якобиан преобразования, заданного в предыдущей контрольной точке: T(u,v)=(u+v,2v). J(u,v)=∂(x,y)∂(u,v)=\|∂x∂u∂x∂v∂y∂u∂y∂v\|=\|1102\|=2 Подсказка Выполните действия, описанные в двух предыдущих примерах. Мы уже видели, что при замене переменных T(u,v)=(x,y) , где х=g(u,v) и у=ч(и,в), небольшая область ΔA в плоскости xy относится к площади, образованной произведением ΔuΔv в уф-плоскости по приближению ΔA≈J(u,v)Δu,Δv. Теперь вернемся на минутку к определению двойного интеграла: ∬Rf(x,y)dA=limm,n→∞∑i=1m∑j=1nf(xij,yij)ΔA. Ссылаясь на [ссылка], обратите внимание, что мы разделили область S в уф-плоскости на маленькие подпрямоугольники Sij и пусть подпрямоугольники Rij в плоскости xy быть образами Сиджа при преобразовании T(u,v)=(x,y). Тогда двойной интеграл становится равным ∬Rf(x,y)dA=limm,n→∞∑i=1m∑j=1nf(xij,yij)∆A=limm,n→∞∑i=1m∑j=1nf(g(uij,vij) ,h(uij,vij))\|J(uij,vij)\|∆u∆v. Обратите внимание, что это в точности двойная сумма Римана для интеграла ∬Sf(g(u,v),h(u,v))\|∂(x,y)∂(u,v)\|dudv. Замена переменных для двойных интегралов Пусть T(u,v)=(x,y) , где x=g(u,v) и y=h(u,v) — единица. преобразование в одно C1 с ненулевым якобианом внутри области S в уф-плоскости; он отображает S в область R в плоскости xy. Если f непрерывно на R, , то ∬Rf(x,y)dA=∬Sf(g(u,v),h(u,v))\|∂(x,y) ∂(u,v)\|дудв. С помощью этой теоремы для двойных интегралов мы можем заменить переменные из (x,y) до (u, v) в двойном интеграле, просто заменив dA=dxdy=\|∂(x,y)∂(u,v)\|dudv , когда мы используем замены x=g(u,v) и у=ч(и,в) , а затем соответствующим образом измените пределы интегрирования. Такая замена переменных часто значительно упрощает любые вычисления. Изменение переменных с прямоугольных на полярные координаты Рассмотрим интеграл ∫02∫02x−x2x2+y2dydx. Используйте замену переменных x=rcosθ и y=rsinθ, и найдите полученный интеграл. Сначала нам нужно найти область интегрирования. Эта область ограничена снизу y=0 и выше на y=2x−x2 (см. следующий рисунок). Возводя в квадрат и собирая члены, получаем, что областью является верхняя половина круга x2+y2−2x=0, , то есть y2+(x−1)2=1. В полярных координатах окружность равна r=2cosθ , поэтому область интегрирования в полярных координатах ограничена 0≤r≤cosθ и 0≤θ≤π2. Якобиан равен J(r,θ)=r, , как показано в [ссылка]. Поскольку r≥0, имеем \|J(r,θ)\|=r. Подынтегральная функция x2+y2 изменяется на r в полярных координатах, поэтому двойной повторный интеграл равен |drdθ=∫0π/2∫02cosθr2drdθ. Рассматривая интеграл ∫01∫01−x2(x2+y2)dydx, используем замену переменных x=rcosθ и y=rsinθ, и находим полученный интеграл. ∫0π/2∫01r3drdθ Подсказка Выполните действия, описанные в предыдущем примере. Обратите внимание, что в следующем примере область, по которой мы должны интегрировать, может предложить подходящее преобразование для интеграции. Это распространенная и важная ситуация. Замена переменных Рассмотрим интеграл ∬R(x−y)dydx, где R — параллелограмм, соединяющий точки (1,2), (3,4),(4,3), и (6,5) ([ссылка]). Во-первых, нам нужно понять регион, в котором мы должны интегрироваться. Стороны параллелограмма равны x−y+1=0,x−y−1=0, x−3y+5=0 иx−3y+9=0 ([ссылка]). Другой способ взглянуть на них: x−y=−1,x−y=1, x−3y=−5, и x−3y=9. Ясно, что параллелограмм ограничен линиями y=x+1,y=x−1,y=13(x+5), и y=13(x+9). Обратите внимание, что если бы мы сделали u=x−y и v=x−3y, , то пределы интеграла были бы −1≤u≤1 и −9≤v≤−5. Чтобы найти x и y, , мы умножаем первое уравнение на 3 и вычитаем второе уравнение, 3u−v=(3x−3y)−(x−3y)=2x. Тогда мы имеем x=3u−v2. Более того, если мы просто вычтем второе уравнение из первого, мы получим u−v=(x−y)−(x−3y)=2y и y=u−v2. Таким образом, мы можем выбрать преобразование T(u,v)=(3u−v2,u−v2) и вычислить якобиан J(u,v). Имеем J(u,v)=∂(x,y)∂(u,v)=\|∂x∂u∂x∂v∂y∂u∂y∂v\|=\|3 /2−1/21/2−1/2\|=−34+14=−12. Следовательно, \|J(u,v)\|=12. Кроме того, исходное подынтегральное выражение принимает вид x−y=12[3u−v−u+v]=12[3u−u]=12[2u]=u. Следовательно, с помощью преобразования T, интеграл изменится на ∬R(x−y)dydx=∫−9−5∫−11J(u,v)ududv=∫−9−5∫ −11(12)ududv, , что гораздо проще вычислить. Сделать соответствующие замены переменных в интеграле ∬R4(x−y)2dydx, , где R — трапеция, ограниченная линиями x−y=2,x−y=4,x=0,andy=0. Запишите полученный интеграл. x=12(v+u) и y=12(v−u) и ∫−44∫−224u2(12)dudv. Подсказка Выполните действия, описанные в предыдущем примере. Мы готовы дать стратегию решения проблемы замены переменных. Стратегия решения проблем: замена переменных , а затем напишите уравнения кривых, образующих границу. и или в зависимости от того, что произойдет, на В следующем примере мы находим замену, которая значительно упрощает вычисление подынтегральной функции. Вычисление интеграла Используя замену переменных u=x−y и v=x+y, вычислить интеграл ∬R(x−y)ex2−y2dA, где R область, ограниченная линиями x+y=1 и x+y=3 и кривыми x2−y2=−1 и x2−y2=1 (см. первый регион в [ссылка]). Как и прежде, сначала найдите область R и изобразите преобразование, чтобы было легче получить пределы интегрирования после выполнения преобразований ([ссылка]). Учитывая u=x−y и v=x+y, , мы имеем x=u+v2 и y=v−u2 и, следовательно, используемое преобразование T(u,v )=(u+v2,v−u2). Строки x+y=1 и x+y=3 становятся v=1 и v=3, соответственно. Кривые x2-y2=1 и x2-y2=-1 становятся uv=1 и uv=-1, соответственно. Таким образом, мы можем описать область S (см. вторую область [ссылка]) как S={(u,v)\|1≤v≤3,−1v≤u≤1v}. Якобиан для этого преобразования равен J(u,v)=∂(x,y)∂(u,v)=\|∂x∂u∂x∂v∂y∂u∂y∂v\| =\|1/2−1/21/21/2\|=12. Следовательно, с помощью преобразования T, интеграл изменится на ∬R(x−y)ex2−y2dA=12∫13∫−1/v1/vueuvdudv. При оценке имеем 12∫13∫−1/v1/vueuvdudv=43e≈0,490. С помощью подстановок x=v и y=u+v, вычислить интеграл ∬Rysin(y2−x)dA , где R — область, ограниченная линиями y=x,x=2, энду=0. 12(sin2−2) Подсказка Нарисуйте рисунок и найдите пределы интегрирования. Замена переменных в тройных интегралах работает точно так же. Замены цилиндрических и сферических координат являются частными случаями этого метода, которые мы демонстрируем здесь. Предположим, что G — это регион в uvw-пространстве и сопоставлен с D в xyz-пространстве ([ссылка]) по индивидуальному C1 преобразование T(u,v,w)=(x,y,z) , где х=g(u,v,w), и z=k(u,v,w). Тогда любая функция F(x,y,z) определено на D можно рассматривать как другую функцию H(u,v,w) то что определяется на G: F(x,y,z)=F(g(u,v,w),h(u,v,w),k(u,v,w))=H(u,v,w). Теперь нам нужно определить якобиан для трех переменных. Определение Определитель Якоби J(u,v,w) от трех переменных определяется следующим образом: J(u,v,w)=\|∂x∂u∂y∂u∂z∂u ∂x∂v∂y∂v∂z∂v∂x∂w∂y∂w∂z∂w\|. Тоже самое, что и J(u,v,w)=\|∂x∂u∂x∂v∂x∂w∂y∂u∂y∂v∂y∂w∂z∂u∂z∂v∂z∂w\ |. Якобиан можно также просто обозначить как ∂(x,y,z)∂(u,v,w). С преобразованиями и якобианом для трех переменных мы готовы установить теорему, описывающую замену переменных для тройных интегралов. Замена переменных для тройных интегралов Пусть T(u,v,w)=(x,y,z) где x=g(u,v,w),y=h(u,v,w) , и z=k(u,v,w), взаимно однозначно C1 9Преобразование 0013 с ненулевым якобианом, которое отображает область G в плоскости uvw в область D в плоскости xyz. Как и в двумерном случае, если F непрерывно на D, , то ∭RF(x,y,z)dV=∭GF(g(u,v,w),h(u ,v,w),k(u,v,w))\|∂(x,y,z)∂(u,v,w)\|dudvdw=∭GH(u,v,w)\|J( u,v,w)\|dudvdw. Посмотрим теперь, как эта теорема влияет на изменение тройных интегралов для цилиндрических и сферических координат. Мы ожидаем получить те же формулы, что и в тройных интегралах в цилиндрических и сферических координатах. Получение формул в тройных интегралах для цилиндрических и сферических координат Вывести формулы в тройных интегралах для из декартова на декартову ([ссылка]). Здесь и Якобиан преобразования равен J(r,θ,z)=∂(x,y,z)∂(r,θ,z)=\|∂x∂r∂x∂θ∂x∂z∂y∂r∂y∂θ ∂y∂z∂z∂r∂z∂θ∂z∂z\|=\|cosθ−rsinθ0sinθrcosθ0001\|=rcos2θ+rsin2θ=r(cos2θ+sin2θ)=r. Мы знаем, что , поэтому Тогда тройной интеграл равен ∭Df(x,y,z)dV=∭Gf(rcosθ,rsinθ,z)rdrdθdz. из декартова к декартовой ([ссылка]). Здесь и Якобиан преобразования равен J(ρ,θ,φ)=∂(x,y,z)∂(ρ,θ,φ)=\|∂x∂ρ∂x∂θ∂x∂φ∂y∂ρ∂y∂θ ∂y∂φ∂z∂ρ∂z∂θ∂z∂φ\|=\|sinφcosθ−ρsinφsinθρcosφcosθsinφsinθ−ρsinφcosθρcosφsinθcosθ0−ρsinφ\|. Разложение определителя по третьей строке: =cosφ\|−ρsinφsinθρcosφcosθρsinφsinθρcosφsinθ\|−ρsinφ\|sinφcosθ−ρsinφsinθsinφsinθρsinφcosθ\|=cosφ(−ρ2sinφcosφsin2θ−ρ2sinφcosφcos2θ)−ρsinφ(ρsin2φcos2θ+ρsin2φsin2θ)=−ρ2sinφcos2φ(sin2θ+cos2θ)−ρ2sinφsin2φ(sin2θ+cos2θ)= −ρ2sinφcos2φ−ρ2sinφsin2φ=−ρ2sinφ(cos2φ+sin2φ)=−ρ2sinφ. С у нас должно быть Так Тогда тройной интеграл становится ∭Df(x,y,z)dV=∭Gf(ρsinφcosθ,ρsinφsinθ,ρcosφ)ρ2sinφdρdφdθ. Давайте попробуем другой пример с другой заменой. Вычисление тройного интеграла с заменой переменных Вычисление тройного интеграла ∫03∫04∫y/2(y/2)+1(x+z3)dxdydz в пространстве xyz с помощью преобразование u=(2x−y)/2,v=y/2 иw=z/3. Затем проинтегрируйте по соответствующей области в uvw-пространстве. Как и прежде, идентифицировать область D в uvw-пространстве может помочь некий набросок области G в xyz-пространстве , по которой мы должны выполнить интегрирование ([ссылка]). Ясно, что G в xyz-пространстве ограничен плоскостями x=y/2,x=(y/2)+1,y=0, y=4,z=0 и z=4. Мы также знаем, что мы должны использовать u=(2x−y)/2,v=y/2, и w=z/3 для преобразований. Нам нужно решить для x, y, и z. Здесь мы находим, что x=u+v, y=2v, и z=3w. Используя элементарную алгебру, мы можем найти соответствующие поверхности для области G и пределы интегрирования в uvw-пространстве. Эти уравнения удобно представить в виде таблицы. для региона D для региона G |
{: valign=»top»}{: . Теперь мы можем вычислить якобиан для преобразования: w∂z∂u∂z∂v∂z∂w\|=\|110020003\|=6. Интегрируемая функция становится f(x,y,z)=x+z3=u+v+3w3=u+v+w. Теперь мы готовы собрать все воедино и решить задачу. ∫03∫04∫y/2(y/2)+1(x+z3)dxdydz=∫01∫02∫01(u+v+w)\|J(u,v,w)\|dudvdw =∫01∫02∫01(u+v+w)\|6\|dudvdw=6∫01∫02∫01(u+v+w)dudvdw=6∫01∫02[u22+vu+wu]01dvdw =6∫01∫02(12+v+w)dvdw=6∫01[12v+v22+wv]02dw=6∫01(3+2w)dw=6[3w+w2]01=24. Пусть D — область в xyz-пространстве , определяемая соотношениями 1≤x≤2,0≤xy≤2 и 0≤z≤1. Вычислите ∭D(x2y+3xyz)dxdydz с помощью преобразования u=x,v=xy, и w=3z. ∫03∫02∫12(v3+vw3u)dudvdw=2+ln8 Подсказка Составьте таблицу для каждой поверхности областей и выберите пределы, как показано в примере. — функция, преобразующая область в одной плоскости (пространстве) в область в другой плоскости (пространстве) заменой переменных. определяется как называется взаимно-однозначным преобразованием, если никакие две точки не отображаются в одно и то же точка изображения. непрерывен на , затем продолжается на , затем ∭RF(x,y,z)dV=∭GF(g(u,v,w),h(u,v,w),k(u,v,w))\|∂(x,y ,z)∂(u,v,w)\|dudvdw=∭GH(u,v,w)\|J(u,v,w)\|dudvdw. В следующих упражнениях функция T:S→R,T(u,v)=(x,y) на область S={(u,v)\|0≤u≤1,0≤v≤1} , ограниченный единичным квадратом, где R⊂R2 это образ S под Т. это . через функцию единицы площади и начертите его. х=2u,y=3v х=u2,y=v3 а. T(u,v)=(g(u,v),h(u,v)),x=g(u,v)=u2 и y=h(u,v)=v3. Функции g и h непрерывны и дифференцируемы, а частные производные gu(u,v)=12, gv(u,v)=0,hu(u,v)=0 и hv(u,v)=13 непрерывны на S; б. Т(0,0)=(0,0), Т(1,0)=(12,0),Т(0,1)=(0,13), и Т(1,1) =(12,13); в. — прямоугольник вершин (0,0), (12,0), (12,13) и (0,13) в плоскости xy; следующий рисунок.* * * х=и-в,у=и+в х=2u−v,y=u+2v а. T(u,v)=(g(u,v),h(u,v)),x=g(u,v)=2u−v, и y=h(u,v)=u+ 2м. Функции g и h непрерывны и дифференцируемы, а частные производные gu(u,v)=2, gv(u,v)=−1,hu(u,v)=1, и hv(u,v)=2 непрерывны на S; б. Т(0,0)=(0,0), Т(1,0)=(2,1),Т(0,1)=(-1,2), и Т(1,1 )=(1,3); в. R — параллелограмм вершин (0,0), (2,1), (1,3) и (−1,2) в плоскости xy; см. следующий рисунок.* * * х=и2,у=v2 х=u3,y=v3 а. T(u,v)=(g(u,v),h(u,v)),x=g(u,v)=u3, и y=h(u,v)=v3. Функции g и h непрерывны и дифференцируемы, а частные производные gu(u,v)=3u2, gv(u,v)=0,hu(u,v)=0, и hv(u,v)=3v2 непрерывны на S; б. Т(1,0)=(1,0),Т(0,1)=(0,1), и Т(1,1) =(1,1); в. Р — единичный квадрат в плоскости xy; см. рисунок в ответе на предыдущее упражнение. В следующих упражнениях определите, выполняются ли преобразования T:S→R , являются ли они один к одному или нет. x=u2,y=v2, где S — прямоугольник вершин (−1,0), (1,0), (1,1) и (−1,1). x=u4,y=u2+v, где S — треугольник вершин (−2,0),(2,0) и (0,2). T не один к одному: две точки S имеют такое же изображение. Действительно, Т(−2,0)=Т(2,0)=(16,4). x=2u,y=3v, где S — квадрат вершин (−1,1),(−1,−1),(1,−1) и (1,1). T(u,v)=(2u−v,u), , где S — треугольник вершин (−1,1),(−1,−1) и (1,−1). T взаимно однозначно: Мы рассуждаем от противного. подразумевает 2u1−v1=2u2−v2 и u1=u2. Таким образом, u1=u2 и v1=v2. х=и+в+ш,у=и+в,г=ш, , где S=R=R3. x=u2+v+w,y=u2+v,z=w, , где S=R=R3. T не взаимно однозначно: T(1,v,w)=(−1,v,w) В следующих упражнениях преобразования T:S→R являются один к одному. Найдите связанные с ними обратные преобразования T−1:R→S. x=4u,y=5v, , где S=R=R2. x=u+2v,y=-u+v, , где S=R=R2. и=х-2у3,в=х+у3 x=e2u+v,y=eu−v, , где S=R2 и R={(x,y)\|x>0,y>0} x=lnu,y=ln(uv), , где S={(u,v)\|u>0,v>0} и R=R2. u=ex,v=e−x+y x=u+v+w,y=3v,z=2w, , где S=R=R3. x=u+v,y=v+w,z=u+w, , где S=R=R3. u=x-y+z2,v=x+y-z2,w=-x+y+z2 В следующих упражнениях преобразование T:S→R,T(u,v)=(x,y) и область R⊂R2 дано. Найдите область S⊂R2. x=au,y=bv,R={(x,y)\|x2+y2≤a2b2}, , где a,b>0 x=au,y=bv,R={(x,y)\|x2a2+y2b2≤1}, , где a,b>0 S={(u,v)\|u2+v2≤ 1} x=ua,y=vb,z=wc,R={(x,y)\|x2+y2+z2≤1}, , где a,b,c>0 x=au,y=bv,z=cw,R={(x,y)\|x2a2−y2b2−z2c2≤1,z>0}, , где a,b,c>0 R= {(u,v,w)\|u2−v2−w2≤1,w>0} В следующих упражнениях найдите якобиан J трансформации. х=и+2в,у=-и+в х=u32,y=vu2 32 х=e2u-v,y=eu+v x=uev,y=e−v −1 x=ucos(ev),y=usin(ev) х=vsin(u2),y=vcos(u2) 2uv х=укошв,у=исхв,г=ш х=vсh(1u),y=vsinh(1u),z=u+w2 vu2 х=и+в,у=в+ш,г=и х=u−v,y=u+v,z=u+v+w 2 Треугольная область R с вершинами (0,0),(1,1) и (1,2) показан на следующем рисунке. , где и — действительные числа с такое, что и найти площадь региона Треугольная область R с вершинами (0,0), (2,0) и (1,3) показана на следующем рисунке. , где и — действительные числа с такое, что и найти площадь региона а. б. Площадь R равна* * * A(R)=∫03∫y/3(6−y)/3dxdy=∫01∫01−u\|∂(x,y)∂(u,v )\|dvdu=∫01∫01−u6dvdu=3. В следующих упражнениях используйте преобразование u=y−x,v=y, для вычисления интегралов на параллелограмме R вершин (0,0),(1,0),(2,1)и(1,1) показан на следующем рисунке.* * * ∬R(y−x)dA ∬R(y2−xy)dA −14 В следующих упражнениях используйте преобразование y−x=u,x+y=v для вычисления интегралов по квадрату R определяется линиями y=x,y=−x+2,y=x+2, и у=-х показан на следующем рисунке.* * * ∬Rex+ydA ∬Rsin(x−y)dA −1+cos2 В следующих упражнениях используйте преобразование x=u,5y=v для вычисления интегралов по области R ограничено эллипсом x2+25y2=1 показан на следующем рисунке. ∬Rx2+25y2dA ∬R(x2+25y2)2dA π15 В следующих упражнениях используйте преобразование u=x+y,v=x−y для вычисления интегралов на трапециевидной области R определяется точками (1,0),(2,0),(0,2)и(0,1) показан на следующем рисунке.* * * ∬R(x2−2xy+y2)ex+ydA ∬R(x3+3x2y+3xy2+y3)dA 315 Сектор кругового кольца R , ограниченный окружностями 4×2+4y2=1 и 9×2+9y2=64, линией x=y3, и осью y , показан на следующем рисунке. Найдите преобразование T из прямоугольной области S в плоскости rθ в область R в плоскости xy. График С. Тело R , ограниченное круговым цилиндром x2+y2=9 и плоскостями z=0,z=1, x=0,andy=0 , показано на следующем рисунке. из цилиндрического ящика S в пространстве rθz в тело R в пространстве xyz. T(r,θ,z)=(rcosθ,rsinθ,z);S=[0,3]×[0,π2]×[0,1] в rθz-пространстве Покажите, что ∬Rf(x23+y23)dA=2π15∫01f(ρ)ρdρ, , где f — непрерывная функция на [0,1] , а R — область, ограниченная эллипсом 5×2+3y2=15. Покажите, что ∭Rf(16×2+4y2+z2)dV=π2∫01f(ρ)ρ2dρ, , где f — непрерывная функция на [0,1] , а R — область, ограниченная эллипсоид 16×2+4y2+z2=1. [T] Найдите площадь области, ограниченной кривыми xy=1,xy=3,y=2x, и y=3x , используя преобразование u=xy и v=yx. Используйте систему компьютерной алгебры (CAS) для построения графика граничных кривых области R. [T] Найдите площадь области, ограниченной кривыми x2y=2,x2y=3,y=x, и y=2x , используя преобразование u=x2y и v=yx. Используйте CAS для построения граничных кривых области R. Площадь R равна 10−46; граничные кривые R представлены на следующем рисунке.* * * Вычислите тройной интеграл ∫01∫12∫zz+1(y+1)dxdydz с помощью преобразования u=x−z, v=3y и w=z2. Вычислите тройной интеграл ∫02∫46∫3z3z+2(5−4y)dxdzdy , используя преобразование u=x−3z,v=4y иw=z. 8 Преобразование T:R2→R2,T(u,v)=(x,y) вида x=au+bv,y=cu+dv, , где a,b,c и d являются действительными числами, называется линейным. Покажите, что линейное преобразование, для которого ad−bc≠0 отображает параллелограммы в параллелограммы. Преобразование Tθ:R2→R2,Tθ(u,v)=(x,y), , где x=ucosθ−vsinθ, y=usinθ+vcosθ, , называется поворотом на угол θ. Покажите, что обратное преобразование Tθ удовлетворяет условию Tθ−1=T−θ, , где T−θ — поворот на угол −θ. [T] Найти область S в uv-плоскости изображение которой через поворот на угол π4 — область R , заключенная в эллипс x2+4y2=1. Используйте CAS, чтобы ответить на следующие вопросы. Округлите ответ до двух знаков после запятой. [T] Преобразования Ti:ℝ2→ℝ2, i=1,…,4, определяемые T1(u,v)=(u,−v), T2(u,v) =(−u,v),T3(u,v)=(−u,−v), и T4(u,v)=(v,u) называются отражениями относительно оси x, оси y, начала координат и линии y=x, соответственно. в через преобразование с помощью CAS. Округлите ответ до двух знаков после запятой. а. R={(x,y)\|y2+x2−2y−4x+1≤0}; б. R изображен на следующем рисунке* * * c. 3.16 [T] Преобразование Tk,1,1:ℝ3→ℝ3,Tk,1,1(u,v,w)=(x,y,z) вида x=ku, y =v,z=w, , где k≠1 — положительное действительное число, называется растяжением, если k>1 , и сжатием, если 0 в направлении x. Используйте CAS для вычисления интеграла ∭Se−(4×2+9y2+25z2)dxdydz на твердом S={(x,y,z)\|4×2+9y2+25z2≤1} , учитывая сжатие T2,3,5(u,v,w)=(x,y,z) определяется как x=u2,y=v3, и z=w5. Округлите ответ до четырех знаков после запятой. [T] Преобразование Ta,0:ℝ2→ℝ2,Ta,0(u,v)=(u+av,v), , где a≠0 — действительное число, называется сдвигом в направлении х. Преобразование, Tb,0:R2→R2,To,b(u,v)=(u,bu+v), , где b≠0 — действительное число, называется сдвигом в направлении Y. трапециевидной области ограничен и через преобразование в , используя площадь региона а. T0,2∘T3,0(u,v)=(u+3v,2u+7v); б. Изображение S представляет собой четырехугольник вершин (0,0), (3,7), (2,4) и (4,9); в. S показан на следующем рисунке* * * d. 32 Используйте преобразование x=au,y=av,z=cw и сферические координаты, чтобы показать, что объем области, ограниченной сфероидом x2+y2a2+z2c2=1 — это 4πa2c3. Найдите объем футбольного мяча, имеющего форму сфероида x2+y2a2+z2c2=1 , длина которого от кончика до кончика равна 11 дюймов, а длина окружности в центре равна 22 дюймов. Округлите ответ до двух знаков после запятой. 26623π≃282,45 дюйма3 [T] Овалы Ламе (или суперэллипсы) — это плоские кривые уравнений (xa)n+(yb)n=1, , где a , b и n — положительные действительные числа. , ограниченный овалами Ламе для и соответственно. , ограниченный овалом Ламе , также называемое сквирклом и изображенное на следующем рисунке, в единичный диск. региона ограничен Округлите ответ до двух знаков после запятой. [T] Овалы Ламе постоянно используются дизайнерами и архитекторами. Например, Джеральд Робинсон, канадский архитектор, спроектировал гараж в торговом центре в Питерборо, Онтарио, в форме суперэллипса уравнения (xa)n+(yb)n=1 с ab=97 и n=e. Используйте CAS, чтобы найти приблизительную площадь гаража в случае a = 900 ярдов, b = 700 ярдов и n = 2,72 ярдов. A(R)≃83 999,2 Правда или ложь? Обоснуйте свой ответ доказательством или контрпримером. ∫ab∫cdf(x,y)dydx=∫cd∫abf(x,y)dydx Теорему Фубини можно распространить на три измерения, если f непрерывна по всем переменным. Верно. Интеграл ∫02π∫01∫r1dzdrdθ представляет объем прямого конуса. Якобиан преобразования для x=u2−2v,y=3v−2uv задается как −4u2+6u+4v. Ложь. Оцените следующие интегралы. ∬R(5x3y2−y2)dA,R={(x,y)\|0≤x≤2,1≤y≤4} ∬Dy3x2+1dA,D={(x,y)\|0≤x≤1,−x≤y≤x} 0 ∬Dsin(x2+y2)dA , где D — диск радиуса 2 с центром в начале координат ∫01∫y1xyex2dxdy 14 ∫−11∫0z∫0x−z6dydxdz ∭R3ydV, где R={(x,y,z)\|0≤x≤1,0≤y≤x,0≤z≤9−y2} 1,475 ∫02∫02π∫r1rdzdθdr ∫02π∫0π/2∫13ρ2sin(φ)dρdφdθ 523π ∫01∫-1-x21-x2∫-1-x2-y21-x2-y2dzdydx Для следующих проблем найдите указанную область или объем. Площадь области, ограниченной одним лепестком r=cos(4θ). №16 Объем тела, лежащего между параболоидом z=2×2+2y2 и плоскости z=8. Объем твердого тела, ограниченного цилиндром x2+y2=16 и от z=1 до z+x=2. 93.291 Объем пересечения двух сфер радиусом 1, верхней с центром в (0,0,0,25) и нижней с центром в (0,0,0). Для следующих задач найдите центр масс области. ρ(x,y)=xy на окружности радиусом 1 только в первом квадранте. (815 815) ρ(x,y)=(y+1)x в области, ограниченной y=ex, y=0, и x=1. ρ(x,y,z)=z на перевернутом конусе радиусом 2 и высотой 2. (0,0,85) Объем рожка мороженого, заданный твердым телом выше z=(x2+y2) и ниже z2+x2+y2=z. Следующие задачи исследуют гору Холли в штате Мичиган. Маунт-Холли — это свалка, превращенная в горнолыжный курорт. Форма горы Холли может быть аппроксимирована прямым круглым конусом высотой 1100 9 .0013 футов и радиус 6000 футов Если уплотненный мусор, используемый для строительства горы Холли, в среднем имеет плотность 400 фунтов/фут3, найдите количество работы, необходимой для строительства горы. 1,452π×1015 фут-фунт На самом деле очень вероятно, что мусор на дне горы Остролист стал более уплотненным под всей тяжестью вышеупомянутого мусора. Рассмотрим функцию плотности относительно высоты: плотность на вершине горы по-прежнему равна плотности 400 фунтов/фут3 и плотность увеличивается. Каждые 100 футов глубины плотность удваивается. Каков общий вес горы Холли? Следующие задачи рассматривают температуру и плотность слоев Земли. [T] Температура слоев Земли показана в таблице ниже. Используйте свой калькулятор, чтобы подогнать полином степени 3 к температуре по радиусу Земли. Затем найдите среднюю температуру Земли. ( Подсказка : начинается с 0 во внутреннем ядре и увеличивается по направлению к поверхности) y=-1,238×10-7×3+0,001196×2-3,666x+7208; средняя температура около 2800°C [T] Плотность слоев Земли показана в таблице ниже. Следующие задачи касаются Теоремы Паппа (см. Моменты и центры масс для освежения знаний), метода вычисления объема с использованием центроидов. Предполагая регион R, при вращении вокруг оси x объем определяется как Vx=2πAy–, и когда вы вращаетесь вокруг оси Y объем определяется выражением Vy=2πAx–, , где А это площадь р. Рассмотрим область, ограниченную x2+y2=1 и выше y=x+1. Найдите объем при вращении области вокруг оси X. №3 Найдите объем при вращении области вокруг оси Y. в двух переменных равно определитель: J(u,v)=\|∂x∂u∂y∂u∂x∂v∂y∂v\|; Якобиан в трех переменных равно определитель: J(u,v,w)=\|∂x∂u∂y∂u∂z∂u∂x∂v∂y∂v∂z∂v∂x∂w∂y∂w∂z∂w\ | определяется как называется взаимно однозначным, если никакие две точки не сопоставляются с одной и той же точкой изображения , преобразующий регион в одной плоскости в область в другой плоскости заменой переменных в одной плоскости в область в другой плоскости заменой переменных Вы также можете скачать бесплатно по адресу http://cnx.org/contents/[email protected] Атрибуция: Разделение переменных — это специальный метод решения некоторых дифференциальных уравнений Дифференциальное уравнение – это уравнение с функцией и одной или несколькими ее производными: Разделение переменных можно использовать, когда: Все члены y (включая dy) можно переместить в одну сторону уравнения, а Все члены x (включая dx) — в другую сторону. Три шага: dy dx = ky Шаг 1 Разделите переменные, переместив все члены y в одну часть уравнения, а все члены x в другую: Умножьте обе части на dx: dy = ky dx Разделите обе части уравнения на y: dy y = k dx Шаг 2 Проинтегрируйте обе части уравнения отдельно: Поставьте знак интеграла перед: = ∫ k dx Интегрируем левую часть: ln(y) + C = ∫ k dx Интегрируем правую часть: ln(y) + C = kx + D C — постоянная интегрирования. И мы используем D для другого, так как это другая константа. Шаг 3 = y , поэтому возьмем показатели с обеих сторон: y = e kx + a И e kx + a = e kx e a поэтому мы получаем: y = e kx e a e e e 9 поэтому мы просто заменяем c на1 9 :y = ce kx Мы решили это: y = ce kx Это общий тип дифференциального уравнения первого порядка, который появляется во многих неожиданных местах в реальных примерах. Мы использовали и и x , но тот же метод работает и для других имен переменных, например: Чем больше у вас будет кроликов, тем больше у вас будет крольчат. Потом эти кролики вырастают и тоже рожают малышей! Население будет расти все быстрее и быстрее. Важными частями этого являются: Скорость изменения в любое время равна скорости роста, умноженной на население: dN dt = rN Но эй! Это то же самое, что и уравнение, которое мы только что решили! Просто у него другие буквы: Итак, мы можем перейти к решению: N = ce rt А вот пример, график N = 0.3e 2t : Есть и другие уравнения, которые следуют этому шаблону, например, непрерывные сложные проценты. Хорошо, теперь несколько примеров разделения переменных: dy dx = 1 y Шаг 1 Разделите все члены уравнения x на одну сторону y другая сторона: Умножить обе части на dx:dy = (1/y) dx Умножить обе части на y: y dy = dx Шаг 2 Интегрировать обе части уравнения отдельно: Поставить знак интеграла впереди :∫ y dy = ∫ dx Проинтегрируем каждую сторону: (y 2 )/2 = x + C Мы проинтегрировали обе стороны в одну прямую. Мы также использовали сокращение только одной константы интегрирования C. Это совершенно нормально, поскольку мы могли бы иметь +D на одном, +E на другом и просто сказать, что C = E−D. 9Шаг 3 Примечание. Это не то же самое, что y = √(2x) + C, потому что C было добавлено до того, как мы взяли квадратный корень. Мы решили: у = ±√(2(х + С)) Более сложный пример: DY DX = 2xy 1+x 2 Шата 1 Отдельные DISLIDED: . y: 1 y dy = 2x 1+x 2 dx Шаг 2 Интегрируем обе части уравнения по отдельности ∫ 1 Y DY = ∫ 2x 1+x 2 DX Левая сторона — простая логарифм, правая сторона может быть интегрирован с использованием upitation: . мы получаем C = ln(k) :ln(y) = ln(u) + ln(k) Итак, мы можем получить это: y = uk Теперь положим u = 1 + x 2 обратно: y = k(1 + x 2 ) Шаг 3 Упростим: Это уже настолько просто, насколько это возможно. y = k(1 + x 2 ) Еще более сложный пример: знаменитое уравнение Ферхюльста Помните о нашем росте Дифференциальное уравнение: dN dt = rN Ну, этот рост не может продолжаться вечно, так как скоро у них закончится доступная еда. Парень, называемый Verhulst, включал K (максимальная популяция, которую поддерживает продукты питания), чтобы получить: DN DT = RN (1–N/K) . Можно ли это решить? Да, с помощью одной хитрости… Шаг 1 Разделить переменные: Умножить обе части на dt: dN = rN(1−N/k) dt Разделить обе части на N(1-N/k): 1 N(1−N/k) dN = r dt Шаг 2 Интегрируем: ∫ 1 N(1−N/k) dN = ∫ r dt Хмммм. Начнем с этого: 1 N(1−N/k) Умножить верх и низ на k: k N(k−N) А вот и хитрость: прибавь N и −N к вершине: N+k−N N( k−N) и разделить его на две дроби: N N(k−N) + k−N N(k−N) Упростить каждую дробь: 1



Якобианцы

 Перекрестное произведение) приблизительно равно \|Δuru×Δvrv\|=\|ru×rv\|ΔuΔv.
Перекрестное произведение) приблизительно равно \|Δuru×Δvrv\|=\|ru×rv\|ΔuΔv.
Замена переменных для двойных интегралов



 Сделайте соответствующие замены переменных и запишите полученный интеграл.
Сделайте соответствующие замены переменных и запишите полученный интеграл.



Замена переменных для тройных интегралов





Уравнения в xyz Соответствующие уравнения в uvw Ограничения на интеграцию в uvw {: valign=»верх»} ———- х=у/2 и+в=2в/2=в {: valign=»верх»} х=у/2 u+v=(2v/2)+1=v+1 {: valign=»верх»} г=0 {: valign=»верх»} у=4 {: valign=»верх»} г=0 {: valign=»верх»} г=3 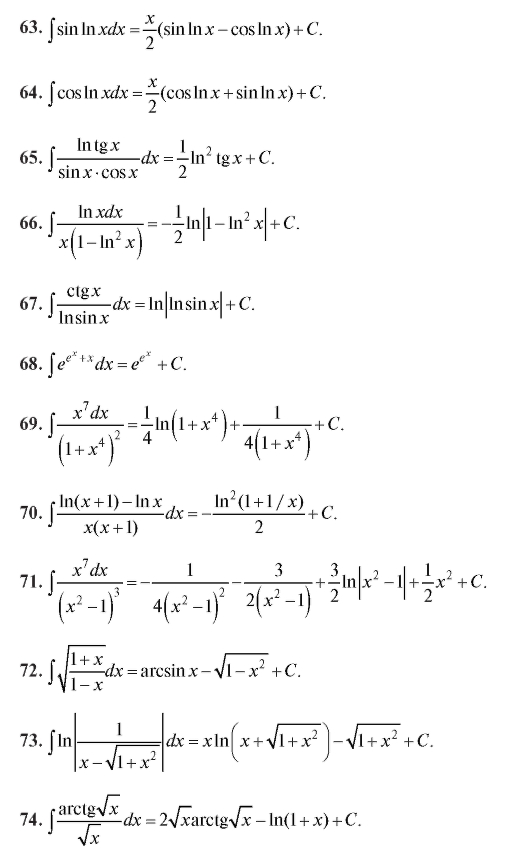 unnumbered summary=»Эта таблица состоит из трех столбцов и семи строк. Первая строка является строкой заголовка и читает Уравнения в x y z для области D, Соответствующие уравнения в u v w для области G и Пределы интегрирования в u v w. В первом столбце внизу написано x = y/2, x = (y/2) + 1, y =, y = 4, z = 0 и z = 3. Во втором столбце внизу написано u + v = 2v/2 = v, u + v = (2v/2) + 1 = v + 1, 2v = 0, 2v = 4, 3w = 0 и 3w = 3. В последнем столбце указано u = 0, u = 1, v = 0. , v = 2, w = 0 и w = 1». метка данных = «»}
unnumbered summary=»Эта таблица состоит из трех столбцов и семи строк. Первая строка является строкой заголовка и читает Уравнения в x y z для области D, Соответствующие уравнения в u v w для области G и Пределы интегрирования в u v w. В первом столбце внизу написано x = y/2, x = (y/2) + 1, y =, y = 4, z = 0 и z = 3. Во втором столбце внизу написано u + v = 2v/2 = v, u + v = (2v/2) + 1 = v + 1, 2v = 0, 2v = 4, 3w = 0 и 3w = 3. В последнем столбце указано u = 0, u = 1, v = 0. , v = 2, w = 0 и w = 1». метка данных = «»}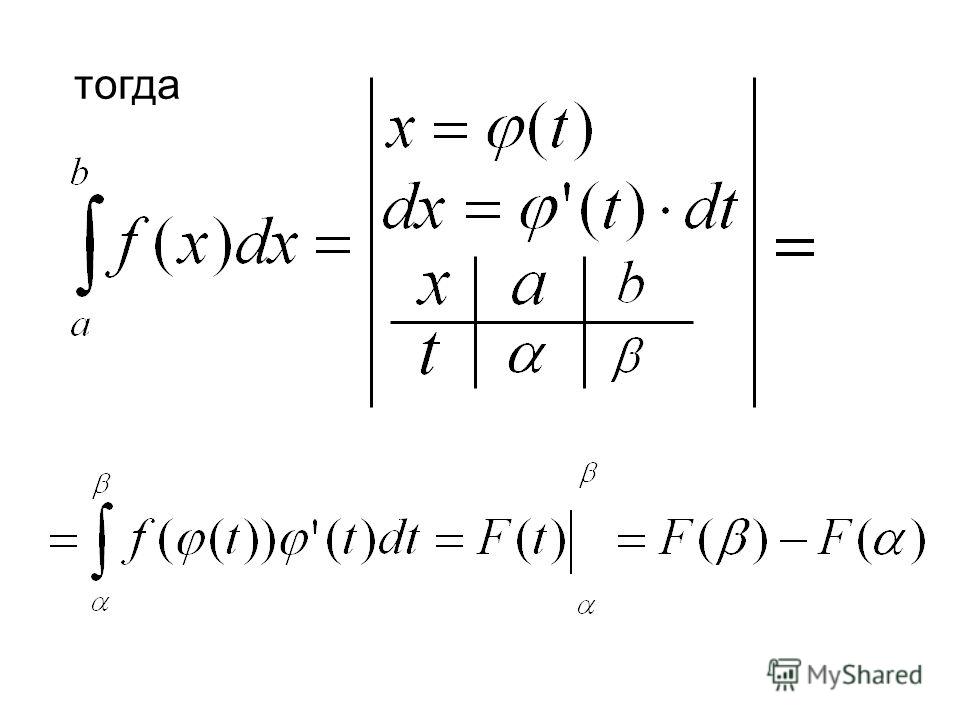
Основные понятия

 R
R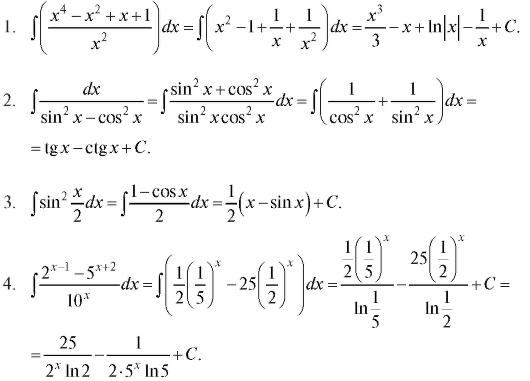 Т(0,0)=(0,0),
Т(0,0)=(0,0),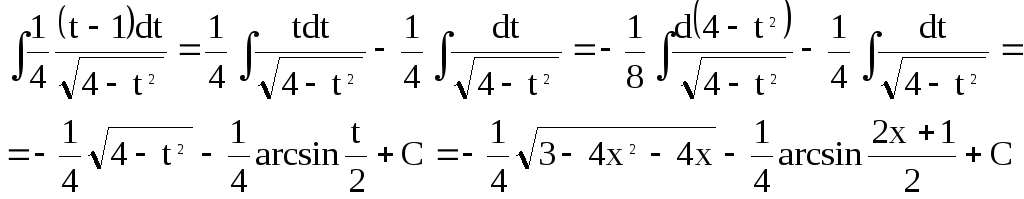 T(u1,v1)=T(u2,v2)
T(u1,v1)=T(u2,v2)

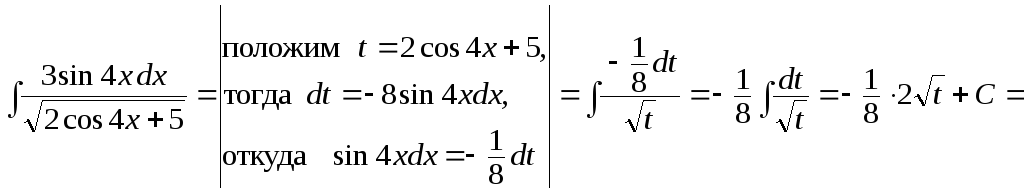 Т(и,в)=(2и+в,3в);
Т(и,в)=(2и+в,3в); * * *
* * * Найдите преобразование T
Найдите преобразование T





Упражнения на обзор глав



These two layers are grouped together as the Lithosphere, and the line between them is marked as the Mohorovicic Discontinuity. Then the next layer is the Mantle, 400 to 650 km, 870 degrees C; Inner mantle (semi-rigid), 650 to 2700 km, 870 degrees C. Then there is a short region between 2700 and 2890 km marked the Gutenberg Discontinuity, which has temperature 3700 degrees C. The next layer is the Molten Outer Core (Iron/nickel) from 2890 to 5150, 4300 degrees C; and finally there is the inner core (Iron/nickel) from 5150 to 6378, 7200 degrees C.» data-label=»»>
Глубина от центра (км) Температура °C Каменистая корка от 0 до 40 0 Верхняя мантия от 40 до 150 870 Мантия от 400 до 650 870 Внутренняя каминная доска от 650 до 2700 870 Расплавленное внешнее ядро 2890 до 5150 4300 Внутреннее ядро 5150 до 6378 7200  С помощью калькулятора или компьютерной программы найдите наиболее подходящее квадратное уравнение для плотности. Используя это уравнение, найдите полную массу Земли.
С помощью калькулятора или компьютерной программы найдите наиболее подходящее квадратное уравнение для плотности. Используя это уравнение, найдите полную массу Земли. Слой Глубина от центра (км) Плотность (г/см3) Внутреннее ядро 0 12,95 Внешний сердечник 1228 11.  05
05 Мантия 3488 5,00 Верхняя мантия 6338 3,90 Корка 6378 2,55 
Глоссарий
Эта работа находится под лицензией Creative Commons Attribution 4. 0 International License.
0 International License. org/contents/[email protected]».
org/contents/[email protected]». Разделение переменных
Пример: уравнение с функцией y и ее производная dy dx Когда я могу его использовать?
Метод
 Не забудьте «+ C» (константа интегрирования).
Не забудьте «+ C» (константа интегрирования). Пример: Решите (k — константа):

Пример: Кролики!
Экспоненциальный рост
Больше примеров
Пример: Решите:
 Это часто происходит с дифференциальными уравнениями. Мы не можем просто добавить C в конце процесса. Он добавляется при интеграции.
Это часто происходит с дифференциальными уравнениями. Мы не можем просто добавить C в конце процесса. Он добавляется при интеграции. Пример: решить это:
 Мы решили ее:
Мы решили ее: Пример: Снова кролики!
 .. На самом деле это можно сделать с помощью небольшой хитрости из Частичных дробей… мы переставляем это так:
.. На самом деле это можно сделать с помощью небольшой хитрости из Частичных дробей… мы переставляем это так:
Теперь решить намного проще. Мы можем интегрировать каждый термин отдельно, например:
Теперь наше полное уравнение выглядит следующим образом: ∫ 1 k−N dN + ∫ 1 N dN = ∫ r dt
Интегрируем: −ln(k−N) + ln(N) + ln(N) C
(Почему получилось минус ln(k−N)? Потому что мы интегрируем по N.) −N) − ln(N) = −rt − C
Объединить ln():ln((k−N)/N) = −rt − C
Теперь возьмем показатели с обеих сторон: (k−N)/ N = е −rt−C
Разделить степени e:(k−N)/N = e −rt e −C
e −C — константа, которую можно заменить на A: (k−N)/N = Ae −rt
Мы приближаемся! Еще немного алгебры, чтобы получить N само по себе:
Разделите члены дроби: (k/N)−1 = Ae −rt
Добавьте 1 к обеим частям: k/N = 1 + Ae −rt
Разделите оба на k:1/N = (1 + Ae −rt )/k
Величина, обратная обеим сторонам: N = k/(1 + Ae −rt )
И у нас есть решение:
N = k 1 + Ae
1 −rtВот Пример , график 40 1 + 5E −2t
Это начинает повышать экспресс.
Методы интеграции
Многие формулы интегрирования могут быть получены непосредственно из соответствующих формул производных, в то время как другие проблемы интеграции требуют дополнительной работы. Некоторые из них требуют дополнительной работы: замена и замена переменных, интегрирование по частям, тригонометрические интегралы и тригонометрические замены.Основные формулы
Большинство следующих основных формул непосредственно следуют правилам дифференцирования.
Пример 1: Оценка
Используя формулу (4) из предыдущего списка, вы находите, что .
Пример 2: Оценка .
Поскольку использование формулы (4) из предыдущего списка дает
Пример 3: Оценка
Применяя формулы (1), (2), (3) и (4), находим, что
Пример 4: Оценка
Используя формулу (13), находим, что
Пример 5: Оценка
Используя формулу (19) с a = 5, вы находите, что
Подстановка и изменение переменных
Одним из методов интегрирования, полезных при вычислении неопределенных интегралов, которые, кажется, не соответствуют основным формулам, является подстановка и замена переменных. Этот метод часто сравнивают с цепным правилом дифференцирования, поскольку оба они применимы к составным функциям. В этом методе внутренняя функция композиции обычно заменяется одной переменной (часто 9).0151 и ). Обратите внимание, что производная или постоянное кратное производной внутренней функции должно быть фактором подынтегрального выражения.
Цель использования метода подстановки состоит в том, чтобы переписать задачу интегрирования в терминах новой переменной, чтобы затем можно было применить одну или несколько основных формул интегрирования. Хотя поначалу этот подход может показаться более трудоемким, в конечном итоге он значительно упростит вычисление неопределенного интеграла.
Обратите внимание: чтобы окончательный ответ имел смысл, он должен быть записан в терминах исходной переменной интегрирования.
Пример 6: Оценка
Поскольку внутренняя функция композиции x 3 + 1, замените на
Пример 7:
Поскольку внутренняя функция композиции равна 5 x , замените на
.Пример 8: Оценка
Поскольку внутренняя функция композиции 9 – x 2 , замените на
Интеграция по частям
Другим методом интегрирования, который следует учитывать при вычислении неопределенных интегралов, которые не соответствуют основным формулам, является интегрирование по частям. Вы можете рассмотреть этот метод, когда подынтегральная функция является одной трансцендентной функцией или произведением алгебраической функции и трансцендентной функции. Основная формула интегрирования по частям:
Вы можете рассмотреть этот метод, когда подынтегральная функция является одной трансцендентной функцией или произведением алгебраической функции и трансцендентной функции. Основная формула интегрирования по частям:
где у и у — дифференциальные функции переменной интегрирования.
Общее практическое правило состоит в том, чтобы сначала выбрать dv как наиболее сложную часть подынтегральной функции, которую можно легко проинтегрировать, чтобы найти v . Функция u будет оставшейся частью подынтегральной функции, которая будет дифференцирована, чтобы найти du . Цель этого метода состоит в том, чтобы найти интеграл ∫ v du , который легче вычислить, чем исходный интеграл.
Пример 9: Оценка ∫ x сек 2 x dx .
Пример 10: Оценка ∫ x 4 In x dx .
Пример 11: Вычислить ∫ arctan x dx .
Интегралы, включающие степени тригонометрических функций, часто должны быть изменены, чтобы привести их к форме, в которой можно применить основные формулы интегрирования. Для вас чрезвычайно важно знать основные тригонометрические тождества, потому что вы часто использовали их, чтобы переписать подынтегральную функцию в более удобной форме. Как и при интегрировании по частям, цель состоит в том, чтобы найти интеграл, который легче вычислить, чем исходный интеграл.
Пример 12: Вычислить ∫ cos 3 x sin 4 x dx
Пример 13: Оценка ∫ сек 6 x dx
Пример 14: Вычислить ∫ sin 4 x dx
Если подынтегральное выражение содержит подкоренное выражение вида, при вычислении неопределенного интеграла может быть полезна определенная тригонометрическая замена . Некоторые общие правила, которым необходимо следовать,
Некоторые общие правила, которым необходимо следовать,
1. Если подынтегральная функция содержит
2. Если подынтегральная функция содержит
3. Если подынтегральная функция содержит
Прямоугольные треугольники могут использоваться в каждом из трех предыдущих случаев для определения выражения для любой из шести тригонометрических функций, которые появляются при вычислении неопределенного интеграла.
Пример 15: Оценка
Поскольку радикал имеет форму
Рисунок 1 Схема для примера 15.
Пример 16: Оценка
Поскольку радикал имеет форму
Рисунок 2 Схема для примера 16.
Введение в интеграцию – Интеграция посредством U-замены – Метод изменения переменной – Правило обратной цепочки
Перейти к содержимому youtube.com/embed/0A2RlnutO8U?start=184&feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>В предыдущем разделе мы узнали о концепции неопределенного интеграла и о том, как найти первообразную простых, распространенных функций, используя таблицу интегралов. Однако для более сложных функций использование базовых методов антидифференцирования или таблицы интегралов не сработает. В этом разделе будет рассмотрен один из наиболее продвинутых методов нахождения неопределенного интеграла для более сложных функций: U-подстановка.
U-подстановка помогает найти интеграл функций y = f(g(x))g'(x), в котором внешняя функция u’ = g'(x) является производной внутренней функции u = g( Икс).
Прежде чем рассматривать интегрирование с помощью U-подстановки, нам нужно определить, можем ли мы выполнить U-подстановку для функции: )?
Решение : Во-первых, нам нужно определить внутреннюю функцию.
Внутренняя функция u = x 2 .
Далее нам нужно найти du и посмотреть, соответствует ли он внешней функции:
du =(x 2 )’ = 2x
du= 2x находится в функции. Следовательно, U-замещение может быть выполнено. u и du можно подставить в исходную функцию, чтобы получить:
f(x) = du cos(u) или cos(u)du
: Во-первых, нам нужно определить внутреннюю функцию.
Внутренняя функция u = x 2 +1
Далее нам нужно найти du и посмотреть, соответствует ли она внешней функции.
du = (x 2 +1)’ = 2x
Мы можем разделить каждую сторону на 2, чтобы du соответствовал члену в числителе:
½ du = x
Таким образом, U-подстановка может быть выполнена . u и ½du можно подставить в исходную функцию, чтобы получить:
Пример 3 : Можем ли мы выполнить U-подстановку на f(x) = 6x 2 (2x 4 +5) 6 ?
Решение : Во-первых, нам нужно определить внутреннюю функцию.
Внутренняя функция u = 2x 4 +5
Далее нам нужно найти du и посмотреть, соответствует ли она внешней функции.
du = (2x 4 +5)’ = 8x 3
Мы видим, что du = 8x 3 не равно 6x 2 , как видно из функции. Следовательно, U-замещение не может быть выполнено.
Пример 4 : Можем ли мы выполнить U-подстановку на f(x) = 3x(2x+7) 6 ?
Решение : Во-первых, нам нужно определить внутреннюю функцию.
Внутренняя функция u = 2x+7
Далее нам нужно найти du и посмотреть, соответствует ли она внешней функции.
du = (2x+7)’ = 2
Мы видим, что du =2 не равно 3x, как видно из функции. Следовательно, U-замещение не может быть выполнено.
Пример 5 : Можем ли мы выполнить U-подстановку на f(x) = cos(3x+2)?
Решение : Во-первых, нам нужно определить внутреннюю функцию.
Внутренняя функция u = 3x+2
Далее нам нужно найти du и посмотреть, соответствует ли она внешней функции.
du = u ‘= 3
Мы видим, что du = 3, что не соответствует ничему в исходной функции. Однако мы можем разделить обе части на 3, чтобы получить:
⅓ du = 1
Однако мы не видим 1 в функции. Хотя это верно, функция f(x) cos(3x+2) может быть записана как cos(3x+2) * 1 (оба означают одно и то же). Следовательно, 1/3 ду действительно находится в функции. Следовательно, U-замещение может быть выполнено.
u и du можно подставить в исходную функцию, чтобы получить:
f(x) = cos(3x+2) * 1
f(x) = cos(u) * ⅓ du
В каждой составной функции , мы определили внутреннюю функцию u и взяли производную от нее du, которая является внешней функцией. Если u = g(x) и du = g'(x), то наша составная функция равна
y = f(g(x))*g'(x) = f(u) * u’
Это похоже на цепное правило дифференцирования.
Следовательно, если мы интегрируем, то, по сути, меняем цепное правило на противоположное. Следовательно, U-подстановка также называется «правилом обратной цепи».
Хотя обозначение не совсем то же самое, связь постоянна.
Таким образом, интегрирование с помощью U-подстановки можно записать следующим образом:
| Формула: U – Подстановка Если u = g(x) и du = g'(x), то интеграл от составной функции f(g(x))*g'(x) равен Руководство по применению U-замены:
|
Пример 1: Предположим, у вас есть неопределенный интеграл
Найдите первообразную, используя метод U-подстановки.
Решение:
Определите внутреннюю функцию u = g(x).
Мы видим, что x 2 находится внутри функции синуса. Поэтому выберем u = x 2
. Возьмем производную от u, чтобы получить du = g’(x)dx.
u = x 2
du = 2xdx
Перепишем интеграл через u и du.
Замените x 2 на u и 2xdx на du.
Найдите полученный интеграл через u.
Проинтегрируем нашу функцию, рассматривая u как переменную:
F(x) = ∫ Sin (u) d (u)
F(x) = – Cos (u) + C, как интеграл от синуса is –косинус,
После интегрирования замените u = g(x) внутри первообразной.
Наконец, поместите u = x 2 обратно в ‘u’,
F(x) = – Cos (x 2 ) + C
Бонус: проверьте свою работу, дифференцируя первообразную с помощью цепного правила.
Внешняя функция равна f(x) = -cos(x), поэтому производная равна f’(x) = sin(x). Внутренняя функция u = g(x) = x 2 , поэтому u’ = g’(x) = 2x. Выполнение цепного правила:
F’ (x) = f’(g(x) )* g’(x) = sin (x 2 )*2x + 0 = sin (x 2 )*2x
Поскольку результат F’(x) соответствует подынтегральной функции, U-подстановка выполнена правильно.
Пример 2: Найдите результат F(x) = ∫ (2x + 5)dx.
Решение:
Определите внутреннюю функцию u = g(x).
Мы видим, что 2x + 5 находится внутри скобок. Поэтому выберем u = 2x + 5
. Возьмем производную от u, чтобы получить du = g’(x)dx.
u = 2x + 5
du = 2dx
du точно не соответствует ни одной функции в подынтегральном выражении.
Следовательно, при du = 2xdx разделим обе части на 2:
½du = dx
Следовательно, ½du = dx и u =2x+5.
Перепишем интеграл через u и du.
Замените ½du = dx и u =2x+5 внутри подынтегральной функции:
Разложите ½ под интегралом:
∫ (u)½du = ½ ∫ (u)du
Найдите интеграл в результате 9042 условия у.
Давайте проинтегрируем нашу функцию, рассматривая u как переменную. Применяя степенное правило интегрирования,
В этом примере мы не будем проверять нашу работу дифференцированием, но если это сделать, то F’(x) будет равно исходному выражению под интегралом.
Рассмотрим пример для определенных интегралов:
Пример 3: Найдите площадь под кривой f(x) = cos(x) esin(x) от x = 0 до x = 1.
Решение:
По сути, мы находим определенный интеграл от f(x) на интервале [0,1]:
Определите вашу внутреннюю функцию u = g(x).
Между sin(x), cos(x) и e x нам нужно выбрать функцию, которая, если взять производную, будет равна другой функции под интегралом.
Попробуем u = e x :
u = e x
du = e x dx
Так как du = e x dx не соответствует ни одной функции в подынтегральном выражении, необходимо выбрать новый u.
Давайте попробуем u = cos(x)
du = -sin(x)dx
Несмотря на то, что у нас есть sin(x) в показателе степени, du не будет показателем, потому что у показателя нет дифференциала dx.
Попробуем u = sin(x)
du = cos(x) dx
В этом случае cos(x)dx существует под интегралом. Поэтому воспользуемся u = sin(x) и du = cos(x)dx
Поэтому воспользуемся u = sin(x) и du = cos(x)dx
. Возьмем производную от u, чтобы получить du = g’(x)dx.
Как уже определено на предыдущем шаге,
u = x 2
du = 2xdx
Перепишем интеграл через u и du.
Замените sin(x) на u, а cos(x)dx на du.
Найдите определенный интеграл:
F(b) – F(a) = e 1 -e 0 = e-1
Без учета пределов интегрирования неопределенный интеграл будет:
F(x) = e u du = e u + C
Подставляя u = sin(x) обратно в первообразную,
F(x) = e sin(x) + C
Бонус: проверьте свою работу, продифференцировав первообразную с помощью цепное правило.
Внешняя функция равна f(x) = e (x) , поэтому производная равна f’(x) = 1*e (x) = e x . Внутренняя функция u = g(x) = sin(x), поэтому u’ = g’(x) = cos(x). Выполните цепное правило,
Выполните цепное правило,
F’ (x) = f’(g(x) )* g’(x) =e sin(x) *cos(x)= e sin(x) cos(x)
Поскольку результат F’(x) соответствует подынтегральной функции, U-подстановка выполнена правильно.
Пример 4 : Найдите первообразную
Решение : Определите внутреннюю функцию u = g(x).
Между 3x и 6x 2 +5 нам нужно выбрать функцию, которая, если взять производную, будет равна другой функции под интегралом.
Давайте попробуем u = 3x:
du = 3dx
Поскольку du = 3dx не соответствует никакой функции под интегралом, необходимо выбрать новое значение u.
Попробуем u = 6x 2 +5
du = 12xdx
Наше уравнение du не соответствует 3xdx под интегралом. Однако мы можем исправить это одним из двух способов:
- Фактор 3 от интеграла, чтобы получить:
Затем разделите уравнение du = 12xdx на 12 с обеих сторон, чтобы получить:
1/12 du = x dx
Теперь уравнение du соответствует внешней функции под интегралом.
- Разделите каждую часть уравнения du на 4, чтобы получить:
¼du = 3xdx
Теперь уравнение du соответствует внешней функции под интегралом.
Воспользуемся первым вариантом.
Возьмите производную от u, чтобы получить du = g’(x)dx.
Как уже определено на предыдущем шаге,
u = 6x 2 +5
1/12 du = xdx
Перепишите интеграл через u и du.
Замените 6x 2 +5 на u и xdx на du. пример 5
Мы видим, что 4x – 1 является внутренней функцией. Возьмем u = 4x – 1
. Возьмем производную от u, чтобы получить du = g’(x)dx.
и = 4х – 1
du = 4 dx
Однако мы не видим 4 dx в подынтегральном выражении. Однако мы можем изменить это, либо разделив на 4 с обеих сторон, либо умножив на ¼ с обеих сторон:
du = 4 dx
¼* du = ¼ * 4 dx
¼du = dx
Теперь уравнение du соответствует дифференциал под интегралом.
Однако нам все равно нужно заменить x перед подынтегральным выражением. Нам нужно вернуться к нашему уравнению u и найти x:
u = 4x -1
u + 1 = 4x
u/4 + 1/4 = x
Таким образом, подынтегральная функция может быть заменена следующим: /4 = x
Перепишем интеграл через u и du.
Замените 4x – 1 = u, dx = ¼ du и x = u/4 + ¼ внутри подынтегральной функции:
| Резюме раздела U-подстановка помогает нам найти интеграл составных функций, в котором функция снаружи du является производной внутренней функции u. U-подстановка (обратное цепное правило) и цепное правило интегрирования являются операциями, обратными друг другу. Если часть подынтегральной функции является композицией функций, f(g(x)), то попробуйте установить u = g(x), «внутреннюю» функцию. Если у нас есть функция в виде y = f(g(x))*g’(x), мы можем подставить u = g(x) и du = g’(x) в формулу. |
Ссылки:
https://www.mathsisfun.com/calculus/integration-by-substitution.html
https://www.khanacademy.org/math/ap-calculus-ab/ab-integration-new /аб-6-9/a/review-applying-u-substitution
https://calcworkshop.com/integrals/u-substitution/
http://scidiv.bellevuecollege.edu/dh/Calculus_all/CC_4_6_FindingAntider.pdf
http://www. opentextbookstore.com/appcalc/Chapter3-4.pdf
Перейти к началу
Интеграция и подстановка U — Уроки Византа
Автор: преподаватель Майкл Б.
Введение
К настоящему времени вы познакомились с одним или несколькими основными правилами интегрирования. Эти правила настолько важны и широко используются, что многие исчисления 9В 2416 книгах эти формулы указаны на внутренней стороне передней и/или задней обложки. Вот некоторые из них (возможно, вы еще не все изучили):
Эти правила так часто публикуются, и все же в них есть тонкий и вводящий в заблуждение момент, который, кажется, обсуждается очень немногими книгами. И это
И это
прискорбно, потому что этот вопрос можно было бы так легко прояснить, если бы только в книгах были опубликованы те же самые формулы в немного отличающейся форме
, показанной ниже.
Видите разницу? Что ж, во втором наборе уравнений используется переменная «u» вместо «x».
«Но», я слышал, вы говорите, «нет никакой реальной разницы. Выбор переменной в любом уравнении произволен.
не должно иметь значения, что я пишу «у» вместо «х», верно?» И да, вы правы. Однако тот факт, что это должны быть общие правила
, противоречит тому факту, что большинство функций, которые мы пишем, уже используют переменную «x». Дело не в том, что обычно публикуемый общий 9Уравнения 2416 неверны, просто они не способствуют прохождению одного из самых важных правил, которым вы должны следовать при решении задач интеграции
, и это тот факт, что вам разрешено интегрировать ТОЛЬКО в соответствии с ИЗВЕСТНЫМИ правила интеграции.
«Но», вы продолжаете возражать, «Я точно знаю, что можно интегрировать некоторые выражения, даже если они не написаны как правила».
Опять же, вы были бы правы. Но чаще всего в таких ситуациях происходит то, что некоторые шаги не отображаются, потому что после
определенного опыта и практики, эти шаги считаются тривиальными, и часто предполагается, что читатель понимает, как применялись правила
для выполнения интеграции. Эти скрытые шаги имеют решающее значение, когда вы учитесь интеграции. Итак, позвольте мне
переформулировать самое важное правило интеграции из всех: вам разрешено интегрировать ТОЛЬКО те выражения, которые ТОЧНО соответствуют ИЗВЕСТНЫМ
правилам интеграции, и никакие другие. Другими словами, пока вы не наберетесь опыта, если то, что вы пытаетесь интегрировать, не совсем соответствует
известному правилу интеграции, вы не сможете это интегрировать.
Итак, какое отношение все это имеет к « U-Substitution »? Что ж, U-подстановка — один из наиболее распространенных методов, которые можно использовать для преобразования проблемы, которая не совсем соответствует известному правилу интегрирования, в ту, которая ему соответствует, без изменения сути проблемы. Затем,
Затем,
, потому что есть точное совпадение, вы можете выполнить интеграцию.
На самом деле эта концепция не должна быть такой уж странной. U-подстановка — это только один метод преобразования, и на самом деле вы, вероятно, уже использовали другие методы преобразования для решения задач интеграции, для которых не требовался метод U-подстановки. Вот пример:
Так что это не выглядит слишком сложно. Но прежде чем мы интегрируем его, давайте вернемся к самому важному правилу. Вы когда-нибудь видели опубликованное правило, в котором
описывает, как интегрировать именно «(x+1)²»? Возможно нет! Поэтому по важнейшему правилу это выражение не может быть проинтегрировано.
Но самое главное правило не говорит о том, что мы не можем преобразовать выражение в эквивалентную форму, что можно проинтегрировать . Мы можем сделать это
довольно легко, применив FOIL к выражению (x+1)(x+1)dx, в результате чего получится (x² + 2x + 1)dx. Но подождите, нет опубликованного правила, определяющего
, как интегрировать (x² + 2x + 1)dx! Но теперь мы можем использовать свойства интегралов, чтобы разбить их на три интеграла, извлечь константы и
, а затем каждый интеграл означает, что в точности соответствует правилу, а именно степенному правилу интегралов:
Следовательно,
Однако проницательный читатель укажет на трудности с этим подходом. Что, если бы мы не просто возводили (x+1) в квадрат, а возводили в 215-ю степень?
Что, если бы мы не просто возводили (x+1) в квадрат, а возводили в 215-ю степень?
Конечно, должен быть более простой способ проинтегрировать (x+1) 215 , чем разложение многочлена! И да, есть — здесь на помощь приходит U-подстановка
. Короче говоря, U-подстановка позволяет в некоторых случаях сделать имеющуюся задачу интеграции похожей на одну из известных задач интеграции 9.2416 правил. Точно так же, как FOILing (x+1)² не меняет выражение, так же как и U-подстановка, с наивной точки зрения. U-подстановка может быть очень
мощным методом преобразований, и это не сложно, но у него есть некоторые особенности, с которыми мы должны быть осторожны, чтобы обращаться с ними должным образом.
Выполнение U-подстановки
Я начал эту статью с отказа от традиционного метода представления формул интегрирования с x вместо u. Причина этого, хотя это несколько надумано, состоит в том, что это затрудняет понимание того, зачем нам нужно изучать u-подстановку. Конечная цель U-Substitution 9Метод 2416 заключается в написании выражения для u как функции x, которое упрощает интеграл, в результате чего получается выражение, которое точно соответствует одному из
известных правил интегрирования, но при этом учитываются детали, которые исчисление налагает на такое действие. Этот метод также часто называют методом
Этот метод также часто называют методом
«замены переменной», потому что мы, по сути, заменяем выражения «x» выражениями «u». Но это не так просто, как заменить x на
u — сделать это считается тривиальным изменением, которое, в конечном счете, вообще не меняет проблему.
Давайте вернемся к приведенному выше примеру и посмотрим, как мы можем выполнить ту же интеграцию, используя технику U-подстановки. Если мы посмотрим на правило степени для интегрирования
, сказав «что-то» вместо «u» или «x», это можно будет прочитать вслух как «интеграл нечто , возведенное в степень n, равен
». что-то , возведенное в степень n+1, деленное на n+1». Ну, (x+1) — это «что-то», не так ли?
Итак, поскольку мы можем присвоить переменной все, что захотим, мы можем присвоить u=x+1. Тогда мы могли бы наивно написать:
Причина, по которой второй интеграл определяется как плохой, заключается в том, что вы не можете (в контексте этого обсуждения U-подстановки) интегрировать
переменную «u» с «dx». Интеграл с «u» должен соответствовать «du». Так как же нам получить «du» вместо «dx»? Это достигается
Интеграл с «u» должен соответствовать «du». Так как же нам получить «du» вместо «dx»? Это достигается
путем взятия производной u по x:
Поскольку du=dx (или, что то же самое, dx=du), теперь мы можем правильно записать интеграл через u и du, завершить интегрирование , а затем повторно подставляем
выражение, которое мы выбрали для u, обратно в уравнение, чтобы завершить решение:
Обратите внимание, что этот ответ точно такой же , как ответ, который мы ранее получили с помощью FOILing (x+1)², хотя он может не сразу казаться таким.
Если мы разложим (x+1) 3 , полученное методом U-подстановки, мы получим x 3 +3x²+3x+1, что при делении всех
этих слагаемых на 3 дает получить (1/3)x 3 +x²+x+(1/3). Может показаться, что в ответе, полученном методом FOILing, отсутствует константа 1/3, но в
на самом деле это нормально, потому что оба интеграла содержат «неизвестную константу C». Тот факт, что член 1/3 отсутствует, просто означает, что он учитывается
Тот факт, что член 1/3 отсутствует, просто означает, что он учитывается
в C из версии интеграла с FOIL. Другими словами, два C различны, и эта разница точно объясняет отсутствующую константу.
Примечание: Довольно часто выбор правильного u является скорее искусством, чем наукой. Иногда вы можете выбрать u только для того, чтобы обнаружить, что вы не можете сделать
замена выглядит как известный интеграл. Возможно, вам нужно выбрать другое u или, возможно, вам нужно сделать что-то немного другое.
Более интересный пример #1
Приведенный выше пример был немного тривиален, потому что мы определили, что dx=du. Давайте теперь рассмотрим более интересный пример, в котором
это не так. В этом процессе мы теперь увидим, что выбор «u» должен быть тщательно выбран, чтобы наш du точно соответствовал всем
других переменных составляющих интеграла.
Как и во всех задачах U-подстановки, наша цель состоит в том, чтобы выбрать выражение x, которое мы можем присвоить u, и, более конкретно, такое выражение, для которого
производная u покрывает любые оставшиеся переменные части интеграла, которые не покрываются вами. При работе с полиномиальными выражениями это часто означает
При работе с полиномиальными выражениями это часто означает
, что мы выбираем более высокую степень из двух многочленов, поскольку производная от многочленов всегда приводит к многочлену более низкой степени. В этом примере
, поэтому естественным выбором будет u = x 4 +2x 2 +5, и, следовательно, du = (4x 3 +8x)dx = 4(x 3 +2x)dx. Это выражение
du содержит член (x 3 +2x)dx, который представляет собой часть интеграла, которая не заменяется нашим выбором «u». Однако он также содержит
постоянных членов 4, но это нормально, потому что константу можно поставить перед интегралом, а наши замены для u и du теперь точно покрывают выражения
x и dx. Мы не можем игнорировать постоянный член, но это не создает проблемы. Вот окончательное решение:
Обратная замена
Иногда после выбора u и решения du вы можете обнаружить, что у вас осталась степень x. Например, рассмотрим следующий пример:
В этом случае вы можете выбрать u=2x+1, а затем du=2dx. Но как насчет x, который остался? Мы можем решить это, решив уравнение u относительно x!
Но как насчет x, который остался? Мы можем решить это, решив уравнение u относительно x!
Это позволяет нам распределить u ½ через член (u+1), а затем мы просто продолжим интегрирование, используя степенное правило:
Определенные интегралы – преобразование пределов
9001 In во всех приведенных выше примерах интегралы были неопределенными интегралами — другими словами, интегралами без пределов интегрирования («а» и «b» в утверждении«интеграл от а до b»). Когда есть ограничения и нам нужно использовать U-замену, нужно помнить о нескольких вещах:
- Пределы не совпадают, когда вы записываете интеграл с u вместо x
- Следовательно, пределы следует либо опустить (как если бы мы вычисляли неопределенный интеграл), либо записать через u
- Если вы решите записать пределы в терминах u, то просто примените уравнение, которое вы присвоили u, чтобы определить новые пределы
- Если вы решите записать пределы через u, то после выполнения интегрирования вы можете напрямую подставить u
ограничивает u-версию интеграла — нет необходимости повторно заменять u на x! В противном случае вы должны вычислить
интеграл с исходными пределами x.
Этот последний пункт может помочь сэкономить много времени при выполнении U-подстановки с определенными интегралами. Следующий пример демонстрирует, что
оба метода дают один и тот же ответ:
Обратите внимание, что при подстановке исходных пределов x первый шаг — точно такая же операция («x+1»), которую вы выполняете. при преобразовании пределов.
Вот почему эти два метода полностью эквивалентны, но метод «преобразования пределов» просто позволяет избежать повторной подстановки
исходного выражения x обратно в интеграл, что помогает устранить ошибки. Также заметьте, что при написании интеграла в методе 2,
, я не указал пределы интегрирования даже для интеграла по х, потому что было бы неправильно говорить, что определенный интеграл от х равен
неопределенный интеграл от и .
Соответствие шаблону вашего du
При выборе вашего u помните, что ваш du также должен быть в уравнении и должен точно учитывать оставшиеся переменные члены x.
Вы не можете добавлять новые переменные, а также (в большинстве случаев) добавлять аддитивные константы к интегралу, чтобы сделать его согласованным. (Вы можете более легко добавлять мультипликативные константы
по мере необходимости, одновременно применяя обратную, чтобы результирующее уравнение было таким же).
Это не обязательно означает, что интеграл не может быть выполнен, но метод U-подстановки строг в том, что вы должны точно сопоставить
u и du в терминах x и dx. Вот пример задачи, которую нельзя решить напрямую с помощью U-замены, но можно решить, предварительно немного поработав
.
Первым шагом к решению этой проблемы может стать установка u=x²+1. Однако если вы это сделаете, то du=2x·dx, и, следовательно, результирующая замена
будет выглядеть так:
известных правил интегрирования из-за того, что
маленький «+1», застрявший в числителе. Вы можете возразить, что мы могли бы разделить этот интеграл на два интеграла, один для du/u, а другой для 1/u,
, но тогда у второго интеграла нет даже du для интегрирования, так что это не работает. .
.
Но, как я уже упоминал изначально, тот факт, что U-Substitution не работает напрямую , не означает, что интеграция не может быть выполнена. Это просто
, для начала нужно немного алгебраических манипуляций:
После выполнения этого алгебраического шага первый интеграл теперь может быть легко обработан с помощью U-подстановки (подробные шаги оставлены читателю
в качестве упражнения, подсказка: u=x²+1), а второй интеграл представляет собой известное интегрирование
Упражнения
Используйте U-подстановку, чтобы вычислить каждый из следующих интегралов и убедиться, что уравнение верно. Возможно, вам придется использовать дополнительные методы
, описанные выше, или другие математические тождества, чтобы решить некоторые из них.
| Легко | Средний | Жесткий |
|---|---|---|
| | | |
| | | |
Изменение переменных
Изменение переменных замена переменных формула для множественных
интегралы подобны u-замене интегралов с одной переменной. Больной
сначала дайте общую формулу замены переменных и рассмотрите
конкретные случаи в более низких измерениях ниже.
Больной
сначала дайте общую формулу замены переменных и рассмотрите
конкретные случаи в более низких измерениях ниже.
Теорема. Пусть U открытое множество в . Пусть функция, которая удовлетворяет:
(a) T инъективен: если , то .
(b) T имеет непрерывные частные производные.
(c) Якобиан отличен от нуля для всех .
Предположим, это интегрируемая функция. затем
Условия на T гарантируют, что замена переменных «прилично себя вели» — например, у нас нет региона U удваивается на себя.
Этот термин состоит из f и T: вы измените переменные в функции, которую вы интегрируете, заменив используя преобразование Т.
Термин приблизительно является фактором, по которому объемы «расширяются» на T. Например, при преобразовании от прямоугольного до полярного в двойном интеграле, это множитель «р» в » «.
В этом курсе важные случаи находятся в более низких измерениях.
Предположим, это координата трансформация самолета. Предположим, что T берет область U в u-v плоскости в область R в плоскости x-y.
В компонентном виде выглядит как
Как и в теореме, мне нужно предположить сделать некоторые технические предположения чтобы убедиться, что преобразование достаточно «хорошее». Конкретно:
1. Т инъективен.
1. T имеет непрерывные первые частные производные.
3. Якобиан отличен от нуля на Q.
Обычно вы можете избежать некоторых исключений из этих условий, если множество исключительных точек «маленькое». Например, если на кривой (технически, на наборе из content 0 ) результат по-прежнему верен. Избегать технические детали, я буду рассматривать только ситуации, в которых можно продолжить.
Согласно вышеприведенным предположениям, изменение формула переменных говорит, что
Чтобы применить формулу для вычисления, вам необходимо:
1. Замените пределы для R на пределы для U.
Замените пределы для R на пределы для U.
2. Используйте уравнения преобразования, чтобы заменить u и v вместо x и у.
3. Вычислите абсолютное значение якобиана и подставьте его в интеграл.
Шаги 1 и 2 кажутся разумными; как насчет шага 3? Идея в том, что для небольшой области в плоскости u-v картина выглядит так:
Для малых приращений u и v, T хорошо аппроксимируется производная . Примените к сторонам маленького прямоугольника в плоскости u-v, чтобы получить маленький параллелограмм в плоскости x-y:
Таким образом, и являются соседними стороны параллелограмма. Площадь параллелограмма равна
То есть якобиан представляет собой фактор, с помощью которого малые площади масштабируется трансформацией. Этим объясняется его присутствие в формула замены переменных.
Пример. Вычислите якобиан трансформация
Пример. Вычислите якобиан
трансформация
Вычислите якобиан
трансформация
Пример. (a) Найдите преобразование, которое переводит единичный квадрат
(Вершины перечислены против часовой стрелки вокруг параллелограмма.)
(b) Пусть R — параллелограмм с вершинами , , , . (Вершины перечислены против часовой стрелки вокруг параллелограмма.)
Используйте преобразование в (а) и замену переменных для вычисления
(a) и , поэтому преобразование
В компонентной форме это
+
(b) Подынтегральная функция
Якобиан
Следовательно,
Пример. (a) Пусть R будет областью в x-y
плоскость, ограниченная слева , , справа , , сверху
, а ниже через . Используйте горизонтальный
сегменты, чтобы найти преобразование координат, которое несет единицу
квадрат, до Р.
(б) Вычислить.
а) Вот область:
Обратите внимание, что его можно разбить на горизонтальные сегменты. Я буду параметризовать сегмент на высоте .
Напомним, что если P и Q — точки, то отрезок от P до Q может быть параметризованным
Вы можете получить эту формулу, найдя векторное уравнение линию через P и Q. Однако проще просто заметить, что она имеет правильная форма для линейного уравнения, и оно проходит через P (множество) и Q (множество) — поэтому оно должно быть правильная вещь.
Левая кривая есть. Set : Then , поэтому я получаю — мне нужен положительный квадратный корень, так как область находится в первом квадранте. Левая точка пересечения является .
Правая кривая есть. Сет: Тогда, так что я получаю. Точка пересечения справа.
Теперь я строю отрезок, соединяющий точки пересечения. Посредством обсуждение выше, это
Каковы пределы? Для параметризации сегмента, которую я использую, u
всегда идет от 0 до 1. v — высота сегмента, а
область простирается от 0 до 1.
v — высота сегмента, а
область простирается от 0 до 1.
Таким образом, преобразование координат
(б) Мы используем преобразование из (а):
Якобиан
Подынтегральная функция
Следовательно,
Пример. (а) Рассмотрим координату трансформация
Найдите изображение R в плоскости x-y квадрата , .
(b) Является ли преобразование инъективным (однозначным) на квадрате?
(c) Используйте формулу замены переменных для вычисления . Проверить вычислением интеграл напрямую. Это работает?
(a) В компонентной форме преобразование
Разумный способ найти изображение — посмотреть, где четыре стороны площади идти.
Посмотрите на сторону А: , . Уравнения становятся , . Устранив тебя, я получаю . Таким образом, эта сторона квадрата отображается на
парабола . Так как и , это часть
парабола, идущая от к .
Так как и , это часть
парабола, идущая от к .
Посмотрите на сторону B: , . Уравнения становятся , . Тогда, так. Это парабола; так как и , у меня есть . Следовательно, я хотите часть параболы, которая идет от до .
Посмотрите на сторону C: , . Уравнения становятся , . Теперь так. Это снова парабола; так как и , я хочу часть параболы, которая удовлетворяет . Он простирается от до .
Наконец, посмотрите на сторону D: , . Уравнения становятся , . Тогда , что является другой параболой. Так как и , я хочу часть параболы, для которой . Это простирается от до .
Область R выглядит как два лепестка или листа. Я нарисовал их ниже, с их ребрами, помеченными в соответствии со сторонами квадрата, который сопоставлены с ними.
(b) Всегда ли разные входные данные дают разные результаты? Нет — если
, то и . То есть все на диагональной линии отображается в начало координат в плоскости x-y. это не
один к одному.





 Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.
Кроме того, уже в этом примере использование метода подведения функции под знак дифференциала значительно повышает риск запутаться в решении.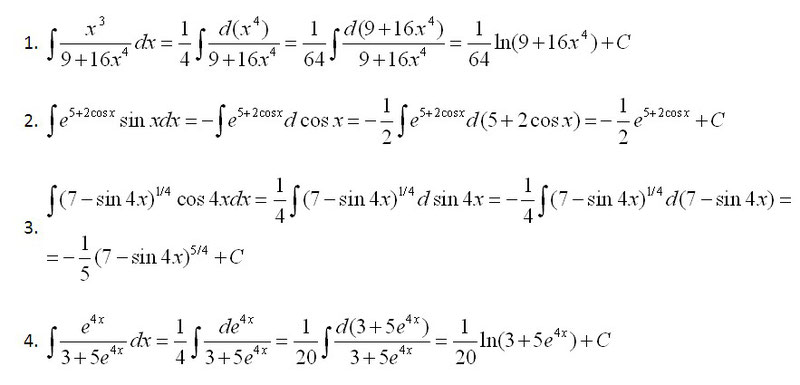


 Примеры решений
Примеры решений Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей. … что-то лирической получается статья, ах да… весна же пришла.
… что-то лирической получается статья, ах да… весна же пришла.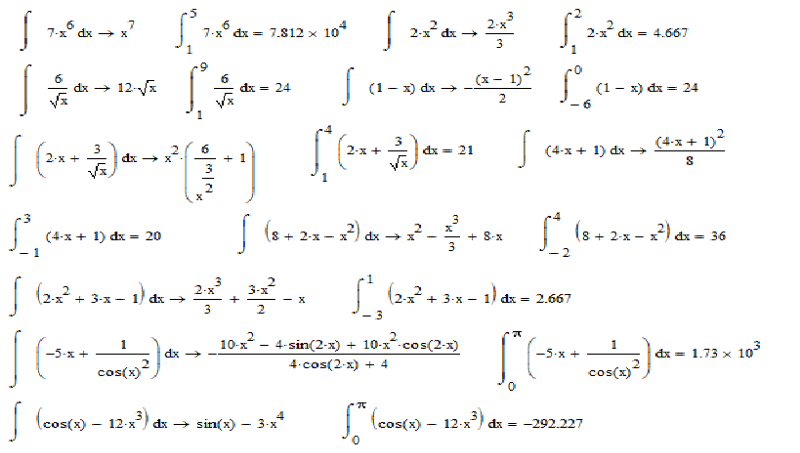 ..
..
 Тогда интеграл сложной функции:
Тогда интеграл сложной функции: