Заказать решение линейного программирования — выполнение задач и заданий на заказ онлайн
Оглавление:
| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказаМинимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказСначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибокВ течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила примеры оформления заказов по некоторым темам предмета линейного программирования, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Основная задача линейного программированияФормулировка основной задачи. Основная задача линейного программирования формулируется так:
Дана линейная форма (целевая функция)
и задана система линейных неравенств (ограничений)
которую перепишем в виде
Найти максимум (минимум) формы (2.1) при выполнении условий (2.2).
Другими словами, среди решений системы (2.2) (образующих многогранник ) надо отыскать такое, для которого форма (2.1) принимает наибольшее (наименьшее) значение.
Как будет показано в следующей главе, эта задача служит математической моделью многих важных практических задач.
- Геометрическая интерпретация. Основную задачу линейного программирования можно легко интерпретировать геометрически.
 Каждое неравенство
Каждое неравенство
системы (2.2) определяет в евклидовом -мерном пространстве полупространство, состоящее из точек расположенных «по одну сторону» от плоскости
и на самой этой плоскости. Точки же, принадлежащие всем полупространствам (2.2) (т. е. множество всех решений системы (2.2)) как пересечение выпуклых множеств, образуют некоторый выпуклый многогранник *).
Значение функции
в точке можно рассматривать как уклонение точки от плоскости
понимая (как в п. 2 § 1 гл. I) под уклонением данной точки от этой плоскости число, которое получим, подставив в левую часть уравнения (*) вместо координаты этой точки. Так, например, уклонение точки (1, —2, 5) от плоскости
равно числу
Уклонение точки от плоскости (*) пропорционально расстоянию от точки до этой плоскости.
Таким образом, геометрический смысл задачи линейного программирования заключается в отыскании в многограннике точки, которая наиболее (наименее) уклонена от плоскости (*).
В случае двумерного пространства имеем картину, изображенную на рис. 1—4.
Здесь многогранником является многоугольник, плоскостями
прямые, полупространствами — полуплоскости (на рисунках они отмечены штриховкой).
Ясно, что решением задачи линейного программирования будет какая-то вершина многогранника 2. На рис. 1 решение задачи максимизации формы (2.1) дает вершина , а задачи минимизации этой формы —вершина , причем эти решения единственны.
На рисунках 2 — 4 приведены: случай существования бесчисленного множества решений (рис. 2), случай неограниченности функции на (рис. 3) и, наконец, случай отсутствия решения (рис. 4).
Другую геометрическую интерпретацию задачи линейного программирования получим, если будем рассматривать эту
задачу в -мерном пространстве переменных в котором линейная форма
является уравнением плоскости (проходящей через начало координат). Система же неравенств
определяет в этом пространстве некоторую выпуклую призму гранями (-мерными) которой служат плоскости
параллельные оси . В «горизонтальной» плоскости , т. е. в л-мерном пространстве переменных эти плоскости ограничивают многогранник , на который проектируется часть плоскости (2.1)—«срез», вырезаемый призмой (2.2), так что можно рассматривать как область определения линейной функции (2.1). Надо найти ту из вершин , в которую проектируется вершина «среза» с наибольшей (наименьшей) координатой (в трехмерном пространстве — аппликатой) .
В «горизонтальной» плоскости , т. е. в л-мерном пространстве переменных эти плоскости ограничивают многогранник , на который проектируется часть плоскости (2.1)—«срез», вырезаемый призмой (2.2), так что можно рассматривать как область определения линейной функции (2.1). Надо найти ту из вершин , в которую проектируется вершина «среза» с наибольшей (наименьшей) координатой (в трехмерном пространстве — аппликатой) .
На рис. 5 изображение дано для случая . «Срез» заштрихован. Наибольшее на значение линейная функция (2.1) достигает в вершине , в которую проектируется вершина «среза» с наибольшей аппликатой.
О методе решения задачи линейного программирования. Нетрудно понять, что обычные методы классического математического анализа для отыскания наибольшего (наименьшего) значения функции неприменимы к рассматриваемой задаче.
Эти методы, сводя задачу к отысканию множества точек, «подозрительных на экстремум», и к сравнению значений функции в этих точках, становятся малопригодными, если число таких точек велико.
Линейная же форма (2.1), определенная на многограннике , заданном неравенствами (2.2), достигает своего наибольшего (наименьшего) значения в некоторой вершине этого многогранника, так что множеством точек, «подозрительных на экстремум», является множество всех вершин многогранника , число которых обычно бывает огромным.
Основным методом решения общей задачи линейного программирования, позволяющим преодолеть эти затруднения, является так называемый симплекс-метод Данцига [30а, 306], подробное описание которого дано в §§ 2, 3.
Симплекс-метод состоит из алгорифма отыскания какого-нибудь опорного среди решений системы линейных неравенств (2.2), т. е. решения-вершины многогранника (или из установления факта несовместности системы), и из алгорифма последовательного перехода от полученного уже опорного решения системы (2.2) к новому опорному решению, для которого форма (2.1) имеет большее (меньшее) значение (до получения максимизирующего (минимизирующего), т. е. оптимального решения).
Пример оформления заказа №1.Основу вычислительной схемы симплекс-метода составляют модифицированные жордановы исключения.
Найти какое-нибудь опорное
Составляем таблицу
и исключаем лишь свободную переменную (см. замечание в конце п. 2). Для этого делаем шаг модифицированного жорданова исключения с разрешающим элементом 1, взятым в рамку. Получим таблицу
из которой выписываем выражение для :
и переходим к отысканию опорного решения. Третья строка содержит отрицательный свободный член. В этой же строке есть два отрицательных коэффициента — 2 и — 11. Выбираем в качестве разрешающего, например, первый столбец, содержащий коэффициент — 2, и сравниваем все неотрицательные отношения свободных* членов к соответствующим коэффициентам первого столбца:
Меньшее из них , однако в случае вырождения мы берем знаменатель разрешающим элементом, лишь если он положителен. Поэтому берем следующее по величине отношение у и его знаменатель 1 будет разрешающим элементом.
После шага модифицированного жорданова исключения получим таблицу
в которой остался отрицательный свободный член —1. Превратим его в положительный, сделав шаг модифицированного жорданова исключения с разрешающим элементом — 1, взятым в рамку, так как есть всего одно положительное отношение свободных членов к коэффициентам второго столбца, взятого разрешающим.
Из полученной таблицы
в которой нет отрицательных свободных членов, находим опорное решение нашей системы. Для этого полагаем
Тогда
Подставив значения для в выражение для находим
Мы получили, таким образом, следующее опорное решение:
Пример оформления заказа №2.Найти опорное решение системы
Составляем таблицу
и приступаем к отысканию опорного решения системы, не производя исключения координат.
Четвертая строка содержит отрицательный свободный член —7. Просматриваем, например, первый столбец коэффициентов, содержащий отрицательный коэффициент —1 этой строки, составляем неотрицательные отношения свободных членов к коэффициентам этого столбца и находим наименьшее из них:
так что разрешающим элементом будет 1 из первой строки.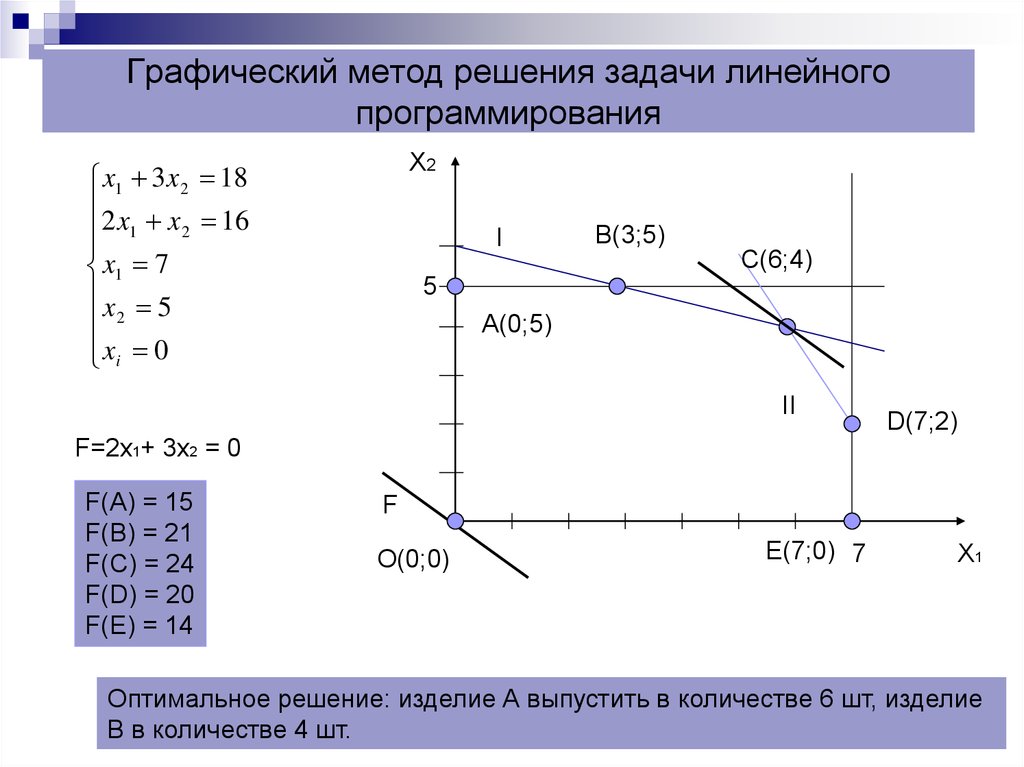
В результате шага модифицированного жорданова исключения с этим разрешающим элементом получаем таблицу
в которой еще остается отрицательный свободный член —1, но строка, в которой он находится, не содержит отрицательных коэффициентов, следовательно, система несовместна.
Возможно эти страницы вам будут полезны:
Решение задач линейного программирования симплекс-методом
Замечание 1
Решение задач линейного программирования симплекс-методом — это решение задач линейного программирования путём нахождения исходного допустимого плана с последующим улучшением плана, вплоть до достижения экстремального значения целевой функции.
Введение
Симплекс метод — это метод поочерёдного перемещения от одного основного решения системы ограничений задачи линейного программирования к другому основному решению до того момента, пока целевая функция не достигнет требуемого экстремального значения, то есть, своих максимальных или минимальных значений.
Симплекс-метод считается универсальным методом, при помощи которого может быть решена любая задача линейного программирования, при этом, следует отметить, что графический метод может быть использован только для системы ограничений с двумя переменными. Симплекс метод разработал американский математик Р. Данциг в 1947-ом году, с той поры многие специалисты при помощи этого метода решают задачи линейного программирования, в которых присутствуют многие тысячи переменных и ограничений.
Решение задач линейного программирования симплекс-методом
Любое неотрицательное решение системы ограничений именуется допустимым решением. Предположим есть система m ограничений с n переменными (m меньше n). Допустимым базисным решением считается решение, которое содержит m неотрицательных основных, то есть базисных, переменных и (n – m) неосновных, то есть небазисных или свободных переменных. Неосновные переменные в базисном решении равняются нулю, основные же переменные обычно отличаются от нуля, что означает, что они положительные числа.
Любые m переменных системы m линейных уравнений с n переменными являются основными в случае, когда определитель из коэффициентов при них отличается от нуля. В таком случае остальные n — m переменных могут считаться неосновными или свободными.
Симплекс метод может быть представлен следующим алгоритмом:
- Сначала следует представить задачу линейного программирования в канонической форме. Для этого необходимо перенести все свободные члены в правые части (в случае, когда среди данных свободных членов имеются также отрицательные, то такие уравнения или неравенства следует умножить на минус единицу) и во все ограничения добавить дополнительные переменные, имеющие знак плюс, если в исходном неравенстве знак «меньше или равно», и имеющие знак минус, если в исходном неравенстве «больше или равно».
- Если в сформированной системе получилось m уравнений, то m переменных следует считать основными. Далее нужно отобразить основные переменные через неосновные и определить необходимое базисное решение.
 Если вычисленное базисное решение будет допустимое, то следует перейти к допустимому базисному решению.
Если вычисленное базисное решение будет допустимое, то следует перейти к допустимому базисному решению. - Далее необходимо найти выражение функции цели через неосновные переменные допустимого базисного решения. В случае, когда ищется экстремум линейной формы и в его выражении не присутствуют неосновные переменные с отрицательными (положительными) коэффициентами, то условие оптимальности считается выполненным и найденное базисное решение может считаться оптимальным, то есть, процесс решения завершён. Если при определении экстремума линейной формы в её выражении присутствует одна или больше неосновных переменных с отрицательными (положительными) коэффициентами, то следует осуществить переход к новому базисному решению.
- Из совокупности неосновных переменных, которые входят в линейную форму с отрицательными (положительными) коэффициентами, следует выбрать ту, которой будет соответствовать самый большой (по модулю) коэффициент, и перевести её в основные. Далее необходимо перейти ко второму этапу.

При реализации алгоритма симплекс-метода, необходима соблюдать следующие важные условия:
- В случае, когда допустимое базисное решение представляет собой оптимум линейной формы, то есть исполнен критерий оптимальности, а в выражении линейной формы, представленной неосновными переменными, не присутствует хотя бы одна из них, то, следовательно, найденное оптимальное решение не является единственным.
- В случае, когда в выражении линейной формы присутствует неосновная переменная с отрицательным коэффициентом в варианте нахождения её максимума (с положительным коэффициентом в случае нахождения её минимума), а в каждое уравнение системы ограничений данного этапа эта переменная включена также с отрицательным коэффициентом или отсутствует, то линейная форма ничем не ограничивается при существующей ограничительной системе. В таком варианте экстремум линейной формы будет равняться плюс или минус бесконечности.
Следует отметить, что в сети Интернет имеются сайты с онлайн калькуляторами, предназначенными для решения задач линейного программирования симплекс-методом.
Рассмотрим стандартный пример, когда система ограничений рассматривается как совместимая и присутствует единственное конечное оптимальное решение.
Задачи линейного программирования могут решаться также симплекс-методом, но с использованием специальных симплексных таблиц. Построение симплексных таблиц позволяет найти решение задачи линейного программирования значительно проще, чем при использовании алгебраических преобразований. Симплексные таблицы обладают достаточно наглядным отображением. Известны различные наборы правил по работе с симплексными таблицами. В том числе правило, которое наиболее часто рассматривается как правило ведущих столбцов и ведущих строк.
Необходимо определить максимум следующей функции:
$F=x_1 + 2x_2$
При наличии следующих ограничений:
Рисунок 1. Ограничения. Автор24 — интернет-биржа студенческих работ
$x_1≥0, x_2 ≤ 0$
Сначала необходимо добавить некоторые переменные x3, x4, x5, x6, которые должны быть неотрицательными, и свести эту систему неравенств к эквивалентной ей системе уравнений:
Рисунок 2. Система уравнений. Автор24 — интернет-биржа студенческих работ
Система уравнений. Автор24 — интернет-биржа студенческих работ
$ X_j ≥0 (j=1, 2, …6)$
Из коэффициентов при переменных (неизвестных) может быть построена симплексная таблица. В последнюю строку таблицы должна быть записана целевая функция. Эта строка называется индексной строкой.
Задачи по линейному программированию с решением онлайн
Если у вас нет времени на выполнение заданий по линейному программированию, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.
Ответы на вопросы по заказу заданий по линейному программированию:
Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.
Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ.
 Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Линейное программирование», если у вас есть желание и много свободного времени!
Содержание:
- Ответы на вопросы по заказу заданий по линейному программированию:
- Линейное программирование
- Задача 1.

- Задача 2.
- Графический метод решения задачи линейного программирования
- Задача 3.
- Симплексный метод решения задачи линейною программирования
- Задача 4.
- Задача 5.
- Задача 6.
- Метод искусственных переменных
- Задача 7.
- Взаимно двойственные задачи линейного программирования
- Задача 8.
- Задача 9.
- Задача 10.
Линейное программирование
Задача линейного программирования. Каноническая и стандартная формы
Основные сведения
Пусть — множество, заданное системой ограничений
где каждый из знаков означает или Предполагается, что система (7.1) содержит неравенства
Пусть также задана линейная функция
Множество называется допустимым, а любая точка — допустимым решением; функция называется целевой функцией. Задача линейного программирования (ЛП) состоит в отыскании наибольшего или наименьшего значения целевой функции (7.3) на множестве допустимых решений. Записывается это следующим образом:
Записывается это следующим образом:
при
Любая точка для которой — наибольшее (наименьшее) значение на называется оптимальным решением.
Если система (7.1) состоит только из уравнений и неравенств вида (7.2), то говорят о канонической форме задачи ЛП, если же в системе (7.1) присутствуют только неравенства, то говорят о стандартной форме задачи ЛП. Если предполагается, что
целые числа, то соответствующая задача называется целочисленной. Любая задача ЛГ1 может быть сведена как к канонической, так и к стандартной форме.
Возможно, вас также заинтересует эта ссылка:
Решение задач по линейному программированию с примерами онлайн |
Задача 1.
Стальные прутья длиной 110 см требуется разрезать на заготовки длиной 50, 45, 30 см. Заготовок длиной 50 см должно быть изготовлено не менее 20, длиной 45 см — не менее 40, длиной 30 см не менее 60. Сколько прутьев и каким способом следует разрезать, чтобы получить указанное количество заготовок при минимальных отходах? Составить математическую модель этой задачи.
Сколько прутьев и каким способом следует разрезать, чтобы получить указанное количество заготовок при минимальных отходах? Составить математическую модель этой задачи.
- Решение:
Нетрудно перебрать все возможные варианты разреза (табл. 7.1):
Пусть — количество прутьев, разрезаемых по варианту с номером Набор натуральных чисел составляет план разреза. Из условий задачи вытекают следующие oipa-ничения на неизвестные
Суммарное количество отходов описывается функцией
В итоге приходим к следующей стандартной задаче ЛП:
при условиях (7.4).
Сформулированную задачу можно привести к канонической форме. Это достигается введением дополнительных (балансовых) переменных
Возможно, вас также заинтересует эта ссылка:
Контрольная работа по линейному программированию заказать |
Задача 2.

На двух складах имеется 50 и 100 тонн товара соответственно. Потребности магазинов в товаре соответственно равны 30, 40, 80 тонн. Известны тарифы перевозок , где — стоимость в рублях перевозки одной тонны товара со склада в магазин Найти минимальный по стоимости план перевозки товара со складов в магазины. Составить математическую модель этой задачи.
- Решение:
Пусть — количество товара в тоннах, предназначенное к перевозке из склада в магазин. Набор чисел
составляет план перевозок. Так как в данном случае суммарные запасы равны суммарным потребностям: 50 + 100 = 30 + 40 + 80, то с каждого склада должен быть вывезен весь товар. Это приводит к уравнениям
Поскольку потребность каждого магазина также должна быть удовлетворена, то имеем еще три уравнения: Очевидно также, что
Суммарная стоимость всех перевозок задается линейной функцией
В итоге имеем каноническую задачу линейного программирования:
при условиях (7. 5) — (7.7).
5) — (7.7).
Данная задача приводится к стандартной форме следующим образом. Преобразуем систему (7.5), (7.6) методом Гаусса к виду с базисными неизвестными и свободными неизвестными В силу (7.7) справедливы неравенства
Заменив в (7.8) базисные неизвестные по формулам (7.9), приведем целевую функцию к виду Таким образом, получаехМ задачу линейного программирования в стандартной форме
при условиях (7.10), (7.11), эквивалентную задаче в канонической форме.
Возможно, вас также заинтересует эта ссылка:
Помощь по линейному программированию онлайн |
Графический метод решения задачи линейного программирования
Основные сведения
Рассматривается задача ЛП в стандартной форме при Допустимое множество (заданное неравенствами) — выпуклое множество на плоскости Целевая функция имеет вид
Прямые вида где — постоянная, называются линиями уровня. Все линии уровня параллельны друг другу
Все линии уровня параллельны друг другу
и перпендикулярны общему вектору нормали
Задача линейного программирования с двумя переменными допускает решение графическим методом, который состоит в следующем:
- 1) строится допустимое множество
- 2) если — пустое множество, то задача неразрешима, так как система ограничений противоречива;
- 3) если — непустое множество, то рассматриваются линии уровня При монотонном увеличении от прямые смещаются параллельно в направлении вектора
Если при таком перемещении линии уровня существует первая общая точка линии уровня и множества то — минимум на множестве Если — последняя точка пересечения
линии уровня и множества то в этой точке достигается максимум на множестве Если при неограниченном уменьшении
параметра прямая пересекает множество то
Если аналогичное свойство справедливо при неограниченном увеличении параметра то
Задачи линейного программирования общего вида допускают решение графическим методом, если их можно преобразовать к задаче с двумя независимыми переменными.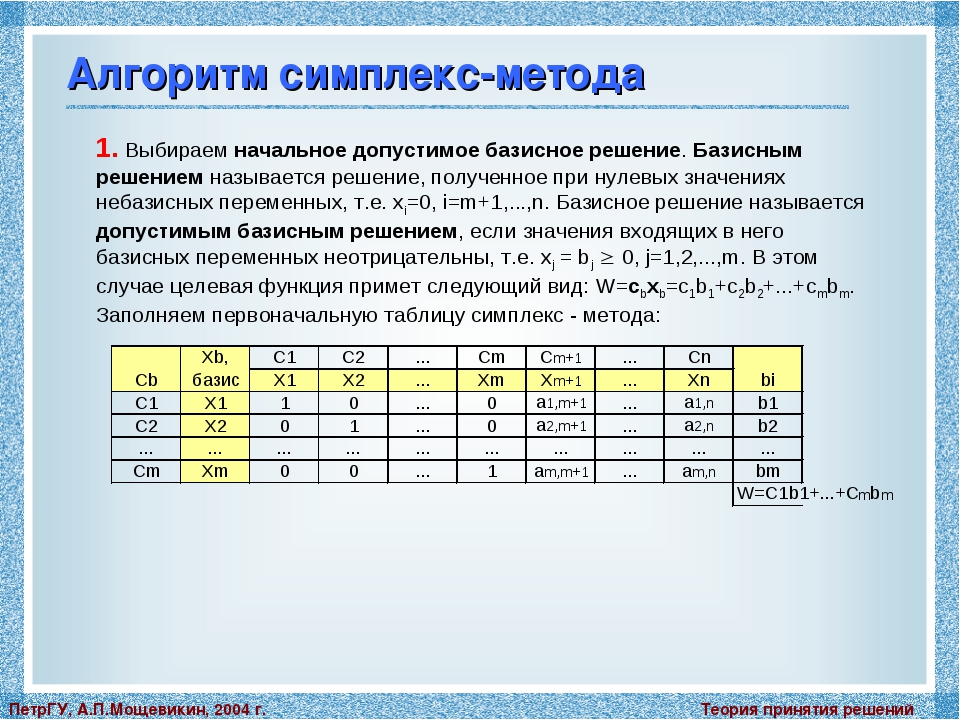
Возможно, вас также заинтересует эта ссылка:
Курсовая работа по линейному программированию заказать готовую онлайн |
Задача 3.
Найти минимальное и максимальное значения целевой функции при условиях:
- Решение:
На рис. 7.1 изображены допустимое множество линия уровня и вектор нормали Перемещая линию
уровня по направлению вектора находим сначала точку минимума целевой функции а затем точку максимума
2. Решить следующую задачу линейного программирования:
После исключения переменных получим задачу с двумя переменными:
Решая последнюю задачу графическим методом (рис. 7.2), находим ее оптимальное решение
Затем вычисляем значения переменных исходной задачи, соответствующие координатам точки
В результате получаем оптимальное решение исходной задачи:
Возможно, вас также заинтересует эта ссылка:
РГР по линейному программированию расчетно графическая работа |
Симплексный метод решения задачи линейною программирования
Основные сведения
Для решения задач линейного программирования симплексным методом следует выполнить ряд подготовительных операций.
- 1. Привести задачу к каноническому виду.
- 2. Преобразовать систему ограничений (уравнений) к специальному виду, в котором переменные разделены на базисные и свободные, а соответствующее базисное решение — неотрицательное (оно называется допустимым базисным решением или опорным решением).
Пример такой системы:
где — базисные переменные, — свободные переменные
3. Исключить из целевой функции базисные переменные с помощью (7.12) и записать ее в виде
Коэффициенты называются оценками соответствующих переменных
Из (7.12), (7.13) следует, что на допустимом базисном решении
целевая функция принимает значение
После выполнения подготовительного этапа заполняется начальная симплекс-таблица (табл. 7.12):
Здесь и ниже используются следующие сокращения:
- 1. — базисные неизвестные.
- 2. — свободные члены.
Таблица соответствует системе уравнений (7.12) с присоединенной целевой функцией (7. 13). Последняя строка таблицы называется строкой оценок.
13). Последняя строка таблицы называется строкой оценок.
Пусть решается задача о нахождении минимума функции
Тогда цель дальнейших симплексных преобразований таблиц состоит в нахождении новых допустимых базисных решений, на которых значение целевой функции уменьшается (или не увеличивается). Алгоритм симплексных преобразований следующий.
1. Если в строке оценок среди чисел имеется хотя бы одна положительная (например, а в соответствующем столбце
(разрешающем столбце) хотя бы один положительный элемент, то решение может быть улучшено. Среди указанных положительных элементов столбца в качестве разрешающего элемента выбирается тот, которому отвечает минимальное отношение
Если имеется несколько элементов с подобным свойством, то в качестве разрешающего выбирается любой из них. В таблице таким элементом является Далее над таблицей проводятся элементарные преобразования: переменная становится базисной, a — свободной. На новом базисном решении значение целевой функции не увеличивается, и снова анализируется строка оценок.
2. Если в строке оценок нет положительных чисел, то оптимальное решение найдено.
3. Если в строке оценок есть положительное число, а в соответствующем ей столбце нет положительных элементов, то задача линейного программирования не имеет решения. В задаче о нахождении минимума функции это обозначается так:
4. Если в последней строке нет положительных оценок, но при этом имеются свободные переменные, равные нулю, то задача имеет, по крайней мере, одно альтернативное решение (чтобы его получить, следует сделать еще одно преобразование, выбрав разрешающий столбец с нулевой оценкой).
Как правило, множество оптимальных решений совпадает с выпуклой оболочкой всех альтернативных (базисных) решений. Исключением является случай, когда в процессе перебора альтернативных решений возникает нулевая оценка, такая, что в соответствующем столбце нет положительных чисел.
При решении задачи о поиске максимума функции алгоритм меняется только в том, что разрешающий столбец выбирается по отрицательной оценке в последней строке.
Задача 4.
Решить симплекс-методом задачу:
- Решение:
Переменные — базисные. Исключив их из целевой функции, получаем На исходном базисном решении значение целевой функции
Заполним начальную симплексную таблицу 7.13 и преобразуем ее.
Все оценки в последней строке неположительные, следовательно, получено оптимальное решение
Заметим, что значения базисных переменных и целевой функции получены из первого столбца симплекс-таблицы.
Задача 5.
Решить задачу линейного программирования:
- Решение:
Преобразуем целевую функцию: Система имеет исходное базисное решение со значением целевой функции Заполним симплексную таблицу (табл. 7.14) и преобразуем ее в соответствии с алгоритмом.
В последней строке есть положительная оценка но в соответствующем столбце нет ни одного положительного элемента, следовательно, задача не имеет решения:
Задача 6.
Решить задачу линейного программирования:
- Решение:
Исходное базисное решение Заполним начальную симплексную таблицу с учетом того, что и выполним последовательность преобразований таблиц в соответствии с алгоритмом симплекс-метода.
Анализ третьей и четвертой таблиц показывает, что минимальное значение целевой функции достигается на соответствующих этим таблицам базисных решениях: и Следовательно, общее оптимальное решение имеет вид:
Использование симплекс-метода
для отыскания допустимого базисного решения.
Метод искусственных переменных
Основные сведения
Для решения задачи линейного программирования симплексным методом необходимо, чтобы исходная система ограничений-уравнений имела вид, допускающий неотрицательное базисное решение. Вели это пребование не выполнено, то можно решить симплекс-методом вспомогательную задачу, что приведет систему ограничений к нужному виду. Алгоритм решения вспомогательной задачи следующий.
1. Исходная система ограничений- уравнений переписывается в виде
где все свободные члены
2. В каждое уравнение системы (7.14) вводятся искусственные переменные
Решение системы (7.15) а сама система имеет допустимое базисное решение
3. Рассматривается вспомогательная целевая функция
и симплексным методом решается задача линейного программирования
при ограничениях (7.15).
Если эта задача имеет решение, то возможны два случая.
1) Тогда исходная система (7.14) не имеет неотрицательных решений.
2) Система (7.14) имеет неотрицательное базисное решение. Если в последней симплекс-таблице вспомогательной задачи все искусственные переменные — свободные, то из этой таблицы несложно получить систему уравнений, эквивалентную (7.14) и преобразованную к виду, необходимому для решения исходной задачи линейного программирования.
Задача 7.
Преобразовать следующую систему уравнений к виду, допускающему неотрицательное базисное решение:
- Решение:
Введем искусственные переменные в двух последних уравнениях (в первом уравнении уже имеется базисная переменная
и рассмотрим вспомогательную целевую функцию Учитывая (7. 16), получаем
16), получаем
Решим задачу при ограничениях (7.16). Решение дано в виде последовательности симплекс-таблиц (табл. 7.15).
Вспомогательная задача решена, искусственные переменные стали свободными переменными. Это означает, что система уравнений (7.15) преобразована к нужному виду
допускающему неотрицательное базисное решение
Взаимно двойственные задачи линейного программирования
Основные сведения
Следующие задачи линейного программирования в стандартной форме, записанные в матричной форме, называются симметричной парой взаимно двойственных задач:
— матрица коэффициентов и транспонированная матрица; — столбцы неотрицательных иеизвестпых; — столбцы правых частей; — константа.
Решения задач I и II взаимосвязаны. Решив любую из них (исходную задачу), можно восстановить решение другой (двойственной задачи).
Первая теорема двойственности. Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны:
При этом оптимальные значения целевых функций обеих задач равны:
Вторая теорема двойственности. Оптимальные решения
пары двойственных задач связаны между собой следующими соотношениями:
Замечание. Если исходная задача неразрешима из-за неограниченности целевой функции, то двойственная задача неразрешима из-за отсутствия допустимых решений (и наоборот).
Пусть теперь рассматривается общая задача линейного программирования. Приведем правила построения двойственной задачи. Матрицу коэффициентов при неизвестных дополним справа столбцом знаков неравенств и равенств для соответствующих ограничений, а также столбцом правых частей. Снизу матрицу дополним строкой ограничений для неизвестных: если при отсутствии ограничения на знак неизвестной; еще ниже добавим строку коэффициентов целевой функции. В результате получим следующую матрицу:
Тогда аналогичная матрица двойственной задачи выглядит следующим образом:
Из сравнения матриц (7.17) и (7. 18) видно, что числовые части этих матриц получаются друг из друга транспонированием. Строка неравенств исходной задачи переходит без изменения в столбец неравенств двойственной задачи, причем символ переходит в знак Столбец неравенств исходной задачи переходит в строку ограничений на неизвестные, причем знаки неравенства меняются на противоположные, а знаки на знаки
18) видно, что числовые части этих матриц получаются друг из друга транспонированием. Строка неравенств исходной задачи переходит без изменения в столбец неравенств двойственной задачи, причем символ переходит в знак Столбец неравенств исходной задачи переходит в строку ограничений на неизвестные, причем знаки неравенства меняются на противоположные, а знаки на знаки
При этом для пары двойственных задач с матрицами (7.17) и (7.18) остаются в силе формулировки первой и второй теорем двойственности.
Преобразуем пару двойственных задач в стандартной форме к канонической форме. При этом в задаче I появятся дополнительных неизвестных по числу основных ограничений, а в задаче дополнительных неизвестных Поэтому
число неизвестных в каждой задаче станет равным одному и тому же числу Можно установить взаимнооднозначное соответствие между этими неизвестными, а именно, основные неизвестные задачи I будут соответствовать дополнительным неизвестным задачи И, и дополнительные неизвестные задачи 1 — основным неизвестным задачи II.
Установленное соответствие позволяет находить решение двойственной задачи по заключительной симплекс-таблице основной задачи. А именно, выделим из последней симплекс-таблицы строку целевой функции. Если число, стоящее в ней, начиная со второго, взять с противоположным знаком, а затем воспользоваться соответствием между неизвестными обеих задач, то получим оптимальное решение двойственной задачи. Первое число в указанной строке дает искомый оптимум целевой функции.
Задача 8.
Сформулировать двойственную задачу линейного программирования для следующей задачи:
- Решение:
Составим расширенную матрицу данной задачи:
В соответствии с указанными правилами расширенная матрица двойственной задачи будет выглядеть следующим образом:
Поэтому развернутая запись двойственной задачи имеет вид:
Задача 9.
Найти решение следующей задачи линейного программирования, используя первую и вторую теоремы двойственности:
- Решение:
По общему правилу составим двойственную задачу:
Двойственная задача совпадает с задачей из § 7. 2, которая была решена графическим методом, и ее оптимальное решение
2, которая была решена графическим методом, и ее оптимальное решение
Чтобы найти оптимальное решение исходной задачи, заметим, прежде всего, что выполняются строгие неравенства Этим переменным соответствуют первые два неравенства исходной задачи, которые по второй теореме двойственности обращаются в равенства:
Чтобы найти недостающее уравнение, подставим значения в неравенства двойственной задачи:
Поскольку третье неравенство строгое, то по второй теореме двойственности соответствующая этому неравенству переменная Таким образом, имеем систему уравнений:
откуда При этом достигается минимум функции что совпадает с ранее найденным значением
Задача 10.
Решить симплексным методом задачу ЛП. По заключительной таблице найти решение двойственной задачи.
- Решение:
Для решения задачи ЛП симплекс-методом введем дополнительные переменные и изменим знак целевой функции
Запишем исходную симилекс-таблицу для данной задачи и решим ее симплекс-методом (табл. 7.16):
7.16):
Поскольку в строке коэффициентов целевой функции все коэффициенты неположительные, то решение исходной задачи таково: на базисном решении Поэтому исходная задача имеет решение
Двойственная задача к исходной выглядит следующим образом:
Установим соответствие между неизвестными исходной и двойственной задач, записанными в канонической форме:
поэтому из строки коэффициентов целевой функции последовательно находим:
Таким образом, решение двойственной задачи на базисном решении
Возможно, вас также заинтересует эта ссылка:
Заказать работу по линейному программированию помощь в учёбе |
Кафедры — Механико-математический факультет
- НГУ org/Breadcrumb» itemprop=»child» itemref=»bx_breadcrumb_2″>Механико-математический факультет
- Кафедры
- Кафедра теоретической кибернетики
Задать вопрос
О кафедре
Подробнее
Кафедра теоретической кибернетики – одна из старейших и основных выпускающих кафедр механико-математического факультета. Она создана в 1965 году известным математиком, членом-корреспондентом АН СССР А.А. Ляпуновым, возглавлявшим ее до 1973 года. В разные годы ею руководили такие выдающиеся ученые, как чл.-корр. АН СССР А.П. Ершов, чл.-корр. АН СССР В.Л. Макаров и проф. В.Т. Дементьев. Ежегодно на кафедру приходит специализироваться около 30 студентов, а общее число единовременно специализирующихся студентов и аспирантов доходит до 80 человек. Значительная часть выпускников впоследствии успешно защищают кандидатские и докторские диссертации и продолжают работать в академических институтах и вузах.
Старый сайт кафедры.
Заведующий кафедрой
Ерзин Адиль Ильясович
д.ф.-м.н., профессор
Телефон: +7 (383) 329 7540
E-mail: [email protected]
Секретарь кафедры
Тахонов Иван Иванович
к. ф.-м.н.
ф.-м.н.
Телефон: +7 (383) 363-41-52 (tone) 5351
E-mail: [email protected]
Новости/объявления
Подробнее
Объявления общего характера
- В настоящий момент идёт перенос инф. со старого сайта old-tc.nsu.ru, который стало невозможно поддерживать…
- Для получения подписи зав. кафедрой оставьте документы (подписанные вами и, если требуется, вашим науч. руководителем) в папке Ерзина на вахте ИМ
Ознакомительный семинар для 3-курсников
Для студентов 3 курса ММФ с 4 октября начинает работать семинар, который поможет выбрать научного руководителя. На каждом семинаре выступят 1-3 преподавателя с рассказами о предлагаемой тематике исследований. Семинар будет проходить очно в течение 1 часа по вторникам с 16:30 в к. 220 ИМ. Пополняемая программа:
(1) 4 октября:
- зав. каф., проф. А.И. Ерзин (60 мин.
 ). «О специализации на кафедре и о задачах комбинаторной оптимизации»
). «О специализации на кафедре и о задачах комбинаторной оптимизации»
(2)
11 октября:
- проф. А.А. Евдокимов (30 мин.). «Комбинаторика символьных последовательностей в приложениях к задачам анализа генетической информации»
(3)
18 октября:
- проф. Ю.А. Кочетов (30 мин.). «Дискретные задачи размещения»
(4)
25 октября:(5) 1 ноября:
(6) 8 ноября:
Объявления о спецкурсах и семинарах
- Семинар «Теория графов» (заседание №1521): 4 октября, 16.20, к.344 ИМ СО РАН.
- С.В. Августинович, Профили инвариантов оптимизационных задач.
- Математические модели принятия решений: вторник, 27 сентября, 11.
 00, online.
00, online.
- Шперлинг Софья — Обзор подходов к решению задач фигурного раскроя
- Семинар «Криптография и криптоанализ». вторник, 27 сентября, 14:30, ау. 1155 (новый корпус НГУ).
- Куценко А.В. «Введение в квантовые вычисления: приложения к криптоанализу»
- Годовой спецкурс «Методы принятия решений» (рук. Э.Х. Гимади) начинает работу. Организационное собрание состоится во вторник, 27.09, 16.20, 220 ИМ
- Учебный семинар для студентов 4 курса: понедельник, 26 сентября, в 18:10, https://meet.google.com/vbb-xamy-jvu
- Бутикова Е.А. «Влияние террагерцового излучения на различные типы клеток»
- Гривкин А.А. «Нейросетевой анализ трехмерных томографических изображений»
- Бунькова Е.А. «Полиномиальная разрешимость двухстадийной трёхмашинной задачи Open Shop».
- Годовой спецкурс для студентов и аспирантов «Теория оптимальных процессов» (рук.
 к.ф.-м.н. Коробов А.А., д.ф.-м.н. Ломов А.А. ) проходит по вторникам в 12:40, ауд. 220 ИМ
к.ф.-м.н. Коробов А.А., д.ф.-м.н. Ломов А.А. ) проходит по вторникам в 12:40, ауд. 220 ИМ
- 1 семестр: обратные задачи теории оптимальных процессов: восстановление решений разностных уравнений по наблюдениям с возмущениями, идентификация параметров; задачи типа Прони по невязке уравнения и с вариационными целевыми функциями; условия единственности, устойчивости, состоятельности решений; алгоритмы вычислений.
- 2 семестр: прямые задачи теории оптимальных процессов: примеры задач оптимального управления, классификация; принцип максимума Понтрягина и классические задачи вариационного исчисления; системы с запаздыванием и др. связанные вопросы.
- Начинает работу (обязательный) учебный семинар для студентов 4 курса. Орг.собрание состоится в понедельник, 12 сентября, в 18.20: https://meet.google.com/vbb-xamy-jvu
- Спецкурс «Алгебраическая теория графов» будет доступен онлайн на платформе Skillbox! Если Вы желаете получить бесплатный доступ к этому онлайн-курсу, сообщите лектору (Константинова Елена Валентиновна, e_konsta@math.
 nsc.ru) Ваш e-mail на домене @nsu.ru до 18:00 нск 9 сентября.
nsc.ru) Ваш e-mail на домене @nsu.ru до 18:00 нск 9 сентября.
Начинают работу спецкурсы
- Методы принятия решений (рук. Э.Х. Гимади) — вторник, 16.20, online. 220 ИМ. Организационное собрание — 27.09, 16.20, 220 ИМ
- Машинное обучение и анализ данных (рук. В.М. Неделько, В.Б. Бериков) — вторник, 09.00, 115 ИМ. Первое занятие — 13.09
- Теория оптимальных процессов (рук. А.А. Коробов, А.А. Ломов) — вторник, 12.40, 220 ИМ. Первое занятие — 13.09
- Дискретный анализ и комбинаторика (рук. А.А. Евдокимов) — вторник, 12.40, 312 ГК НГУ. Первое занятие — 13.09
- Теория расписаний (рук. И.Д. Черных) — вторник, 18.10, 220 ИМ. Первое занятие — 13.09
- Теория графов (рук. А.Н. Глебов) — четверг, 18.10, 2240 НГУ. Первое занятие — 15.09
- Дискретные экстремальные задачи (рук. А.Н. Глебов) — пятница, 18.10, 2240 НГУ. Первое занятие — 16.09
- Коды и схемы (1/2 года, рук.
 И.Ю. Могильных) — четверг, 18.10, 2241 НГУ. Первое занятие — 29.09
И.Ю. Могильных) — четверг, 18.10, 2241 НГУ. Первое занятие — 29.09
Начинают работу семинары
- Учебный семинар для студентов 4 курса (рук. А.А. Евдокоимов, А.В. Плясунов) — понедельник, 18.20, online. Орг.собрание — 12.09: https://meet.google.com/vbb-xamy-jvu
- Учебный семинар для магистрантов (рук. Е.В. Константинова, И.Д. Черных) — вторник, 09.00, 220 ИМ. Орг.собрание — 13.09
- Теория статистических решений (рук. В.М. Неделько, В.Б. Бериков, А.А. Викентьев) — вторник, 10.50, 115 ИМ. Первое занятие — 13.09
- Математические модели принятия решений (рук. Ю.А. Кочетов) — вторник, 10.50, online. Первое занятие — 20.09
- Теория оптимальных процессов (рук. А.А. Коробов, А.А. Ломов) — четверг, 10.50, 220 ИМ. Даты заседаний будут объявлены дополнительно
- Дискретные экстремальные задачи (рук. А.В. Пяткин, И.Д. Черных) — вторник, 14.30, 220 ИМ. Первое занятие — 13.
 09. Желающие посещать, напишите на почту [email protected] для включения в рассылку.
09. Желающие посещать, напишите на почту [email protected] для включения в рассылку. - Теория графов (рук. Е.В. Константинова, А.А. Добрынин) — вторник, 16.20, 344 ИМ. Первое занятие — 20.09
- Дискретный анализ (рук. А.А. Евдокимов) — пятница, 16.20, 417 ИМ или online. Даты заседаний будут объявлены дополнительно
- Введение в дискретную математику (рук. А.А. Тараненко) — понедельник, 18.10,
417344 ИМ. Первое занятие — 19.09 - Криптография и криптоанализ (рук. Н.Н. Токарева) — вторник, 14.30, 1155 НГУ. Первое занятие — 20.09
- Криптография в задачах (рук. Н.А. Коломеец) — вторник, 16.20, 2241 НГУ. Первое занятие — 27.09
Проект расписания ск и сс на 1 семестр 2022/23 года доступен в этой таблице. В данный момент информация еще уточняется и может изменяться, подтвержденная информация выделена синим.(6)
Научные направления
Подробнее
- Анализ данных и распознавание образов
- Дискретная оптимизация
- Дискретные математические модели генных сетей
- Дискретный анализ и комбинаторика
- Исследование операций
- Криптология
- Маршрутизация
- Непрерывная оптимизация
- Оптимальное управление
- Теория графов
- Теория кодирования
- Теория расписаний
Аспирантура
Подробнее
Список аспирантов кафедры
Учебные курсы
Подробнее
- Обязательные курсы
Курсы, выделенные красным, в настоящее время не проводятсяЛекторы Название Поток Семестры Бериков В.  Б.
Б.
Математические методы анализа данных маг. ММФ (ПМИ, МиКН) 1 Бериков В.Б. Теория вероятностей и математическая статистика бак/спец. ФЕН (Химия) 4 ван Беверн Р.А. Общая теория сложности маг. ММФ (МиКН) 1 Глебов А.Н. Графы и алгоритмы ФИТ (в данный момент нет) 5-6 Горкунов Е.В. Дополнительные главы теории информации маг.  (МиКН)
(МиКН)
3 Городилова А.А. Криптографические булевы функции крипт. 11 Давыдов И.А. Компьютерное моделирование в оптимизации бак. ММФ (ПМИ, МиКН) 6 Давыдов И.А. Методы оптимизации бак. ММФ (ПМИ, МиММ) 5 Давыдов И.А. Методы исследования операций маг.  ММФ (AI&BDA)
ММФ (AI&BDA)1 Ерзин А.И. Исследование операций бак ММФ (ПМИ) 8 Коломеец Н.А. Дизайн шифров крипт. 11 Кононов А.В. Приближённые алгоритмы маг. ММФ (МиКН) 2 Константинова Е.В. Графы и алгоритмы бак. ММФ (МиКН) 5 Константинова Е.В. Алгебраическая теория графов маг.  ММФ (МиКН)
ММФ (МиКН)
1 Кочетов Ю.А. Исследование операций бак. ММФ (инж. шк.) 5 Кочетов Ю.А. Исследование операций бак. ММФ (Мат) 7 Кочетов Ю.А., Мельников А.А. Дискретные задачи принятия решений 1 бак. ММФ (МиКН) 7 Кочетов Ю.А., Мельников А.А. Дискретные задачи принятия решений 2 бак.  ММФ (МиКН)
ММФ (МиКН)
8 Куценко А.В. Основы теории информации маг. ММФ (AI&BDA) 1 Куценко А.В., Токарева Н.Н. Квантовые технологии и защита информации крипт. 12 Облаухов А.К., Токарева Н.Н. Технология блокчейн: математические задачи и приложения крипт. 11 Панин А.А. Методы оптимизации бак.  ММФ (инж. шк.)
ММФ (инж. шк.)3 Плясунов А.В. Методы оптимизации бам. ММФ (иссл. группа) 5 Постовалов С.Н. Машинное обучение маг. ММФ (AI&BDA) 1 Пяткин А.В. Методы оптимизации бак. ММФ (Мат, МиКН) 5 Тахонов И.И. Дискретная оптимизация и теория графов маг.  ММФ (ПМИ)
ММФ (ПМИ)
1 Тахонов И.И. Основы дискретной математики бак. ММФ (инж. шк.) 1 Коломеец Н.А. Основы теории информации и криптографии бак. ММФ (МиКН) 5 Токарева Н.Н. Криптосистемы с открытым ключом и их криптоанализ крипт. 11 Токарева Н.Н. Основы теории информации иск.  инт.
инт.
9 Черных И.Д. Теория расписаний маг. ММФ (МиКН) 2
Спецкурсы и спецсеминары
Подробнее
- Проект расписания ск и сс на 1 семестр 2022/23 года доступен в этой таблице. В данный момент информация еще уточняется и может изменяться, подтвержденная информация выделена синим.
- Спецкурсы
Лекторы Название Длительность Дни недели Время ауд. Августинович С.  В.
В.
Замощения групп 1 год Бериков В.Б.,
Неделько В.М.Теория статистических решений 1 год Борисова И.А. Интеллектуальный анализ данных 0.5 года Валюженич А.А. Факторные языки 0.5 года ван Беверн Р.  А.
А.
Общая теория сложности 2 0.5 года ван Беверн Р.А. Рандомизированные алгоритмы 0.5 года ван Беверн Р.А. Алгоритмы для анализа больших объёмов данных 0.5 года Васильева А.Ю. Алгебраическая комбинаторика (2 сем.  )
)
0.5 года Гимади Э.Х. Методы принятия решений 1 год Глебов А.Н. Дискретные экстремальные задачи 1 год Глебов А.Н. Теория графов 1 год Городилова А.  А.
А.
Булевы функции в криптографии 0.5 года Евдокимов А.А. Дискретный анализ и комбинаторика 1 год Идрисова В.А.,
Токарева Н.Н.Криптография и криптоанализ. Современные методы 0.5 года Константинова Е.В. Комбинаторные задачи на графах Кэли 0.  5 года
5 года
Константинова Е.В.,
Сотникова Е.В.Алгебраическая теория графов 0.5 года Coursera Константинова Е.В.,
Сотникова Е.В.Алгебраическая теория графов 2 0.5 года Коробов А.А.,
Ломов А.А.Теория оптимальных процессов
Математические основы и приложения1 год Куценко А.  В.,
В.,
Токарева Н.Н.Математические основы и приложения квантовой информатики: криптография и вычисления 0.5 года Могильных И.Ю. Коды и схемы (1 сем.) 0.5 года Облаухов А.К.,
Токарева Н.Н.Блокчейн: математические задачи и приложения 0.5 года Панасенко А.  В.,
В.,
Хандеев В.И.Экстремальные задачи анализа данных и распознавания образов 0.5 года Потапов В.Н. Совершенные структуры в кодировании и криптографии 0.5 года Цидулко О.Ю. Параметризованные алгоритмы 1 год Черных И.Д. Теория расписаний 1 год discord - Спецсеминары
Руководители Название Длительность Дни недели Время ауд. 
Августинович С.В. Семинар кафедры теоретической кибернетики 1 год среда 15:00 220 ИМ Бериков В.Б.,
Викентьев А.А.Теория статистических решений 1 год ван Беверн Р.А.,
Цидулко О.Ю.Computer Science Club 1 год Воробьев К.В.,
Тараненко А.А.Введение в дискретную математику 1 год Добрынин А.  А.,
А.,
Константинова Е.В.Теория графов 1 год Евдокимов А.А. Дискретный анализ 1 год Евдокимов А.А.,
Пережогин А.Л.Комбинаторика и дискретные модели генных сетей 1 год Евдокимов А.А.,
Плясунов А.В.Обязательный учебный семинар для студ. 4 курса 1 год Ерзин А.  И.
И.Обязательный учебный семинар для студ. 3 курса 0.5 года Коломеец Н.А. Криптография в задачах 1 год Константинова Е.В.,
Черных И.Д.Обязательный учебный семинар для студ. магистратуры 1 год Коробов А.А.,
Ломов А.А.Теория оптимальных процессов 1 год Кочетов Ю.  А.
А.
Математические модели принятия решений 1 год Пяткин А.В.,
Черных И.Д.Дискретные экстремальные задачи 1 год Токарева Н.Н. Криптография и криптоанализ 1 год
Преподаватели
Подробнее
| ФИО | степень | звание | должность | тлф | кабинет |
дата переизбрания |
|
| Августинович Сергей Владимирович |
avgust@math. nsc.ru nsc.ru
|
к.ф.-м.н. | почасовик | 3297510 | 333 ИМ | ||
| Бериков Владимир Борисович | [email protected] | д.т.н. | проф. | проф. | 3297575 | 281 ИМ | |
| Борисова Ирина Артёмовна | [email protected] | к.т.н. | ассистент | 3297565 | 271 ИМ | ||
| Валюженич Александр Андреевич |
graphkiper@mail. ru ru
|
к.ф.-м.н. | ассистент | 3297557 | 247 ИМ | ||
| ван Беверн Рене Андреасович | [email protected] | Dr.rer.nat. | доц. | ||||
| Гимади Эдуард Хайрутдинович | [email protected] | д.ф.-м.н. | проф. | проф. | 3297541 | 224 ИМ | |
| Глебов Алексей Николаевич |
angle@math. nsc.ru nsc.ru
|
к.ф.-м.н. | доц. | 3297624 | 211 ИМ | ||
| Гончаров Евгений Николаевич | [email protected] | к.ф.-м.н. | ст. преп. | 3297535 | 218 ИМ | ||
| Горкунов Евгений Владимирович | [email protected] | к.ф.-м.н. | 3297568 | 274 ИМ | |||
| Городилова Анастасия Александровна |
gorodilova@math. nsc.ru nsc.ru
|
к.ф.-м.н. | доц. | 3297505 | |||
| Давыдов Иван Александрович | [email protected] | к.ф.-м.н. | ст. преп. | 3297566 | 272 ИМ | ||
| Добрынин Андрей Алексеевич | [email protected] | к.ф.-м.н. |
доц.
|
доц. | 3297529 | 211 ИМ | |
| Евдокимов Александр Андреевич | [email protected] | к.ф.-м.н. | доц. | проф. | 3297639 | 361 ИМ | |
| Ерзин Адиль Ильясович | [email protected] | д.ф.-м.н. | проф. | зав. каф. | 3297540 | 223 ИМ | |
| Идрисова Валерия Александровна |
vitkup@math. nsc.ru nsc.ru
|
к.ф.-м.н. | ИМ | ||||
| Коломеец Николай Александрович | [email protected] | к.ф.-м.н. | ассистент | 3297505 | 291 ИМ | ||
| Кононов Александр Вениаминович | [email protected] | д.ф.-м.н. |
доц.
|
проф. | 3297580 | 286 ИМ | |
| Константинова Елена Валентиновна | [email protected] | к.т.н. | доц. | доц. | 3297547 | 230 ИМ | |
| Коробов Алексей Александрович | [email protected] | к.ф.-м.н. | ст. преп. | 3297534 | 217 ИМ | ||
| Кочетов Юрий Андреевич |
jkochet@math. nsc.ru nsc.ru
|
д.ф.-м.н. | проф. | проф. | 3297583 | 289 ИМ | |
| Кротов Денис Станиславович | [email protected] | д.ф.-м.н. | проф. РАН | ст. преп. | 3297542 | 225 ИМ | |
| Куценко Александр Владимирович | [email protected] | к.ф.-м.н. | ассистент | ||||
| Ломов Андрей Александрович |
lomov@math. nsc.ru nsc.ru
|
д.ф.-м.н. | доц. | проф. | 3297558 | 264 ИМ | |
| Мельников Андрей Андреевич | [email protected] | к.ф.-м.н. | ст. преп. | 3297566 | 272 ИМ | ||
| Могильных Иван Юрьевич | [email protected] | к.ф.-м.н. |
ст. преп. преп.
|
3297568 |
274 ИМ | ||
| Неделько Виктор Михайлович | [email protected] | к.ф.-м.н. | доц. | доц. | 3297561 | 267 ИМ | |
| Пережогин Алексей Львович | [email protected] | к.ф.-м.н. | ст. преп. | 3297644 | 366 ИМ | ||
| Плясунов Александр Владимирович |
apljas@math. nsc.ru nsc.ru
|
д.ф.-м.н. | доц. | доц. | 3297581 | 287 ИМ | |
| Постовалов Сергей Николаевич | [email protected] | д.т.н. | доц. | проф. | +79139556300 | ||
| Потапов Владимир Николаевич | [email protected] | к.ф.-м.н. |
доц.
|
3297627 | 349 ИМ | ||
| Пяткин Артём Валерьевич | [email protected] | д.ф.-м.н. | проф. РАН | проф. | 3297617 | 336 ИМ | |
| Севастьянов Сергей Васильевич | [email protected] | д.ф.-м.н. | проф. | проф. | 3297539 | 222 ИМ | |
| Сом Людмила Васильевна |
som@math. nsc.ru nsc.ru
|
ассистент | |||||
| Тараненко Анна Александровна | [email protected] | к.ф.-м.н. | ассистент | 137 ИМ | |||
| Тахонов Иван Иванович | [email protected] | к.ф.-м.н. |
доц.
|
3634020 | 4114 НГУ | ||
| Токарева Наталья Николаевна | [email protected] | к.ф.-м.н. | доц. | 3297640 | 262 ИМ | ||
| Хандеев Владимир Ильич | [email protected] | к.ф.-м.н. | ст. преп. | 3297562 | 268 ИМ | ||
| Цидулко Оксана Юрьевна |
tsidulko. [email protected] [email protected]
|
к.ф.-м.н. | ассистент | 3297532 | 215 ИМ | ||
| Черных Илья Дмитриевич | [email protected] | к.ф.-м.н. | доц. | 3297535 | 218 ИМ |
Студенты
Подробнее
Список студентов кафедры
Премия Ляпунова
Подробнее
Премия им. А.А. Ляпунова присуждается выпускникам магистратуры кафедры с 2010 года.
А.А. Ляпунова присуждается выпускникам магистратуры кафедры с 2010 года.
В 2022 г. лауреатами стали:
Дипломы 1 степени:
- Мелиди Г.Е., Назаренко С.А. (н. рук. Ерзин А.И.)
- Сон Ен Гун (н. рук. Константинова Е.В.)
- Черных О.И. (н. рук. Пяткин А.В.)
Дипломы 2 степени:
- Ратушный А.В. (н. рук. Кочетов Ю.А.)
Дипломы 3 степени:
- Керкеснер Д.В. (н. рук. Горкунов Е.В.)
Математическое программирование 03
Контрольная работа оформляется в виде файла в Word, с приложением решения 2-й задачи в Excel. Рисунок к 1-й задаче может быть выполнен вручную, сканирован и приложен отдельно или вставлен в текст контрольной. (Выбираете по порядковому номеру в списке группы)
Вариант 2.
1. Решить задачу линейного программирования графическим методом: Найти F = 2×1 — x2 ® min при ограничениях
.
Решение
Необходимо найти минимальное значение целевой функции F = 2×1-x2 → min, при системе ограничений:
|
X1+x2≥4 |
(1) |
|
-x1+2×2≤2 |
(2) |
|
X1+2×2≤10 |
(3) |
|
X1≥0 |
(4) |
|
X2≥0 |
(5) |
Построим область допустимых решений, т. е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Построим уравнение x1+x2=4 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=4. Для нахождения второй точки приравниваем x2=0. Находим x1=4. Соединяем точку (0;4) с (4;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 1•0 +1•0-4≤0, т. е. x1+x2 — 4≥ 0 в полуплоскости выше прямой.
Построим уравнение — x1+2×2=2 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=1. Для нахождения второй точки приравниваем x2=0. Находим x1=-2. Соединяем точку (0;1) с (-2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: -1•0+2•0-2≤0, т. е. — x1+2×2-2≤ 0 в полуплоскости ниже прямой.
Построим уравнение x1+2×2=10 По двум точкам.
Для нахождения первой точки приравниваем x1=0. Находим x2=5. Для нахождения второй точки приравниваем x2=0. Находим x1=10. Соединяем точку (0;5) с (10;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0;0), определим знак неравенства в полуплоскости: 1•0+2•0-10≤0, т. е. x1+2×2-10≤0 в полуплоскости ниже прямой.
Границы области допустимых решений
Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Рассмотрим целевую функцию задачи F=2×1-x2→min.
Построим прямую, отвечающую значению функции F=0: F=2×1-x2=0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0;0), конец – точка (2;-1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.
Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
X1+x2=4
-x1+2×2=2
Решив систему уравнений, получим: X1=2, x2=2
Откуда найдем минимальное значение целевой функции:
F(X)=2*2-1*2=2
Ответ: x1 = 2, x2 = 2, F(X) = 2
2. Решить задачу симплекс-методом и проверить решение, используя программное средство Excel (команду «поиск решения»):
Решение
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 6×1 + x2 — x3 — 2×4 при следующих условиях-ограничений.
X1 + 2×2 + x3 + 6×4 + x5=4
3×1 — x2 — 3×3 + x4=1
X1 + 3×2 + 5×3=9
Введем Искусственные переменные x: в 1-м равенстве переменную x5 принимаем в качестве базисной; в 2-м равенстве вводим переменную x6; в 3-м равенстве вводим переменную x7;
1×1 + 2×2 + 1×3 + 6×4 + 1×5 + 0x6 + 0x7 = 4
3×1-1×2-3×3 + 1×4 + 0x5 + 1×6 + 0x7 = 1
1×1 + 3×2 + 5×3 + 0x4 + 0x5 + 0x6 + 1×7 = 9
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 6×1+x2-1×3-2×4 — Mx6 — Mx7 → max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x6 = 1-3×1+x2+3×3-x4
X7 = 9-x1-3×2-5×3
Которые подставим в целевую функцию:
F(X) = 6×1 + x2-x3-2×4 — M(1-3×1+x2+3×3-x4) — M(9-x1-3×2-5×3) → max
Или F(X) = (6+4M)x1+(1+2M)x2+(-1+2M)x3+(-2+M)x4+(-10M) → max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
|
1 |
2 |
1 |
6 |
1 |
0 |
0 |
|
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
|
1 |
3 |
5 |
0 |
0 |
0 |
1 |
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x5, x6, x7
Полагая, что Свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,0,4,1,9).
Базисное решение называется допустимым, если оно неотрицательно.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
4 |
1 |
2 |
1 |
6 |
1 |
0 |
0 |
|
X6 |
1 |
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
|
X7 |
9 |
1 |
3 |
5 |
0 |
0 |
0 |
1 |
|
F(X0) |
-10M |
-6-4M |
-1-2M |
1-2M |
2-M |
0 |
0 |
0 |
Переходим к основному алгоритму симплекс-метода.
Итерация №0.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее: min (4 : 1 , 1 : 3 , 9 : 1 ) = 1/3
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
4 |
1 |
2 |
1 |
6 |
1 |
0 |
0 |
4 |
|
X6 |
1 |
3 |
-1 |
-3 |
1 |
0 |
1 |
0 |
1/3 |
|
X7 |
9 |
1 |
3 |
5 |
0 |
0 |
0 |
1 |
9 |
|
F(X1) |
-10M |
-6-4M |
-1-2M |
1-2M |
2-M |
0 |
0 |
0 |
0 |
4. Пересчет симплекс-таблицы.
Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x6 в план 1 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x6 плана 0 на разрешающий элемент РЭ=3
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x1 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ,
СТЭ — элемент старого плана, РЭ — разрешающий элемент (3), А и В — элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
11/3 |
0 |
7/3 |
2 |
17/3 |
1 |
-1/3 |
0 |
|
X1 |
1/3 |
1 |
-1/3 |
-1 |
1/3 |
0 |
1/3 |
0 |
|
X7 |
26/3 |
0 |
10/3 |
6 |
-1/3 |
0 |
-1/3 |
1 |
|
F(X1) |
2-82/3M |
0 |
-3-31/3M |
-5-6M |
4+M |
0 |
2+11/3M |
0 |
Итерация №1.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai3
и из них выберем наименьшее: min (32/3 : 2 , — , 82/3 : 6 ) = 14/9
Следовательно, 3-ая строка является ведущей.
Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
32/3 |
0 |
21/3 |
2 |
52/3 |
1 |
-1/3 |
0 |
15/6 |
|
X1 |
1/3 |
1 |
-1/3 |
-1 |
1/3 |
0 |
1/3 |
0 |
— |
|
X7 |
82/3 |
0 |
31/3 |
6 |
-1/3 |
0 |
-1/3 |
1 |
14/9 |
|
F(X2) |
2-82/3M |
0 |
-3-31/3M |
-5-6M |
4+M |
0 |
2+11/3M |
0 |
0 |
4. Пересчет симплекс-таблицы.
Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x7 в план 2 войдет переменная x3.
Строка, соответствующая переменной x3 в плане 2, получена в результате деления всех элементов строки x7 плана 1 на разрешающий элемент РЭ=6
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x3 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x3 и столбец x3.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X5 |
7/9 |
0 |
11/9 |
0 |
52/9 |
1 |
-2/9 |
-1/3 |
|
X1 |
16/9 |
1 |
2/9 |
0 |
5/18 |
0 |
5/18 |
1/6 |
|
X3 |
13/9 |
0 |
5/9 |
1 |
-1/18 |
0 |
-1/18 |
1/6 |
|
F(X2) |
92/9 |
0 |
-2/9 |
0 |
313/18 |
0 |
113/18+M |
5/6+M |
Итерация №2.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее: min (7/9 : 12/9 , 17/9 : 2/9 , 14/9 : 5/9 ) = 7/11
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (12/9) и находится на пересечении ведущего столбца и ведущей строки.
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
Min |
|
X5 |
7/9 |
0 |
12/9 |
0 |
57/9 |
1 |
-2/9 |
-1/3 |
7/11 |
|
X1 |
17/9 |
1 |
2/9 |
0 |
5/18 |
0 |
5/18 |
1/6 |
8 |
|
X3 |
14/9 |
0 |
5/9 |
1 |
-1/18 |
0 |
-1/18 |
1/6 |
23/5 |
|
F(X3) |
92/9 |
0 |
-2/9 |
0 |
313/18 |
0 |
113/18+M |
5/6+M |
0 |
4. Пересчет симплекс-таблицы.
Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x5 в план 3 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 3, получена в результате деления всех элементов строки x5 плана 2 на разрешающий элемент РЭ=12/9
На месте разрешающего элемента в плане 3 получаем 1.
В остальных клетках столбца x2 плана 3 записываем нули.
Таким образом, в новом плане 3 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.
Получаем новую симплекс-таблицу:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X2 |
7/11 |
0 |
1 |
0 |
52/11 |
9/11 |
-2/11 |
-3/11 |
|
X1 |
18/11 |
1 |
0 |
0 |
-17/22 |
-2/11 |
7/22 |
5/22 |
|
X3 |
12/11 |
0 |
0 |
1 |
-59/22 |
-5/11 |
1/22 |
7/22 |
|
F(X3) |
94/11 |
0 |
0 |
0 |
417/22 |
2/11 |
115/22+M |
17/22+M |
1. Проверка критерия оптимальности.
Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
|
Базис |
B |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|
X2 |
7/11 |
0 |
1 |
0 |
52/11 |
9/11 |
-2/11 |
-3/11 |
|
X1 |
18/11 |
1 |
0 |
0 |
-17/22 |
-2/11 |
7/22 |
5/22 |
|
X3 |
12/11 |
0 |
0 |
1 |
-59/22 |
-5/11 |
1/22 |
7/22 |
|
F(X4) |
94/11 |
0 |
0 |
0 |
417/22 |
2/11 |
115/22+M |
17/22+M |
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым.
Оптимальный план можно записать так:
X2 = 7/11
X1 = 17/11
X3 = 11/11
F(X) = 1•7/11 + 6•17/11 -1•11/11 = 94/11
Ответ: x2 = 7/11, x1 = 17/11, x3 = 11/11, F(X) = 94/11
| < Предыдущая | Следующая > |
|---|
Линейное программирование — Образовательная платформа «Юрайт». Для вузов и ссузов.
- Скопировать в буфер библиографическое описание
Палий, И. А. Линейное программирование : учебное пособие для вузов / И. А. Палий. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. — 175 с. — (Высшее образование). — ISBN 978-5-534-04716-5. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/448940 (дата обращения: 03.10.2022).
- Добавить в избранное
2-е изд. , испр. и доп. Учебное пособие для вузов
, испр. и доп. Учебное пособие для вузов
- Нравится
- 14 Посмотреть кому понравилось
- Поделиться
- Описание
- Программа курса
- Видео: 1
- Нет в мобильном приложении
- Аннотация
- Программа курса
- Медиаматериалы 1
Данное учебное пособие посвящено изучению основ линейного программирования. Изложение теоретического материала сопровождается большим количеством подробно разобранных примеров решения задач, что облегчает усвоение доказательств теорем и принципов работы алгоритмов. В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории двойственности, основы теории потоков в сетях, обоснование метода потенциалов и венгерского алгоритма решения транспортной задачи, научатся находить решения различных задач линейного программирования с использованием изученных алгоритмов, выполнять анализ чувствительности, исследуя поведение решения в зависимости от изменения исходных параметров задачи. В 2006 году книге «Линейное программирование» был присвоен гриф Министерства образования и науки Российской федерации. В 2018 году книга получила диплом конкурса «Университетская книга 2018».
Изложение теоретического материала сопровождается большим количеством подробно разобранных примеров решения задач, что облегчает усвоение доказательств теорем и принципов работы алгоритмов. В результате изучения данного учебного пособия студенты узнают принципы построения математических моделей задач линейного программирования, обоснование симплекс-метода решения задач линейного программирования, основы теории двойственности, основы теории потоков в сетях, обоснование метода потенциалов и венгерского алгоритма решения транспортной задачи, научатся находить решения различных задач линейного программирования с использованием изученных алгоритмов, выполнять анализ чувствительности, исследуя поведение решения в зависимости от изменения исходных параметров задачи. В 2006 году книге «Линейное программирование» был присвоен гриф Министерства образования и науки Российской федерации. В 2018 году книга получила диплом конкурса «Университетская книга 2018».
Проблемы и решения линейного программирования
Введение
Оптимизация ресурсов (стоимости и времени) требуется во всех аспектах нашей жизни. Нам нужна оптимизация, потому что у нас ограниченные временные и финансовые ресурсы, и нам нужно выжать из них максимум. Каждый аспект современного делового мира, от производства до решения проблем с цепочками поставок, требует оптимизации для сохранения конкурентоспособности.
Нам нужна оптимизация, потому что у нас ограниченные временные и финансовые ресурсы, и нам нужно выжать из них максимум. Каждый аспект современного делового мира, от производства до решения проблем с цепочками поставок, требует оптимизации для сохранения конкурентоспособности.
Линейное программирование предлагает самый простой способ оптимизации, поскольку оно упрощает ограничения и помогает найти жизнеспособное решение сложной проблемы. В этой статье мы решим некоторые задачи линейного программирования с помощью графического метода.
Лучшие репетиторы по математике
Поехали
Упражнение 1
Транспортная компания имеет два типа грузовых автомобилей, тип A и тип B. Тип A имеет холодильную мощность и неохлаждаемую мощность в то время как Тип В имеет одинаковый общий объем с равными секциями для охлаждаемого и неохлаждаемого инвентаря. Бакалейщику необходимо нанять грузовики для перевозки охлажденных и неохлажденных товаров. Стоимость километра для типа А составляет 40 для типа В. Сколько грузовиков каждого типа должен арендовать бакалейщик, чтобы получить минимальную общую стоимость?
Сколько грузовиков каждого типа должен арендовать бакалейщик, чтобы получить минимальную общую стоимость?
Упражнение 2
Школа готовит поездку для 400 учеников. Компания, предоставляющая транспорт, имеет 10 автобусов по 50 мест каждый и 8 автобусов по 40 мест, но имеет только 9 водителей. Стоимость аренды большого автобуса составляет 600 для маленького автобуса. Подсчитайте, сколько автобусов каждого типа нужно использовать для поездки с наименьшими возможными затратами.
Упражнение 3
Магазин хочет продать 200 рубашек и 100 пар брюк прошлого сезона. Они решили составить два предложения, A и B. Предложение A — это упаковка из одной рубашки и пары брюк, которая будет продаваться по 50. Магазин не хочет продавать менее 20 упаковок предложения A и менее 10 упаковок. предложения B. Сколько упаковок каждого из них они должны продать, чтобы максимизировать деньги, полученные от рекламной акции?
Решение упражнения 1
Транспортная компания имеет два типа грузовых автомобилей, тип A и тип B. Тип A имеет холодильную и неохлаждаемую вместимость, а тип B имеет одинаковый общий объем с равные секции для охлаждаемого и неохлаждаемого инвентаря. Бакалейщику необходимо нанять грузовики для перевозки охлажденных и неохлажденных товаров. Стоимость километра для типа А составляет 40 для типа В. Сколько грузовиков каждого типа должен арендовать бакалейщик, чтобы получить минимальную общую стоимость?
Тип A имеет холодильную и неохлаждаемую вместимость, а тип B имеет одинаковый общий объем с равные секции для охлаждаемого и неохлаждаемого инвентаря. Бакалейщику необходимо нанять грузовики для перевозки охлажденных и неохлажденных товаров. Стоимость километра для типа А составляет 40 для типа В. Сколько грузовиков каждого типа должен арендовать бакалейщик, чтобы получить минимальную общую стоимость?
а) Выберите неизвестные.
x = грузовые автомобили типа A
y = грузовые автомобили типа B
b) Напишите целевую функцию .
c) Запишите ограничения в виде системы неравенств.
d) Найдите множество допустимых решений, которые графически представляют ограничения.
Пример 1 — часть dд) Рассчитать координаты вершин из совокупности возможных решений.
Пример 1 — часть д f) Вычислить значение целевой функции в каждой из вершин, чтобы определить, какая из них имеет максимальное или минимальное значение.
Поскольку x и y должны быть натуральными числами, округленными до значения y.
По умолчанию мы видим, что принимает значение x в y = 66 в уравнении, которое находится в допустимых решениях.
Минимальная стоимость 800 и f(x,y) = 600x + 800y40x + 50y geq 400x + y leq 9x geq 0y geq 0f(0,8) = 600 cdot 0 + 800 cdot 8 = 6400(0,9) = 600 cdot 0 + 800 cdot 9 = 72000f(5,4) = 600 cdot 5 + 800 cdot 4 = 62006200. Это достигается с помощью 4 больших автобуса, и 5 маленьких автобусов.
Мы подставили точки (0,9), (0,8) и (5,4) в уравнение, чтобы определить минимальную стоимость. Однако вы можете сказать это, непосредственно взглянув на график. Координата (5,4) попадает под допустимую область и является ее точкой минимума.
Решение упражнения 3
Магазин хочет продать 200 рубашек и 100 пар брюк прошлого сезона. Они решили составить два предложения, A и B. Предложение A — это упаковка из одной рубашки и пары брюк, которая будет продаваться по 50. Магазин не хочет продавать менее 20 упаковок предложения A и менее 10 упаковок. предложения B. Сколько упаковок каждого из них они должны продать, чтобы максимизировать деньги, полученные от рекламной акции?
Магазин не хочет продавать менее 20 упаковок предложения A и менее 10 упаковок. предложения B. Сколько упаковок каждого из них они должны продать, чтобы максимизировать деньги, полученные от рекламной акции?
а) Выберите неизвестные.
x = количество пакетов Предложения A
y = количество пакетов Предложения B
б) Запишите целевую функцию .
c) Запишите ограничения в виде системы неравенств.
г) Найдите множество допустимых решений, которые графически представляют ограничения.
Пример 3 — часть de) Рассчитайте координаты вершин из совокупности допустимых решений.
Пример 3 — часть ef) Вычислить значение целевой функции в каждой из вершин, чтобы определить, какая из них имеет максимальное или минимальное значение.
50 пакетов каждого предложения приносят максимальную сумму продаж 4000 долларов США.
Решатель линейных программ загрузить | SourceForge.net
Решение задач линейного программирования
Статус: Бета
Привлечены к вам: конобей
СкачатьПолучить обновления
ФИО
Номер телефона
Название работы
Промышленность
Компания
Размер компании Размер компании: 1 — 2526 — 99100 — 499500 — 9991,000 — 4,9995,000 — 9,99910,000 — 19,99920,000 или больше
Получайте уведомления об обновлениях для этого проекта. Получите информационный бюллетень SourceForge. Получайте информационные бюллетени и уведомления, содержащие новости сайта, специальные предложения и эксклюзивные скидки на ИТ-продукты и услуги.
Я понимаю, что нажав кнопку ниже, я соглашаюсь с Условиями и положениями SourceForge. Я согласен получать эти сообщения от SourceForge.net. Я понимаю, что могу отозвать свое согласие в любое время. Пожалуйста, ознакомьтесь с нашими Условиями использования и Политикой конфиденциальности или свяжитесь с нами для получения более подробной информации.
Я понимаю, что нажав кнопку ниже, я соглашаюсь с Условиями и положениями SourceForge. Я согласен получать эти сообщения от SourceForge.net. Я понимаю, что могу отозвать свое согласие в любое время. Пожалуйста, ознакомьтесь с нашими Условиями использования и Политикой конфиденциальности или свяжитесь с нами для получения более подробной информации.
Пожалуйста, ознакомьтесь с нашими Условиями использования и Политикой конфиденциальности или свяжитесь с нами для получения более подробной информации.
Я понимаю, что нажав кнопку ниже, я соглашаюсь с Условиями и положениями SourceForge. Я согласен получать эти сообщения от SourceForge.net. Я понимаю, что могу отозвать свое согласие в любое время. Пожалуйста, ознакомьтесь с нашими Условиями использования и Политикой конфиденциальности или свяжитесь с нами для получения более подробной информации.
Для этой формы требуется JavaScript.
Похоже, у вас отключен CSS. Пожалуйста, не заполняйте это поле.
Похоже, у вас отключен CSS. Пожалуйста, не заполняйте это поле.
Нет, спасибо
Поделись
Windows
Linear Program Solver (LiPS) — это пакет оптимизации, ориентированный на решение задач линейного, целочисленного и целевого программирования.
Основные особенности LiPS:
● LiPS основан на эффективной реализации модифицированного симплексного метода, который решает крупномасштабные задачи.
● LiPS предоставляет не просто ответ, а подробный процесс решения в виде последовательности симплексных таблиц, поэтому вы можете использовать его для изучения/обучения линейному программированию.
● LiPS дает процедуры анализа чувствительности, которые позволяют изучить поведение модели при изменении ее параметров, в том числе: анализ изменения правых частей ограничений, анализ изменения коэффициентов целевой функции, анализ изменения в столбце/строке матрицы технологий. Такая информация может оказаться чрезвычайно полезной для практического применения моделей LP.
● LiPS предоставляет методы целевого программирования, в том числе лексикографические и взвешенные методы GP, ориентированные на многокритериальную оптимизацию.
Функции
- Решатель линейного и целочисленного программирования
- Анализ чувствительности
- Целевое программирование (экспериментальное)
- Простой в использовании графический интерфейс (GUI)
Образцы проектов
Деятельность по проекту
Просмотреть все действия >
{{ this. obj.activity_extras.summary }}
obj.activity_extras.summary }}
{{/каждый}}
Категории
Алгоритмы, математика, моделированиеЛицензия
Лицензия MITДжира | Программное обеспечение для отслеживания проблем и проектов для Agile-команд
Инструмент №1 для разработки программного обеспечения, используемый agile-командами
Jira, которой доверяют тысячи команд, предлагает доступ к широкому спектру инструментов для планирования, отслеживания и выпуска программного обеспечения мирового класса, захвата и организация проблем, назначение работы и отслеживание командной деятельности. Он также интегрируется с ведущими инструментами разработчиков для сквозной прослеживаемости.
Подробнее
Оцените этот проект
Войдите, чтобы оценить этот проект
Рейтинг пользователей
4.7 из 5 звезд★★★★★
★★★★
★★★
★★
★
легкость 1 из 5 2 из 5 3 из 5 4 из 5 5 из 5 4 / 5
характеристики 1 из 5 2 из 5 3 из 5 4 из 5 5 из 5 3 / 5
дизайн 1 из 5 2 из 5 3 из 5 4 из 5 5 из 5 2 / 5
поддержка 1 из 5 2 из 5 3 из 5 4 из 5 5 из 5 3 / 5
Отзывы пользователей
Отфильтровать отзывы:
Все
Решите эту задачу линейного программирования (ЛП), используя транспортный метод.
 — Tutorspoint.com
— Tutorspoint.comРезультаты представлены в виде целых дробей, а не чисел с плавающей запятой, и я не вижу возможности изменить это. Мне приходится тратить много времени на преобразование результатов в числа с плавающей запятой с помощью калькулятора. Я действительно ненавижу, когда люди делают сложную часть проекта правильно, а простую часть неправильно. И помощи нет, только притворная помощь с «?» и нажатие на него ничего не делает. Я тоже не люблю, когда меня дразнят.
Уважаемый разработчик, Спасибо, что поделились таким замечательным проектом Он отлично работает у меня. У меня есть предложение, которое заключается в том, чтобы написать формулировку в матричном формате (в текстовом режиме), как в Matlab. еще раз спасибо за вашу работу 🙂
Липсайд отлично работает.
Липсайд отлично работает.
1 пользователь считает этот отзыв полезным.
Дополнительные сведения о проекте
Языки
Бразильский португальский, английский, русский, испанскийПредполагаемая аудитория
Образование, конечные пользователи/настольные компьютеры, информационные технологии, наука/исследованияПользовательский интерфейс
Win32 (MS Windows)Язык программирования
C++ 2010-07-06Сообщить о неприемлемом содержимом
LP с Solver
LP с SolverПрименимо к Excel 2002-2016 (включая Office 365)
(процедуры Google Drive Solver доступны отдельно) 1.
 Прежде чем пытаться решить задачу линейного программирования с помощью
Excel, убедитесь, что надстройка «Поиск решения»
активирован. См. Надстройки Excel
веб-страницу для получения подробной информации.
Прежде чем пытаться решить задачу линейного программирования с помощью
Excel, убедитесь, что надстройка «Поиск решения»
активирован. См. Надстройки Excel
веб-страницу для получения подробной информации. 2. Введите все данные задачи в ячейки. Формат
ниже допустимо, но не обязательно (Excel не волнует, где вы что-то кладете, но
вы должны указать программе Solver, где находятся ключевые элементы
расположен). Примечания.
- содержат отдельные ячейки как для значений, так и для объективных коэффициентов в переменные решения.
- целевые коэффициенты – это числа в целевой функции
- «значения» представляют фактические значения переменных решения. Первоначально «значения» обычно устанавливаются равными нуль. После решения Excel поместит оптимальное решение значения переменных в ячейках значений.
- включает один
ячейка, в которой прибыль вычисляется из значений переменной решения и
объективные коэффициенты (проще всего с помощью функции суммы произведений — щелкните здесь для объяснения).

- включают ячейки, в которых общее количество использованных ограничений вычисляется, т. е. левая часть ограничения (опять же, проще всего с суммовым произведением).
- осторожное использование абсолютных ссылок на ячейки позволит вам ввести
только первую формулу, затем скопируйте ее в оставшиеся строки — см. пример
ниже.
- включают ячейки, содержащие правую часть каждого ограничения.
- вы можете дополнительно включить ячейки для типа ограничения (<=, >= или =). Это рекомендуется сделать вашу электронную таблицу более читабельной и напомнить вам о типы ограничений, но эти ячейки не используется решателем.
- не включают ограничения неотрицательности в электронной таблице (неотрицательность обрабатывается в разделе «Параметры решателя»).
Макс. Z= 5 X1 + 8 X2
СТ 2 X1 + 4 X2 <= 40
6 X1 + 3 X2 <= 42
X1 >= 3
X1, X2 >= 0Вы можете настроить электронную таблицу следующим образом, в которой стрелки указывают куда Примеры формул ячеек идут.
 Примечание: нет необходимости
поместите данные именно в этом формате (нажмите здесь, например, электронную таблицу):
Примечание: нет необходимости
поместите данные именно в этом формате (нажмите здесь, например, электронную таблицу): Следующие шаги немного различаются в зависимости от версии Excel:
3. Запустите Solver:
Excel 2002/03: нажмите Инструменты вверху, затем Solver.
Excel 2007/13/16/10: нажмите
в
Вкладка «Данные» вверху, затем нажмите «Решатель» в разделе «Анализ».
в правом верхнем углу (называется «Анализ» в Excel 2016).
4. Нажмите в поле "Установить целевую ячейку" для Excel 2002/03/07 или поле «Установить цель» для Excel 2010/13/16, затем выберите одну ячейку содержащий целевая функция формула. Также нажмите кнопку Max или Min, если это применимо. (линейное программирование не использует опцию «Значение»).
5. Нажмите в поле "Изменение ячеек" для Excel 2002/03/07 или поле «Изменяя ячейки переменных» для Excel 2010/13/16, затем выберите ячейки значения переменной решения.
6. Нажмите кнопку "Добавить" рядом с надписью "При условии
Ограничения», в котором выводится:
Нажмите кнопку "Добавить" рядом с надписью "При условии
Ограничения», в котором выводится:
Для каждого ограничения:
- нажмите кнопку «Ячейка Ссылка", затем щелкните ячейку, содержащую формулу для левая сторона всего
- при необходимости измените тип ограничения
- щелкните поле "Ограничение" и выберите ячейку, содержащую правую часть ограничения
- нажмите Добавить в закончить ограничение
В Excel 2010/13/16 это будет выглядеть так:
7. Важно: должны быть установлены два параметра:
В Excel 2002/03/07: Нажмите «Параметры», затем нажмите чтобы поставьте галочки «Предполагать линейную модель» и «Предполагать Неотрицательный" следующим образом:
Оставьте другие варианты в покое.
 Нажмите OK, чтобы вернуться к Солверу.
Поле параметров, которое должно выглядеть так же, как показано на шаге 6 выше.
Нажмите OK, чтобы вернуться к Солверу.
Поле параметров, которое должно выглядеть так же, как показано на шаге 6 выше. В Excel 2010/13/16:
необходимые параметры находятся на главном экране Solver Parameters, показанном выше:
- Установите флажок «Сделать переменные без ограничений неотрицательными»
- Щелкните стрелку вниз справа от «Выберите метод решения». и измените его с "GRG Nonlinear" на "Simplex LP".
См. советы ниже, если вы открываете электронную таблицу в версии Excel, отличной от тот, в котором он был создан.
8. Проверьте введенную проблему. Если все выглядит правильно, нажмите «Решить». Если все хорошо, вы увидите «Решатель найдено решение." Если решатель говорит что-то еще, это НЕ нашел решения - см. Советы ниже.
9. После того, как Solver найдет решение, нажмите, чтобы выбрать ответ
и/или отчеты о конфиденциальности в разделе «Отчеты». требуется для вашего задания. Не изменяйте никакие другие настройки. Нажмите OK, и Solver
создать новую электронную таблицу(ы), содержащую отчеты. Решатель также
поместите оптимальные значения переменных решения в соответствующие ячейки
оригинальный лист. Нажмите на вкладку внизу экрана
для просмотра или печати каждого отчета. (нажмите здесь, чтобы просмотреть пример электронной таблицы).
Отчет об ответах на вышеуказанную проблему должен выглядеть примерно так
в Excel 2016, с некоторыми изменениями в других версиях Excel:
требуется для вашего задания. Не изменяйте никакие другие настройки. Нажмите OK, и Solver
создать новую электронную таблицу(ы), содержащую отчеты. Решатель также
поместите оптимальные значения переменных решения в соответствующие ячейки
оригинальный лист. Нажмите на вкладку внизу экрана
для просмотра или печати каждого отчета. (нажмите здесь, чтобы просмотреть пример электронной таблицы).
Отчет об ответах на вышеуказанную проблему должен выглядеть примерно так
в Excel 2016, с некоторыми изменениями в других версиях Excel:
Возможная ошибка: если вы используете Excel 2007, вы можете столкнуться с ошибкой при попытке создать отчеты. Если вы получили решение, но оно не создает отчеты, посетите следующую веб-страницу для временного решения:
http://faculty.sfasu.edu/fisherwarre/solver_workaround.html
Еще лучше, нажмите здесь, чтобы получить инструкции о том, как получить Office 365 бесплатно!
Советы:
- при правильном использовании абсолютных ссылок на ячейки вам нужно только
войти в первый
формула левой части ограничения.
 Затем его можно скопировать в
другие строки ограничений. Это сделано в приведенном выше примере.
Затем его можно скопировать в
другие строки ограничений. Это сделано в приведенном выше примере. - не используйте Кнопка «Угадай» в Excel 2002/03/07 Параметры решателя. Это почти никогда не угадывает правильно.
- если
у вас есть два или более ограничения в строке одного типа
(<=, например), вы можете ввести их одновременно. Для этого
перетащите через обе левые итоговые формулы для ссылки на ячейку,
и перетащите через обе правые ячейки для ограничения
коробка. Хотя это выглядит как одно ограничение в Solver, Excel
обрабатывает каждую пару ячеек «Ссылка на ячейку/ограничение» как отдельную
ограничение.
- , если открыть электронную таблицу с линейным программированием в версии Excel, отличная от версии, используемой для создания электронной таблицы, еще раз проверьте, что параметры установлены правильно (см. шаг 7 выше).
- , если проблема не устранена, еще раз проверьте все вышеперечисленные шаги, включая параметры настройки (шаг
7).
 Все равно не решит? На занятия доктора Фишера приносите
электронную таблицу ему на флеш-накопителе или по электронной почте. В
другие классы, следуйте инструкциям своего преподавателя.
Все равно не решит? На занятия доктора Фишера приносите
электронную таблицу ему на флеш-накопителе или по электронной почте. В
другие классы, следуйте инструкциям своего преподавателя.
Линейный
Программирование: задачи Word (стр. Разделы: Оптимизация линейные системы, Постановка текстовых задач
Если каждый научный калькулятор продано результатов в $2 потери, но каждый графический калькулятор выдает $5 прибыль, сколько каждого типа следует производить ежедневно, чтобы максимизировать чистую прибыль? Вопрос требует оптимального числа калькуляторов, поэтому мои переменные будут обозначать это: Так как они не могут производить отрицательные числа
калькуляторов, у меня есть два ограничения, x > 0 и y > 0. Р = 2 х + 5 у ,
предмет: График области осуществимости выглядит следующим образом: Авторские права Элизабет Стапель 2006-2011 Все права защищены При проверке угловых точек в точках (100,
170), (200, 170), (200, 80), (120, 80),
и (100, 100),
вы должны получить максимальное значение P = 650 в ( х , у ) = (100, 170).
Вопрос по количеству шкафов Мне нужно купить, поэтому мои переменные будут обозначать это: Естественно, x > 0 и у > 0. Я должен рассмотреть
затраты и площадь («занимаемая площадь» каждой единицы), в то время как
максимально увеличить объем хранилища, поэтому моими ограничениями будут затраты и площадь пола,
в то время как объем будет моим уравнением оптимизации. стоимость: 10 х + 20 у < 140 или г < ( 1 / 2 ) х + 7 Эта система (вместе с первыми двумя ограничения) графики как: При проверке угловых точек в точках (8, 3), (0, 7) и (12, 0), вы должны получить максимальную громкость из 100 кубических футов, купив восемь моделей X и три модели Y. << Предыдущий Топ | 1 | 2 | 3 | 4 | 5 | Вернуться к индексу Далее >>
|
|
|
Линейное программирование (ЛП) — введение в основы
Обратите внимание, вы также можете увидеть список примеров кода для различных языков программирования на нашей странице примеров кода линейного программирования .
Линейное программирование (ЛП) — мощная основа для описания и решения задач оптимизации. Он позволяет указать набор переменных решения, а также линейную цель и набор линейных ограничений для этих переменных. В качестве простого и широко используемого примера рассмотрим задачу минимизации стоимости выбора продуктов, отвечающих всем рекомендуемым ежедневным нормам питательных веществ. Модель LP будет иметь набор переменных решения, которые фиксируют количество каждого продукта для покупки, линейную цель, которая минимизирует общую стоимость покупки выбранных продуктов, и линейное ограничение для каждого питательного вещества, требующее, чтобы выбранные продукты вместе содержали достаточное количество этого питательного вещества. Используя обозначения линейной алгебры, линейную программу можно описать следующим образом: Цель: минимизировать c T x Ограничения: A x = b (линейные ограничения) l ≤ x ≤ u (граничные ограничения) При описании в этой форме вектор x представляет переменные решения, вектор c задает линейную целевую функцию, матричное уравнение Ax = b задает линейные ограничения для x , а векторы l и u задают нижнюю и верхнюю границы для x . Набор приложений линейного программирования буквально слишком длинный, чтобы его перечислять. Он включает в себя все: от планирования производства до оптимизации веб-рекламы и производства одежды. LP так или иначе затрагивает почти каждую коммерческую отрасль.
Набор приложений линейного программирования буквально слишком длинный, чтобы его перечислять. Он включает в себя все: от планирования производства до оптимизации веб-рекламы и производства одежды. LP так или иначе затрагивает почти каждую коммерческую отрасль.
Алгоритмы линейного программирования
Первым алгоритмом для решения задач линейного программирования был симплекс-метод, предложенный Джорджем Данцигом в 1947 году. Примечательно, что этот 65-летний алгоритм остается одним из самых эффективных и надежных методов решения таких задач. Cегодня. Основной альтернативой симплексному методу является барьерный метод или метод внутренней точки. Этот подход имеет долгую историю, но его популярность в последнее время связана с доказательством полиномиальной сложности Кармаркара в 1984 году. Методы внутренних точек значительно выиграли от последних достижений в компьютерной архитектуре, включая введение многоядерных процессоров и наборов инструкций SIMD, и обычно считаются более быстрыми, чем симплексные, для решения задач LP с нуля. Однако огромное разнообразие различных моделей LP и множество различных способов использования LP означает, что на практике ни один из алгоритмов не доминирует над другим. Оба важны в вычислительном линейном программировании.
Однако огромное разнообразие различных моделей LP и множество различных способов использования LP означает, что на практике ни один из алгоритмов не доминирует над другим. Оба важны в вычислительном линейном программировании.
Вычислительное линейное программирование
Учитывая возраст этих алгоритмов (65 лет для симплексного метода и 28 лет для методов внутренних точек), можно ожидать, что вопросы реализации, связанные с этими методами, будут хорошо изучены и что разные реализации дадут похожие результаты. Удивительно, но это далеко не так. Вычислительные тесты для ряда моделей показывают большие различия в производительности и надежности между различными реализациями. Например, симплексные решатели с открытым исходным кодом CLP и GLPK в среднем в 2,5 и 58 раз медленнее симплексного решателя Gurobi соответственно. Чем объясняются такие большие различия между реализациями таких старых и хорошо зарекомендовавших себя методов? Различия в основном сводятся к трем факторам.
Разреженная линейная алгебра
Первый фактор — это разреженная линейная алгебра. Матрицы ограничений, возникающие в линейном программировании, обычно чрезвычайно разрежены. Разреженные матрицы содержат очень мало ненулевых элементов. Нередко можно найти матрицы ограничений, содержащие только 3 или 4 ненулевых значения в столбцах A. Шаги как симплексного алгоритма, так и алгоритма внутренней точки включают ряд вычислений с чрезвычайно разреженными матрицами и чрезвычайно разреженными векторами. Разреженные матрицы должны быть разложены на множители, системы разреженных линейных уравнений должны быть решены с использованием результирующих матриц факторов, матрицы факторов должны быть изменены и т. д. Требуется многолетний опыт работы с разреженной числовой линейной алгеброй и линейным программированием, чтобы понять вычислительные проблемы, связанные с построением эффективные алгоритмы разреженных матриц для LP.
Плотная матрица
Разреженная матрица
Численные ошибки
Второй фактор — осторожное обращение с числовыми ошибками. Всякий раз, когда вы решаете системы линейных уравнений в арифметике с конечной точностью, вы всегда будете получать небольшие числовые ошибки в результатах. Важнейшей частью построения эффективного алгоритма LP является разработка эффективных стратегий для управления такими ошибками — невыполнение этого может означать разницу между решением модели за доли секунды и отсутствием решения вообще.
Всякий раз, когда вы решаете системы линейных уравнений в арифметике с конечной точностью, вы всегда будете получать небольшие числовые ошибки в результатах. Важнейшей частью построения эффективного алгоритма LP является разработка эффективных стратегий для управления такими ошибками — невыполнение этого может означать разницу между решением модели за доли секунды и отсутствием решения вообще.
Эвристические стратегии
Третий фактор – это разработка эффективных эвристических стратегий для принятия разнообразных решений, возникающих в процессе решения. Чтобы привести один пример, симплекс-алгоритм должен многократно выбирать одну переменную из многих, чтобы войти в базис. Используемая стратегия может сильно повлиять на время выполнения алгоритма. Различия между различными стратегиями часто довольно тонкие, и во многих случаях они просто основаны на эмпирических наблюдениях за тем, какие схемы наиболее эффективны на практике. Опять же, выбор эффективных стратегий требует многолетнего опыта.
Результаты тестов
Публичные тесты различных коммерческих LP-решателей демонстрируют эффективность подходов, которые Гуроби использовал для решения каждой из этих проблем. Как для симплексного, так и для барьерного методов решатели Gurobi обеспечивают как более высокую производительность, так и лучшую численную надежность, чем конкурирующие решатели. Это различие, конечно, имеет значение, когда вы решаете модели LP, но, что более важно, оно также обеспечивает более прочную основу для построения множества алгоритмов, которые полагаются на LP как на подпрограмму. Одним из очень важных примеров является алгоритм ветвей и границ, который используется для решения моделей смешанного целочисленного программирования (MIP).
Ссылки
Если вам нужна дополнительная информация об этих методах, мы отсылаем вас к следующим книгам:
- Bertsimas, D., and Tsitsiklis, J., Introduction to Linear Optimization , 1995.
- Вандербей, Р.
 , Линейное программирование: основы и расширения , 2010
, Линейное программирование: основы и расширения , 2010 - Райт, С., Первично-двойственные методы внутренней точки , 1997.
Интерактивный симплексный метод — численная оптимизация
Этот модуль предназначен только для образовательных целей , поддерживает обучение и знакомство с симплекс-методом.
Вы хотите эффективно решать линейные программы? использовать MixedIntegerLinearProgram вместо .
Реализованные здесь методы позволяют решать задачи линейного программирования (ЗПП) в несколькими способами, может потребоваться подробное (и правильное!) описание шагов и вероятно, будут намного медленнее, чем «обычные» LP-решатели. Если же вы хотите узнать, как работает симплекс-метод, и посмотреть, что происходит в разных ситуациях использовать разные стратегии, но не хотите заниматься утомительной арифметикой, это модуль для вас!
Исторически он был создан в дополнение к курсу Math 373 по математике. Программирование и оптимизация в Университете Альберты, Эдмонтон, Канада.
Программирование и оптимизация в Университете Альберты, Эдмонтон, Канада.
АВТОРОВ:
ПРИМЕРЫ:
Большая часть функциональности модуля демонстрируется на следующей задаче.
Кукуруза и ячмень
У фермера есть 1000 акров земли для выращивания кукурузы и ячменя. Кукуруза имеет чистую прибыль в размере 10 долларов с акра, в то время как ячмень имеет чистую прибыль. прибыль 5 долларов с акра. У фермера есть 1500 кг удобрений из расчета 3 кг на акр. для кукурузы и 1 кг на акр для ячменя. Фермер хочет максимизировать прибыль. (Иногда мы также добавляем еще одно ограничение, чтобы исходный словарь невыполнимо: фермер должен использовать не менее 40% доступной земли.)
Используя переменные \(C\) и \(B\) для земли, используемой для выращивания кукурузы и ячменя соответственно, в акрах, мы можем построить следующую задачу ЛП:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: П Проблема с LP (для получения подробной информации используйте "view(...)" или "%display typeset")
Рекомендуется скопировать и вставить такие примеры в свой рабочий лист, чтобы
вы можете запускать эти команды в режиме верстки ( %display typeset ) и получаем
\[\begin{split}\begin{массив}{l} \begin{массив}{lcrcrcl} \max \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} 10 C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu} &\mspace{-6mu} 5 B \mspace{-6mu} \\ \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}&\mspace {-6mu} B \mspace{-6mu}&\mspace{-6mu} \leq \mspace{-6mu}&\mspace{-6mu} 1000 \\ \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} 3 C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}&\ mspace{-6mu} B \mspace{-6mu}&\mspace{-6mu} \leq \mspace{-6mu}&\mspace{-6mu} 1500 \\ \конец{массив} \\ С, В \geq 0 \конец{массив}\конец{разделить}\]
Поскольку у него только две переменные, мы можем решить его графически:
мудрец: P.plot() Графический объект, состоящий из 19 графических примитивов.
Симплекс-метод применим только к задачам стандартной формы , которые могут быть созданы либо напрямую
шалфей: InteractiveLPProblemStandardForm(A, b, c, ["C", "B"]) Проблема LP (используйте ...)
или из уже построенной задачи «общего типа»:
мудрец: P = P.standard_form()
В этом случае задача не требует каких-либо изменений для записи в стандартная форма, но этот шаг по-прежнему необходим для включения методов, связанных с симплексный метод.
Самый простой способ использовать симплекс-метод:
мудрец: P.run_simplex_method()
\begin{уравнение*}
...
Оптимальное значение: $6250$. Оптимальное решение: $\left(250,\,750\right)$.
(Этот метод дает довольно длинные формулы, которые здесь не приводятся.) Но, конечно, гораздо веселее выполнять большинство шагов вручную. Давайте начнем путем создания исходного словаря:
мудрец: D = P.initial_dictionary() мудрец: Д Словарь проблем LP (используйте ...)
Используя рекомендованный режим верстки, вы увидите
\[\begin{split}\renewcommand{\arraystretch}{1.5} \begin{массив}{|rcrcrcr|} \hline x_{3} \mspace{-6mu}&\mspace{-6mu} = \mspace{-6mu}&\mspace{-6mu} 1000 \mspace{-6mu}&\mspace{-6mu} - \mspace{- 6mu}&\mspace{-6mu} C \mspace{-6mu}&\mspace{-6mu} - \mspace{-6mu}&\mspace{-6mu} B\\ x_{4} \mspace{-6mu}&\mspace{-6mu} = \mspace{-6mu}&\mspace{-6mu} 1500 \mspace{-6mu}&\mspace{-6mu} - \mspace{- 6mu}&\mspace{-6mu} 3 C \mspace{-6mu}&\mspace{-6mu} - \mspace{-6mu}&\mspace{-6mu} B\\ \hline z \mspace{-6mu}&\mspace{-6mu} = \mspace{-6mu}&\mspace{-6mu} 0 \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}& \mspace{-6mu} 10 C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}&\mspace{-6mu} 5 B\\ \hline \конец{массив}\конец{разделить}\]
С начальным или любым другим словарем можно выполнить ряд проверок:
мудрец: D.is_feasible() Истинный мудрец: D.is_optimal() ЛОЖЬ
Вы можете просмотреть многие его части и связанные с ними данные:
мудрец: D.basic_variables() (х3, х4) мудрец: D.basic_solution() (0, 0) мудрец: D.objective_value() 0
Самое главное, вы можете выполнять шаги симплекс-метода, выбирая входная переменная, выходная переменная и обновление словаря:
мудрец: D.enter("C")
мудрец: Д.уйти(4)
мудрец: D.update()
Если все сделано правильно, новый словарь по-прежнему возможен и объективное значение не уменьшилось:
мудрец: D.is_feasible() Истинный мудрец: D.objective_value() 5000
Если вы не уверены в выборе входных и выходных переменных, вы можете использовать вспомогательные методы, которые сделают все возможное, чтобы сказать вам, что будет вашим следующим опции:
мудрец: D.possible_entering() [Б] мудрец: D.possible_leaving() Traceback (последний последний вызов): ... ValueError: можно определить оставшиеся переменные для допустимых словарей с заданной входной переменной или для двойных допустимых словарей
Также возможно получить возможных набора и итоговых словаря задачи, работа с исправленными словарями ,
и используйте метод двойного симплекса!
Примечание
В настоящее время не имеет формата отображения для терминала.
- класс sage.numerical.interactive_simplex_method.InteractiveLPProblem( A , b , c , x='x' , limited_type='<=' , variable_type='' , problem_type='max' , base_ring=Нет , is_primal=True , target_constant_term=0 )
Базы:
sage.structure.sage_object.SageObjectПостроить задачу LP (линейное программирование).
Примечание
Этот класс предназначен только для образовательных целей : если вы хотите решить Линейные программы эффективно, используйте
MixedIntegerLinearProgramвместо.Этот класс поддерживает задачи LP с ограничениями «переменные слева».
ВВОД:
А– матрица коэффициентов ограниченийб– вектор постоянных членов ограниченияc– вектор объективных коэффициентовx– (по умолчанию:"x") вектор переменных решения или строка, задающая базовое имяlimited_type– (по умолчанию:"<=") строка, указывающая ограничение тип(ы): либо"<=",">=","==", либо их списокvariable_type– (по умолчанию:"") строка, определяющая переменную тип(ы): либо">=","<=",""(пустая строка), либо список их, соответствующих, соответственно, неотрицательным, неположительные и свободные переменныеproblem_type– (по умолчанию:"max") строка, определяющая тип задачи:"max","min","-max"или"-min"base_ring— (по умолчанию: дробное поле общего кольца для всех входные коэффициенты) поле, в которое будут помещены все входные коэффициенты. переделанный
переделанныйis_primal— (по умолчанию:True) является ли эта проблема первичной или двойная: каждая проблема, конечно, двойственна своей собственной двойственности, этот флаг в основном для внутреннего использования и влияет только на имена переменных по умолчаниюtarget_constant_term– (по умолчанию: 0) постоянный срок цель
ПРИМЕР:
Построим следующую задачу:
\[\begin{split}\begin{массив}{l} \begin{массив}{lcrcrcl} \max \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} 10 C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu} &\mspace{-6mu} 5 B \mspace{-6mu} \\ \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}&\mspace {-6mu} B \mspace{-6mu}&\mspace{-6mu} \leq \mspace{-6mu}&\mspace{-6mu} 1000 \\ \mspace{-6mu}&\mspace{-6mu} \mspace{-6mu}&\mspace{-6mu} 3 C \mspace{-6mu}&\mspace{-6mu} + \mspace{-6mu}&\ mspace{-6mu} B \mspace{-6mu}&\mspace{-6mu} \leq \mspace{-6mu}&\mspace{-6mu} 1500 \\ \конец{массив} \\ С, В \geq 0 \конец{массив}\конец{разделить}\]
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=")
Та же проблема, но более явно:
мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], .
 ...:Ограничение_тип="<=", переменная_тип=">=")
...:Ограничение_тип="<=", переменная_тип=">=")
Еще более явно:
мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], problem_type="max", ....: тип_ограничения=["<=", "<="], тип_переменной=[">=", ">="])
Используя последнюю форму, вы сможете представить любую задачу LP, если так как все подобные термины собраны и в ограничениях переменные и константы находятся по разные стороны.
- А ()
Возвращает коэффициенты ограничений
self, т.е. \(A\).ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.constraint_coefficients() [1 1] [3 1] мудрец: П.А.() [1 1] [3 1]
- Abcx()
Вернуть \(A\), \(b\), \(c\) и \(x\) из
себяв виде кортежа.ВЫВОД:
кортеж
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.
 Abcx()
(
[1 1]
[3 1], (1000, 1500), (10, 5), (В, Б)
)
Abcx()
(
[1 1]
[3 1], (1000, 1500), (10, 5), (В, Б)
)
- add_constraint( коэф.
Возвратите новую задачу LP, добавив ограничение к ``self``.
ВВОД:
коэффициенты– коэффициенты нового ограниченияConstant_term– постоянный член нового ограниченияlimited_type– (по умолчанию:"<=") строка, указывающая тип ограничения нового ограничения
ВЫХОД:
и
Проблема LP
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c) мудрец: P1 = P.add_constraint(([2, 4]), 2000, "<=") мудрец: P1.Abcx() ( [1 1] [3 1] [2 4], (1000, 1500, 2000), (10, 5), (х1, х2) ) мудрец: P1.constraint_types() ('<=', '<=', '<=') мудрец: P.Abcx() ( [1 1] [3 1], (1000, 1500), (10, 5), (х1, х2) ) мудрец: P. constraint_types()
('<=', '<=')
мудрец: P2 = P.add_constraint(([2, 4, 6]), 2000, "<=")
Traceback (последний последний вызов):
...
TypeError: количество столбцов должно быть одинаковым, а не 2 и 3
мудрец: P3 = P.add_constraint(([2, 4]), 2000, "<")
Traceback (последний последний вызов):
...
ValueError: неизвестный тип ограничения
constraint_types()
('<=', '<=')
мудрец: P2 = P.add_constraint(([2, 4, 6]), 2000, "<=")
Traceback (последний последний вызов):
...
TypeError: количество столбцов должно быть одинаковым, а не 2 и 3
мудрец: P3 = P.add_constraint(([2, 4]), 2000, "<")
Traceback (последний последний вызов):
...
ValueError: неизвестный тип ограничения
- б()
Возвращает постоянные условия ограничений
self, т. е. \(b\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.constant_terms() (1000, 1500) мудрец: П.б() (1000, 1500)
- base_ring()
Верните базовое кольцо
на себя.Примечание
Базовое кольцо задач LP всегда является полем.
ВЫВОД:
кольцо
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.
 base_ring()
Рациональное поле
мудрец: с = (10, 5.)
мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=")
мудрец: P.base_ring()
Real Field с точностью до 53 бит
base_ring()
Рациональное поле
мудрец: с = (10, 5.)
мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=")
мудрец: P.base_ring()
Real Field с точностью до 53 бит
- с()
Коэффициенты возврата цели
self, т.е. \(c\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.objective_coefficients() (10, 5) мудрец: п.с() (10, 5)
- константа_термины()
Возвращает постоянные условия ограничений
self, т. е. \(b\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.constant_terms() (1000, 1500) мудрец: П.
 б()
(1000, 1500)
б()
(1000, 1500)
- ограничение_коэффициентов ()
Возвращает коэффициенты ограничений
self, то есть \(A\).ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.constraint_coefficients() [1 1] [3 1] мудрец: П.А.() [1 1] [3 1]
- ограничения_типы()
Вернуть кортеж со списком типов ограничений для всех строк.
ВЫХОД:
набор строк
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=", limited_type=["<=", "=="]) мудрец: P.constraint_types() ('<=', '==')
- решение_переменные()
Вернуть переменные решения
self, т. е. \(x\).
е. \(x\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.decision_variables() (С, Б) мудрец: П.х() (С, Б)
- двойной( y=нет )
Построить двойную задачу ЛП для
self.ВВОД:
ВЫВОД:
и
InteractiveLPПроблема
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: DP = P.dual() мудрец: DP.b() == P.c() Истинный мудрец: DP.dual(["C", "B"]) == P Истинный
- выполнимый_набор ()
Вернуть допустимый набор
self.ВЫВОД:
а
Многогранник
- is_bounded()
Проверить, ограничено ли
self.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.is_bounded() Истинный
Обратите внимание, что неразрешимые задачи всегда ограничены:
мудрец: b = (-1000, 1500) мудрец: P = InteractiveLPProblem(A, b, c, variable_type=">=") мудрец: P.is_feasible() ЛОЖЬ мудрец: P.is_bounded() Истинный
- is_feasible( *x )
Проверить, возможно ли
самоили заданное решение.ВВОД:
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, variable_type=">=") мудрец: P.is_feasible() Истинный мудрец: P.is_feasible(100, 200) Истинный мудрец: P.is_feasible(1000, 200) ЛОЖЬ мудрец: P.is_feasible([1000, 200]) ЛОЖЬ мудрец: P.is_feasible(1000) Traceback (последний последний вызов): .
 ..
TypeError: данный ввод не является решением этой проблемы
..
TypeError: данный ввод не является решением этой проблемы
- is_negative()
Вернуть \(True\), если проблема имеет тип
"-max"или"-min".ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.is_negative() ЛОЖЬ мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=", problem_type="-min") мудрец: P.is_negative() Истинный
- is_optimal( *x )
Проверить допустимость данного решения.
ВВОД:
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (15, 5) мудрец: P = InteractiveLPProblem(A, b, c, variable_type=">=") мудрец: P.is_optimal(100, 200) ЛОЖЬ мудрец: P.is_optimal(500, 0) Истинный мудрец: P.is_optimal(499, 3) Истинный мудрец: P.is_optimal(501, -3) ЛОЖЬ
- is_primal()
Проверить, считаем ли мы эту задачу простой или двойственной.

Это различие влияет только на некоторые автоматически выбранные имена переменных.
ВЫВОД:
логический
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.is_primal() Истинный мудрец: P.dual().is_primal() ЛОЖЬ
- м()
Возвращает количество ограничений
self, т.е. \(m\).ВЫВОД:
целое число
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.n_constraints() 2 мудрец: Пм() 2
- п()
Вернуть число переменных решения
self, то есть \(n\).ВЫВОД:
целое число
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.
 n_variables()
2
мудрец: п.н()
2
n_variables()
2
мудрец: п.н()
2
- n_constraints()
Возвращает количество ограничений
self, т.е. \(m\).ВЫВОД:
целое число
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.n_constraints() 2 мудрец: Пм() 2
- n_variables()
Возвращает число переменных решения
self, т. е. \(n\).ВЫВОД:
целое число
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.n_variables() 2 мудрец: п.н() 2
- объективные_коэффициенты()
Коэффициенты возврата цели
self, т.е. \(c\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.
 objective_coefficients()
(10, 5)
мудрец: п.с()
(10, 5)
objective_coefficients()
(10, 5)
мудрец: п.с()
(10, 5)
- target_constant_term()
Возвращает постоянный член цели.
ВЫВОД:
номер
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.objective_constant_term() 0 мудрец: P.optimal_value() 6250 мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], ....: variable_type=">=", target_constant_term=-1250) мудрец: P.objective_constant_term() -1250 мудрец: P.optimal_value() 5000
- target_value( *x )
Возвращает значение цели для данного решения.
ВВОД:
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, variable_type=">=") мудрец: P.objective_value(100, 200) 2000 г.

- оптимальное_решение()
Возврат оптимальное решение
сам.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.optimal_solution() (250, 750)
- оптимальное_значение()
Вернуть оптимальное значение для
self.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.optimal_value() 6250
- график ( * аргументы , ** kwds )
Вернуть график для решения
selfграфически.ВВОД:
xmin,xmax,ymin,ymax– границы осей, если не указано, будет предпринята попытка подобрать разумные значенияальфа— (по умолчанию: 0,2) определяет, насколько непрозрачны тени
ВЫХОД:
участок
Это работает только для задач с двумя переменными решения.
 На участке
черная стрелка указывает направление роста объектива.
линии, перпендикулярные ему, являются кривыми уровня объектива. Если там
являются оптимальными решениями, стрелка начинается в одном из них, а
соответствующая кривая уровня сплошная: все точки допустимого множества
на нем находятся оптимальные решения. В противном случае стрелка помещается в
центр. Если проблема неразрешима или цель равна нулю, сюжет
возвращается только допустимое множество.
На участке
черная стрелка указывает направление роста объектива.
линии, перпендикулярные ему, являются кривыми уровня объектива. Если там
являются оптимальными решениями, стрелка начинается в одном из них, а
соответствующая кривая уровня сплошная: все точки допустимого множества
на нем находятся оптимальные решения. В противном случае стрелка помещается в
центр. Если проблема неразрешима или цель равна нулю, сюжет
возвращается только допустимое множество.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: p = P.plot() мудрец: p.show()
В этом случае график лучше работает со следующими диапазонами осей:
мудрец: p = P.plot(0, 1000, 0, 1500) мудрец: p.show()
- plot_feasible_set( xmin=Нет , xmax=Нет , ymin=Нет , ymax=Нет , альфа = 0,2 )
Вернуть график допустимого множества
self.
ВВОД:
xmin,xmax,ymin,ymax– границы осей, если не указано, будет предпринята попытка подобрать разумные значенияальфа— (по умолчанию: 0,2) определяет, насколько непрозрачны тени
ВЫХОД:
участок
Это работает только для задачи с двумя переменными решения. Сюжет показывает границы ограничений тенью с одной стороны для неравенства. Если
возможных_set()не пусто и хотя бы часть его находится в заданных границах, она будет закрашена серым цветом и \(F\) будет размещен в его середине.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: p = P.plot_feasible_set() мудрец: p.show()
В этом случае график лучше работает со следующими диапазонами осей:
мудрец: p = P.
 plot_feasible_set (0, 1000, 0, 1500)
мудрец: p.show()
plot_feasible_set (0, 1000, 0, 1500)
мудрец: p.show()
- проблема_тип()
Вернуть тип проблемы.
Необходимо использовать вместе с
is_negative.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.problem_type() 'Максимум' мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=", problem_type="-min") мудрец: P.problem_type() 'мин'
- standard_form (преобразование = False , **kwds )
Построить задачу LP в стандартной форме, эквивалентной
self.ВВОД:
преобразование— (по умолчанию:False) еслиTrue, карта преобразование решений задачи в стандартной форме в исходную один будет также возвращенможно пройти (только как ключевые слова)
slack_variables,вспомогательная_переменная,``objective_name`` в конструкторInteractiveLPProblemStandardForm
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, variable_type=">=") мудрец: DP = P.
 dual()
мудрец: DPSF = DP.standard_form()
мудрец: DPSF.b()
(-10, -5)
мудрец: DPSF.slack_variables()
(у3, у4)
мудрец: DPSF = DP.standard_form(slack_variables=["L", "F"])
мудрец: DPSF.slack_variables()
(Л, Ж)
мудрец: DPSF, f = DP.standard_form(True)
мудрец: ф
Морфизм векторного пространства представлен матрицей:
[1 0]
[0 1]
Домен: векторное пространство размерности 2 над рациональным полем.
Codomain: векторное пространство размерности 2 над Rational Field
dual()
мудрец: DPSF = DP.standard_form()
мудрец: DPSF.b()
(-10, -5)
мудрец: DPSF.slack_variables()
(у3, у4)
мудрец: DPSF = DP.standard_form(slack_variables=["L", "F"])
мудрец: DPSF.slack_variables()
(Л, Ж)
мудрец: DPSF, f = DP.standard_form(True)
мудрец: ф
Морфизм векторного пространства представлен матрицей:
[1 0]
[0 1]
Домен: векторное пространство размерности 2 над рациональным полем.
Codomain: векторное пространство размерности 2 над Rational Field
Более сложная карта трансформации:
мудрец: P = InteractiveLPProblem(A, b, c, variable_type=["<=", ""], ....: target_constant_term=42) мудрец: PSF, f = P.standard_form(True) мудрец: ф Морфизм векторного пространства представлен матрицей: [-1 0] [ 0 1] [ 0 -1] Домен: векторное пространство размерности 3 над рациональным полем. Codomain: векторное пространство размерности 2 над Rational Field мудрец: PSF.optimal_solution() (0, 1000, 0) мудрец: P.optimal_solution() (0, 1000) мудрец: P.is_optimal(PSF.optimal_solution()) Traceback (последний последний вызов): .
 ..
TypeError: данный ввод не является решением этой проблемы
мудрец: P.is_optimal(f(PSF.optimal_solution()))
Истинный
мудрец: PSF.optimal_value()
5042
мудрец: P.optimal_value()
5042
..
TypeError: данный ввод не является решением этой проблемы
мудрец: P.is_optimal(f(PSF.optimal_solution()))
Истинный
мудрец: PSF.optimal_value()
5042
мудрец: P.optimal_value()
5042
- переменные_типы()
Вернуть кортеж со списком типов переменных всех переменных решения.
ВЫВОД:
набор строк
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=[">=", ""]) мудрец: P.variable_types() ('>=', '')
- х()
Вернуть переменные решения
self, т. е. \(x\).ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblem(A, b, c, ["C", "B"], variable_type=">=") мудрец: P.decision_variables() (С, Б) мудрец: П.х() (С, Б)
- класс sage.
 numerical.interactive_simplex_method.InteractiveLPProblemStandardForm( A , B , C , x = 'x' , Проблема_type = 'max' , Slack_variables = None , Auxiliarial_var_var_variables = None , Auxiliarial_var_VAR = None 9075, 9075, 9075, 9075, 9075, 9075, 9075, 9075, 9075, , , = 9075, , . , target_name=Нет , target_constant_term=0 )
numerical.interactive_simplex_method.InteractiveLPProblemStandardForm( A , B , C , x = 'x' , Проблема_type = 'max' , Slack_variables = None , Auxiliarial_var_var_variables = None , Auxiliarial_var_VAR = None 9075, 9075, 9075, 9075, 9075, 9075, 9075, 9075, 9075, , , = 9075, , . , target_name=Нет , target_constant_term=0 ) Базы:
sage.numerical.interactive_simplex_method.InteractiveLPProblemСоздайте задачу LP (линейное программирование) в стандартной форме.
Примечание
Этот класс предназначен только для образовательных целей : если вы хотите решить Линейные программы эффективно, используйте
MixedIntegerLinearProgramвместо.Используемая стандартная форма:
\[\begin{split}\begin{массив}{l} \макс\макс сх\\ Топор \leq b\\ х \geq 0 \конец{массив}\конец{разделить}\]
ВВОД:
А– матрица коэффициентов ограниченийб– вектор постоянных членов ограниченияc– вектор объективных коэффициентовx– (по умолчанию:"x") вектор переменных решения или строка базовое имя, дающееproblem_type– (по умолчанию:"max") строка, определяющая тип задачи: либо"max", либо"-max"slack_variables— (по умолчанию: зависит от стиля()) вектор резервных переменных или строка, задающая базовое имявспомогательная_переменная– (по умолчанию: то же, что и параметрxс присоединенным"0"если было задано как строка, иначе"x0") вспомогательный имя, которое, как ожидается, будет таким же, как первая переменная решения для вспомогательные задачиbase_ring— (по умолчанию: дробное поле общего кольца для всех входные коэффициенты) поле, в которое будут помещены все входные коэффициенты. переделанный
переделанныйis_primal— (по умолчанию:True) является ли эта проблема первичной или двойная: каждая проблема, конечно, двойственна своей собственной двойственности, этот флаг в основном для внутреннего использования и влияет только на имена переменных по умолчаниюtarget_name– строка или символьное выражение для цель, используемая в словарях, по умолчанию зависит отstyle()target_constant_term– (по умолчанию: 0) постоянный срок цель
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c)
В отличие от
InteractiveLPProblem, этот класс не позволяет настраивать типы ограничения (они всегда"<=") и переменные (они всегда">="), а тип проблемы может быть только"max"или"-max". Вы можете давать собственные имена slack-переменным и вспомогательным переменным, но в
в большинстве случаев должны работать значения по умолчанию:
Вы можете давать собственные имена slack-переменным и вспомогательным переменным, но в
в большинстве случаев должны работать значения по умолчанию:мудрец: P.decision_variables() (х1, х2) мудрец: P.slack_variables() (х3, х4)
- add_constraint( коэффициенты , Constant_term , slack_variable=None )
Возвратите новую задачу LP, добавив ограничение к ``self``.
ВВОД:
коэффициенты– коэффициенты нового ограниченияConstant_term– постоянный член нового ограниченияslack_variable— (по умолчанию: зависит от стиля()) строка, задающая имя резервной переменной нового ограничения
ВЫХОД:
задача
LP в стандартной форме
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.
 Abcx()
(
[1 1]
[3 1], (1000, 1500), (10, 5), (х1, х2)
)
мудрец: P.slack_variables()
(х3, х4)
мудрец: P1 = P.add_constraint(([2, 4]), 2000)
мудрец: P1.Abcx()
(
[1 1]
[3 1]
[2 4], (1000, 1500, 2000), (10, 5), (х1, х2)
)
мудрец: P1.slack_variables()
(х3, х4, х5)
мудрец: P2 = P.add_constraint(([2, 4]), 2000, slack_variable='c')
мудрец: P2.slack_variables()
(х3, х4, в)
мудрец: P3 = P.add_constraint(([2, 4, 6]), 2000)
Traceback (последний последний вызов):
...
TypeError: количество столбцов должно быть одинаковым, а не 2 и 3
Abcx()
(
[1 1]
[3 1], (1000, 1500), (10, 5), (х1, х2)
)
мудрец: P.slack_variables()
(х3, х4)
мудрец: P1 = P.add_constraint(([2, 4]), 2000)
мудрец: P1.Abcx()
(
[1 1]
[3 1]
[2 4], (1000, 1500, 2000), (10, 5), (х1, х2)
)
мудрец: P1.slack_variables()
(х3, х4, х5)
мудрец: P2 = P.add_constraint(([2, 4]), 2000, slack_variable='c')
мудрец: P2.slack_variables()
(х3, х4, в)
мудрец: P3 = P.add_constraint(([2, 4, 6]), 2000)
Traceback (последний последний вызов):
...
TypeError: количество столбцов должно быть одинаковым, а не 2 и 3
- вспомогательная_проблема( target_name=Нет )
Построить вспомогательную задачу для
self.ВВОД:
ВЫВОД:
задача
LP в стандартной форме
Вспомогательная задача со вспомогательной переменной \(x_0\) равна
\[\begin{split}\begin{массив}{l} \макс - х_0 \\ - x_0 + A_i x \leq b_i \text{ для всех } i \\ х \geq 0 \конец{массив}\ .
 \конец{разделить}\]
\конец{разделить}\]Такие проблемы возникают, когда
initial_dictionary()невыполнимо.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: AP = P.auxiliary_problem()
- вспомогательная_переменная()
Вернуть вспомогательную переменную
self.Обратите внимание, что вспомогательная переменная может быть или не быть среди
решение_переменные().ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.auxiliary_variable() х0 мудрец: P.decision_variables() (х1, х2) мудрец: AP = P.auxiliary_problem() мудрец: AP.auxiliary_variable() х0 мудрец: AP.decision_variables() (х0, х1, х2)
- координата_кольцо ()
Возврат координатного кольца
сам.
ВЫВОД:
полиномиальное кольцо над
base_ring()изselfввспомогательная_переменная (),решение_переменных (), иslack_variables()с заказом «neglex»
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.coordinate_ring() Многомерное полиномиальное кольцо в x0, x1, x2, x3, x4, x5 над рациональным полем мудрец: P.base_ring() Рациональное поле мудрец: P.auxiliary_variable() х0 мудрец: P.decision_variables() (х1, х2) мудрец: P.slack_variables() (х3, х4, х5)
- словарь( *x_B )
Создать словарь для
себяс заданными базовыми переменными.ВВОД:
ВЫВОД:
словарь
Примечание
Это синоним
self.revised_dictionary(x_B)., но основные переменные являются обязательными. dictionary()
dictionary() ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.dictionary("x1", "x2") мудрец: D.basic_variables() (х1, х2)
- выполнимый_словарь( вспомогательный_словарь )
Создать допустимый словарь для
себя.ВВОД:
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: AP = P.auxiliary_problem() мудрец: D = AP.initial_dictionary() мудрец: D.enter(0) мудрец: Д.уйти(5) мудрец: D.update() мудрец: D.enter(1) мудрец: Д.уйти(0) мудрец: D.update() мудрец: D.is_optimal() Истинный мудрец: D.objective_value() 0 мудрец: D.basic_solution() (0, 400, 0) мудрец: D = P.feasible_dictionary(D) мудрец: D.is_optimal() ЛОЖЬ мудрец: D.
 is_feasible()
Истинный
мудрец: D.objective_value()
4000
мудрец: D.basic_solution()
(400, 0)
is_feasible()
Истинный
мудрец: D.objective_value()
4000
мудрец: D.basic_solution()
(400, 0)
- final_dictionary()
Вернуть окончательный словарь симплекс-метода, примененного к
self.См.
run_simplex_method()для описания возможностей.ВЫВОД:
словарь
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.final_dictionary() мудрец: D.is_optimal() Истинный
- final_revised_dictionary()
Вернуть окончательный словарь измененного примененного симплекс-метода к
себе.См.
run_revised_simplex_method()для описания возможности.ВЫВОД:
a
пересмотренный словарь
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 final_revised_dictionary()
мудрец: D.is_optimal()
Истинный
final_revised_dictionary()
мудрец: D.is_optimal()
Истинный
- начальный_словарь()
Построить исходный словарь
из себя.Исходный словарь «определяет»
slack_variables()в терминах изsolution_variables(), т. е. имеет резерв переменные как базовые.ВЫВОД:
словарь
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary()
- inject_variables( объем=нет , многословный=истина )
Вставить переменные
selfв область видимостиВВОД:
ВЫВОД:
нет
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.
 inject_variables()
Определение x0, x1, x2, x3, x4
шалфей: 3*x1 + x2
х2 + 3*х1
inject_variables()
Определение x0, x1, x2, x3, x4
шалфей: 3*x1 + x2
х2 + 3*х1
- имя_цели()
Вернуть имя задачи, используемое в словарях для этой задачи.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.objective_name() г мудрец: sage.numerical.interactive_simplex_method.style ("Вандербей") 'Вандербей' мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.objective_name() дзета шалфей: sage.numerical.interactive_simplex_method.style("UAlberta") 'УАльберта' мудрец: P = InteractiveLPProblemStandardForm(A, b, c, target_name="custom") мудрец: P.objective_name() обычай
- static random_element( m , n , bound=5 , special_probability=0.2 , **kwds )
Создать случайную форму
InteractiveLPProblemStandardForm.
ВВОД:
m– количество ограничений/базовых переменныхn– количество решающих/неосновных переменныхbound– (по умолчанию: 5) ограничение на коэффициентыspecial_probability– (по умолчанию: 0,2) вероятность построение задачи, исходный словарь которой разрешен быть изначально невозможным или двойственно возможным
Все остальные аргументы ключевого слова передаются конструктору.
ПРИМЕРЫ:
мудрец: InteractiveLPProblemStandardForm.random_element(3, 4) Проблема с LP (для получения подробной информации используйте "view(...)" или "%display typeset")
- пересмотренный_словарь ( *x_B )
Создать новый словарь для
себя.ВВОД:
основные переменные для создаваемого словаря; если не дано,
slack_variables()будет использоваться, возможно, свспомогательная_переменная()для получения подходящего словаря
ВЫХОД:
a
пересмотренный словарь
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary("x1", "x2")
мудрец: D.basic_variables()
(х1, х2)
revised_dictionary("x1", "x2")
мудрец: D.basic_variables()
(х1, х2)
Если базовые переменные не заданы, исходный словарь построено:
мудрец: P.revised_dictionary().basic_variables() (х3, х4) мудрец: P.initial_dictionary().basic_variables() (х3, х4)
Если это невозможно, в этом случае допустимый словарь для построена вспомогательная задача:
мудрец: A = ([1, 1], [3, 1], [-1,-1]) мудрец: b = (1000, 1500, -400) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.initial_dictionary().is_feasible() ЛОЖЬ мудрец: P.revised_dictionary().basic_variables() (х3, х4, х0)
- run_revised_simplex_method()
Применить пересмотренный симплекс-метод и возвратить все шаги.
ВЫВОД:
Примечание
Вы можете получить доступ к
final_revised_dictionary(), который может быть одно из следующих:оптимальный словарь с
вспомогательной_переменной()средиbasic_variables()и ненулевой оптимальное значение, указывающее чтосамоневозможно;неоптимальный словарь с пометкой входа переменная, для которой нет выбора уходящей переменной, указание того, что
selfне ограничено;оптимальный словарь.

ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.run_revised_simplex_method() \begin{уравнение*} ... \end{уравнение*} Ввод: $x_{1}$. Выезд: $x_{0}$. \begin{уравнение*} ... \end{уравнение*} Ввод: $x_{5}$. Выезд: $x_{4}$. \begin{уравнение*} ... \end{уравнение*} Ввод: $x_{2}$. Выезд: $x_{3}$. \begin{уравнение*} ... \end{уравнение*} Оптимальное значение: $6250$. Оптимальное решение: $\left(250,\,750\right)$.
- run_simplex_method()
Применить симплекс-метод и вернуть все шаги и промежуточные состояния.
ВЫВОД:
Примечание
Вы можете получить доступ к
final_dictionary(), который может быть одним из следующего:оптимальный словарь для
вспомогательной_проблемы()с ненулевое оптимальное значение, указывающее, чтоselfневозможно;неоптимальный словарь на
selfкоторый отметил вход переменная, для которой нет выбора уходящей переменной, указание того, чтоselfне ограничено;оптимальный словарь для
self.
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.run_simplex_method() \begin{уравнение*} ... \end{уравнение*} Исходный словарь недопустим, что решает вспомогательную задачу. ... Ввод: $x_{0}$. Выезд: $x_{5}$. ... Ввод: $x_{1}$. Выезд: $x_{0}$. ... Вернемся к исходной проблеме. ... Ввод: $x_{5}$. Выезд: $x_{4}$. ... Ввод: $x_{2}$. Выезд: $x_{3}$. ... Оптимальное значение: $6250$. Оптимальное решение: $\left(250,\,750\right)$.
- slack_variables()
Вернуть резервные переменные
self.Slack-переменные — это разница между постоянными условиями и левые части ограничений.
Если вы хотите дать пользовательские имена слабым переменным, вы должны сделать это при построении задачи.
ВЫВОД:
кортеж
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: P.
 slack_variables()
(х3, х4)
мудрец: P = InteractiveLPProblemStandardForm(A, b, c, ["C", "B"],
....: slack_variables=["L", "F"])
мудрец: P.slack_variables()
(Л, Ж)
slack_variables()
(х3, х4)
мудрец: P = InteractiveLPProblemStandardForm(A, b, c, ["C", "B"],
....: slack_variables=["L", "F"])
мудрец: P.slack_variables()
(Л, Ж)
- класс sage.numerical.interactive_simplex_method.LPAbstractDictionary
Базы:
sage.structure.sage_object.SageObjectАбстрактный базовый класс для словарей для задач LP.
Непосредственное создание экземпляра этого класса бессмысленно, см.
LPDictionaryиLRevisedDictionaryдля полезных расширений.- add_row( неосновные_коэффициенты , константа , basic_variable=нет )
Вернуть словарь с дополнительной строкой на основе заданного словаря.
ВВОД:
nonbasic_coefficients– список коэффициентов для новая строка (с которой вычитаются неосновные переменные в отношении для новой базовой переменной)константа– константа для новой строкибазовая_переменная— (по умолчанию: зависит от стиля()) строка, задающая имя базовой переменной новой строки
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([-1, 1, 7], [8, 2, 13], [34, 17, 12]) мудрец: б = (2, 17, 6) мудрец: с = (55/10, 21/10, 14/30) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 dictionary("x1", "x2", "x4")
мудрец: D1 = D.add_row([7, 11, 19], 42, basic_variable='c')
мудрец: D1.row_coefficients("c")
(7, 11, 19)
dictionary("x1", "x2", "x4")
мудрец: D1 = D.add_row([7, 11, 19], 42, basic_variable='c')
мудрец: D1.row_coefficients("c")
(7, 11, 19)
- base_ring()
Вернуть базовое кольцо
себе, т.е. кольцо коэффициентов.ВЫВОД:
кольцо
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.base_ring() Рациональное поле мудрец: D = P.revised_dictionary() мудрец: D.base_ring() Рациональное поле
- basic_solution ( include_slack_variables = False )
Вернуть базовое решение
себе.Основное решение, связанное со словарем, получается путем установки обнулить все
nonbasic_variables(), и в этом случаеbasic_variables()должны быть равныConstant_terms()в уравнениях. Он может относиться только к значениям
Он может относиться только к значениям solution_variables()или также включитеslack_variables().ВВОД:
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.basic_solution() (0, 0) мудрец: D.basic_solution(True) (0, 0, 1000, 1500) мудрец: D = P.revised_dictionary() мудрец: D.basic_solution() (0, 0) мудрец: D.basic_solution(True) (0, 0, 1000, 1500)
- основные_переменные()
Вернуть базовые переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.basic_variables() (х3, х4)
- столбец_коэффициенты ( против )
Возвращает коэффициенты неосновной переменной.

ВВОД:
v– неосновная переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.column_coefficients(1) (1, 3)
- константа_термс ()
Вернуть постоянные условия отношений
себе.ВЫВОД:
вектор.
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.constant_terms() (1000, 1500)
- координата_кольцо ()
Возврат координатного кольца
сам.
ВЫВОД:
кольцо полиномов в
вспомогательная_переменная(),решение_переменных()иslack_variables()изсебяпоbase_ring()
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.coordinate_ring() Многомерное полиномиальное кольцо в x0, x1, x2, x3, x4 над рациональным полем мудрец: D = P.revised_dictionary() мудрец: D.coordinate_ring() Многомерное полиномиальное кольцо в x0, x1, x2, x3, x4 над рациональным полем
- двойные_отношения()
Коэффициенты возврата, используемые для определения входной переменной на основе выхода.
ВЫВОД:
Список пар \((r_j, x_j)\), где \(x_j\) — неосновная переменная, а \(r_j = c_j / a_{ij}\) - отношение объективного коэффициента \(c_j\) к коэффициенту \(a_{ij}\) при \(x_j\) в соотношении для ухода переменная \(x_i\):
\[x_i = b_i - \cdots - a_{ij} x_j - \cdots.
 \]
\]Порядок пар совпадает с порядком
неосновные_переменные(), но учитываются только \(x_j\) с отрицательным \(a_{ij}\).
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.dictionary(2, 3, 5) мудрец: Д.уйти(3) мудрец: D.dual_ratios() [(5/2, х1), (5, х4)] мудрец: D = P.revised_dictionary(2, 3, 5) мудрец: Д.уйти(3) мудрец: D.dual_ratios() [(5/2, х1), (5, х4)]
- введите ( v )
Установите
vв качестве входной переменнойself.ВВОД:
v— неосновная переменнаяself, может быть задана в виде строки, фактическая переменная или целое число, интерпретируемое как индекс переменная. Также можно ввестиНетдля сброса выбора.
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.enter("x1")
initial_dictionary()
мудрец: D.enter("x1")
Мы также можем использовать индексы переменных:
мудрец: D.enter(1)
Или имена переменных без кавычек после их внедрения:
мудрец: P.inject_variables() Определение x0, x1, x2, x3, x4 мудрец: D. введите (x1)
То же самое работает и с исправленными словарями:
мудрец: D = P.revised_dictionary() мудрец: D. введите (x1)
- ввод()
Вернуть текущую выбранную входную переменную.
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.entering() - None Истинный мудрец: D.enter(1) мудрец: D.вход() х1
- ввод_коэффициентов()
Возвращает коэффициенты введенной переменной.
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.enter(1)
мудрец: D.entering_coefficients()
(1, 3)
initial_dictionary()
мудрец: D.enter(1)
мудрец: D.entering_coefficients()
(1, 3)
- is_dual_feasible()
Проверить, является ли
selfдвойственно возможным.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.is_dual_feasible() ЛОЖЬ мудрец: D = P.revised_dictionary() мудрец: D.is_dual_feasible() ЛОЖЬ
- is_feasible()
Проверить, если
selfвозможно.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.is_feasible() Истинный мудрец: D = P.revised_dictionary() мудрец: D.is_feasible() Истинный
- is_optimal()
Проверить, является ли
selfоптимальным.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.is_optimal() ЛОЖЬ мудрец: D = P.revised_dictionary() мудрец: D.is_optimal() ЛОЖЬ мудрец: D = P.revised_dictionary(1, 2) мудрец: D.is_optimal() Истинный
- уйти( v )
Установить
vкак выходную переменнуюself.ВВОД:
v– базовая переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменная. Также можно оставитьNoneдля сброса выбора.
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.
 leave ("x4")
leave ("x4")
Мы также можем использовать индексы переменных:
мудрец: Д.уйти(4)
Или имена переменных без кавычек после их внедрения:
мудрец: P.inject_variables() Определение x0, x1, x2, x3, x4 мудрец: D.уйти(x4)
То же самое работает и с исправленными словарями:
мудрец: D = P.revised_dictionary() мудрец: D.уйти(x4)
- уход()
Вернуть текущую выбранную уходящую переменную.
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.leaving() — None Истинный мудрец: Д.уйти(4) мудрец: Д.уходя() х4
- покидающие_коэффициенты ()
Возвращает коэффициенты уходящей переменной.
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 dictionary(2, 3)
мудрец: Д.уйти(3)
мудрец: D.leaving_coefficients()
(-2, -1)
dictionary(2, 3)
мудрец: Д.уйти(3)
мудрец: D.leaving_coefficients()
(-2, -1)
То же самое работает и с исправленными словарями:
мудрец: D = P.revised_dictionary(2, 3) мудрец: Д.уйти(3) мудрец: D.leaving_coefficients() (-2, -1)
- неосновные_переменные()
Вернуть неосновные переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.nonbasic_variables() (х1, х2)
- объективные_коэффициенты()
Возвратные коэффициенты цели
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.objective_coefficients()
(10, 5)
initial_dictionary()
мудрец: D.objective_coefficients()
(10, 5)
- имя_цели()
Вернуть имя цели
self.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.objective_name() г
- target_value()
Вернуть значение цели в
basic_solution()изself.ВЫХОД:
номер
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.objective_value() 0
- возможно_двойной_симплекс_метод_степс()
Вернуть возможные шаги двойного симплексного метода для
self.ВЫВОД:
Список пар
(выход, вход), гдепокидаетбазовая переменная, которая можетоставить()ивводпредставляет собой список неосновные переменные, которые могутвойти (), когдапокидаетуходит. Обратите внимание, что
Обратите внимание, что , вводя, может быть пустым, указывая на то, что проблема недопустимо (поскольку двойственное неограниченно).
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.dictionary(2, 3) мудрец: D.possible_dual_simplex_method_steps() [(x3, [x1])] мудрец: D = P.revised_dictionary(2, 3) мудрец: D.possible_dual_simplex_method_steps() [(x3, [x1])]
- возможно_ввод()
Вернуть возможные вводимые переменные для
self.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.possible_entering() [х1, х2] мудрец: D = P.revised_dictionary() мудрец: D.possible_entering() [х1, х2]
- возможное_оставление()
Вернуть возможные выходные переменные для
self.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.enter(1) мудрец: D.possible_leaving() [x4] мудрец: D = P.revised_dictionary() мудрец: D.enter(1) мудрец: D.possible_leaving() [x4]
- возможно_simplex_method_steps()
Вернуть возможные шаги симплексного метода для
self.ВЫВОД:
Список пар
(входящий, выходящий), гдевходящийявляется неосновная переменная, которая можетвойти()иоставитьсписок основных переменных, которые могутвыйти (), когдавходитвходит. Обратите внимание, что, оставляя, может быть пустым, указывая на то, что проблема неограниченный.
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.possible_simplex_method_steps()
[(x1, [x4]), (x2, [x3])]
мудрец: D = P.revised_dictionary()
мудрец: D.possible_simplex_method_steps()
[(x1, [x4]), (x2, [x3])]
initial_dictionary()
мудрец: D.possible_simplex_method_steps()
[(x1, [x4]), (x2, [x3])]
мудрец: D = P.revised_dictionary()
мудрец: D.possible_simplex_method_steps()
[(x1, [x4]), (x2, [x3])]
- коэффициенты ()
Коэффициент возврата, используемый для определения исходящей переменной на основе ввода.
ВЫВОД:
Список пар \((r_i, x_i)\), где \(x_i\) — базовая переменная, а \(r_i = b_i / a_{ik}\) есть отношение постоянного члена \(b_i\) к коэффициент \(a_{ik}\) входящей переменной \(x_k\) в отношении для \(x_i\):
\[x_i = b_i - \cdots - a_{ik} x_k - \cdots.\]
Порядок пар совпадает с порядком
базовые_переменные(), но учитываются только \(x_i\) с положительным \(a_{ik}\).
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.enter(1) мудрец: D.
 ratios()
[(1000, x3), (500, x4)]
мудрец: D = P.revised_dictionary()
мудрец: D.enter(1)
мудрец: D.ratios()
[(1000, x3), (500, x4)]
ratios()
[(1000, x3), (500, x4)]
мудрец: D = P.revised_dictionary()
мудрец: D.enter(1)
мудрец: D.ratios()
[(1000, x3), (500, x4)]
- row_coefficients( против )
Вернуть коэффициенты базовой переменной
v.Это коэффициенты, с которыми вычитаются неосновные переменные в отношении
к.ВВОД:
v– базовая переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([-1, 1], [8, 2]) мудрец: b = (2, 17) мудрец: с = (55/10, 21/10) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.final_dictionary() мудрец: D.row_coefficients("x1") (1/10, -1/5)Мы также можем использовать индексы переменных:
мудрец: D.row_coefficients(1) (1/10, -1/5)
Или использовать имена переменных без кавычек после их внедрения:
мудрец: P.
 inject_variables()
Определение x0, x1, x2, x3, x4
мудрец: D.row_coefficients(x1)
(1/10, -1/5)
inject_variables()
Определение x0, x1, x2, x3, x4
мудрец: D.row_coefficients(x1)
(1/10, -1/5)
- run_dual_simplex_method()
Применить метод двойного симплекса и возвратить все шаги/промежуточные состояния.
Если входные или выходные переменные уже были установлены, они будут использовал.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.run_dual_simplex_method() Traceback (последний последний вызов): ... ValueError: оставшиеся переменные могут быть определены для возможного словари с заданной входной переменной или для двойного возможного словари
Давайте начнем с двойного возможного словаря, тогда:
мудрец: D = P.dictionary(2, 3, 5) мудрец: D.is_dual_feasible() Истинный мудрец: D.is_optimal() ЛОЖЬ мудрец: D.run_dual_simplex_method() \begin{уравнение*} . ..
\end{уравнение*}
Выезд: $x_{3}$. Ввод: $x_{1}$.
\begin{уравнение*}
...
\end{уравнение*}
мудрец: D.is_optimal()
Истинный
..
\end{уравнение*}
Выезд: $x_{3}$. Ввод: $x_{1}$.
\begin{уравнение*}
...
\end{уравнение*}
мудрец: D.is_optimal()
Истинный
Этот метод обнаруживает неразрешимые проблемы:
мудрец: A = ([1, 0],) мудрец: b = (-1,) мудрец: с = (0, -1) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.run_dual_simplex_method() \begin{уравнение*} ... \end{уравнение*} Задача неразрешима из-за ограничения $x_{3}$.
- run_simplex_method()
Применить симплекс-метод и вернуть все шаги и промежуточные состояния.
Если входные или выходные переменные уже были установлены, они будут использовал.
ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.run_simplex_method() Traceback (последний последний вызов): ... ValueError: ввод переменных может быть определен для возможного словари или для двойных допустимых словарей с набором, оставляющим переменная
Давайте начнем с подходящего словаря, тогда:
мудрец: D = P.
 dictionary(1, 3, 4)
мудрец: D.is_feasible()
Истинный
мудрец: D.is_optimal()
ЛОЖЬ
мудрец: D.run_simplex_method()
\begin{уравнение*}
...
\end{уравнение*}
Ввод: $x_{5}$. Выезд: $x_{4}$.
\begin{уравнение*}
...
\end{уравнение*}
Ввод: $x_{2}$. Выезд: $x_{3}$.
\begin{уравнение*}
...
\end{уравнение*}
мудрец: D.is_optimal()
Истинный
dictionary(1, 3, 4)
мудрец: D.is_feasible()
Истинный
мудрец: D.is_optimal()
ЛОЖЬ
мудрец: D.run_simplex_method()
\begin{уравнение*}
...
\end{уравнение*}
Ввод: $x_{5}$. Выезд: $x_{4}$.
\begin{уравнение*}
...
\end{уравнение*}
Ввод: $x_{2}$. Выезд: $x_{3}$.
\begin{уравнение*}
...
\end{уравнение*}
мудрец: D.is_optimal()
Истинный
Этот метод обнаруживает неограниченные проблемы:
мудрец: A = ([1, 0],) мудрец: б = (1,) мудрец: с = (0, 1) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.run_simplex_method() \begin{уравнение*} ... \end{уравнение*} Задача не ограничена в направлении $x_{2}$.
- обновить()
Обновите
себя, используя ранее установленные входные и выходные переменные.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.
 * + с х_N\\
\hline
\конец{массив}\конец{разделить}\] 9*\)
* + с х_N\\
\hline
\конец{массив}\конец{разделить}\] 9*\)
basic_variables– список базовых переменных \(x_B\)nonbasic_variables– список небазовых переменных \(x_N\)target_name– «имя» для цели \(z\)ВЫХОД:
-
словарь
для задачи LP
Примечание
Этот конструктор не проверяет правильность ввода, т.к. предназначен для внутреннего использования
InteractiveLPProblemStandardForm.ПРИМЕРЫ:
Предполагается косвенное использование этого класса:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: Д Словарь проблем LP (используйте ...)
Но если вы хотите, вы можете создать словарь, не начиная с LP проблема, вот построение того же словаря, что и выше:
мудрец: A = матрица (QQ, ([1, 1], [3, 1])) мудрец: b = вектор (QQ, (1000, 1500)) мудрец: c = вектор (QQ, (10, 5)) мудрец: R = PolynomialRing(QQ, "x1, x2, x3, x4", order="neglex") шалфей: из sage.
 numerical.interactive_simplex_method \
....: импорт LPDictionary
мудрец: D2 = LPDictionary(A, b, c, 0, R.gens()[2:], R.gens()[:2], "z")
мудрец: D2 == D
Истинный
numerical.interactive_simplex_method \
....: импорт LPDictionary
мудрец: D2 = LPDictionary(A, b, c, 0, R.gens()[2:], R.gens()[:2], "z")
мудрец: D2 == D
Истинный
- add_row( nonbasic_coefficients , константа , basic_variable=None )
Вернуть словарь с дополнительной строкой на основе заданного словаря.
ВВОД:
nonbasic_coefficients– список коэффициентов для новая строка (с которой вычитаются неосновные переменные в отношении для новой базовой переменной)константа– константа для новой строкиbasic_variable– (по умолчанию: зависит отstyle()) строка, задающая имя базовой переменной новой строки
ВЫХОД:
словарь
ПРИМЕР:
мудрец: A = ([-1, 1, 7], [8, 2, 13], [34, 17, 12]) мудрец: б = (2, 17, 6) мудрец: с = (55/10, 21/10, 14/30) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 dictionary("x1", "x2", "x4")
мудрец: D1 = D.add_row([7, 11, 19], 42, basic_variable='c')
мудрец: D1.row_coefficients("c")
(7, 11, 19)
мудрец: D1.constant_terms()[-1]
42
мудрец: D1.basic_variables()[-1]
с
dictionary("x1", "x2", "x4")
мудрец: D1 = D.add_row([7, 11, 19], 42, basic_variable='c')
мудрец: D1.row_coefficients("c")
(7, 11, 19)
мудрец: D1.constant_terms()[-1]
42
мудрец: D1.basic_variables()[-1]
с
- основные_переменные()
Вернуть базовые переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.basic_variables() (х3, х4)
- столбец_коэффициенты ( против )
Возвращает коэффициенты неосновной переменной.
ВВОД:
v– неосновная переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫХОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.column_coefficients(1)
(1, 3)
initial_dictionary()
мудрец: D.column_coefficients(1)
(1, 3)
- константа_термс ()
Вернуть постоянные условия отношений
себе.ВЫВОД:
вектор.
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.constant_terms() (1000, 1500)
- неосновные_переменные()
Вернуть неосновные переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.nonbasic_variables() (х1, х2)
- объективные_коэффициенты()
Возвратные коэффициенты цели
self.
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.objective_coefficients() (10, 5)
- имя_цели()
Вернуть имя цели
self.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.objective_name() г
- target_value()
Вернуть значение цели в
basic_solution()изself.ВЫВОД:
номер
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 initial_dictionary()
мудрец: D.objective_value()
0
initial_dictionary()
мудрец: D.objective_value()
0
- статический random_element( m , n , bound=5 , special_probability=0.2 )
Создать случайный словарь.
ВВОД:
m– количество ограничений/базовых переменныхn– количество решающих/неосновных переменныхпривязка— (по умолчанию: 5) привязка к словарным статьямspecial_probability– (по умолчанию: 0,2) вероятность построения потенциально невозможный или потенциально оптимальный словарь
ВЫХОД:
и
Словарь задач LP
ПРИМЕР:
шалфей: из sage.numerical.interactive_simplex_method \ ....: импортировать random_dictionary sage: random_dictionary(3, 4) # косвенный doctest Словарь проблем LP (для получения подробной информации используйте «view(.
 ..)» или «%display typeset»)
..)» или «%display typeset»)
- row_coefficients( против )
Вернуть коэффициенты базовой переменной
v.Это коэффициенты, с которыми вычитаются неосновные переменные в отношении
к.ВВОД:
v– базовая переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([-1, 1], [8, 2]) мудрец: b = (2, 17) мудрец: с = (55/10, 21/10) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.final_dictionary() мудрец: D.row_coefficients("x1") (1/10, -1/5)Мы также можем использовать индексы переменных:
мудрец: D.row_coefficients(1) (1/10, -1/5)
Или использовать имена переменных без кавычек после их внедрения:
мудрец: P.inject_variables() Определение x0, x1, x2, x3, x4 мудрец: D.
 row_coefficients(x1)
(1/10, -1/5)
row_coefficients(x1)
(1/10, -1/5)
- обновить()
Обновите
себя, используя ранее установленные входные и выходные переменные.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.initial_dictionary() мудрец: D.objective_value() 0 мудрец: D.enter("x1") мудрец: D.leave ("x4") мудрец: D.update() мудрец: D.objective_value() 5000
- класс sage.numerical.interactive_simplex_method.LPRevisedDictionary( проблема , basic_variables )
Базы:
sage.numerical.interactive_simplex_method.LPAbstractDictionaryСоздать пересмотренный словарь для задачи LP.
ВВОД:
ВЫВОД:
пересмотренный словарь
для задачи LP
Пересмотренный словарь кодирует те же отношения, что и
обычный словарь, но хранит только то, что есть «необходим для эффективного вычисления данных для симплексного метода».
Пусть исходная задача будет
\[\begin{split}\begin{массив}{l} \макс\макс сх\\ Топор \leq b\\ х \geq 0 \конец{массив}\конец{разделить}\]
Пусть \(\bar{x}\) будет вектором
option_variables()\(x\) за которым следуетslack_variables(). Пусть \(\bar{c}\) будет векторомобъективных_коэффициентов()\(c\) за которыми следуют нули для всех резервных переменных. Пусть \(\bar{A} = (A | I)\) — матрицаограничение_коэффициентов ()\(A\) дополнено идентификатором матрица в виде столбцов, соответствующих резервным переменным. Тогда проблема выше можно записать как\[\begin{split}\begin{массив}{l} \pm \max \bar{c} \bar{x} \\ \бар{А} \бар{х} = б \\ \bar{x} \geq 0 \конец{массив}\конец{разделить}\]
и любой словарь представляет собой систему уравнений, эквивалентную \(\bar{A} \bar{x} = b\), но разрешено для
basic_variables()\(x_B\) в условияnonbasic_variables()\(x_N\) вместе с выражением для цель с точки зрения \(x_N\). Пусть 9{-1}\), поэтому мы отслеживаем его
через этапы обновления.
Пусть 9{-1}\), поэтому мы отслеживаем его
через этапы обновления.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) шалфей: из sage.numerical.interactive_simplex_method \ ....: импортировать LPRevisedDictionary мудрец: D = LPRevisedDictionary(P, [1, 2]) мудрец: D.basic_variables() (х1, х2) мудрец: Д Словарь проблем LP (используйте ...)
Такой же словарь можно построить через задачу:
9{-1}\) и несколько дополнительных столбцов, а нижний показывает несколько строк: они связаны со столбцами и строками словарные статьи.- А( против )
Вернуть столбец коэффициентов ограничений, соответствующий
v.ВВОД:
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: Д.А.(1)
(1, 3)
мудрец: Д.А.(0)
(-1, -1)
мудрец: DA("x3")
(1, 0)
revised_dictionary()
мудрец: Д.А.(1)
(1, 3)
мудрец: Д.А.(0)
(-1, -1)
мудрец: DA("x3")
(1, 0)
- А_Н()
Возвращает матрицу \(A_N\), коэффициенты ограничения неосновные переменные.
ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.A_N() [1 1] [3 1]
- Б()
Возвращает матрицу \(B\), т.е. коэффициенты ограничения основные переменные.
ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary(1, 2) мудрец: Д.Б.() [1 1] [3 1]
- B_inverse()
Возвращает обратную матрицу
B().
Эта обратная матрица сохраняется и вычисляется во время обновления словаря в более эффективный способ, чем общая инверсия.
ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary(1, 2) мудрец: D.B_inverse() [-1/2 1/2] [ 3/2 -1/2]
- Э()
Возвращает эта-матрицу между
собственными следующим словарем.ВЫВОД:
матрица
Если \(B_{\mathrm{old}}\) — текущая матрица \(B\) и \(B_{\mathrm{new}}\) является матрицей \(B\) следующего словаря (после шага обновления), тогда \(B _ {\ mathrm {новый}} = B _ {\ mathrm {старый}} E \).
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: D.enter(1)
мудрец: Д.уйти(4)
мудрец: D.E()
[1 1]
[0 3]
revised_dictionary()
мудрец: D.enter(1)
мудрец: Д.уйти(4)
мудрец: D.E()
[1 1]
[0 3]
- E_inverse()
Возвращает обратную матрицу
E().Эта обратная матрица вычисляется более эффективным способом, чем обычная инверсия.
ВЫВОД:
матрица
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.enter(1) мудрец: Д.уйти(4) мудрец: D.E_inverse() [ 1 -1/3] [ 0 1/3]
- add_row( nonbasic_coefficients , константа , basic_variable=None )
Вернуть словарь с дополнительной строкой на основе заданного словаря.
Реализация этого метода для исправленных словарей добавляет к задаче новое ограничение неравенства, в котором заданное \(basic_variable\) становится резервной переменной.
 Полученный словарь
(с добавлением \(basic_variable\) к основе) будет иметь заданное
\(неосновные_коэффициенты\) и \(константа\) в качестве новой строки.
Полученный словарь
(с добавлением \(basic_variable\) к основе) будет иметь заданное
\(неосновные_коэффициенты\) и \(константа\) в качестве новой строки.ВВОД:
nonbasic_coefficients– список коэффициентов для новая строка (с которой вычитаются неосновные переменные в отношении для новой базовой переменной)константа– константа для новой строкиbasic_variable– (по умолчанию: зависит отstyle()) строка, задающая имя базовой переменной новой строки
ВЫХОД:
a
пересмотренный словарь
ПРИМЕР:
мудрец: A = ([-1, 1111, 3, 17], [8, 222, 7, 6], ....: [3, 7, 17, 5], [9, 5, 7, 3]) мудрец: б = (2, 17, 11, 27) мудрец: с = (5/133, 1/10, 1/18, 47/3) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.final_revised_dictionary() мудрец: D1 = D.add_row([7, 11, 13, 9], 42) мудрец: D1.
 row_coefficients("x9")
(7, 11, 13, 9)
мудрец: D1.constant_terms()[-1]
42
мудрец: D1.basic_variables()[-1]
х9мудрец: А = ([-9, 7, 48, 31, 23], [5, 2, 9, 13, 98],
....: [14, 15, 97, 49, 1], [9, 5, 7, 3, 17],
....: [119, 7, 121, 5, 111])
мудрец: б = (33, 27, 1, 272, 61)
мудрец: с = (51/133, 1/100, 149/18, 47/37, 13/17)
мудрец: P = InteractiveLPProblemStandardForm(A, b, c)
мудрец: D = P.revised_dictionary("x1", "x2", "x3", "x4", "x5")
мудрец: D2 = D.add_row([5 ,7, 11, 13, 9], 99, basic_variable='c')
мудрец: D2.row_coefficients("c")
(5, 7, 11, 13, 9)
мудрец: D2.constant_terms()[-1]
99
мудрец: D2.basic_variables()[-1]
с
мудрец: D = P.revised_dictionary(0, 1, 2, 3, 4)
мудрец: D.add_row([1, 2, 3, 4, 5, 6], 0)
Traceback (последний последний вызов):
...
ValueError: сумма коэффициентов неосновных переменных резерва имеет
быть равным -1 при вставке строки в словарь для
вспомогательная задача
мудрец: D3 = D.add_row([1, 2, 3, 4, 5, -15], 0)
мудрец: D3.row_coefficients(11)
(1, 2, 3, 4, 5, -15)
row_coefficients("x9")
(7, 11, 13, 9)
мудрец: D1.constant_terms()[-1]
42
мудрец: D1.basic_variables()[-1]
х9мудрец: А = ([-9, 7, 48, 31, 23], [5, 2, 9, 13, 98],
....: [14, 15, 97, 49, 1], [9, 5, 7, 3, 17],
....: [119, 7, 121, 5, 111])
мудрец: б = (33, 27, 1, 272, 61)
мудрец: с = (51/133, 1/100, 149/18, 47/37, 13/17)
мудрец: P = InteractiveLPProblemStandardForm(A, b, c)
мудрец: D = P.revised_dictionary("x1", "x2", "x3", "x4", "x5")
мудрец: D2 = D.add_row([5 ,7, 11, 13, 9], 99, basic_variable='c')
мудрец: D2.row_coefficients("c")
(5, 7, 11, 13, 9)
мудрец: D2.constant_terms()[-1]
99
мудрец: D2.basic_variables()[-1]
с
мудрец: D = P.revised_dictionary(0, 1, 2, 3, 4)
мудрец: D.add_row([1, 2, 3, 4, 5, 6], 0)
Traceback (последний последний вызов):
...
ValueError: сумма коэффициентов неосновных переменных резерва имеет
быть равным -1 при вставке строки в словарь для
вспомогательная задача
мудрец: D3 = D.add_row([1, 2, 3, 4, 5, -15], 0)
мудрец: D3.row_coefficients(11)
(1, 2, 3, 4, 5, -15)
- базовые_индексы()
Вернуть основные индексы
self.
Примечание
Базовые индексы — это индексы
basic_variables()в списке генераторыкоординаты_кольца()проблема()изself, они могут не совпадать с индексы переменных, которые являются частью их имен. (Они будут для индексированные имена по умолчанию.)ВЫВОД:
список.
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.basic_indices() [3, 4]
- основные_переменные()
Вернуть базовые переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.basic_variables() (х3, х4)
- c_B()
Возвращает вектор \(c_B\), целевые коэффициенты основных переменных.

ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary(1, 2) мудрец: D.c_B() (10, 5)
- c_N()
Возвращает вектор \(c_N\), целевые коэффициенты неосновных переменных.
ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.c_N() (10, 5)
- столбец_коэффициенты ( против )
Возвращает коэффициенты неосновной переменной.
ВВОД:
v– неосновная переменнаяself, может быть задан как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫХОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: D.column_coefficients(1)
(1, 3)
revised_dictionary()
мудрец: D.column_coefficients(1)
(1, 3)
- константа_термс ()
Возврат постоянных условий в отношениях
с самим собой.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.constant_terms() (1000, 1500)
- словарь()
Вернуть обычный словарь LP, соответствующий
self.ВЫВОД:
и
Словарь LP
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1], [-1, -1]) мудрец: b = (1000, 1500, -400) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.словарь() Словарь проблем LP (используйте ...)
- небазовые_индексы ()
Вернуть неосновные индексы
self.
Примечание
Небазовые индексы — это индексы
nonbasic_variables()в список генераторовкоордината_кольцо()изпроблема()изself, они могут не совпадать с индексами переменных, которые являются частью их имен. (Они будут для индексированные имена по умолчанию.)ВЫВОД:
список
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.nonbasic_indices() [1, 2]
- неосновные_переменные()
Вернуть неосновные переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.
 nonbasic_variables()
(х1, х2)
nonbasic_variables()
(х1, х2)
- объективные_коэффициенты()
Возвратные коэффициенты цели
self.ВЫВОД:
вектор
Это коэффициенты неосновных переменных, когда основные переменные устранено.
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.objective_coefficients() (10, 5)
- имя_цели()
Вернуть имя цели
self.ВЫВОД:
ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.objective_name() г
- target_value()
Вернуть значение цели в базовом решении
self.ВЫХОД:
номер
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: D.objective_value()
0
revised_dictionary()
мудрец: D.objective_value()
0
- проблема()
Вернуть исходную задачу.
ВЫВОД:
задача
LP в стандартной форме
ПРИМЕР:
мудрец: А = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.problem() — это P Истинный
- row_coefficients( против )
Вернуть коэффициенты базовой переменной
v.Это коэффициенты, с которыми вычитаются неосновные переменные в отношении
к.ВВОД:
v— базовая переменнаяself, может быть задана как строка, фактическая переменная или целое число, интерпретируемое как индекс переменной
ВЫХОД:
ПРИМЕРЫ:
мудрец: A = ([-1, 1], [8, 2]) мудрец: b = (2, 17) мудрец: с = (55/10, 21/10) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: D.row_coefficients("x3")
(-1, 1)
revised_dictionary()
мудрец: D.row_coefficients("x3")
(-1, 1)
Мы также можем использовать индексы переменных:
мудрец: D.row_coefficients(3) (-1, 1)
Или имена переменных без кавычек после их внедрения:
мудрец: P.inject_variables() Определение x0, x1, x2, x3, x4 мудрец: D.row_coefficients(x3) (-1, 1)
- обновить()
Обновите
себя, используя ранее установленные входные и выходные переменные.ПРИМЕРЫ:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.objective_value() 0 мудрец: D.enter("x1") мудрец: D.leave ("x4") мудрец: D.update() мудрец: D.objective_value() 5000
- х_В()
Вернуть базовые переменные
self.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.
 revised_dictionary()
мудрец: D.basic_variables()
(х3, х4)
revised_dictionary()
мудрец: D.basic_variables()
(х3, х4)
- х_N()
Возвращает неосновные переменные
сам.ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: D.nonbasic_variables() (х1, х2)
- у ()
Возвращает вектор \(y\), произведение
c_B()иB_inverse().ВЫВОД:
вектор
ПРИМЕР:
мудрец: A = ([1, 1], [3, 1]) мудрец: б = (1000, 1500) мудрец: с = (10, 5) мудрец: P = InteractiveLPProblemStandardForm(A, b, c) мудрец: D = P.revised_dictionary() мудрец: Д.у() (0, 0)
- sage.numerical.interactive_simplex_method.default_variable_name( переменная )
Вернуть имя переменной по умолчанию для текущего
style().
ВВОД:
ВЫВОД:
ПРИМЕРЫ:
шалфей: sage.numerical.interactive_simplex_method.default_variable_name("первоначальный резерв") 'Икс' шалфей: sage.numerical.interactive_simplex_method.style('Вандербей') 'Вандербей' sage: sage.numerical.interactive_simplex_method.default_variable_name("первоначальная слабина") 'ж' мудрец: sage.numerical.interactive_simplex_method.style('UAlberta') 'УАльберта'
- sage.numerical.interactive_simplex_method.random_dictionary( м , n , bound=5 , special_probability=0,2 )
Создать случайный словарь.
ВВОД:
m– количество ограничений/базовых переменныхn– количество решающих/неосновных переменныхпривязка— (по умолчанию: 5) привязка к словарным статьямspecial_probability– (по умолчанию: 0,2) вероятность построения потенциально невозможный или потенциально оптимальный словарь
ВЫХОД:
и
Словарь задач LP
ПРИМЕР:
шалфей: из sage.
 numerical.interactive_simplex_method \
....: импортировать random_dictionary
sage: random_dictionary(3, 4) # косвенный doctest
Словарь проблем LP (для получения подробной информации используйте «view(...)» или «%display typeset»)
numerical.interactive_simplex_method \
....: импортировать random_dictionary
sage: random_dictionary(3, 4) # косвенный doctest
Словарь проблем LP (для получения подробной информации используйте «view(...)» или «%display typeset»)
- sage.numerical.interactive_simplex_method.style( new_style=Нет )
Установить или получить текущий стиль задач и словарей.
ВВОД:
ВЫВОД:
Если ввод не распознается как допустимый стиль, возникает исключение
ValueError. Поднялся.В настоящее время поддерживаются следующие стили:
‘UAlberta’ (по умолчанию): соответствует стилю, используемому в курсе Math 373. по математическому программированию и оптимизации в Университете г. Альберта, Эдмонтон, Канада; по книге Чватала.
Имена переменных по умолчанию равны
.\(z\) для основной цели
\(z\) для двойного объектива
\(w\) для вспомогательного объектива
\(x_1, x_2, \dots, x_n\) для основных переменных решения
\(x_{n+1}, x_{n+2}, \dots, x_{n+m}\) для первичных резервных переменных
\(y_1, y_2, \dots, y_m\) для двойных переменных решения
\(y_{m+1}, y_{m+2}, \dots, y_{m+n}\) для двойных резервных переменных
«Вандербей»: соответствует стилю учебника Роберта Вандербая, Линейное программирование — основы и расширения.

Имена переменных по умолчанию равны
.\(дзета\) для основной цели
\(xi\) для двойного объектива
\(xi\) для вспомогательного объектива
\(x_1, x_2, \dots, x_n\) для основных переменных решения
\(w_1, w_2, \dots, w_m\) для первичных резервных переменных
\(y_1, y_2, \dots, y_m\) для двойных переменных решения
\(z_1, z_2, \dots, z_n\) для двойных резервных переменных
ПРИМЕР:
шалфей: sage.numerical.interactive_simplex_method.style() 'УАльберта' шалфей: sage.numerical.interactive_simplex_method.style('Вандербей') 'Вандербей' шалфей: sage.numerical.interactive_simplex_method.style('Не существует') Traceback (последний последний вызов): ... ValueError: Стиль должен быть одним из: UAlberta, Vanderbei мудрец: sage.numerical.interactive_simplex_method.style('UAlberta') 'УАльберта'
- sage.
 numerical.interactive_simplex_method.variable( Р , v )
numerical.interactive_simplex_method.variable( Р , v ) Интерпретировать
vкак переменнуюR.ВВОД:
R– кольцо многочленовv– переменнаяRили конвертируемая вR, строка с именем переменнойRили индексом переменнойR
ВЫХОД:
переменная
R
ПРИМЕР:
шалфей: из sage.numerical.interactive_simplex_method \ ....: переменная импорта мудрец: R = PolynomialRing(QQ, "x3, y5, x5, y") мудрец: R.inject_variables() Определение x3, y5, x5, y шалфей: переменная (R, "x3") х3 шалфей: переменная (R, x3) х3 шалфей: переменная (R, 3) х3 мудрец: переменная (R, 0) Traceback (последний последний вызов): ... ValueError: нет переменной с данным индексом шалфей: переменная (R, 5) Traceback (последний последний вызов): ...


 Каждое неравенство
Каждое неравенство Если вычисленное базисное решение будет допустимое, то следует перейти к допустимому базисному решению.
Если вычисленное базисное решение будет допустимое, то следует перейти к допустимому базисному решению.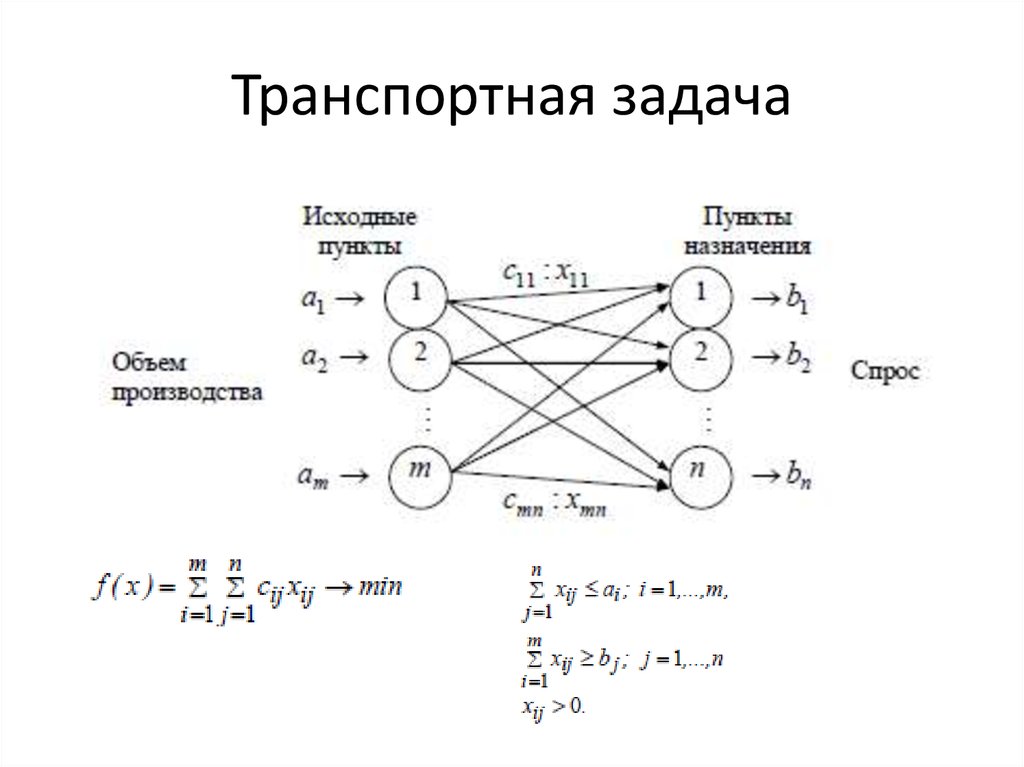
 Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.
 ). «О специализации на кафедре и о задачах комбинаторной оптимизации»
). «О специализации на кафедре и о задачах комбинаторной оптимизации» 00, online.
00, online.
 к.ф.-м.н. Коробов А.А., д.ф.-м.н. Ломов А.А. ) проходит по вторникам в 12:40, ауд. 220 ИМ
к.ф.-м.н. Коробов А.А., д.ф.-м.н. Ломов А.А. ) проходит по вторникам в 12:40, ауд. 220 ИМ
 nsc.ru) Ваш e-mail на домене @nsu.ru до 18:00 нск 9 сентября.
nsc.ru) Ваш e-mail на домене @nsu.ru до 18:00 нск 9 сентября.
 И.Ю. Могильных) — четверг, 18.10, 2241 НГУ. Первое занятие — 29.09
И.Ю. Могильных) — четверг, 18.10, 2241 НГУ. Первое занятие — 29.09 09. Желающие посещать, напишите на почту
09. Желающие посещать, напишите на почту  Б.
Б.
 (МиКН)
(МиКН)
 ММФ (AI&BDA)
ММФ (AI&BDA) ММФ (МиКН)
ММФ (МиКН)
 ММФ (МиКН)
ММФ (МиКН)
 ММФ (инж. шк.)
ММФ (инж. шк.) ММФ (ПМИ)
ММФ (ПМИ)
 инт.
инт.
 В.
В.
 А.
А.
 )
)
 А.
А.
 5 года
5 года
 В.,
В.,  В.,
В.,
 А.,
А.,  И.
И. А.
А.