Тригонометрия. Материалы для подготовки к ЕГЭ по Математике
Тригонометрия для многих старшеклассников представляется сложной темой. Но на самом деле это не так. Тригонометрия проста и логична. Главное – начать с самых основ. Вспомнить, что такое градусы и радианы. Что такое синус и что такое косинус для произвольного угла.
Тригонометрию можно понять! И мы поможем вам это сделать. Ведь понимание намного лучше зубрежки. Читайте статьи этого раздела:
New Задачи из сборников Ященко, 2021 год
Измерение углов: градусы и радианы
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрические формулы
Формулы приведения
Все формулы тригонометрии
Тригонометрические функции
Обратные тригонометрические функции
Простейшие тригонометрические уравнения, 1
Простейшие тригонометрические уравнения, 2
Тригонометрические уравнения. Методы решения
Повторим самое главное в тригонометрии.
— Выучи,
Из курса геометрии ты помнишь, что синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе. Однако это частные случаи для углов, больших нуля и меньших 90 градусов. А мы говорим о произвольном угле. Определения синуса и косинуса произвольного угла – в этом разделе.
— Тригонометрический круг, или тригонометрическая окружность, – твоя универсальная шпаргалка. Значения синусов и косинусов основных углов, знаки синуса и косинуса в четвертях, четность и нечетность синуса и косинуса и многое другое – на тригонометрическом круге.
— Формулы приведения не надо зубрить наизусть! Надо понять, как они получаются.
— Сколько формул тригонометрии нужно знать, чтобы уверенно решать задачи? Три – это мало.
— Как решать тригонометрические уравнения? Не спеши учить формулы. Сначала разберись, почему их решения именно такие. Выучи определения и свойства обратных тригонометрических функций – арксинуса, арккосинуса, арктангенса и арккотангенса.
И тренируйся на реальных задачах ЕГЭ!
Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Тригонометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 25.12.2022
ЕГЭ МАТЕМАТИКА профиль 2022 | LANCMAN SCHOOL
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»).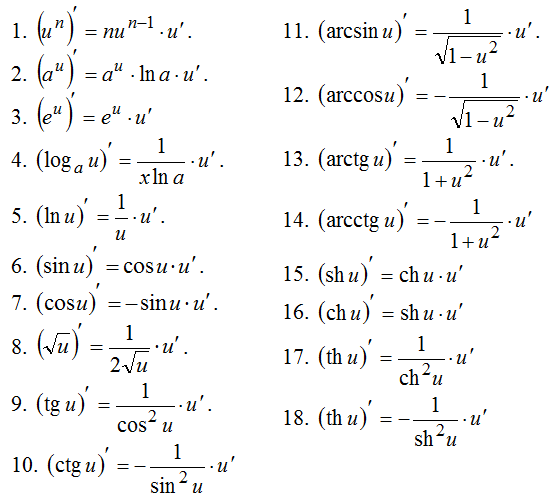 Сегодня мы расскажем о том, как готовиться к ЕГЭ по профильной математике 2022 года.
Сегодня мы расскажем о том, как готовиться к ЕГЭ по профильной математике 2022 года.
Нелюбовь к тригонометрии в 10-11 классах может побить разве что страх перед стереометрией. Обычно опасение вызывают бесконечные столбцы формул и таблицы, которые заставляют учить для работы с тригонометрическими выражениями.
Но в ЕГЭ с тригонометрией всё достаточно просто. В первую очередь потому, что наизусть учить формул нужно даже меньше, чем для логарифмов. Вот популярный сборник формул для алгебры 10-11 класса. В нем мы выделили красным то, что нужно реально учить для экзамена.
Видно, что номинально объем по тригонометрии в 2 раза превосходит всю остальную алгебру (в этом сборнике нет разве что производной). А вот почему на деле так мало нужно учить наизусть – мы и расскажем ниже.
1. Справочные материалы
Во-первых, несколько формул дадут прямо на самом экзамене (речь про профильный ЕГЭ по математике), вместе с КИМами. Вот они:
2.
 Где и какая тригонометрия встречается на ЕГЭ
Где и какая тригонометрия встречается на ЕГЭФормулы из третьего, самого правого столбца в большом сборнике формул либо уже есть среди этой пятерки выше, либо попросту не встречаются при решении ЕГЭшных задач. В крайнем случае что-то можно за несколько секунд вывести из этих пяти формул. Например,
Давайте тут же разберемся, где вообще можно встретить тригонометрию в профильной математике – чтоб вы понимали, стоит ли вся игра свеч.
А вообще-то стоит. Тригонометрия может попасться в целых 4 из 18 заданий ЕГЭ.
1) Задание 4. Преобразование выражений. Пример:
2) Задание 7. Практическая работа с формулами. Пример:
3) Задание 12. Уравнения, письменная часть. Пример:
4) Задание 17. Выражение с параметром, письменная часть. Пример:
В Задании 17, пожалуй, совсем редко встречается тригонометрия, но в остальных точно нужно быть к ней готовым. При этом самое большое разнообразие задач бывает в Задании 4.
Получается, нужно сфокусироваться на среднем столбце из большого сборника формул. И тут начинается самое интересное.
3. Большинство формул выводится
В самом деле, посмотрите на обведенные формулы в среднем столбце. Их очень мало, верно? Давайте разбираться по порядку с этим сборником, пойдем по его разделам.
1) Основные тождества
Из этих тождеств в ЕГЭ используется определение тангенса и котангенса (слева), это и правда надо выучить. А все остальное – либо следует или выводится из этих определений (попробуйте, например, перемножить дроби у тангенса и котангенса), либо уже дано в справочных материалах.
2) Тригонометрические уравнения
Вместо заучивания кучи этих формул лучше заняться изучением тригонометрической окружности. Все равно для более уверенного решения №12 – особенно пункта б) – потребуется в ней хорошо ориентироваться. Возможно, на изучение окружности потребуется примерно столько же времени, что и на заучивание соответственных формул.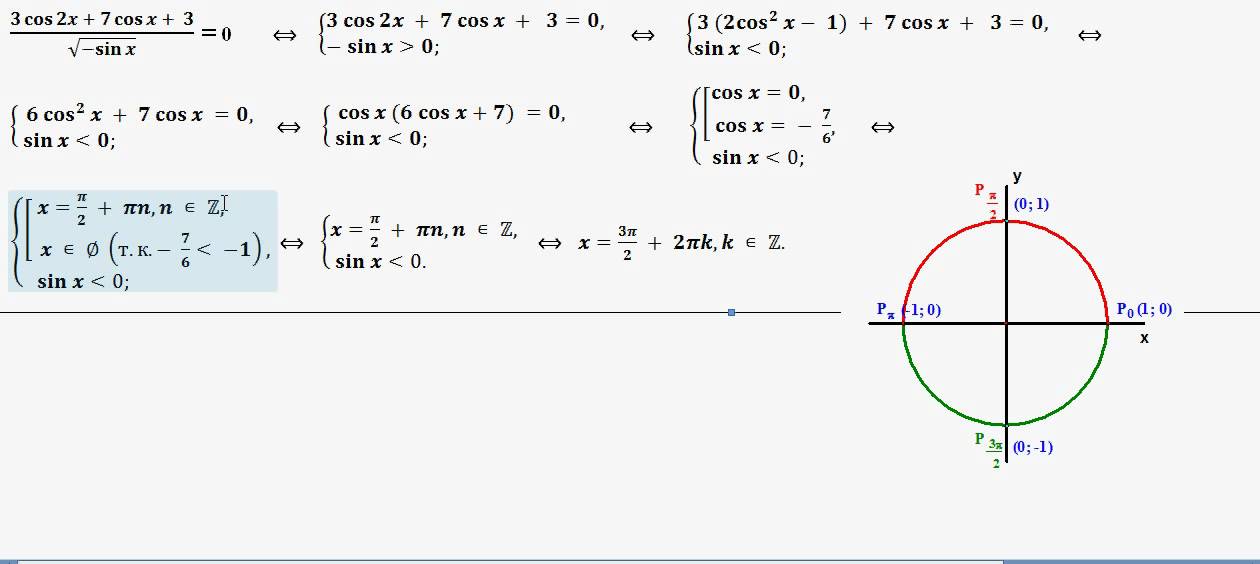 Но, во-первых, в отличие от механически выученного материала – практический навык не пропадет из памяти из-за волнения и стресса на экзамене. Во-вторых, именно работа с окружностью поможет сориентироваться в более сложных и непривычных ситуациях.
Но, во-первых, в отличие от механически выученного материала – практический навык не пропадет из памяти из-за волнения и стресса на экзамене. Во-вторых, именно работа с окружностью поможет сориентироваться в более сложных и непривычных ситуациях.
В таблице предлагается выучить в сумме значений больше в 5 раз, чем предлагаем мы (обведено красным). И это еще не самая обширная таблица.
4) Формулы приведения
Как раз в виде формул заучивать эту тему – крайне неблагодарное дело. Приглядитесь: с учетом различных знаков из таблицы ниже придется извлечь и выучить 36 формул, едва отличающихся друг от друга!
Первый столбец вообще объясняется четностью-нечетностью функций и легко показывается (и вспоминается) через окружность. Другие формулы лучше не заучивать, а запомнить простой алгоритм в 2 шага. Сейчас мы им поделимся.
Шаг 2. Если исходная функция при исходном угле положительна, то знак перед выражением после «отбрасывания» не меняется. Если отрицательная – меняется на противоположный (или, можно сказать, происходит домножение на –1). В какой четверти какая функция положительна/отрицательна лучше не заучивать (см. рисунок ниже), а ориентироваться на оси.
Если исходная функция при исходном угле положительна, то знак перед выражением после «отбрасывания» не меняется. Если отрицательная – меняется на противоположный (или, можно сказать, происходит домножение на –1). В какой четверти какая функция положительна/отрицательна лучше не заучивать (см. рисунок ниже), а ориентироваться на оси.
Да, почему ось Y – ось sin, а ось X – ось cos весьма легко понять, не заучивая этот факт. Вспомните определение, например, косинуса из геометрии: «прилежащий катет делить на гипотенузу». А теперь подставьте вместо прилежащего катета координату по оси X для треугольника, скажем, в 30° и вспомните, что в тригонометрической окружности r=1.
Вот и разобрались со всеми формулами. Ведь третий столбец в большом списке учить вообще не надо, как мы писали выше.
Конечно, ответ в этой статье получился сложнее, чем просто «учите вот этот и этот параграф наизусть», потому что изучать всегда сложнее, чем заучивать. Да еще и самостоятельно. Поэтому желаем вам найти преподавателя, который прислушается к вашим запросам и учтет индивидуальные особенности вашего стиля обучения. И – если у вас возникнут проблемы с запоминанием – сможет показать, как разобраться с любой сложной темой, не заучивая механически большие объемы материала наизусть.
Поэтому желаем вам найти преподавателя, который прислушается к вашим запросам и учтет индивидуальные особенности вашего стиля обучения. И – если у вас возникнут проблемы с запоминанием – сможет показать, как разобраться с любой сложной темой, не заучивая механически большие объемы материала наизусть.
Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны.
Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Обложка поста: pixabay.com
Тригонометрические рабочие листы, вопросы и вопросы
Уровень 4-5GCSEAQAEdexcelOCRWJEC
Уровень 4-5GCSE
SOHCATOAСначала нам нужно обозначить каждую сторону прямоугольного треугольника:
Гипотенуза всегда самая длинная сторона ; это тот напротив прямого угла .
напротив 9Сторона 0018 – это сторона, расположенная напротив от угла .
Сторона , примыкающая к , — это сторона, которая прилегает к (рядом с) углом .
\textcolor{purple}{\sin(x)}=\dfrac{\textcolor{red}{\text{напротив}}}{\textcolor{синий}{\text{гипотенуза}}}
\textcolor{ фиолетовый}{\cos(x)}=\dfrac{\textcolor{limegreen}{\text{adjacent}}}{\textcolor{blue}{\text{гипотенуза}}}
\textcolor{purple}{\tan (x)}=\dfrac{\textcolor{red}{\text{напротив}}}{\textcolor{limegreen}{\text{adjacent}}}
Если мы допустим, что O будет противоположным, A будет соседним, а H будет гипотенузой, то они будут сокращены до:
В результате аббревиатура: SOHCAHTOA полезна для запоминания того, какие стороны соответствуют какой функции.
Уровень 4-5GCSE
Углы возвышения и падения Если вы смотрите на что-то, что не находится на уровне глаз , угол, который ваши глаза образуют с объектом, равен углу возвышения / углубления .
угол возвышения — это когда вы смотрите вверх на что-то.
Угол наклона — это когда вы смотрите вниз на что-то.
Эти углы можно использовать для расчета высоты и расстояния до объектов .
Пример: Билл находится в 30\text{ м} от церкви. Угол возвышения , когда он смотрит на вершину шпиля церкви, составляет 45°. Если Биллу уровень глаз 1,5\text{ м} над землей, какой высоты шпиль церкви?
Сторона, которую мы хотим проработать, находится напротив угла, который у нас есть. У нас также есть длина соседней стороны. Это означает, что мы хотим использовать TOA, или \tan=\dfrac{\text{напротив}}{\text{смежный}}
\tan(45)=\dfrac{h}{30}, где h — высота мы хотим вычислить.
ч=30\загар(45)
Теперь мы можем использовать \tan(45)=1, чтобы найти, что h=30\text{ m}
Однако это не высота шпиля , так как это было рассчитано по уровню глаз Билла . Таким образом, мы должны добавить к этому уровень глаз Билла , чтобы получить реальную высоту шпиля .
Таким образом, мы должны добавить к этому уровень глаз Билла , чтобы получить реальную высоту шпиля .
\text{Высота}=30+1,5=31,5\text{м}
Уровень 4-5GCSE
Продукт
Переходные математические карточки
8,99 фунтов стерлингов
Переходные математические карточки — идеальный способ охватить темы более высокого уровня GCSE, а также познакомиться с новыми темами по математике уровня A, которые помогут вам подготовиться к 12-му классу. Ваше идеальное руководство для начала работы с математикой уровня А! Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.
Посмотреть продукт
Пример 1: Недостающая длина Найдите длину стороны, отмеченной буквой y, до 1 dp.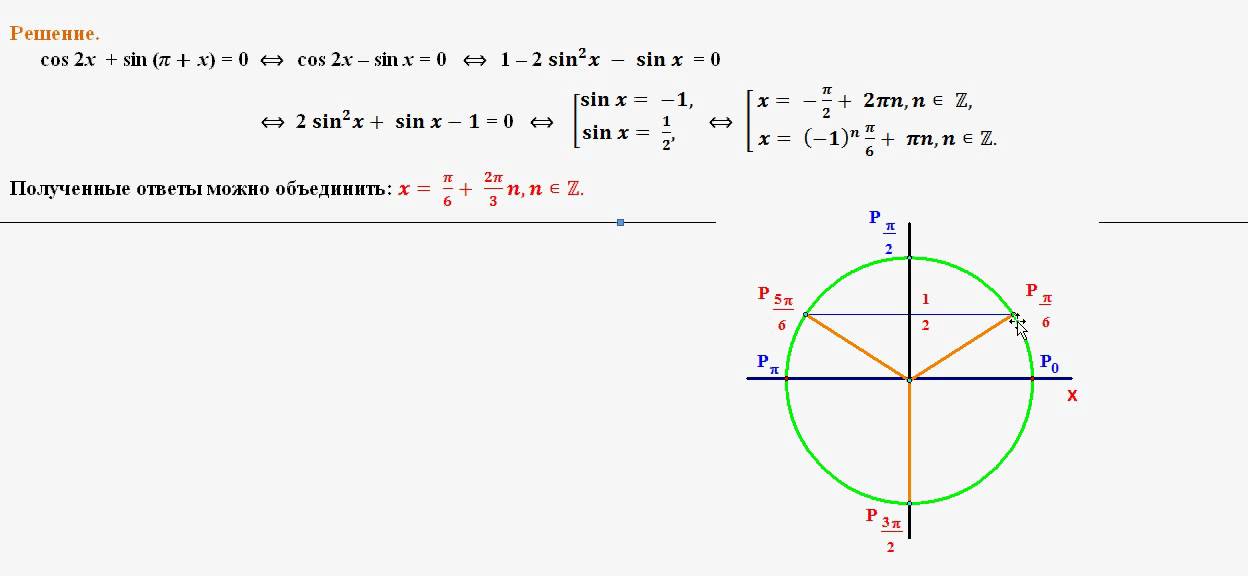
[2 балла]
Прежде всего нам нужно найти, какое уравнение нам нужно использовать.
У нас есть гипотенуза \textcolor{blue}{H} = \textcolor{blue}{12} см
У нас также есть смежная сторона \textcolor{limegreen}{A} = \textcolor{limegreen} {y}
Итак, если \textcolor{limegreen}{A} и \textcolor{blue}{H} — это две стороны, с которыми мы работаем, то это
‘\textcolor{purple}{C}\textcolor{limegreen}{A}\textcolor{blue}{H}’ часть SOHCATOA , которую нам нужно использовать.
\textcolor{purple}{\cos(x)}=\dfrac{\textcolor{limegreen}{A}}{\textcolor{blue}{H}}
Подставляя две стороны и один угол, получаем :
\textcolor{purple}{\cos(38°)} =\dfrac{\textcolor{limegreen}{y}}{\textcolor{blue}{12}}
Далее нам нужно решить уравнение. Умножение обеих сторон на 12 дает нам:
\textcolor{limegreen}{y}=\textcolor{blue}{12} \textcolor{purple}{\cos(38°)}
Подставив это в наш калькулятор, мы получим:
\textcolor{limegreen}{y}=9. 456129043…
456129043…
\textcolor{limegreen}{y}=9,5 см (1 dp)
Уровень 4-5GCSE
Пример 2: Недостающий уголНайдите размер угла z до 2 фут.
[2 балла]
Прежде всего нам нужно найти, какое уравнение нам нужно использовать.
У нас есть противоположная сторона = \textcolor{red}{5} мм
У нас также есть смежный сторона = \textcolor{limegreen}{8} мм
Так как мы работаем с \textcolor{red}{O} и \textcolor{limegreen}{A}, то ‘\textcolor{purple}{T}\ textcolor{red}{O}\textcolor{limegreen}{A}’ является частью SOHCAHTOA , которую мы будем использовать:
\textcolor{purple}{\tan(z)}=\dfrac{\textcolor{red} {O}}{\textcolor{limegreen}{A}}
Замена двух известных сторон дает нам:
\textcolor{purple}{\tan(z)}=\dfrac{\textcolor{red}{5 }}{\textcolor{лаймзеленый}{8}} 9{-1}.
Уровень 4-5GCSE
Пример 3: Углы подъема и падения Джесс смотрит вниз на фрисби, приземлившуюся в 4\text{ м} от ее ног. Если уровень глаз Джесс находится на высоте 1,7\text{м} над землей, найдите угол наклона .
Если уровень глаз Джесс находится на высоте 1,7\text{м} над землей, найдите угол наклона .
Дайте ответ с точностью до одного десятичного знака.
[2 балла]
У нас есть противоположных и смежных длин сторон угла, который мы хотим найти, поэтому нам нужно использовать TOA или \tan=\dfrac{\text{напротив}}{ \текст{смежный}} 9{-1}\left(\dfrac{4}{1.7}\right)
x=67.0\степень
Уровень 4-5GCSE
Пример вопросов
В данном случае нас интересуют две стороны: гипотенуза и сторона , примыкающая к заданному углу. Поэтому нам нужна часть «CAH» «SOH CAH TOA», где A = 35, H = p, а угол равен 43 градусам:
\cos(43°)=\dfrac{35}{p }
Далее нам нужно найти p. Умножая обе стороны на p, получаем:
p\times\cos(43°)=35
Тогда, поскольку \cos(43°) — это просто число , мы можем разделить обе части на \cos(43°):
p = \ dfrac {35} {\ cos (43 °)}
Наконец, вкладывая это в калькулятор. м (3 сф)
м (3 сф)
Две стороны, с которыми мы работаем, это гипотенуза и сторона , противоположная стороне , поэтому нам нужна часть SOH от SOH CAH TOA, где O=13, H=15, а угол равен Q°: 92=4+4=8
Квадратный корень с обеих сторон, мы получаем:
c=\sqrt{8}=2\sqrt{2}
Теперь у нас есть гипотенуза, мы можем использовать ‘SOH’:
\sin(w)=\dfrac{2}{2\sqrt{2}}
Обратите внимание, что сверху и снизу есть 2, которые могут отменить:
\sin(w)=\dfrac{2}{2\sqrt{2}}=\dfrac{1}{\sqrt{2}}
В данном случае две стороны, с которыми мы работаем, это гипотенуза , а сторону напротив на заданный угол. Следовательно, нам нужна часть SOH в SOH CAH TOA, где O=CB, H=12 и угол равен 30°:
\sin(30°)=\dfrac{CB}{12 }
Затем мы можем решить это, умножив обе стороны на 12, чтобы получить:
12\sin(30°)=CB
Наконец, подставив это в калькулятор, мы получим:
2
33
3 СВ=6,00 см (3 ст. ф.)
ф.) Две стороны, с которыми мы работаем, это 9{-1}\left(\dfrac{4}{7}\right)=29,7448813…
x=29,7° (1 дп).
У нас есть угол 87\градус, смежный с ним угол 4\text{ m}, и мы хотим найти противоположный угол, поэтому нам нужно использовать TOA.
\tan(87\степень)=\dfrac{h}{4} где h — высота здания.
ч = \ загар (87) \ раз 4
Выполнение этого на калькуляторе дает:
ч = 76,3 \ текст {м}
Похожие темы
MME
Пифагор
Уровень 4-5GCSEKS3 Пересмотреть
Рабочий лист и примеры вопросов
(НОВИНКА) Вопросы в стиле экзамена по тригонометрии — MME
Уровень 4–5 GCSENewOfficial MME Экзаменационные вопросы Отметить схему
Учебные вопросы
Тригонометрия 1. Вопросы для тренировки
Уровень 4-5 GCSE Экзаменационные вопросы
Вам также может понравиться.
 ..
.. Что дальше?
Рабочие листы по тригонометрии, вопросы и редакция был добавлен в ваши сохраненные темы. Вы можете просмотреть все свои
сохраненные темы, посетив
Мои сохраненные темы.
Тригонометрические рабочие листы, вопросы и редакция были удалены из ваших сохраненных тем. Вы можете просмотреть все
ваши сохраненные темы, посетив
Мои сохраненные темы.
Тригонометрия — Математика GCSE — шаги, примеры и рабочий лист
Здесь мы узнаем о тригонометрии , включая то, как использовать SOHCATOA, обратные тригонометрические функции, точные тригонометрические значения и гипотенузу. Мы также узнаем о правиле синуса, правиле косинуса, о том, как найти площадь треугольника с помощью ½abSinC, трехмерной тригонометрии и о том, как использовать графики синуса, косинуса и тангенса.
Существуют также рабочие листы по тригонометрии, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое тригонометрия?
Тригонометрия — отношение между углами и длинами сторон в треугольниках; оно происходит от греческих слов «тригонон», означающих треугольник, и «метрон», означающих меру.
Тригонометрия изначально использовалась вавилонянами, более чем за 1500 лет до греческой формы, которую мы используем сегодня. Он широко используется в науке, технике и дизайне продукции.
Высшая учебная программа GCSE расширяет использование тригонометрических функций для непрямоугольных треугольников, развиваясь на основе фундаментальных знаний о трех тригонометрических отношениях (выраженных как мнемоника SOHCAHTOA) и точных тригонометрических значениях в прямоугольных треугольниках.
См. также: 15 вопросов по тригонометрии
Что такое тригонометрия
Рабочий лист по тригонометрии
Получите бесплатный рабочий лист по тригонометрии, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс Рабочий лист по тригонометрии
Получите бесплатный рабочий лист по тригонометрии, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
СОХКАТОА
Что такое СОХКАТОА?
SOHCAHTOA — это аббревиатура, используемая для описания трех тригонометрических соотношений для функций синуса , косинуса и тангенса .
Чтобы определить, какую тригонометрическую функцию нужно использовать для ответа на вопрос, это зависит от расположения угла и сторон треугольника, которые будут использоваться.
Тригонометрические функции применимы к прямоугольным треугольникам.
- Если вы знаете гипотенузу и противоположную сторону угла, вы должны использовать функцию синуса .

- Если вы знаете гипотенузу и смежную сторону (рядом с) угол, вы должны использовать функцию косинуса .
- Если вы знаете противоположных и смежных сторон угла, вы используете касательную 9Функция 0018.
Мы можем использовать SOHCATOA для вычисления длин и углов в 2D и 3D формах путем распознавания прямоугольных треугольников.
Мы можем найти длину AC параллелограмма или длину AH прямоугольного параллелограмма ниже.
Пошаговое руководство: SOHCATOA
Гипотенуза
Что такое гипотенуза?
Гипотенуза — самая длинная сторона прямоугольного треугольника. Это сторона, противоположная прямому углу.
Гипотенуза не встречается в других типах треугольников, если мы не знаем больше информации (например, равнобедренный треугольник можно составить из 2 одинаковых прямоугольных треугольников, расположенных задними сторонами).
Обозначение других сторон треугольника Зная, какой угол мы используем, мы можем обозначить противоположные стороны (O), смежные (A) и гипотенузу (H).
Мы знаем, что гипотенуза лежит напротив прямого угла.
Сторона , противоположная , находится напротив угла, который мы используем.
Сторона , смежная со стороной , находится рядом с углом, который мы используем.
Треугольник ниже обозначен на основе использования угла θ .
Пошаговое руководство: Гипотенуза (скоро)
Пример 1: найти сторону по углу и гипотенузе
ABC — прямоугольный треугольник. Размер угла ACB = 60º, а длина BC = 16см.
Вычислите значение x.
Обозначив стороны OAH по отношению к углу 60º, мы можем использовать гипотенузу, и нам нужно найти прилежащую сторону. Поэтому нам нужно использовать функцию косинуса.
\[ \begin{выровнено}
потому что (\ тета) & = \ frac {A} {H} \\\\
cos(60)&=\frac{x}{16} \\\\
16\times cos(60&)=x\\\\
х&=8см. \end{align} \]
\end{align} \]
Обратные тригонометрические функции
Что такое обратные тригонометрические функции?
Обратные тригонометрические функции позволяют вычислить величину угла θ для прямоугольного треугольника.
Обратные тригонометрические функции выглядят так:
\[ \begin{align}
&\квадратный \;\; \text{синус} \quad \quad \quad \quad \quad \quad \quad \text{cosine} \quad \quad \quad \quad \quad \;\; \quad \text{тангенс} \\\\
\text{тригонометрический} \quad \quad \quad &\ sin(\theta) = \frac{O}{H} \quad \quad \quad \quad \;\; \cos(\theta)=\frac{A}{H}
\quad \quad \quad \quad \;\; \tan(\theta)=\frac{O}{A} \\
\text{функция} \quad \quad \quad \quad &\\\\\\
\text{other} \quad \quad \quad \quad \quad &H=\frac{O}{\sin(\theta)} \quad \quad \quad \quad \;\; H=\frac{A}{\cos(\theta)} \quad \quad \quad \quad \;\; A=\frac{O}{\tan(\theta)} \\
\text{forms} \quad \quad \quad \quad \quad &\\
\quad \quad \quad \quad &O=H\times\sin(\theta) \quad \quad \quad A=H\times\cos(\theta) \quad \quad \quad O=A\times\tan( \тета) \\\\\\
\text{обратный} \;\; \quad \quad \quad \quad & \\
\text{тригонометрический} \quad \quad \quad &\theta=\sin^{-1}(\frac{O}{H}) \quad \quad \quad \;\; \theta=\cos^{-1}(\frac{A}{H}) \quad \quad \quad \;\;\; \ тета = \ загар ^ {- 1} (\ гидроразрыва {O} {A}) \\
\text{функция} \quad \quad \quad \quad &
\конец{выровнено}\]
Пошаговое руководство: Тригонометрические функции
Пример 2: найти угол с помощью обратных тригонометрических функций
Вычислите величину угла θ с точностью до 2 знаков после запятой.
Двумя сторонами, которые можно использовать для вычисления значения θ, являются противоположность и гипотенуза, поэтому мы применяем функцию синуса к θ, чтобы получить
\[ sin(\theta)=\frac{8}{10} . \]
Чтобы вычислить θ, мы переформулируем уравнение, используя функцию обратного синуса. 9{\ круг} \\\\
\text{sin}(x) \quad\quad \quad \quad &0 \; \ quad \ quad \ quad \ quad \ frac {1} {2} \ quad \ quad \ quad \ quad \ frac {1} {\ sqrt {2}} \ quad \ quad \ quad \ quad \ frac {\ sqrt { 3}}{2} \quad \quad \quad \quad 1 \\\\
\text{cos}(x) \quad\quad \quad \quad &1 \; \четырехъядерный \четырехъядерный \четырехъядерный \;\; \ гидроразрыва {\ sqrt {3}} {2} \; \; \quad \quad \quad \frac{1}{\sqrt{2}}\;\; \quad \quad \quad \quad \frac{1}{2} \quad \quad \quad \quad \; 0 \\\\
\text{tan}(x) \quad\quad \quad \quad &0 \; \четырехъядерный \четырехъядерный \четырехъядерный \;\; \frac{1}{\sqrt{3}} \; \quad \quad \quad \quad 1 \;\;\; \quad \quad \quad \quad \sqrt{3} \quad \quad \quad \text{Undefined}
\конец{выровнено}\]
Пример 3: использование точных тригонометрических значений
ABC — равносторонний треугольник. {\circ}\\
\end{выровнено} \]
{\circ}\\
\end{выровнено} \]
Пифагор или тригонометрия?
Нам нужно уметь интерпретировать проблемы и понимать, нужно ли нам использовать теорему Пифагора в 2D, 3D или в одном из трех тригонометрических соотношений.
В этой блок-схеме представлена информация, которую необходимо знать о фигуре, чтобы решить проблему.
Важно понимать, что в большинстве этих задач вам может понадобиться использовать теорему Пифагора, тригонометрию или и то, и другое в рамках одного и того же вопроса, поэтому вы должны быть уверены в этих темах по отдельности, чтобы получить полный доступ к этой теме.
Below is a summary of methods that can be used for right angled triangles:
Name
Pythagoras’ Theorem in 2D
Sine function
Cosine function
Тангенс функция0532
Обратная тангенсная функция
Теорема Pythagoras ‘3D
Используется для поиска…
Гипотенуза (C)
А.
Недостающая сторона:
гипотенуза (H)
или напротив (O)
Недостающая сторона:
9053 2 {2}}
Пример 4: найти гипотенузу с помощью тригонометрии
Вычислить длину гипотенузы прямоугольного треугольника x с точностью до 1 знака после запятой.
Две важные стороны в этом вопросе — это сторона, противоположная углу (O), и гипотенуза (H), поэтому нам нужно использовать функцию синуса для вычисления значения x.
\[ \begin{выровнено}
H&=\frac{O}{\sin(\theta)}\\
\\H&=\frac{56}{\sin(63)}\\
\\H&=62.9м\quad(1dp)\\
\end{выровнено} \]
Решение непрямоугольных треугольников
Правило синусов (закон синусов)
Что такое правило синусов?
Правило синусов (или закон синусов) представляет собой зависимость между величиной угла в треугольнике и противолежащей стороной. В треугольнике есть три отношения, так как есть 3 угла с противоположными сторонами, но вам нужно будет использовать только два.
Теорему Пифагора нельзя использовать для нахождения третьей стороны непрямоугольного треугольника. Вместо этого мы можем использовать правило синусов или правило косинусов, в зависимости от информации, которую мы знаем о треугольнике.
Чтобы найти недостающий угол:
\frac{\sin (A)}{a}=\frac{\sin (B)}{b}
Чтобы найти недостающую сторону:
\frac{a} {\sin (A)}=\frac{b}{\sin (B)}
Пошаговое руководство: Правило синусов
Пример 5. Нахождение недостающей стороны треугольника с помощью правила синусов
Рассчитайте длину AB. Запишите свой ответ с точностью до 2 знаков после запятой.
Обозначьте каждый угол A, B и C и каждую сторону a, b и c:
Здесь мы знаем сторону a и хотим найти длину c, поэтому мы можем сказать:
\начало{массив}{л}
\frac{a}{\sin (A)}=\frac{c}{\sin (C)}\\
\\\frac{6}{\sin (55)}=\frac{c}{\sin (73)}\\
\\c=\frac{6}{\sin (55)}\times\sin(73)\\
\\c=\frac{6\sin(73)}{\sin(55)}\\
\\c=7. 00\quad(2dp)
\end{array}
00\quad(2dp)
\end{array}
Здесь длина AB = 7,00 см (2dp).
Правило косинусов (закон косинусов)
Что такое правило косинусов?
Правило косинусов (или закон косинусов) — это формула, которую можно использовать для вычисления недостающих сторон треугольника или для нахождения недостающего угла. Для этого нам нужно знать две схемы формулы и то, что представляет каждая переменная. 92}{2bc})
Пошаговое руководство: Правило косинуса
Пример 6: Найдите недостающую сторону, используя правило косинуса
Найдите длину x треугольника ABC, исправьте до 2 знаков после запятой.
Вершины уже помечены буквой A, расположенной на используемом нами угле, поэтому нам нужно только пометить противоположные стороны a, b и c.
Здесь нам нужно найти недостающую сторону а, поэтому нам нужно сформулировать правило косинусов с 2 в качестве подлежащего: 9{2}=14,38516072…\\
\\x=\sqrt{14. 38516072…}\\
\\x=3,79 см\quad(2dp)\\
\end{массив}
38516072…}\\
\\x=3,79 см\quad(2dp)\\
\end{массив}
1/2abSin(C) (площадь треугольника)
Что такое 1/2abSin(C)?
\frac{1}{2}abSin(C) – это формула для вычисления площади любого треугольника.
\[ Площадь =\frac{1}{2}ab\sin(C). \]
Пошаговое руководство: Площадь треугольника треугольника
Пример 7: площадь с использованием A=1/2abSin(C)
Вычислите площадь треугольника ABC. Запишите свой ответ с точностью до 2 знаков после запятой. 9{2}\квадрат(2дп)\\
\end{array}
Трехмерная тригонометрия
Что такое трехмерная тригонометрия?
Трехмерная тригонометрия представляет собой применение тригонометрических навыков, разработанных для двумерных треугольников.
Чтобы найти отсутствующие стороны или углы в трехмерных фигурах, нам нужно четко знать правила и формулы для нахождения этих разных углов и длин сторон.
Приведенная ниже блок-схема может помочь определить, какую функцию вам нужно использовать:
Как только вы сможете обосновать, какое правило или формулы вам нужно использовать, вам, возможно, придется повторить этот процесс еще раз для другого треугольника в вопросе.
Главный совет: ищите общие углы или общие стороны.
Пошаговое руководство: Трехмерная тригонометрия
Пример 8: найти недостающий угол в треугольной призме
Вычислить величину угла в треугольной призме ABCDEF.
Мы видим, что треугольник ABF и треугольник ACF имеют общую сторону AF. Мы можем использовать треугольник ACF для вычисления длины AF, что затем поможет нам вычислить величину угла θ.
Этот треугольник не содержит информации об углах, поэтому нам нужно использовать теорему Пифагора. 9{\ круг}
\end{align}
Тригонометрические графики Тригонометрические функции синуса, косинуса и тангенса могут быть представлены в виде графиков.
Например, при изменении угла изменяется и значение синуса. Это можно изобразить на графике.
Угол 0 15 30 45 60 75 90 Синус (до 3 знаков после запятой) 0 0,259 0,5 0,707 0,866 0,966 1
Рассмотрим это подробнее ниже.
Графики синуса, косинуса и тангенса
Что такое графики синуса, косинуса и тангенса?
Тригонометрические графики являются визуальным представлением функций синуса, косинуса и тангенса. Горизонтальная ось представляет собой угол, обычно обозначаемый как θ, а вертикальная ось представляет собой триггерную функцию.
См. ниже все три тригонометрических графика для всех углов θ между -360° и 360° (-360 < θ < 360).
График y = sin(θ)
Пошаговое руководство: График Sin
График y = cos(θ)
Пошаговое руководство Cos graph
График y = tan(θ)
Пошаговое руководство: Tan graph
Пример 9: указать значение tan(θ) при известном θ
Используйте график y = tan(θ) для оценки значения y при θ = 120º.
Здесь мы рисуем вертикальную линию под углом 120º, пока она не достигнет касательной кривой, а затем горизонтальную линию по направлению к оси Y.
Поскольку масштаб каждой отметки на оси Y равен 0,25, значение tan(120) приблизительно равно -1,7 (1dp).
Распространенные заблуждения
- Неправильная маркировка треугольника
Напр.
Сторона этого треугольника неправильно обозначена рядом с углом.
Это повлияет на формулу для правила синусов, правила косинуса и площади треугольника.
- Использование неправильной тригонометрической функции
Неправильная маркировка треугольника может привести к использованию неправильной стандартной или обратной тригонометрической функции.
- Слишком раннее округление десятичной дроби
Это может привести к потере меток точности. Всегда используйте как можно больше знаков после запятой в расчетах, а затем округляйте решение.
- Теорема Пифагора или тригонометрия?
Используйте блок-схему, чтобы понять, когда следует использовать теорему Пифагора, а когда — тригонометрию. Помните, что вам может понадобиться использовать оба.
Помните, что вам может понадобиться использовать оба.
- Использование правила синусов вместо правила косинусов
Чтобы использовать правило синусов, нам нужно иметь пары противоположных углов и сторон.
- Без использования внутреннего угла
Для правила косинуса и площади треугольника, использующего A=1/2absin(C), угол включается между двумя сторонами. Использование любого другого угла приведет к неправильному решению.
- Используя A = b × h ÷ 2
Если вертикальная высота треугольника недоступна, мы не можем вычислить площадь, разделив основание пополам на высоту.
- Вместо этого используется обратная триггерная функция, вызывающая математическую ошибку
Если вместо стандартной функции триггера используется обратная триггерная функция, калькулятор может выдать математическую ошибку, поскольку решения не существует.
- Графики синуса и косинуса перепутаны
Графики синуса и косинуса очень похожи, и их легко спутать друг с другом. Совет, который следует помнить, заключается в том, что вы «синусируете вверх» от 0 для синусоидального графика, поэтому линия увеличивается, тогда как вы «косинусируете вниз» от 1, поэтому линия уменьшается для косинусного графика.
- Неправильно построены асимптоты для графика функции тангенса
Функция тангенса имеет асимптоту на 90º, поскольку это значение не определено. Поскольку кривая повторяется каждые 180º, следующая асимптота находится на 270º и т. д.
- Графики нарисованы с помощью линейки
Каждый тригонометрический график представляет собой кривую, поэтому единственный раз, когда вам нужно использовать линейку, это нарисовать набор осей. Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.
Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.
Вопросы по практической тригонометрии
17,87см
13,96см
0,06см
0,21см
Это прямоугольный треугольник с углами, поэтому используйте SOHCAHTOA.
Сначала нам нужно обозначить стороны O, A и H.
Мы знаем A и хотим найти H, поэтому нам нужно использовать cos.
\begin{выровнено}
H&=\frac{A}{\cos(\theta)}\\\\
H&=\frac{11}{\cos(52)}\\\\
В&=17,87\mathrm{см}
\end{выровнено}
9{2}
\end{выровнено}
9,11 см
7,81 см
10,39 см
10,91 см
Треугольники AGH и AEH имеют общую прямую AH.
Используя треугольник AGH, мы можем вычислить длину прямой AH.
\begin{выровнено}
A &= \frac{O}{\tan(\theta)}\\\\
A &= \frac{6}{\tan(30)}\\\\
A &= 6\sqrt{3} \mathrm{см}
\end{выровнено}
Используя треугольник AEH, мы можем вычислить длину AE. 9{2}&=83\\\\
AE&=\sqrt{3}\\\\
AE&=9,11 \mathrm{см}
\end{выровнено}
9{2}&=83\\\\
AE&=\sqrt{3}\\\\
AE&=9,11 \mathrm{см}
\end{выровнено}
(90, -1)
(180, 0)
(180, -1)
(90, 0)
Минимальная точка приходится на (180, -01) 3
Вопросы GCSE по тригонометрии
1. Ниже представлен рисунок футбольного поля ABCD.
(a) Игрок F стоит ровно в 60 м перпендикулярно игроку E на линии ворот и в 75 м от угла, где стоит игрок A. 9{\ Circ}
(1)
(B)
(1)
FG = \ FRAC {45} {SIN (60)}
7777777777777 (45} {SIN (60)}
9000 2 77777777777777777777777777777777777777777 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 77777 (45}. 1)
FG = 51,96 м
(1)
2. Треугольники ABE и ACD подобны с отношением AB:BC = 1:3. Используя информацию на диаграмме, вычислите площадь заштрихованной области BCDE.
Треугольники ABE и ACD подобны с отношением AB:BC = 1:3. Используя информацию на диаграмме, вычислите площадь заштрихованной области BCDE.
В ответе укажите единицы измерения.
9{2} = 43,97 м (1)
BX = 6,63 м
(1)
Контрольный список обучения
Вы узнали, как:
- решать задачи, связанные с прямоугольными треугольниками
- распознавать, чертить и интерпретировать графики тригонометрических функций (с аргументами в градусах) y = sin x, y = cos x и y = tan x для углов любой величины
- применять тригонометрические соотношения к находить углы и длины в прямоугольных треугольниках и, по возможности, общих треугольниках в 2-х и 3-х мерных фигурах
- знать точные значения sin θ и cos θ для θ = 0°, 30°, 45°, 60° и 90°; знать точное значение тангенса θ для θ = 0°, 30°, 45°, 60°
- знать и применять правила синуса и косинуса для нахождения неизвестных длин и углов
- знать и применять area = \frac{ 1}{2}abSinC для вычисления площади, сторон или углов любого треугольника
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.
 ф.)
ф.)Две стороны, с которыми мы работаем, это 9{-1}\left(\dfrac{4}{7}\right)=29,7448813…
x=29,7° (1 дп).
У нас есть угол 87\градус, смежный с ним угол 4\text{ m}, и мы хотим найти противоположный угол, поэтому нам нужно использовать TOA.
\tan(87\степень)=\dfrac{h}{4} где h — высота здания.
ч = \ загар (87) \ раз 4
Выполнение этого на калькуляторе дает:
ч = 76,3 \ текст {м}
Похожие темы
MME
Пифагор
Уровень 4-5GCSEKS3Пересмотреть
Рабочий лист и примеры вопросов
(НОВИНКА) Вопросы в стиле экзамена по тригонометрии — MME
Уровень 4–5 GCSENewOfficial MMEЭкзаменационные вопросы Отметить схему
Учебные вопросы
Тригонометрия 1. Вопросы для тренировки
Уровень 4-5 GCSEЭкзаменационные вопросы
Вам также может понравиться.
 ..
..Что дальше?
Рабочие листы по тригонометрии, вопросы и редакция был добавлен в ваши сохраненные темы. Вы можете просмотреть все свои сохраненные темы, посетив Мои сохраненные темы.
Тригонометрические рабочие листы, вопросы и редакция были удалены из ваших сохраненных тем. Вы можете просмотреть все ваши сохраненные темы, посетив Мои сохраненные темы.
Тригонометрия — Математика GCSE — шаги, примеры и рабочий лист
Здесь мы узнаем о тригонометрии , включая то, как использовать SOHCATOA, обратные тригонометрические функции, точные тригонометрические значения и гипотенузу. Мы также узнаем о правиле синуса, правиле косинуса, о том, как найти площадь треугольника с помощью ½abSinC, трехмерной тригонометрии и о том, как использовать графики синуса, косинуса и тангенса.
Существуют также рабочие листы по тригонометрии, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое тригонометрия?
Тригонометрия — отношение между углами и длинами сторон в треугольниках; оно происходит от греческих слов «тригонон», означающих треугольник, и «метрон», означающих меру.
Тригонометрия изначально использовалась вавилонянами, более чем за 1500 лет до греческой формы, которую мы используем сегодня. Он широко используется в науке, технике и дизайне продукции.
Высшая учебная программа GCSE расширяет использование тригонометрических функций для непрямоугольных треугольников, развиваясь на основе фундаментальных знаний о трех тригонометрических отношениях (выраженных как мнемоника SOHCAHTOA) и точных тригонометрических значениях в прямоугольных треугольниках.
См. также: 15 вопросов по тригонометрии
Что такое тригонометрия
Рабочий лист по тригонометрии
Получите бесплатный рабочий лист по тригонометрии, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист по тригонометрии
Получите бесплатный рабочий лист по тригонометрии, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
СОХКАТОА
Что такое СОХКАТОА?
SOHCAHTOA — это аббревиатура, используемая для описания трех тригонометрических соотношений для функций синуса , косинуса и тангенса .
Чтобы определить, какую тригонометрическую функцию нужно использовать для ответа на вопрос, это зависит от расположения угла и сторон треугольника, которые будут использоваться.
Тригонометрические функции применимы к прямоугольным треугольникам.
- Если вы знаете гипотенузу и противоположную сторону угла, вы должны использовать функцию синуса .

- Если вы знаете гипотенузу и смежную сторону (рядом с) угол, вы должны использовать функцию косинуса .
- Если вы знаете противоположных и смежных сторон угла, вы используете касательную 9Функция 0018.
Мы можем использовать SOHCATOA для вычисления длин и углов в 2D и 3D формах путем распознавания прямоугольных треугольников.
Мы можем найти длину AC параллелограмма или длину AH прямоугольного параллелограмма ниже.
Пошаговое руководство: SOHCATOA
Гипотенуза
Что такое гипотенуза?
Гипотенуза — самая длинная сторона прямоугольного треугольника. Это сторона, противоположная прямому углу.
Гипотенуза не встречается в других типах треугольников, если мы не знаем больше информации (например, равнобедренный треугольник можно составить из 2 одинаковых прямоугольных треугольников, расположенных задними сторонами).
Зная, какой угол мы используем, мы можем обозначить противоположные стороны (O), смежные (A) и гипотенузу (H).
Мы знаем, что гипотенуза лежит напротив прямого угла.
Сторона , противоположная , находится напротив угла, который мы используем.
Сторона , смежная со стороной , находится рядом с углом, который мы используем.
Треугольник ниже обозначен на основе использования угла θ .
Пошаговое руководство: Гипотенуза (скоро)
Пример 1: найти сторону по углу и гипотенузе
ABC — прямоугольный треугольник. Размер угла ACB = 60º, а длина BC = 16см.
Вычислите значение x.
Обозначив стороны OAH по отношению к углу 60º, мы можем использовать гипотенузу, и нам нужно найти прилежащую сторону. Поэтому нам нужно использовать функцию косинуса.
\[ \begin{выровнено}
потому что (\ тета) & = \ frac {A} {H} \\\\
cos(60)&=\frac{x}{16} \\\\
16\times cos(60&)=x\\\\
х&=8см. \end{align} \]
\end{align} \]
Обратные тригонометрические функции
Что такое обратные тригонометрические функции?
Обратные тригонометрические функции позволяют вычислить величину угла θ для прямоугольного треугольника.
Обратные тригонометрические функции выглядят так:
\[ \begin{align} &\квадратный \;\; \text{синус} \quad \quad \quad \quad \quad \quad \quad \text{cosine} \quad \quad \quad \quad \quad \;\; \quad \text{тангенс} \\\\ \text{тригонометрический} \quad \quad \quad &\ sin(\theta) = \frac{O}{H} \quad \quad \quad \quad \;\; \cos(\theta)=\frac{A}{H} \quad \quad \quad \quad \;\; \tan(\theta)=\frac{O}{A} \\ \text{функция} \quad \quad \quad \quad &\\\\\\ \text{other} \quad \quad \quad \quad \quad &H=\frac{O}{\sin(\theta)} \quad \quad \quad \quad \;\; H=\frac{A}{\cos(\theta)} \quad \quad \quad \quad \;\; A=\frac{O}{\tan(\theta)} \\ \text{forms} \quad \quad \quad \quad \quad &\\ \quad \quad \quad \quad &O=H\times\sin(\theta) \quad \quad \quad A=H\times\cos(\theta) \quad \quad \quad O=A\times\tan( \тета) \\\\\\ \text{обратный} \;\; \quad \quad \quad \quad & \\ \text{тригонометрический} \quad \quad \quad &\theta=\sin^{-1}(\frac{O}{H}) \quad \quad \quad \;\; \theta=\cos^{-1}(\frac{A}{H}) \quad \quad \quad \;\;\; \ тета = \ загар ^ {- 1} (\ гидроразрыва {O} {A}) \\ \text{функция} \quad \quad \quad \quad & \конец{выровнено}\]
Пошаговое руководство: Тригонометрические функции
Пример 2: найти угол с помощью обратных тригонометрических функций
Вычислите величину угла θ с точностью до 2 знаков после запятой.
Двумя сторонами, которые можно использовать для вычисления значения θ, являются противоположность и гипотенуза, поэтому мы применяем функцию синуса к θ, чтобы получить
\[ sin(\theta)=\frac{8}{10} . \]
Чтобы вычислить θ, мы переформулируем уравнение, используя функцию обратного синуса. 9{\ круг} \\\\ \text{sin}(x) \quad\quad \quad \quad &0 \; \ quad \ quad \ quad \ quad \ frac {1} {2} \ quad \ quad \ quad \ quad \ frac {1} {\ sqrt {2}} \ quad \ quad \ quad \ quad \ frac {\ sqrt { 3}}{2} \quad \quad \quad \quad 1 \\\\ \text{cos}(x) \quad\quad \quad \quad &1 \; \четырехъядерный \четырехъядерный \четырехъядерный \;\; \ гидроразрыва {\ sqrt {3}} {2} \; \; \quad \quad \quad \frac{1}{\sqrt{2}}\;\; \quad \quad \quad \quad \frac{1}{2} \quad \quad \quad \quad \; 0 \\\\ \text{tan}(x) \quad\quad \quad \quad &0 \; \четырехъядерный \четырехъядерный \четырехъядерный \;\; \frac{1}{\sqrt{3}} \; \quad \quad \quad \quad 1 \;\;\; \quad \quad \quad \quad \sqrt{3} \quad \quad \quad \text{Undefined} \конец{выровнено}\]
Пример 3: использование точных тригонометрических значений
ABC — равносторонний треугольник. {\circ}\\
\end{выровнено} \]
{\circ}\\
\end{выровнено} \]
Пифагор или тригонометрия?
Нам нужно уметь интерпретировать проблемы и понимать, нужно ли нам использовать теорему Пифагора в 2D, 3D или в одном из трех тригонометрических соотношений.
В этой блок-схеме представлена информация, которую необходимо знать о фигуре, чтобы решить проблему.
Важно понимать, что в большинстве этих задач вам может понадобиться использовать теорему Пифагора, тригонометрию или и то, и другое в рамках одного и того же вопроса, поэтому вы должны быть уверены в этих темах по отдельности, чтобы получить полный доступ к этой теме.
Below is a summary of methods that can be used for right angled triangles:
Name
Pythagoras’ Theorem in 2D
Sine function
Cosine function
Тангенс функция0532
Обратная тангенсная функция
Теорема Pythagoras ‘3D
Используется для поиска…
Гипотенуза (C)
А.
Недостающая сторона:
гипотенуза (H)
или напротив (O)
Недостающая сторона:
9053 2 {2}}
Пример 4: найти гипотенузу с помощью тригонометрии
Вычислить длину гипотенузы прямоугольного треугольника x с точностью до 1 знака после запятой.
Две важные стороны в этом вопросе — это сторона, противоположная углу (O), и гипотенуза (H), поэтому нам нужно использовать функцию синуса для вычисления значения x.
\[ \begin{выровнено} H&=\frac{O}{\sin(\theta)}\\ \\H&=\frac{56}{\sin(63)}\\ \\H&=62.9м\quad(1dp)\\ \end{выровнено} \]
Решение непрямоугольных треугольников
Правило синусов (закон синусов)
Что такое правило синусов?
Правило синусов (или закон синусов) представляет собой зависимость между величиной угла в треугольнике и противолежащей стороной. В треугольнике есть три отношения, так как есть 3 угла с противоположными сторонами, но вам нужно будет использовать только два.
Теорему Пифагора нельзя использовать для нахождения третьей стороны непрямоугольного треугольника. Вместо этого мы можем использовать правило синусов или правило косинусов, в зависимости от информации, которую мы знаем о треугольнике.
Чтобы найти недостающий угол:
\frac{\sin (A)}{a}=\frac{\sin (B)}{b}
Чтобы найти недостающую сторону:
\frac{a} {\sin (A)}=\frac{b}{\sin (B)}
Пошаговое руководство: Правило синусов
Пример 5. Нахождение недостающей стороны треугольника с помощью правила синусов
Рассчитайте длину AB. Запишите свой ответ с точностью до 2 знаков после запятой.
Обозначьте каждый угол A, B и C и каждую сторону a, b и c:
Здесь мы знаем сторону a и хотим найти длину c, поэтому мы можем сказать:
\начало{массив}{л}
\frac{a}{\sin (A)}=\frac{c}{\sin (C)}\\
\\\frac{6}{\sin (55)}=\frac{c}{\sin (73)}\\
\\c=\frac{6}{\sin (55)}\times\sin(73)\\
\\c=\frac{6\sin(73)}{\sin(55)}\\
\\c=7. 00\quad(2dp)
\end{array}
00\quad(2dp)
\end{array}
Здесь длина AB = 7,00 см (2dp).
Правило косинусов (закон косинусов)
Что такое правило косинусов?
Правило косинусов (или закон косинусов) — это формула, которую можно использовать для вычисления недостающих сторон треугольника или для нахождения недостающего угла. Для этого нам нужно знать две схемы формулы и то, что представляет каждая переменная. 92}{2bc})
Пошаговое руководство: Правило косинуса
Пример 6: Найдите недостающую сторону, используя правило косинуса
Найдите длину x треугольника ABC, исправьте до 2 знаков после запятой.
Вершины уже помечены буквой A, расположенной на используемом нами угле, поэтому нам нужно только пометить противоположные стороны a, b и c.
Здесь нам нужно найти недостающую сторону а, поэтому нам нужно сформулировать правило косинусов с 2 в качестве подлежащего: 9{2}=14,38516072…\\
\\x=\sqrt{14. 38516072…}\\
\\x=3,79 см\quad(2dp)\\
\end{массив}
38516072…}\\
\\x=3,79 см\quad(2dp)\\
\end{массив}
1/2abSin(C) (площадь треугольника)
Что такое 1/2abSin(C)?
\frac{1}{2}abSin(C) – это формула для вычисления площади любого треугольника.
\[ Площадь =\frac{1}{2}ab\sin(C). \]
Пошаговое руководство: Площадь треугольника треугольника
Пример 7: площадь с использованием A=1/2abSin(C)
Вычислите площадь треугольника ABC. Запишите свой ответ с точностью до 2 знаков после запятой. 9{2}\квадрат(2дп)\\ \end{array}
Трехмерная тригонометрия
Что такое трехмерная тригонометрия?
Трехмерная тригонометрия представляет собой применение тригонометрических навыков, разработанных для двумерных треугольников.
Чтобы найти отсутствующие стороны или углы в трехмерных фигурах, нам нужно четко знать правила и формулы для нахождения этих разных углов и длин сторон.
Приведенная ниже блок-схема может помочь определить, какую функцию вам нужно использовать:
Как только вы сможете обосновать, какое правило или формулы вам нужно использовать, вам, возможно, придется повторить этот процесс еще раз для другого треугольника в вопросе.
Главный совет: ищите общие углы или общие стороны.
Пошаговое руководство: Трехмерная тригонометрия
Пример 8: найти недостающий угол в треугольной призме
Вычислить величину угла в треугольной призме ABCDEF.
Мы видим, что треугольник ABF и треугольник ACF имеют общую сторону AF. Мы можем использовать треугольник ACF для вычисления длины AF, что затем поможет нам вычислить величину угла θ.
Этот треугольник не содержит информации об углах, поэтому нам нужно использовать теорему Пифагора. 9{\ круг} \end{align}
Тригонометрические графикиТригонометрические функции синуса, косинуса и тангенса могут быть представлены в виде графиков.
Например, при изменении угла изменяется и значение синуса. Это можно изобразить на графике.


Сторона этого треугольника неправильно обозначена рядом с углом.
Это повлияет на формулу для правила синусов, правила косинуса и площади треугольника.
 Помните, что вам может понадобиться использовать оба.
Помните, что вам может понадобиться использовать оба.
 Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.
Потренируйтесь рисовать каждую кривую от руки и отмечайте важные значения на каждой оси.Используя треугольник AGH, мы можем вычислить длину прямой AH.
 9{2}&=83\\\\
AE&=\sqrt{3}\\\\
AE&=9,11 \mathrm{см}
\end{выровнено}
9{2}&=83\\\\
AE&=\sqrt{3}\\\\
AE&=9,11 \mathrm{см}
\end{выровнено} Треугольники ABE и ACD подобны с отношением AB:BC = 1:3. Используя информацию на диаграмме, вычислите площадь заштрихованной области BCDE.
Треугольники ABE и ACD подобны с отношением AB:BC = 1:3. Используя информацию на диаграмме, вычислите площадь заштрихованной области BCDE.

 Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.