Экономический смысл двойственной задачи: 4.3. Экономический смысл двойственной задачи

4.3. Экономический смысл двойственной задачи

Рассмотрим следующую производственную задачу.

Предприятие после выпуска основной продукции имеет излишки ресурсов двух типов: R₁ – 10 единиц, R₂ – 8 единиц. Существует два способа распорядиться этими ресурсами:

Рассмотрим оба способа.

Исходные данные приведены в таблице:

Ресурсы	Расход ресурса на  единицу продукции			Запас ресурсов
	P1	P2	P3
R1	1	2	1	10
R2	2	1	3	8
Удельная прибыль	6	4	4

Согласно первому способу, надо составить такой план выпуска продукции, который максимизирует суммарную прибыль. Построим математическую модель этой задачи.

Пусть  x_j – план выпуска продукции P_j .

Тогда целевая функция будет  выглядеть следующим образом:

f(x) = 6x₁ + 4x₂ + 4x₃  max;

Ограничения по ресурсам:

x₁ + 2x₂ + x₃  10 ,

2x₁ + x₂ + 3x₃  8 ,

x_j  0 ,  j=1,2,3.

Получили стандартную задачу ЛП.

Рассмотрим второй способ использования ресурсов, а именно, их продажу.

Интерес предприятия состоит в том, чтобы продать ресурсы  по таким ценам, при которых доход от реализации ресурсов будет не меньше прибыли, которую можно получить от реализации продукции, изготовленной из этих ресурсов.

В свою очередь, покупатель заинтересован  в приобретении  ресурсов  по таким ценам, при которых затраты на покупку будут минимальны. 

Задача согласования цен на ресурсы, устраивающих обе стороны, может быть описана следующей математической моделью. 

Пусть y₁ – цена одной единицы ресурса R₁ , y₂ – цена одной единицы ресурса R₂ .

Интерес покупателя будет выражаться целевой функцией, равной суммарной стоимости приобретаемых ресурсов

g(y) = 10 y₁ + 8 y₂  min .

Интерес продавца будет описываться ограничениями:

y₁

+ 2y₂  6 ,

2y₁ + y₂  4 ,

y₁ + 3y₂  4 ,

в которых левая часть означает стоимость ресурсов, затраченных на выпуск единицы соответствующей продукции, а правая – удельную прибыль от ее реализации.

Присоединяя естественные условия неотрицательности цен:

y₁, y₂, y₃   0 ,

получаем  двойственную задачу ЛП.

    

Таким образом, симметричной паре двойственных задач можно придать определенный экономический смысл.

Прямая задача Определить такой план выпуска  продукции  x = ( x1 , x2 ,…, xn), используя  ограниченные запасы ресурсов, при котором прибыль от реализации продукции будет максимальной.

Двойственная задача Установить такой набор цен ресурсов y =( y1 , y2 ,. .., ym), при которых стоимость ресурсов, затраченных на выпуск единицы продукции, будет не ниже прибыли от ее реализации, но при этом суммарная стоимость затрат будет минимальна.

    

Цены ресурсов  y₁ , y₂ ,…,y_m  носят названия теневых, неявных или внутренних цен. Эти названия отличают их от «внешних», заранее известных цен  с₁, с₂,…,с_n  на выпускаемую продукцию. Цены  y₁ , y₂ ,…,y_m на ресурсы определяются из решения двойственной задачи и характеризуют стоимость затрат на выпуск конкретных видов продукции, поэтому их часто называют двойственными оценками ресурсов.

 

Интерпретация двойственных задач в экономике качества

Главная » Интерпретация двойственных задач в экономике качества

Interpretation of Dual Problems in Economics of Quality

М. С. Бабарин
M.S. Babaryn
[email protected]
генеральный директор ЗАО «Инвестиционная компания «Энергокапитал»
General Director of Energocapital Investment Company
г. Санкт-Петербург
St. Petersburg
Рассмотрены проблемы экономической интерпретации двойственных задач линейного программирования применительно к экономике качества. Представлены математические модели, раскрыта экономическая сущность целевой функции и ограничений для прямой и двойственной задачи оптимизации качества на основе полезности. Сделаны теоретические выводы для развития экономики качества.
The problems of economic interpretation of dual linear programming relating to the economics of quality are considered in the article. Mathematical models are presented, the economic essence of an objective function and constraints for a primal and dual quality optimization problem on the basis of utility is revealed. The theoretical conclusions for the development of economics of quality are made.
Ключевые слова: экономика качества полезность прямая и двойственная задачи линейного программирования	Keywords: economics of quality utility primal and dual problems of linear programming
В статье рассмотрены актуальные проблемы экономической интерпретации двойственных задач линейного программирования применительно к экономике качества. Одной из задач экономики качества является нахождение оптимального плана по качеству продукции в условиях ограниченных ресурсов. Для решения данной задачи представлены математические модели прямой и двойственной задач линейного программирования, раскрыта экономическая сущность целевой функции и ограничений для прямой и двойственной задачи оптимизации плана производства по качеству на основе полезности, как общепризнанной фундаментальной экономической переменной, связанной с качеством. Автором сделаны теоретические выводы для развития экономики качества, а именно: раскрыто экономическое содержание задач линейного программирования для экономики качества; представлена интерпретация прямых и двойственных задач с использованием в целевой функции и ограничениях показателей полезности; выявлен двоякий экономический смысл цен оптимального плана по качеству в двойственных задачах линейного программирования; обосновано правило экономики качества о принятии экономических решений для альтернативы производства или потребления.
The article deals with topical problems of the economic interpretation of dual linear programming regarding to quality economics. One of the objectives of the economics of quality is finding the optimal quality plan for the product in resource-limited settings. The author presents mathematical models of primal and dual linear programming problems; defines the economic essence of an objective function and constraints for a primal and dual optimization problem of a product quality planning based on utility, as a universally recognized fundamental economic variable related to quality. The author makes theoretical conclusions for the economics of quality development, namely: the economic content of linear programming problems for the economics of quality is set forth; interpretation of primal and dual problems with the use of an objective function and constrains of utility indicators are presented; the double economic meaning of the prices of the optimal quality plan in dual linear programming problems is defined; the rule of economics of quality about economic decision-making for the alternative of production or consumption is validated.
Обзор статьи В теории всеобщего управления качеством (TQM) категория качества применяется к продукции, процессам, организациям, обществу и в настоящее время приобретает решающее значение в экономических отношениях людей. Встают вопросы улучшения качества продукции, качества государственных услуг, качества жизни людей и другие вопросы, связанные с качеством. С развитием экономики, ростом благосостояния людей и общества возрастают требования к качеству различных объектов и возникает необходимость его постоянного повышения. Вместе с тем, экономический аспект устойчивого развития и постоянного улучшения качества еще не полностью решен и находится в области исследований экономики качества. Академик В.В. Окрепилов определяет содержание экономики качества как части экономической науки, изучающей взаимосвязь качественных характеристик объектов или явлений с экономическими показателями [6. С. 124]. Экономика качества как научное направление определяет оптимальные решения социально-экономических проблем, связанных с качеством [1; 2]. В круг вопросов экономики качества, таким образом, попадают проблемы достижения наилучшего качества продукции и процессов для удовлетворенности потребителей такого уровня, которое возможно достигнуть в реальных условиях. В связи с этим одной из задач экономики качества может являться нахождение оптимального плана по качеству выпускаемой продукции в условиях ограниченных ресурсов.
Список использованной литературы 1. Горбашко Е.А. Управление качеством. М.: Юрайт, 2012. 2. Демиденко Д.С., Леонова Т.И., Бабарин М.С. Координаты экономики качества // Стандарты и качество. 2013. № 5. 3. Долан Э. Дж., Линдсей Д. Рынок: микроэкономическая модель / под общ. ред. Б. Лисовика, Л. Лукашевича. СПб.: Автокомп, 1992. 4. Макконнелл К.Р., Брю С.Л. Экономикс: принципы, проблемы и политика. В 2-х т. М.: Республика, 1992. 5. Обросова Н.К., Шананин А.А. Экономическая интерпретация двойственности в задачах линейного программирования. М.: Изд-во Ун-та Дружбы народов, 2007. 6. Окрепилов В.В. Экономика качества. СПб.: Наука, 2011.

Экономическая интерпретация двойственности

1. Экономическая интерпретация двойственных переменных 2. Экономическая интерпретация двойственных ограничений

ЭКОНОМИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ДВОЙСТВЕННОСТИ

 

задачу линейного программирования можно рассматривать как модель распределения ресурсов в целью которого является максимизация дохода при условии наличия ограниченные ресурсы. Рассматривая проблему с этой точки зрения, двойная проблема предлагает интересные экономические интерпретации ресурса LP модель распределения.

 

Кому формализовать обсуждение, рассмотрим следующее представление общие прямые и двойственные задачи:

модель распределения ресурсов, основная задача имеет n видов экономической деятельности и m Ресурсы. Коэффициент Cj в основном представляет выручка на единицу деятельности j. Ресурс i, чей максимальная доступность б _я , это потребляется из расчета аиж единиц на единицу деятельности дж.

 

1. Экономическая интерпретация двойных переменных

 

Раздел 4.2.3 утверждает, что для любых двух первичных и двойственных допустимых решений значения целевых функций, когда конечно, должны удовлетворять следующему неравенству:

строгое равенство, z =  w, выполняется, когда и первичное, и двойные решения оптимальны. Рассмотрим сначала оптимальное условие z = w . Учитывая, что основная проблема представляет собой модель распределения ресурсов, мы можем думать о z как о доходах в долларах. Потому что б _я представляет количество доступных единиц ресурса i, the уравнение

z =   w может быть выражается размерно как

Это означает, что двойная переменная y _i представляет стоимость единицы ресурса i.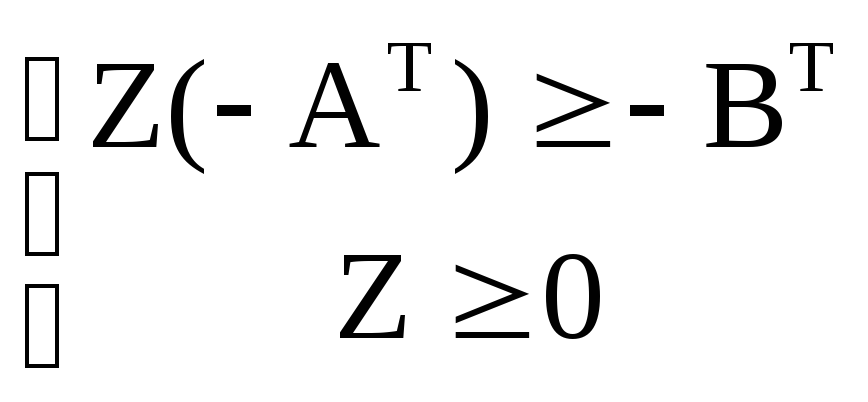 Как указано в разделе 3.6, стандартное имя dual (или тень) цена ресурса и заменяет имя стоит за единицу во всех LP литература и программные пакеты.

 

Использование по той же логике, неравенство z < w , связанное с любыми двумя допустимыми первичное и двойное решения интерпретируются как

 

(доход) < (Стоимость ресурсов)

 

Это отношение говорит о том, что до тех пор, пока общий доход от всех видов деятельности меньше, чем ценность ресурсов, соответствующие первичная и двойная решения не оптимальны. Оптимальность (максимальный доход) достигается только тогда, когда ресурсы были полностью использованы, что может произойти только тогда, когда вход (стоимость ресурсов) равен результату (доход в долларах). В экономической терминах, говорят, что система нестабильный (неоптимальный) когда вход (стоимость ресурсов) превышает выход (доход). Стабильность возникает только тогда, когда две величины равный.

 

Пример 4.3-1

 

Редди Модель Миккса (пример 2.1-1) и ее двойник задаются как:

Вкратце, модель Reddy Mikks занимается производством двух видов краски (внутренняя и экстерьер) с использованием двух исходных материалов М1 и M2 (ресурсы 1 и 2) и в зависимости от рынка и ограничений спроса представлены третьим и четвертым ограничениями. Модель определяет количества (тонн/день) красок для внутренних и наружных работ, которые максимизируют ежедневную доход (выраженный в тысячах долларов).

 

оптимальное двойное решение показывает, что двойная цена (стоимость единицы) сырья материал Ml (ресурс 1) равен y _l = 0,75 (или $750 за тонну), а сырье М2 (ресурс 2) равен y ₂ = 0,5 (или 500 долларов за тонну). Эти результаты справедливы для конкретных диапазонов выполнимости , как мы показали в разделе 3. 6. Для ресурсов 3 и 4, представляющий пределы рынка и спроса, обе двойные цены равны нулю, что указывает на то, что связанные с ними ресурсы в изобилии. Следовательно, их стоимость единицы равна нулю.

 

 

НАБОР ЗАДАЧ 4.3A

 

1. В В примере 4.3-1 вычислите изменение оптимального дохода в каждом из следующих случаях (используйте выходные данные TORA для получения допустимых диапазонов):

 

a. ограничение для сырья M1 (ресурс 1) равно 6x _l   + 4x ₂ ≤ 22.

 

3 b. ограничение по сырью M2 (ресурс 2) равен х ₁ + 2x ₂ ≤ 4,5.

 

c. рыночное состояние, представленное ресурсом 4, равно x ₂   ≤ 10.

 

*2. СЗАК Electronics производит четыре типа простых кабелей для оборонного подрядчика. Каждый кабель должны пройти четыре последовательные операции: сращивание, пайка, оплетка и осмотр. В следующей таблице приведены соответствующие данные о ситуации.

Подрядчик гарантирует минимальный уровень производства 100 единиц для каждого из четыре кабеля.

 

а. Сформулировать задача как модель линейного программирования, и определить оптимальную производительность расписание.

 

б. На основе двойные цены, вы рекомендуете увеличить суточную мощность любая из четырех операций? Объяснять.

 

в. Есть ли минимальные производственные требования для четырех кабелей представляют собой преимущество или недостаток для NWAC Electronics? Дайте объяснение, основанное на двойном Цены.

 

д. Может ли текущая удельная доля дохода в соответствии с двойной ценой должна быть гарантировано, если мы увеличим мощность пайки на 10%?

 

3. БагКо производит кожаные куртки и сумки. На куртку требуется 8 м ² из кожа, а сумка всего 2 м ² • Требования к рабочей силе для двух произведения соответственно 12 и 5 часов. Текущие еженедельные поставки кожа и работа ограничены 1200 м ² и 1850 часов. Компания продает куртки и сумки по 350 и 120 долларов соответственно. Цель определить график производства, который максимизирует чистый доход. БэгКо это с учетом расширения производства. Какова максимальная цена покупки компания должна платить за дополнительную кожу? Для дополнительной работы?

 

2. Экономическая интерпретация двойных ограничений

 

Двойственное ограничения можно интерпретировать с помощью формулы 2 в разделе 4.2.4, которая утверждает, что на любой первичной итерации

Таким образом, условие оптимальности максимизации говорит о том, что это экономически выгодно увеличить деятельность до положительного уровня, если доход от ее единицы превышает вмененная стоимость единицы.

 

Мы используйте модель TOYCO из раздела 3.6, чтобы продемонстрировать вычисления. Детали модели приведены здесь для удобства.

 

 

Пример 4.3-2

 

TOYCO собирает три типа игрушек: поезда, грузовики и автомобили, используя три операции. Доступное время сборки для трех операций: 430, 460 и 420 минут. в день соответственно, а доход от игрушечного поезда, грузовика и автомобиля составляет 3 доллара, 2 и 5 долларов соответственно. Время сборки поезда для трех операций равны 1,3 и 1 минуте соответственно. Соответствующее время на грузовик и на car равны (2,0,4) и (1,2,0) минуты (нулевое время означает, что операция не используется).

Сдача в аренду x ₁ ,x ₂ и x ₃ представляет собой ежедневное количество единиц, собранных из поездов, грузовиков и легковых автомобилей, соответствующая модель LP и ее двойник задаются как:

оптимальное первичное решение требует не производить игрушечных поездов, 100 игрушечных грузовиков и 230 игрушечных автомобилей. Предположим, что TOYCO также заинтересованы в производстве игрушечных поездов. Как этого добиться? Смотрящий на проблему с точки зрения интерпретации снижена стоимость для xl> игрушечные поезда станут экономически привлекательным только в том случае, если вмененная стоимость ресурсов, используемых для производство одного игрушечного поезда строго меньше его удельного дохода. Таким образом, TOYCO может либо увеличить удельный доход на единицу за счет повышения цены за единицу, либо он может уменьшить вмененную стоимость использованных ресурсов (= y ₁ + 3y ₂ + у ₃ ). Увеличение цена за единицу может оказаться невозможной из-за рыночной конкуренции. Снижение удельные условно исчисленные затраты более правдоподобны, поскольку они влекут за собой внесение улучшений в сборочные операции. Сдача г ₁ , r ₂ , и r ₃ представляют пропорции, в которых единица времени три операции сокращаются, задача требует определения r ₁ , r ₂ и r3 таких, что новые вмененные затраты на единицу на игрушечный поезд меньше, чем его удельный доход, то есть

Таким образом, любой значения r ₁ и r ₂ между 0 и 1, которые удовлетворяют r ₁ + 6r ₂ > 4 должны сделать игрушечные поезда выгодно. Однако эта цель может оказаться недостижимой, поскольку она требует практически невозможное сокращение времени операций 1 и 2. Для Например, даже сокращение на 50% в эти моменты времени (то есть r ₁ = r ₂ = 0,5) не удовлетворяет заданному условию. Таким образом, TOYCO не должна производить игрушечные поезда, за исключением случаев, когда увеличение цены за единицу продукции возможный.

ПРОБЛЕМА НАБОР 4.3B

 

1. В Пример 4.3-2, предположим, что для игрушечных поездов единица времени работы 2 может быть сокращено с 3 минут до максимум 1,25 минут. На сколько должен на единицу времени работы 1 сократить, чтобы игрушечные поезда стали просто прибыльными?

 

*2. В Пример 4.3-2, предположим, что TOYCO изучает возможность введения четвертая игрушка: пожарные машины. Сборка не использует операцию 1. Ее время сборки блока на операции 2 и 3 составляет 1 и 3 минуты соответственно. Доход на единицу составляет 4 доллара. Не посоветуете ли TOYCO представить новую продукт?

*3. JoShop использует токарные станки и сверлильные станки для производства деталей машин четырех типов: PP1, PP2, , PP3, и PP4. Стол ниже приведены соответствующие данные.

Для части, которые не производятся настоящим оптимальным решением, определяют скорость ухудшения оптимального дохода на единицу увеличения каждого из этих продукты.

 

4. Рассмотрим оптимальное решение JoShop в задаче 3. Компания оценивает что для каждой не произведенной детали (согласно оптимальному решению) повсеместно 20% пере. сокращение времени обработки может быть реализовано за счет процесса улучшения. Сделают ли эти улучшения прибыльными эти детали? Если нет, то каков минимум процентное сокращение, необходимое для реализации рентабельности?

Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, объяснение, краткая информация

Исследование операций: Введение: Двойственность и постоптимальный анализ: Экономическая интерпретация двойственности |

Концепция двойственности в теории потребления-микроэкономике

1 Комментарий / Микроэкономика, Учебные материалы / Автор Энотес Мир

Распространяйте любовь

Содержание

Значение двойственности

Термин двойственность обычно используется для обозначения несходства между двумя коррелирующими понятиями, такими как дуальные характеристики развивающихся экономик. Это означает, что двойственность связана с поиском конкретной вещи двумя разными альтернативными способами. Таким образом, в теории потребителей двойственность — это альтернативный взгляд на решение потребителя о максимизации полезности. Здесь мы объясняем концепцию и механизм двойственности в теории потребления.

В микроэкономическом анализе двойственность относится к отношениям между количествами и ценами, которые растут в результате гипотез оптимизации и выпуклости. В связи с этим двойственность представляет собой логическую связь между функциями полезности и расходов (а также функциями прибыли и производства), первичной и двойственной линейными программами, теневыми ценами и рядом других экономических концепций. В теории потребления двойственность между, скажем, функцией полезности и функцией расходов возникает в результате ловкости рук/искусного трюка с условиями первого порядка для оптимизации. Эти двойственные отношения, однако, не являются естественным продуктом исчисления.

Изучая теорию потребления, мы можем исследовать поведение с точки зрения максимизации полезности в зависимости от денежного дохода или бюджетного ограничения или минимизации расходов/затрат в зависимости от ограничения полезности. Это означает, что мы можем рассматривать поведение потребителей с обеих этих точек зрения, и это известно как двойственность потребления или концепция двойственности в теории потребления.

Концепция двойственности, связанная с потребительским поведением (концепция двойственности в теории потребления), основана на том факте, что предпочтения могут быть представлены в двух формах, отличных от функции полезности; это функция расходов и косвенная функция полезности. Практичность двойственности вытекает из двух фактов. Во-первых, это функция спроса Маршалла. Его можно измерить по косвенной функции полезности путем дифференцирования. Во-вторых, это функция спроса Хикса. Его можно вычислить из функции расходов дифференцированием. Функции спроса Маршалла и Хикса получаются только как неявные функции, в то время как спрос выводится непосредственно из функции полезности с помощью обычного метода Лагранжа.

Таким образом, концепция двойственности показывает, что существует четкая связь между задачей максимизации функции с учетом ограничения и задачей присвоения значений ограничениям. Любая ограниченная максимизация, которая фокусируется на ограничении в исходной (основной) задаче. Здесь его двойная задача состоит в минимизации затрат или затрат, необходимых для достижения заданной полезности. Или основная проблема фирмы может состоять в том, чтобы минимизировать общую стоимость ресурсов, используемых для производства данного уровня выпуска, тогда как двойная задача состоит в том, чтобы максимизировать выпуск при заданном уровне общей стоимости приобретенных ресурсов.

Пример двойственности

Основное решение

Например, мы задали основную задачу как задачу максимизации полезности как;

Maximize U= f (X ₁ , X ₂ )

Subject to B= P ₁ X ₁ +P ₂ X ₂

Where X ₁ and X ₂ являются потребительскими товарами. «B» — денежный доход или бюджетное ограничение для потребителя, а P ₁ и P ₂ — цены за единицу товара.

Теперь установим выражение Лагранжа как;

L= X ₁ X ₂ + λ(B-P ₁ X ₁ -P ₂ X ₂ ) ………………. множитель. Условиями максимизации первого порядка являются;

∂l/∂x ₁ = 0 или, ∂ {x ₁ x ₂ + λ (B -P ₁ x ₁ -P ₂ x ₂ )}/acm37 _{777. 1} = 0 Или, ∂L/∂X ₁ =X ₂ -λP ₁ =0

∂L/∂X ₂ = 0 Или, ∂{07 0 3 х _{1 90 λ (B -P 1 x 1 -P 2 x 2 )}/∂x 2 = 0 или, ∂L/∂x 2 = x 1 -λp 2 = x 1 -λp 2 или , B=P 1 X 1+ P 2 X 2}

Чтобы найти значения X ₁ , X _{2 ,} и λ, необходимо решить три приведенных выше уравнения одновременно. Решив приведенные выше уравнения, мы получим, X ₁ = B/2P ₁ и X ₂ = B/2P ₂ .

Здесь X ₁ и X ₂ — функции спроса Маршалла. Таким образом, косвенная функция полезности имеет вид V=B/2P ₁ * B/2P ₂ =B ² /4P ₁ P ₂ =U*

Двойственность или двойное решение

Двойственность этой задачи максимизации с ограничениями состоит в том, что для заданной полезности потребитель желает минимизировать затраты, необходимые для получения заданного уровня полезности. Математически задача состоит в том, чтобы минимизировать

Стоимость E=P ₁ X ₁ + P ₂ X ₂

С учетом ограничения U*= f (X _{1 0 3} , X )

Настройка выражения Лагранжа как

L ^D = [P ₁ x ₁ + P ₂ x ₂ + λ (U*-x ₁ x ₂ )]

, где D DANOTES DANOTES ). concept

Для задачи минимизации необходимы следующие условия первого порядка + λ(U*-X ₁ X ₂ )]/ ∂X ₁ =0 Или, P ₁ -λX ₂ = 0

∂L ^D /∂x ₂ = 0 или, ∂ [P ₁ x ₁ + P ₂ x ₂ + λ (u*-x ₁ x ₂ + λ (u*-x ₁ x ₂ + λ (u*-x ₁ x _{. 2 )] / ∂x 2 = 0 или, p 2 -λx 1 = 0}

∂L ^D / ∂λ = 0, ∂ [P ₁ X ₁ +P ₂ X ₂ + λ(U*-X ₁ X ₂ )]/λ=0 Или, U*=X ₁ X ₂

Решая вышеприведенные уравнения получить X ₁ = {U*P ₂ /P ₁ } ^1/2 и X ₂ = {U*P ₁ /P ₂ } ^1/2

900 * из прямого решения в значение X ₁ и X ₂ в двойственном решении получаем;

X ₁ =B/2P ₁ и X ₂ =B/2P ₂ .