4. Из параллельности сторон вытекает равенство частей углов. Например:
\(\angle DAC = \angle BCA\)
\(\angle CBD = \angle BDA\)
5. Две диагонали делят параллелограмм на две пары равных (по стороне и двум углам) треугольников:
\(\mathrm{\Delta}ABC = \mathrm{\Delta}BCD\)
\(\mathrm{\Delta}ABD = \mathrm{\Delta}ACD\)
6. Диагонали параллелограмма точкой пересечения делятся пополам:
\(AO = OC\)
\(BO = OD\)
Также параллелограмм обладает необычными свойствами, связанные с биссектрисами:
Пусть AL и СК – биссектрисы противоположных углов, а ВМ – биссектриса смежного с ними угла.
Тогда:
1. Биссектрисы противоположных углов параллельны:
\(AL\ ||\ CK\)
2. Биссектрисы смежных углов перпендикулярны:
\(AL,\ CK\bot BM\)
3. Биссектриса параллелограмма отсекает от него два равных угла. Например:
\(\mathrm{\Delta}ABL\ — \ равнобедренный,\ т.к.\ \angle BAL = \angle BLA\)
\(\mathrm{\Delta}ABM\ — \ равнобедренный,\ т. к.\ \angle ABM = \angle AMB\)
к.\ \angle ABM = \angle AMB\)
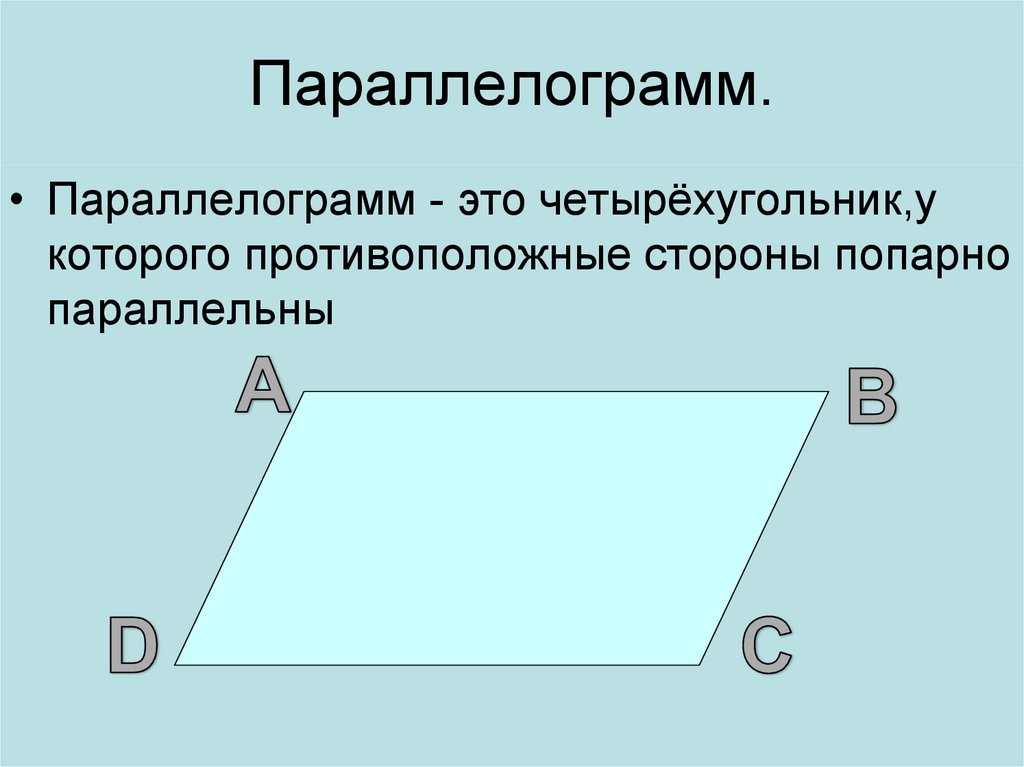
ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА:
Для того, чтобы доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
\(AB\ ||\ CD\)
\(BC\ ||\ AD\)
2. Четырехугольник имеет пару параллельных и равных сторон:
\(AB\ ||\ CD,\ AB = CD\)
\(или\)
\(BC\ ||\ AD,\ BC = AD\)
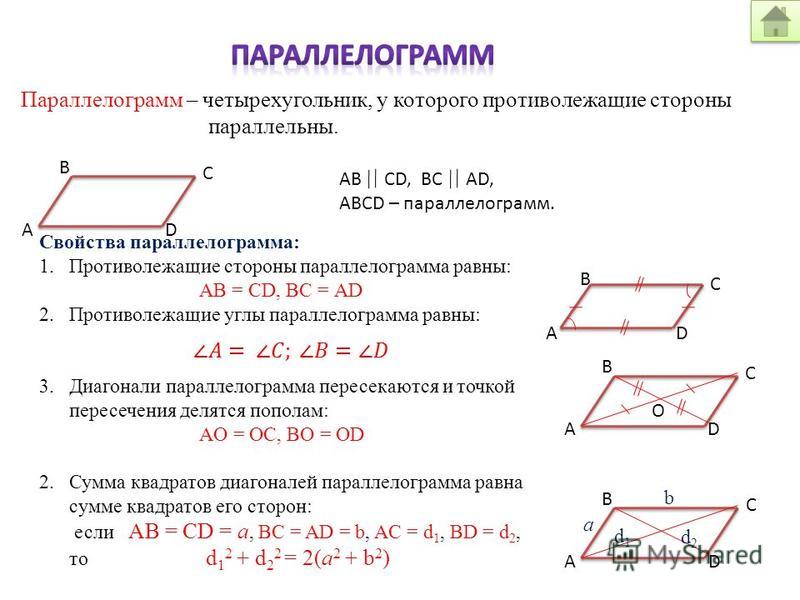
3. В четырехугольнике противоположные стороны попарно равны:
\(AB = CD\)
\(BC = AD\)
4. В четырехугольнике противоположные углы попарно равны:
\(\angle DAB = \angle BCD\)
\(\angle ABC = \angle CDA\)
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
\(AO = OC\)
\(BO = OD\)
6. Сумма углов четырехугольника, прилегающих к любой стороне, равна 180°:
\(\angle ABC + \angle BCD = \angle BCD + \angle CDA = \angle CDA + \angle DAB = \angle DAB + \angle ABC = 180{^\circ}\)
ПЛОЩАДЬ ПАРАЛЕЛОГРАММА:
1. Через высоту и сторону
Через высоту и сторону
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
\(S = ah_{1} = bh_{2}\)
2. Через две стороны и угол между ними
Площадь параллелограмма равна произведению его сторон на синус угла между ними.
\(S = ab \bullet \sin\alpha\)
3. Через диагонали и угол между ними
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
\(S = \frac{1}{2}d_{1}d_{2} \bullet \sin\gamma\)
Почему теорема называется теоремой
Андрей Щетников
«Квантик» №9, 2021
Слово «теорема» известно нам из школьного учебника геометрии: так называется утверждение, истинность которого следует доказать. Однокоренное с ним и слово «теория». Как и многие другие слова, связанные с наукой, они пришли к нам из Древней Греции. Полюбопытствуем, что эти слова означали в древности, и откроем словарь древнегреческого языка.
ϑεωρiα — 1) смотрение на зрелище; зрелище, празднество; 2) посольство или депутация, посылаемая греческими государствами для присутствия на играх Олимпийских, Истмийских, Пифейских и Немейских; священное посольство, посылаемое афинянами в Делос; 3) наблюдение, рассмотрение, исследование, научное познание, наука, учение, теория.
ϑεώρημα — 1) зрелище, увеселение; 2) позд. исследованное и доказанное положение, правило, учение.
Удивительно, правда?! Особенно странным кажется упоминание об Олимпийских играх; разве есть что-то общее между ними и геометрией? Но такая связь есть, и чтобы понять, почему древнегреческие математики стали называть открытые ими геометрические факты теоремами, к истории Олимпийских игр надо обратиться в первую очередь.
Сегодня Олимпийские игры — это большие соревнования по многим видам спорта, проводимые раз в четыре года. Но раньше этим дело не ограничивалось.
Древние Олимпийские игры были общегреческим религиозным праздником в честь одного из олимпийских богов — Зевса Олимпийского. Святилище Зевса находилось, конечно же, не на Олимпе, но в Олимпии — небольшом греческом государстве на западе Пелопоннеса. Здесь росла священная роща. В роще стоял храм, когда-то деревянный, а впоследствии каменный, и его мраморные колонны сами были похожи на стволы деревьев. Рядом с храмом росла древняя олива. Когда-то предки греков жили в лесах и поклонялись деревьям, и эта олива была сама предметом такого поклонения. Считалось, что божество любит втайне от людей посещать свой храм и свою рощу; а олива была если и не воплощением божества, то чем-то очень близко с ним связанным.
Святилище Зевса находилось, конечно же, не на Олимпе, но в Олимпии — небольшом греческом государстве на западе Пелопоннеса. Здесь росла священная роща. В роще стоял храм, когда-то деревянный, а впоследствии каменный, и его мраморные колонны сами были похожи на стволы деревьев. Рядом с храмом росла древняя олива. Когда-то предки греков жили в лесах и поклонялись деревьям, и эта олива была сама предметом такого поклонения. Считалось, что божество любит втайне от людей посещать свой храм и свою рощу; а олива была если и не воплощением божества, то чем-то очень близко с ним связанным.
Праздник Зевса Олимпийского проводился раз в четыре года. Летом этого года все греческие города-государства объявляли священное перемирие. Всякая война прекращалась на время, чтобы все путники могли добраться в Олимпию беспрепятственно. Уже в самом начале лета на олимпийских тренировочных площадках собирались молодые люди, готовившиеся принять участие в состязаниях. Ближе к празднику в Олимпию приезжали торговцы с товарами из самых дальних краёв греческого мира, от Геркулесовых столбов до Чёрного моря. Конечно же, торговля велась не в храмовой округе, но за её пределами; и этот рынок был самым большим и шумным из всех греческих рынков. И наконец, в Олимпию прибывали официальные посольства из всех греческих городов. Понятно, что в их состав входили самые уважаемые в своём городе люди. А назывались эти посольства, как мы помним из словаря, теориями.
Конечно же, торговля велась не в храмовой округе, но за её пределами; и этот рынок был самым большим и шумным из всех греческих рынков. И наконец, в Олимпию прибывали официальные посольства из всех греческих городов. Понятно, что в их состав входили самые уважаемые в своём городе люди. А назывались эти посольства, как мы помним из словаря, теориями.
Основу Олимпийского праздника составляло — и тут история делает неожиданный для неспециалистов поворот! — принесение божеству даров и жертв. У каждого города в Олимпии была своя дарохранительница и свой алтарь. На алтаре сжигались части жертвенных животных, и дым поднимался к небу; а послы принимали участие в священной трапезе, становясь тем самым сотрапезниками божества.
А дальше начинается самое интересное. Грекам очень хотелось узнать, насколько благосклонно божество отнеслось к их дарам, приняло их или отвергло. Выяснить это и помогали Олимпийские игры!
Я думаю, греки представляли это так. Вообразим себе первый старт — в беге на один стадий. Первая четвёрка бегунов замерла на стартовой черте. Звучит команда — и бегуны устремляются вперёд. Все они — молодые, сильные, красивые, и они бегут грудь в грудь.
Первая четвёрка бегунов замерла на стартовой черте. Звучит команда — и бегуны устремляются вперёд. Все они — молодые, сильные, красивые, и они бегут грудь в грудь.
Но в это время где-то в священной роще находится невидимое божество, привлечённое вчерашними дарами. Греки были любознательным народом, и такими же любознательными и любопытными были и их боги. И вот, привлечённый красотой состязания, на стадионе незримо появляется сам Зевс. Он глядит на бегунов и думает: кто ему больше по душе? Вот он делает свой выбор и простирает над головой бегуна свою незримую длань. И тут — о чудо! — этот бегун вырывается вперёд так, как будто остальные его соперники стоят на месте, а ведь они тоже бегут изо всей силы. Финишная черта, победа!
А за победой приходит слава, которую так ценили древние греки. После бегуну поставят памятник, будут кормить целый год за общественный счёт. Ведь на нём остановился выбор божества, и его сограждане тоже были отмечены этим выбором. Но сначала победителя награждают венком из ветвей той самой оливы, которая растёт рядом с храмом.
А что же зрители, сидящие на трибунах олимпийского стадиона? Они, конечно, болеют за своих, кричат изо всей силы — но и участвуют в священнодействии: ведь они наблюдают за знаками, которые подаёт божество. Бегуны и открывающееся через них божество — это и есть теорема в исходном смысле этого слова; а зрители на трибунах — это теоретики, созерцатели божественных знаков. Впрочем, это высокое занятие не мешает им кричать и махать руками — разве мы сумеем постичь красоту состязаний, сидя на трибуне в молчании?
Но причём здесь геометрическая теорема? Чтобы ответить на этот вопрос, расскажем немного о Пифагоре и пифагорейцах, ведь, возможно, о геометрических теоремах впервые заговорили именно в их сообществе. До нас дошла легенда о том, что сам Пифагор в молодости был победителем олимпийских состязаний; а в зрелом возрасте он почти наверняка, и не раз, побывал в Олимпии зрителем.
«Говорят, что Пифагор первый стал называть себя философом, не только придумав новое слово, но и прекрасно разъясняя, что оно обозначает. Он говорил, что приход людей в жизнь подобен толпе на игрищах. Там суетятся разные люди, пришедшие каждый со своей целью (один стремится продать товар подороже, другой — добиться славы и показать телесную силу; но есть и третий вид людей, причём самый свободный, которые собираются ради зрелищ, прекрасных творений, благих деяний и речей, обычно представляемых на праздниках). Так и в жизни всевозможные люди собираются в одном месте, движимые различными интересами: одних обуревает жажда денег и роскоши, других привлекает власть, первенство, соперничество и честолюбие. Но самый чистый образ жизни у того, кто занимается созерцанием (θεωρiα) прекрасного, и он называется философским».
Будучи философом, Пифагор учит правильной, достойной жизни. Но какую роль в этой жизни играет геометрия? Почему именно пифагорейцы стали заниматься теоретической геометрией и сделали в ней ряд первых крупных открытий? И почему они удостоили свои открытия высокого звания теорем? Чтобы ответить на этот вопрос, давайте рассмотрим какую-нибудь из теорем, открытых пифагорейцами. Можно взять знаменитую теорему Пифагора; но я предпочитаю свой любимый пример.
Можно взять знаменитую теорему Пифагора; но я предпочитаю свой любимый пример.
Для начала начертим произвольный параллелограмм и проведём в нём диагональ. Далее, поставим точку в произвольном месте на этой диагонали. Затем проведём через эту точку два отрезка, соединяющие противоположные стороны параллелограмма: один отрезок параллельно одной паре сторон параллелограмма, другой — параллельно другой паре сторон. Наконец, закрасим два внутренних параллелограмма, лежащих по разные стороны от диагонали. Доказанная пифагорейцами теорема утверждает, что эти параллелограммы имеют равную площадь.
Чтобы установить истинность теоремы, простого взгляда на чертёж отнюдь не достаточно! Один параллелограмм у нас более широкий, зато менее высокий; возможно, эта разница в размерах и приводит к равенству площадей, но само это равенство не очевидно; оно скрывается от нашего глаза.
Но посмотрим на чертёж, подключив ещё и свой ум. Мы видим большой параллелограмм, разделённый диагональю на два треугольника. Эти треугольники очевидно одинаковы, а значит, равны и по площади. Далее, есть два меньших незакрашенных параллелограмма, также разделённые диагональю пополам; и их частями опять будут равные треугольники. А теперь смотрите: мы берём большие треугольники и отнимаем от них малые треугольники, сначала из одной пары, а потом из другой. Но если от равных величин отнять равные, то и остатки будут равны. А остатки у нас — это закрашенные параллелограммы; вот мы и доказали, что они равны по площади.
Эти треугольники очевидно одинаковы, а значит, равны и по площади. Далее, есть два меньших незакрашенных параллелограмма, также разделённые диагональю пополам; и их частями опять будут равные треугольники. А теперь смотрите: мы берём большие треугольники и отнимаем от них малые треугольники, сначала из одной пары, а потом из другой. Но если от равных величин отнять равные, то и остатки будут равны. А остатки у нас — это закрашенные параллелограммы; вот мы и доказали, что они равны по площади.
Равенство площадей сперва было скрыто от нас, а потом на помощь зрению пришёл ум, они соединились в умозрении, и равенство стало явным, теперь мы отчётливо видим его и понимаем, откуда оно возникает. Надо думать, именно эта аналогия с подающим знаки скрытым божеством заставила Пифагора считать свои открытия божественными; ведь по преданию, за открытие одной из своих теорем он принёс в жертву богам сто быков (хотя другое предание говорит, что Пифагор проповедовал отказ от животной пищи и приносил в жертву фигурки быков, изготовленные из медового теста).
Удивительное свойство открытых Пифагором теорем состоит ещё и в другом. Мы рассматривали на чертеже конкретный параллелограмм, но полученное знание относится не только к нему, но и ко всем параллелограммам сразу. Выходит, наш ум способен охватить в единой теории бесконечное множество размеров и пропорций, подведя их под общее понятие, а такая способность ума несомненно является даром богов. Прокл, один из последних античных философов, живший через тысячу лет после Пифагора, сказал об этом так: «Пифагор преобразовал занятия геометрией в форму свободного образования, изучая сами её начала отвлечённо от материи и умозрительно». Такую свободу надо ценить в себе и развивать, и поэтому изучение геометрии со времён Пифагора навсегда стало важнейшей частью образования, и люди ценят её в первую очередь не за «пользу», которую геометрические знания приносят, а за то совершенствование человеческой души, к которому приводит геометрия, если ей заниматься правильно.
Всякому, кто хочет больше узнать о древних Олимпийских играх и о Пифагоре, я рекомендую несколько книг: Ян Парандовский «Олимпийский диск»; А. В. Волошинов «Пифагор. Союз истины, добра и красоты»; М. Л. Гаспаров «Занимательная Греция».
В. Волошинов «Пифагор. Союз истины, добра и красоты»; М. Л. Гаспаров «Занимательная Греция».
Художник Алексей Вайнер
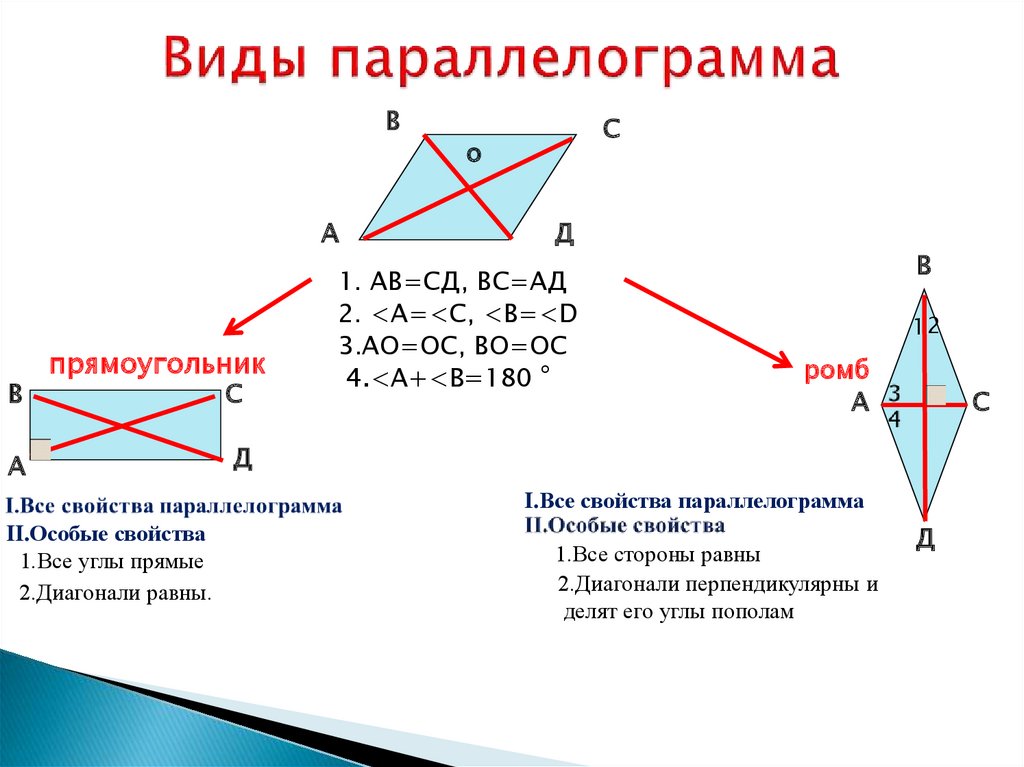
Содержание | Введение | Дом П л а н е Геометрия Приключение в языке и логике на основе Предложение 33 Предложение 34 МЫ ДЕЛАЕМ НАШ окончательный подход к теореме Пифагора. Но сначала мы должны установить, когда числа, которые не конгруэнтны, будут равны. Для этого рассмотрим четырехугольники, у которых противоположные стороны параллельны. Такая фигура называется параллелограммом. (Определение 15.) Следующее предложение эффективно показывает, что такая фигура существует.
Предложение доказывает, что если две стороны четырехугольника равны и параллельны , то фигура это параллелограмм. (Определение 14.) Следовательно, мы можем построить параллелограмм; ибо предложение 31 показывает, как построить прямую линию, параллельную данной прямой. Следующая теорема имеет своей гипотезой, что фигура является параллелограммом, то есть противоположные стороны параллельны. Эта теорема будет фундаментальной для теории равных площадей. На самом деле, как мы неоднократно указывали, когда мы говорим, что две фигуры «равны», мы имеем в виду, что они равны по площади. См. задачи 1 и 2 после предложения 4. Учащийся должен посмотреть на рисунок ниже, и, учитывая, что это параллелограмм, должно быть ясно, почему эти два треугольника равны. Почему? С.А.С.
Пожалуйста, «переверните» страницу и сделайте несколько Задач. или Перейдите к следующему предложению. Предыдущее предложение Содержание | Введение | Дом Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн. Copyright © 2021 Лоуренс Спектор Вопросы или комментарии? Электронная почта: [email protected] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Параллелограммные дизайны, темы, шаблоны и загружаемые графические элементы на Dribbble
Посмотреть складку флага
Складной флаг
Посмотреть Акита Эдж
Акита Эдж
Посмотреть полушеврон Акита
Полушеврон Акита
Просмотр движущихся баз
Подвижные базы
Просмотр KMRE 102.
 3FM
3FMКМРЭ 102.3FM
Посмотреть параллелограмм космического тона
Параллелограмм космических тонов
- 904:30
Посмотреть портфолио 2020 — Заголовок и навигация
Портфолио 2020 — Заголовок и навигация
Посмотреть параллелограмм
Параллелограмм
Посмотреть параллелограмм
Параллелограмм
Просмотр воздушных змеев (реприза).

Воздушные змеи (реприза).
Просмотр геометрического градиента Wipe 3 Действия
Геометрическое градиентное вытеснение 3 действия
Просмотр всегда привлекателен
Всегда привлекательный
Посмотреть синий сэндвич
Синий сэндвич
- 904:30
Посмотреть концепцию портфолио
Концепция портфеля
Посмотреть Год Обезьяны Параллелограмм
Год Обезьяны Параллелограмм
Посмотреть Изготовление выкройки
Изготовление моделей
Посмотреть параллелограф
Параллелограмм
Посмотреть выращивание с теплицей
Выращивание в теплице
Просмотр стационарных
Стационарный
Просмотр параллелограммов
Параллелограммы
- 904:30
Посмотреть Handy камуфляж Parallelogram
Handy камуфляж Parallelogram
Посмотреть надпись SXSW
Надпись SXSW
Просмотр параллелограммов
Параллелограммы
Вид четырехугольника нет.


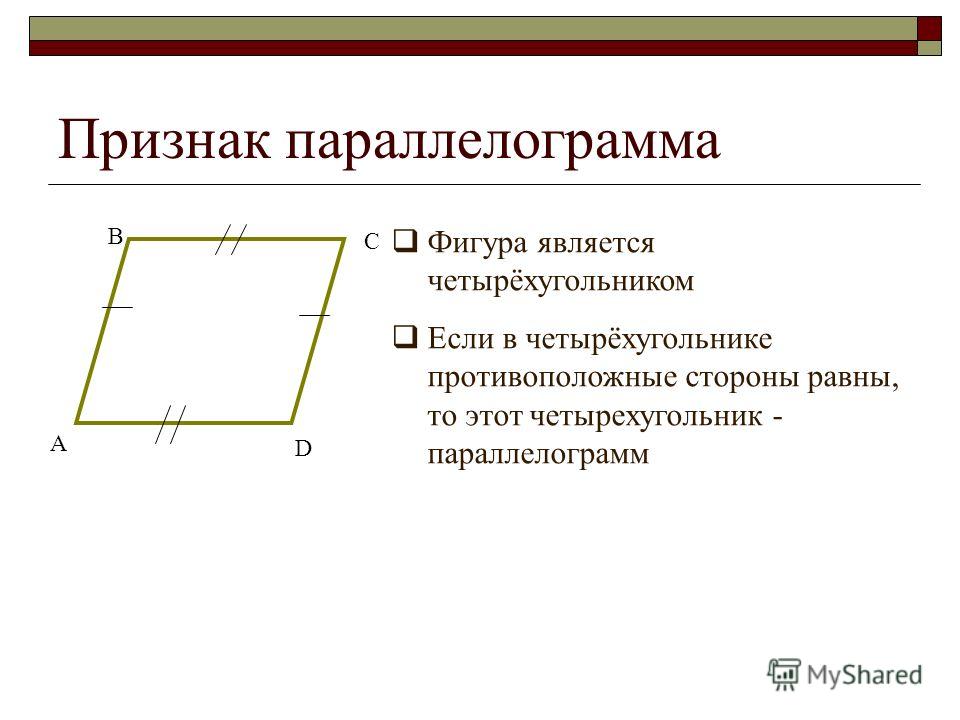
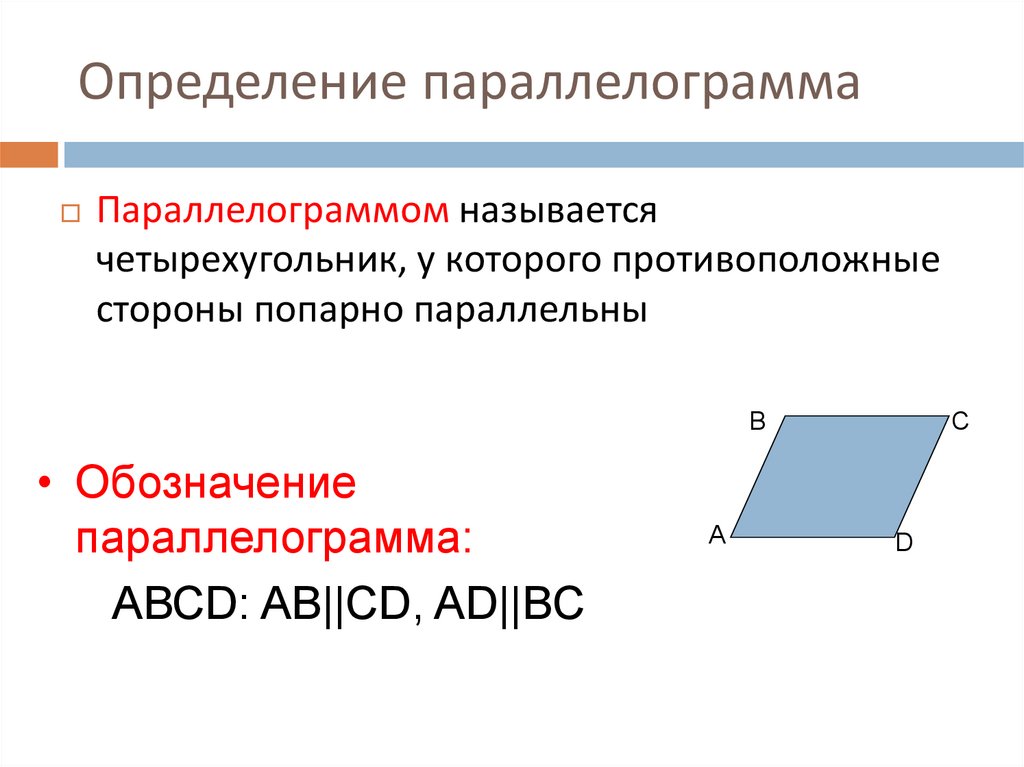 И это доказывает очевидное для глаза: противоположные стороны равны.
И это доказывает очевидное для глаза: противоположные стороны равны. 29)
29)
 д. К.Э.Д.
д. К.Э.Д.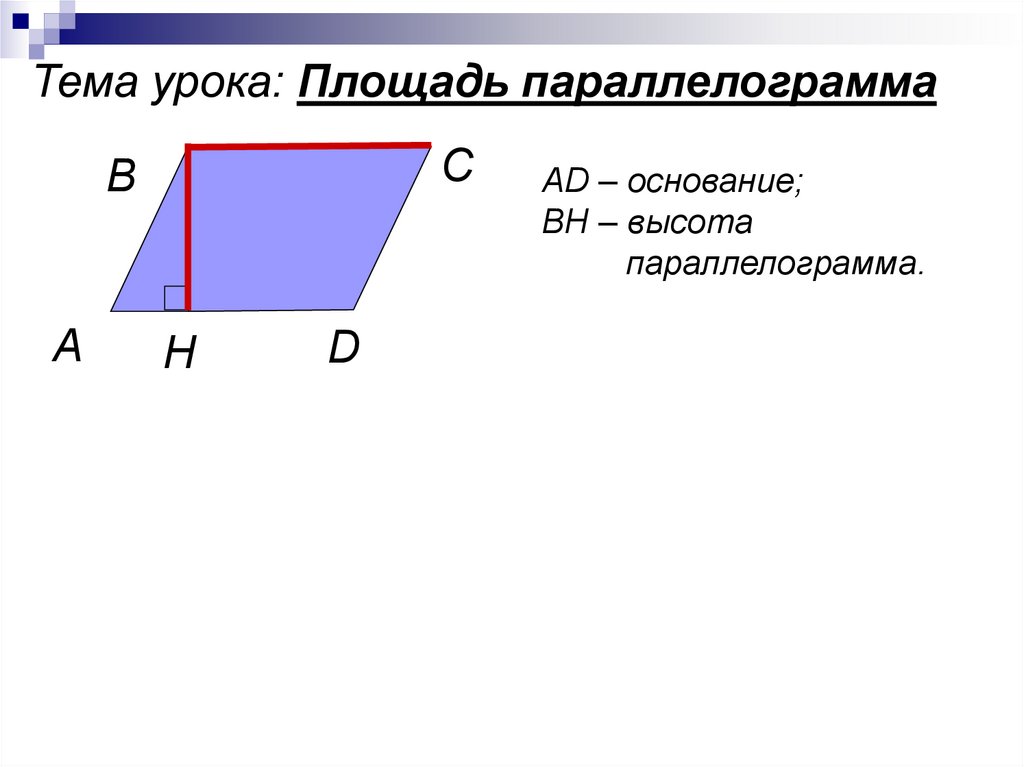 3FM
3FM