Опыт Юнга. Расчет интерференционной картины от двухисточников. Расстояние между полосами.
Главная
» Самолетостроение
» Физика (3 семестр)
» Опыт Юнга. Расчет интерференционной картины от двухисточников. Расстояние между полосами.
Первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга свет от источника, в качестве которого служила узкая щель S, падал на экран с двумя близко расположенными щелями S1 и S2 (рис. 3.7.3). Проходя через каждую из щелей, световой пучок уширялся вследствие дифракции, поэтому на белом экране Э световые пучки, прошедшие через щели S В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
| Рисунок 3.7.3. Схема интерференционного опыта Юнга |
Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Поэтому в его опыте щели S1 и S2, которые в соответствии с принципом Гюйгенса можно рассматривать как источники вторичных волн, освещались светом одного источника S. При симметричном расположении щелей вторичные волны, испускаемые источниками S1 и S2, находятся в фазе, но эти волны проходят до точки наблюдения P разные расстояния r1и r2. Следовательно, фазы колебаний, создаваемых волнами от источников S 1 и S2 в точке P, вообще говоря, различны. Таким образом, задача об интерференции волн сводится к задаче о сложении колебаний одной и той же частоты, но с разными фазами. Утверждение о том, что волны от источников S1 и S2распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.
Утверждение о том, что волны от источников S1 и S2распространяются независимо друг от друга, а в точке наблюдения они просто складываются, является опытным фактом и носит название принципа суперпозиции.
Монохроматическая (или синусоидальная) волна, распространяющаяся в направлении радиус-вектора , записывается в виде
| E = a cos (ωt – kr), |
где a – амплитуда волны, k = 2π / λ – волновое число, λ – длина волны, ω = 2πν – круговая частота. В оптических задачах под E следует понимать модуль вектора напряженности электрического поля волны. При сложении двух волн в точке P результирующее колебание также происходит на частоте ω и имеет некоторую амплитуду A и фазу φ:
E = a1 · cos (ωt – kr1) + a2 · cos (ωt – kr2) = A · cos (ωt – φ). |
Приборов, которые способны были бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существует; наблюдаемой величиной является поток энергии, который прямо пропорционален квадрату амплитуды электрического поля волны. Физическую величину, равную квадрату амплитуды электрического поля волны, принято называть интенсивностью: I = A2.
Несложные тригонометрические преобразования приводят к следующему выражению для интенсивности результирующего колебания в точке P:
| (*) |
где Δ = r2 – r1 – так называемая разность хода.
Из этого выражения следует, что интерференционный максимум (светлая полоса) достигается в тех точках пространства, в которых Δ = mλ (m = 0, ±1, ±2, .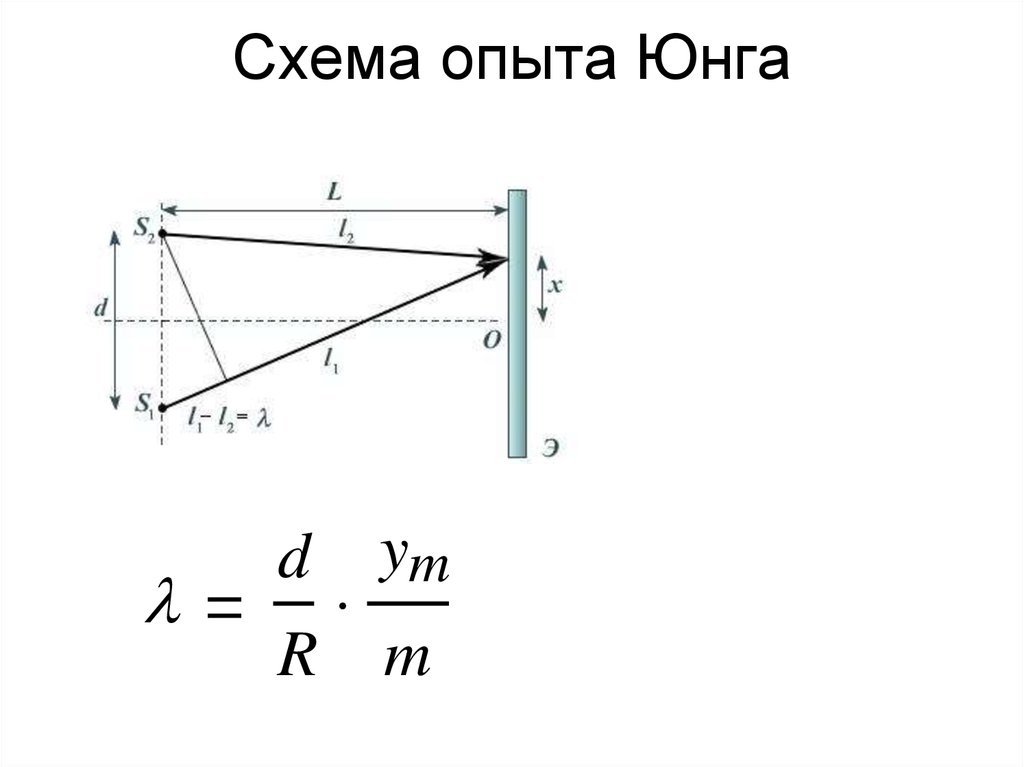 ..). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивностиImin = (a1 – a2)2 < I1 + I2
..). При этом Imax = (a1 + a2)2 > I1 + I2. Интерференционный минимум (темная полоса) достигается при Δ = mλ + λ / 2. Минимальное значение интенсивностиImin = (a1 – a2)2 < I1 + I2
| Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – порядок интерференционного максимума |
В частности, если I1 = I2 = I0, т. е. интенсивности обеих интерферирующих волн одинаковы, выражение (*) приобретает вид:
| (**) |
В этом случае Imax = 4I 0, Imin = 0.
Формулы (*) и (**) являются универсальными. Они применимы к любой интерференционной схеме, в которой происходит сложение двух монохроматических волн одной и той же частоты.
Если в схеме Юнга через y обозначить смещение точки наблюдения от плоскости симметрии, то для случая, когда d << L и y << L (в оптических экспериментах эти условия обычно выполняются), можно приближенно получить:
При смещении вдоль координатной оси y на расстояние, равное ширине интерференционной полосы Δl, т. е. при смещении из одного интерференционного максимума в соседний, разность хода Δ изменяется на одну длину волны λ. Следовательно,
где ψ – угол схождения «лучей» в точке наблюдения P.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Физика для углубленного изучения. 2. Электродинамика. Оптика
Физика для углубленного изучения. 2. Электродинамика. Оптика
ОглавлениеВведениеI. ЭЛЕКТРОСТАТИКА § 1. Электрический заряд. Закон Кулона § 3. Теорема Гаусса § 4. Потенциал электростатического поля. Энергия системы зарядов § 5. Расчет электрических полей § 6. 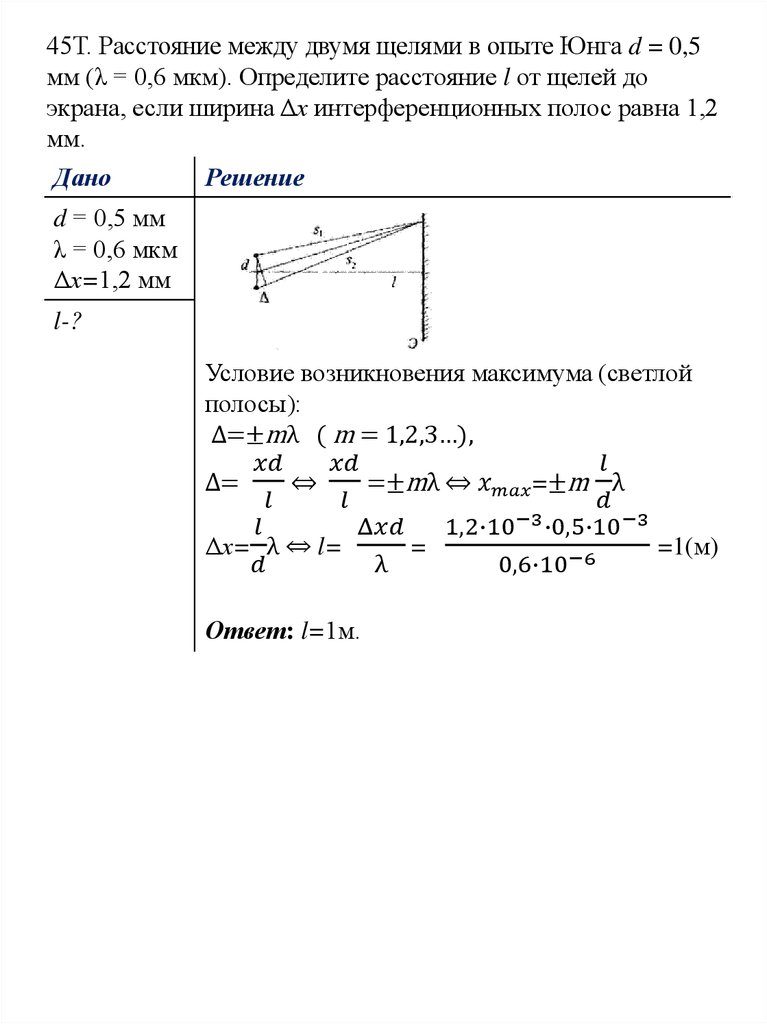 Проводники в электрическом поле Проводники в электрическом поле§ 7. Силы в электростатическом поле § 8. Конденсаторы. Электроемкость § 9. Энергия электрического поля II. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 10. Характеристики электрического тока. Закон Ома § 11. Соединение проводников в электрические цепи § 12. Закон Ома для неоднородной цепи § 13. Расчет цепей постоянного тока § 14. Работа и мощность постоянного тока § 15. Магнитное поле постоянного тока § 16. Действие магнитного поля на движущиеся заряды III. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 17. Явление электромагнитной индукции § 18. Электрические машины постоянного тока § 19. Энергия магнитного поля § 20. Основы теории электромагнитного поля § 21. Квазистационарные явления в электрических цепях IV. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 22. Цепи переменного тока. Закон Ома § 23. Работа и мощность переменного тока. Передача электроэнергии § 24. Трехфазный ток. Электрические машины переменного тока V.  ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ§ 25. Колебательный контур § 26. Вынужденные колебания в контуре. Резонанс § 27. Незатухающие электромагнитные колебания § 28. Электромагнитные волны § 29. Свойства и применения электромагнитных волн VI. ОПТИКА § 30. Свет как электромагнитные волны. Интерференция § 31. Дифракция света § 32. Спектральные приборы. Дифракционная решетка § 33. Протяженные источники света § 34. Интерференция немонохроматического света § 35. Физические принципы голографии § 36. Геометрическая оптика |
В опыте Юнга с двумя щелями получают полосы на экране, расположенном на определенном расстоянии от щелей. Если экран сдвинуть на 5 см в сторону щели, ширина полосы изменится на 30 мкм. Учитывая, что щели находятся на расстоянии 1 мм друг от друга. Вычислите длину волны красного света.
Обновлено: 27-06-2022
Текст Решение
Решение
Здесь d=1мм=1×10-3м, изменение расстояния экрана от щелей ΔD=5см=5×10-2м
изменение ширины полосы Δβ=мкм=30×10−6м.
Из соотношения β=λDd имеем Δβ=λΔDd
⇒λ=dΔβΔD=(1×10−3)×(30×10−6)(5×10−2)=6×10−7m=600 нм
U-LIKE СЕРИЯ-ВОЛНОВАЯ ОПТИКА-КОРОТКИЕ ОТВЕТЫ НА ВОПРОСЫ
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro and dekho sari videos бина киси ад ки рукаават ке!
Похожие видео
В эксперименте Юнга с двумя щелями две щели на расстоянии 0,15 мм друг от друга освещаются светом с длиной волны 450 нм. Экран находится на расстоянии 1,0 м от щелей. Найдите расстояние от центрального максимума до второй яркой и второй темной полос. Как изменится рисунок полос, если экран отодвинуть от щелей?
12014479
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 1 мм, между щелью и экраном — 1 метр, а 10-я полоса находится на расстоянии 5 мм от центральной яркой полосы, тогда длина волны используемого света будет
16267102
В эксперименте Юнга с двумя щелями используется красный свет с длиной волны 620 нм, а расстояние между двумя щелями составляет 0,3 мм. Интерференционные полосы наблюдаются на экране на расстоянии 1,3 мм друг от друга. Вычислите (i) расстояние щелей от экрана и (ii) ширину полосы, если это расстояние увеличить вдвое.
Интерференционные полосы наблюдаются на экране на расстоянии 1,3 мм друг от друга. Вычислите (i) расстояние щелей от экрана и (ii) ширину полосы, если это расстояние увеличить вдвое.
17960020
В двухщелевом эксперименте Юнга с монохромным светом на экране, расположенном на некотором расстоянии от плоскости щелей, получаются полосы. Если экран переместить на 5 см в сторону щелей, то изменение ширины полос составит 30 мкм, если расстояние между щелями 1 мм, то рассчитайте длину волны используемого света.
31093554
Если две щели в эксперименте Юнга находятся на расстоянии 0,4 мм друг от друга, а ширина полос на экране на расстоянии 200 см составляет 2 мм, то длина волны света, освещающего щели, равна
31093845
Две щели в эксперименте Юнга с двойными щелями расположены на расстоянии 0,1 миллиметра друг от друга. Если ширина полосы получается равной 5 мм на экране в 1,5 м от щелей. Найдите длину волны используемого света.
74385142
В двухщелевом опыте Юнга с монохроматическим светом интерференционные полосы получаются на экране, расположенном на некотором расстоянии от щелей. При перемещении экрана на 5×10-2 м в сторону щели изменение ширины полосы составит 3×10-5 м. При расстоянии между щелями 10-3 м используемая длина волны
При перемещении экрана на 5×10-2 м в сторону щели изменение ширины полосы составит 3×10-5 м. При расстоянии между щелями 10-3 м используемая длина волны
127272595
В эксперименте Юнга с двумя щелями щели на расстоянии 3 мм освещаются источником монохроматического света с длиной волны 6000 Å. Интерференционные полосы получаются на экране на расстоянии 1 м от щелей. Ширина полосы будет
127272706
В двойном опыте расстояние между щелями 1 мм и экраном на расстоянии 25 см от щелей. Длина волны света составляет 6000Å. Ширина полосы на экране
141173930
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 1 мм, а расстояние между щелью и экраном — 1 метр. Если 10-я яркая полоса находится на расстоянии 5 мм от центральной яркой полосы, то используемая длина волны света будет
531857853
Text Solution
В эксперименте Юнга с двумя щелями на экране, находящемся на определенном расстоянии, появляются полосы определенной ширины.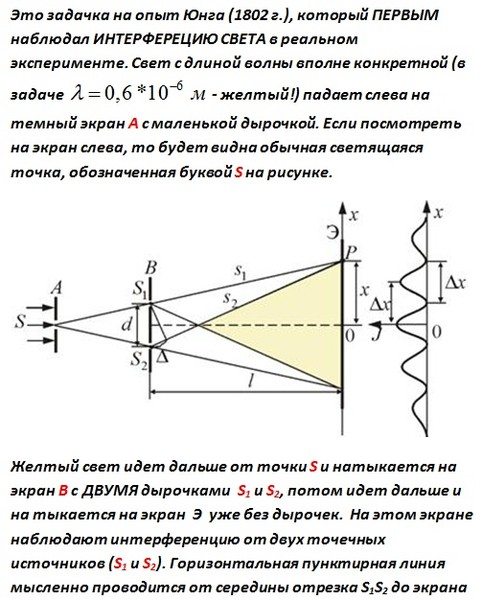 из щелей. При удалении экрана от щелей на 0,1 м ширина полос увеличивается на 6×10–5 м. Расстояние между щелями 1 мм. рассчитать длину волны используемого света.
из щелей. При удалении экрана от щелей на 0,1 м ширина полос увеличивается на 6×10–5 м. Расстояние между щелями 1 мм. рассчитать длину волны используемого света.
557953130
В эксперименте Юнга с двумя щелями на экране, находящемся на определенном расстоянии от щелей, появляются полосы определенной ширины. При удалении экрана от щелей на 0,1 м ширина полос увеличивается на 6×10–5 м. Расстояние между щелями 1 мм. рассчитать длину волны используемого света.
573864087
В эксперименте Юнга с двумя щелями две щели на расстоянии 0,15 мм друг от друга освещаются светом с длиной волны 450 нм. Экран находится на расстоянии 1,0 м от щелей. Найдите расстояние от центрального максимума до второй яркой и второй темной полос. Как изменится рисунок полос, если экран отодвинуть от щелей?
642521229
В двухщелевом эксперименте Юнга с монохромным светом на экране, расположенном на некотором расстоянии от плоскости щелей, получаются полосы. Если экран переместить на 5 см в сторону щелей, то изменение ширины полос составит 30 мкм, если расстояние между щелями 1 мм, то рассчитайте длину волны используемого света.
643196832
Если две щели в эксперименте Юнга находятся на расстоянии 0,4 мм друг от друга, а ширина полос на экране на расстоянии 200 см составляет 2 мм, то длина волны света, освещающего щели, равна
643197028
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 0,3 мм, а экран находится на расстоянии 1,5 м. Вторая яркая полоса оказывается смещенной на 6 мм от центральной полосы. Длина волны света (в нм), используемого в эксперименте, составляет
. Обновлено: 27 июня 2022 г.
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
В эксперименте Юнга с двумя щелями две щели на расстоянии 0,15 мм друг от друга освещаются светом с длиной волны 450 нм. Экран находится на расстоянии 1,0 м от щелей. Найдите расстояние от центрального максимума до второй яркой и второй темной полос.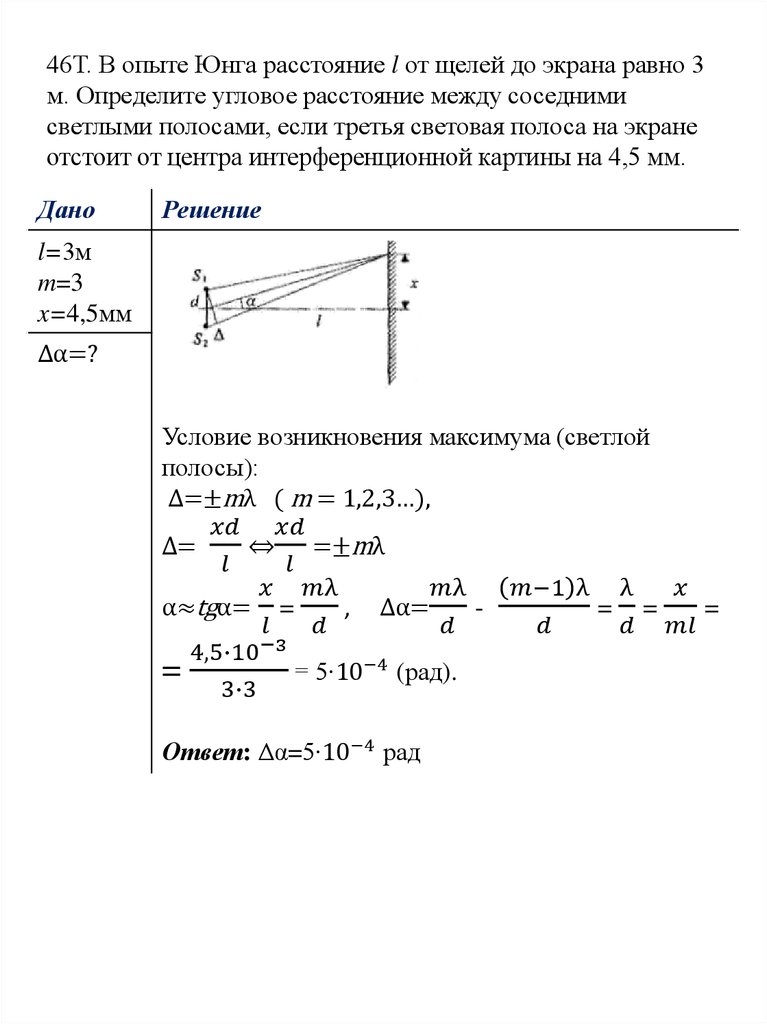 Как изменится рисунок полос, если экран отодвинуть от щелей?
Как изменится рисунок полос, если экран отодвинуть от щелей?
12014479
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 0,2 мм, а расстояние до экрана составляет 1,5 м. Замечено, что расстояние между центральной светлой полосой и четвертой темной полосой составляет 1,8 см. Рассчитайте длину волны используемого света.
12015170
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 1 мм, между щелью и экраном — 1 метр, а 10-я полоса находится на расстоянии 5 мм от центральной яркой полосы, тогда длина волны используемого света будет
16267102
(a) В эксперименте Юнга с двумя щелями монохроматический источник света S находится на равном расстоянии от щелей S1 и S2. Объясните информацию о темных и светлых полосах на экране.
(b) Пучок света, состоящий из двух длин волн, 650 нм и 520 нм, используется для получения интерференционных полос в двухщелевом эксперименте Юнга.
(i) Найдите расстояние третьей яркой полосы на экране от центрального максимума для длин волн 650 нм.
(ii) На каком наименьшем расстоянии от центрального максимума совпадают яркие полосы, обусловленные обеими длинами волн?
Дано: Расстояние между щелями 4 мм, расстояние между экраном и плоскостью щелей 1,2 м.
56435594
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 0,28 мм, а экран расположен на расстоянии 1,4 м. Расстояние между центральной яркой полосой и четвертой яркой полосой составляет 1,2 см. Определите длину волны света, использованного в эксперименте.
113075420
Интерференционные полосы получены в эксперименте Юнга с двумя щелями с использованием пучка света, состоящего из двух длин волн 500 нм и 600 нм. Яркие полосы обеих длин волн совпадают на расстоянии 2,5 мм от центрального максимума. Если расстояние между щелями 3 мм, то расстояние между экраном и плоскостью щелей равно
233091291
В эксперименте Юнга с двумя щелями щели разнесены на 0,28 мм, а экран расположен на расстоянии 1,4 мм. Расстояние между центральной светлой каймой и четвертой светлой каймой измерено как 1,2 см. определить длину волны света, используемого в эксперименте.
определить длину волны света, используемого в эксперименте.
531857684
Текст Решение
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 1 мм, а расстояние между щелью и экраном — 1 метр. Если 10-я яркая полоса находится на расстоянии 5 мм от центральной яркой полосы, то используемая длина волны света будет равна
531857853
Text Solution
Луч света, состоящий из двух длин волн 500 нм и 400 нм, используется для получения интерференционных полос в эксперименте Юнга с двумя щелями. Расстояние между щелями 0,3 мм, расстояние между щелями и экраном 1,5 м. Вычислите наименьшее расстояние точки от центрального максимума, где яркие полосы, обусловленные обеими длинами волн, совпадают.
573864084
В эксперименте Юнга с двумя щелями две щели на расстоянии 0,15 мм друг от друга освещаются светом с длиной волны 450 нм. Экран находится на расстоянии 1,0 м от щелей. Найдите расстояние от центрального максимума до второй яркой и второй темной полос. Как изменится рисунок полос, если экран отодвинуть от щелей?
Как изменится рисунок полос, если экран отодвинуть от щелей?
642521229
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 0,03 см, а экран расположен на расстоянии 1,5 м. Расстояние между центральной каймой и четвертой светлой каймой равно 1 см. Определите длину волны света, использованного в эксперименте.
642692293
В двухщелевом опыте Юнга расстояние между щелями 0,5 мм и интерференция наблюдается на экране на расстоянии 100 см от щелей. Установлено, что девятая яркая полоса находится на расстоянии 7,5 мм от второй темной бахромы от центра рисунка бахромы. Длина волны используемого света в нм составляет
642750741
В эксперименте Юнга с двумя щелями расстояние между щелями составляет 0,56 мм, а экран находится на расстоянии 2,8 м. Расстояние между центральной светлой каймой и пятой светлой каймой 1,5 см. Найдите длину волны используемого света.
642764893
В эксперименте Юнга расстояние между щелями составляет 0,28 мм.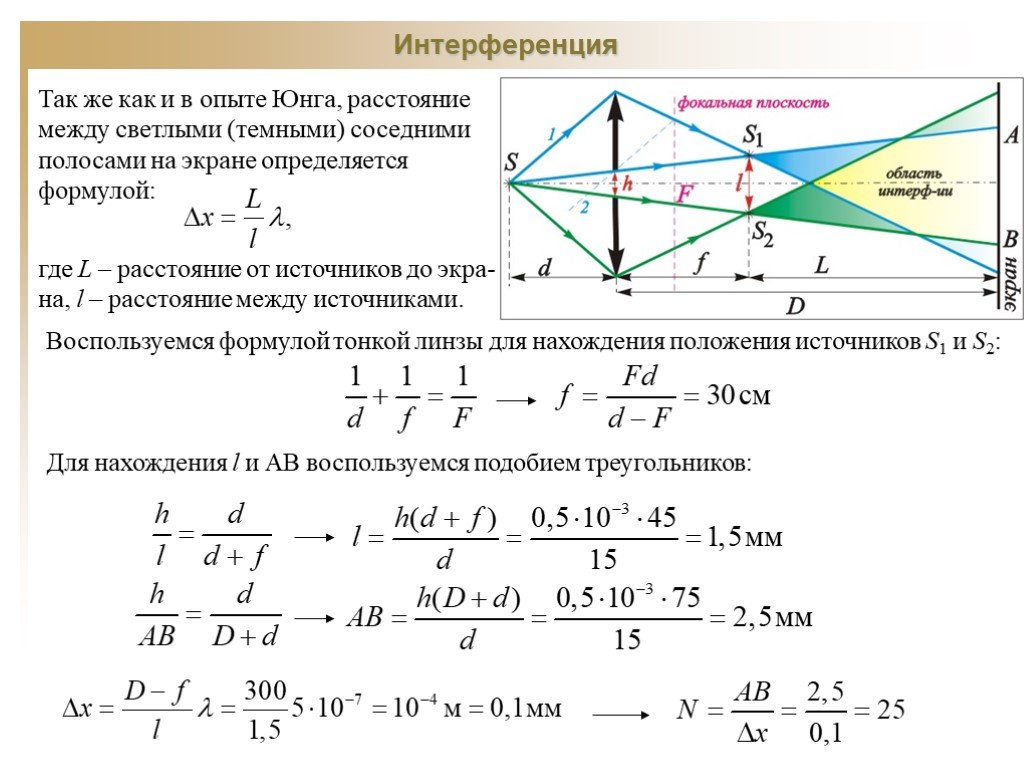


 Том 2. М.: Физматлит. — 336 с.
Том 2. М.: Физматлит. — 336 с.