Excel метод наименьших квадратов: Метод Наименьших Квадратов в EXCEL. Примеры и описание

alexxlab / / Разное

Метод наименьших квадратов в Excel

Перейти к содержанию

Search for:

Главная » Уроки MS Excel

Автор Елизавета КМ На чтение 5 мин Опубликовано

Табличный процессор Эксель способен реализовывать большое число математических операций. Из статьи вы узнаете, как используется метод наименьших квадратов, который применяется для осуществления решения разнообразных задач.

Содержание

  1. Первоначальные настройки: включение параметра «Поиск решения»
  2. Что такое метод наименьших квадратов
  3. Шаг первый: исходные данные решаемой задачи
  4. Шаг второй: решение задачки с использованием МНК
  5. Заключение

Первоначальные настройки: включение параметра «Поиск решения»

Изначально необходимо включить «Поиск решения», так как по умолчанию он находится в выключенном состоянии. Пошаговое руководство выглядит следующим образом:

  1. Переходим в раздел «Файл», который находится в левом верхнем углу интерфейса табличного процессора.
1
  1. На экране отобразилось новое окошко. Здесь, в левой колонке, необходимо кликнуть на элемент «Параметры».
2
  1. В появившемся окне выбираем раздел «Надстройки». В правой части окошка находим надпись «Управление:» и раскрываем список. В списке выбираем пункт «Надстройки Excel». Щёлкаем кнопку «ОК».
3
  1. Появилось еще одно окошко с названием «Надстройки». Около элемента «Поиск решения» ставим галочку. После проведения всех манипуляций кликаем «ОК».
4
  1. Готово! Параметр включился, и теперь мы можем приступить к разбору метода наименьших квадратов.

Что такое метод наименьших квадратов

Для начала вспомним, что метод наименьших квадратов — математический метод, используемый для решения задач, основанный на минимизации суммы квадратов отклонений некоторых функций от изначальных значений.

Он может применяться для «решения» переопределенных систем уравнений (когда число уравнений больше числа неизвестных), для поиска решения в случае стандартных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.

Шаг первый: исходные данные решаемой задачи

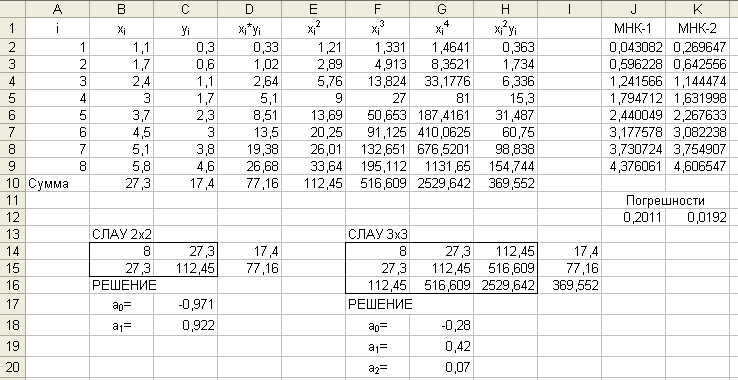
На конкретном примере начнем разбор метода наименьших квадратов. К примеру, у нас есть 2 колонки – X и Y:

5

Эта зависимость описывается уравнением: Y=A+NX.

Мы прекрасно знаем, что если Х равен нулю, то и Y равен нулю. Следовательно, это уравнение можно привести к следующему виду: Y=NX. Начнём реализацию этой задачи. Нам нужно найти сумму квадратов разности.

Шаг второй: решение задачки с использованием МНК

Пошаговое руководство выглядит следующим образом:

  1. Столбику, который располагается левее показателя Х, даем название N и прописываем единицу рядом с 1-м показателем колонки Х. Единица – это примерное значение 1-го коэффициента N.
6
  1. Столбику, который располагается правее показателя Y, даем наименование NX.
  2. В ячейку D1, находящуюся около первых показателей X и Y, прописываем специальную формулу произведения коэффициента N на показатель из столбика Х. Сама формула выглядит следующим образом: =$А$2*В2. Стоит заметить, что адрес ячейки с коэффициентом необходимо привести к абсолютному типу. Абсолютный тип в табличном процессоре позволяет зафиксировать строчку или столбик (или все вместе одновременно). Иными словами, при копировании значений в другие ячейки абсолютные ссылки не будут меняться. После проведения всех манипуляций жмем клавишу «Enter».
7
  1. Перемещаем курсор мышки на сектор с выведенным результатом. Наведя указатель в правый верхний уголок, он превратится в маленький плюсик темного цвета, который называется маркером заполнения. Зажимаем ЛКМ и перетягиваем маркер в самый низ до крайней строчки табличных данных.
8
  1. После проведения этих манипуляций мы получили результаты вычислений во всех секторах колонки NX.
9
  1. Далее переходим к подсчету суммы разностей квадратов показателей Y и NX. Перемещаемся в ячейку E1, располагающуюся правее от показателя NX, нажимаем на элемент «Вставить функцию», который находится рядом со строкой для ввода формул, и имеет внешний вид «fx».
10
  1. Первым делом, находим надпись «Категории:» и раскрываем список, находящийся рядом. В обширном списке выбираем элемент «Математические». В блоке «Выберите функцию:» отыскиваем функцию «СУММКВРАЗН» и выбираем ее. После проведения всех манипуляций жмем на кнопку «ОК».
11
  1. Открылось небольшое окошко «Аргументы функции». Для дальнейшей работы необходимо заполнить все строки формы. В строчку «Массив_х» вводим адрес диапазона ячеек столбика Y. Координаты можно вписать самостоятельно ручным вводом, используя клавиатуру, или же путем их выбора в самих табличных данных.
  2. В строчку «Массив_у» вводим адрес диапазона ячеек столбика NX. После проведения всех манипуляций щёлкаем клавишу «Enter».
12
  1. Перемещаемся в раздел «Данные», который находится в верхней части интерфейса табличного процессора. Находим блок команд под названием «Анализ» и выбираем элемент «Поиск решения».
13
  1. На экране отобразилось окошко с огромным количеством настроек, которые необходимо заполнить. В строчку «Оптимизировать целевую функцию» вводим ссылку на ячейку с оператором «СУММКВРАЗН». Реализовать это действие можно самостоятельно ручным вводом, используя клавиатуру, или же выбрав сектор в самой табличке. Ставим отметку около надписи «Минимум», которая располагается в блоке «До:». В строчку «Изменяя ячейки переменных» вбиваем адрес сектора, в котором располагается показатель коэффициента N –
    $    A$2. После проведения всех манипуляций щелкаем на «Найти решение».
14
  1. После того, как «Поиск решения» будет выполнен, на экране компьютера отобразится окошко с выведенными результатами поиска решения, а затем реализуется замена числовых значений в столбике N. Отображенный результат – это наименьший квадрат функции. Если выведенный результат удовлетворяет тому, что нужно было найти, то нажимаем «ОК».
15

Заключение

Таким образом, мы на конкретном примере рассмотрели способ использования метода наименьших квадратов в табличном процессоре Microsoft Excel и ознакомились со стандартным алгоритмом действий при решении похожих задач.

Оцените качество статьи. Нам важно ваше мнение:

Excel задачи метод наименьших квадратов МНК формулы Эксель

Adblock
detector

Применение метода наименьших квадратов в Excel: пример

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Уроки Excel Метод наименьших квадратов в Excel

Программа Excel – мощный табличный редактор, позволяющий выполнять огромное количество различных операций и задач.

В данной статье мы разберем, как можно применить метод наименьших квадратов (МНК), который используется для решения различных задач с минимизацией суммы квадратов отклонений некоторых функций от искомых переменных.

Содержание

  • Подготовительный этап: активируем надстройку “Поиск Решения”
  • Этап 1: исходные данные
  • Этап 2: решаем задачу с применением МНК
  • Заключение

Подготовительный этап: активируем надстройку “Поиск Решения”

Прежде, чем приступить к решению основной задачи, потребуется активировать надстройку “Поиск решения” в программе.

  1. Идем в меню “Файл”.
  2. В перечне слева выбираем пункт “Параметры”.
  3. В правой части подраздела “Надстройки” выбираем для параметра “Управление” вариант “Надстройки Excel” и жмем “Перейти”.
  4. Появится окно для выбора нужных надстроек. Устанавливаем галочку напротив пункта “Поиск решения”
    и щелкаем OK.

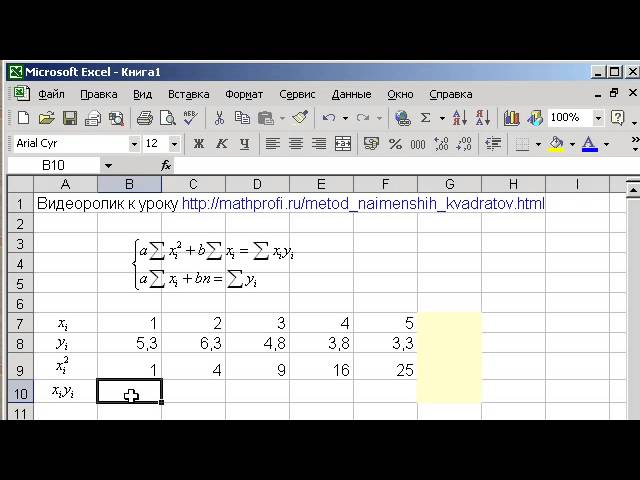
Этап 1: исходные данные

Давайте разберем применение метода наименьших квадратов, решив конкретный пример. Допустим, у нас есть два ряда числовых значений – X и Y.

Данная зависимость может быть описана уравнением ниже:

Y=A+NX

Также, мы знаем, что если X=0, то и Y=0. А значит, данное уравнение можно записать так:

Y=NX

Приступим к выполнению нашей задачи, которая заключается в нахождении суммы квадратов разности.

Этап 2: решаем задачу с применением МНК

  1. Столбцу, находящемся слева от X, задаем имя N пишем число “1” (примерное значение первого коэф. N) напротив первого значения ряда X.
  2. Столбцу с правой стороны от Y задаем название NX. Затем в самой верхней ячейке (напротив первых значений рядов X и Y) пишем формулу произведения коэф. N на соответствующее ему значение из столбца X. При этом адрес ячейки с коэффициентом нужно сделать абсолютным, чтобы он не менялся при копировании формулы. По готовности жмем Enter.
  3. Наводим указатель мыши на ячейку с полученным результатом. Как только появится черный плюсик (маркер заполнения), зажав левую кнопку мыши тянем его вниз до последней строки таблицы.
  4. Получаем результаты расчетов в каждой ячейке столбца NX.
  5. Теперь нужно посчитать сумму разностей квадратов значений Y и NX. Встаем в самую верхнюю ячейку столбца справа от NX (не считая шапки таблицы) и щелкаем по значку “Вставить функцию” (fx).
  6. В окне вставки функции выбираем категорию “Математические”, находим оператор “СУММКВРАЗН” и щелкаем OK.
  7. Теперь нужно заполнить аргументы функции:
    • в поле “Массив_x”  указываем координаты диапазона ячеек столбца Y (без шапки). Адреса ячеек можно указать как вручную, напечатав их с клавиатуры, так и путем выделения с помощью зажатой левой кнопки мыши в самой таблице.
    • в поле “Массив_y” указываем диапазон ячеек столбца NX.
    • жмем Enter, когда все готово.
  8. Переключаемся во вкладку “Данные”. В группе “Анализ” щелкаем по функции “Поиск решения”.
  9. Нам предстоит заполнить параметры поиска решения:
    • в поле “Оптимизировать целевую функцию” следует указать ссылку на ячейку с функцией “СУММКВРАЗН”. Сделать это можно вручную или выбрав элемент в таблице.
    • для опции “До” выбираем вариант – “Минимум”.
    • в поле “Изменяя ячейки переменных” нужно указать координаты ячейки, в которой находится соответствующее значение коэф. N.
    • по готовности нажимаем “Найти решение”.
  10. После выполнения функции появится окно с результатами поиска решения и произойдет замена значения в столбце N. Найденная величина является наименьшим квадратом функции. Нажимаем OK, если полученный результат удовлетворителен.

Заключение

Итак, мы только что разобрали на практическом примере, каким образом можно применить метод наименьших квадратов в Эксель. На практике могут встречаться более сложные задачи, однако, в целом логика действий схожа с той, что мы описали.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Построение графика методом наименьших квадратов с помощью Microsoft Excel

Построение графика методом наименьших квадратов с помощью Microsoft Excel
Построение графика методом наименьших квадратов с использованием Microsoft Excel

Простые программы для работы с электронными таблицами, такие как Microsoft Excel или Quattro Pro , являются мощными инструментами. для многих типов расчетов в химии. Одна из наиболее часто используемых функций программа для работы с электронными таблицами предназначена для построения графиков. Процедура построения графа наименьших квадратов используя Microsoft Excel описан ниже.

Обратите внимание, что « click » означает поместить курсор мыши в позицию и нажать левую кнопку мыши. кнопка один раз; « двойной щелчок » означает быстрое двойное нажатие левой кнопки мыши; к « драг » означает поместить курсор мыши в позицию, нажать и удерживать левую кнопку мыши, переместить курсор мыши в другую позицию, затем отпустите кнопку мыши. Перетаскивание используется не только для перемещения объектов, но и для выделения текста, данных и т. д.

  1. Введите свои данные в электронную таблицу. Часто бывает проще поместить подобные типы данных в столбцы, а не строки (хотя это не является обязательным требованием).
  2. Выберите (выделите) данные, которые вы хотите включить в график. Например, если вы хотите построить данные, содержащиеся в ячейках 1-4 столбцов A и B, поместите курсор мыши в ячейке A1 и перетащите курсор мыши в ячейку B4.

    Если данные, которые вы хотите включить, находятся в двух несмежных столбцах (например, ячейки 1-4 столбцов A и C), поместите курсор мыши на ячейку A1 и перетащите курсор мыши в ячейку A4. Затем, удерживая клавишу CTRL на клавиатуры, поместите курсор мыши в ячейку C1 и перетащите его в ячейку C4. Обе колонки данных следует выделить.

  3. Нажмите Вставить в строке меню.
  4. Нажмите на диаграмму ….
  5. Ниже Стандартные типы , Тип диаграммы: , нажмите XY (Scatter) .
  6. Под типом диаграммы : щелкните диаграмму только с маркерами данных и без линий.
  7. Нажмите Далее> .
  8. Нажмите Далее> .
  9. Под Заголовки ,
    1. щелкните в текстовом поле под Название диаграммы: и введите название диаграммы.
    2. щелкните в текстовом поле под осью Категория (X): и введите заголовок для ось х.
    3. щелкните в текстовом поле под осью значений (Y): и введите заголовок для оси Y.
  10. Нажмите на вкладку Gridlines . Установите флажки, чтобы включить или выключить линии сетки.
  11. Нажмите на вкладку Легенда . Установите флажок рядом с Показать легенду , чтобы включить легенда включена или выключена. Здесь также можно выбрать размещение легенды на графике.
  12. Перейдите на вкладку Метки данных . Нажмите на переключатели, чтобы включить метки данных. или выкл.
  13. Щелкните вкладку Таблица данных . Установите флажки, чтобы включить таблицу данных или выключенный.
  14. Нажмите Далее> .
  15. Под Место диаграммы: , нажмите на переключатель рядом с Как новый лист: . Введите имя графика в выделенном текстовом поле.
  16. Нажмите Готово . На данный момент вы создали график X-Y данных.
    1. Переместите курсор мыши на любую точку данных и нажмите левую кнопку мыши. Теперь все точки данных должны быть выделены. Теперь, пока мышь курсор все еще находится на любой из выделенных точек данных, нажмите правую кнопку мыши и нажмите Добавить линию тренда… из появившегося меню.
    2. В окне Добавить линию тренда под Введите , щелкните поле с нужным типом посадки (например, Linear ).
    3. Нажмите Options в верхней части окна Add Trendline .
    4. Установите флажок рядом с Показать уравнение на графике и флажок рядом с Показать значение R-квадрата на графике . Не нажимайте на флажок рядом с «Set Intercept = 0».
    5. Нажмите OK .
Форматирование графика методом наименьших квадратов в
Microsoft Excel
Некоторые общие операции в
Microsoft Excel

Метод наименьших квадратов | Реальная статистика с использованием Excel

В разделе «Корреляция» мы изучаем линейную корреляцию между двумя случайными величинами x и у. Теперь посмотрим на линию на плоскости x y, которая лучше всего соответствует данным ( x 1 , y 1 ), …, ( x n , y n ).

Напомним, что уравнение для прямой имеет вид y = bx + a , где

b = наклон прямой
a = y-пересечение, т.е. значение y в месте пересечения прямой с ось Y

Для наших целей мы запишем уравнение линии наилучшего соответствия как

and so the y-intercept is

For each i , we define ŷ i as the y-value of x i on this line, and so

Линия наилучшего соответствия — это линия, для которой сумма расстояний между каждой из n точек данных и линией как можно меньше. Таким образом, математически полезный подход состоит в том, чтобы найти линию со свойством, что сумма следующих квадратов минимальна.

Теорема 1 : наилучшая посадка для точек ( x 1 , Y 1 ),… ( x N , Y n n n n n n n y .

где

Щелкните здесь для доказательства теоремы 1. Даны два доказательства, одно из которых не использует исчисление.

Определение 1 : Линия наилучшего соответствия называется линией регрессии .

Наблюдение : Теорема показывает, что линия регрессии проходит через точку ( x̄ , ȳ) и имеет уравнение

, где наклон равен

, а точка пересечения по оси Y равна

. Обратите внимание, что b = cov ( x ,y)/ var ( x ). Поскольку члены, включающие n , сокращаются, это можно рассматривать либо как ковариацию и дисперсию генеральной совокупности, либо как ковариацию и дисперсию выборки. Таким образом a и b можно вычислить в Excel следующим образом, где R1 = массив значений y и R2 = массив значений x : R2) / VARP(R2)

a = INTERCEPT(R1, R2) = AVERAGE(R1) – b * AVERAGE(R2)

Свойство 1 : 

Доказательство корреляции: по определению, 2

и, таким образом, по приведенному выше наблюдению мы имеем

Функции Excel : Excel предоставляет следующие функции для прогнозирования значения y для любого x на основе линии регрессии.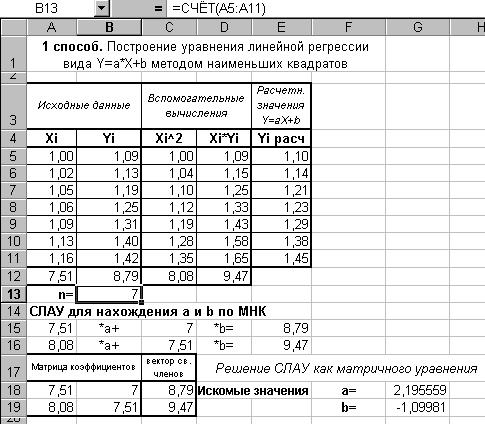 Здесь R1 = массив значений данных y, а R2 = массив значений данных x :

НАКЛОН (R1, R2) = наклон линии регрессии, как описано выше

ПЕРЕСЕЧЕНИЕ (R1, R2) = y-пересечение линии регрессии, как описано выше0161 х . Таким образом, ПРОГНОЗ (x, R1, R2) = a + b * x , где a = ПЕРЕСЕЧЕНИЕ (R1, R2) и b = НАКЛОН (R1, R2).

TREND (R1, R2) = функция массива, которая создает массив предсказанных значений y, соответствующих x значениям, хранящимся в массиве R2, на основе линии регрессии, вычисленной из x значений, хранящихся в массиве R2, и значений y хранится в массиве R1.

TREND (R1, R2, R3) = функция массива, которая предсказывает значения y, соответствующие 9Значения 0161 x в R3 на основе линии регрессии на основе значений x , хранящихся в массиве R2, и значений y, хранящихся в массиве R1.

Чтобы использовать TREND(R1, R2), выделите диапазон, в котором вы хотите сохранить предсказанные значения y. Затем введите TREND и левую скобку. Затем выделите массив наблюдаемых значений для y (массив R1), введите запятую и выделите массив наблюдаемых значений для x (массив R2), за которым следует правая скобка. Наконец нажмите Ctrl-Shft-Enter .

Чтобы использовать TREND(R1, R2, R3), выделите диапазон, в котором вы хотите сохранить предсказанные значения y. Затем введите TREND и левую скобку. Затем выделите массив наблюдаемых значений для y (массив R1), введите запятую и выделите массив наблюдаемых значений для x (массив R2), затем еще одну запятую и выделите массив R3, содержащий значения для x , для которых вы хотите предсказать значения y на основе линии регрессии. Теперь введите правую скобку и нажмите Ctrl-Shft-Enter .

Функция Excel 2016 : В Excel 2016 представлена ​​новая функция ПРОГНОЗ.ЛИНЕЙНЫЙ , эквивалентная ПРОГНОЗУ.

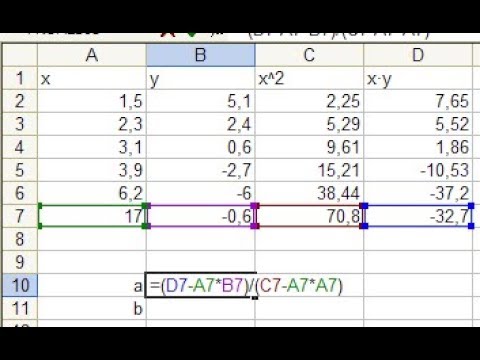
Пример 1 : Рассчитайте линию регрессии для данных в Примере 1 проверки гипотезы одной выборки на предмет корреляции и нанесите результаты на график.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *