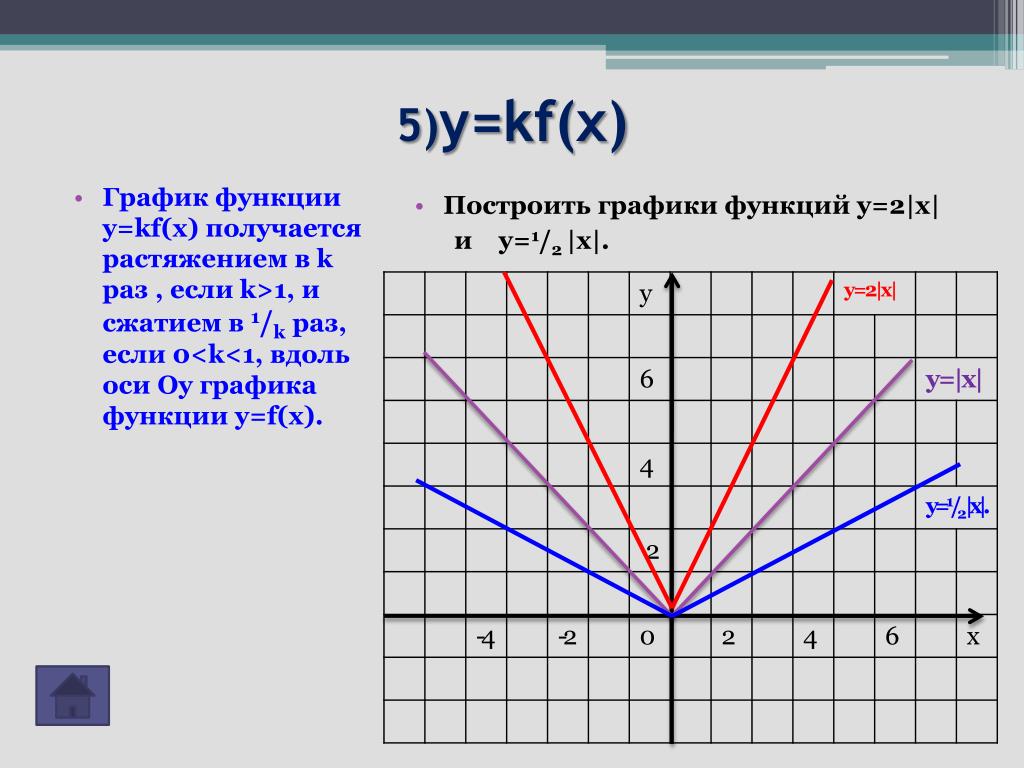
2 x функция
Вы искали 2 x функция? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 2 y x 3 и y x, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 x функция».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 x функция,2 y x 3 и y x,2 х в квадрате график,2x функция,2х2 график,3 x функция,3 в степени x график,4 x функция,e x график функции,f x 1 x график,x 2 2x функция,x 2 функция,x в квадрате график функции,x у 2,y 2 x какой график,y 2 х,y 2x,y 2×2 функция,y x 2,y x 2 2x,y x 2 и y 2x 2,y x 2 парабола,y x 2 при x 2,y x 5 функция,y x 7 функция,y x в 2 степени график,y x в 5 степени график,y x в квадрате график,y x2,y x2 1 функция y,y x2 график функций,y x2 парабола,y x3 x,y х 2,y х в квадрате,y2 x,график 2х2,график f x 1 x,график x в 3 степени,график x в квадрате,график y 6 x,график y a x,график y x 2 2x,график y x в квадрате,график параболы y x2,график функции 2 х,график функции f x 1 x,график функции f x y построить,график функции x в квадрате,график функции x квадрат y квадрат,график функции y,график функции y 2 x в квадрате,график функции y 2 х,график функции y 2x x 2,график функции y 3 2x x 2,график функции y x 2,график функции y x 2 2x,график функции y x a,график функции y x в квадрате,график функции y x2 2x,график функции y х 2,график функции найти,график функции х 2,график функции х в квадрате,график функции х2,график функций y x2,график х квадрат у квадрат,икс в квадрате функция,исследование и построение графика функции онлайн калькулятор,калькулятор для функций онлайн,калькулятор онлайн функции,онлайн решение функции,парабола y 2 x,парабола y 2x 2,парабола y x 2,парабола y x2,парабола график функции y x2,построить график y x в квадрате,построить график функции f x,построить график функции y 2 x,построить график функции y 2x,построить график функции y 2x в квадрате,построить график функции y x в квадрате,построить график функции у х 2,построить графики функций f x и g x,постройте график функции y 2 х,постройте график функции y x 2 2x,постройте график функции y x 2 2x 2,постройте график функции y x в квадрате,у 2 x,у 2х 2 график,у x 2,у х 2 2х,у х2 2 х,у х2 2х,формула y x в квадрате,функции x 2 x 3,функция 1 x 3,функция 2x x 2,функция x 2,функция x 2 y 4,функция x y 2,функция y 2 x,функция y 2 x 2,функция y 2 x2,функция y 2x 2,функция y 2×2,функция y 2×2 и ее график,функция y 3 2x,функция y 3x 2,функция y x 1 x 2,функция y x 2,функция график,функция калькулятор,функция х 1 х 2 1,функция х в квадрате,х 2 y,х y 2,х в квадрате 2 график,х в квадрате график,х в квадрате функция,х у в квадрате график,что за функция y 2 x 2.
Решить задачу 2 x функция вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Задание 6 ЕГЭ по математике (профиль)
Открытый банк заданий mathege.ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege.ru.
Номер заданий соответствует номеру заданий в базе mathege.ru.
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7).
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) положительна?
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12. В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках возрастания функции f(x)?
317542.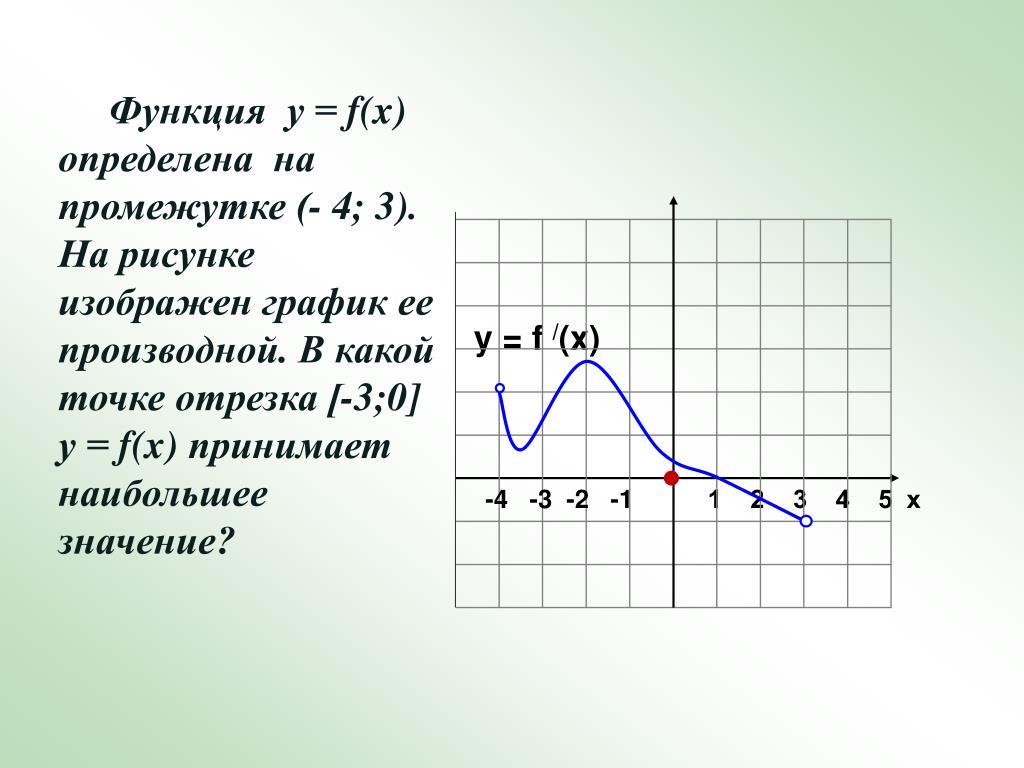 На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x2 + 6x — 8. Найдите абсциссу точки касания.
27486. Прямая y = -4x — 11 является касательной к графику функции y = x3 + 7x2 + 7x — 6. Найдите абсциссу точки касания.
27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2).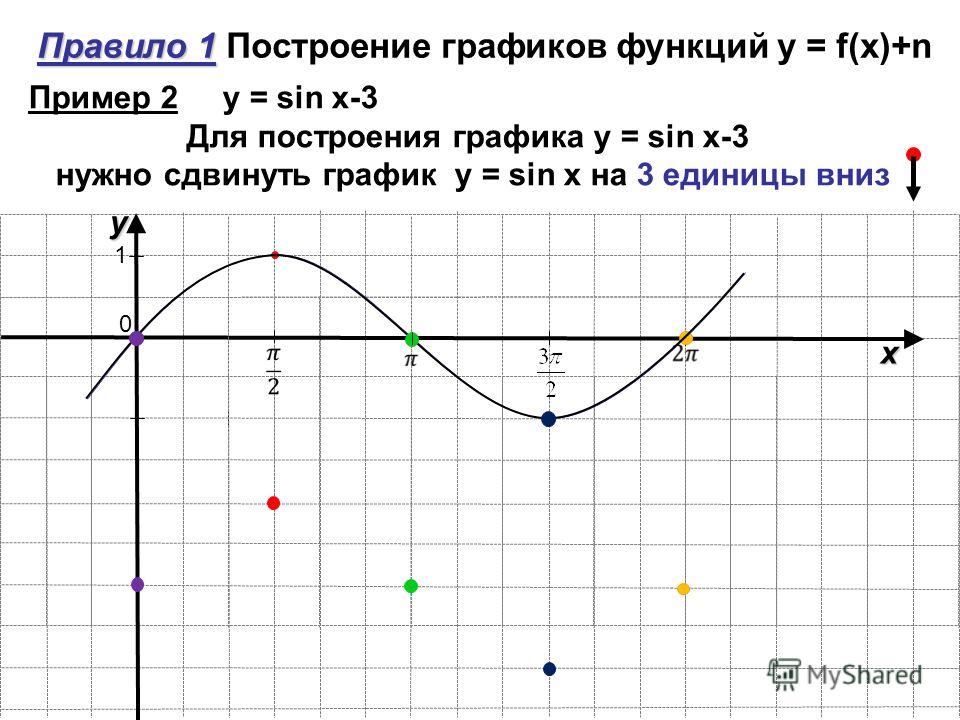 Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0
27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27505. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.
40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
119972. Прямая y = 3x +1 является касательной к графику функции ax2 + 2x + 3. Найдите a.
119973. Прямая y = -5x + 8 является касательной к графику функции 28x2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
119974. Прямая y = 3x + 4 является касательной к графику функции 3x2 — 3x + c. Найдите c.
317543. На рисунке изображён график функции y = f(x).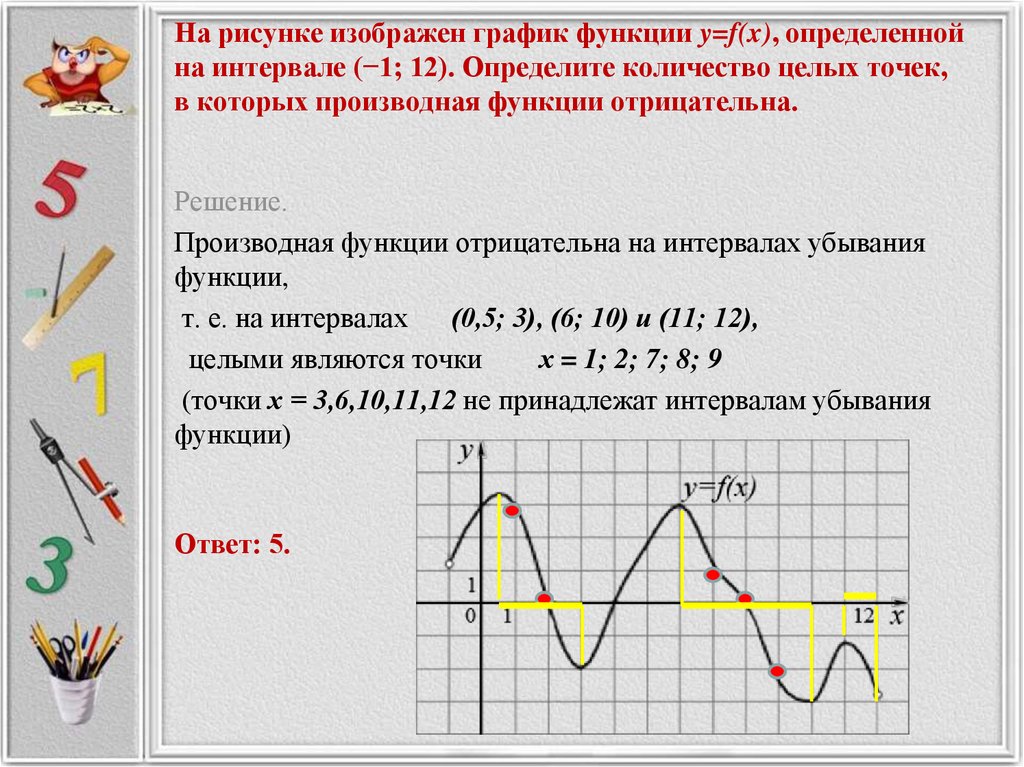 На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» class=»»]
4
[/su_expand]
119975. Материальная точка движется прямолинейно по закону x(t) = 6t2 — 48t +17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 9 с.
119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t3 — 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
119977. Материальная точка движется прямолинейно по закону x(t) = -t4 + 6t3 + 5t + 23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3 с.
119978. Материальная точка движется прямолинейно по закону x(t) = t2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t3 — 3t2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x3 + 30x2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= -x3 — 27x2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Понравилось это:
Нравится Загрузка…
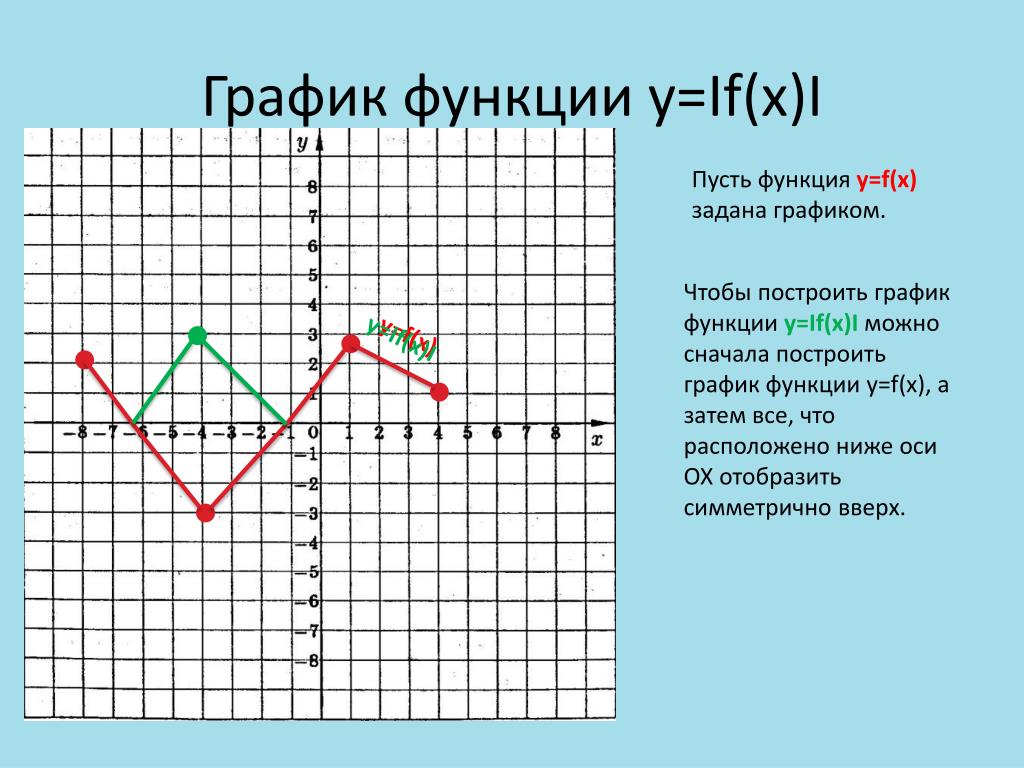
Характеристики рациональных функций | Колледж Алгебра
Результаты обучения
- Используйте обозначения со стрелками для описания локального и конечного поведения рациональных функций.

- Определение горизонтальных и вертикальных асимптот рациональных функций по графикам.
- Нарисуйте график рациональной функции при заданных горизонтальных и вертикальных смещениях.
- Напишите рациональную функцию, описывающую смешивание.
Мы видели графики основной обратной функции и квадрат обратной функции из нашего исследования функций инструментария. Изучите эти графики и обратите внимание на некоторые их особенности.
Несколько вещей становятся очевидными, если мы исследуем график [латекс]f\left(x\right)=\dfrac{1}{x}[/latex].
- На левой ветви графика кривая приближается к оси [latex]x[/latex] [latex]\left(y=0\right) \text{ as } x\to -\infty [/ латекс].
- Когда график приближается к [latex]x=0[/latex] слева, кривая падает, но когда мы приближаемся к нулю справа, кривая поднимается.
- Наконец, на правой ветви графика кривые приближаются к оси [латекс]x[/латекс] – [латекс]\влево(у=0\вправо) \текст{ as } x\to \infty [ /латекс].

Подводя итог, мы используем обозначение со стрелкой , чтобы показать, что [latex]x[/latex] или [latex]f\left(x\right)[/latex] приближается к определенному значению.
| Стрелочное обозначение | |
|---|---|
| Символ | Значение |
| [latex]x[/latex] приближается к [latex]a[/latex] справа ([latex]x | |
| [латекс]х\до \infty[/латекс] | [latex]x[/latex] приближается к бесконечности ([latex]x[/latex] неограниченно возрастает) |
| [латекс]х\к -\infty [/латекс] | [latex]x[/latex] приближается к отрицательной бесконечности ([latex]x[/latex] убывает неограниченно) |
| [латекс]f\влево(х\вправо)\в \infty [/латекс] | выход приближается к бесконечности (выход неограниченно увеличивается) |
| [латекс]f\влево(х\вправо)\в -\infty [/латекс] | выход приближается к отрицательной бесконечности (выход неограниченно уменьшается) |
| [латекс]ж\влево(х\вправо)\к[/латекс] | вывод приближается к [latex]a[/latex] |
Локальное поведение [latex]f\left(x\right)=\frac{1}{x}[/latex]
Начнем с обратной функции [latex]f\left(x \right)=\frac{1}{x}[/latex]. Мы не можем делить на ноль, что означает, что функция не определена в [latex]x=0[/latex]; так что ноль не в домене .
Мы не можем делить на ноль, что означает, что функция не определена в [latex]x=0[/latex]; так что ноль не в домене .
Когда входные значения приближаются к нулю с левой стороны (становятся очень маленькими, отрицательными значениями), значения функции неограниченно уменьшаются (другими словами, они приближаются к отрицательной бесконечности). Мы можем видеть это поведение в таблице ниже.
| [латекс]x[/латекс] | –0,1 | –0,01 | –0,001 | –0,0001 |
| [латекс]f\left(x\right)=\frac{1}{x}[/latex] | 9{-},f\left(x\right)\to -\infty [/latex]
| [латекс]x[/латекс] | 0,1 | 0,01 9{+}, f\left(x\right)\to \infty [/latex]. Когда [latex]x[/latex] приближается к [latex]0[/latex] с правой (положительной) стороны, [latex]f(x)[/latex] будет приближаться к бесконечности. Такое поведение создает вертикальную асимптоту , которая представляет собой вертикальную линию, к которой график приближается, но никогда не пересекает. В этом случае график приближается к вертикальной линии [latex]x=0[/latex] , когда вход становится близким к нулю. A Общее примечание: вертикальная асимптотаA вертикальная асимптота графика — это вертикальная линия [latex]x=a[/latex], где график стремится к положительной или отрицательной бесконечности по мере того, как входные данные приближаются к [latex]x[/latex]. Мы пишем [латекс]\текст{As }x\to a,f\left(x\right)\to \infty , \text{или как }x\to a,f\left(x\right)\ в -\infty [/латекс]. End Поведение [latex]f\left(x\right)=\frac{1}{x}[/latex]Когда значения [latex]x[/latex] приближаются к бесконечности, значения функции приближаются 0. По мере того, как значения [latex]x[/latex] приближаются к отрицательной бесконечности, значения функции приближаются к 0. Символически, используя обозначение со стрелкой [латекс]\текст{As}x\to\infty,f\left(x\right)\to 0,\text{и as}x\to-\infty,f\left(x\right)\ до 0[/латекс]. Основываясь на этом общем поведении и графике, мы можем видеть, что функция приближается к 0, но на самом деле никогда не достигает 0; кажется, что он выравнивается, когда входные данные становятся большими. Такое поведение создает горизонтальную асимптоту , горизонтальную линию, к которой график приближается по мере неограниченного увеличения или уменьшения входных данных. В этом случае график приближается к горизонтальной линии [latex]y=0[/latex]. A Общее примечание: Горизонтальная асимптота Горизонтальная асимптота графика представляет собой горизонтальную линию [latex]y=b[/latex], где график приближается к линии по мере неограниченного увеличения или уменьшения входных данных. [латекс]\текст{As }x\to \infty \text{ или }x\to \infty ,\text{ }f\left(x\right)\to b[/latex]. Пример: использование стрелочной нотацииИспользуйте стрелочную нотацию для описания конечного поведения и локального поведения функции ниже. Показать решение ПопробуйтеИспользуйте обозначения со стрелками для описания конечного поведения и локального поведения функции обратного квадрата. Показать решение Пример: использование преобразований для построения графика рациональной функцииНарисуйте график обратной функции, сдвинутой на две единицы влево и на три единицы вверх. Определите горизонтальную и вертикальную асимптоты графика, если они есть. Показать раствор Попробуйте Показать решение Задача смешиванияВ предыдущем примере мы сдвинули функцию инструментария таким образом, что в результате получилась функция [латекс]f\left(x\right)=\dfrac{3x+7}{x+2}[ /латекс]. Это пример рациональной функции. Рациональная функция — это функция, которую можно записать как частное двух полиномиальных функций. Многие реальные задачи требуют от нас найти отношение двух полиномиальных функций. Задачи, связанные со скоростями и концентрациями, часто связаны с рациональными функциями. 9{q — 1}+…+{b}_{1}x+{b}_{0}},Q\left(x\right)\ne 0[/latex] Пример. Решение прикладной задачи, включающей Rational Function Большой смесительный бак в настоящее время содержит 100 галлонов воды, в которых смешано 5 фунтов сахара. Откроется кран, из которого в бак будет выливаться 10 галлонов воды в минуту, в то же время в бак будет высыпаться сахар со скоростью 1 фунт в минуту. Найдите концентрацию (фунтов на галлон) сахара в баке через 12 минут. Показать решение Попробуй1200 первокурсников и 1500 второкурсников собрались на подготовительном митинге в полдень. После 12 часов каждые пять минут на митинг прибывают 20 первокурсников, а 15 второкурсников покидают митинг. Найдите соотношение первокурсников и второкурсников в 13:00. Показать раствор Поддержите!У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад. Улучшить эту страницуПодробнее Докажите домен и является ли функция — f(x) = 1/(1 + |x|) один к одному.Задавать вопрос спросил Изменено 2 года, 4 месяца назад Просмотрено 201 раз $\begingroup$ Я учусь на первом курсе компьютерных наук и в этом семестре изучаю исчисление и линейную алгебру. У меня есть два вопроса:
Вопрос — 1 — Домен — Мое понимание f(x) = 1/(1+ |x|)
Однако решение следующее, и я не понимаю этого решения. 1 + |х| >= 1 1/(1 + |х|) <= 1 0 < 1/(1 + |x|) <= 1 для всех x E (-α, α) Вопрос - 2 - Функция один к одному или нет y = 1/(1 + |x|) 1 + |х| = 1/год |х| = 1/г -1 х = +- (1/у -1) Отсюда я вижу, что y должен быть больше 0, так как знаменатель не может быть равен 0. Я застрял здесь. Мне пришлось использовать сайт wolframalpha для построения графика. Без использования этого веб-сайта, как я должен проверить функцию «один к одному»?
Графический график для проверки взаимно однозначной функции
Насколько я понимаю, поскольку для каждого соответствующего y есть два значения x (+-), это не один к одному. |


 Мы можем видеть это поведение в таблице ниже.
Мы можем видеть это поведение в таблице ниже.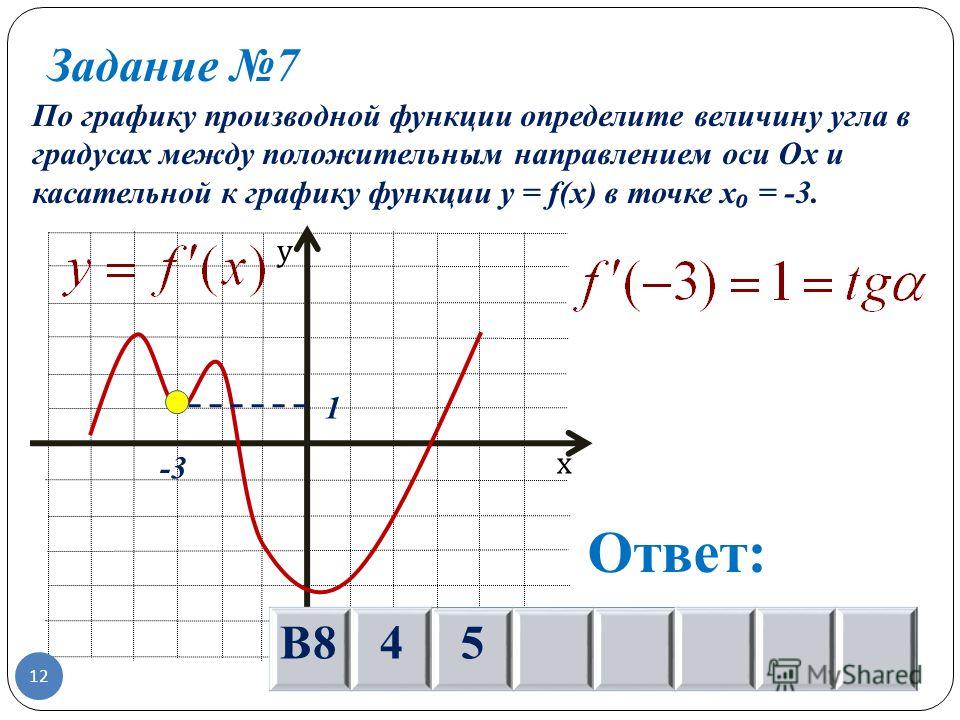
 Мы пишем
Мы пишем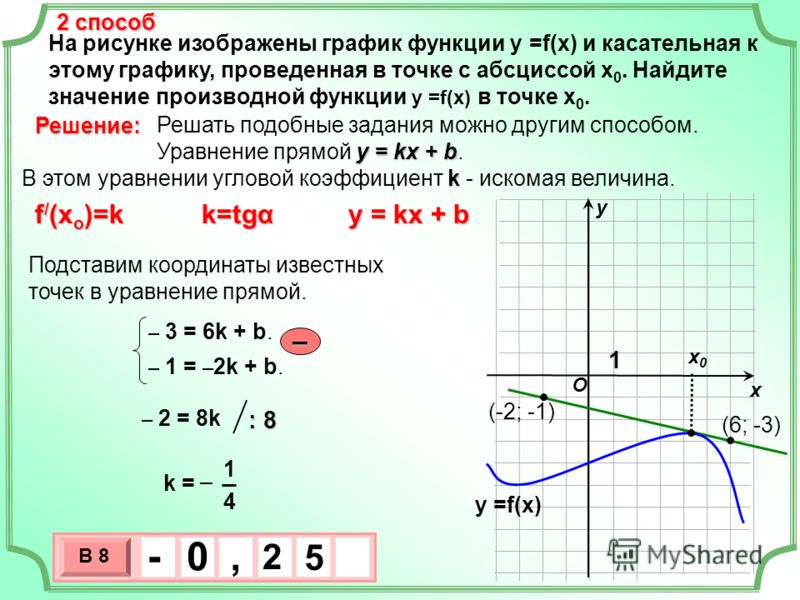
 Это большая концентрация, чем в начале?
Это большая концентрация, чем в начале?