Функция ДВФАКТР
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ДВФАКТР в Microsoft Excel.
Описание
Возвращает двойной факториал числа.
Синтаксис
ДВФАКТР(число)
Аргументы функции ДВФАКТР описаны ниже.
Замечания
-
Если число не является числом, функция FACTDOUBLE возвращает #VALUE! (значение ошибки).
-
Если значение аргумента «число» является четным числом:
-
Если значение аргумента «число» является нечетным числом:
Если число отрицательное, функция FACTDOUBLE возвращает #NUM! (значение ошибки).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу Enter. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ДВФАКТР(6) |
Двойной факториал числа 6. n!! = n*(n-2)*(n-4)…(4)(2) |
48 |
|
=ДВФАКТР(7) |
Двойной факториал числа 7. Для этого нечетного числа двойной факториал равен 7*5*3; используя такое уравнение: n!! = n*(n-2)*(n-4)…(3)(1) |
105 |
§ Факториал. Как посчитать факториал
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы.
 Разрядные слагаемые
Разрядные слагаемые - Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция.
 Парабола
Парабола - Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Умный человек создаёт больше возможностей, чем находит. Фрэнсис Бэкон
на главную
Введите тему
Русский язык Поддержать сайт
Слово факториал произошло от латинского factor (делающий, производящий).
Запомните!
Факториал числа — это произведение натуральных чисел от
1 до самого числа (включая
данное число).
Обозначается факториал восклицательным знаком
«!».
Примеры:
- 3! = 1 · 2 · 3 = 6
- 6! = 1 · 2 · 3 · 4 · 5 · 6 = 720
Факториал определён только для натуральных чисел и нуля.
Запомните!
Факториал нуля и единицы это 1.
- 0! = 1
- 1! = 1
Термин факториал ввел в 1800 году францзузский математик Аргобаст Луи Франсуа Антуан.
Обозначение «n!» придумал чуть позже немецкий математик Кристиан Крамп в 1808 году.
Интересные факториалы проверьте сами:
- 145 = 1! + 4! + 5! = 1 + 24 + 120 = 145
- 40 585 = 4! + 0! + 5! +8! + 5!
На нашем ресурсе вы также можете посчитать факториал онлайн.
Урок Видео: Факториалы | Nagwa
Стенограмма видео
В этом видео мы узнаем, как
найти факториал любого числа 𝑛, являющегося произведением всех целых чисел, меньших
или равно 𝑛 и больше или равно единице. Мы также научимся находить
факториалы для решения задач и решения задач, содержащих перестановки и
факториалы. Начнем с изучения письменного
и алгебраическое определение факториала.
Мы также научимся находить
факториалы для решения задач и решения задач, содержащих перестановки и
факториалы. Начнем с изучения письменного
и алгебраическое определение факториала.
Факториал положительного целого числа
𝑛 — это произведение всех натуральных чисел, меньших или равных 𝑛. Мы используем обозначение 𝑛, за которым следует
восклицательный знак, который читается как 𝑛 факториал. 𝑛 факториал равен 𝑛
умножить на 𝑛 минус один умножить на 𝑛 минус два и так далее умножить на два
умножить на единицу. Определим также факториал
ноль равен единице; то есть нулевой факториал равен единице. Мы также знаем, что для любого целого числа
𝑛 больше или равно единице, 𝑛 факториал равен 𝑛, умноженному на 𝑛 минус
один факториал. Мы видим, что из общего
правило для факториала 𝑛 выше. Это свойство будет очень полезно
при решении более сложных задач в этом видео.
Вычислить четыре факториала.
Напомним, что факториал любого положительное целое число 𝑛 — это произведение всех положительных целых чисел, меньших или равных к 𝑛. Это означает, что 𝑛 факториал равно 𝑛, умноженное на 𝑛 минус один, умноженное на 𝑛 минус два, и так далее по всем вплоть до одного. Таким образом, факториал четырех равен четыре умножить на три умножить на два умножить на один. Четыре умножить на три равно до 12. Умножение этого на два дает нам 24, а умножение 24 на единицу равно 24. Мы можем умножать целые числа четыре, три, два и один в любом порядке, чтобы дать нам ответ 24. Следовательно, четыре факториала равны 24.
В нашем следующем вопросе мы решим более сложная проблема.
Упростите выражение шесть
факториал более четырех факториал минус 27 факториал более 28 факториал.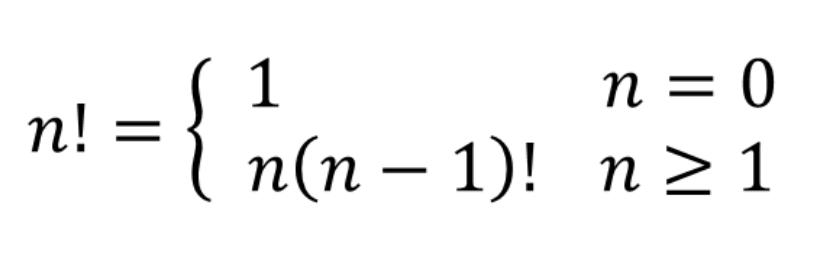 Дайте ответ в виде дроби.
Дайте ответ в виде дроби.
Напомним, что факториал 𝑛 равно 𝑛, умноженное на 𝑛 минус один, умноженное на 𝑛 минус два, и так далее по всем вплоть до одного. Это означает, что мы могли вычислить шесть факториалов путем умножения шести на пять, на четыре, на три, на два и на один. Хотя это было бы не слишком сложно для первой дроби, вычислив 27 факториалов и 28 факториалов в этой путь займет очень много времени. Поэтому мы можем вспомнить еще один правило вычисления 𝑛 факториала. Это равно 𝑛, умноженному на 𝑛 минус один факториал. Мы также могли видеть, что факториал 𝑛 равно 𝑛, умноженному на 𝑛 минус один, умноженному на 𝑛 минус два факториала. Это позволяет нам переписать шесть факториал как шесть умножить на пять умножить на четыре факториал.
Первый член в нашем вопросе
упрощает до шести умножить на пять умножить на четыре факториал все разделить на
четыре факториала. Поскольку четыре факториала сокращаются, мы
осталось шесть умножить на пять. Это равно 30. Мы можем снова использовать этот метод для
вторая дробь как факториал 28 равна 28, умноженному на 27 факториал. На этот раз 27 факториалов
отменить, оставив нам одного старше 28. Нам нужно вычесть один больше 28 или
одна двадцать восьмая от 30. Это равно смешанному числу
29и двадцать семь двадцать восьмых.
Поскольку четыре факториала сокращаются, мы
осталось шесть умножить на пять. Это равно 30. Мы можем снова использовать этот метод для
вторая дробь как факториал 28 равна 28, умноженному на 27 факториал. На этот раз 27 факториалов
отменить, оставив нам одного старше 28. Нам нужно вычесть один больше 28 или
одна двадцать восьмая от 30. Это равно смешанному числу
29и двадцать семь двадцать восьмых.
Для того, чтобы написать наш ответ просто как дробь, нам нужно будет преобразовать это в неправильную или тяжелую сверху дробная часть. Мы делаем это, сначала умножая целое число 29 в знаменателе 28. Это равно 812. Затем мы добавляем числитель 27, что дает нам 839. Выражение six factorial over четыре факториала минус 27 факториалов больше 28 факториалов равно дроби 839старше 28 лет.
В нашем следующем вопросе мы будем использовать наш
Знание факториалов для решения алгебраического уравнения.![]()
Найдите набор решений одного больше 𝑛 плюс семь факториалов плюс один больше 𝑛 плюс восемь факториалов равно 256 больше 𝑛 плюс девять факториалов.
Есть много способов начать этот вопрос. Одним из способов было бы умножить оба сторон на 𝑛 плюс девять факториалов. Умножение первого члена на 𝑛 плюс девять факториалов дает нам 𝑛 плюс девять факториалов над 𝑛 плюс семь факториал. Второй член слева сторона становится 𝑛 плюс девять факториалов над 𝑛 плюс восемь факториалов. Как 𝑛 плюс девять факториалов разделить на 𝑛 плюс девять факториал равен единице, правая часть становится 256.
Напомним, что 𝑟 факториал
равно 𝑟, умноженному на 𝑟 минус один факториал. Это означает, что 𝑛 плюс девять
факториал можно переписать как 𝑛 плюс девять умножить на 𝑛 плюс восемь факториал или
𝑛 плюс девять умножить на 𝑛 плюс восемь умножить на 𝑛 плюс семь факториал. Таким образом, первый член упрощает
на 𝑛 плюс девять умножить на 𝑛 плюс восемь. Второй член упрощается до 𝑛
плюс девять. 𝑛 плюс девять умножить на 𝑛 плюс
восемь плюс 𝑛 плюс девять равно 256.
Таким образом, первый член упрощает
на 𝑛 плюс девять умножить на 𝑛 плюс восемь. Второй член упрощается до 𝑛
плюс девять. 𝑛 плюс девять умножить на 𝑛 плюс
восемь плюс 𝑛 плюс девять равно 256.
Мы можем распределить скобки или раскройте скобки, используя метод FOIL. Умножение первых членов дает нам 𝑛 в квадрате, внешние члены восемь 𝑛, внутренние члены девять 𝑛 и последние члены 72. Теперь у нас есть уравнение 𝑛 в квадрате плюс восемь 𝑛 плюс девять 𝑛 плюс 72 плюс 𝑛 плюс девять равно 256. Собирая подобные члены, левая часть упрощается до 𝑛 в квадрате плюс 18𝑛 плюс 81. Затем мы можем вычесть 256 из обоих стороны уравнения такие, что 𝑛 в квадрате плюс 18𝑛 минус 175 равно нулю.
Теперь мы можем разложить этот квадратичный
выражение в два набора скобок. Первый член в каждом из них равен
𝑛, так как 𝑛, умноженное на 𝑛, равно 𝑛 в квадрате. Вторые члены будут иметь сумму
18, а произведение отрицательных 175. 25, умноженных на семь, равно 175. Это означает, что положительные 25
умноженное на минус семь равно минус 175. Положительные числа 25 и
отрицательные семь также имеют сумму 18. Поскольку это выражение равно нулю, один
наших скобок должны быть равны нулю. Это означает, что либо 𝑛 равно
на минус 25 или 𝑛 равно семи. Факториалы определены только для
неотрицательные целые числа. Это означает, что мы можем отказаться от
решение 𝑛 равно отрицательному числу 25. Значение 𝑛, удовлетворяющее
уравнение 𝑛 равно семи. Множество решений уравнения
просто содержит число семь.
Вторые члены будут иметь сумму
18, а произведение отрицательных 175. 25, умноженных на семь, равно 175. Это означает, что положительные 25
умноженное на минус семь равно минус 175. Положительные числа 25 и
отрицательные семь также имеют сумму 18. Поскольку это выражение равно нулю, один
наших скобок должны быть равны нулю. Это означает, что либо 𝑛 равно
на минус 25 или 𝑛 равно семи. Факториалы определены только для
неотрицательные целые числа. Это означает, что мы можем отказаться от
решение 𝑛 равно отрицательному числу 25. Значение 𝑛, удовлетворяющее
уравнение 𝑛 равно семи. Множество решений уравнения
просто содержит число семь.
Наш последний вопрос касается
перестановки и факториалы. Прежде чем перейти к этому, мы
Вспомните определение перестановки. Перестановка – это перестановка
коллекция предметов. определяется как количество способов
мы можем упорядочить 𝑟 элементов из набора 𝑛 элементов без повторения. Мы пишем это как нижний индекс 𝑛
заглавная буква P, индекс 𝑟. Это просто читается как 𝑛P𝑟. Он определяется 𝑛 факториалом
разделить на 𝑛 минус 𝑟 факториал. Например, девять P пять равно
девять факториалов разделить на девять минус пять факториалов. Это упрощает до девяти факториалов
разделить на четыре факториала.
определяется как количество способов
мы можем упорядочить 𝑟 элементов из набора 𝑛 элементов без повторения. Мы пишем это как нижний индекс 𝑛
заглавная буква P, индекс 𝑟. Это просто читается как 𝑛P𝑟. Он определяется 𝑛 факториалом
разделить на 𝑛 минус 𝑟 факториал. Например, девять P пять равно
девять факториалов разделить на девять минус пять факториалов. Это упрощает до девяти факториалов
разделить на четыре факториала.
Использование свойства, которое 𝑛 факториал равен 𝑛, умноженному на 𝑛 минус один факториал, девять факториалов равно равно девяти умножить на восемь умножить на семь умножить на шесть умножить на пять умножить на четыре факториала. Поскольку четыре факториала сокращаются, мы затем можно умножить пять целых чисел девять, восемь, семь, шесть и пять, что даст нам 15 120.
Сейчас мы ответим на вопрос
с перестановками и факториалами.
Учитывая, что 𝑛P𝑟 равно 504 и 𝑟 факториал равен шести, найдите значения 𝑛 и 𝑟.
Напомним, что при работе с перестановок, 𝑛P𝑟 равно 𝑛 факториалу по 𝑛 минус 𝑟 факториалу. Нам также говорят в вопросе что факториал 𝑟 равен шести. Это факториал, который мы можем решить довольно легко. Мы знаем, что три умножить на два умножить на один равно шести. Это означает, что три факториала равно шести. Следовательно, наше значение 𝑟 равно до трех.
Нам сказали, что 𝑛P𝑟 равно
504. Следовательно, 𝑛P три равно
504. Подстановка 𝑟 равняется трем в
наша общая формула для перестановок, у нас есть 𝑛 факториал, деленный на 𝑛 минус три
факториал равен 504. 𝑛 факториал можно переписать как 𝑛
умножить на 𝑛 минус один умножить на 𝑛 минус два умножить на 𝑛 минус три
факториал. Разделив это на 𝑛 минус три
факториал, у нас остается 𝑛, умноженное на 𝑛 минус один, умноженный на 𝑛 минус
два. Это равно 504. Поэтому мы ищем три
последовательные целые числа, которые умножаются, чтобы дать нам 504.
Это равно 504. Поэтому мы ищем три
последовательные целые числа, которые умножаются, чтобы дать нам 504.
Мы могли бы попытаться решить эти
ценности методом проб и улучшений. Тем не менее, есть трюк, который мы можем
используйте, чтобы найти три последовательных целых числа, которые умножаются, чтобы дать число. Начнем с извлечения кубического корня из
это число. Кубический корень из 504 равен 7,958.
скоро. Ну, как это нам поможет? Это не целое число. Что мы можем сделать, так это взять целые числа
по обе стороны от этого числа. В данном случае это семь и
восемь. Теперь мы можем разделить наше число на
в данном случае 504, двумя целыми числами. 504 разделить на семь равно
72. Следовательно, семь умножить на 72.
равно 504. Теперь делим 72 на секунду
целое число восемь. 72 разделить на восемь равно
девять. Следовательно, восемь умножить на девять
72,
Следовательно, восемь умножить на девять
72,
Теперь мы записали 504 как произведение трех последовательных целых чисел. Эти целые числа семь, восемь, и девять, которые соответствуют 𝑛 минус два, 𝑛 минус один и 𝑛 соответственно. Наше значение 𝑛 равно девяти. Если 𝑛P𝑟 равно 504 и 𝑟 факториал равен шести, 𝑟 равно трем, а 𝑛 равно девяти. Есть немного разные методы, которые мы могли бы использовать для вычисления 𝑟, а затем для вычисления 𝑛. Вернемся к факту что мы знаем, что факториал 𝑟 равен шести.
При попытке найти неизвестное
целое число, учитывая его факториал, мы можем разделить на последовательные положительные целые числа. Это означает, что мы начинаем с
делим наше число шесть на один. Это равно шести. Затем делим на следующий положительный
целое число два. Шесть разделить на два равно
три. Затем делим на следующий положительный
целое число три, и три разделить на три равно единице. Как шесть разделить на один разделить на
два разделить на три равно единице, тогда шесть тоже равно трем умножить на
два умножить на один. Мы еще раз доказали, что
три факториала равно шести. Следовательно, 𝑟 равно трем.
Как шесть разделить на один разделить на
два разделить на три равно единице, тогда шесть тоже равно трем умножить на
два умножить на один. Мы еще раз доказали, что
три факториала равно шести. Следовательно, 𝑟 равно трем.
Когда мы добрались до сцены, что 𝑛
умножить на 𝑛 минус один умножить на 𝑛 минус два равно 504, мы могли бы
использовали наши знания о простых множителях, чтобы попытаться перестроить их в последовательные
целые числа. 504 равно двум, умноженным на
252. 252 равно двум, умноженным на
126. Повторение этого процесса путем деления
по простым числам мы можем записать 504 как произведение его простых множителей. 504 равно двум, умноженным на
два умножить на два умножить на семь умножить на три умножить на
три. Это можно переписать как два в кубе
умножить на семь умножить на три в квадрате. Два в кубе равно восьми, а
три в квадрате равно девяти. И снова нас трое
последовательные целые числа семь, восемь и девять, такие что семь равно 𝑛 минус
два, восемь равно 𝑛 минус один, а девять равно 𝑛.
Два в кубе равно восьми, а
три в квадрате равно девяти. И снова нас трое
последовательные целые числа семь, восемь и девять, такие что семь равно 𝑛 минус
два, восемь равно 𝑛 минус один, а девять равно 𝑛.
Теперь мы суммируем ключ
очки из этого видео. Факториал положительного целого числа
𝑛 определяется как произведение всех положительных целых чисел, меньших или равных 𝑛. Основное свойство факториала
заключается в том, что 𝑛 факториал равен 𝑛, умноженному на 𝑛 минус один факториал. Мы можем использовать это, чтобы упростить
выражения с использованием факториалов, а также решать факториальные уравнения. При попытке найти неизвестное
целое число по его факториалу, мы делим на последовательные положительные целые числа, пока не получим
достичь ответа один. Наконец, мы увидели, что число
перестановки размера 𝑟, взятые из набора размера 𝑛, задаются как 𝑛P𝑟 равно 𝑛
факториал разделить на 𝑛 минус 𝑟 факториал.
Алгоритм на день: Вычислить факториал числа | by Marina Shemesh
Фоновое изображение создано Bedneyimages — Freepik.comЧто такое факториал?
В математике факториал неотрицательного целого числа представляет собой произведение всех положительных целых чисел, меньших или равных этому неотрицательному целому числу.
Символом функции факториала является восклицательный знак после числа.
Например: 5!
Итак, если вы видите что-то вроде 5! , вы знаете, что вам придется умножать ряд убывающих положительных целых чисел.
Например:
5! = 5 * 4 * 3 * 2 * 1 = 120
и
4! = 4 * 3 * 2 * 1 = 24
Целые числа или целые числа или натуральные числа?Если вы немного погуглите, то заметите, что определение «что такое фактория l» немного отличается друг от друга:
Mathsisfun.com:
Результат умножения последовательности убывания натуральных чисел до 1 (например, 4 × 3 × 2 × 1).
Decodedscience.org:
Обычное определение «n-факториала» — «n! = n * (n — 1) * (n — 2) *…* 2 * 1», где n — положительное целое число .
Wikipedia.org:
В математике факториал неотрицательного целого числа n , обозначаемый n !, является произведением всех положительных целых чисел, меньших или равных 9098п .
Использование целых неотрицательных чисел , целых положительных чисел и натуральных чисел в этих определениях означает, что все числа, используемые в факториалах, не должны быть десятичными, например, отрицательные числа (-10). ) или дроби.
****************************************************** ******************
Натуральные числа : Числа, которые вы используете для счета: 1, 2, 3, 4…и так далее и тому подобное. Ноль не является натуральным числом.
Ноль не является натуральным числом.
Целые числа : Все числа «целые» — нет дробей, отрицательных чисел или десятичных знаков. Единственная разница между целыми и натуральными числами заключается в том, что 0 — это целое число.
Целые числа : Положительные и отрицательные целые числа, например -6, 0, -200,
1660, 2 и т. д.
********************** ************************************************
А как насчет «0!»
ЕСТЬ 0! Он существует? Можем ли мы его использовать?
Было согласовано, что можно использовать нулевой факториал и что 0! = 1.
Я согласен, что кажется странным, что умножение чисел не может дать вам одно. Салман Кхан из Академии Хана очень хорошо объясняет аргументацию в этом видео.
Кое-что интересное
Мы можем вычислить факториал из предыдущего. Взгляните на это:
1! = 1
2! = 2 * 1 = 2
3! = 3 * 2 * 1 = 6
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1= 120
Обратите внимание, что 3! (6) умножить на 4 = 24 или факториал 4!
Продолжаем в том же духе и находим 4! умножить на 5 = 120 или 5!
И 6! равно 5! * 6 (120 * 6) = 720
Таким образом, мы можем сделать вывод, что: n! = n × (n−1)!
Функция JavaScript
А теперь немного действия JavaScript! Как всегда в кодировании, часто существует более одного способа написать функцию. Итак, рассмотрим два варианта. Первый использует рекурсию. Рекурсия означает, что функция вызывает сама себя .
Итак, рассмотрим два варианта. Первый использует рекурсию. Рекурсия означает, что функция вызывает сама себя .
факториал функции (n) {
if (n === 0) { // помните, что 0! определяется как 1
return 1;
}
return n * factorial(n — 1)//рекурсия
}factorial(3) //возвращает 6
factorial(0) //возвращает 1
factorial(4) // возвращает 24 Если это ищет вам нравится цикл внутри функции, вы абсолютно правы. Мы также можем вычислить факториал числа с помощью цикла for:
function newFactorial (num) {
var result = 1; for (var i = 2; i <= num; i++){ результат *=i
}
return result
}newFactorial(0)//return 1
newFactorial(3)//return 6
newFactorial(5)//return 120 Мы начинаем наш цикл с 2, потому что 1 уже позаботился с var результатом = 1;
Я рекомендую вам скопировать код в консоль и немного поиграть с ним.
Использование в реальной жизни
Используются ли факториалы в реальной жизни или это просто математические упражнения? Ах да, факториалы могут быть очень полезными.

 Для этого четного числа двойной факториал равен 6*4*2; используя такое уравнение:
Для этого четного числа двойной факториал равен 6*4*2; используя такое уравнение: Разрядные слагаемые
Разрядные слагаемые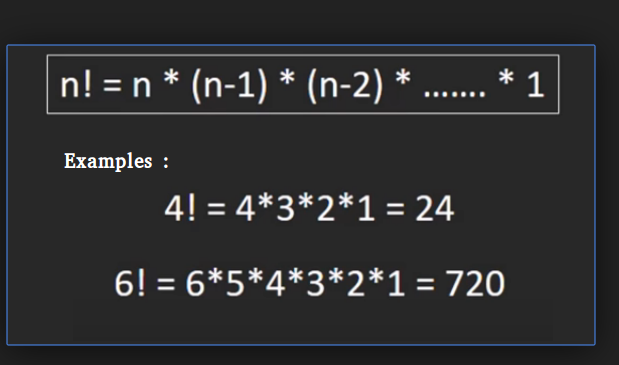 Парабола
Парабола