[Прелесть математики] Теорема Байеса
Все статьи из цикла «В чем прелесть предмета»
Другие статьи из цикла «В чем прелесть математики»:
Визуальные доказательства
Красота рассуждений
Режем провода
Прятки с геометрией
Бесконечность
Теорема Пифагора
Благодаря ей был дешифрован шифр “Энигмы”, благодаря ей работает ваш спам-фильтр, благодаря ей искусственный интеллект может диагностировать диабет. Теорема Байеса – не просто математические символы, которые позволяют нам что-то высчитывать. Теорема Байеса – это записанная в одну строчку философия принятия решений, которой придерживается человечество.
Знакомство с Дариной
Для начала познакомимся с Дариной. Дарина живёт в Америке. Она спокойная, любит проводить время с собой и тишину. Кем, по-вашему, работает Дарина: медсестрой или библиотекарем?
Скажем, \(80\%\) библиотекарей спокойные и любят тишину прямо как Дарина. А сколько таких среди медсестёр? Скажем, \(10\%\). Или это много? Тогда пусть будет \(5\%\). \(5\%\) медсестёр спокойные, любят проводить время с собой и тишину. Ну тогда всё очевидно! \(80\%\) против \(5\%\). Скорее всего Дарина работает библиотекарем.
Или это много? Тогда пусть будет \(5\%\). \(5\%\) медсестёр спокойные, любят проводить время с собой и тишину. Ну тогда всё очевидно! \(80\%\) против \(5\%\). Скорее всего Дарина работает библиотекарем.
А вот не совсем!
В Америке медсестёр намного больше, чем библиотекарей, примерно в \(30\) раз. Для простоты скажем, что в Америке \(100\) библиотекарей и \(3000\) медсестёр. Точные числа не так важны, важно лишь их отношение.
Известно, что \(80%\) библиотекарей подходят под описание самой Дарины. А раз \(100\cdot 0.80=80\), то Дарина может оказаться одной из этих восьмидесяти библиотекарей. Также мы сказали, что среди медсестёр \(5\%\) имеют схожие с Дариной качества \(3000\cdot 0.05=150\), значит Дарина может быть либо одной из \(80\) библиотекарей, либо одной из \(150\) медсестёр.
Таким образом, \(\frac{80}{80+150}\approx 35\%\) — вероятность, что Дарина библиотекарь, а \(\frac{150}{80+150}\approx 65\%\) — вероятность, что Дарина медсестра.
Байес в жизни и плоская ЗемляТак, хорошо. А где же философия принятия решений? На самом деле, обновлять вероятность пребывания Дарины библиотекарем можно бесконечно: учесть процентные соотношения женщин и мужчин в рассматриваемых профессиях, учесть расу, возраст и многое другое. Можно обновлять нашу уверенность в чём-то вновь и вновь. Именно эта идея лежит в сердце теоремы Байеса. Это бесконечное переплетение предположений и новых фактов, которые приводят к выводам.
А где же философия принятия решений? На самом деле, обновлять вероятность пребывания Дарины библиотекарем можно бесконечно: учесть процентные соотношения женщин и мужчин в рассматриваемых профессиях, учесть расу, возраст и многое другое. Можно обновлять нашу уверенность в чём-то вновь и вновь. Именно эта идея лежит в сердце теоремы Байеса. Это бесконечное переплетение предположений и новых фактов, которые приводят к выводам.
Давайте познакомимся поближе с математической записью теоремы Байеса:
\[P(A | B)= \frac{P(B | A)\cdot P(A)}{P(B)}\]
\(A\) и \(B\) – это ситуации, некоторые события. Знак «|» можно читать как «зная» или «при условии». Таким образом, \(P(A | B)\) читается как «вероятность события \(А\), зная, что \(B\)» или «вероятность \(А\) при условии, что \(B\) произошло».
В жизни человек применяет теорему Байеса в такой форме:
\[P(Гипотеза\ |\ Наблюдение)= \frac{P(Наблюдение\ |\ Гипотеза)\cdot P(Гипотеза)}{P(Наблюдение)}\]
Перед тем, как разобрать эту запись теоремы Байеса, давайте взглянем на неё под другим углом.
\[P(Гипотеза\ |\ Наблюдение)= \frac{P(Наблюдение\ |\ Гипотеза)}{P(Наблюдение)}\cdot P(Гипотеза)\]
Теорема Байеса связывает \(P(Гипотеза)\) и \(P(Гипотеза\ |\ Наблюдение)\) – “изначальную”(априорную) и “обновлённую”(апостериорную) вероятности. Сначала существует некая уверенность в какой-то гипотезе, затем эту гипотезу тестируют. После тестирования новые экспериментальные данные обновляют эту уверенность. Коэффициентом пропорциональности между “изначальной” и “обновлённой” вероятностями выступает \(\frac{P(Наблюдение\ |\ Гипотеза)}{P(Наблюдение)}\).
Давайте представим ситуацию из жизни:
Вы верите, что Земля круглая. Однажды решив это подтвердить, вы вышли на улицу искать шарообразность и кривизну. Обойдя кучу мест, выехав даже в широкое поле, кривизны вы так и не заметили – вокруг всё плоское.
Итак, у вас была “изначальная” вероятность, что Земля круглая (\(P(Земля\: круглая))\). Затем, пронаблюдав, что всё вокруг плоское, вы хотите оценить “обновлённую” вероятность, что Земля круглая (\(P(Земля\:круглая\ |\ Всё\: плоское)\). Ход мыслей:
Ход мыслей:
1) Я всё обошёл, но везде всё плоское.
2) Если бы Земля была круглой, была бы кривизна.
Вывод: видимо, Земля не круглая, вопреки прошлым убеждениям.
Вот так в голове происходит обновление уверенности в теории после получения новой информации. Переведём слова на язык математики:
- Вы верите, что Земля круглая = \(P(Земля\: круглая) = 1\)
- Вы всё обошли, но везде всё плоское = \(P(Окрестности\: плоские) = 1\)
- Если бы Земля была круглой, была бы кривизна, и вы бы это заметили = \(P(Окрестности\: плоские\ |\ Земля\: круглая) = 0.01\), то есть вероятность того, что всё вокруг будет плоским, если Земля круглая, очень мала
Подставим всё в теорему Байеса и найдём “обновлённую” вероятность:
\[P(Земля\: круглая\ |\ Окрестности\: плоские)=\] \[=\frac{P(Окрестности\: плоские\ |\ Земля\: круглая)}{P(Окрестности\: плоские)}\cdot P(Земля\: круглая) = \frac{0.01}{1}\cdot 1 = 0.01\]
Конечно, Земля круглая, и можно сделать много других наблюдений, доказывающих это, но благодаря этому примеру мы увидели, как повседневные мыслительные процессы подчиняются теореме Байеса.
Теперь вернёмся к Дарине и найдём вероятность, что она работает библиотекарем, всё так же используя теорему Байеса. Что мы знаем про Дарину? Дарина работает библиотекарем — «Библиотекарь». Дарина спокойная, любит проводить время с собой и тишину — «Тихая». Мы хотим найти \(P(Библиотекарь\ |\ Тихая)\) — вероятность, что Дарина библиотекарь при условии, что она тихая. Чтобы визуально представить это, сохраним отношение библиотекарей к медсёстрам и скажем, что первых всего \(10\) человек, а вторых – \(300\).
Сначала выделим зеленым и оранжевым цветами всех, кто попадает под условие «Тихая». Вспомним, что среди библиотекарей тихих \(80\) процентов, то есть \(8\) человек из \(10\). Среди медсестёр \(5\) процентов тихих, то есть \(15\) человек из \(300\).
Таким образом, мы имеем \(8 + 15\) тихих людей — условие «тихости» выполнено. Теперь нужно найти вероятность, что Дарина библиотекарь. Для этого поделим количество библиотекарей среди тихих на общее количество тихих людей. \[P(Библиотекарь\ |\ Тихая) = \frac{8}{8 + 15} \approx 35\%\]Интуитивно мы разобрались с процессом, и настало время узнать, какая математика скрывается за этими библиотекарями и медсёстрами. Что есть эти \(8\) и \(15\)?
\[P(Библиотекарь\ |\ Тихая) = \frac{8}{8 + 15} \approx 35\%\]Интуитивно мы разобрались с процессом, и настало время узнать, какая математика скрывается за этими библиотекарями и медсёстрами. Что есть эти \(8\) и \(15\)?
Для начала разберёмся с событиями, происходящими вместе, то есть с событиями «и»-типа. В школе учили, что если мы видим «и» между событиями, то нужно перемножить вероятности этих событий, чтобы получить вероятность их одновременного свершения. Например, какова вероятность, что выпадут два орла подряд при подбрасывании монетки? Легко! Вероятность выпадения орла в первый раз умножаем на вероятность выпадения орла во второй: \(\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}\).
Как оказалось, нельзя всегда так просто ставить знак умножения между двумя вероятностями — нужно быть предельно аккуратным. К примеру, вероятность, что пойдёт дождь равна \(10\%\), а вероятность надеть пальто прямо перед выходом — \(20\%\). Подметим, что во время дождя вы обычно надеваете пальто. Какова вероятность, что вы наденете пальто, когда на улице идет дождь?
Подметим, что во время дождя вы обычно надеваете пальто. Какова вероятность, что вы наденете пальто, когда на улице идет дождь?
Очевидно, не \(0.1\cdot 0.2=0.02\). Иначе получается, что одновременно вы надели пальто и идёт дождь в \(2\) днях из \(100\), а вообще дождь идёт в \(10\) днях из \(100\). Получается, \(8\) из \(10\) дней, когда идёт дождь, вы ходите без пальто. Что-то не сходится.
Зависимые событияНо что пошло не так? В примере с дождём события зависимые. Если есть дождь, скорее всего есть и пальто. Пришло время познакомиться с новой формулой для «и»-событий: \[P(A \cap B) = P(A)\cdot P(B | A) \tag{$1$}\]Здесь запись \(P(A\cap B)\) означает вероятность, что произошли оба события \(A\) и \(B\). Прелесть этой формулы заключается в том, что она еще более логична и интуитивно понятна, чем простое перемножение вероятностей.
Понимать можно так. События \(A\) и \(B\) происходят вместе в том случае, если:
- Происходит событие \(A\)
- Происходит событие \(B\) с учётом, что \(A\) произошло
Для простоты можно считать, будто события \(A\) и \(B\) происходят одно за другим: сначала происходит \(A\) (вероятность чего \(P(A))\), а затем происходит \(B\), вероятность которого обозначаем как \(P(B | A)\). Думать о событиях как о происходящих одно за другим помогает понять формулу, но на деле порядок свершения событий не важен.
Думать о событиях как о происходящих одно за другим помогает понять формулу, но на деле порядок свершения событий не важен.
Давайте пересчитаем вероятность дождя и ношения пальто, чтобы закрепить. Добавим условие: если идёт дождь, вы надеваете пальто в \(90\%\) случаев, то есть \(P(Пальто\ |\ Дождь)=0.9\)\[P(Дождь\ \cap\ Пальто)=\]\[=P(Дождь)\cdot P(Пальто\ |\ Дождь)=0.1\cdot 0.9=0.09\]Так-то лучше! Каждые \(10\) из \(100\) дней льёт дождь, а каждые \(9\) из \(100\) дней льёт дождь и вы носите пальто. \(9\) из \(10\) — \(90\%\). Всё сходится!
Если вам интересно, что тогда делать с монетками и орлами, то вот ответ: каждое подбрасывание монетки не зависит от предыдущего. На математическом языке это означает \[P(Орёл\ второй\ |\ Орёл\ первый) = P(Орёл\ второй)\]Другими словами, вероятность того, что во второй раз выпадает орёл при условии, что в первый раз выпал орёл, просто равна вероятности, что во второй раз выпал орёл. Это работает так, потому что первый орёл никак не влияет на исход второго подбрасывания. Каждое подбрасывание монетки – независимое событие. Таким образом, \[P(Орёл\ первый \cap Орёл\ второй)=\]\[=P(Орёл\ первый)\cdot P(Орёл\ второй\ |\ Орёл\ первый)=\]\[=P(Орёл\ первый)\cdot P(Орёл\ второй)\]это старое доброе правило «и».
Это работает так, потому что первый орёл никак не влияет на исход второго подбрасывания. Каждое подбрасывание монетки – независимое событие. Таким образом, \[P(Орёл\ первый \cap Орёл\ второй)=\]\[=P(Орёл\ первый)\cdot P(Орёл\ второй\ |\ Орёл\ первый)=\]\[=P(Орёл\ первый)\cdot P(Орёл\ второй)\]это старое доброе правило «и».
Предоставленная формула (\(1\)) для высчитывания вероятности происхождения двух событий была не строго выведена из здравого смысла, а определена математиками. Это как с определениями слов в словаре, только у математиков вместо слов формулы.
P.S. Кто-то даже считает формулу (\(1\)) аксиомой теории вероятности!
Условная вероятность и доказательство теоремы БайесаОпределение условной вероятности:\[P(A\ |\ B)=\frac{P(A\ \cap\ B)}{P(B)}\] Отсюда и взялась формула (\(1\)), нужно только перекинуть \(P(B)\) влево. Теперь используем ту же формулу, но переставим местами \(A\) и \(B\):\[P(B | A)=\frac{P(A\cap B)}{P(A)}\]Выразим из обоих равенств \(P(A\cap B)\):\[P(A\cap B)=P(A | B)\cdot P(B)\]\[P(A\cap B)=P(B | A)\cdot P(A)\]Отсюда, приравняв \(P(A\cap B)\), получим\[P(A | B)\cdot P(B)=P(B | A)\cdot P(A) \implies P(A | B)=\frac{P(B | A)\cdot P(A)}{P(B)}\]
Библиотекари, медсёстры, “тихие” и теорема БайесаВернёмся к \(\frac{8}{8 + 15}\). Здесь \(8\) – это количество тихих библиотекарей. Количество тихих библиотекарей – это количество всех людей, умноженное на вероятность пребывания тихим библиотекарем. Воспользуемся новым правилом «и»: \[8 =310\cdot P(Библиотекарь)\cdot P(Тихая\ |\ Библиотекарь)\]В свою очередь, \(15\) это количество тихих людей, не являющихся библиотекарями. «Не» в математике записывается как \(\neg\). \(Не\ библиотекарь\ = \neg\ Библиотекарь\). Количество тихих людей, не являющихся библиотекарями, равно количеству всех людей, умноженному на вероятность пребывания тихим не-библиотекарем.
Здесь \(8\) – это количество тихих библиотекарей. Количество тихих библиотекарей – это количество всех людей, умноженное на вероятность пребывания тихим библиотекарем. Воспользуемся новым правилом «и»: \[8 =310\cdot P(Библиотекарь)\cdot P(Тихая\ |\ Библиотекарь)\]В свою очередь, \(15\) это количество тихих людей, не являющихся библиотекарями. «Не» в математике записывается как \(\neg\). \(Не\ библиотекарь\ = \neg\ Библиотекарь\). Количество тихих людей, не являющихся библиотекарями, равно количеству всех людей, умноженному на вероятность пребывания тихим не-библиотекарем.
Таким образом, \[15 = 310 \cdot P(\neg Библиотекарь)\cdot P(Тихая\ |\ \neg Библиотекарь)\]Подставим всё это в \(\frac{8}{8+15}\) и получим \[\frac{310\cdot P(Б)\cdot P(Т\ |\ Б)}{310\cdot P(Б)\cdot P(Т\ |\ Б) + 310\cdot P(\neg Б)\cdot P(Т\ |\ \neg Б)}\]Сократим \(310\):\[\frac{P(Б)\cdot P(Т\ |\ Б)}{P(Б)\cdot P(Т\ |\ Б) + P(\neg Б)\cdot P(Т\ |\ \negБ)}\]
* «Библиотекарь» = Б, «Тихая» = Т.
Удобно изобразить все графически. В первой картинке площадь синего прямоугольника обозначает вероятность, что Дарина работает библиотекарем – \(P(Б)\), а площадь красного прямоугольника обозначает вероятность, что Дарина не библиотекарь – \(P(\neg Б)\). Во второй картинке зеленым мы выделили вероятность, что Дарина тихий библиотекарь – \(P(Б)\cdot P(T\ |\ Б)\), а оранжевым – вероятность, что Дарина тихий не библиотекарь \(P(\neg Б)\cdot P(Т\ |\ \neg Б)\). Тогда вероятность, что Дарина библиотекарь, зная, что она тихая, будет как раз то, что мы написали сверху.
В первой картинке площадь синего прямоугольника обозначает вероятность, что Дарина работает библиотекарем – \(P(Б)\), а площадь красного прямоугольника обозначает вероятность, что Дарина не библиотекарь – \(P(\neg Б)\). Во второй картинке зеленым мы выделили вероятность, что Дарина тихий библиотекарь – \(P(Б)\cdot P(T\ |\ Б)\), а оранжевым – вероятность, что Дарина тихий не библиотекарь \(P(\neg Б)\cdot P(Т\ |\ \neg Б)\). Тогда вероятность, что Дарина библиотекарь, зная, что она тихая, будет как раз то, что мы написали сверху.
Последний штрих: заметим, что знаменатель гласит «вероятность, что Дарина тихая и библиотекарь или что она тихая и не библиотекарь». Это просто равно вероятности того, что она тихая. В итоге мы получаем \[\frac{8}{8+15} = P(Библиотекарь\ |\ Тихая) = \frac{P(Т\ |\ Б)\cdot P(Б)}{P(Т)}\]А это, если приглядеться, и есть теорема Байеса \[P(A\ |\ B)= \frac{P(B\ |\ A)\cdot P(A)}{P(B)}\]Сегодня теорема Байеса присутствует везде: и в вычислениях учёных, и в наших головах. Но сам Томас Байес не ожидал такой славы. На деле, он вообще не возлагал на неё никаких надежд. Теорема Байеса пылилась более десяти лет среди других работ британского математика и была обнаружена только после его смерти, когда семья попросила знакомого посмотреть, нет ли в записях Байеса ничего достойного публикации. Таким образом священник и математик Томас Байес, сам того не осознавая, положил начало современной философии теории вероятности.
Но сам Томас Байес не ожидал такой славы. На деле, он вообще не возлагал на неё никаких надежд. Теорема Байеса пылилась более десяти лет среди других работ британского математика и была обнаружена только после его смерти, когда семья попросила знакомого посмотреть, нет ли в записях Байеса ничего достойного публикации. Таким образом священник и математик Томас Байес, сам того не осознавая, положил начало современной философии теории вероятности.
Кто знает, может и у вас в голове таится какая-то революционная мысль, которую вы не замечаете. Может и у вас есть шанс каким-то маленьким открытием запустить цепочку событий, которая определит будущее человечества.
Применение и задачиОсталось научиться применять эту теорему. Она полезна, когда вы имеете дело со странными условными вероятностями. Например, “вероятность того, что вы в пальто, если идёт дождь” — интуитивно понятная вещь. Но “вероятность, что идёт дождь, если вы в пальто” — уже не очень.
Давайте как раз это и вычислим. Вспомним условия: \(P(Дождь)=0.1\), \(P(Пальто)=0.2\), \(P(Пальто\ |\ Дождь)=0.9\)
Вспомним условия: \(P(Дождь)=0.1\), \(P(Пальто)=0.2\), \(P(Пальто\ |\ Дождь)=0.9\)
По теореме Байеса, \[P(Дождь\ |\ Пальто)=\frac{P(Пальто\ |\ Дождь)\cdot P(Дождь)}{P(Пальто)}=\]\[=\frac{0.9\cdot 0.1}{0.2}=0.45\]
Задача о гене гениальностиПредположим, учёные выяснили, что ген гениальности существует и есть он у \(0.1\%\) населения Земли. Чтобы искать гениев, те же учёные изобрели тест, показывающий наличие или отсутствие гена гениальности. Точность этого теста — \(99\%\). Вы решили из интереса провериться и отдали биоматериал на исследование. Вскоре вам звонят и сообщают, что тест показал, что вы носитель гена гениальности. С какой вероятностью он у вас есть?
Решение
На первый взгляд суть вопроса может быть вообще непонятна. Что значит «с какой вероятностью»? Там же написано, что \(99\%\). Что ж, давайте считать.
Пусть \(P(Гений)\) — вероятность наличия гена гениальности. \(P(Положительный\ |\ Гений)\) — вероятность положительного результата теста при условии, что у вас есть ген гениальности. \(P(Положительный)\) — вероятность того, что результат теста положительный.
\(P(Положительный)\) — вероятность того, что результат теста положительный.
Всё это мы используем в формуле \[P(Гений\ |\ Положительный)=\frac{P(Положительный\ |\ Гений)\cdot P(Гений)}{P(Положительный)}\] и найдём ответ на вопрос нашей задачи.
Начнём с нахождения \(P(Гений)\), \(P(Положительный\ |\ Гений)\), \(P(Положительный)\).
\(P(Гений)=0.001\), так как ген гениальности встречается с вероятностью \(0.1\%\) — у каждого тысячного человека. \(P(Положительный\ |\ Гений)=0.99\), так как точность теста \(99\%\). C \(P(Положительный)\) чуть сложнее. Сначала нужно расписать эту вероятность как сумму. Тест может показать “+”, когда он правильно определяет наличие гена в \(99\%\) случаев и когда он ошибается в \(1\%\) случаев, выдавая ложный положительный результат. Снова, чтобы уместить все в строку заменим «Положительный» на «П», а «Гений» на «Г». Учитывая вышеуказанные выводы, получим: \[P(П)=P(П\cap Г) + P(П\cap \neg Г)=P(Г)\cdot P(П\ |\ Г)+P(\neg Г)\cdot P(П\ |\ \neg Г)\]А последнее выражение посчитать мы можем. \(P(Г)=0.001\), так как каждый тысячный человек – гений. \(P(\neg Г)=0.999\), так как все остальные \(999\) человек из тысячи не гении. \(P(П\ |\ Гений)=99\%\), так как это точность теста. \(P(П\ |\neg Г)=1\%\), так как это вероятность, что тест ошибётся.
\(P(Г)=0.001\), так как каждый тысячный человек – гений. \(P(\neg Г)=0.999\), так как все остальные \(999\) человек из тысячи не гении. \(P(П\ |\ Гений)=99\%\), так как это точность теста. \(P(П\ |\neg Г)=1\%\), так как это вероятность, что тест ошибётся.
Подставим:\[P(Положительный)=0.001\cdot 0.99 + 0.999\cdot 0.01=0.01098\]Теперь можно и всё подставлять в основную формулу!\[P(Г\ |\ П)=\frac{P(П\ |\ Г)\cdot P(Г)}{P(П)}=\frac{0.99\cdot 0.001}{0.01098}\approx 0.09016%\]Следовательно, если тест выдал положительный результат, то вы являетесь гением с вероятностью \(9\%\)!
Но почему так? Тест ведь \(99\)-процентный! Может теорема Байеса не работает?
Давайте поймем на уровне интуиции, почему всё-таки \(9\%\). Вспомним, что гением является лишь один человек из тысячи. Пусть учёные взяли биоматериал у каждого из этой тысячи и провели тесты. Так как точность теста лишь \(99\%\), \(1\%\) людей получили неправильный результат. Грубо говоря, \(1000\cdot 0.01=10\) человек получили положительный результат, не являясь гениями. Если прибавить к ним настоящего гения, получится \(11\) человек. И лишь один среди них будет гением. Так и получается примерно \(9\%\).
Если прибавить к ним настоящего гения, получится \(11\) человек. И лишь один среди них будет гением. Так и получается примерно \(9\%\).
Надо заметить, что здесь всё не так просто: тест мог бы и не выявить гения из-за возможности ошибки. В объяснении учтены не все варианты, но оно выполняет свою работу, давая интуицию.
Продолжение
Вы уверены в своей гениальности и решили снова сдать тот же тест. Какова вероятность, что вы гений, если во второй раз результат тоже положительный?
Задача о машинках и инспектореНа заводе производятся игрушечные машинки. \(10\%\) из них оказываются бракованными. Инспектор, который отвечает за проверку машинок на наличие брака, проверяет их выборочно. Через него проходят \(60\%\) бракованных и \(20\%\) исправных машинок. Какова вероятность, что выбранная инспектором машинка окажется бракованной?
Решение
\(P(Брак)\) — вероятность того, что машинка бракованная. По условию, \(P(Брак)=10\%\)
По условию, \(P(Брак)=10\%\)
\(P(Тест)\) – вероятность того, что инспектор выберет конкретную машинку.
Так сразу \(P(Тест)\) из условия мы взять не можем, но зато у нас есть \(P(Тест\ |\ Брак)\) и \(P(Тест \ |\ \negБрак)\) – вероятности, что бракованная и не бракованная машинки попадут к инспектору.
\(P(Тест\ |\ Брак) = 60\%\)
\(P(Тест \ |\ \negБрак) = 20\%\)
Мы извлекли из условия все полезные данные, теперь поймём, что нужно найти. Вероятность того, что выбранная машинка окажется бракованной, на математическом языке означает \(P(Брак\ |\ Тест)\)
По теореме Байеса
\[P(Брак\ |\ Тест) = \frac{P(Тест\ |\ Брак)\cdot P(Брак)}{P(Тест)}\]
\(P(Тест\ |\ Брак)\) и \(P(Брак)\) у нас есть, а \(P(Тест)\) придётся найти. Так как события \(Брак\) и \(\negБрак\) взаимоисключающие, \[P(Тест) = P(Тест\ \cap\ Брак) + P(Тест\ \cap\ \negБрак)\]
На русском это означает, что вероятность выбора машинки для инспекции равна сумме двух вероятностей: машинка выбрана и бракована, машинка выбрана и не бракована.
Из определения условной вероятности,
\[P(Тест\ \cap\ Брак) = P(Тест\ |\ Брак)\cdot P(Брак)\]\[P(Тест\ \cap\ \negБрак) = P(Тест\ |\ \negБрак)\cdot P(\negБрак)\]
Следовательно,
\[P(Тест) = P(Тест\ |\ Брак)\cdot P(Брак) + P(Тест\ |\ \negБрак)\cdot P(\negБрак)\]
Подставив это в теорему Байеса, получим:
\[P(Брак\ |\ Тест) = \frac{P(Тест\ |\ Брак)\cdot P(Брак)}{P(Тест\ |\ Брак)\cdot P(Брак) + P(Тест\ |\ \negБрак)\cdot P(\negБрак)}\]
Подставим все значения:
\[P(Брак\ |\ Тест) = \frac{0.6\cdot 0.1}{0.6\cdot 0.1 + 0.2\cdot 0.9} = \frac{0.06}{0.06 + 0.18} = 0.25\]
Задача о красоте картинАндрей, Борис и Влад написали картины для школьной ярмарки. Они написали разное их количество и имеют разные уровни профессионализма:
Андрей написал \(5\) картин, \(80\%\) его картин красивые.
Борис написал \(15\), \(60\%\) его картин красивые.
Влад написал \(10\), \(30\%\) его картин красивые.
Какова вероятность, что выбранная красивая картина была написана Борисом?
Решение
Из условия:
\(P(Красивая\ |\ Андрей) = 0. 8\) – вероятность, что выбранная картина Андрея красивая. Аналогично, \(P(Красивая\ |\ Борис) = 0.6\) и \(P(Красивая\ |\ Влад) = 0.3\)
8\) – вероятность, что выбранная картина Андрея красивая. Аналогично, \(P(Красивая\ |\ Борис) = 0.6\) и \(P(Красивая\ |\ Влад) = 0.3\)
Найти: \(P(Борис\ |\ Красивая)\)
По теореме Байеса \[P(Борис\ |\ Красивая) = \frac{P(Красивая\ |\ Борис)\cdot P(Борис)}{P(Красивая)}\]
Найдём \(P(Борис)\) и \(P(Красивая)\):
Всего у нас \(5 + 15 + 10 = 30\) картин, 15 из которых написал Борис, поэтому \[P(Борис) = \frac{Написанные\ Борисом}{Всего\ картин} = \frac{15}{30} = 0.5\]
Красивых картин у нас \(5\cdot0.8 + 15\cdot0.6 + 10\cdot0.3 = 4 + 9 + 3 = 16\). Значит \(P(Красивая)=\frac{Красивые\ картины}{Всего\ картин} = \frac{16}{30} = \frac{8}{15} = 0.5(3)\)
Подставим:
\[P(Борис\ |\ Красивая) = \frac{P(Красивая\ |\ Борис)\cdot P(Борис)}{P(Красивая)} = \frac{0.6\cdot 0.5}{0.5(3)}=0.562\]
Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.
Редактор статьи: Дарина Мухамеджанова
Формула Байеса (формула вероятностей гипотез) — Мегаобучалка
Если до опыта вероятности гипотез H1, H2, … Hn были равны P(H1), P(H2), …, P(Hn), а в результате опыта произошло событие А, то новые (условные) вероятности гипотез вычисляются:
(2.14)
Доопытные (первоначальные) вероятности гипотез P(H1), P(H2), …, P(Hn) называются априорными, а послеопытные — P(H1| А), … P(Hn| А) – апостериорными.
Формула Байеса позволяет «пересмотреть» возможности гипотез с учетом полученного результата опыта.
Доказательство формулы Байеса следует из предшествующего материала. Поскольку P(Hi А) = P(Hi) P(А| Hi) = P(Hi)·P(Hi| А):
(2.15)
откуда, с учетом (2.13), получается выражение (2.
Если после опыта, давшего событие А, проводится еще один опыт, в результате которого может произойти или нет событие А1, то условная вероятность этого последнего события вычисляется по (2.13), в которую входят не прежние вероятности гипотез P(Hi), а новые — P(Hi| А):
(2.16)
Выражение (2.16) называют формулой для вероятностей будущих событий.
Контрольные вопросы и задачи:
1. Перечислите показатели безотказности объекта и поясните, чем отличаются статистическая (выборочные оценки) и вероятностная форма (определения)?
2. Поясните «схему испытаний» объекта при определении выборочных оценок показателей безотказности?
3. Дайте определение «оценки» вероятности события и объясните условие сходимости оценки и вероятности события?
4. Перечислите и поясните основные аксиомы вероятности?
5. Перечислите и поясните смысл основных правил (теорем) теории вероятностей?
6. Назовите следствия основных теорем теории вероятностей?
Назовите следствия основных теорем теории вероятностей?
7. Прибор может работать в двух режимах: «1» и «2». Режим «1» наблюдается в 80% случаев, режим «2» — в 20% случаев за время работы T. Вероятность того, что прибор откажет при работе в режиме «1» равна 0.1, а вероятность отказа прибора в режиме «2» — 0.7. Найти вероятность отказа прибора за время T?
Ответ: 0.22
8. Прибор состоит из 3-х блоков, которые независимо друг от друга могут отказать. Отказ каждого из блоков приводит к отказу всего прибора. Вероятность того, что за время T работы прибора откажет первый блок, равна 0.2, второй – 0.1, третий – 0.3. Найти вероятность того, что за время T прибор проработает безотказно?
Ответ: 0.504
9. Прибор состоит из 2-х блоков, дублирующих друг друга. Вероятность того, что за время T каждый из блоков проработает безотказно, равна 0.9. Отказ прибора произойдет при отказе обоих блоков. Найти вероятность того, что за время T прибор проработает безотказно?
Ответ: 0. 99
99
ПОКАЗАТЕЛИ БЕЗОТКАЗНОСТИ: ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ОТКАЗОВ, ИНТЕНСИВНОСТЬ ОТКАЗОВ
Общие понятия о показателях безотказности, формах их представления и схеме испытаний объектов (элементов системы управления) приведены в разделе 2.
Узнайте определение, формулу, доказательство и примеры здесь!
Теорема Байеса/Теорема Байеса — это простой математический метод, используемый для вычисления условных вероятностей. Теорема Байеса была придумана в честь британского математика Томаса Байеса. Теорема Байеса также определяется как правило Байеса / закон Байеса и является основой области байесовской статистики.
Формула Байеса представляет собой вероятность возникновения события при любом условии. Это полезно для случая условной вероятности. Прокручивая вниз, мы узнаем об определении теоремы Байеса, формуле Байеса, концепциях условной вероятности и теореме Байеса с решенными примерами и многим другим.
Содержание
- Что такое теорема Байеса?
- Условная вероятность.
Теорема Байеса определяет условную вероятность события при условии, что другое событие уже произошло. Просто мы можем заявить, что это процесс ограничения вероятности события в зависимости от возникновения предыдущих событий, который также понимается как правило Байеса или закон Байеса.
С точки зрения математической формулировки теорема читается как:
P(A/B) = насколько вероятно, что произойдет A при условии, что B произошло
Аналогично,
P(B/A) = насколько вероятно, что B произойдет при условии, что произошло А.
Прежде чем перейти к формуле и теореме Байеса, давайте изучим некоторые важные термины, связанные с ними.
- Событие: Возможные подмножества выборочного пространства, связанные со случайным экспериментом, называются событием эксперимента.

- Случайный эксперимент: Это действие, результат которого неизвестен, то есть эксперимент, результат которого нельзя предсказать с уверенностью. Например, бросок игральной кости или монеты, или выбор карты из группы карт и т. д.
- Вероятность : Вероятность события определяется как отношение числа случаев в его пользу к общее количество дел. Рассмотрим S как выборочное пространство, а E — событие, такое что n(S) = n, n(E) = m и каждый исход равновероятен. Тогда:
- \(p\left(E\right)=\frac{n\left(E\right)}{n\left(S\right)}=\frac{m}{n}=\frac{\text {Количество благоприятных исходов E}}{\text{Общее число возможных исходов}}\)
- Случайные величины: Случайная величина обозначает вещественную переменную, потенциальные значения которой определяются случайным экспериментом.
- Условная вероятность: Условная вероятность — это вероятность события, устанавливаемая при наступлении другого события.
 Математически выражается как P (A | B). Выражение представляет собой вероятность A при условии, что событие B уже произошло.
Математически выражается как P (A | B). Выражение представляет собой вероятность A при условии, что событие B уже произошло. - Апостериорная вероятность: Когда вероятность события рассчитывается после того, как собраны все данные, связанные с событием, такая вероятность называется апостериорной вероятностью.
- Априорная вероятность : Как следует из названия, это вероятность исхода, которая определяется на основе существующих знаний до выполнения эксперимента.
Изучите различные концепции биномиальной теоремы здесь.
Условная вероятностьТеория формулы условной вероятности фундаментально связана с теоремой Байеса, которая является одной из самых влиятельных теорий в статистике. Условная вероятность — это вероятность того, что одно событие произойдет в той или иной степени по отношению к одному или нескольким другим событиям.
Пусть A и B — любые два события, связанные со случайным экспериментом.
 Тогда вероятность наступления события A при условии, что B уже произошло, так что вероятность B не равна нулю (P(B) ≠ 0), называется условной вероятностью и обозначается P(A | Б).
Тогда вероятность наступления события A при условии, что B уже произошло, так что вероятность B не равна нулю (P(B) ≠ 0), называется условной вероятностью и обозначается P(A | Б).\(P\left(A\mid\B\right)=\frac{P\left(A\\cap B\right)}{P\left(B\right)},\ \text{где } P\left(B\right)\ne0 \)
Аналогично,
\(P\left(B\mid\ A\right)=\frac{P\left(A\ \cap B\right)}{ P\left(A\right)},\text{ где } P\left(A\right)\ne0 \)
Формула теоремы БайесаТеорема Байеса определяет вероятность события, скажем, «A» при условии, что событие «В» уже произошло. Это процесс определения вероятности события на основе возникновения предыдущих событий.
Формулы теоремы Байеса выводятся из определения условной вероятности. Его можно вывести для событий A и B, а также для непрерывных случайных величин X и Y.
Рассмотрим \(E1, E2, ….., En \) n взаимоисключающих и исчерпывающих событий, связанных со случайным экспериментом, и пусть S — выборочное пространство.
Доказательство теоремы Байеса nP\left( E_i\вправо)\times P\влево(A\середина E_i\вправо)},\ i=1,2,……,n \).
nP\left( E_i\вправо)\times P\влево(A\середина E_i\вправо)},\ i=1,2,……,n \).\(P(A\mid B)=\frac{P\left(B\mid A\right)P(A)}{P(B)}\ где\ P(B )\ne0\\ \)
По определению условной вероятности.
\(P(A\mid B)=\frac{P(A∩B)}{P(B)},\ P(B)\ne0\ and\ P(A∩B)=P(B∩ A)=P(B\mid A)P(A)\\ \)
Поэтому \( P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B )} \)
Если вы освоили теорему Байеса, вы также можете узнать о теореме Ролля и теореме Лагранжа о среднем значении
Применение теоремы БайесаТеорема Байеса применяется для определения условной вероятности.
- Некоторые из наиболее популярных применений условной вероятности включают прогноз результатов в случае подбрасывания монеты, выбора карты из колоды и бросания игральной кости.
- Он также помогает специалистам по обработке и анализу данных получать лучшие результаты при анализе заданного набора данных.
- Для инженеров по машинному обучению он служит для подготовки более подробных моделей прогнозирования.

- Теорема Байеса используется в байесовском выводе, особом методе статистического вывода.
- Байесовский вывод нашел применение в различных проектах, включая медицину, спорт, философию, науку, инженерию, юриспруденцию и т. д.
- Теорему Байеса можно использовать для определения эффективности результатов медицинских тестов путем изучения вероятности есть это заболевание и общая эффективность теста.
- Теорема Байеса имеет различные приложения; Байесовский вывод в области здравоохранения используется для выявления вероятности роста проблем со здоровьем с увеличением возраста и многих других проблем.
Зная определение, формулу и связанные термины, давайте попрактикуемся в решении некоторых примеров:
Решенный пример 1: Есть две сумки. В мешке А 7 красных и 4 синих шара, а в мешке Б 5 красных и 9 синих шаров. Случайным образом вытягивается один шар, и он оказывается красным.
 Определить вероятность того, что мяч был из мешка А, используя теорему Байеса.
Определить вероятность того, что мяч был из мешка А, используя теорему Байеса.Решение: Пусть U и V будут событиями, когда мяч достается из мешка A и мешка B соответственно. Предположим, что X — это событие выбора красного шара. Мы помним, что вероятность подобрать мешочек для вытягивания шара равна 1/2, то есть:
\(P(U)=P(V)=\frac{1}{2} \)
\(\text{Поскольку из 11 шаров в мешке A 7красных,} \)
\(\text{отсюда P(извлечение красного шара из мешка A)}=P(X\mid U)=\frac{7}{11} \)
\(\text{Аналогично, P ( вытягивание красного шара из мешка B)}=P(X\mid V)=\frac{5}{14} \)
\(\text{Нам нужно найти значение:}\)
\( \text{P(мяч взят из мешка A, учитывая, что это красный шар), то есть},\ P(U\mid X). \)
\(\text{Используя теорему Байеса, мы имеем следующий результат :}\)
\(P(U\mid X)=\frac{P\left(X\mid U\right)P\left(U\right)}{P\left(X\mid U\right)P\left (U \ справа) + P \ слева (X \ середина V \ справа) P (\ слева (V \ справа)} \\ \)
\ (= \ гидроразрыва {\ влево (\ гидроразрыва {7} {11} \right)\left(\frac{1}{2}\right)}{\left(\frac{7}{11}\right)\left(\frac{1}{2}\right)+\left (\frac{5}{14}\right)\left(\frac{1}{2}\right)}=0,64\\ \)
\(\text{Поэтому вероятность того, что шар вытащен, равна из мешка А равно 0,64.
 } \)
} \)Если вы читаете теорему Байеса, прочтите также о множествах.0003
Решено Пример 2: Предположим, в мешке A 4 красных и 5 черных шаров, а в другом мешке B 6 красных и 7 черных шаров. Из одного из мешков наугад вынимают один шар, и он оказывается красным. Найдите вероятность того, что он взят из мешка B?
Решение:
Концепция:
Теорема Байеса:
Пусть \(E_{1}, E_{2}, ….., E_{n} \) будет n взаимоисключающими и исчерпывающими событиями, случайный эксперимент, и пусть S будет выборочным пространством. Пусть A — любое событие, которое происходит вместе с любым из \(E_1\text{ или}\ E_2\text{ или }\cdots\text{ или }E_n \), такое, что P(A) ≠ 0. Тогда 9nP\left(E_i\right)\times P\left(A\mid E_i\right)},\ i=1,2,……,n \)
Расчет:
Пусть E1 — событие выбора мешок A, E2 — событие выбора мешка B, а X — событие извлечения красного шара.
\(\Стрелка вправо P\влево(E_1\вправо)=P\влево(E_2\вправо)=\frac{1}{2}.
 \)
\)\(\Стрелка вправо P\влево(X\середина E_1\ right)=P(\text{Вытягивание красного шара из мешка A})=\frac{4}{9} \)
Аналогично,
\(P\left(X\mid E_2\right)=P( \text{Вытягивание красного шара из мешка B})=\frac{6}{13} \) 9nP\left(E_i\right)\times P\left(A\mid E_i\right)},\ i=1,2,……,n \)
\(P\left(E_2\mid X\right )=\frac{P\left(E_2\right)\times P\left(X\mid E_2\right)}{P\left(E_1\right)\times P\left(X\mid E_1\right)+ P\left(E_2\right)\times P\left(X\mid E_2\right)} \)
\(P\left(E_2\mid X\right)=\frac{P\left(E_2\right) )\times P\left(X\mid E_2\right)}{P\left(E_1\right)\times P\left(X\mid E_1\right)+P\left(E_2\right)\times P\ влево (X \ середина E_2 \ вправо)} = \ гидроразрыва {\ гидроразрыва {1} {2} \ раз \ гидроразрыва {6} {13}} {\ гидроразрыва {1} {2} \ раз \ гидроразрыва {4} { 9}+\frac{1}{2}\times\frac{6}{13}} \)
\(P\left(E_2\mid X\right)=\frac{\frac{1}{2} \times\frac{6}{13}}{\frac{1}{2}\times\frac{4}{9}+\frac{1}{2}\times\frac{6}{13}} =\frac{27}{53} \)
Также изучите различные типы отношений и функций.

Решено Пример 3: Если в мешке A 4 красных и 4 черных шара, а в другом мешке B 2 красных и 6 черных шаров. Наугад выбирается один из двух мешков, из мешка вынимается шар, и оказывается, что он красный. Найдите вероятность того, что он взят из мешка А? 9nP\left(E_i\right)\times P\left(A\mid E_i\right)},\ i=1,2,……,n \)
Расчет:
Пусть E1 — событие выбора мешка A, E2 — событие выбора мешка B, а X — событие извлечения красного шара.
\(\Стрелка вправо P\влево(E_1\вправо)=P\влево(E_2\вправо)=\frac{1}{2}. \)
\(\Стрелка вправо P\влево(X\середина E_1\ right)=P(\text{Вытягивание красного шара из мешка A})=\frac{4}{8}=\frac{1}{2} \)
\(P\left(X\mid E_2\ right)=P(\text{Вытягивание красного шара из мешка B})=\frac{2}{8}=\frac{1}{4} \)
Здесь мы должны найти вероятность вытащить шар из мешка A при условии, что шар красного цвета, т.е. \(P\left(E_1\mid X\right). \)
Применяя теорему Байеса, получаем :
\(P\left(E_1\mid X\right)=\frac{P\left(E_1\right)\times P\left(X\mid E_1\right)}{P\left(E_1\right) )\times P\left(X\mid E_1\right)+P\left(E_2\right)\times P\left(X\mid E_2\right)} \)
\(P\left(E_1\mid X\right)=\frac{P\left(E_1\right)\times P\left(X\mid E_1\right)}{P\left(E_1\right)\times P\left(X\mid E_1\ вправо)+P\влево(E_2\вправо)\times P\left(X\mid E_2\right)}=\frac{\frac{1}{2}\times\frac{1}{2}}{\ frac{1}{2}\times\frac{1}{2}+\frac{1}{2}\times\frac{1}{4}} \)
\(P\left(E_1\mid X\right)=\frac{\frac{1}{2}\times\frac{1}{2}}{\frac{1}{2}\times\ frac{1}{2}+\frac{1}{2}\times\frac{1}{4}}=\frac{2}{3} \)
Ознакомьтесь с этой статьей о последовательностях и сериях.

Решено Пример 4: Два игральных кубика бросаются одновременно. Найдите вероятность того, что сумма выпавших на них чисел будет простым числом?
Решение:
Пример пространства для одновременного броска двух игральных костей:
S = {(a, b)} {где a = 1, 2, ….., 6 и b = 1, 2, ……, 6}
⇒ n (S) = 36
Решение. Пусть A — подмножество S, определенное как A = {(a, b) | a + b — простое число.
А = {(1, 1), (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (4, 1), (4, 3), (5, 2), (5, 6), (6, 1), (6, 5)}
⇒ n ( A) = 15
Как мы знаем,
\(P\left(A\right)=\frac{n\left(A\right)}{n\left(S\right)}\\ \)
\(P\left(A\right)=\frac{n\left(A\right)}{n\left(S\right)}=\frac{15}{36}=\frac{5} {12} \)
Мы надеемся, что приведенная выше статья о теореме Байеса поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам.
Часто задаваемые вопросы по теореме Байеса Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.В.1 Что такое теорема Байеса простыми словами?
Ответ 1 Теорема Байеса или теорема Байеса Теорема Байеса — это простой математический метод, используемый для вычисления условных вероятностей. Теорема Байеса была названа в честь британского математика Томаса Байеса.
В.2 Где можно использовать правило Байеса?
Ответ 2 Теорема Байеса применяется для определения условной вероятности. Он используется в байесовском выводе, особом способе статистического вывода. Он также помогает специалистам по обработке и анализу данных получать лучшие результаты при анализе заданного набора данных.
Q.3 Что такое формулировка теоремы Байеса?
Ответ 3 Теорема Байеса определяет вероятность события, скажем, «А», при условии, что событие «В» уже произошло.
Это процесс определения вероятности события на основе возникновения предыдущих событий.
Q.4 Что такое теорема Байеса в вероятности?
Ответ 4 Теорема Байеса утверждает, что условная вероятность события A при наличии другого события B равна произведению вероятности B при данном A и вероятности A
В.5. Что такое пример теоремы Байеса?
Ans.5 Теорема Байеса также признана формулой для вероятности «причин». Например: если нам требуется определить вероятность вынуть красный шар из второго мешка из трех разных мешков с шарами, где каждый мешок содержит три шара разного цвета, а именно. красный, черный, желтый.
Скачать публикацию в формате PDFЕще на testbook.com
Величина: знание определения, величины действительного числа и векторы с примерами Режим: определение, формулы, типы и примеры решения Формула расстояния: знание определения с подробными формулами и примерами решения 9 Элемент , соединения и молекулы — определение, законы и объяснение Основные понятия химии — определение, классификация, важность и другие примечания Что это такое, формула и примеры
Что такое теорема Байеса?
Теорема Байеса, названная в честь британского математика XVIII века Томаса Байеса, представляет собой математическую формулу для определения условной вероятности.
 Условная вероятность — это вероятность возникновения исхода, основанная на предыдущем исходе, произошедшем в аналогичных обстоятельствах. Теорема Байеса дает возможность пересмотреть существующие прогнозы или теории (обновить вероятности) с учетом новых или дополнительных доказательств.
Условная вероятность — это вероятность возникновения исхода, основанная на предыдущем исходе, произошедшем в аналогичных обстоятельствах. Теорема Байеса дает возможность пересмотреть существующие прогнозы или теории (обновить вероятности) с учетом новых или дополнительных доказательств.В финансах теорему Байеса можно использовать для оценки риска кредитования потенциальных заемщиков. Эта теорема также называется правилом Байеса или законом Байеса и является основой области байесовской статистики.
Ключевые выводы
- Теорема Байеса позволяет обновлять предсказанные вероятности события путем включения новой информации.
- Теорема Байеса была названа в честь математика 18-го века Томаса Байеса.
- Часто используется в финансах для расчета или обновления оценки риска.
- Теорема стала полезным элементом в реализации машинного обучения.
- Теорема не использовалась в течение двух столетий из-за большого объема вычислительных мощностей, необходимых для выполнения ее транзакций.

Понимание теоремы Байеса
Применение теоремы Байеса широко распространено и не ограничивается финансовой сферой. Например, теорему Байеса можно использовать для определения точности результатов медицинских анализов, принимая во внимание вероятность заболевания любого конкретного человека и общую точность теста. Теорема Байеса основана на включении априорных распределений вероятностей для получения апостериорных вероятностей.
Априорная вероятность в байесовском статистическом выводе — это вероятность того, что событие произойдет до того, как будут собраны новые данные. Другими словами, он представляет собой наилучшую рациональную оценку вероятности определенного результата, основанную на текущих знаниях до проведения эксперимента.
Апостериорная вероятность — это пересмотренная вероятность события, происходящего после учета новой информации. Апостериорная вероятность рассчитывается путем обновления априорной вероятности с использованием теоремы Байеса.
 В терминах статистики апостериорная вероятность — это вероятность наступления события А при условии, что произошло событие В.
В терминах статистики апостериорная вероятность — это вероятность наступления события А при условии, что произошло событие В.Особые указания
Таким образом, теорема Байеса дает вероятность события на основе новой информации, которая связана или может быть связана с этим событием. Формулу также можно использовать для определения того, как гипотетическая новая информация может повлиять на вероятность события, если предположить, что новая информация окажется верной.
Например, вытяните одну карту из полной колоды из 52 карт.
Вероятность того, что карта является королем, равна четырем, разделенным на 52, что равно 1/13 или приблизительно 7,69.%. Помните, что в колоде четыре короля. Теперь предположим, что выяснилось, что выбранная карта является лицевой. Вероятность того, что выбранная карта является королем, если это фигурная карта, равна четырем, деленным на 12, или примерно 33,3%, поскольку в колоде 12 лицевых карт.
Формула для теоремы Байеса
п ( А ∣ Б ) знак равно п ( А ⋂ Б ) п ( Б ) знак равно п ( А ) ⋅ п ( Б ∣ А ) п ( Б ) куда: п ( А ) знак равно Вероятность возникновения А п ( Б ) знак равно Вероятность появления B п ( А ∣ Б ) знак равно Вероятность A при B п ( Б ∣ А ) знак равно Вероятность B при условии A п ( А ⋂ Б ) ) знак равно Вероятность того, что произойдут события А и В.
 \begin{align} &P\left(A|B\right)=\frac{P\left(A\bigcap{B}\right)}{P\left(B\right)}=\frac{P\left (A\right)\cdot{P\left(B|A\right)}}{P\left(B\right)}\\ &\textbf{где:}\\ &P\left(A\right)= \text{ Вероятность появления A}\\ &P\left(B\right)=\text{ Вероятность появления B}\\ &P\left(A|B\right)=\text{Вероятность заданного A B}\\ &P\left(B|A\right)=\text{ Вероятность B при данном A}\\ &P\left(A\bigcap{B}\right))=\text{ Вероятность обоих A и B встречается}\\ \end{выровнено}
P(A∣B)=P(B)P(A⋂B)=P(B)P(A)⋅P(B∣A)где: P(A) = вероятность наступления A P(B )= Вероятность В появления P(A∣B)= Вероятность A при заданном BP(B∣A)= Вероятность B при заданном AP(A⋂B))= Вероятность нахождения A и B
\begin{align} &P\left(A|B\right)=\frac{P\left(A\bigcap{B}\right)}{P\left(B\right)}=\frac{P\left (A\right)\cdot{P\left(B|A\right)}}{P\left(B\right)}\\ &\textbf{где:}\\ &P\left(A\right)= \text{ Вероятность появления A}\\ &P\left(B\right)=\text{ Вероятность появления B}\\ &P\left(A|B\right)=\text{Вероятность заданного A B}\\ &P\left(B|A\right)=\text{ Вероятность B при данном A}\\ &P\left(A\bigcap{B}\right))=\text{ Вероятность обоих A и B встречается}\\ \end{выровнено}
P(A∣B)=P(B)P(A⋂B)=P(B)P(A)⋅P(B∣A)где: P(A) = вероятность наступления A P(B )= Вероятность В появления P(A∣B)= Вероятность A при заданном BP(B∣A)= Вероятность B при заданном AP(A⋂B))= Вероятность нахождения A и B Примеры теоремы Байеса
Ниже приведены два примера теоремы Байеса, в которых первый пример показывает, как формула может быть получена на примере инвестирования в акции с использованием Amazon.com Inc. (AMZN). Второй пример применяет теорему Байеса к тестированию фармацевтических препаратов.

Вывод формулы теоремы Байеса
Теорема Байеса следует просто из аксиом условной вероятности. Условная вероятность — это вероятность события при условии, что произошло другое событие. Например, простой вероятностный вопрос может звучать так: «Какова вероятность падения курса акций Amazon.com?» Условная вероятность поднимает этот вопрос еще на один шаг, спрашивая: «Какова вероятность того, что цена акций AMZN упадет 9?0417, учитывая, что промышленный индекс Доу-Джонса (DJIA) упал ранее?»
Условная вероятность A при условии, что B произошло, может быть выражена как:
Если A означает: «цена AMZN падает», то P(AMZN) — это вероятность того, что AMZN упадет; и B: «DJIA уже упал», а P(DJIA) — вероятность того, что DJIA упал; тогда выражение условной вероятности читается как «вероятность того, что AMZN упадет при снижении индекса DJIA, равна вероятности того, что цена AMZN упадет, а индекс DJIA упадет по сравнению с вероятностью снижения индекса DJIA».

P(AMZN|DJIA) = P(AMZN и DJIA) / P(DJIA)
P(AMZN и DJIA) – это вероятность того, что 90 417 произойдут как 90 418 A, так и B. Это также то же самое, что вероятность A, умноженная на вероятность B при условии, что A произойдет, выраженная как P(AMZN) x P(DJIA|AMZN). Тот факт, что эти два выражения равны, приводит к теореме Байеса, которая записывается как:
если P(AMZN и DJIA) = P(AMZN) x P(DJIA|AMZN) = P(DJIA) x P(AMZN|DJIA)
тогда P(AMZN|DJIA) = [P(AMZN) x P(DJIA|AMZN)] / P(DJIA).
Где P(AMZN) и P(DJIA) — вероятности падения Amazon и Dow Jones независимо друг от друга.
Формула объясняет взаимосвязь между вероятностью гипотезы до того, как будут получены доказательства P(AMZN), и вероятностью гипотезы после получения доказательств P(AMZN|DJIA), учитывая гипотезу для Amazon с учетом доказательств в индексе Доу.
Численный пример теоремы Байеса
В качестве числового примера представьте, что есть тест на наркотики, который составляет 9Точность 8% означает, что в 98% случаев он показывает истинно положительный результат для тех, кто употребляет наркотик, и в 98% случаев показывает истинно отрицательный результат для тех, кто не употребляет наркотик.

Далее предположим, что 0,5% людей употребляют наркотики. Если случайно выбранный человек дал положительный результат на наркотик, можно сделать следующий расчет, чтобы определить вероятность того, что человек действительно употребляет наркотик.
(0,98 х 0,005) / [(0,98 х 0,005) + ((1 — 0,98) х (1 — 0,005))] = 0,0049 / (0,0049+ 0,0199) = 19,76%
Теорема Байеса показывает, что даже если человек дал положительный результат в этом сценарии, вероятность того, что человек не примет наркотик, составляет примерно 80%.
Какова история теоремы Байеса?
Теорема была обнаружена среди бумаг английского пресвитерианского министра и математика Томаса Байеса и опубликована посмертно, будучи прочитанной в Королевском обществе в 1763 году. вычислительная мощность для выполнения сложных расчетов.
Эти достижения привели к увеличению числа приложений, использующих теорему Байеса. В настоящее время он применяется для самых разных вероятностных расчетов, включая финансовые расчеты, генетику, употребление наркотиков и борьбу с болезнями.

Что утверждает теорема Байеса?
Теорема Байеса утверждает, что условная вероятность события, основанная на появлении другого события, равна вероятности второго события при первом событии, умноженной на вероятность первого события.
Что вычисляется в теореме Байеса?
Теорема Байеса вычисляет условную вероятность события на основе значений конкретных связанных известных вероятностей.
Что такое калькулятор теоремы Байеса?
Калькулятор теоремы Байеса вычисляет вероятность события A при условии другого события B, учитывая априорные вероятности A и B, и вероятность B при условии A. Он вычисляет условные вероятности на основе известных вероятностей.
Как теорема Байеса используется в машинном обучении?
Теорема Байеса предлагает полезный метод для размышлений о взаимосвязи между набором данных и вероятностью. Другими словами, теорема гласит, что вероятность того, что данная гипотеза верна на основе конкретных наблюдаемых данных, может быть сформулирована как нахождение вероятности наблюдения данных с учетом гипотезы, умноженной на вероятность того, что гипотеза верна независимо от данных, разделенная вероятностью наблюдения данных независимо от гипотезы.

- Событие: Возможные подмножества выборочного пространства, связанные со случайным экспериментом, называются событием эксперимента.


 Математически выражается как P (A | B). Выражение представляет собой вероятность A при условии, что событие B уже произошло.
Математически выражается как P (A | B). Выражение представляет собой вероятность A при условии, что событие B уже произошло. Тогда вероятность наступления события A при условии, что B уже произошло, так что вероятность B не равна нулю (P(B) ≠ 0), называется условной вероятностью и обозначается P(A | Б).
Тогда вероятность наступления события A при условии, что B уже произошло, так что вероятность B не равна нулю (P(B) ≠ 0), называется условной вероятностью и обозначается P(A | Б). nP\left( E_i\вправо)\times P\влево(A\середина E_i\вправо)},\ i=1,2,……,n \).
nP\left( E_i\вправо)\times P\влево(A\середина E_i\вправо)},\ i=1,2,……,n \).
 Определить вероятность того, что мяч был из мешка А, используя теорему Байеса.
Определить вероятность того, что мяч был из мешка А, используя теорему Байеса.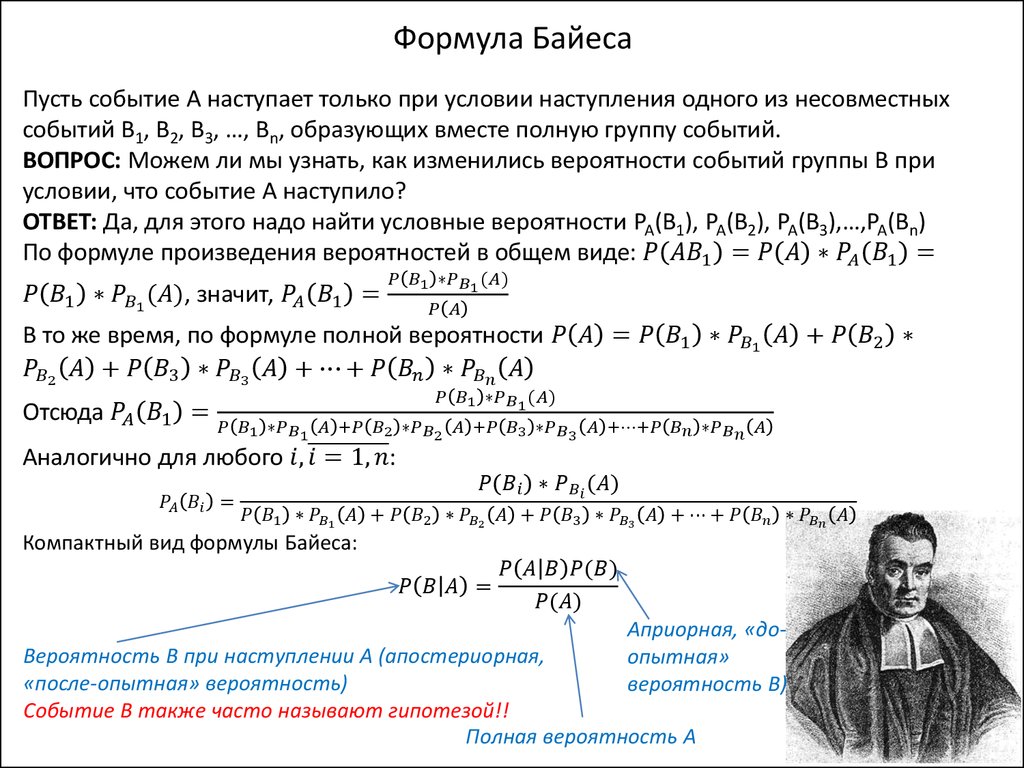 } \)
} \) \)
\)

 Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.


 В терминах статистики апостериорная вероятность — это вероятность наступления события А при условии, что произошло событие В.
В терминах статистики апостериорная вероятность — это вероятность наступления события А при условии, что произошло событие В. \begin{align} &P\left(A|B\right)=\frac{P\left(A\bigcap{B}\right)}{P\left(B\right)}=\frac{P\left (A\right)\cdot{P\left(B|A\right)}}{P\left(B\right)}\\ &\textbf{где:}\\ &P\left(A\right)= \text{ Вероятность появления A}\\ &P\left(B\right)=\text{ Вероятность появления B}\\ &P\left(A|B\right)=\text{Вероятность заданного A B}\\ &P\left(B|A\right)=\text{ Вероятность B при данном A}\\ &P\left(A\bigcap{B}\right))=\text{ Вероятность обоих A и B встречается}\\ \end{выровнено}
P(A∣B)=P(B)P(A⋂B)=P(B)P(A)⋅P(B∣A)где: P(A) = вероятность наступления A P(B )= Вероятность В появления P(A∣B)= Вероятность A при заданном BP(B∣A)= Вероятность B при заданном AP(A⋂B))= Вероятность нахождения A и B
\begin{align} &P\left(A|B\right)=\frac{P\left(A\bigcap{B}\right)}{P\left(B\right)}=\frac{P\left (A\right)\cdot{P\left(B|A\right)}}{P\left(B\right)}\\ &\textbf{где:}\\ &P\left(A\right)= \text{ Вероятность появления A}\\ &P\left(B\right)=\text{ Вероятность появления B}\\ &P\left(A|B\right)=\text{Вероятность заданного A B}\\ &P\left(B|A\right)=\text{ Вероятность B при данном A}\\ &P\left(A\bigcap{B}\right))=\text{ Вероятность обоих A и B встречается}\\ \end{выровнено}
P(A∣B)=P(B)P(A⋂B)=P(B)P(A)⋅P(B∣A)где: P(A) = вероятность наступления A P(B )= Вероятность В появления P(A∣B)= Вероятность A при заданном BP(B∣A)= Вероятность B при заданном AP(A⋂B))= Вероятность нахождения A и B 



