Факториал таблица – Таблица факториалов · Математика

Таблица факториалов — энциклопедический справочник и словарь для студента от А до Я

Ответ

\(\ 6 !=720 \)

Факториальная таблица натуральных чисел от 1 до 50

Укажем точные значения факториалов натуральных чисел от 1 до 50

\(\ 1 !=1 \)

\(\ 2 !=2 \)

\(\ 3 !=6 \)

\(\ 4 !=24 \)

\(\ 5 !=120 \)

\(\ 6 !=720 \)

\(\ 7 !=5040 \)

\(\ 8 !=40320 \)

\(\ 9 !=362880 \)

\(\ 10 !=3628800 \)

\(\ 11 !=39916800 \)

\(\ 12 !=479001600 \)

\(\ 13 !=6227020800 \)

\(\ 14 !=87178291200 \)

\(\ 15 !=1307674368000 \)

\(\ 16 !=20922789888000 \)

\(\ 17 !=355687428096000 \)

\(\ 18 !=6402373705728000 \)

\(\ 19 !=12164510040832000 \)

\(\ 20 !=2432902008176640000 \)

\(\ 21 !=51090942171709440000 \)

\(\ 22 !=1124000727777607680000 \)

\(\ 23 !=25852016738884976640000 \)

\(\ 24 !=620448401733239439360000 \)

\(\ 25 !=15511210043330985984000000 \)

\(\ 26 !=403291461126605635584000000 \)

\(\ 27 !=10888869450418352160768000000 \)

\(\ 28 !=3048883444611713860501504000000 \)

\(\ 29 !=884176199373970195454361600000 \)

\(\ 30 !=265252859812191058636308480000000 \)

\(\ 31 !=8222838654177922817725562880000000 \)

\(\ 32 !=26313083693693369353016721801216000000 \)

\(\ 33 !=8683317618811886495518194401280000000 \)

\(\ 34 !=29523279903960414084761860964552000000 \)

\(\ 35 !=1033314796638614492966665133752320000000 \)

\(\ 36 !=371993326789901217467999448150835200000000 \)

\(\ 37 !=13763753091226345046315979581580902400000000 \)

\(\ 38 !=52302261746661111760007224100074291200000000 \)

\(\ 39 !=203978820811974435864028173990289735680000 \)

\(\ 40 !=815915283247897734345611269596115894272000000000 \)

\(\ 41 !=33452526613807108170062053440751665152000000 \)

\(\ 42 !=1405006117752879898543142606244511569936384000000000 \)

\(\ 43 !=604152630633738356373555637355513997507264512000000000 \)

\(\ 44 !=2658271574788448768043625811014619838528000000000 \)

\(\ 45 !=11962222086548019456196316149565771506438373376000000 \)

\(\ 46 !=5502622159812088949850305428800254892961651752960000000000 \)

\(\ 47 !=258623241511168180642964355153611979969197632389120000000000 \)

\(\ 48 !=12413915592536072670862289047373750385214863546777600000000 \)

\(\ 49 !=608281864034267560872252163321295376887552831379210240000000000 \)

\(\ 50 !=3041409320171337804361660647688443776415689605120000000000000 \)

ПРИМЕР 2

Задача

Рассчитать \(\ 9 !-5 ! \)

Решение

Согласно факториальной таблице, \(\ 9 !=362880 \) и \(\ 5 !=120 \). Тогда

\(\ 9 !-5 !=362880-120=362760 \)

Ответ

\(\ 9 !-5 !=362760 \)

Приблизительные факториальные значения от 1 до 100

Поскольку факториал является быстро растущей функцией, т. Е. Его значения, начиная с некоторого n, очень велики, удобно использовать следующие факториальные значения в математических вычислениях, которые собраны в следующей таблице для чисел от 1 до 100:

\(\ \begin{array}{|c|c|c|c|} \hline Факториал&Значение&Факториал&Значение \\ \hline 1 !&1&51 !& 1,55 \cdot 10^{66} \\ \hline 2 !&2&52 !& 8,07 \cdot 10^{67} \\ \hline 3 !&6&53 !& 4,28 \cdot 10^{69} \\ \hline 4 !&24&54 !& 2,31 \cdot 10^{71} \\ \hline 5 !& 1,2 \cdot 10^{2}&55 !& 1,27 \cdot 10^{73} \\ \hline 6 !& 7,2 \cdot 10^{2}&56 !& 7,11 \cdot 10^{74} \\ \hline 7 !& 5,04 \cdot 10^{3}&57 !& 4,05 \cdot 10^{76} \\ \hline 8 !& 4,03 \cdot 10^{4}&58 !& 2,35 \cdot 10^{78} \\ \hline 9 !& 3,62 \cdot 10^{5}&59 !& 1,39 \cdot 10^{80} \\ \hline 10 !& 3,62 \cdot 10^{6}&60 !& 8,32 \cdot 10^{81} \\ \hline 11 !& 3,99 \cdot 10^{7}&61 !& 5,08 \cdot 10^{83} \\ \hline 12 !& 4,79 \cdot 10^{8}&62 !& 3,15 \cdot 10^{85} \\ \hline 13 !& 6,22 \cdot 10^{9}&63 !& 1,98 \cdot 10^{87} \\ \hline 14 !& 8,71 \cdot 10^{10}&64 !& 1,27 \cdot 10^{89} \\ \hline 15 !& 1,30 \cdot 10^{12}&65 !& 8,25 \cdot 10^{90} \\ \hline 16 !& 2,09 \cdot 10^{13}&66 !& 5,44 \cdot 10^{92} \\ \hline 17 !& 3,55 \cdot 10^{14}&67 !& 3,65 \cdot 10^{94} \\ \hline 18 !& 6,40 \cdot 10^{15}&68 !&2,48 \cdot 10^{96}\\ \hline 19 !& 1,21 \cdot 10^{17}&69 !& 1,71 \cdot 10^{98} \\ \hline 20 !& 2,43 \cdot 10^{18}&70 !& 1,20 \cdot 10^{100} \\ \hline 21 !& 5,10 \cdot 10^{19}&71 !& 8,50 \cdot 10^{101} \\ \hline 22 !& 1,12 \cdot 10^{21}&72 !& 6,12 \cdot 10^{103} \\ \hline 23 !& 2,58 \cdot 10^{22}&73 !& 4,47 \cdot 10^{105} \\ \hline 24 !& 6,20 \cdot 10^{23}&74 !& 3,31 \cdot 10^{107} \\ \hline 25 !& 1,55 \cdot 10^{25}&75 !& 2,48 \cdot 10^{109} \\ \hline 26 !& 4,03 \cdot 10^{26}&76 !& 1,89 \cdot 10^{111} \\ \hline 27 !& 1,08 \cdot 10^{28}&77 !& 1,45 \cdot 10^{113} \\ \hline 28 !& 3,05 \cdot 10^{29}&78 !& 1,13 \cdot 10^{115} \\ \hline 29 !& 8,84 \cdot 10^{30}&79 !& 8,95 \cdot 10^{116} \\ \hline 30 !& 2,65 \cdot 10^{32}&80 !& 7,16 \cdot 10^{118} \\ \hline 31 !& 8,22 \cdot 10^{33}&81 !& 5,80 \cdot 10^{120} \\ \hline 32 !& 2,63 \cdot 10^{35}&82 !& 4,75 \cdot 10^{122} \\ \hline 33 !& 8,68 \cdot 10^{36}&83 !& 3,95 \cdot 10^{124} \\ \hline 34 !& 2,95 \cdot 10^{38}&84 !& 3,31 \cdot 10^{126} \\ \hline 35 !& 1,03 \cdot 10^{40}&85 !& 2,82 \cdot 10^{128} \\ \hline 36 !& 3,72 \cdot 10^{41}&86 !& 2,42 \cdot 10^{130} \\ \hline 37 !& 1,38 \cdot 10^{43}&87 !& 2,11 \cdot 10^{132} \\ \hline 38 !& 5,23 \cdot 10^{44}&88 !& 1,85 \cdot 10^{134} \\ \hline 39 !& 2,04 \cdot 10^{46}&89 !& 1,65 \cdot 10^{136} \\ \hline 40 !& 8,16 \cdot 10^{47}&90 !& 1,49 \cdot 10^{138}\\ \hline 41 !& 3,35 \cdot 10^{49}&91 !& 1,35 \cdot 10^{140} \\ \hline 42 !& 1,41 \cdot 10^{51}&92 !& 1,24 \cdot 10^{142} \\ \hline 43 !& 6,04 \cdot 10^{52}&93 !& 1,16 \cdot 10^{144} \\ \hline 44 !& 2,66 \cdot 10^{54}&94 !& 1,09 \cdot 10^{146} \\ \hline 45 !& 1,19 \cdot 10^{56}&95 !& 1,03 \cdot 10^{148} \\ \hline 46 !& 5,50 \cdot 10^{57}&96 !& 9,92 \cdot 10^{149} \\ \hline 47 !& 2,59 \cdot 10^{59}&97 !& 9,62 \cdot 10^{151} \\ \hline 48 !& 1,24 \cdot 10^{61}&98 !& 9,43 \cdot 10^{153} \\ \hline 49 !& 1,24 \cdot 10^{61}&99 !& 9,33 \cdot 10^{155} \\ \hline 50 !& 3,04 \cdot 10^{64}&100 !& 9,33 \cdot 10^{157} \\ \hline \end{array} \)

ПРИМЕР 3

Задача

Найдите значение выражения \(\ 14 ! \cdot 27 ! \)

Решение.

В таблице находим значения каждого фактора: \(\ 14 !=8,71 \cdot 10^{10} \) и \(\ 27 !=1,08 \cdot 10^{28} \)

Тогда \(\ 14 ! \cdot 27 !=8,71 \cdot 10^{10} \cdot 1,08 \cdot 10^{28}=9,4068 \cdot 10^{38} \)

Ответ

\(\ 14 ! \cdot 27 !=9,4068 \cdot 10^{38} \)

sciterm.ru

Таблица факториалов.

Факториал n! произвольного целого числа n≥0 определяется по формуле:

n! = 1 · 2 · 3 · … · (n — 1) · n

Таблица факториалов чисел от 1 до 50

1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200 15! = 1307674368000 16! = 20922789888000 17! = 355687428096000 18! = 6402373705728000 19! = 121645100408832000 20! = 2432902008176640000 21! = 51090942171709440000 22! = 1124000727777607680000 23! = 25852016738884976640000 24! = 620448401733239439360000 25! = 15511210043330985984000000 26! = 403291461126605635584000000 27! = 10888869450418352160768000000 28! = 304888344611713860501504000000 29! = 8841761993739701954543616000000 30! = 265252859812191058636308480000000 31! = 8222838654177922817725562880000000 32! = 263130836933693530167218012160000000 33! = 8683317618811886495518194401280000000 34! = 295232799039604140847618609643520000000 35! = 10333147966386144929666651337523200000000 36! = 371993326789901217467999448150835200000000 37! = 13763753091226345046315979581580902400000000 38! = 523022617466601111760007224100074291200000000 39! = 20397882081197443358640281739902897356800000000 40! = 815915283247897734345611269596115894272000000000 41! = 33452526613163807108170062053440751665152000000000 42! = 1405006117752879898543142606244511569936384000000000 43! = 60415263063373835637355132068513997507264512000000000 44! = 2658271574788448768043625811014615890319638528000000000 45! = 119622220865480194561963161495657715064383733760000000000 46! = 5502622159812088949850305428800254892961651752960000000000 47! = 258623241511168180642964355153611979969197632389120000000000 48! = 12413915592536072670862289047373375038521486354677760000000000 49! = 608281864034267560872252163321295376887552831379210240000000000 50! = 30414093201713378043612608166064768844377641568960512000000000000

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0oq.ru

Таблица факториалов от 1 до 2000 (файл в формате rar) — Разное — Каталог файлов

  Таблица факториалов от 1 до 2000. Расчеты получены в рамках дипломного проекта студента Ветер Д.А. (руководитель Чурсин В.Б.).   , (файл в формате rar), 2,2 МБ. Если кто-то обнаружит ошибки, то просьба сообщать об этом по адресу [email protected] 

(В разделе «Разное» представлены  также Таблицы факториалов от 2001 до 3000 и от 3001 до 4000)

1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
11! = 39916800
12! = 479001600
13! = 6227020800
14! = 87178291200
15! = 1307674368000
16! = 20922789888000
17! = 355687428096000
18! = 6402373705728000
19! = 121645100408832000
20! = 2432902008176640000
21! = 51090942171709440000
22! = 1124000727777607680000
23! = 25852016738884976640000
24! = 620448401733239439360000
25! = 15511210043330985984000000
26! = 403291461126605635584000000
27! = 10888869450418352160768000000
28! = 304888344611713860501504000000
29! = 8841761993739701954543616000000
30! = 265252859812191058636308480000000
31! = 8222838654177922817725562880000000
32! = 263130836933693530167218012160000000
33! = 8683317618811886495518194401280000000
34! = 295232799039604140847618609643520000000
35! = 10333147966386144929666651337523200000000
36! = 371993326789901217467999448150835200000000
37! = 13763753091226345046315979581580902400000000

38! = 523022617466601111760007224100074291200000000
39! = 20397882081197443358640281739902897356800000000
40! = 815915283247897734345611269596115894272000000000
41! = 33452526613163807108170062053440751665152000000000
42! = 1405006117752879898543142606244511569936384000000000
43! = 60415263063373835637355132068513997507264512000000000
44! = 2658271574788448768043625811014615890319638528000000000
45! = 119622220865480194561963161495657715064383733760000000000
46! = 5502622159812088949850305428800254892961651752960000000000
47! = 258623241511168180642964355153611979969197632389120000000000
48! = 12413915592536072670862289047373375038521486354677760000000000
49! = 608281864034267560872252163321295376887552831379210240000000000
50! = 30414093201713378043612608166064768844377641568960512000000000000
51! = 1551118753287382280224243016469303211063259720016986112000000000000
52! = 80658175170943878571660636856403766975289505440883277824000000000000
53! = 4274883284060025564298013753389399649690343788366813724672000000000000
54! = 230843697339241380472092742683027581083278564571807941132288000000000000
55! = 12696403353658275925965100847566516959580321051449436762275840000000000000
56! = 710998587804863451854045647463724949736497978881168458687447040000000000000
57! = 40526919504877216755680601905432322134980384796226602145184481280000000000000
58! = 2350561331282878571829474910515074683828862318181142924420699914240000000000000
59! = 138683118545689835737939019720389406345902876772687432540821294940160000000000000
60! = 8320987112741390144276341183223364380754172606361245952449277696409600000000000000
61! = 507580213877224798800856812176625227226004528988036003099405939480985600000000000000
62! = 31469973260387937525653122354950764088012280797258232192163168247821107200000000000000
63! = 1982608315404440064116146708361898137544773690227268628106279599612729753600000000000000
64! = 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000
65! = 8247650592082470666723170306785496252186258551345437492922123134388955774976000000000000000
66! = 544344939077443064003729240247842752644293064388798874532860126869671081148416000000000000000
67! = 36471110918188685288249859096605464427167635314049524593701628500267962436943872000000000000000
68! = 2480035542436830599600990418569171581047399201355367672371710738018221445712183296000000000000000
69! = 171122452428141311372468338881272839092270544893520369393648040923257279754140647424000000000000000
70! = 11978571669969891796072783721689098736458938142546425857555362864628009582789845319680000000000000000
71! = 850478588567862317521167644239926010288584608120796235886430763388588680378079017697280000000000000000
72! = 61234458376886086861524070385274672740778091784697328983823014963978384987221689274204160000000000000000
73! = 4470115461512684340891257138125051110076800700282905015819080092370422104067183317016903680000000000000000
74! = 330788544151938641225953028221253782145683251820934971170611926835411235700971565459250872320000000000000000
75! = 24809140811395398091946477116594033660926243886570122837795894512655842677572867409443815424000000000000000000
76! = 1885494701666050254987932260861146558230394535379329335672487982961844043495537923117729972224000000000000000000
77! = 145183092028285869634070784086308284983740379224208358846781574688061991349156420080065207861248000000000000000000
78! = 11324281178206297831457521158732046228731749579488251990048962825668835325234200766245086213177344000000000000000000
79! = 894618213078297528685144171539831652069808216779571907213868063227837990693501860533361810841010176000000000000000000
80! = 71569457046263802294811533723186532165584657342365752577109445058227039255480148842668944867280814080000000000000000000
81! = 5797126020747367985879734231578109105412357244731625958745865049716390179693892056256184534249745940480000000000000000000
82! = 475364333701284174842138206989404946643813294067993328617160934076743994734899148613007131808479167119360000000000000000000
83! = 39455239697206586511897471180120610571436503407643446275224357528369751562996629334879591940103770870906880000000000000000000
84! = 3314240134565353266999387579130131288000666286242049487118846032383059131291716864129885722968716753156177920000000000000000000
85! = 281710411438055027694947944226061159480056634330574206405101912752560026159795933451040286452340924018275123200000000000000000000
86! = 24227095383672732381765523203441259715284870552429381750838764496720162249742450276789464634901319465571660595200000000000000000000
87! = 2107757298379527717213600518699389595229783738061356212322972511214654115727593174080683423236414793504734471782400000000000000000000
88! = 185482642257398439114796845645546284380220968949399346684421580986889562184028199319100141244804501828416633516851200000000000000000000
89! = 16507955160908461081216919262453619309839666236496541854913520707833171034378509739399912570787600662729080382999756800000000000000000000
90! = 1485715964481761497309522733620825737885569961284688766942216863704985393094065876545992131370884059645617234469978112000000000000000000000
91! = 135200152767840296255166568759495142147586866476906677791741734597153670771559994765685283954750449427751168336768008192000000000000000000000
92! = 12438414054641307255475324325873553077577991715875414356840239582938137710983519518443046123837041347353107486982656753664000000000000000000000
93! = 1156772507081641574759205162306240436214753229576413535186142281213246807121467315215203289516844845303838996289387078090752000000000000000000000
94! = 108736615665674308027365285256786601004186803580182872307497374434045199869417927630229109214583415458560865651202385340530688000000000000000000000
95! = 10329978488239059262599702099394727095397746340117372869212250571234293987594703124871765375385424468563282236864226607350415360000000000000000000000
96! = 991677934870949689209571401541893801158183648651267795444376054838492222809091499987689476037000748982075094738965754305639874560000000000000000000000
97! = 96192759682482119853328425949563698712343813919172976158104477319333745612481875498805879175589072651261284189679678167647067832320000000000000000000000
98! = 9426890448883247745626185743057242473809693764078951663494238777294707070023223798882976159207729119823605850588608460429412647567360000000000000000000000
99! = 933262154439441526816992388562667004907159682643816214685929638952175999932299156089414639761565182862536979208272237582511852109168640000000000000000000000

и т.д.

 

chursinvb.ucoz.ru

Таблицы факториалов — сборник таблиц

Приблизительная таблицы факториалов (1-255)

Факториал n! произвольного целого числа n≥0 определяется по формуле:

Факториал	Значение	Факториал	Значение	Факториал	Значение
1!	1	86!	2,42*10130	171!	1,24*10309
2!	2	87!	2,11*10132	172!	2,13*10311
3!	6	88!	1,85*10134	173!	3,69*10313
4!	24	89!	1,65*10136	174!	6,43*10315
5!	1,2*102	90!	1,49*10138	175!	1,12*10318
6!	7,2*102	91!	1,35*10140	176!	1,98*10320
7!	5,04*103	92!	1,24*10142	177!	3,50*10322
8!	4,03*104	93!	1,16*10144	178!	6,24*10324
9!	3,62*105	94!	1,09*10146	179!	1,12*10327
10!	3,62*106	95!	1,03*10148	180!	2,01*10329
11!	3,99*107	96!	9,92*10149	181!	3,64*10331
12!	4,79	97!	9,62*10151	182!	6,62*10333
13!	6,22*109	98!	9,43*10153	183!	1,21*10336
14!	8,71*1010	99!	9,33*10155	184!	2,23*10338
15!	1,30*1012	100!	9,33*10157	185!	4,12*10340
16!	2,09*1013	101!	9,43*10159	186!	7,68*10342
17!	3,55*1014	102!	9,61*10161	187!	1,43*10345
18!	6,40*1015	103!	9,9*10163	188!	2,69*10347
19!	1,21*1017	104!	1,03*10166	189!	5,09*10349
20!	2,43*1018	105!	1,08*10168	190!	9,68*10351
21!	5,10*1019	106!	1,15*10170	191!	1,85*10354
22!	1,12*1021	107!	1,23*10172	192!	3,55*10356
23!	2,58*1022	108!	1,32*10174	193!	6,85*10358
24!	6,20*1023	109!	1,44*10176	194!	1,33*10361
25!	1,55*1025	110!	1,59*10178	195!	2,59*10363
26!	4,03*1026	111!	1,76*10180	196!	5,08*10365
27!	1,08*1028	112!	1,97*10182	197!	1,00*10368
28!	3,05*1029	113!	2,23*10184	198!	1,98*10370
29!	8,84*1030	114!	2,54*10186	199!	3,94*10372
30!	2,65*1032	115!	2,93*10188	200!	7,89*10374
31!	8,22*1033	116!	3,39*10190	201!	1,59*10377
32!	2,63*1035	117!	3,97*10192	202!	3,20*10379
33!	8,68*1036	118!	4,68*10194	203!	6,50*10381
34!	2,95*1038	119!	5,57*10196	204!	1,33*10384
35!	1,03*1040	120!	6,69*10198	205!	2,72*10386
36!	3,72*1041	121!	8,09*10200	206!	5,60*10388
37!	1,38*1043	122!	9,88*10202	207!	1,16*10391
38!	5,23*1044	123!	1,21*10205	208!	2,41*10393
39!	2,04*1046	124!	1,51*10207	209!	5,04*10395
40!	8,16*1047	125!	1,88*10209	210!	1,06*10398
41!	3,35*1049	126!	2,37*10211	211!	2,23*10400
42!	1,41*1051	127!	3,01*10213	212!	4,73*10402
43!	6,04*1052	128!	3,86*10215	213!	1,01*10405
44!	2,66*1054	129!	4,97*10217	214!	2,16*10407
45!	1,19*1056	130!	6,47*10219	215!	4,64*10409
46!	5,50*1057	131!	8,47*10221	216!	1,00*10412
47!	2,59*1059	132!	1,12*10224	217!	2,17*10414
48!	1,24*1061	133!	1,49*10226	218!	4,74*10416
49!	6,08*1062	134!	1,99*10228	219!	1,04*10419
50!	3,04*1064	135!	2,69*10230	220!	2,28*10421
51!	1,55*1066	136!	3,66*10232	221!	5,04*10423
52!	8,07*1067	137!	5,01*10234	222!	1,12*10426
53!	4,28*1069	138!	6,92*10236	223!	2,50*10428
54!	2,31*1071	139!	9,62*10238	224!	5,60*10430
55!	1,27*1073	140!	1,35*10241	225!	1,30*10433
56!	7,11*1074	141!	1,90*10243	226!	2,85*10435
57!	4,05*1076	142!	2,7*10245	227!	6,46*10437
58!	2,35*1078	143!	3,85*10247	228!	1,47*10440
59!	1,39*1080	144!	5,55*10249	229!	3,37*10442
60!	8,32*1081	145!	8,05*10251	230!	7,76*10444
61!	5,08*1083	146!	1,17*10254	231!	1,79*10447
62!	3,15*1085	147!	1,73*10256	232!	4,16*10449
63!	1,98*1087	148!	2,56*10258	233!	9,69*10451
64!	1,27*1089	149!	3,81*10260	234!	2,67*10454
65!	8,25*1090	150!	5,71*10262	235!	5,33*10456
66!	5,44*1092	151!	8,63*10264	236!	1,26*10459
67!	3,65*1094	152!	1,31*10267	237!	2,98*10461
68!	2,48*1096	153!	2,01*10269	238!	7,09*10463
69!	1,71*1098	154!	3,09*10271	239!	1,70*10466
70!	1,20*10100	155!	4,79*10273	240!	4,07*10468
71!	8,50*10101	156!	7,47*10275	241!	9,80*10470
72!	6,12*10103	157!	1,17*10278	242!	2,37*10473
73!	4,47*10105	158!	1,85*10280	243!	5,77*10475
74!	3,31*10107	159!	2,95*10282	244!	1,41*10478
75!	2,48*10109	160!	4,71*10284	245!	3,45*10480
76!	1,89*10111	161!	7,59*10286	246!	8,48*10482
77!	1,45*10113	162!	1,23*10289	247!	2,09*10485
78!	1,13*10115	163!	2,00*10291	248!	5,19*10487
79!	8,95*10116	164!	3,29*10293	249!	1,29*10490
80!	7,16*10118	165!	5,42*10295	250!	3,23*10492
81!	5,80*10120	166!	9,00*10297	251!	8,11*10494
82!	4,75*10122	167!	1,50*10300	252!	2,04*10497
83!	3,95*10124	168!	2,53*10302	253!	5,17*10499
84!	3,31*10126	169!	4,27*10304	254!	1,31*10502
85!	2,82*10128	170!	7,26*10306	255!	3,35*10504

 

www.funtable.ru

Факториалы Таблицы — Энциклопедия по машиностроению XXL

Вальцы листоправильные 319 Величины обратные факториалов — Таблицы 40  [c.1109]

При вычислении значений р (jf,) можно пользоваться таблицей значений факториалов (стр. 33, табл. IV) и таблицей значений (стр. 86, табл. VII]).  [c.296]

При р= 1/4, п = 20 несимметричность уменьшается. При вычислениях следует пользоваться таблицами факториалов и степеней целых чисел.  [c.323]

Фазы синусоидальных величин 98 Факториалы целых чисел — Таблицы 41 Факториальные функции — см. Функции факториальные Фермы 419  [c.589]

Так как биномиальное распределение двухпараметрическое, то для него не удается составить достаточно подробные и в то же время компактные таблицы. При вычислении значений Р (х) удобно пользоваться таблицами биномиальных коэффициентов или значений факториалов [4].  [c.63]

Ввиду ТОГО что гипергеометрическое распределение трехпараметрическое, его табулирование затруднено. Значения Р (х) при гипергеометрическом распределении можно вычислять с помощью таблиц биномиальных коэффициентов или таблиц факториалов [4], если значения их аргументов сравнительно невелики. При больших значениях их аргументов можно пользоваться приближенной формулой Стирлинга  [c.65]

ТАБЛИЦА IX. ФАКТОРИАЛЫ ЦЕЛЫХ ЧИСЕЛ ОТ 1 ДО 20 И ЛОГАРИФМЫ ФАКТОРИАЛОВ  [c.41]

Фазы синусоидальных величин 98 Факториалы целых чисел — Таблицы 41  [c.564]

Обращаем особое внимание читателя на то обстоятельство, что во всех численных таблицах, за исключением таблицы факториалов чисел, приводятся квадраты значений коэффициентов. Если сам коэффициент является отрицательной величиной, то перед его квадратом стоит значок .  [c.224]

Таблица 14. Некоторые степени, факториалы, и обратные величины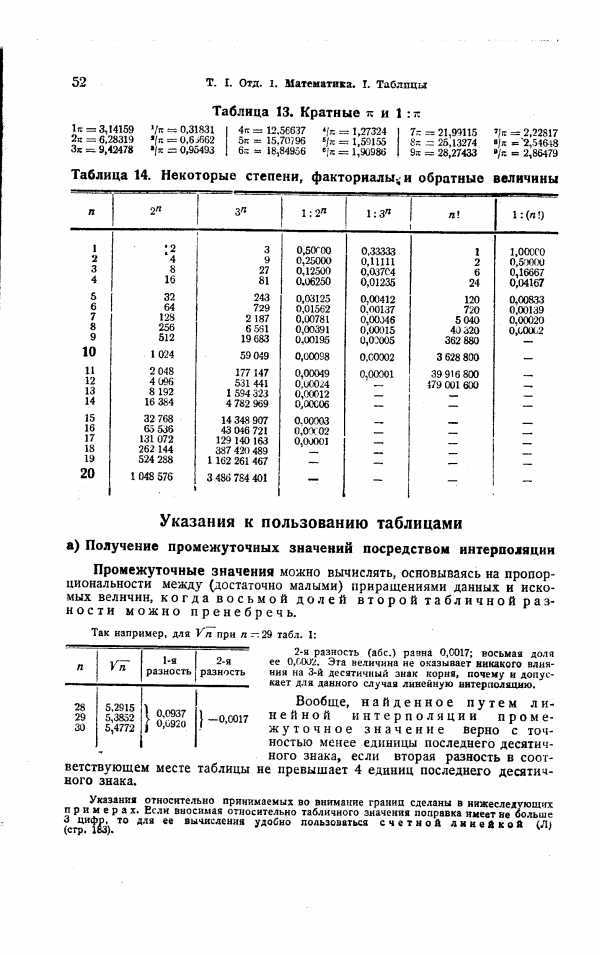

Таблица коэфициентов бинома — см. стр. 51, таблица факториалов — стр. 52,  [c.61]

Фазы синусоидальных величин I — 98 Факториалы чисел — Таблицы 1—41 Факториальные функции 1—302 Фальц на слоистых пластиках — Фрезерование 5 — 612 Фанера 3 — 22, 351 6 — 337  [c.488]

Таблица факториалов (п ) приведена на стр. 82 (О принимают равным единице).  [c.101]

Теперь покажем в явном виде, что для очень большой системы (Л >> 1) функция ц(М,т), определенная соотношением (12), имеет резкий максимум при значении т = 0. Найдем сначала приближение, которое позволит нам исследовать зависимость ц Ы,т) от т при 1 и т [c.23]

Вычисление моментов по способу произведений требует большой вычислительной работы по перемножению каждой частоты таблицы распределения на различные степени отклонений значений статистических величин от их начальных значений, или на различные факториалы отклонений. Кроме того, для уверенности в правильности вычислений необходимо обращаться к специальным проверочным таблицам или же лроизводить вычисления по два раза, что при наличии обширной таблицы распределения представляет большое затруднение.  [c.149]

---

mash-xxl.info

definition of факториал and synonyms of факториал (Russian)

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

Например:

По определению полагают . Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, … (последовательность A000142 в OEIS)

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

  Свойства

  Рекуррентная формула

  Комбинаторная интерпретация

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.

  Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

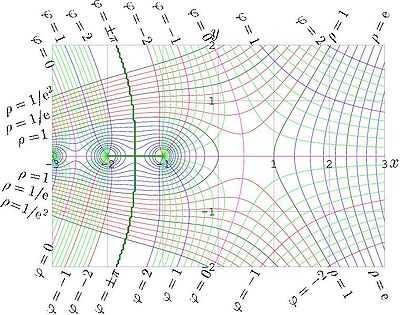
  Амплитуда и фаза факториала комплексного аргумента.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

  Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

  Разложение на простые числа

Каждое простое число p входит в разложение на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

  Другие свойства

• Для натурального числа n

  Обобщения

  Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают .

Последовательность значений n!! начинается так:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, … (последовательность A006882 в OEIS)

  Кратный факториал

m-кратный факториал числа n обозначается и определяется следующим образом:

Пусть число n представимо в виде , где , . Тогда^[1]

Двойной факториал является частным случаем m-кратного факториала для m = 2.

  Связь с гамма-функцией

^[2]

  Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

  Возрастающий факториал

Возрастающим факториалом называется выражение

  Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n#  и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов (включая ) начинается так:

1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

  Суперфакториалы

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал числа n как произведение первых n (m-1)-уровневых факториалов, то есть

где для и .

  Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

  Ссылки

  См. также

  Примечания

1. ↑ «Энциклопедия для детей» Аванта+. Математика
2. ↑ wolframalpha.com

   

dictionary.sensagent.com