Физический и геометрический смысл определенного интеграла: Геометрический смысл определенного интеграла

Геометрический и физический смысл определенного интеграла

Возвратимся к задаче о площади криволинейной трапеции и определению определенного интеграла. Мы видим, что площадь криволинейной трапеции, ограниченной кривой y=f(x), где f(x)0 на отрезке [a, b], осью x и прямыми x = a и x = b численно равна определенному интегралу, т. е.

.

До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Если изменять, например, верхний предел, не выходя из отрезка [a, b], величина интеграла будет меняться. Другими словами, интеграл c переменным верхним пределом представляет собой функцию своего верхнего предела. Таким образом, если мы имеем интеграл

с постоянным нижним пределом а и переменным верхним пределом х, то величина этого интеграла будет функцией верхнего предела х. Обозначим эту функцию через Ф(х), т. е. положим

(2.1)

и назовем ее определенным интегралом с переменным верхним пределом. Геометрически функция Ф(х) представляет собой площадь заштрихованной криволинейной трапеции, если f(x)0 (рис. 2)

Рис. 2

Теперь рассмотрим доказательство теоремы, одной из основных теорем математического анализа.

Теорема 3. Если f(t) – непрерывная функция и

то имеет место равенство

или (2.2)

Иными словами, производная определенного интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в верхнем пределе.

Доказательство. Возьмем любое значение x[a,b] и придадим ему приращение x  0 такое, чтобы x + x  [a,b], т. е. . Тогда функция Ф(х) получит новое значение:

Находим приращение функции Ф(х):

Ф = Ф(x+x) – Ф(x) =

Применяя теорему о среднем к последнему интегралу получим:

где С – число, заключенное между числами x и x + x. Отсюда

Если теперь x 0, то c  x и f(c )  f(x) (в силу непрерывности f(x) на [a,b]). Поэтому переходя к пределу в последнем равенстве получаем

f (x) или ,

что и требовалось доказать.

Следствие. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции. Другими словами, для любой непрерывной функции существует первообразная,

Замечание. Интеграл с переменным верхним пределом интегрирования используется при определении многих

новых функций, например:

.

Как мы уже отмечали, вычисление определенного интеграла методом, основанным на нахождении предела интегральных сумм, как правило, связано с большими трудностями. Поэтому существует другой как правило более удобный метод вычисления определенных интегралов, который основан на тесной связи, существующей между понятиями определенного и неопределенного интеграла. Эту связь выражает следующая

Теорема 4. Определенный интеграл от непрерывной функции равен разности значений любых ее первообразных для верхнего и нижнего предела интегрирования.

Доказательство. Мы установили, что функция f(x), непрерывная на [a,b] имеет на этом отрезке первообразную, причем, одной из первообразных является функция

.

Пусть F(x) — любая другая первообразная для функции f(x) на том же отрезке [a, b]. Так как первообразные Ф(х) и F(х) отличаются на постоянную (см. свойства первообразных), то имеет место равенство

где С – некоторое число. Подставляя в это равенство значение x = a будем иметь 0 = F(a) + C, C = — F(a), т. е. для x  [a, b] имеем

Полагая x = b, получаем соотношение

(3. 1)

Формула (3.1) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) принято условно записывать в виде

и тогда формула (3.1) принимает вид

Итак, полученная нами формула (3.1)с одной стороны, устанавливает связь между определенным и неопределенным интегралами, с другой стороны, она дает простой метод вычисления определенного интеграла :

определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленной для верхнего и нижнего пределов интегрирования.

Различные способы решения задач по теме «Геометрический смысл определенного интеграла»

Ключевые слова: интеграл, определенный интеграл, площадь криволинейной трапеции, формула Ньютона-Лейбница, преобразования графиков

Интегрирование, пожалуй, вызывает наибольшие трудности в школьном курсе математики, несмотря на то, что даются только самые общие представления об интеграле.

Тем не менее, в профильном варианте ЕГЭ встречаются задания, использующие, например, геометрический смысл определенного интеграла (задание №7).

В геометрическом смысле и раскрывается наглядность определенного интеграла, его связь со знакомыми для учеников линиями и фигурами. При вычислении площадей в данной теме, во-первых, формируется умение интегрировать и видеть ту криволинейную трапецию, для которой площадь равна интегралу. Во-вторых, можно использовать известные фигуры планиметрии (треугольники, четырехугольники, круг и т.д.) и для них подсчитывать площадь. В-третьих, можно использовать симметрию некоторых графиков, их параллельный перенос для удобства вычислений. Самое главное – увидеть, распознать все это из условия задачи.

После сложных формул интегрирования такое обилие наглядного материала дает простор для мыслительной деятельности учащихся, позволяет активизировать работу как в общеобразовательных классах, так и в профильных. Учитель может выбирать задания, предложенные в презентации, ориентируясь на конкретный состав учеников.

Например, для учащихся, которым трудно дается математика, можно рассмотреть раздел “Вычисление площадей (легкие случаи)”, задачу 1, пример 1 из раздела “Площадь как способ вычисления интеграла”.

Подчеркнем, что в большинстве заданий предлагаются два доминирующих способа решения: “алгебраический”, использующий в основном формулы, связанные с интегралом, и “геометрический”, для которого на первый план выходят свойства некоторых линий и фигур. Названия этих способов условны, потому что иногда тот и другой вид решения могут пересекаться. Но примечательно, что ученики, ознакомившись с общими приемами решения, могут затем выбирать свой способ и сравнивать его с теми, которые предложат остальные. Тут очень ярко могут себя проявить индивидуальные особенности мышления учеников.

Дети получают возможность сравнивать разные способы, обсуждать их достоинства и недостатки, при этом развивается критическое мышление учеников, умение общаться друг с другом. Когда основные приемы решения известны, урок можно построить более динамично, в виде деловой игры (конференции, соревнования и т. д.), где обсуждаются полученные способы решения.

Для вычисления площадей нужно напомнить ученикам самое важное из предыдущих уроков: геометрический смысл определенного интеграла, площадь криволинейной трапеции (слайд 3), площадь фигуры, расположенной между графиком функции, которая принимает только отрицательные значения, и осью Ox (слайд 4), площадь между графиками двух функций, один из которых всегда выше другого на заданном промежутке [1], (

слайд 5), формула Ньютона-Лейбница (слайд 6).

Сначала рассматриваем легкие случаи.

Слайд 7.

На рисунке мы видим закрашенную фигуру между прямой у=2х и осью Ох на отрезке [1;3]. Ее площадь и равна найденному интегралу. Проверим это с помощью геометрических рассуждений. Закрашенная фигура – трапеция. Мы знаем ее основания и высоту, площадь равна 8.

Слайд 8.

Найдем площадь фигуры, заключенной между графиком y=sinx и осью Ох на [0; ]. Эта площадь равна интегралу

Слайды 9, 10, 11.

Рассмотрим дополнительные вопросы.

Эти интегралы можно не считать, а использовать их геометрический смысл. Мы уже знаем результат (*).

Используя свойства синусоиды, получаем в первом случае 1. Во втором случае интеграл равен числу, противоположному (*), т.е. -2. На рисунках все это хорошо видно.

Далее мы переходим к подробному рассмотрению разных способов вычисления площадей в более трудных заданиях.

Слайд 12.

Задача 1. Найти площадь фигуры, ограниченной линиями у=х² и у=4.

Можно ученикам предложить самим сделать чертеж и найти нужную фигуру, а потом сверить свой рисунок с тем, что на слайде. В классах, где много слабых учеников, лучше сразу показать готовый рисунок. После подготовки чертежа идет обсуждение возможных способов решения.

Важно подчеркнуть, что выделенная фигура при данных условиях не является криволинейной трапецией, т.е. ее площадь нельзя просто приравнять интегралу. А вот площадь фигуры S₁ – можно.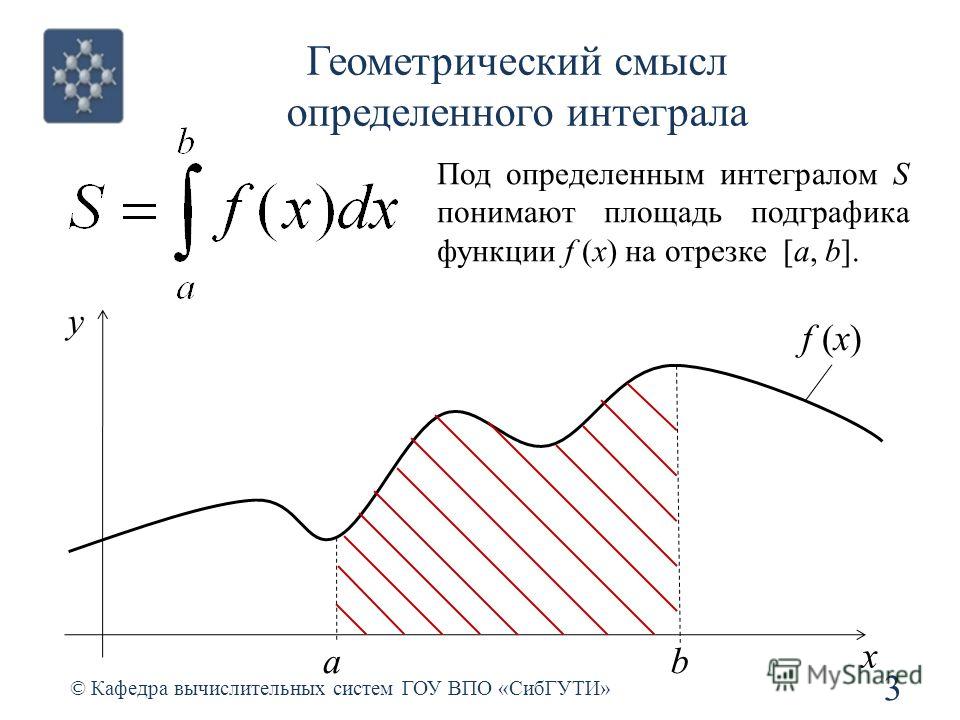 Обязательно надо обратить внимание детей на симметричность чертежа!

Слайд 13.

Первый способ вполне согласуется с [2], нам он тоже представляется самым естественным: S

Ф = S_ABCD — 2S₁ (см. слайд 13).

Слайд 14.

Проводятся вычисления, получен ответ.

Слайд 15.

Второй способ. Используется тот факт, что график у=4 выше графика у= х² на отрезке [-2;2] (точки пересечения не учитываем). Поэтому можем подсчитать искомую площадь как интеграл от разности двух функций.

Слайд 16.

Приводится подсчет интеграла.

Вроде бы, второй способ должен быть короче: сразу начинаем интегрировать и не нужно выделять дополнительные фигуры, как в первом способе. Но подсчет длинный! И вот здесь дети сразу чувствуют разницу – в “геометрическом” способе сначала больше рассуждений, но зато потом вычисления легкие. В “алгебраическом” сразу получена нужная формула, но она подразумевает громоздкие вычисления.

Слайд 17.

Эти вычисления в данном случае можно слегка упростить, используя опять же симметрию и делая расчет для того интеграла, где нижний предел интегрирования 0. Ученики замечают, что в этом случае считать намного быстрее.

Слайд 18.

Задача 2. Найти площадь фигуры, ограниченной линиями у=4х² + 16х + 19, у=0, х=-3, х=-1.

Вершина параболы (-2;3) – на чертеже это должно быть выделено.

Слайд 19.

Первый способ могут предложить сами ребята, так как наша фигура представляет собой именно криволинейную трапецию, и, значит, ее площадь равна интегралу от данной функции.

Слайд 20.

Но вычисление этого интеграла снова непростое. Если предложить детям подсчитать его самостоятельно, то вполне вероятны ошибки из-за невнимательности. Многие из учеников сами начнут думать о другом подходе, где вычислительных усилий будет меньше. Современные дети не любят утомительных длинных вычислений!

Слайд 21, 22.

Какие же могут быть другие способы? Может быть, вспоминая предыдущую задачу, ученики будут искать фигурку, “близкую” к параболе. И тогда естественно будет провести прямую у=3.

S_Ф = S_{прямоуг.} — 2S₁

Слайд 23.

Как подсчитать S₁? Для этого рассмотрим нашу параболу в другой системе координат (см. слайд). Получаем в этой системе координат параболу у=4х².

Слайд 24.

Слайд 25.

Получаем окончательный ответ:

Слайд 26.

Задача 3. Найти площадь фигуры, ограниченной линиями у = -х² + 4х, у=3, у=0.

Сложность этой задачи в том, что искомая фигура вроде бы “похожа” на криволинейную трапецию, но на самом деле принципиально отличается от нее.

Слайды 27, 28

“Настоящая” криволинейная трапеция хорошо видна на чертеже, и если от нее “отрезать” верхнюю часть (мы ее обозначили S₀), то тогда получим искомую площадь.

Слайд 29.

Проводим расчеты (см. слайд) и получаем: S_ф=

Вполне закономерно может последовать вопрос какого-либо ученика: “А нельзя ли и здесь найти другой способ, в котором бы не было больших вычислений?” Замечаем, что данная фигура может быть разбита на “внутренний” прямоугольник (его площадь равна 6) и два боковых криволинейных треугольника. Площадь левого треугольника считаем через интеграл (он равен ). Площадь всей фигуры: 6+2 * =9

Этим способом ученики вполне могут решить задачу самостоятельно.

Слайд 30.

Но дети могут предложить и другой способ (по аналогии с задачей 1), в котором из “внешнего” прямоугольника вырезаются две фигуры площадью S₁. Рассмотрим этот подход.

Итак, ищем площадь (см. слайд): S_Ф = S_ОАВС — 2S₁.

Слайды 31, 32, 33

Для подсчета S₁ введем новую систему координат (см.слайд 31) такую, чтобы наша парабола была в ней задана формулой у=х²+2х. Это удобно для вычисления площади S₁.

Итак, мы получаем:

S_ф=

Слайды 34 – 39 посвящены задачам, где значение интеграла находится с помощью площади. Приведем условия этих задач, подробное решение дано на слайдах.

На рисунке дан график функции f(x). Найдите значение интеграла

В заключение отметим, что приведенные задачи настраивают детей на поиск необычного решения, использование геометрического материала, пространственного воображения, применение преобразований графиков элементарных функций. Все это сопутствует новой теме интегрирования и позволяет расширять общий кругозор ребенка. Тем самым его деятельность на уроке становится активной и творческой.

Литература.

1. Виленкин Н.Я. и др. Алгебра и математический анализ для 11 класса – М.: Просвещение, 1995.
2. Колмогоров А.Н. и др. Алгебра и начала анализа. 10–11 класс. – М.: Просвещение, 2009.

Геометрическая интерпретация определенного интеграла как площади под кривой — Интегральное исчисление

Используя интегрирование, мы можем оценить площадь, ограниченную кривыми с осями координат.

Площадь области, ограниченной кривыми

Используя интегрирование, мы можем оценить площадь, ограниченную кривыми с осями координат. Мы также можем вычислить площадь между двумя заданными кривыми.

Геометрическая интерпретация определенных Интеграл как площадь под кривой:

Предположим, мы хотим узнать площадь области, которая ограничен сверху кривой y = f ( x ), ниже на x − ось и строки х = и х = б .

Теперь из рис. 3.1 пусть интервал [a b] делится на n подинтервалы [x _i-1 , x _i ] одинаковой длины ∆ x _i , т.е. x _я -х _я-1 = ∆ _xi для любого x _i ’ ∈ [x _i-1 ,x _i ], пусть f(x′ _i ) быть высотой n прямоугольников, имеющих x _i -x _i-1 = ∆x _i в качестве его основания. Тогда площадь A _i = ∆x _i f (x _i ’).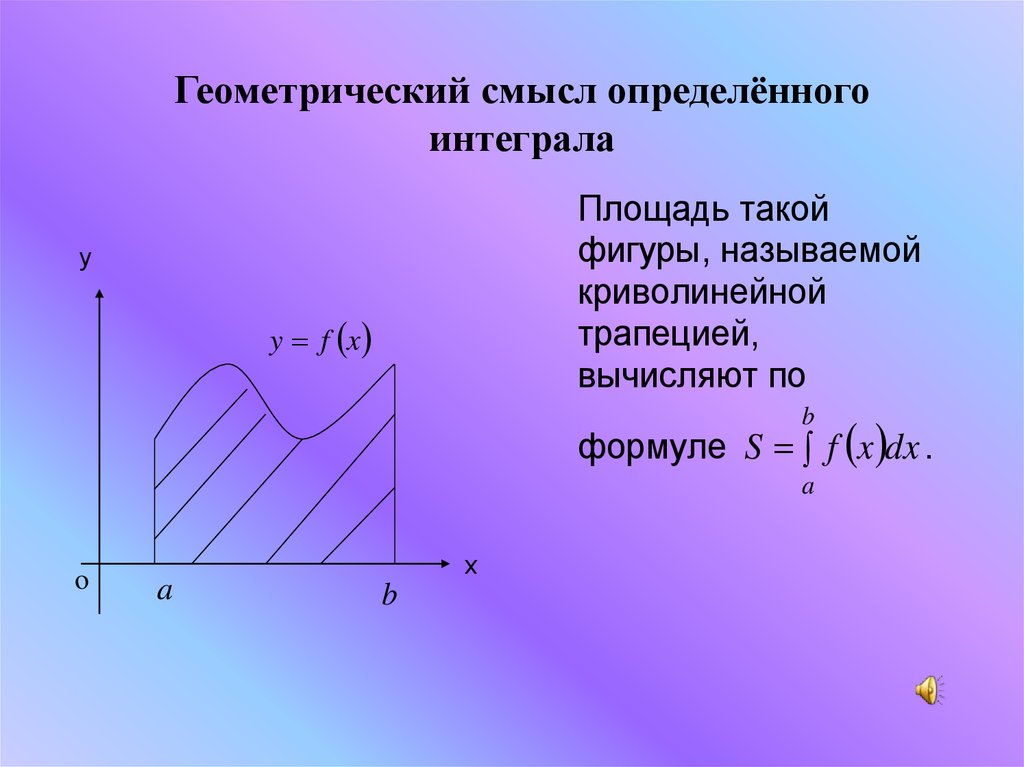 Теперь общая площадь А = 

Теперь из определения определенного интеграла, если f ( x ) является функцией, определенной на [ a , b ] с a < b тогда определенный интеграл равен

Площадь под кривой исчерпывается увеличением числа прямоугольные полосы до ∞

Таким образом, геометрическая интерпретация определенного интеграла есть площадь под кривой между заданными пределами.

Площадь области, ограниченной кривой y = f ( x ), с x — ось и ордината на x = A и x = B , приведенный

Примечание

(I) Область региона, связанная по Curv ) между пределами x = a , x = b и лежит ниже оси x, составляет

(ii) Площадь область, ограниченная кривой x = f (y) между пределами y = c и y = d при y − ось и площадь лежат справа оси Y, составляет

(iii) Площадь, ограниченная кривой x = f ( y ) between the limits y = c and y = d with y − axis and the area lies to the left of y — axis, is

Let f ( x ) и г ( x ) два непрерывных функции, определенные на x в интервале [ а , б ]. Также ф ( x ) > г ( x ), a ≤ B

Затем площадь между этими двумя кривыми от x = от a до x = B ,

Пример 3,10006

. на y = 4 х + 3 с x — ось между строками x = 1 и x = 4

Решение:

. x − 2 y −12 = 0 , ось y и строки y = 2, y = 5.

Решение:

х − 2 y −12 = 0

x = 2 y + 12

Требуемая область

. парабола y = 4 − x ² , x − ось и строки x = 0, x = 2

Solutions:

 

Example 3. 4

Find the area bounded by y = x между линиями x = -1 и x = 2 с осью x .

Решения:

 

Пример 3.5

Найдите площадь параболы y ² = 8 x , ограниченной его широкая прямая кишка.

Решение

y ² =8x (1)

По сравнению со стандартной формой y ² = 4 ax ,

4 a = 8

a = 2

Уравнение широкой прямой кишки: x = 2

Поскольку уравнение (1) симметрично относительно x — оси

Требуемая площадь = 2[Площадь в первом квадранте между пределами x = 0 и x = 2]

 

| х + 3| и оцените 

Решение:

 

Пример 3.7

Используя интегрирование, найдите площадь круга, центр которого находится в начало координат и радиус равны единицам.

Решение

Уравнение искомого круга x ² + y ² = a ²                (1)

положить y = 0, x ² = a ²

⇒ x = ± a

Поскольку уравнение (1) симметрично относительно обеих осей

требуемая площадь = 4 [Площадь в первом квадранте между пределом 0 и а.]

 

линия х = 4 и парабола y ² = 16 х .

Решение:

Уравнение y ² = 16 x представляет собой параболу (открытая справа)

Теги: Интегральное исчисление — II, 12-я Бизнес-математика и статистика: Глава 3: Интегральное исчисление — II и статистика: Глава 3: Интегральное исчисление-II: Геометрическая интерпретация определенного интеграла как площади под кривой | Интегральное исчисление — II

интегрирование — Геометрическая интерпретация определенных интегралов с $\pi$ в результате

спросил 9 лет, 9 месяцев назад

Изменено 9 лет, 9 месяцев назад

Просмотрено 3к раз

$\begingroup$

Какова геометрическая интерпретация следующего интеграла?

Какова хорошая геометрическая интерпретация следующего интеграла (возможно, по отношению к окружности), которая подчеркивает, почему мы получаем результат π в правой части? 9{-1} х$.

В ответах я также был бы признателен за примеры других интегралов с геометрической интерпретацией.

• интеграция
• мягкий вопрос
• неправильные интегралы
• геометрическая интерпретация

$\endgroup$

9

$\begingroup$

Рассмотрим стереографическую проекцию линии на окружность.

$\hspace{1cm}$ 92}$ из-за того, что линия $x=1$ имеет переменный наклон по отношению к направлению световых лучей. Поэтому я думаю, что аргумент «первоапрельской шутки» можно спасти, но он, вероятно, не стоит того, учитывая ясный аргумент Робджона (не зависящий от физики, света и т. д.).

$\endgroup$

4

$\begingroup$

По определению :

$$a,b\in\Bbb R\;,\;a,b>0\;:\;\;\int\limits_{-\infty}^\infty\frac {dx}{1+x^2}=\lim_{a,b\to\infty}\int\limits_{-a}^b\frac{dx}{1+x^2} =\left.

No related posts.