Формулы сокращенного умножения. Разность квадратов, квадрат суммы, разность кубов, бином Ньютона.
Откровенно говоря, эти формулы должен помнить любой ученик седьмого класса. Изучать алгебру даже на школьном уровне и не знать формулу разности квадратов или квадрата суммы просто невозможно. Они постоянно встречаются при упрощении алгебраических выражений, при сокращении дробей и даже могут помочь в арифметических вычислениях. Ну, например, вам нужно вычислить в уме: 3,162 — 2 • 3,16 • 1,16 + 1,162. Если вы начнете считать это «в лоб», получится долго и скучно, а если воспользуетесь формулой квадрата разности, ответ получите за 2 секунды!
Итак, семь формул «школьной» алгебры, которые должны знать все:
| Название | Формула |
| Квадрат суммы | (A + B)2 = A2 + 2AB + B2 |
| Квадрат разности | (A — B)2 = A2 — 2AB + B2 |
| Разность квадратов | (A — B)(A + B) = A2 — B2 |
| Куб суммы | (A + B)3 = A3 + 3A2B + 3AB2+ B3 |
| Куб разности | (A — B)3 = A3 — 3A2B + 3AB2 — B3 |
| Сумма кубов | A3 + B3 = (A + B)(A2 — AB + B2) |
| Разность кубов | A3 — B3 = (A — B)(A2 + AB + B2) |
Версия для печати в формате png
Обратите внимание: никакой формулы суммы квадратов не существует! Не позволяйте своей фантазии заходить слишком далеко.
Как проще всего запомнить все эти формулы? Ну, скажем, увидеть определенные аналогии. Например, формула квадрата суммы похожа на формулу квадрата разности (отличие лишь в одном знаке), а формула куба суммы — на формулу куба разности. Далее, в составе формул разности кубов и суммы кубов мы видим нечто похожее на квадрат суммы и квадрат разности (только коэффициента 2 не хватает).
Но лучше всего эти формулы (как и любые другие!) запоминаются на практике. Решайте больше примеров на упрощение алгебраических выражений, и все ф-лы запомнятся сами собой.
Любознательным школьникам будет, вероятно, интересно обобщить приведенные факты. Вот, скажем, существуют формулы квадрата и куба суммы. А что, если рассмотреть выражения типа (A + B)4, (A + B)5 и даже (A + B)n, где n — произвольное натуральное число? Можно ли увидеть здесь какую — либо закономерность?
Да, подобная закономерность существует. Выражение вида (A + B)n называется биномом Ньютона. Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
Я рекомендую пытливым школьникам самим вывести формулы для (A + B)4 и (A + B)5, а далее попытаться увидеть общий закон: сравнить, например, степень соответствующего бинома и степень каждого из слагаемых, которые получаются при раскрытии скобок; сравнить степень бинома с количеством слагаемых; попытаться найти закономерности в коэффициентах. Мы не будем сейчас углубляться в эту тему (для этого нужен отдельный разговор!), а лишь запишем готовый результат:
(A + B)n = An + Cn1An-1B + Cn2An-2B2 + … + CnkAn-kBk + … + Bn.
Здесь Cnk = n!/(k! • (n-k)!).
Напоминаю, что n! — это 1 • 2 • … • n — произведение всех натуральных чисел от 1 до n. Называется это выражение факториалом числа n. Например, 4! = 1 • 2 • 3 • 4 = 24. Факториал нуля считается равным единице!
А что можно сказать по поводу разности квадратов, разности кубов и т. п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
п.? Существует ли здесь какая-либо закономерность? Можно ли привести общую формулу для An — Bn?
Да, можно. Вот эта формула:
An — Bn = (A — В)(An-1 + An-2B + An-3B2 + … + Bn-1).
Более того, для нечетных степеней n существует аналогичная ф-ла и для суммы:
An + Bn = (A + В)(An-1 — An-2B + An-3B2 — … + Bn-1).
Мы не будем сейчас выводить эти формулы (кстати, это не очень сложно), но знать об их существовании, безусловно, полезно.
Возможно, вам будут интересны другие материалы:
- Тест по математике для 7 класса
- Тест по математике для 8 класса
- Проценты. Задачи «на проценты». Часть I
- Четность. Задачи: от элементарных до «олимпиадных»
- ОГЭ по математике — пробный тест № 1
- Подготовка к ОГЭ-2021 по математике
Зачем нужны формулы сокращенного умножения / Бери и делай
Умножение чисел не вызывает особых трудностей до тех пор, пока мы не сталкиваемся со сложными выражениями, где есть не только числа, но и переменные. Чтобы преобразовать или упростить такие выражения, можно использовать формулы сокращенного умножения. Они кажутся сложными, но лишь на первый взгляд.
Чтобы преобразовать или упростить такие выражения, можно использовать формулы сокращенного умножения. Они кажутся сложными, но лишь на первый взгляд.
«Бери и Делай» объясняет, что из себя представляют формулы сокращенного умножения, как их понять и использовать для решения разных задач.
Зачем нужны формулы сокращенного умножения
С этой темой чаще всего впервые сталкиваются в средней школе в рамках курса алгебры. На первый взгляд, все выглядит сложным, но формулы сокращенного умножения действительно помогают быстро и компактно произвести вычисления в определенных ситуациях.
Ситуация № 1. Вы не хотите в уме возводить в степень большие числа, а затем производить математические действия с полученными результатами. Посмотрите на картинку выше: вместо того чтобы возводить числа 89 и 88 в квадрат, а затем заниматься вычитанием больших чисел, как это сделано на картинке слева, легче воспользоваться формулой разности двух квадратов a2 − b2 = (a − b) × (a + b), как это сделано на картинке справа.
Аналогично, чтобы возвести в квадрат большое число, можно воспользоваться формулой квадрата разности (a − b)2 = a2 − 2ab + b2. Например: 792 = (80 − 1)2 = 6400 − 160 + 1 = 6241.
Ситуация № 2. Вы хотите избавиться от скобок в выражении, выполнив минимум действий. В примере выше для того, чтобы вынести из скобок выражение (5 + b)2, справа мы воспользовались формулой квадрата суммы двух чисел (a + b)2 = a2 + 2ab + b2, в результате получив выражение 25 + 10b + b2. К этому же выражению можно прийти и без формулы, выполнив все действия последовательно, но именно благодаря формуле это быстрее и проще.
Ситуация № 3. Вам нужно привести многочлен (сумму произведений чисел и переменных) к стандартному виду. Для этого в примере на картинке выше мы снова использовали формулу квадрата суммы (a + b)2 = a2 + 2ab + b2 и превратили (1 + 5x)2 − 12x − 1 в 25×2 − 2x.
Какие бывают формулы сокращенного умножения
Математически доказать эти формулы несложно. Достаточно последовательно выполнить действия.
Пример № 1. Возьмем правую часть разности квадратов (a − b) × (a + b) и избавимся от скобок, получив (a − b) × (a + b) = a2 + ab − ab − b2. Так как ab − ab = 0, в итоге получаем, что (a − b) × (a + b) = a2 − b2.
Пример № 2. Возьмем правую часть формулы квадрата суммы (a + b)2 и избавимся от степени, получив (a + b)2 = (a + b) × (a + b). Уберем скобки, получив a2 + ab + b2 + ab, а затем a2 + 2ab + b2. В итоге получаем, что (a + b)2 = a2 + 2ab + b2.
Пример № 3. Часто встречается формула квадрата суммы трех чисел, но что делать, если нам нужна формула квадрата разницы трех чисел? Попробуем ее получить самостоятельно:
(a − b − c)2 = (a − b − c) × (a − b − c) = a2 − ab − ac − ba + b2 + bc − ca + cb + c2 = a2 − 2ab − 2ac + b2 + 2bc + c2. Для удобства восприятия ее можно записать так: (a − b − c)2 = a2 + b2 + c2 − 2ab − 2ac + 2bc.
Для удобства восприятия ее можно записать так: (a − b − c)2 = a2 + b2 + c2 − 2ab − 2ac + 2bc.
Формулы для кубов доказать можно точно так же.
Пример № 1. Возьмем правую часть формулы разности кубов (a − b) × (a2 + ab + b2) и избавимся от скобок, получив a3 + a2b + ab2 − ba2 − ab2 − b3 = a3 + a2b − ba2 − b3 = a3 − b3. В итоге получаем, что (a − b) × (a2 + ab + b2) = a3 − b3.
Как запомнить формулы сокращенного умножения
В школе формулы сокращенного умножения учат наизусть. Если вы их случайно забудете, всегда можно с помощью нескольких действий привести выражение к упрощенному виду, как мы делали это выше в доказательствах. Но есть пара способов, которые могут облегчить запоминание.
Обычно сложнее всего запомнить коэффициенты и знаки в середине формулы, если речь идет об n-й степени суммы или разницы (квадрате суммы, квадрате разницы, кубе суммы, кубе разницы и так далее). Но можно их не запоминать, если на черновике рисовать небольшую подсказку — треугольник Паскаля.
Но можно их не запоминать, если на черновике рисовать небольшую подсказку — треугольник Паскаля.
Для начала на листке бумаге расположите три единицы: одна в середине, две другие у нее по бокам, но так, чтобы они все вместе образовывали треугольник.
Строку с одной единицей будем считать нулевой. Таким образом, на первой строке располагаются две единицы. Чтобы получить вторую строчку, по краям снова расположим единицы, а между ними число, которое в сумме дают два вышестоящих над ним числа (единицы). Так в середине второй строчки появляется двойка.
Теперь записываем третью строку. По краям ставим единицы (так будет всегда), затем между ними снова добавляем те числа, которые получаются в результате сложения вышестоящих, то есть тройки.
Продолжим заполнять таким образом треугольник до четвертой строчки. Что мы получили? Посмотрите на картинку выше. В каждой строке у нас коэффициенты из разложения двучлена в многочлен.
Теперь осталось разобраться со знаками. Как их запомнить? Первый из них будет таким же, как в раскладываемом двучлене (если раскладываем сумму, то это плюс, если разность — минус), а дальше знаки будут чередоваться.
Альтернативный способ. Некоторым людям легче запомнить формулы, представляя вместо переменных абстрактные фигуры, как на изображении выше.
Как правильно читать формулы сокращенного умножения
- a2 + b2 = (a + b)2 − 2ab
Сумма квадратов двух выражений равна разности квадрата суммы этих чисел и их удвоенного произведения.
- a2 − b2 = (a − b) × (a + b)
Разность квадратов двух выражений равна произведению их разности и их суммы.
- (a + b)2 = a2 + 2ab + b2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого на второе плюс квадрат второго выражения.
- (a − b)2 = a2 − 2ab + b2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого на второе плюс квадрат второго выражения.
- a3 + b3 = (a + b) × (a2 − ab + b2)
Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- a3 − b3 = (a − b) × (a2 + ab + b2)
Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго выражения.
- (a − b)3 = a3 − 3a2b + 3ab2 − b3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго выражения.
Какие ошибки чаще всего допускают люди при использовании этих формул
- Путают сумму квадратов и квадрат суммы, разность квадратов и квадрат разности, сумму кубов и куб суммы, разность кубов и куб разности.
- Путают формулы сокращенного умножения и формулы умножения и деления переменных со степенями.
- Не замечают, что в выражении есть часть, которую можно упростить или решить с помощью формулы сокращенного умножения.
- Не видят формулу сокращенного умножения в выражении, потому что забывают, что иногда вместо одной переменной могут быть целые выражения.
Как раскрывается разность куба. Формулы сокращенного умножения
При расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения . Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
a 2 — b 2 = (a — b)(a + b)
Квадрат суммы
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
(a + b) 2 = a 2 + 2ab + b 2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел , не используя калькулятор или умножение в столбик. Поясним на примере:
Найти 112 2 .
Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2
112 = 100 + 1
Запишем сумму чисел в скобки и поставим над скобками квадрат.
112 2 = (100 + 12) 2
Воспользуемся формулой квадрата суммы:
112 2 = (100 + 12) 2 = 100 2 + 2 x 100 x 12 + 12 2 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.
(8a + с) 2 = 64a 2 + 16ac + c 2
Предостережение!!!
(a + b) 2 не равно a 2 + b 2
Квадрат разности
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
(a — b) 2 = a 2 — 2ab + b 2
Также стоит запомнить весьма полезное преобразование:
(a — b)
2
= (b — a)
2
(a — b)
2
= a
2
— 2ab + b
2
= b
2
— 2ab + a
2
= (b — a)
2
Куб суммы
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Запомнить эту «страшную» на вид формулу довольно просто.
Выучите, что в начале идёт a 3 .
Два многочлена посередине имеют коэффициенты 3.
В
спомним, что любое число в нулевой степени есть 1. (a 0 = 1, b 0 = 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b. В этом можно убедиться:
(a + b) 3 = a 3 b 0 + 3a 2 b 1 + 3a 1 b 2 + b 3 a 0 = a 3 + 3a 2 b + 3ab 2 + b 3
Предостережение!!!
(a + b) 3 не равно a 3 + b 3
Куб разности
Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a 3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.
(a — b) 3 = + a 3 — 3a 2 b + 3ab 2 — b 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сумма кубов ( Не путать с кубом суммы!)
Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
a 3 + b 3 = (a + b)(a 2 — ab + b 2)
Сумма кубов — это произведение двух скобок.
Первая скобка — сумма двух чисел.
Вторая скобка — неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
A 2 — ab + b 2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубов (Не путать с кубом разности!!!)
Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
a 3 — b 3 = (a — b)(a 2 + ab + b 2)
Будьте внимательны при записи знаков. Следует помнить, что все формулы, приведённые выше, используется также и справа налево.
Трудно запоминаются формулы сокращенного умножения? Делу легко помочь. Нужно просто запомнить, как изображается такая простая вещь, как треугольник Паскаля. Тогда вы вспомните эти формулы всегда и везде, вернее, не вспомните, а восстановите.
Что же такое треугольник Паскаля? Этот треугольник состоит из коэффициентов, которые входят в разложение любой степени двучлена вида в многочлен.
Разложим, например, :
В этой записи легко запоминается, что вначале стоит куб первого, а в конце — куб второго числа. А вот что посередине — запоминается сложно. И даже то, что в каждом следующем слагаемом степень одного множителя все время уменьшается, а второго — увеличивается — несложно заметить и запомнить, труднее дело обстоит с запоминанием коэффициентов и знаков (плюс там или минус?).
Итак, сначала коэффициенты. Не надо их запоминать! На полях тетрадки быстренько рисуем треугольник Паскаля, и вот они — коэффициенты, уже перед нами. Рисовать начинаем с трех единичек, одна сверху, две ниже, правее и левее — ага, уже треугольник получается:
Первая строка, с одной единичкой — нулевая. Потом идет первая, вторая, третья и так далее. Чтобы получить вторую строку, нужно по краям снова приписать единички, а в центре записать число, полученное сложением двух чисел, стоящих над ним:
Записываем третью строку: опять по краям единицы, и опять, чтобы получить следующее число в новой строке, сложим числа, стоящие над ним в предыдущей:
Как вы уже догадались, мы получаем в каждой строке коэффициенты из разложения двучлена в многочлен:
Ну а знаки запомнить еще проще: первый — такой же, как в раскладываемом двучлене (раскладываем сумму — значит, плюс, разность — значит, минус), а дальше знаки чередуются!
Вот такая это полезная штука — треугольник Паскаля. Пользуйтесь!
Пользуйтесь!
В предыдущем уроке мы разобрались с разложением на множители. Освоили два способа: вынесение общего множителя за скобки и группировку. В этом уроке — следующий мощный способ: формулы сокращённого умножения . В краткой записи — ФСУ.
Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.
Разбираемся?)
Откуда берутся формулы сокращённого умножения?
Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.
Они берутся из умножения.) Например:
(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2
Вот и всё, никаких научных хитростей. Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
Просто перемножаем скобки и приводим подобные. Так получаются все формулы сокращённого умножения. Сокращённое умножение — это потому, что в самих формулах нет перемножения скобок и приведения подобных. Сокращены.) Сразу дан результат.
ФСУ нужно знать наизусть. Без первых трёх можно не мечтать о тройке, без остальных — о четвёрке с пятёркой.)
Зачем нужны формулы сокращённого умножения?
Есть две причины, выучить, даже зазубрить эти формулы. Первая — готовый ответ на автомате резко уменьшает количество ошибок. Но это не самая главная причина. А вот вторая…
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой , которую мы рекомендуем распечатать и все время держать перед глазами:
Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a
и b
на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2
) и разности двух выражений a
и b
на неполный квадрат их суммы (a 2 +a·b+b 2
) соответственно.
Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a
и b
на их неполный квадрат разности (так называют выражение вида a 2 −a·b+b 2
) и разности двух выражений a
и b
на неполный квадрат их суммы (a 2 +a·b+b 2
) соответственно.
Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество . Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.
При решении примеров, особенно в которых имеет место разложение многочлена на множители , ФСУ часто используют в виде с переставленными местами левыми и правыми частями:
Три последних тождества в таблице имеют свои названия. Формула a 2 −b 2 =(a−b)·(a+b)
называется формулой разности квадратов , a 3 +b 3 =(a+b)·(a 2 −a·b+b 2
) — формулой суммы кубов , а a 3 −b 3 =(a−b)·(a 2 +a·b+b 2
) — формулой разности кубов . Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.
Дополнительные формулы
В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.
Сферы применения формул сокращенного умножения (фсу) и примеры
Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений . Наиболее часто эти формулы используются в процессе упрощения выражений .
Пример.
Упростите выражение 9·y−(1+3·y) 2 .
Решение.
В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y) 2 =9·y−(1 2 +2·1·3·y+(3·y) 2) . Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1 2 +2·1·3·y+(3·y) 2)= 9·y−1−6·y−9·y 2 =3·y−1−9·y 2 .
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук. Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей , решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х 2 — у 2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у) 2 = х 2 + 2ху + у 2 . Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у) 2 = х 2 — 2ху + у 2 . Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у) 3 = х 3 + 3х 2 у + 3ху 2 + у 3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х — у) 3 = х 3 — 3х 2 у + 3ху 2 — у 3 . Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестая х 3 + у 3 = (х + у) (х 2 — ху + у 2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х 3 — у 3 = (х — у) (х 2 + ху + у 2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей з нали еще около 4 тысяч лет тому назад. Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b) 2 = a 2 +2ab +b 2 .
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
A 2 b 2 c 2, сложение квадратов
Рассмотрим квадрат трех слагаемых:
(a + b + c)2
Представим его в таком виде:
((a + b) + c)2
Если рассматривать (a + b) как одно слагаемое, то мы можем применить формулу квадрата суммы для двух слагаемых:
((a + b) + c)2 = (a + b)2 + 2(a + b)c + c2 = a2 + 2ab + b2 + 2ac + 2bc + c2
Итак в результате преобразования мы получили:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
Если бы слагаемых было 4, то в результате преобразования выглядели так:
(a + b + c + d)2 = ((a + b) + (c + d))2 = (a + b)2 + 2(a+b)(c+d) + (c + d)2 = a2 + 2ab + b2 + 2ac + 2ad + 2bc + 2bd + c2 + 2cd + d2
В результате была бы получена следующая формула:
(a + b + c + d)2 = a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
Вообще независимо от того, сколько слагаемых в квадрате суммы, при раскрытии скобок получается сумма квадратов всех слагаемых плюс удвоенные пары произведений этих слагаемых. 2=21 и a+b-c=7. найдите значение выражения ab-bc-ac
2=21 и a+b-c=7. найдите значение выражения ab-bc-ac
- Пример 1 Преобразуйте выражение в многочлен
- Пример 2 Преобразуйте выражение в многочлен
- Пример 3 Выполните умножение
- Больше информации по теме
Квадрат суммы и разности
Квадрат суммы
Выражение (a + b)2 — это квадрат суммы чисел a и b. По определению степени выражение (a + b)2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что
По определению степени выражение (a + b)2 представляет собой произведение двух многочленов (a + b)(a + b). Следовательно, из квадрата суммы мы можем сделать выводы, что
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2,
т. е. квадрат суммы двух чисел равен квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата суммы, без промежуточных преобразований, будет выглядеть так:
(a + b)2 = a2 + 2ab + b2
Многочлен a2 + 2ab + b2 называется разложением квадрата суммы.
Так как a и b обозначают любые числа или выражения, то правило даёт нам возможность сокращённым путём возводить в квадрат любое выражение, которое может быть рассмотрено как сумма двух слагаемых. 2=21 и a+b-c=7. найдите значение выражения ab-bc-ac
2=21 и a+b-c=7. найдите значение выражения ab-bc-ac
У нас должна получиться сумма квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(3x2 + 2xy)2 = (3x2)2 + 2(3x2 · 2xy) + (2xy)2
Теперь, пользуясь правилами умножения и возведения в степень одночленов, упростим получившееся выражение:
(3x2)2 + 2(3x2 · 2xy) + (2xy)2 = 9x4 + 12x3y + 4x2y2
Квадрат разности
Выражение (a — b)2 — это квадрат разности чисел a и b. Выражение (a — b)2 представляет собой произведение двух многочленов (a — b)(a — b). Следовательно, из квадрата разности мы можем сделать выводы, что
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2,
т. е. квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
е. квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа.
Из правила следует, что общая формула квадрата разности, без промежуточных преобразований, будет выглядеть так:
(a — b)2 = a2 — 2ab + b2
Многочлен a2 — 2ab + b2 называется разложением квадрата разности.
Это правило применяется к сокращённому возведению в квадрат выражений, которые могут быть представлены как разность двух чисел.
Пример. Представьте квадрат разности в виде трёхчлена:
(2a2 — 5ab2)2
Решение: используя формулу квадрата разности находим:
(2a2 — 5ab2)2 = (2a2)2 — 2(2a2 · 5ab2) + (5ab2)2
Теперь преобразуем выражение в многочлен стандартного вида:
(2a2)2 — 2(2a2 · 5ab2) + (5ab2)2 = 4a4 — 20a3b2 + 25a2b4
Разность квадратов
Выражение a2 — b2 — это разность квадратов чисел a и b.
Выражение a2 — b2 представляет собой сокращённый способ умножения суммы двух чисел на их разность:
(a + b)(a — b) = a2 + ab — ab — b2 = a2 — b2,
т. е. произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
Из правила следует, что общая формула разности квадратов выглядит так:
a2 — b2 = (a + b)(a — b)
Это правило применяется к сокращённому умножению таких выражений, которые могут быть представлены: одно — как сумма двух чисел, а другое — как разность тех же чисел.
Пример. Преобразуйте произведение в двучлен:
(5a2 + 3)(5a2 — 3)
Решение:
(5a2 + 3)(5a2 — 3) = (5a2)2 — 32 = 25a4 — 9
В примере мы применили формулу разности квадратов справа налево, то есть нам дана была правая часть формулы, а мы преобразовали её в левую:
(a + b)(a — b) = a2 — b2
На практике все три рассмотренные формулы применяются и слева направо и справа налево, в зависимости от ситуации.
Выражения, преобразование выражений
Формулы сокращенного умножения (ФСУ): таблица, формулировки, примеры применения.
Для умножения и возведения в степень чисел и выражений (в частности многочленов) в некоторых случаях могут быть использованы так называемые формулы сокращенного умножения. Из названия понятно, что эти формулы позволяют проводить умножение сокращенно, то есть, быстрее при более компактной записи решения.
В этой статье мы перечислим все основные наиболее часто используемые формулы сокращенного умножения. Для удобства запоминания занесем их в таблицу. Дальше дадим формулировки – они позволят читать формулы сокращенного умножения. После этого остановимся на принципах доказательства этих формул. Наконец, дадим обзор задач, для решения которых применяются формулы сокращенного умножения, и рассмотрим несколько примеров с подробными решениями.
Список формул сокращенного умножения (ФСУ) в виде таблицы
Формулы сокращенного умножения (фсу) изучаются на уроках алгебры в 7 классе после разговора про действия с многочленами и одночленами, при этом рассматриваются 7 основных формул. 3;
3;
Под буквами a и b понимаются числа, переменные, или, вообще, любые числовые и буквенные выражения.
Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой таблица формул сокращенного умножения, которую мы рекомендуем распечатать и все время держать перед глазами:
Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a2−a·b+b2) и разности двух выражений a и b на неполный квадрат их суммы (a2+a·b+b2) соответственно.
Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество. Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.
При решении примеров, особенно в которых имеет место разложение многочлена на множители, ФСУ часто используют в виде с переставленными местами левыми и правыми частями:
Три последних тождества в таблице имеют свои названия.
Формула a2−b2=(a−b)·(a+b) называется формулой разности квадратов, a3+b3=(a+b)·(a2−a·b+b2) — формулой суммы кубов, а a3−b3=(a−b)·(a2+a·b+b2) — формулой разности кубов. Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.
К началу страницы
Дополнительные формулы
В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.
Во-первых, полезной будет формула бинома Ньютона вида , где — биномиальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. С ее помощью можно сокращенно возводить сумму двух выражений в любую натуральную степень. Кстати, ФСУ квадрата и куба суммы и разности являются частными случаями формулы бинома Ньютона при n=2 и n=3.
Во-вторых, полезной бывает формула возведения в квадрат суммы трех, четырех и большего количества слагаемых вида
(a1+a2+…+an)2=a12+a22+…+an−12+an2+
+2·a1·a2+2·a1·a3+2·a1·a4+…+
+2·a1·an−1+2·a1·an+
+2·a2·a3+2·a2·a4+…+2·a2·an−1+2·a2·an+
+…+
+2·an−1·an.
Она читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых a, b и c, имеем (a+b+c)2=a2+b2+c2+2·a·b+2·a·c+2·b·c. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.
И еще не помешает держать перед глазами формулу разности n-ых степеней двух слагаемых вида an−bn=
=(a−b)·(an−1+an−2·b+an−3·b2+…+a·bn−2+bn−1), которую обычно представляют раздельно для четных и нечетных показателей. Для четных показателей 2·m она имеет вид a2·m−b2·m=
=(a2−b2)·(a2·m−2+a2·m−4·b2+a2·m−6·b4+…+b2·m−2), а для нечетных показателей 2·m+1 – вид a2·m+1−b2·m+1=
=(a−b)·(a2·m+a2·m−1·b+a2·m−2·b2+…+b2·m).
Частными случаями этой формулы являются формулы разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).
К началу страницы
Как читаются формулы сокращенного умножения?
Чтобы рассказать решение примера, в котором были использованы формулы сокращенного умножения, нужно знать, как эти формулы читаются. Дадим соответствующие формулировки.
Сначала разберемся с принципом чтения формул сокращенного умножения. Это удобнее всего сделать, рассмотрев любую и них, например, первую формулу квадрата суммы вида (a+b)2=a2+2·a·b+b2.
В левой ее части находится выражение (a+b)2, которое представляет собой квадрат суммы двух выражений a и b, оно так и читается (отсюда понятно и название формулы). Дальше стоит знак равно, он и произносится как равно. В правой части формулы расположена сумма трех слагаемых a2, 2·a·b и b2. a2 и b2 – это квадраты первого и второго выражений соответственно, а 2·a·b читается как удвоенное произведение выражений a и b, слово «удвоенное» отвечает числовому коэффициенту2. Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.
Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.
Итак, квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения первого и второго выражений и квадрата второго выражения.
Аналогично читаются и остальные фсу.
Так квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения. Эта формулировка второй фсу вида (a−b)2=a2−2·a·b+b2.
Дальше читаем формулу (a+b)3=a3+3·a2·b+3·a·b2+b3. Куб суммы двух выражений a и b равен сумме куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения.
Аналогично читается и формула куба разности (a−b)3=a3−3·a2·b+3·a·b2−b3. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.
Переходим к чтению пятой по списку формулы сокращенного выражения (a−b)·(a+b)=a2−b2. Произведение разности двух выражений и их суммы равно разности квадратов первого и второго выражений.
А для удобства чтения шестой и, последней, седьмой ФСУ используют термины «неполный квадрат суммы» и «неполный квадрат разности» выражений a и b, которыми называют выражения a2+a·b+b2 и a2−a·b+b2 соответственно. (В свою очередь выражения a2+2·a·b+b2 и a2−2·a·b+b2 называют полным квадратом суммы и разности соответственно.)
Итак, произведение суммы двух выражений на их неполный квадрат разности равно сумме кубов этих выражений.
Теорема косинусов. Доказательство теоремы косинусов.

Так читается формула (a+b)·(a2−a·b+b2)=a3+b3. И произведение разности двух выражений на неполный квадрат их суммы равен разности кубов этих выражений, этому утверждению отвечает формула сокращенного умножения вида (a−b)·(a2+a·b+b2)=a3−b3.
К началу страницы
Доказательство
Сейчас самое время остановиться на доказательстве формул сокращенного умножения.
Доказать их достаточно легко – для этого нужно лишь выполнить возведение в степень или умножение выражений, находящихся в левых частях формул, основываясь на свойствах умножения.
Для примера докажем формулу квадрата разности (a−b)2=a2−2·a·b+b2. Возведем разность a−b во вторую степень. Для этого степень заменяем умножением, и выполняем это действие: (a−b)2=(a−b)·(a−b)=
=a·(a−b)−b·(a−b)=a·a+a·(−b)−b·a−b·(−b)=
=a2−a·b−b·a+b·b=a2−a·b−a·b+b2=
=a2−2·a·b+b2.
Абсолютно аналогично доказывается любая другая из 7 основных формул сокращенного умножения.
Доказательство дополнительных ФСУ можно провести с использованием метода наименьших квадратов.
К началу страницы
Сферы применения формул сокращенного умножения (фсу) и примеры
Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.
Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений. Наиболее часто эти формулы используются в процессе упрощения выражений.
Упростите выражение 9·y−(1+3·y)2.
В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y)2=9·y−(12+2·1·3·y+(3·y)2). Остается лишь раскрыть скобки и привести подобные члены: 9·y−(12+2·1·3·y+(3·y)2)=9·y−1−6·y−9·y2=3·y−1−9·y2.
9·y−(1+3·y)2=3·y−1−9·y2.
И если в 7 классе речь идет о преобразовании целых выражений с помощью формул сокращенного умножения, то в старших классах можно будет видеть применение ФСУ к преобразованию выражений всех других видов – дробных, иррациональных, логарифмических, тригонометрических и других. К примеру, тождества сокращенного умножения с переставленными частями позволяют представлять выражения в виде степеней или произведений, в частности, выполнять разложение многочленов на множители. Это очень полезно, к примеру, при сокращении алгебраических дробей.
Сократите дробь .
В числителе выражение представляет собой разность кубов двух выражений 2·x и z2, а в знаменателе – разность квадратов этих выражений. После применения соответствующих формул исходная дробь примет вид . Теперь можно сократить одинаковые множители в числителе и знаменателе: .
Оформим все решение кратко:
.
Формулы сокращенного умножения иногда позволяют рационально вычислять значения выражений. В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 792=(80−1)2=802−2·80·1+12=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.
В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 792=(80−1)2=802−2·80·1+12=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.
В заключение скажем еще про одно важное преобразование – выделение квадрата двучлена, в основе которого лежит формула сокращенного умножения квадрат суммы. Например, выражение 4·x2+4·x−3 может быть преобразовано к виду (2·x)2+2·2·x·1+12−4, и первые три слагаемых заменяются с использованием формулы квадратом суммы. Так что выражение принимает вид (2·x+1)2−4. Подобные преобразования широко используются, например, при интегрировании.
Профиль автора статьи в Google+
К началу страницы
- Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008.
 — 240 с. : ил. — ISBN 978-5-09-019315-3.
— 240 с. : ил. — ISBN 978-5-09-019315-3. - Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Формули скороченого множення застосовують для спрощення обчислень, а також розкладання многочленів на прості множники, швидкого множення многочленів. Більшість формул скороченого множення можна отримати з біному Ньютона, в цьому Ви скоро переконаєтеся.
Формули для квадратів застосовують в обчисленнях найчастіше. Їх починають вивчати в шкільній програми починаючи з 7 класу і до кінця навчання формули для квадратів та кубів школярі повинні знати на зубок.
Формули для кубів теж не надто складні і їх потрібно знати при зведенні многочленів до стандартного вигляду, для спрощення піднесення суми чи різниці змінної і числа до кубу.
Формули позначені червоним отримують з попередніх групуванням доданків.
Формули для четвертого степеня та п’ятого степеня в шкільному курсі мало кому пригодяться, однак є завдання при вивченні вищої математики де потрібно обчислювати коефіцієнти при степенях.
Формули для степеня n степеня розписані через біноміальні коефіцієнти з використанням факторіалів наведені нижче
Приклади застосування формул скороченого множення
Приклад 1.Обчислити 512.
Розв’язок.
Якщо маєте калькулятор то без проблем знаходите
Це я пожартував — з калькулятором мудрі усі, без нього … (не будемо про сумне).
Не маючи калькулятора та знаючи наведені вище правила квадрат числа знаходимо за правилом
Саме для таких спрощених обчислень і потрібні формули скороченого множенння.
Приклад 2.Знайти 992.
Розв’язок. Застосуємо формулу для різниці в квадраті
Як можна переконатися з обчислень — це легше, ніж часом знайти в потрібний момент калькулятор.
Приклад 3.Піднести до квадрату вираз
(x+y-3).
Розв’язок. Суму перших двох доданків уявно вважаємо одним доданком і за другою формулою скороченого множення знаходимо
В такий спосіб отримали вадратичну залежність для двох змінних.
Приклад 4.Знайти різницю квадратів
112-92.
Розв’язок. Оскільки числа невеликі то можна просто підставити значення квадратів
Але мета в нас зовсім інша – навчитися використовувати формули скороченого множення для спрощення обчислень. Для цього прикладу застосуємо третю формулу
При великих числах і невеликою різницею між ними така схема набагато ефективніша ніж підносити до квадратів, а пізніше шукати різницю квадратів.
Приклад 5.Знайти різницю квадратів
172-32.
Розв’язок. На цьому прикладі Ви вже захочете вивчити правила, щоб обчислення звести до одного рядка
Як бачите – нічого складного ми не робили. Кінцевий результат в складніших умовах отримують множенням чисел у стовпчик.
Кінцевий результат в складніших умовах отримують множенням чисел у стовпчик.
Приклад 6. Спростити вираз
(x-y)2-(x+y)2.
Розв’язок. Можна розкладати квадрати, а пізніше сумувати подібні доданки. Проте можна прямо застосувати різницю квадратів
Тут пропущені проміжні перетворенн, які займають чимало місця, але наша практика дозволяє на так записати. Для перевіри нас розпишіть добуток дужок самостійно.
Приклад 7.Піднести до кубу многочлен
x3-4.
Розв’язок.
Формула Пифагора a2+b2=c2. Почему квадрат?
Застосуємо 5 формулу скороченого множення
З кубами Вам доведеться часто мати справу в навчанні, тому раджу формуи вивчити або мати на шпаргалці.
Приклад 8. Записати у вигляді різниці квадратів або сумі
а) x2-8x+7
б) x2+4x+29
Розв’язок. а) Перегрупуємо доданки
б) Спрощуємо на основі попередніх міркувань
Такі переторення досить часто доводиться виконувати на інтегруванні, коли наведені квадратичні залежності містяться в чисельнику чи знаменнику і потрібно звести запис під формулу інтегрування.
Приклад 9.Розкласти раціональний дріб
Розв’язок.
Застосуємо формулу різниці квадратів
Складемо систему рівнянь для визначення констант
До потроєного першого рівняння додамо друге. Знайдене значення підставляємо в перше рівняння
Остаточно розклад прийме вигляд
Розкласти раціональний дріб часто необхідно перед інтегруванням, щоб понизити степінь знаменника.
Приклад 10.Використовуючи біном Ньютона розписати
вираз (x-a)7.
Розв’язок. Що таке біном Ньютона Ви мабуть вже знаєте. Якщо ні то нижче наведені біноміальні коефіцієнти
Вони утворюються наступним чином: по краю ідуть одиниці, коефіцієнти між ними в нижньому рядку утворюють сумуванням сусідніх верхніх. Якщо нам потрібно знайти різницю в якомусь степені, то знаки в розкладі чергуються від плюса до мінуса. Таким чином для сьомого порядку отримаємо такий розклад
Уважно також погляньте як змінюються показники – для першої змінної вони спадають на одиницю в кожному наступному доданку, відповідно для другої – на одиницю зростають. В сумі показники при ожному множгику завжди повинні давати степінь розкладу (=7). Використовуйте це правило для самоперевірки.
В сумі показники при ожному множгику завжди повинні давати степінь розкладу (=7). Використовуйте це правило для самоперевірки.
Думаю на основі приведеного вище матеріалу Ви зможете розв’язати задачі на біном Ньютона. Вивчайте формули скороченого множення та застосовуйте всюди, де це може спростити обчислення та зекономити час виконання завдання.
Квадрат суммы нескольких слагаемых
Рассмотрим на примерах применение формул сокращенного умножения.
Пример 1 Преобразуйте выражение в многочлен
Разложим выражение на множители с помощью формулы квадрата суммы
Пример 2 Преобразуйте выражение в многочлен
Воспользуемся формулой квадрата разности
Пример 3 Выполните умножение
Разложим выражение на множители с помощью формулы разности квадратов
Математические выражения (формулы) сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне не заменимы во многих областях точных наук.
Pythagorean theorem
Эти 7 символьных записей не заменимы при упрощении выражений, решении уравнений, при умножении многочленов, сокращении дробей, решении интегралов и многом другом. А значит будет очень полезно разобраться как они получаются, для чего они нужны, и самое главное, как их запомнить и потом применять. Потом применяя формулы сокращенного умножения на практике самым сложным будет увидеть, что есть х и что есть у. Очевидно, что никаких ограничений для a и b нет, а значит это могут быть любые числовые или буквенные выражения.
И так вот они:
Первая х2 — у2 = (х — у) (х+у) .Чтобы рассчитать разность квадратов двух выражений надо перемножить разности этих выражений на их суммы.
Вторая (х + у)2 = х2 + 2ху + у2. Чтобы найти квадрат суммы двух выражений нужно к квадрату первого выражения прибавить удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Третья (х — у)2 = х2 – 2ху + у2. Чтобы вычислить квадрат разности двух выражений нужно от квадрата первого выражения отнять удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Четвертая (х + у)3 = х3 + 3х2у + 3ху2 + у3. Чтобы вычислить куб суммы двух выражений нужно к кубу первого выражения прибавить утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
Пятая (х — у)3 = х3 – 3х2у + 3ху2 — у3. Чтобы рассчитать куб разности двух выражений необходимо от куба первого выражения отнять утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
Шестая х3 + у3 = (х + у) (х2 — ху + у2) Чтобы высчитать сумму кубов двух выражений нужно умножить суммы первого и второго выражения на неполный квадрат разности этих выражений.
Седьмая х3 — у3 = (х — у) (х2 + ху + у2) Чтобы произвести вычисление разности кубов двух выражений надо умножить разность первого и второго выражения на неполный квадрат суммы этих выражений.
Не сложно запомнить, что все формулы применяются для произведения расчетов и в противоположном направлении (справа налево).
О существовании этих закономерностей знали еще около 4 тысяч лет тому назад.
Их широко применяли жители древнего Вавилона и Египта. Но в те эпохи они выражались словесно или геометрически и при расчетах не использовали буквы.
Разберем доказательство квадрата суммы (а + b)2 = a2 +2ab +b2.
Первым эту математическую закономерность доказал древнегреческий учёный Евклид, работавший в Александрии в III веке до н.э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а2”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”.
И так Евклид взял квадрат со стороной (a + b):
S = (a + b)2 – площадь квадрата;
С другой стороны, этот же квадрат он представить иначе, разделив сторону на а и b:
Тогда площадь квадрата можно представить в виде суммы площадей:
И так как квадраты были одинаковы, то их площади равны, и это значит:
Таким образом, была доказана геометрически формула квадрата суммы.
Решение формулы суммы квадратов двух чисел
Цитировать:
Мамарахмонов Н.М., Мамарахмонов М.Х. Решение формулы суммы квадратов двух чисел // Universum: технические науки : электрон. научн. журн. 2020. № 8(77). URL: https://7universum.com/ru/tech/archive/item/10642 (дата обращения: 22.09.2022).
Прочитать статью:
АННОТАЦИЯ
В настоящей статье нами впервые предложено решение формулы сокращенного произведения, которая может широко применена в решении различных математических задач, равенств и неравенств, а также для упрощения сложных алгебраических выражений, имеющих широкое практическое применение в науке и технике.
ABSTRACT
In this article, we first proposed a solution to the abbreviated product formula, which can be used in solving various mathematical problems, equalities and inequalities, as well as to simplify complex algebraic expressions that have wide practical applications in science and technology.
Ключевые слова: формулы сокращенного произведения, сумма квадратов двух чисел.
Keywords: formulas of short multiplication, sum of squares two numbers.
Известно, что при решении задач во всех разделах математики очень часто используют формулы сокращенного произведения (ФСУ) [1. 163-182, 2. 115, 3. 134]. Эти формулы удачно используются при упрощении сложных математических выражений, при решении алгебраических, тригонометрических уравнений, неравенств, геометрических задач, учебных и научных проблем различной сложности. Ниже приведены официально всем известные ФСУ в табличном виде, из учебников Алгебры для 7 класса:
Таблица 1.
Формулы сокращенного умножения
|
Формула |
Название |
Name |
№ |
|
(a+b)2=a2+2ab+b2 |
Квадрат суммы двух чисел |
Square of sum |
(1) |
|
(a-b)2=a2-2ab+b2 |
Квадрат разности двух чисел |
Square of difference |
(2) |
|
(a+b)3=a3+3a2b+3ab2+b3 |
Куб суммы двух чисел |
Cube of sum |
(3) |
|
(a-b)3=a3-3a2b+3ab2-b3 |
Куб разности двух чисел |
Cube of difference |
(4) |
|
a3+b3=(a+b)(a2-ab+b2) |
Сумма кубов двух чисел |
Sum of cubes |
(5) |
|
a3-b3=(a-b)(a2+ab+b2) |
Разность кубов двух чисел |
Difference of cubes |
(6) |
|
a2-b2=(a-b)(a+b) |
Разность квадратов двух чисел |
Difference of squares |
(7) |
|
a2+b2 = ? |
Сумма квадратов двух чисел (Примечание: не разлагающаяся на члены) [8] |
Sum of squares (Note: not expands) [8,10] |
(8) |
Наглядно видно из таблицы 1, что приведенные в ней формулы 1, 2; 3, 4; 5, 6; 7, 8 являются формулами-парами, которые отличаются нежели только со знаками у отдельных членов в левой части равенства. Однако, решение для урувнения формулой a2+b2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена [1-7]. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» [8-10]. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.
Однако, решение для урувнения формулой a2+b2 (8) до настоящего времени ни в официальных источниках, также в учебной и научной литературе не была приведена [1-7]. Тому можно убедиться после ознакомления в электронных интернет учебниках на английском, так и на других языках. В них формула (8) указана как “not expands” – «не разлагающаяся на члены» [8-10]. Также, во всех учебниках для средних образовательных школ по математике, так и в пособиях для ВУЗов Узбекистана, России и Европейских стран, написанные на узбекском, английком, так и на русском языках, формула (8), до настоящего времени обозначается как, “не разлагающаяся на члены”.
В настоящей статье нами впервые предложена конкретное решение для формулы (8), для разложения суммы квадратов двух чисел на многочлены. Она имеет решение следующего вида:
Она имеет решение следующего вида:
(8)
Доказательство. Результат последовательного произведения многочленов в правой части формулы (8), должны равняться сумме квадратов двух чисел, в левой части равенства. Для этого применяем правила последовательного умножения для многочленов к выражениям в скобках, в правой части равенства:
Примечание. Члены с одинаковыми абсолютными значениями, но с различными знаками взаимно сокращаются, как показано ниже:
;
;
В результате упрощения получим результат сумму квадратов двух чисел, идентичный, что в левой части равенства a2+b2.
Конец доказательства.
Предложенная нами формула для суммы квадратов двух чисел (8) является инновационной, новой и имеет в дальнейшем практическое применение как в математике, информатике, ИТ, в точных науках в целом, так и в других отраслях науки и техники.
Список литературы
- Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворов. Алгебра. 7 класс: учебник для общеобразоват. учреждений.: под ред. С.А.Теляковского.- М.: «Просвещение». — 2013. — 256 с.
- Ш.Алимов,О.Р. Холмухамедов, М.А. Мирзаахмедов. Алгебра. 7 класс: учебник для общеобразоват. учреждений.: T.: “Укитувчи”. — 2017. -192 c.
- А.У. Абдухамидов, Х.А.Насимов, Ж.Х.Хусанов. Алгебра и основы математического анализа, I-часть, Учебник для Академических лицеев.: T.: “Укитувчи”. — 2008. — 134-с.
- Ш.Ш.Ботиров, З.Н.Неъматов, Д.Ф.Орипова. Математика. Сборник тематических вопросов-ответов. Бухара.: “Бухоро”. – 2015. – 24с.
- Г. Худойберганов, А.Ворисов, Х.Мансуров, Б.Шоимкулов. Лекции по математическому анализу . T.: “Ворис-нашриёт”. — 2010. — 70 с.
- М. Хушвактов. Матемтический анализ. T.: “Янгиюл Полиграф Сервис”.-2008. – 59 с.
- П.Е.Данько, А.Г.Паров, Т.Е.
 Кожевникова. Высшая сатематика в задачах и упражнениях. T.: “Узбек файласуфлари миллий жамияти” – 2007. – 53 с.
Кожевникова. Высшая сатематика в задачах и упражнениях. T.: “Узбек файласуфлари миллий жамияти” – 2007. – 53 с. - Short multiplication formulas/ MathForYou.net [Электронный ресурс]. – Режим доступа: URL: http://www.mathforyou.net/en/formulas/shortmultiplication-formulas/ (Дата обращения 10.08.2020).
- Формулы сокращенного умножения многочленов / [Электронный ресурс]. – Режим доступа: URL: http://math-https://prosto.ru/?page=pages/fsu/short_multiplication_formula.php
- Short multiplication formulas / [Электронный ресурс]. – Режим доступа: URL: https://www.emathhelp.net/notes/algebra-2/trigonometry/short-multiplication-formulas/ (Дата обращения:10.08.2020).
Формулы сокращенного умножения — МАТВОКС
Формулы сокращенного умножения — МАТВОКСПерейти к содержанию
ПОИСК
Страница Вконтакте открывается в новом окне
Вы здесь:
Содержание раздела
История формул сокращенного умножения
За много веков до нашей эры математикам Китая и Древней Греции были известны формулы сокращённого умножения.
Все алгебраические утверждения тогда выражались в геометрической форме.
Древние греки обозначали величины не числами или буквами, а отрезками прямых. Они говорили не a в квадрате (a2), а «квадрат на отрезке a», не произведение ab, a «прямоугольник, содержащийся между отрезками a и b».
Так как древнегреческие математики решали алгебраические уравнения геометрическим способом, то это направление в математике называлась геометрическая алгебра.
Евклид во второй книге «Начал» сформулировал и доказал ряд алгебраических тождеств.
Например, одно из них сформулировано было так: «если прямая линия как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды взятым прямоугольником, заключенным между отрезками». Другими словами, если прямая рассечена на два отрезка, то квадрат этой прямой будет равен сумме квадратов, построенных на этих отрезках, плюс сумма двух прямоугольников, построенных из длин этих отрезков.
Покажем это на рисунке.
Геометрический способ вывода формулы квадрата суммы
Прямую рассечем на два отрезка отрезок а и отрезок b.
В результате получим на прямой отрезок АВ (обозначим концы всего отрезка прямой буквами А и В). длина отрезка АВ равна сумме длин отрезков a и b:
AB=a+bПокажем, что квадрат всего отрезка равен квадрату суммы отрезков, из которых он состоит:
AB2=(a+b)2
На стороне AB построим квадрат ABCD. Для этого под прямыми углами проведем отрезки, равные АВ (AB=BD=CD=AC)
Внутри квадрата построим квадрат со стороной а и его площадь обозначим S1.
Далее построим квадрат со стороной b и его площадь обозначим S2.
В результате образовались: квадрат, площадью S1, квадрат площадью S2 и два прямоугольника, у которых площади равны a∙b.
Площадь квадрата равна квадрату стороны, значит, по построению: S1= a2, S2=b2.
Площадь прямоугольника равна произведению его сторон. Значит, площадь построенного прямоугольника будет равна a∙b. А так как таких прямоугольников два, то их площади будут в два раза больше: 2a∙b.
Итак, AB2 — это построенный квадрат.
Запишем, из чего он в результате состоит.
И так как, ранее мы показали, что:
AB=a+b
То, можем записать:
Таким же образом, при помощи отрезков были доказаны квадрат разности и разность квадратов.
Древнегреческий ученый математик Диофант Александрийский в третьем веке до новой эры отказался от геометрических способов выражения. Диофант в своём труде «Арифметика» рассматривал формулы квадрата суммы, квадрата разности и разности квадратов уже алгебраическим способом.
Благодаря Виету и Декарту в XVI веке алгебраические тождества получили современную символику.
Исаак Ньютон обосновал математические формулы на современном уровне.
Однако некоторые термины из геометрической алгебры мы используем до сих пор. Например, квадратом мы называем вторую степень числа, кубом третью степень числа.
Треугольник Паскаля
В 1654 году французский математик Блез Паскаль написал «Трактат об арифметическом треугольнике».
В 1303 году в книге китайского математика Чжу Шицзе «Яшмовое зеркало четырех элементов» на иллюстрации уже был изображён подобный треугольник.
Немецкий математик, астроном Петер Апиан такой треугольник изобразил в учебнике арифметики на титульном листе в 1529 году.
Но Паскаль в своем трактате исследует свойства числовой таблицы треугольной формы, которую называли «треугольником Паскаля».
Приведем некоторые свойства треугольника Паскаля:
- Сумма чисел каждой следующей строки в два раза больше суммы чисел предыдущей строки.
- В каждой строке сумма чисел, стоящих на четных местах, равна сумме чисел на нечётных местах.
- Если номер строки является простым числом, то и все числа в этой строке, кроме крайних, делятся на её номер.
Около 1677 г Исаак Ньютон вывел формулу бинома Ньютона для более общего случая, когда показатель степени произвольное действительное число.
Бином Ньютона (a+b)n — формула разложения натуральной степени двучлена (a+b)n в многочлен.
View this post on Instagram
A post shared by Математика для каждого (@mathvox_ru)
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
MATHVOX
Вверх
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Don`t copy text!
A Square Plus B Square Plus C Square Formula — Examples
a 2 + b 2 + c 2 формула используется для нахождения суммы квадратов трех чисел без фактического вычисления квадратов. a 2 + b 2 + c 2 формула является одним из основных алгебраических тождеств. Чтобы получить расширение формулы 2 + b 2 + c 2 , оцените формулу (a + b + c) 2 . Давайте узнаем больше о a 92 Формула?
Чтобы получить расширение формулы 2 + b 2 + c 2 , оцените формулу (a + b + c) 2 . Давайте узнаем больше о a 92 Формула?
Мы только что прочитали, что, умножая (a + b + c) само на себя, мы можем легко получить формулу a 2 + b 2 + c 2 . Давайте посмотрим на расширение формулы 2 + b 2 + c 2 .
(a + b + c) 2 = (a + b + c)(a + b + c)
(a + b + c) 2 = a 2 + ab + ac + ab + b 2 + bc + ca + bc + c 2
(а + б + в) 2 = а 2 + b 2 + c 2 + 2ab + 2bc + 2ca
(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
Вычитая 2ab + 2bc + 2ca из обеих частей приведенной выше формулы, 2 + B 2 + C 2 Формула:
A 2 + B 2 + C 2 = (A + B + C) 2 — 2 (AB + BC + ва)
(или)
а 2 + б 2 + C 2 = (A + B + C) 2 -2AB -2BC -2CA
A 2 + B 2 + C 2 = (A + B + C) 2 — 2 (AB+ BC+ CA)
Мы также можем выразить формулу 2 + B 2 + C 2 AS,
A 2 + B 2 + C 2 = ( a — b — c) 2 + 2ab + 2ac — 2bc
Давайте посмотрим, как использовать формулу a 2 + b 2 + c 2 , в следующем разделе.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Примеры формулы a2 + b2 + c2
Давайте рассмотрим несколько примеров, чтобы лучше понять формулу a 2 + b 2 + c 2 .
Пример 1: Найдите значение 2 + b 2 + c 2 если a + b + c = 10 и ab + bc + ca = -2.
Решение:
Найти: a 2 + b 2 + c 2
Учитывая, что:
а + б + с = 10
аб + бс + са = -2
Используя формулу a 2 + b 2 + c 2 ,
a 2 + b 2 + c 2 = (a + b + c) 2 — 2(ab + bc + ca)
а 2 + B 2 + C 2 = (10) 2 — 2 (-2) = 100+ 4 = 104
Ответ: A 2 + B 2 + C 2 = 104.
Пример 2: Найдите значение a 2 + b 2 + c 2 если a + b + c = -3, 1/a + 1/b + 1/c = -2 и abc = 3.
Решение:
Найти: a 2 + b 2 + c 2
Учитывая, что:
а + b + с = -3 … (1)
1/а + 1/б + 1/с = -2 … (2)
абв = 3 … (3)
Умножение (2) и (3),
abc(1/a + 1/b + 1/c) = (3)(−2)
bc + ca + ab = −6
Используя формулу a 2 + b 2 + c 2 ,
a 2 + b 2 + c 2 = (a + b + c) 2 — 2(ab + bc + ca)
a 2 + b 2 + c 2 = (-3) 2 — 2(-6) = 9 + 12 = 21
Ответ: A 2 + B 2 + C 2 = 21.
Пример 3: Найдите значение 2 + B 2 + C 2 , если A+ B + c = 20 и ab + bc + ca = 100.
Решение:
Найти: a 2 + b 2 + c 2
Учитывая, что:
а + б + с = 20
аб + бк + са = 100
Использование a 2 + b 2 + c 2 формула,
a 2 + b 2 + c 2 = (a + b + c) 2 — 2(ab + bc + ca)
A 2 + B 2 + C 2 = (20) 2 — 2 (100) = 400 — 200 = 200
Ответ: A 2 + B 2 + C 2 = 200.
Часто задаваемые вопросы по a
2 + b 2 + c 2 ФормулыЧто такое расширение формулы a2 + b2 + c2?
а 92 Формула в алгебре?
Формула a 2 + b 2 + c 2 является одним из важных алгебраических тождеств. Оно читается как квадрат плюс квадрат b плюс квадрат c. Его формула a 2 + b 2 + c 2 выражается как + ок).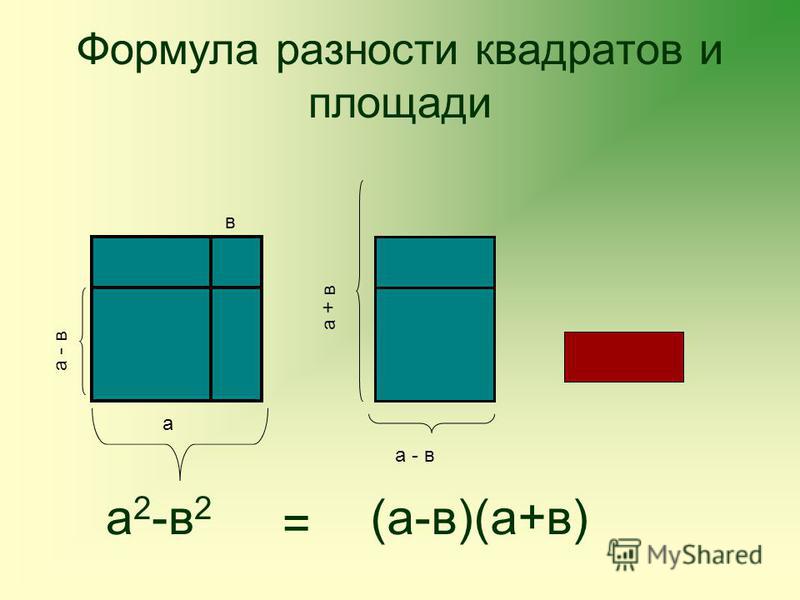
Как упростить числа с помощью формулы a
2 + b 2 + c 2 ? Давайте разберемся в использовании формулы a 2 + b 2 + c 2 с помощью следующего примера.
Пример: Найдите значение (2 2 + 5 2 + 3 2 ), используя формулу a 2 + b 2 + c 29003.
Чтобы найти: (2 2 + 5 2 + 3 2 )
Предположим, что a = 2, b = 5 и c = 3.
Мы подставим их в формулу (a 2 + b 2 + c 2 ).
a 2 + b 2 + c 2 = (a + b + c) 2 — 2(ab + bc + ca)
= (2 + 5 + 3) 2 — 2(2×5 + 5×3 + 3×2)
= 100 — 62 = 38
Ответ: (2 2 + 5 2 + 3 2 ) = 38
Как использовать (A
2 + B 2 + C 2 ) Формула дает шаги? При использовании (a 92 как индивидуальная мощность или нет.
Калькулятор теоремы Пифагора
Создано Петром Малеком и Матеушем Мухой
Отзыв от Ханны Памулы, кандидата наук, и Джека Боуотера
Последнее обновление: 16 января 2022 г.
Содержание:- Что такое теорема Пифагора?
- Как пользоваться теоремой Пифагора
- Что такое формула гипотенузы?
- Другие соображения при работе с треугольниками
Этот калькулятор теоремы Пифагора рассчитает длину любой из недостающих сторон прямоугольного треугольника, если вы знаете длины двух других его сторон. Это включает в себя вычисление гипотенузы. Гипотенуза прямоугольного треугольника — это сторона, противолежащая прямому углу, и самая длинная сторона. Эту сторону можно найти с помощью формулы гипотенузы, другого термина для теоремы Пифагора, когда она решает для гипотенузы. Напомним, что прямоугольный треугольник — это треугольник с углом, равным 90 градусов. Два других угла также должны составлять 90 градусов, так как сумма мер углов любого треугольника равна 180. Читайте дальше, чтобы ответить на вопрос «что такое теорема Пифагора и как она используется?»
Эту сторону можно найти с помощью формулы гипотенузы, другого термина для теоремы Пифагора, когда она решает для гипотенузы. Напомним, что прямоугольный треугольник — это треугольник с углом, равным 90 градусов. Два других угла также должны составлять 90 градусов, так как сумма мер углов любого треугольника равна 180. Читайте дальше, чтобы ответить на вопрос «что такое теорема Пифагора и как она используется?»
Что такое теорема Пифагора?
Теорема Пифагора описывает, как три стороны прямоугольного треугольника связаны в евклидовой геометрии. Он гласит, что сумма квадратов сторон прямоугольного треугольника равна квадрату гипотенузы. Вы также можете думать об этой теореме как о формуле гипотенузы. Если стороны прямоугольного треугольника равны a и b и гипотенуза c , формула
a² + b² = c²
Теорема была приписана древнегреческому философу и математику Пифагору, жившему в шестом веке до нашей эры. Хотя ранее она использовалась индийцами и вавилонянами, Пифагор (или его ученики) считался первым, кто доказал теорему. Следует отметить, что нет никаких конкретных доказательств того, что сам Пифагор работал над этой теоремой или доказал ее.
Хотя ранее она использовалась индийцами и вавилонянами, Пифагор (или его ученики) считался первым, кто доказал теорему. Следует отметить, что нет никаких конкретных доказательств того, что сам Пифагор работал над этой теоремой или доказал ее.
Как использовать теорему Пифагора
- Введите в формулу две длины, которые у вас есть. Например, предположим, что вы знаете
a = 4,b = 8и мы хотим найти длину гипотенузыc. - После подстановки значений в формулу имеем
4²+ 8² = c² - Возведите каждое слагаемое в квадрат, чтобы получить
16 + 64 = c² - Объедините одинаковые члены, чтобы получить
80 = c² - Извлеките квадратный корень из обеих частей уравнения, чтобы получить
с = 8,94. Проверьте это с помощью нашего калькулятора теоремы Пифагора!
Обратите внимание: если вы решаете для a или b , измените уравнение, чтобы изолировать нужную переменную, прежде чем объединять одинаковые члены и извлекать квадратный корень
Калькулятор теоремы Пифагора решит для сторон в одном способ, который мы показали выше. Мы включили метод, чтобы показать вам, как вы можете решить свою проблему, если предпочитаете делать это вручную.
Мы включили метод, чтобы показать вам, как вы можете решить свою проблему, если предпочитаете делать это вручную.
Что такое формула гипотенузы?
Формула гипотенузы просто берет теорему Пифагора и решает для гипотенузы, c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом мы получаем c = √(a² + b²) . Это всего лишь расширение теоремы Пифагора и часто не связанное с именем формула гипотенузы .
Другие соображения при работе с треугольниками
Обратите внимание, что стороны треугольника имеют определенный уклон или наклон. Мы можем использовать калькулятор уклона, чтобы определить наклон каждой стороны. В прямоугольном треугольнике стороны, образующие прямой угол, имеют наклоны, произведение которых равно -1. Формула для уклона, если вы хотите рассчитать вручную:
(y₂ - y₁)/(x₂ - x₁)
Итак, если координаты (3,6) и (7,10) , уклон сегмента (10-6)/(7-3) = 1 . Если наклон другого сегмента, образующего угол, равен
Если наклон другого сегмента, образующего угол, равен -1 , то линии будут перпендикулярны, поскольку 1 * -1 = -1 . Следовательно, треугольник прямоугольный.
Вы также можете вычислить недостающие длины сторон и углы прямоугольного треугольника, используя калькулятор прямоугольного треугольника. Если углы, указанные в задаче, выражены в градусах, и вы хотите преобразовать их в радианы или радианы в градусы, воспользуйтесь нашим конвертером углов. Существует простой способ конвертировать градусы в радианы и радианы в градусы.
Если угол выражен в радианах
- Умножить на
180/π
Если угол выражен в градусах
- Умножить на
π/180
Иногда вы можете столкнуться с проблемой отсутствия длины двух или всех трех сторон. В таких случаях калькулятор теоремы Пифагора не поможет — вы будете использовать тригонометрические функции для решения этих недостающих частей.
Петр Малек и Матеуш Муха
a² + b² = c²
Периметр
Посмотреть 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… Еще 15
Что такое 4 в квадрате c в квадрате плюс? [54 ответа найдено]
Ищете ответ на вопрос: Сколько будет 3 в квадрате плюс 4 в квадрате c в квадрате? Здесь мы собрали для вас 54 самых точных и подробных ответа на вопрос: Сколько будет 3 в квадрате плюс 4 в квадрате c в квадрате?
- Что такое формула a2 b2 c2?
- Как найти C в квадрате по теореме Пифагора?
- Что такое ¾ в квадрате?
- Кто сделал a2 b2 C2?
- Какова формула a3 b3?
- Сколько времени Пифагор жил в Египте?
- Алгебра теоремы Пифагора?
- Как найти C в треугольнике?
- Сколько 3/4 делится на 2 в дроби?
- Чему равно 3 в степени 4?
- Что такое ab3?
- Что такое аб2?
- Кто изобрел ноль в мире?
- Как использовать теорему Пифагора для равнобедренного треугольника?
- Что такое значение C?
- Каково значение C в треугольнике?
- Как найти a2 b2 c2?
- Является ли C квадратом гипотенузы?
- Как найти квадрат?
- Что обозначает C в теореме Пифагора?
- Для чего используется теорема Пифагора?
- Что такое C в теореме Пифагора?
- Почему теорема Пифагора A2 B2 C2?
- Как решить задачу по теореме Пифагора?
- Почему теорема Пифагора верна?
- Что такое x² в математике?
- Что такое правило 3 4 5 в строительстве?
- Что такое Теорема Пифагора словами?
- Как называется сторона c?
- Кто составил формулу a2 b2 c2?
- Является ли a2 b2 c2 только для прямоугольных треугольников?
- Сколько будет 3 в квадрате плюс 4 в квадрате c в квадрате? 8 Ответы экспертов:
- Сколько будет 3 в квадрате плюс 4 в квадрате c в квадрате? Видеоответы:
Сколько будет 3 в квадрате плюс 4 в квадрате c в квадрате? Быстрый ответ:
Ответил King
Учитывая это, как решить 3 в квадрате плюс 4 в квадрате? Например, A = 3 B = 4 C = 5, это также можно назвать треугольником 3, 4, 5. 2. Также спросили, чему равен C в квадрате по теореме Пифагора?0029
2. Также спросили, чему равен C в квадрате по теореме Пифагора?0029
Когда сумма числа плюс 3 возводится в квадрат, она на 11 больше, чем сумма числа плюс 2 в квадрате. Когда сумма числа плюс 3 в квадрате больше, чем сумма числа плюс 2 в квадрате?
Квадрат 4 равен 4×4. Чтобы показать, что число возведено в квадрат, справа вверху от числа ставится маленькая цифра 2. Вот так: Эти знаки аналогичны фразе «3 в квадрате, 4 в квадрате и х в квадрате».
Что такое формула a2 b2 c2?
В любом прямоугольном треугольнике сумма площадей квадратов, образованных катетами треугольника, равна площади квадрата, образованного гипотенузой: a2 + b2 = c2. Теорема Пифагора используется во многих приложениях, связанных с прямоугольными треугольниками.
Как найти C в квадрате в теореме Пифагора?
Формула гипотенузы просто берет теорему Пифагора и вычисляет гипотенузу c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом мы получаем c = √(a² + b²) .
При этом мы получаем c = √(a² + b²) .
Что такое ¾ в квадрате?
(3/4)2 = 9/16, которое нельзя уменьшить. Чтобы доказать это, возведем исходную дробь в квадрат без сокращения: (12/16)2 = (12 х 12/16 х 16) = (144/256)
Кто сделал a2 b2 C2?
Пифагор Самосский (обычно оформляется как a2 + b2 = c2), где и c — длина гипотенузы, а a и b — длины двух других сторон. Он приписывается Пифагору Самосскому, математику, философу и религиозному лидеру.
Какова формула a3 b3?
a3 – b3 = (a – b) (a2 + ab + b2).
Сколько лет Пифагор жил в Египте?
Фалес посоветовал Пифагору посетить Египет, что он и сделал, когда ему было около 22 лет. Пифагору, должно быть, нравился Египет. Он прожил там примерно следующие 22 года своей жизни, осваивая математические и духовные идеи. Пифагор наслаждался жизнью в Египте.
Алгебра теоремы Пифагора?
Теорема Пифагора очень важна для математики. Вы, вероятно, впервые узнаете об этом в алгебре, но вы будете буквально использовать это в алгебре, геометрии, тригонометрии, предварительном исчислении, исчислении и не только!
Как найти C в треугольнике?
Гипотенуза лежит напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом a и b и с гипотенузой c теорема Пифагора утверждает, что: a² + b² = c². Чтобы найти c , возьмите квадратный корень из обеих сторон, чтобы получить c = √(b²+a²) . 93 формула – это формула куба разности двух слагаемых.
В прямоугольном треугольнике с катетом a и b и с гипотенузой c теорема Пифагора утверждает, что: a² + b² = c². Чтобы найти c , возьмите квадратный корень из обеих сторон, чтобы получить c = √(b²+a²) . 93 формула – это формула куба разности двух слагаемых.
Что такое ab2?
Формула (a + b)2 — это алгебраическое тождество, используемое для нахождения квадрата суммы двух чисел. Чтобы найти формулу бинома в виде (a + b)2, мы просто умножим (a + b) (a + b). (а + b)2 = (а + b)(a + b) = a2 + ab + ba + b2. = а2 + 2аб + Ь2.
Кто изобрел ноль в мире?
«Ноль и его действие впервые были определены [индуистским астрономом и математиком] Брахмагуптой в 628 году», — сказал Гобетс. Он разработал символ нуля: точку под цифрами.
Как использовать теорему Пифагора для равнобедренного треугольника?
0:573:53Теорема Пифагора и геометрия 1: площадь равнобедренного …YouTube
Что такое значение C?
Скорость света определяется как скорость, с которой световой фотон движется в вакууме. Он обозначается буквой c и измеряется в единицах СИ м/с. Значение скорости света или значение c является постоянным в любой части Вселенной.
Он обозначается буквой c и измеряется в единицах СИ м/с. Значение скорости света или значение c является постоянным в любой части Вселенной.
Каково значение C в треугольнике?
Общий случай. «С» обычно обозначает третью сторону треугольника.
Как найти a2 b2 c2?
Формула гипотенузы просто берет теорему Пифагора и вычисляет гипотенузу c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом мы получаем c = √(a² + b²) .
Является ли C квадратом гипотенузы?
Самая длинная сторона, гипотенуза, прямо здесь. Итак, если мы подумаем о теореме Пифагора — что А в квадрате плюс В в квадрате равно С в квадрате — 12 можно рассматривать как С. Это гипотенуза. Квадрат С — это квадрат гипотенузы.
Как найти квадрат?
Чтобы найти квадрат числа, умножьте число само на себя. Например, если вы пытаетесь найти квадрат 5, вы должны умножить 5 на 5 и получить 25, то есть квадрат.
Что обозначает C в теореме Пифагора?
Сумма площадей двух квадратов катетов (a и b) равна площади квадрата гипотенузы (c).
Для чего используется теорема Пифагора?
Теорема Пифагора — одна из самых известных теорем в математике. Он описывает особое отношение между сторонами прямоугольного треугольника и может быть использован для нахождения недостающей стороны прямоугольного треугольника.
Что такое C в теореме Пифагора?
гипотенуза
Теорема. Поле. Евклидова геометрия. Заявление. Сумма площадей двух квадратов на катетах (а и б) равна площади квадрата на гипотенузе (с).
Почему теорема Пифагора A2 B2 C2?
Формула A2 + B2 = C2, это так же просто, как один катет треугольника в квадрате плюс другой катет треугольника в квадрате равняется гипотенузе в квадрате.
Как решить задачу по теореме Пифагора?
0:254:21Теорема Пифагора | Найдите неизвестную сторону прямоугольного треугольникаYouTube
Почему теорема Пифагора верна?
Из того факта, что сумма углов в треугольнике составляет 180◦, легко понять, что на самом деле это квадрат). Есть также четыре прямоугольных треугольника с основанием a и высотой b. Вывод состоит в том, что a2 + b2 = c2, что является теоремой Пифагора.
Есть также четыре прямоугольных треугольника с основанием a и высотой b. Вывод состоит в том, что a2 + b2 = c2, что является теоремой Пифагора.
Что такое x² в математике?
Сколько х в квадрате? x в квадрате — это обозначение, которое используется для представления выражения x×x x × x . т. е. х в квадрате равен х, умноженному на самого себя. В алгебре x, умноженный на x, может быть записан как x×x x × x (или) x⋅x x ⋅ x (или) xx (или) x(x) x символ в квадрате равен x2 .
Что такое правило 3 4 5 в строительстве?
Чтобы получить идеально ровный угол, необходимо стремиться к соотношению размеров 3:4:5. Другими словами, вам нужна длина в три фута по прямой линии, длина в четыре фута по перпендикулярной линии и длина в пять футов в поперечнике. Если все три измерения верны, у вас будет идеально прямой угол.
Что такое Теорема Пифагора в словах?
: теорема геометрии: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин двух других сторон.
Как называется сторона с?
Что такое теорема Пифагора в математике? Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Эта теорема может быть выражена как c2 = a2 + b2; где «с» — гипотенуза, а «а» и «b» — катеты треугольника.
Кто составил формулу a2 b2 c2?
Теорема Пифагора — известная теорема. Он также очень древний, он не только носит имя Пифагора, древнего грека, но и был известен еще древним вавилонянам и древним египтянам. Большинство школьников узнают об этом как a2 + b2 = c2.
a2 b2 c2 только для прямоугольных треугольников?
Теорема Пифагора: Если треугольник прямоугольный (имеет прямой угол), то a2+b2=c2. Обратное: если a2+b2=c2 в треугольнике с самой длинной стороной c, то треугольник прямоугольный. Если треугольник не прямоугольный, есть 2 других варианта типов треугольников.
Ответил Chasmine
Три в квадрате плюс четыре в квадрате равно 25, что является значением C в квадрате. Однако, если вы возьмете квадратный корень с обеих сторон, вы получите значение 5, и эта формула применима только к прямоугольным треугольникам. Процедура называется теоремой Пифагора, в которой квадрат одного значения равен судам и суммам двух других сторон.
Однако, если вы возьмете квадратный корень с обеих сторон, вы получите значение 5, и эта формула применима только к прямоугольным треугольникам. Процедура называется теоремой Пифагора, в которой квадрат одного значения равен судам и суммам двух других сторон.
Ответил Iyannah
Учитывая это, как решить 3 в квадрате плюс 4 в квадрате? Например, A = 3 B = 4 C = 5, это также можно назвать треугольником 3,4,5. Вот как вы делаете уравнение, например, 3 в квадрате плюс 4 в квадрате = 5 в квадрате, другими словами, 9 + 16 = 25, поэтому, поскольку все это целые числа, треугольник должен быть пифагорейской тройкой.
Ответил Кимари
Итак, 4 в квадрате плюс 3 в квадрате = 4² + 3² = 16 + 9 = 25 = 5 в квадрате. Надеюсь, вы получили ответ. Джесс Лейтон. Ответил 3 года назад. (4×4)+ (3×3) равно 4 в квадрате плюс 3 в квадрате. Оно на удивление тоже равно 5х5. Если мы думаем с точки зрения площади, у нас есть ящик со сторонами, равными 4, плюс ящик со сторонами, равными 3.
Ответил Вики
Например, A = 3 B = 4 C = 5 это также можно назвать треугольником 3,4,5. Вот как вы делаете уравнение, например, 3 в квадрате плюс 4 в квадрате = 5 в квадрате, другими словами, 9 + 16 = 25, поэтому, поскольку все это целые числа, треугольник должен быть пифагорейской тройкой.
Ответил Raelynn
Числа от 0 до 10 в квадрате . 0 в квадрате равно 0² = 0 × 0 = 0; 1 в квадрате равен 1² = 1 × 1 = 1; 2 в квадрате равно 2² = 2 × 2 = 4; 3 в квадрате это 3² = 3 × 3 = 9; 4 в квадрате равно 4² = 4 × 4 = 16; 5 в квадрате — это 5² = 5 × 5 = 25; 6 в квадрате равно 6² = 6 × 6 = 36; 7 в квадрате равно 7² = 7 × 7 = 49; 8 в квадрате равно 8² = 8 × 8 = 64; 9 в квадрате равно 9² = 9 × 9 = 81; 10 в квадрате — это 10² = 10 × 10 = 100; Ссылки / Дополнительное чтение. Goodman, …
Ответил Rayah
Величина 4 в квадрате и 3 в квадрате выражается уравнением: 16 — 9 равно 7,3 в квадрате равно 3 x 3 = 94 в квадрате равно 4 x 4 = 1616 — 9 = 7.
Ответил Энмануэль
Соответствует ли 1 квадратный метр 1000 квадратных миллиметров? (1 метр) в квадрате = (1000 мм) в квадрате = 1000000 мм в квадрате. Что такое 3 в квадрате х 4 в квадрате? 3 в квадрате = 9 4 …
Что такое 3 в квадрате х 4 в квадрате? 3 в квадрате = 9 4 …
Ответил Брикола
Используйте 3.14 для пи. Радиус цилиндра равен 2, а высота равна 15. A)100,4 см в квадрате B)97,43 см в квадрате C)36,29 см в квадрате*** D)33,14 см в квадрате … Какой координате х соответствует график функции по ряду Маклорена 1 минус 2 умножить на х плюс 4 умножить на х в квадрате на 2 факториал минус 8 умножить на х в кубе на 3 факториал плюс …
Найдите гипотенузу по теореме Пифагора | Дэйв Мэй учит
Теорема Пифагора: A в квадрате ПЛЮС B в квадрате РАВНО C в квадрате . Полезно, если вы знаете 2 стороны прямоугольного треугольника, …
Найдите недостающую сторону треугольника, используя теорему Пифагора
Узнайте о теореме Пифагора. Теорема Пифагора — это фундаментальное соотношение между 90 661 и тремя 90 662 сторонами прямоугольного треугольника …
Единственный президент США, доказавший математическую теорему
В 1880 году Джеймс Гарфилд представил новое доказательство самой известной геометрической теоремы о прямоугольном треугольнике. Математический клад: …
Математический клад: …
Исчисление – КАК: Интегрирование с помощью частичных дробей (начальный уровень, часть 1)
В этом видео рассматриваются 4 практических вопросов и 2 вопросов для начинающих по интегрированию с помощью частичных дробей, часть 1. Урок интеграции 7.11 …
Живой подготовительный класс кAOE/BECE | Обязан посмотреть!! #easymathstutor pt2
———————————————————— 👥 Facebook: https://www.facebook.com/easymathematicsonline/ …
НЕОФИЦИАЛЬНО Математика GCSE Edexcel Paper 3 (2022) — Вопрос 1-4
Пожалуйста, поставьте лайк, поделитесь и подпишитесь! 💡 Online GCSE Maths, English & Science 3 месяца Интенсивная программа Perfect для дома …
Математические выходки. Теорема Пифагора
Узнайте больше на сайте mathantics.com Посетите http://www.mathantics.com для еще бесплатных видео по математике и дополнительной подписки на основе …
Обзор экзамена по геометрии с отличием за 2015 г.
 — Раздел 4, тема 2 (вопросы 45–54)
— Раздел 4, тема 2 (вопросы 45–54)… равно минусу 3 в квадрате , что равно 9 плюс минус 4 в квадрате , что равно 16 9 плюс 16 равно а квадратный корень из 25 равен 5 C d we …
Сколько существует способов доказать теорему Пифагора? — Бетти Фей
Что общего между Евклидом, 12-летним Эйнштейном и американским президентом Джеймсом Гарфилдом? Все они придумали элегантно …
Теорема Пифагора | MathHelp.com
Этот урок посвящен теореме Пифагора, которая утверждает, что сумма квадратов длин катетов прямоугольного треугольника …
Кевин Хаффман
Главный редактор
Здравствуйте, пользователи AnswerOwn. Меня зовут Кевин Хаффман, и я главный редактор AnswerOwn. Мне 32 года, я живу во Флориде, США. Все детство я увлекался видеоиграми, а также различными компьютерными программами. Будучи подростком, я всегда помогал своим одноклассникам с домашним заданием по программированию. В колледже я создал свои первые проекты в Интернете, которые помогали людям находить информацию по разным вопросам. На одном из мероприятий по программированию я познакомился с ребятами, с которыми мы создавали AnswerOwn. Это наш совместный сервис, который помогает людям найти ответы на насущные вопросы, а также является качественным образовательным проектом. Задавайте свои вопросы, и мы обязательно найдем ответ!
В колледже я создал свои первые проекты в Интернете, которые помогали людям находить информацию по разным вопросам. На одном из мероприятий по программированию я познакомился с ребятами, с которыми мы создавали AnswerOwn. Это наш совместный сервис, который помогает людям найти ответы на насущные вопросы, а также является качественным образовательным проектом. Задавайте свои вопросы, и мы обязательно найдем ответ!
Актуальные вопросы
- Как быстро действует байтрил?
- Как активировать соленоид абс?
- Где находится серийный номер общего тренажерного зала?
- Как долго действует каменная броня?
- Что такое преобразователь ржавчины олеум ржавчины?
- Когда был построен торговый центр в Ванкувере?
- Чем можно закрыть пространство для обхода?
- Какова цель викторины о реконструкции?
- Как посадить петунии вокруг дерева?
- Могу ли я покрасить свой каменный камин?
Популярные вопросы
- Какой банк aib?
- Какой глубины должны быть грядки?
- Как почистить террасу, не навредив растениям?
- Восстанавливает ли micrococcus luteus нитраты?
- На каком расстоянии друг от друга должны быть планки кровати?
- Почему Лесото является анклавом Южной Африки?
- Что происходит при Исходе?
- Что увеличивает отношение сигнал/шум?
- Сколько витамина В 12 я должен принимать ежедневно?
- Что такое рекомендация w3c в XML?
Теорема Пифагора – Объяснение и примеры
Теорема Пифагора, , также известная как « Теорема Пифагора, », возможно, самая известная формула в математике , которая определяет отношения между сторонами прямоугольного треугольника.
Теорема приписывается греческому математику и философу по имени Пифагор (569–500 гг. до н. э.). У него много вкладов в математику, но теорема Пифагора — самый важный из них.
Пифагору приписывают несколько вкладов в математику, астрономию, музыку, религию, философию и т. д. Одним из его заметных вкладов в математику является открытие теоремы Пифагора. Пифагор изучал стороны прямоугольного треугольника и обнаружил, что сумма квадрата двух меньших сторон треугольника равна квадрату большей стороны.
В этой статье e будет обсуждаться, что такое теорема Пифагора , ее обращение и Формула теоремы Пифагора . Прежде чем углубиться в тему, давайте вспомним прямоугольный треугольник. Прямоугольный треугольник – это треугольник, у которого один внутренний угол равен 90 градусов. В прямоугольном треугольнике две короткие стороны пересекаются под углом 90 градусов. Гипотенуза треугольника лежит против угла 90 градусов.
Что такое теорема Пифагора?
Теорема Пифагора — математический закон, утверждающий, что сумма квадратов длин двух коротких сторон прямоугольного треугольника равна квадрату длины гипотенузы .
Теорема Пифагора алгебраически записывается как:
a 2 + b 2 = c 2
9
Рассмотрим прямоугольный треугольник выше.
Учитывая, что:
∠ ABC= 90°.
Пусть BD — перпендикуляр к стороне AC.
Подобные ∆s:
∆ADB и ∆ABC — подобные треугольники.
Из правила подобия,
⇒ AD/AB = AB/AC
⇒ AD × AC = (AB) 2 —————– (i)
Аналогично;
∆BDC и ∆ABC — подобные треугольники. Следовательно;
⇒ DC/BC = BC/AC
⇒ DC × AC = (BC) 2 —————– (ii)
Комбинируя уравнения (i) и (ii), мы получаем,
AD × AC + DC × AC = (AB) 2 + (BC) 2
⇒ (AD + DC) × AC = (AB) 2 + (BC) 2
⇒ (AC) 2 = (АВ) 2 + (BC) 2
Следовательно, если положить AC = c; АВ = b и ВС = b, тогда;
⇒ c 2 = a 2 + b 2
Существует множество демонстраций теоремы Пифагора , данных разными математиками.
Другая распространенная демонстрация состоит в том, чтобы нарисовать 3 квадрата таким образом, чтобы между ними образовывался прямоугольный треугольник, а площадь большего квадрата (тот, что находится на гипотенузе) равнялась сумме площадей меньшего два квадрата (те, что с двух сторон).
Рассмотрим 3 квадрата ниже:
Они нарисованы таким образом, что образуют прямоугольный треугольник. Мы можем записать их площади в виде уравнения:
Площадь квадрата III = Площадь квадрата I + Площадь квадрата II
Предположим, длина квадрата I , квадрата II, и квадрат III представляют собой a, b и c соответственно.
Затем,
Площадь площади I = A 2
Площадь квадратной II = B 2
Площадь квадрата III = C 2
. Следовательно, мы можем написать его как:
A 2 2 44444444404. + b 2 = c 2
+ b 2 = c 2
, что является теоремой Пифагора.
Обратная теорема Пифагора
обратная теорема Пифагора — это правило, которое используется для классификации треугольников как прямоугольных, остроугольных или тупоугольных.
Учитывая теорему Пифагоре, A 2 +B 2 = C 2 , затем:
- для острого треугольника, C 2 2 +B 2 , где C сторону, противоположную острому углу.
- Для прямоугольного треугольника c 2 = a 2 + b 2 , где c – сторона угла в 90 градусов.
- Для тупоугольного треугольника c 2 > a 2 + b 2 , где c — сторона, противоположная тупому углу.
Пример 1
Классифицируйте треугольник, размеры которого равны; а = 5 м, b = 7 м и c = 9 м.
Решение
Согласно теореме Пифагора, a 2 + b 2 = c 2 тогда;
A 2 + B 2 = 5 2 + 7 2 = 25+ 49 = 74
Но, C 2 = 9 0003 2 = 81
: 81> 74

Пример 2
Классифицируйте треугольник, длины сторон которого a, b, c равны 8 мм, 15 мм и 17 мм соответственно.
Решение
A 2 + B 2 = 8 2 + 15 2 = 64+ 225 = 289
Но, C 2 = 17 2 = 289
Compare: 289 = 17 2 = 289
289
Следовательно, c 2 = a 2 + b 2 (прямоугольный треугольник).
Пример 3
Классифицируйте треугольник, чьи длина боковой длины приведена как; 11 дюймов, 13 дюймов и 17 дюймов. + 13 2 = 121 + 169 = 290
C 2 = 17 2 = 289
Сравнение: 289 <290
Следовательно, C 2 2
+ B 2 )Теорема Пифагора Формула
Формула теоремы Пифагора имеет следующий вид:
⇒ c 2 = a 2 + b 2
где;
c = длина гипотенузы;
а = длина одной стороны;
b = длина второй стороны.
Мы можем использовать эту формулу для решения различных задач, связанных с прямоугольными треугольниками. Например, мы можем использовать формулу для определения третьей длины треугольника, когда известны длины двух сторон треугольника.
Применение формулы теоремы Пифагора в реальной жизни
- Мы можем использовать теорему Пифагора, чтобы проверить, является ли треугольник прямоугольным или нет.
- В океанографии формула используется для расчета скорости звуковых волн в воде.
- Теорема Пифагора используется в метеорологии и аэрокосмической отрасли для определения источника звука и его диапазона.
- Мы можем использовать теорему Пифагора для расчета электронных компонентов, таких как экраны телевизоров, экраны компьютеров, солнечные батареи и т. д.
- Мы можем использовать теорему Пифагора, чтобы вычислить градиент определенного ландшафта.
- В навигации теорема используется для расчета кратчайшего расстояния между заданными точками.

- В архитектуре и строительстве мы можем использовать теорему Пифагора для расчета уклона крыши, водосточной системы, плотины и т. д.
Примеры применения теоремы Пифагора: Две короткие стороны прямоугольного треугольника равны 5 см и 12 см. Найдите длину третьей стороны
Раствор
Дано, a = 5 см
b = 12 см
c = ?
Из формулы теоремы Пифагора; c 2 = a 2 + b 2 , имеем;
C 2 = A 2 + B 2
C 2 = 12 2 + 5 2
C 2 = 144 + 25
√c 2 = 1444 + 25
. √169
c = 13.
Следовательно, третья равна 13 см.
Пример 5
Длина диагонали и одной стороны треугольной стороны составляет 25 см и 24 см соответственно. Чему равна третья сторона?
Решение
Использование теоремы Пифагора,
c 2 = a 2 + b 2 .
Пусть b = третья сторона
25 2 = 24 2 + b 2
625 = 576 + b 2 –5 6
625 – 5 6
625 –0003 2
49 = B 2
B 2 = 49
B = √49 = 7 см
Пример 6
Найдите размер экрана компьютера. дюймы.
Подсказка: Диагональ экрана равна его размеру .
Решение
Размер экрана компьютера равен диагонали экрана.
Использование теоремы Пифагора,
c 2 = 8 2 + 15 2
Решите для c.
c 2 = 64 + 225
c 2 = 289
c = √289
c = 17
размер экрана компьютера равен 1 дюйму.
Пример 7
Найдите площадь прямоугольного треугольника, если его диагональ и основание равны 8,5 см и 7,7 см соответственно.
Решение
Использование теоремы Пифагора,
8,5 2 = a 2 + 7,5 2
Найдите a.
72,25 = A 2 + 56,25
72,25 — 56,25 = K 2 + 56,25 — 56,25
16 = A 2
A = √16 = 4 CM
AREA TRIANGL ½) x основание x высота
= (½ x 7,7 x 4) см 2
= 15,4 см 2
Объяснение квадратичной формулы | Пурпурная математика
ДискриминантДиск. & Графики
Purplemath
Когда мне следует использовать квадратичную формулу?
Квадратную формулу можно использовать в любое время, когда вы пытаетесь решить квадратное уравнение, если это уравнение имеет форму «(квадратичное выражение), которое установлено равным нулю».
Часто самый простой способ решить « x 2 + bx + c = 0» для значения x — это разложить квадратное число на множители, установить каждый множитель равным нулю, а затем решить каждый фактор. Но иногда квадратное выражение слишком запутано, или оно вообще не учитывается, или, черт возьми, может быть, вам просто не хочется факторизовать. Хотя факторинг не всегда будет успешным, квадратичная формула всегда может найти ответы для вас.
Но иногда квадратное выражение слишком запутано, или оно вообще не учитывается, или, черт возьми, может быть, вам просто не хочется факторизовать. Хотя факторинг не всегда будет успешным, квадратичная формула всегда может найти ответы для вас.
Содержание продолжается ниже
Mathhelp.com
Практика Квадратичная Формула
В квадратичной формуле используется « A », B »и« C »от» AX 7777779 2 9 400047 2 9000 40004779 2 77 2 77 2 7 777 2 77 2 7 7 2 7 2 7 2 7 7 7 7 7 7 2 7 2 7 2 7 2 7 2 7 2 7 77777 2 7 2 C ». bx + c «, где « a «, « b » и « c » — просто числа; это «числовые коэффициенты» квадратного уравнения, которое они дали вам решить.
Квадратичная формула получается из процесса завершения квадрата и формально выражается как:
Что такое квадратичная формула?
Квадратичная формула — это правило, согласно которому в любом уравнении вида x 2 + bx + c = 0 решение x -значения уравнения задаются формулой:
Как использовать квадратичную формулу?
Чтобы использовать квадратную формулу, вы должны:
Приведите уравнение к форме «(квадратичное) = 0».

Расположите члены (уравнения) в порядке убывания (сначала квадратный член, затем член x и, наконец, линейный член).
Вытяните числовые части каждого из этих терминов, а именно « a », « b » и « c » Формулы.
Подставьте эти числа в формулу.
Упростите, чтобы получить ответы.
Рекомендации: «2 a » в знаменателе формулы находится под всем вышеперечисленным, а не только под квадратным корнем. И там внизу «2 a «, а не просто «2». Убедитесь, что вы не уронили квадратный корень или «плюс/минус» в середине ваших вычислений, иначе я могу гарантировать, что вы забудете «вставить их обратно» в своем тесте, и вы запутаетесь. себя вверх. Помните, что « b 2 » означает «квадрат ВСЕХ b , включая его знак», поэтому не оставляйте b 2 отрицательным, даже если b отрицательное, потому что квадрат отрицательного числа является положительным.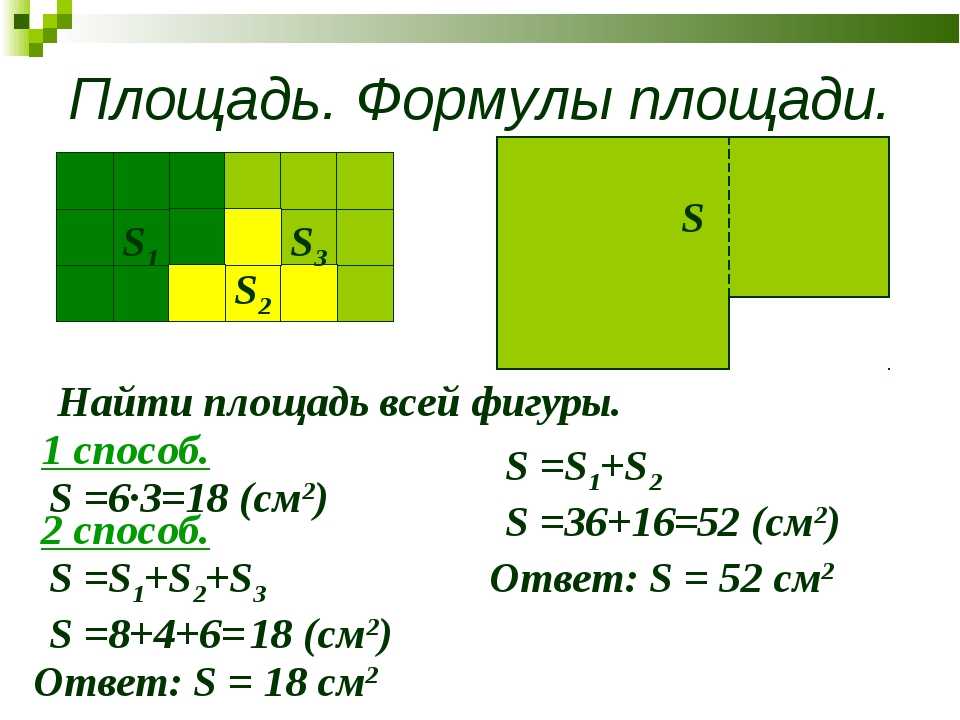
Другими словами, не делайте Будьте небрежны и не пытайтесь срезать путь, потому что это только навредит вам в долгосрочной перспективе Поверьте мне в этом!
Какой пример использования квадратичной формулы?
использовать, чтобы подтвердить то, что я получаю от квадратичной формулы Формула должна дать мне те же ответы.
x 2 + 3 x — 4 = ( x + 4)( x — 1) = 0
… так что я уже знаю, что решения = x 9 4 и x = 1.
Теперь, как бы мое решение выглядело в квадратичной формуле? Используя a = 1, b = 3 и c = −4, мой процесс решения выглядит следующим образом:
Таким образом, как и ожидалось, решение равно x = −4, x = 1.
Для этого конкретного квадратного уравнения факторизация, вероятно, будет более быстрым методом. Но Квадратичная формула — это метод plug-n-chug, при котором 90 576 всегда будет работать как 90 577. У вас «заморозка мозгов» на тесте, и вы не можете ничего стоящего? Используйте формулу plug-n-chug; он всегда будет заботиться о вас!
У вас «заморозка мозгов» на тесте, и вы не можете ничего стоящего? Используйте формулу plug-n-chug; он всегда будет заботиться о вас!
Как квадратичная формула связана с пересечениями по оси x?
Решения квадратного уравнения, представленные Квадратичной формулой, являются точками пересечения x соответствующей параболы, изображенной на графике.
Как? Ну, когда y = 0, вы находитесь на оси x . Точки пересечения x на графике — это места, где парабола пересекает ось x . Вы применяете квадратичную формулу к уравнению x 2 + bx + c = y , где y установлено равным нулю.
Глядя на приведенный выше пример, можно увидеть два решения уравнения x 2 + 3 x − 4 = 0. Это говорит нам о том, что тогда должно быть два x — перехваты на графике. На графике мы получаем следующую кривую:
Как вы можете видеть, точки пересечения x (красные точки выше) соответствуют решениям, пересекая ось x в точке x = −4 и x = 1. Это показывает связь между построением графика и решением: когда вы решаете «(квадратичное) = 0», вы находите x -перехватов графика. Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратную формулу (при необходимости) для решения квадратного уравнения, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые x — точки пересечения имеют те же десятичные значения, что и решения, обеспечиваемые квадратичной формулой.
Это показывает связь между построением графика и решением: когда вы решаете «(квадратичное) = 0», вы находите x -перехватов графика. Это может быть полезно, если у вас есть графический калькулятор, потому что вы можете использовать квадратную формулу (при необходимости) для решения квадратного уравнения, а затем использовать свой графический калькулятор, чтобы убедиться, что отображаемые x — точки пересечения имеют те же десятичные значения, что и решения, обеспечиваемые квадратичной формулой.
Обратите внимание, однако, что отображение графика калькулятором, вероятно, будет иметь некоторую ошибку округления, связанную с пикселями, поэтому вам нужно проверить, чтобы вычисленные и графические значения были достаточно близки; не ждите точного совпадения.
В (2)(−3) = −6 нет множителей, которые в сумме дают −4, поэтому я знаю, что этот квадрат нельзя разложить на множители. Я буду применять квадратную формулу. В этом случае a = 2, b = -4 и c = -3:
Тогда ответ равен x = -0,58, x = 2,58, округленное до двух знаков после запятой.
Можно ли округлить ответы квадратичной формулы?
В общем, нет, не стоит; обычно требуется, чтобы «решение» или «корни» или «нули» квадратного числа были в «точной» форме ответа. Вы можете использовать округленную форму при построении графика (при необходимости), но «ответ(ы)» из квадратичной формулы следует записывать в (часто беспорядочной) «точной» форме.
В приведенном выше примере точной формой является форма с квадратными корнями из десяти. Если вы хотите изобразить в виде графика пересечения x или вам нужно упростить окончательный ответ в словесной задаче, чтобы он имел практическую («реальную») форму, вы можете использовать приближение калькулятора. Но если у вас нет веских оснований полагать, что ответ должен быть округленным, всегда выбирайте точную форму.
Подкрепляя концепцию: сравните решения, которые мы нашли выше для уравнения 2 x 2 − 4 x − 3 = 0 с точками пересечения x графика: . Это всегда верно. «Решением» уравнения также являются x -пересечения соответствующего графика.
«Решением» уравнения также являются x -пересечения соответствующего графика.
Page 2Page 3
URL: https://www.purplemath.com/modules/quadform.htm
Теорема Пифагора и ее многочисленные доказательства
| — Чрезвычайно информативное сообщение, — сказал генерал. — Я вижу, вы дали себе труд основательно вникнуть в суть дела. Это один из секретов успеха в жизни». |
Энтони Пауэлл |
Профессор Р. Смаллян в своей книге 5000 г. до н.э. и другие философские фантазии рассказывает об эксперименте, который он провел на одном из уроков геометрии. Он нарисовал на доске прямоугольный треугольник с квадратами на гипотенузе и катетах и заметил, что квадрат на гипотенузе имеет большую площадь, чем любой из двух других квадратов. Затем он спросил: «Предположим, что эти три квадрата сделаны из чеканного золота, и вам предложили либо один большой квадрат, либо два маленьких квадрата. Что бы вы выбрали?» Интересно, что около половины класса выбрали один большой квадрат, а половина — два маленьких. Обе группы были одинаково поражены, когда им сказали, что это не имеет никакого значения.
Затем он спросил: «Предположим, что эти три квадрата сделаны из чеканного золота, и вам предложили либо один большой квадрат, либо два маленьких квадрата. Что бы вы выбрали?» Интересно, что около половины класса выбрали один большой квадрат, а половина — два маленьких. Обе группы были одинаково поражены, когда им сказали, что это не имеет никакого значения.
Пифагорейская (или пифагорейская ) Теорема есть утверждение, что сумма (площадей) двух маленьких квадратов равна (площади) большого.
В алгебраических терминах a² + b² = c² , где c — гипотенуза, а a и b — катеты треугольника.
Теорема имеет фундаментальное значение в евклидовой геометрии, где она служит основой для определения расстояния между двумя точками. Это настолько просто и хорошо известно, что, я уверен, любой, кто посещал уроки геометрии в старшей школе, не мог не запомнить ее еще долго после того, как другие математические понятия были полностью забыты.
Ниже представлен набор из 118 подходов к доказательству теоремы. Многие доказательства сопровождаются интерактивными иллюстрациями Java.
Примечание
Формулировка теоремы была обнаружена на вавилонской табличке около 1900-1600 гг. до н.э. Был ли Пифагор (ок. 560–480 гг. до н. э.) или кто-то еще из его школы первым, кто обнаружил ее доказательство, нельзя утверждать с какой-либо степенью достоверности. Евклид (около 300 г. до н.э.) Элементы представляют собой первый, а затем и стандартный справочник по геометрии. На самом деле Евклид предоставил два совершенно разных доказательства: Предложение I.47 (Первая книга, Предложение 47) и VI.31. Теорема реверсивный , что означает, что его реверсивный также верен. Обратное утверждение гласит, что треугольник, стороны которого удовлетворяют условию a² + b² = c², обязательно прямоугольный. Евклид был первым (I.48), кто упомянул и доказал этот факт.
У. Данэм [ Математическая Вселенная ] цитирует книгу Пифагорейское Предложение профессора начала 20-го века Элиши Скотт Лумис.
 Книга представляет собой сборник из 367 доказательств теоремы Пифагора и была переиздана NCTM в 1968. В предисловии автор справедливо утверждает, что число алгебраических доказательств безгранично, как и число геометрических доказательств, но что это предложение не допускает тригонометрического доказательства. Любопытно, что нигде в книге Лумис не упоминает VI.31 Евклида, даже когда предлагает его и варианты в качестве алгебраических доказательств 1 и 93 или геометрических доказательств 230.
Книга представляет собой сборник из 367 доказательств теоремы Пифагора и была переиздана NCTM в 1968. В предисловии автор справедливо утверждает, что число алгебраических доказательств безгранично, как и число геометрических доказательств, но что это предложение не допускает тригонометрического доказательства. Любопытно, что нигде в книге Лумис не упоминает VI.31 Евклида, даже когда предлагает его и варианты в качестве алгебраических доказательств 1 и 93 или геометрических доказательств 230.По всей видимости, Лумис черпал вдохновение из серии коротких статей в The American Mathematical Monthly , опубликованный Б. Ф. Янни и Дж. А. Колдерхедом в 1896–1899 гг. С учетом возможных вариаций в расчетах, полученных из одних и тех же геометрических конфигураций, потенциальное количество доказательств выросло до тысяч. Например, авторы насчитали 45 доказательств на основе схемы доказательства № 6 и практически столько же на основе диаграммы № 19 ниже. Я приведу пример их подхода в доказательстве №56.
 (Всего было 100 «стенографических» доказательств.)
(Всего было 100 «стенографических» доказательств.)Должен признаться, что относительно существования тригонометрического доказательства я был на стороне Элиши Лумиса до самого последнего времени, т. е. до тех пор, пока мне не сообщили о доказательстве № 84. На самом деле, для некоторых людей стало неожиданностью, что кто-то может сомневаться в существовании тригонометрических доказательств, поэтому многие из них в конечном итоге попали на эти страницы.
В тригонометрических терминах теорема Пифагора утверждает, что в треугольнике ABC равенство sin²A + sin²B = 1 эквивалентно прямому углу при C. Более симметричное утверждение состоит в том, что ΔABC верно тогда и только тогда, когда sin²A + sin²B + sin²C = 2. По закону синусов последнее эквивалентно a² + b² + c² = 2d², где d — диаметр описанной окружности. Другая форма того же свойства — cos²A + cos²B + cos²C = 1, что мне нравится даже больше.
Теорема Пифагора обобщается на пространства большей размерности.
 Некоторые обобщения далеко не очевидны. Теорема Пифагора служит основой формулы Евклидова расстояния.
Некоторые обобщения далеко не очевидны. Теорема Пифагора служит основой формулы Евклидова расстояния.Ларри Хоэн придумал плоское обобщение, которое связано с законом косинусов, но короче и выглядит красивее.
Теорема, формулировка которой приводит к понятию евклидова расстояния, евклидова и гильбертова пространств, играет важную роль в математике в целом. Существует небольшой набор довольно элементарных фактов, доказательство которых может быть основано на теореме Пифагора. Есть более свежая страница со списком свойств евклидовой диаграммы для I.47.
Везде, где все три стороны прямоугольного треугольника являются целыми числами, их длины образуют пифагорейских чисел (или пифагорейских чисел ). Существует общая формула для получения всех таких чисел.
- Мой первый математический дудл тоже был связан с теоремой Пифагора. В отличие от доказательства без слов, друдл может предложить утверждение, а не просто доказательство.

Также было опубликовано несколько ложных доказательств теоремы. Я собрал несколько на отдельной странице. Лучше учиться на чужих ошибках, чем совершать свои.
Известно, что теорема Пифагора эквивалентна постулату о параллельных.
- Конфигурация Пифагора известна под многими названиями, самым популярным из которых, вероятно, является Стул Невесты. Помимо утверждения теоремы Пифагора, стул Брайда обладает многими интересными свойствами, многие из которых весьма элементарны.
- Покойный профессор Эдсгер В. Дейкстра нашел совершенно потрясающее обобщение теоремы Пифагора. Если в треугольнике углы α, β, γ лежат против сторон длины a, b, c, то
(ЭВД)
знак (α + β — γ) = знак (a² + b² — c²),
, где sign(t) — функция signum :
sign(t) = -1, для t < 0, sign(0) = 0, sign(t) > 170, Теорема, которой посвящена эта страница, трактуется как «Если γ = p/2, то a² + b² = c²».
 Дейкстра заслуженно считает (EWD) более симметричным и информативным. Дополнительным преимуществом считается отсутствие трансцендентных величин (р). Доказательство Дейкстры включено в Доказательство 78 и более подробно описано на отдельной странице.
Дейкстра заслуженно считает (EWD) более симметричным и информативным. Дополнительным преимуществом считается отсутствие трансцендентных величин (р). Доказательство Дейкстры включено в Доказательство 78 и более подробно описано на отдельной странице. Самый известный из прямоугольных треугольников с размерами 3:4:5 был замечен в готическом искусстве и может быть получен складыванием бумаги. Довольно непреднамеренно он появляется в нескольких задачах сангаку.
Возможно, неудивительно, что теорема Пифагора является следствием различных физических законов и встречается в нескольких механических явлениях.
Доказательство №1
Это, вероятно, самое известное из всех доказательств пифагорейского утверждения. Это первое из двух доказательств Евклида (I.47). Базовая конфигурация стала известна под разными названиями, наиболее популярным из которых, вероятно, было кресло невесты .
Доказательство проиллюстрировано отмеченным наградами апплетом Java, написанным Джимом Мори. Я включил его на отдельной странице с любезного разрешения Джима. Приведенное ниже доказательство представляет собой несколько сокращенную версию исходного евклидова доказательства в том виде, в каком оно представлено в переводе сэра Томаса Хита.
Я включил его на отдельной странице с любезного разрешения Джима. Приведенное ниже доказательство представляет собой несколько сокращенную версию исходного евклидова доказательства в том виде, в каком оно представлено в переводе сэра Томаса Хита.
Прежде всего, ΔABF = ΔAEC по SAS. Это потому, что AE = AB, AF = AC и
∠BAF = ∠BAC + ∠CAF = ∠CAB + ∠BAE = ∠CAE.
ΔABF имеет основание AF и высоту от B, равную AC. Следовательно, его площадь равна половине площади квадрата на стороне АС. С другой стороны, ΔAEC имеет AE и высоту от C, равную AM, где M — точка пересечения AB с линией CL, параллельной AE. Таким образом, площадь ΔAEC равна половине площади прямоугольника AELM. Что говорит о том, что площадь AC² квадрата со стороной AC равна площади прямоугольника AELM.
Аналогично, площадь BC² квадрата со стороной BC равна площади прямоугольника BMLD. Наконец, два прямоугольника AELM и BMLD составляют квадрат на гипотенузе AB.
Имеющаяся конфигурация допускает множество вариаций. Б. Ф. Янни и Дж. А. Колдерхед ( Am Math Monthly , v.4, n 6/7, (1987), 168–170 опубликовали несколько доказательств, основанных на следующих диаграммах
Б. Ф. Янни и Дж. А. Колдерхед ( Am Math Monthly , v.4, n 6/7, (1987), 168–170 опубликовали несколько доказательств, основанных на следующих диаграммах
Некоторые свойства этой конфигурации были доказаны на Стуле Невесты, а другие на специальной странице Свойства фигур в Евклиде I.47.
Доказательство №2
Начнем с двух квадратов со сторонами a и b соответственно, расположенных рядом. общая площадь двух квадратов a²+b² .
Построение началось не с треугольника, но теперь мы рисуем два из них, оба с стороны a и b и гипотенуза c . Обратите внимание, что отрезок, общий для двух квадратов, был удаленный. Таким образом, на данный момент у нас есть два треугольника и странная форма.
В качестве последнего шага мы поворачиваем треугольники на 90°, каждый вокруг своей вершины.
правый вращается по часовой стрелке, тогда как левый треугольник вращается против часовой стрелки. Очевидно, что получившаяся фигура представляет собой квадрат со стороной c и площадью c² . Это доказательство появляется в динамическом воплощении.
Очевидно, что получившаяся фигура представляет собой квадрат со стороной c и площадью c² . Это доказательство появляется в динамическом воплощении.
(Вариант этого доказательства можно найти в сохранившейся рукописи Табита ибн Курры, находящейся в библиотеке Музея Айя София в Турции, зарегистрированной под номером 4832. [Р. Шломинг, Табит ибн Курра и теорема Пифагора , Учитель математики 63 (октябрь 1970 г.), 519-528]. Диаграмма ибн Курры аналогична диаграмме в доказательстве № 27. Само доказательство начинается с определения наличия четырех равных прямоугольных треугольников, окружающих странно выглядящую фигуру, как в текущем доказательстве №2. Эти четыре треугольника попарно соответствуют начальной и конечной позициям повернутых треугольников в текущем доказательстве. Эту же конфигурацию можно было бы наблюдать в доказательстве с помощью тесселяции.)
Доказательство №3
Теперь мы начинаем с четырех копий одного и того же треугольника. Три из них были повернуты на 90°, 180° и 270° соответственно. Каждый имеет площадь ab /2. Складываем их вместе без дополнительных поворотов так, чтобы они образовали квадрат со стороной c .
Три из них были повернуты на 90°, 180° и 270° соответственно. Каждый имеет площадь ab /2. Складываем их вместе без дополнительных поворотов так, чтобы они образовали квадрат со стороной c .
Квадрат имеет квадратное отверстие со стороной ( a — b ). Суммируя его площадь ( a — b )² и 2 ab , площадь четырех треугольников (4· аб /2), получаем
| c² | = (a — b)² + 2ab |
| = a² — 2ab + b² + 2ab | |
| = a² + b² |
Доказательство #4
Четвертый подход начинается с тех же четырех треугольников, за исключением того, что на этот раз они образуют квадрат со стороной ( a + b ) и отверстие с бортиком c . Мы можем вычислить площадь большого квадрата двумя способами. Таким образом,
( a + b )² = 4 · ab /2 + c ²
упрощая который получаем нужный идентификатор.
Доказательство, которое объединяет это с доказательством № 3, приписывается индуистскому математику XII века Бхаскаре (Бхаскара II):
Нельсен (стр. 4) отдает должное Бхаскаре также за доказательство №3.
Здесь мы добавляем два тождества
с ² = ( а — б )² + 4· аб /2 и
с ² = ( а + б / )² 6 1· / аб 2 — 6 4 · аб 90
что дает
2 c ² = 2 a ² + 2 b ².
Последнее нужно разделить только на 2. Это алгебраическое доказательство № 36 в коллекции Лумиса. Его вариант, специально примененный к треугольнику 3-4-5, фигурирует в классической китайской девятке.0576 Chou Pei Suan Ching , датированный где-то между 300 г. до н.э. и 200 г. н.э., который Лумис называет доказательством 253.
Доказательство № 5
Это доказательство, обнаруженное президентом Дж. А. Гарфилдом в 1876 году [Папас], является вариацией предыдущего. Но на этот раз мы вообще не рисуем квадратов. Теперь ключом является формула площади трапеции — полусумма оснований, умноженная на высоту — ( a + b )/2·( a + b ). Глядя на картинку с другой стороны, это также можно вычислить как сумму площадей трех треугольников — аб /2 + аб /2 + с · с /2. Как и прежде, упрощения дают a² + b² = c² . (Это еще не все.)
Но на этот раз мы вообще не рисуем квадратов. Теперь ключом является формула площади трапеции — полусумма оснований, умноженная на высоту — ( a + b )/2·( a + b ). Глядя на картинку с другой стороны, это также можно вычислить как сумму площадей трех треугольников — аб /2 + аб /2 + с · с /2. Как и прежде, упрощения дают a² + b² = c² . (Это еще не все.)
Две копии одной и той же трапеции можно объединить двумя способами, прикрепив их вдоль наклонной стороны трапеции. Один ведет к доказательству №4, другой — к доказательству №52.
Другая разработка принадлежит Тони Фостеру: она также вызывает образ трапеции, но в другом свете.
Доказательство #6
Мы начинаем с исходного прямоугольного треугольника, который теперь обозначается как ABC, и нам нужна только одна дополнительная конструкция — высота AD. Треугольники ABC, DBA и DAC подобны, что приводит к двум отношениям:
AB/BC = BD/AB и AC/BC = DC/AC.
При записи по-другому получается
AB·AB = BD·BC и AC·AC = DC·BC
Суммируя получаем
| AB·AB + AC·AC | = BD·BC + DC·BC |
| = (BD+DC)·BC = BC·BC. |
В несколько иной форме это доказательство появилось в Mathematics Magazine , 33 (март 1950 г.), с. 210, в разделе Mathematical Quickies, см. Mathematical Quickies CW Trigg.
Приняв AB = a, AC = b, BC = c и обозначив BD = x, получим, как и выше,
a² = cx и b² = c(c — x),
, что, возможно, более прозрачно ведет к той же идентичности.
В частной переписке д-р Франс Дакар, Любляна, Словения, предположил, что диаграмма справа может служить двум целям. Во-первых, это дает дополнительное графическое представление настоящего доказательства №6. Кроме того, он подчеркивает связь последнего с доказательством № 1.
Р. М. Менток заметил, что небольшая хитрость делает доказательство более кратким. В общепринятых обозначениях c = b cos A + a cos B. Но из исходного треугольника легко увидеть, что cos A = b/c и cos B = a/c, поэтому c = b (b/c) + а (а/с). Этот вариант сразу ставит вопрос: получаем ли мы таким образом тригонометрическое доказательство? Я так не думаю, хотя здесь бросается в глаза тригонометрическая функция (косинус). Отношение двух длин в фигуре является свойством формы, означающим, что оно остается постоянным при переходе между подобными фигурами, т. е. фигурами одинаковой формы. Тот факт, что конкретное отношение, используемое в доказательстве, сыграло достаточно важную роль в тригонометрии и вообще в математике, чтобы заслужить собственное специальное обозначение, не делает доказательство зависимым от этого обозначения. (Тем не менее, проверьте Доказательство 84, где тригонометрические тождества используются существенным образом.)
В общепринятых обозначениях c = b cos A + a cos B. Но из исходного треугольника легко увидеть, что cos A = b/c и cos B = a/c, поэтому c = b (b/c) + а (а/с). Этот вариант сразу ставит вопрос: получаем ли мы таким образом тригонометрическое доказательство? Я так не думаю, хотя здесь бросается в глаза тригонометрическая функция (косинус). Отношение двух длин в фигуре является свойством формы, означающим, что оно остается постоянным при переходе между подобными фигурами, т. е. фигурами одинаковой формы. Тот факт, что конкретное отношение, используемое в доказательстве, сыграло достаточно важную роль в тригонометрии и вообще в математике, чтобы заслужить собственное специальное обозначение, не делает доказательство зависимым от этого обозначения. (Тем не менее, проверьте Доказательство 84, где тригонометрические тождества используются существенным образом.)
Майкл Брозинский придумал вариант доказательства, которое, как мне кажется, можно правильно назвать липограммным .
Наконец, следует отметить, что конфигурация, используемая в этом доказательстве, является частным случаем следующего доказательства — второго и менее известного доказательства пифагорейского утверждения Евклида. Отдельная страница посвящена доказательству по рассуждению подобия.
Отдельная страница посвящена доказательству по рассуждению подобия.
Доказательство №7
Следующее доказательство дословно взято из Евклида VI.31 в переводе сэра Томаса Л. Хит. Великий Г. Поля анализирует ее в своей Индукция и аналогия в математике (II.5), которая рекомендуется к прочтению студентам и учителям математики.
В прямоугольных треугольниках фигура на стороне, опирающейся на прямой угол, равна равным подобным и аналогично описанным фигурам на сторонах, содержащих правую угол.
Пусть ABC прямоугольный треугольник с прямым углом BAC; Я говорю, что фигура на ВС равна аналогичным и аналогично описанным фигурам на БА, АС.
Пусть AD проведен перпендикулярно. Тогда, поскольку в прямоугольном треугольнике ABC из прямого угла проведена точка AD Перпендикуляр к основанию ВС, треугольники ABD, ADC, примыкающие к перпендикуляру, подобны как всему ABC, так и друг другу [VI.8].
И, поскольку ABC подобен ABD, следовательно, как CB соответствует BA, так и AB соответствует BD [VI. Def.1].
Def.1].
И, поскольку три прямые пропорциональны, как первая пропорциональна третьей, так пропорциональна и рисунок на первом к аналогичному и аналогично описанному рисунку на втором [VI.19]. Следовательно, как СВ к BD, так и фигура на CB к подобному и сходно описанному рисунок на БА.
По той же самой причине, как BC относится к CD, так и цифра на BC к фигуре на CA; чтобы, кроме того, как ВС относится к BD, DC, так и фигура на ВС к подобному и подобному описанные фигуры на ВА, АС.
Но ВС равно BD, DC; поэтому цифра на ВС также равна аналогичной и аналогично описаны фигуры на ВА, АС.
Поэтому и т. д. Q.E.D.
Исповедь
Я по-настоящему оценил это доказательство только после прочтения книги Поля I
упомянутое выше. Я надеюсь, что Java-апплет поможет вам
добраться до сути этого замечательного доказательства. Обратите внимание, что утверждение фактически доказано
является гораздо более общей, чем теорема, как она общеизвестна. (В другом обсуждении VI. 31 рассматривается под немного другим углом.)
31 рассматривается под немного другим углом.)
Джон Ариони придумал прекрасную иллюстрацию, которая также проливает свет на доказательство №8.
Доказательство №8
Играя с апплетом, демонстрирующим доказательство Евклида (№7), я обнаружил еще одно тот, который, хотя и уродлив, тем не менее служит цели.
Таким образом, начиная с треугольника 1, мы добавляем еще три, как это было предложено в доказательстве № 7: подобные и одинаково описанные треугольники 2, 3 и 4. Вывод пары отношений как было сделано в доказательстве № 6, мы получаем длины сторон, как показано на диаграмме. В настоящее время, можно посмотреть на конечную форму двумя способами:
- как объединение прямоугольника (1 + 3 + 4) и треугольника 2, или
- как объединение прямоугольника (1 + 2) и двух треугольников 3 и 4.
Приравнивание площадей приводит к
ab/c · (a² + b²)/c + ab/2 = ab + (ab/c · a²/c + ab/c · b²/c)/2
Упрощая получаем
ab/c · (a² + b²)/c/2 = ab/2 или (a² + b²)/c² = 1
Замечание
Оглядываясь назад, можно найти более простое доказательство. Посмотрите на прямоугольник (1 + 3 + 4). Его длинная сторона, с одной стороны, представляет собой простое c, а с другой стороны, это a²/c + b²/c, и мы снова имеем то же самое тождество.
Посмотрите на прямоугольник (1 + 3 + 4). Его длинная сторона, с одной стороны, представляет собой простое c, а с другой стороны, это a²/c + b²/c, и мы снова имеем то же самое тождество.
Владимир Николин из Сербии предоставил прекрасную иллюстрацию:
Доказательство #9
Еще одно доказательство основано на перестановке жестких частей, как и доказательство №2. Это делает алгебраическую часть доказательства № 4 полностью избыточной. К двум картинкам добавить особо нечего.
(Моя искренняя благодарность Монти Фистеру за любезное разрешение использовать графику.)
Есть интерактивная симуляция, с которой можно поиграть. И еще одно, которое ясно показывает его связь с доказательствами № 24 или № 69..
Лумис (стр. 49-50) упоминает, что доказательство «было разработано Морисом Лейснезом, старшеклассником, в средней школе Саут-Бенда, штат Индиана, и прислано мне 16 мая 1939 года. его классным руководителем Уилсоном Торнтоном».
Доказательство было опубликовано Руфусом Исааком в Mathematics Magazine , Vol. 48 (1975), с. 198.
Немного другая перегруппировка приводит к шарнирному рассечению, показанному апплетом Java.
Р. Б. Нельсен воспроизводит доказательство с замечанием «основано на одном из г. Zhou bi suan jing , китайский документ, датируемый примерно 200 г. до н.э.». Сэр Томас Л. Хит упоминает его в своем комментарии (1908 г.) к Евклиду I.47 без указания авторства, но со ссылкой на двух других современных комментаторов.
Профессор Сяолинь Чжун из Калифорнийского университета в Лос-Анджелесе предложил вариант, упакованный в один квадрат: «Доказательство становится очевидным, если просто переместить $\Delta ABH$ и $\Delta BCD$ в $\Delta HGF$ и $\Delta FED,$ соответственно.»
Доказательство №10
Это и следующие 3 доказательства взяты из [ PWW ].
Треугольники в Доказательстве №3 можно переставить еще одним способом, который делает пифагорейское тождество очевидно.
(Более поясняющая диаграмма справа была любезно прислана мне Монти Фистером. Доказательство допускает шарнирное рассечение, проиллюстрированное Java-апплетом.)
Первые две части могут быть объединены в одну. Результат появился в книге 9 1830 года.0576 Санпо Синсё — Новая математика — Чиба Танехидэ (1775-1849), [H. Фукагава, А. Ротман, Священная математика: геометрия японского храма , Princeton University Press, 2008, с. 83].
Доказательство №11
Нарисуйте окружность радиусом c и прямоугольный треугольник со сторонами a и b, как показано на рисунке. В этой ситуации можно применить любой из нескольких хорошо известных фактов. Например, на диаграмме три точки F, G, H, расположенные на окружности, образуют еще один прямоугольный треугольник с высотой FK длины a. Его гипотенуза GH разделена на две части: (c + b) и (c — b). Итак, как и в Доказательстве № 6, мы получаем a² = (c + b)(c — b) = c² — b².
Итак, как и в Доказательстве № 6, мы получаем a² = (c + b)(c — b) = c² — b².
[Loomis, #53] приписывает эту конструкцию великому Лейбницу, но удлиняет доказательство примерно в три раза за счет извилистых и ошибочных выводов.
Б. Ф. Янни и Дж. А. Колдерхед ( Am Math Monthly , v.3, n. 12 (1896), 299-300) предлагают несколько иной маршрут. Представьте, что FK расширен до второго пересечения F’ с окружностью. Тогда по теореме о пересекающихся хордах FK·KF’ = GK·KH с тем же следствием.
Совсем недавно Дэниел Дж. Хардиски пришел к доказательству другим путем. Постройте два равнобедренных треугольника $ABD$ и $ABE,$ с $D$ и $E$ на $AC$ по обе стороны от $A.$ Затем заметьте, что $\угол DBE$ прямой.
Этот аргумент напоминает характеристику прямоугольных треугольников, обсуждавшуюся в другом месте.
Доказательство № 12
Это доказательство является вариацией № 1, одного из оригинальных доказательств Евклида. В частях 1, 2 и 3,
два маленьких квадрата сдвигаются друг к другу так, что общая заштрихованная площадь остается
неизменен (и равен a²+b².) В части 3 длина вертикали
часть границы заштрихованной области точно равна c, потому что два оставшихся треугольника являются копиями
оригинального. Это означает, что можно скользить вниз по заштрихованной области, как в части 4. Отсюда
Теорема Пифагора легко следует.
В частях 1, 2 и 3,
два маленьких квадрата сдвигаются друг к другу так, что общая заштрихованная площадь остается
неизменен (и равен a²+b².) В части 3 длина вертикали
часть границы заштрихованной области точно равна c, потому что два оставшихся треугольника являются копиями
оригинального. Это означает, что можно скользить вниз по заштрихованной области, как в части 4. Отсюда
Теорема Пифагора легко следует.
(Это доказательство можно найти в H. Eves, In Mathematical Circles , MAA, 2002, pp. 74-75)
, a’b’c’, a’x и b’y.) Мы последовательно имеем
у/б = Ь’/с, х/а = а’/с, су + сх = аа’ + bb’.
И, наконец, cc’ = aa’ + bb’. Это очень похоже на доказательство № 6, но результат более общий.
Доказательство №14
Это доказательство H.E. Dudeney (1917) начинает с того, что разрезает квадрат с большей стороны на четыре части, которые затем объединяются с меньшей стороной, образуя квадрат, построенный на гипотенузе.
Грег Фредериксон из Университета Пердью, автор действительно поучительной книги Dissections: Plane & Fancy (Cambridge University Press, 1997), указал на историческую неточность:
Вы приписали доказательство №14 Е.П. Дьюдени (1917 г.), но на самом деле она была опубликована ранее (1872 г.) Генри Перигалом, лондонским биржевым маклером. Другое доказательство вскрытия появилось гораздо раньше, его дал арабский математик и астроном Табит в десятом веке. Подробности об этих и других доказательствах рассечения (включая доказательства закона косинусов) я включил в свою недавнюю книгу «Рассечения: плоскость и фантазии», Cambridge University Press, 19.97. Вам может понравиться веб-страница книги:
. http://www.cs.purdue.edu/homes/gnf/book.html
С уважением,
Грег Фредериксон
Билл Кассельман из Университета Британской Колумбии секундирует информацию Грега. Мой взят из Proofs Without Words Р. Б. Нельсена (MAA, 1993).
Доказательство имеет динамическую версию.
Доказательство № 15
Это замечательное доказательство К. О. Фридрихса является обобщением предыдущего Дьюдени (или Перигала, как указано выше). Это действительно общее. Он общий в том смысле, что из него можно вывести бесконечное множество конкретных геометрических доказательств. (Роджер Нельсен приписывает [PWWII, стр. 3] это доказательство Аннаиризи из Аравии (ок. 9 г. до н. э.).00 г. н.э.)) Особенно красивый вариант Олофа Ханнера представлен на отдельной странице.
Вариант основного доказательства прислал мне Микель Пленс, старшеклассник из Каталонии. Микель рассматривает перекрытие восьми квадратов по трем сторонам прямоугольного треугольника и оставшиеся части. Я поместил его заявление на отдельной странице.
Доказательство №16
Это доказательство приписывается Леонардо да Винчи (1452-1519) [Евс]. Четырехугольники
ABHI, JHBC, ADGC и EDGF равны. (Это следует из наблюдения, что угол ABH
составляет 45°. Это так, потому что ABC прямоугольный, поэтому центр O квадрата ACJI лежит
на окружности, описанной вокруг треугольника ABC. Очевидно, угол ABO равен 45°.) Теперь
Площадь (ABHI) + Площадь (JHBC) = Площадь (ADGC) + Площадь (EDGF). Каждая сумма содержит две площади треугольников, равные ABC
(IJH или BEF), удаление которого дает теорему Пифагора.
Это так, потому что ABC прямоугольный, поэтому центр O квадрата ACJI лежит
на окружности, описанной вокруг треугольника ABC. Очевидно, угол ABO равен 45°.) Теперь
Площадь (ABHI) + Площадь (JHBC) = Площадь (ADGC) + Площадь (EDGF). Каждая сумма содержит две площади треугольников, равные ABC
(IJH или BEF), удаление которого дает теорему Пифагора.
Дэвид Кинг несколько модифицирует аргумент
Длины сторон шестиугольников идентичны. Углы при P (прямой угол + угол между a и c) одинаковы. Углы при Q (прямой угол + угол между b и c) одинаковы. Следовательно, все четыре четырехугольника одинаковы, а значит, и шестиугольники имеют одинаковую площадь.
Доказательство №17
Это доказательство содержится в Книге IV Mathematical Collection Папп Александрийский (ок. 300 г. н.э.) [Евс, Паппас]. Он обобщает теорему Пифагора в двух отношениях: треугольник ABC не обязательно должен быть прямоугольным и
фигуры, построенные на его сторонах, представляют собой произвольные параллелограммы, а не квадраты. Таким образом, постройте параллелограммы CADE и CBFG на сторонах AC и, соответственно, BC. Пусть DE и FG пересекаются в H и рисуют AL и BM параллельно и равны HC. Тогда площадь (ABML) = площадь (CADE) + площадь (CBFG). Действительно, с преобразованием сдвига, уже использованным в доказательствах № 1 и № 12, площадь (CADE) = площадь (CAUH) = площадь (SLAR), а также площадь (CBFG) = площадь (CBVH) = площадь (SMBR). Теперь просто сложите то, что равно.
Таким образом, постройте параллелограммы CADE и CBFG на сторонах AC и, соответственно, BC. Пусть DE и FG пересекаются в H и рисуют AL и BM параллельно и равны HC. Тогда площадь (ABML) = площадь (CADE) + площадь (CBFG). Действительно, с преобразованием сдвига, уже использованным в доказательствах № 1 и № 12, площадь (CADE) = площадь (CAUH) = площадь (SLAR), а также площадь (CBFG) = площадь (CBVH) = площадь (SMBR). Теперь просто сложите то, что равно.
Динамическая иллюстрация доступна в другом месте.
Доказательство №18
Это еще одно обобщение, не требующее прямых углов. Это связано с Табитом ибн Куррой (836-901) [Евами]. Если углы CAB, AC’B и AB’C равны, то AC² + AB² = BC(CB’ + BC’). Действительно, треугольники ABC, AC’B и AB’C подобны. Таким образом, мы имеем AB/BC’ = BC/AB и AC/CB’ = BC/AC, что немедленно приводит к требуемому тождеству. В случае, если угол A прямой, теорема сводится к пифагорову утверждению и доказательству №6.
Та же диаграмма по-другому используется Э. В. Дейкстрой, который концентрируется на сравнении ВС с суммой СВ’ + ВС’.
В. Дейкстрой, который концентрируется на сравнении ВС с суммой СВ’ + ВС’.
Доказательство №19
Это доказательство является вариацией №6. На меньшую сторону AB прибавьте прямоугольный треугольник ABD, подобный к АВС. Тогда, естественно, DBC похож на два других. Из площади (ABD) + площади (ABC) = площади (DBC), AD = AB²/AC и BD = AB·BC/AC, мы получаем (AB²/AC)·AB + AB·AC = (AB·BC/AC)·BC. Деление на AB/AC приводит к AB² + AC² = BC².
Доказательство №20
Это помесь №7 и №19. Постройте треугольники ABC’, BCA’ и ACB’, подобные треугольнику ABC, как на рисунке. По построению ΔABC = ΔA’BC. Кроме того, равны треугольники ABB’ и ABC’. Таким образом, мы заключаем, что площадь (A’BC) + площадь (AB’C) = площадь (ABC’). Из подобия треугольников по-прежнему получаем B’C = AC²/BC и BC’ = AC·AB/BC. Сложив все это вместе, мы получим AC·BC + (AC²/BC)·AC = AB·(AC·AB/BC), что равно
ВС² + АС² = АВ².
Доказательство № 21
Ниже приводится выдержка из письма доктора Скотта Броди из Медицинской школы Маунт-Синай, штат Нью-Йорк.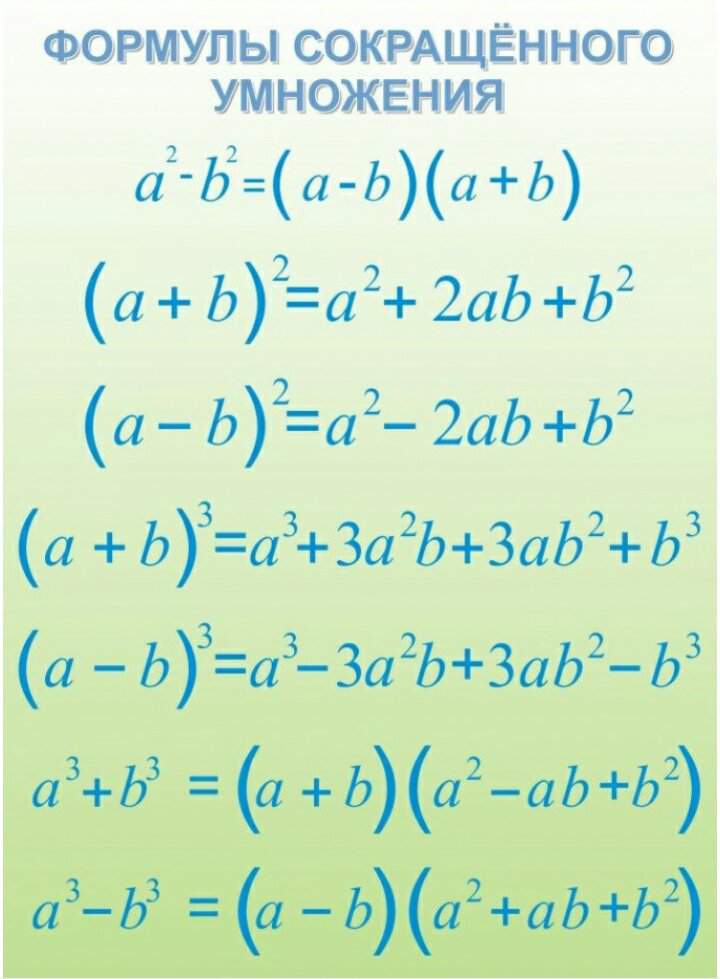 который прислал мне пару доказательств собственно теоремы и ее обобщения на закон косинусов:
который прислал мне пару доказательств собственно теоремы и ее обобщения на закон косинусов:
Первое доказательство я просто перехожу из отличного обсуждения в серии Project Mathematics, основанного на теореме Птолемея о четырехугольниках, вписанных в окружность: для таких четырехугольников сумма произведений длин противоположных сторон, взятых попарно, равна произведение длин двух диагоналей. В случае прямоугольника это немедленно сводится к a² + b² = c².
Доказательство №22
Вот второе доказательство из письма доктора Скотта Броди.
Примем как известную теорему о силе точки: если взять точку вне круга и из этой точки провести отрезок, касающийся круга, и провести другой отрезок (секущую), который делит круг пополам. различных точек, то квадрат длины касательной равен произведению расстояния по секущей от внешней точки до ближайшей точки пересечения с окружностью и расстояния по секущей до дальней точки пересечения с окружностью. круг.
круг.
Пусть ABC прямоугольный треугольник с прямым углом C. Проведите высоту от C до гипотенузы; пусть P обозначает основание этой высоты. Тогда, поскольку CPB прав, точка P лежит на окружности с диаметром BC; а поскольку CPA прав, точка P лежит на окружности с диаметром AC. Поэтому пересечение двух окружностей на катетах ВС, СА исходного прямоугольного треугольника совпадает с Р и, в частности, лежит на АВ. Обозначим через x и y длины отрезков BP и PA соответственно и, как обычно, пусть a, b, c обозначают длины сторон ABC, противоположных углам A, B, C соответственно. Тогда x + y = c .
Поскольку угол C прямой, BC касается окружности диаметром CA, а теорема о силе точки утверждает, что a² = xc ; аналогично AC касается окружности диаметром BC, и b² = yc . Складывая, находим а² + б² = хс + yc = c² , Q.E.D.
Доктор Броди также создал файл Geometer’s SketchPad, чтобы проиллюстрировать это доказательство.
(Это доказательство было опубликовано под номером XXIV в сборнике доказательств Б. Ф. Янни и Дж. А. Колдерхеда в Am Math Monthly , т. 4, № 1 (1897), стр. 11-12.)
Доказательство #23
Другое доказательство основано на формуле Герона. (Попутно с помощью формулы я отобразил площади в апплете, иллюстрирующем Доказательство №7). Это довольно запутанный способ доказательства теоремы Пифагора, который, тем не менее, отражает центральное место теоремы в геометрии плоскости. (Более короткое и более прозрачное применение формулы Герона лежит в основе доказательства № 75.)
Доказательство #24
[Светц] приписывает это доказательство Абу л’Хасану Табиту ибн Курра Марван аль’Харрани (826-901). Это второе из доказательств, данных Сабитом ибн Куррой. Первый из них, по сути, является номером 2 выше.
Доказательство похоже на часть 3 доказательства №12.
ΔАВС =
ΔFLC =
ΔFMC =
ΔBED =
ΔАГ =
ΔФГЭ. С одной стороны, площадь формы ABDFH равна AC² + BC² + Area(ΔABC + ΔFMC + ΔFLC). С другой стороны, площадь (ABDFH) = AB² + площадь (ΔBED + ΔFGE + ΔAGH).
С одной стороны, площадь формы ABDFH равна AC² + BC² + Area(ΔABC + ΔFMC + ΔFLC). С другой стороны, площадь (ABDFH) = AB² + площадь (ΔBED + ΔFGE + ΔAGH).
Табит ибн Курра допускает естественное обобщение доказательства закона косинусов.
Также доступна динамическая иллюстрация доказательства ибн Курры.
Это «развернутый» вариант приведенного выше доказательства. Две пятиугольные области — красная и синяя — заведомо равны и оставляют одинаковую площадь при удалении из каждой трех равных треугольников.
Доказательство популяризирует Монти Фистер, автор неподражаемой Gnarly Math компакт-диск.
Флор ван Ламоен любезно указал мне на более ранний источник. Эдуард Доуэс Деккер, один из самых известных голландских авторов, опубликовал в 1888 году под псевдонимом Мультатули доказательство, сопровождаемое следующей диаграммой.
Скотт Броди указал на очевидную связь этого доказательства с № 9. Это та же самая конфигурация, но без одного треугольника.
Доказательство № 25
Б. Ф. Янни (1903, [Swetz]) дал доказательство, используя «аргумент сдвига», который также использовался в Доказательствах № 1 и № 12. Последовательно, площади LMOA, LKCA и ACDE (что есть AC²) равны, как и площади HMOB, HKCB и HKDF (что есть BC²). БК = ДФ. Таким образом, AC² + BC² = Площадь (LMOA) + Площадь (HMOB) = Площадь (ABHL) = AB².
Доказательство #26
Это доказательство я нашел на сайте Билла Кассельмана, где оно представлено Java-апплетом.
Со всеми приведенными выше доказательствами это должно быть простым. Подобные треугольники, как в доказательствах № 6 или № 13.
Доказательство № 27
Те же части, что и в доказательстве № 26, можно переставить и другим способом.
Это рассечение часто приписывают голландскому математику 17 го века Франсу ван Схоотену. [Фредериксон, с. 35] рассматривает его как шарнирный вариант варианта ибн Курры, см. примечание в скобках после доказательства №2. Доктор Франс Дакар из Словении указал, что эту же диаграмму легко объяснить с помощью тесселяции в доказательстве № 15. На самом деле, это может быть лучше объяснено другой тесселяцией. (Я благодарю Дугласа Роджерса за то, что он разъяснил мне это.)
примечание в скобках после доказательства №2. Доктор Франс Дакар из Словении указал, что эту же диаграмму легко объяснить с помощью тесселяции в доказательстве № 15. На самом деле, это может быть лучше объяснено другой тесселяцией. (Я благодарю Дугласа Роджерса за то, что он разъяснил мне это.)
Имеющаяся конфигурация допускает множество вариаций. Б. Ф. Янни и Дж. А. Колдерхед ( Am Math Monthly , v. 6, n. 2 (1899), 33–34) опубликовали несколько доказательств, основанных на следующих диаграммах (при этом несколько доказательств на диаграмму)
Доказательство № 28
Мелисса Бег с MathForum любезно прислала мне ссылку (которая с тех пор исчезла) на страницу Дональда Б. Вагнера, эксперта по истории науки и техники в Китае. Доктор Вагнер, по-видимому, реконструировал доказательство Лю Хуэя (третий век нашей эры). Однако (см. ниже) есть серьезные сомнения в авторстве доказательства.
Элиша Лумис цитирует это как геометрическое доказательство № 28 со следующим комментарием:
- Бенджир фон Гутейл, оберлерер из Нюрнберга, Германия, представил приведенное выше доказательство.
 Он погиб в окопах во Франции в 1914 году. Так писал Дж. Адамс в августе 1933 года.
Он погиб в окопах во Франции в 1914 году. Так писал Дж. Адамс в августе 1933 года. - Назовем это Доказательством мировой войны Б. фон Гутейля.
Судя по фильму «Сладкая земля», такое снисходительное отношение к немецкому коллеге, возможно, не было обычным явлением в период, близкий к Первой мировой войне. Возможно, в 19 веке его охраняли еще больше.30-е годы в период прихода к власти нацистов в Германии.
(Я благодарю Д. Роджерса за то, что он обратил мое внимание на ссылку на коллекцию Лумиса. Он также сделал оговорку в отношении приписывания доказательства Лю Хуэю и проследил его раннее появление до Geometrische aufgabensamming Ausgabe B Карла Юлиуса Вальтера Литцмана. : fuer Realanstalten , опубликованный в Лейпциге Тойбнером в 1916 году. Интересно, что доказательство не было включено в более ранний Литцмана Der Pythagoreische Lehrsatz , опубликовано в 1912 г.)
Доказательство #29
Механическое доказательство теоремы заслуживает отдельной страницы.
К этому доказательству относится страница «Внегеометрические» доказательства теоремы Пифагора Скотта Броди
Доказательство #30
Это доказательство я нашел в продолжении Р. Нельсена Доказательства без слов II . (Это из-за Пу-Сун Парка и первоначально было опубликовано в Mathematics Magazine , декабрь 1999 г.). Начиная с одной из сторон прямоугольного треугольника, постройте 4 конгруэнтных прямоугольных равнобедренных треугольника с гипотенузами любых двух последующих перпендикуляров и вершинами, удаленными от данного треугольника. Гипотенуза первого из этих треугольников (на схеме выделена красным) должна совпадать с одной из сторон.
Вершины равнобедренных треугольников образуют квадрат со стороной, равной гипотенузе данного треугольника. Гипотенузы этих треугольников пересекают стороны квадрата в их серединах. Таким образом, получилось 4 пары равных треугольников (одна из пар зеленого цвета). Один из треугольников в паре находится внутри квадрата, другой снаружи. Пусть стороны исходного треугольника равны a, b, c (гипотенуза). Если первый равнобедренный треугольник был построен на стороне b, то каждый из них имеет площадь b²/4. Получаем
Пусть стороны исходного треугольника равны a, b, c (гипотенуза). Если первый равнобедренный треугольник был построен на стороне b, то каждый из них имеет площадь b²/4. Получаем
а² + 4b²/4 = с²
Есть динамическая иллюстрация и еще одна диаграмма, показывающая, как разделить два меньших квадрата и переставить их в один большой.
Эта диаграмма также имеет динамический вариант.
Доказательство #31
Для прямой ΔABC обозначим, как обычно, длины сторон BC, AC и гипотенузы как a, b и c соответственно. Постройте квадраты со сторонами ВС и АС, как показано на рисунке. Согласно SAS треугольники ABC и PCQ равны, так что ∠QPC = ∠A. Пусть М — середина гипотенузы. Обозначим пересечение MC и PQ как R. Покажем, что MR PQ.
Медиана гипотенузы равна половине последней. Следовательно, ΔCMB равнобедренный и ∠MBC = ∠MCB. Но у нас также есть ∠PCR = ∠MCB. Отсюда и ∠QPC = ∠A следует, что угол CRP прямой, или MR PQ.
С этими предварительными действиями мы переходим к треугольникам MCP и MCQ. Мы оцениваем их площади двумя разными способами:
Мы оцениваем их площади двумя разными способами:
С одной стороны, высота от M до PC равна AC/2 = b/2. Но также PC = b. Следовательно, площадь (ΔMCP) = b²/4. С другой стороны, Площадь (ΔMCP) = CM·PR/2 = c·PR/4. Точно так же площадь (ΔMCQ) = a²/4, а также площадь (ΔMCQ) = см·RQ/2 = c·RQ/4.
Мы можем суммировать два тождества: a²/4 + b²/4 = c·PR/4 + c·RQ/4 или a²/4 + b²/4 = c·c/4.
(Я благодарен Флору ван Ламоэну, который обратил мое внимание на это доказательство. Оно появилось в Pythagoras — голландском математическом журнале для школьников — в номере за декабрь 1998 года, в статье Бруно Эрнста. Доказательство приписывается ученица американской средней школы по имени Энн Кондит 1938 г. Доказательство включено в качестве геометрического доказательства 68 в сборник Лумиса, стр. 140.)
Доказательство #32
Пусть ABC и DEF — два конгруэнтных прямоугольных треугольника, такие что B лежит на DE, а A, F, C, E коллинеарны. ВС = EF = а, AC = DF = b, AB = DE = c. Очевидно, AB DE. Вычислите площадь ΔADE двумя разными способами.
ВС = EF = а, AC = DF = b, AB = DE = c. Очевидно, AB DE. Вычислите площадь ΔADE двумя разными способами.
Площадь (ΔADE) = AB·DE/2 = c²/2, а также площадь (ΔADE) = DF·AE/2 = b·AE/2.AE = AC + CE = b + CE. CE можно найти из подобных треугольников BCE и DFE: CE = BC·FE/DF = a·a/b. Собираем вещи вместе получаем
c²/2 = b(b + a²/b)/2
(Это доказательство является упрощением одного из доказательств Мишель Уоткинс, студентки Университета Северной Флориды, которое появилось в Math Spectrum 1997/98, v30, n3, 53-54.)
Дуглас Роджерс заметил, что одну и ту же диаграмму можно трактовать по-разному:
Доказательство 32 можно немного упорядочить, в соответствии с более поздними доказательствами, добавленными совсем недавно, и, таким образом, избежать подобных треугольников.
Конечно, ADE — это треугольник на основании DE с высотой AB, т. е. площадью cc/2.
Но его можно разрезать на треугольник FEB и четырехугольник ADBF. Первый имеет основание FE и высоту BC, поэтому площадь aa/2. Последний, в свою очередь, состоит из двух треугольников, расположенных спиной к спине на основании DF с суммой высот AC, поэтому площадь bb/2. Альтернативное рассечение рассматривает треугольник ADE как состоящий из треугольника ADC и треугольника CDE, который, в свою очередь, состоит из двух треугольников, расположенных спиной к спине на основании BC, с объединенными высотами EF.
Последний, в свою очередь, состоит из двух треугольников, расположенных спиной к спине на основании DF с суммой высот AC, поэтому площадь bb/2. Альтернативное рассечение рассматривает треугольник ADE как состоящий из треугольника ADC и треугольника CDE, который, в свою очередь, состоит из двух треугольников, расположенных спиной к спине на основании BC, с объединенными высотами EF.
Следующие два доказательства сопровождали следующее сообщение от Шая Симонсона, профессора Колледжа Стоунхилл в Кембридже, Массачусетс:
Приветствую вас,
Я с удовольствием просматривал ваш сайт и наткнулся на длинный список доказательств теоремы Пифа.
В моем курсе «История математической изобретательности» я использую два доказательства, в которых используется вписанная окружность прямоугольного треугольника. Каждое доказательство использует две диаграммы, каждая из которых представляет собой различное геометрическое представление одного алгебраического
доказательство, которое я обнаружил много лет назад и опубликовал в письме учителю математики.
Два геометрических доказательства не требуют слов, но требуют небольшого размышления.
С наилучшими пожеланиями,
Шай
Доказательство #33
Доказательство № 34
Proof #35
Cracked Domino — доказательство Марио Пачека (также известного как Pakoslaw Gwizdalski) — также требует некоторого размышления.
Доказательство, отправленное по электронной почте, сопровождалось следующим сообщением:
Это новое, экстраординарное и чрезвычайно элегантное доказательство, пожалуй, самой фундаментальной теоремы в математике (безоговорочно победившее по количеству доказательств 367?) превосходит все известные науке, включая китайское доказательство и доказательство Джеймса А. Гарфилда (20-го президента США). ), потому что он прямой, не требует никаких формул и его могут освоить даже дошкольники. Вполне вероятно, что он идентичен утраченному оригиналу, но кто это может доказать? Еще не в Книге рекордов Гиннеса!
Способ соединения частей вполне может быть оригинальным. Само рассечение хорошо известно (см. доказательства 26 и 27) и описано в книге Фредериксона, с. 29. Там же отмечено, что Б. Броди (1884) заметил, что подобное рассечение применимо и к подобным прямоугольникам. Вскрытие также является частным случаем доказательства суперпозиции К. О. Фридрихса.
Само рассечение хорошо известно (см. доказательства 26 и 27) и описано в книге Фредериксона, с. 29. Там же отмечено, что Б. Броди (1884) заметил, что подобное рассечение применимо и к подобным прямоугольникам. Вскрытие также является частным случаем доказательства суперпозиции К. О. Фридрихса.
Доказательство #36
Это доказательство принадлежит Дж. Э. Бётчеру и цитируется Нельсеном ( Доказательства без слов II , с. 6).
Я думаю, что взломать это доказательство без слов — хорошее упражнение для урока геометрии в средней или старшей школе.
С. К. Штейн, ( Mathematics: The Man-Made Universe , Dover, 1999, стр. 74) дает несколько иное рассечение.
Оба варианта имеют динамическую версию. Есть еще одна особенно яркая иллюстрация бетхеровского разложения.
Proof #37
Апплет Дэвида Кинга, демонстрирующий это доказательство, помещен на отдельной странице.
Доказательство #38
Это доказательство также было сообщено мне Дэвидом Кингом. Квадраты и 2 треугольника объединяются, чтобы получить два шестиугольника одинаковой площади, которые можно было бы установить, как в Доказательстве № 9. Однако оба шестиугольника мозаичны на плоскости.
Для каждого шестиугольника в левой мозаике есть шестиугольник в правой мозаике. Обе мозаики имеют одинаковую структуру решетки, которая демонстрируется апплетом. Теорема Пифагора доказана после удаления двух треугольников из каждого из шестиугольников.
Доказательство № 39
(Дж. Барри Саттон, The Math Gazette , v 86, n 505, март 2002 г., стр. 72.)
Пусть в ΔABC угол C = 90°. Как обычно, AB = c, AC = b, BC = a. Определим точки D и E на AB так, чтобы AD = AE = b.
По построению C лежит на окружности с центром A и радиусом b. Угол DCE опирается на диаметр и, следовательно, прямой: DCE = 90°. Отсюда следует, что BCD = ACE. Поскольку ΔACE равнобедренный, CEA = ACE.
Поскольку ΔACE равнобедренный, CEA = ACE.
Треугольники DBC и EBC имеют общий треугольник DBC. Кроме того, BCD = BEC. Следовательно, треугольники DBC и EBC подобны. У нас есть BC/BE = BD/BC, или
а / (с + b) = (с — b) / а.
И, наконец,
а² = с² — b²,
а² + b² = с².
Диаграмма напоминает доказательство Табита ибн Курры. Но они совершенно разные. Однако это и есть доказательство 14 из коллекции Элиши Лумиса. Кроме того, Лумис приводит две более ранние ссылки от 1925 и 1905 годов. С нарисованным кругом в центре точки А Лумис повторяет доказательство как 82 (со ссылками на 1887, 1880, 1859, 1792), а также перечисляет (в качестве доказательства 89) симметричная версия вышеуказанного:
Для прямоугольного треугольника ABC с прямым углом в точке C продлите AB в обоих направлениях так, чтобы AE = AC = b и BG = BC = a. Как и выше, теперь у нас есть подобные треугольники DBC и EBC. Кроме того, треугольники AFC и ACG также подобны, что приводит к двум тождествам:
a² = c² — b², и
б² = с² — а².
Вместо прямого использования одного из идентификаторов Лумис добавляет два:
2(а² + b²) = 2c²,
, который выглядит как графическое и алгебраическое излишество.
Доказательство #40
Это письмо Майкла Харди из Университета Толедо, опубликованное в The Mathematical Intelligencer в 1988 году. К нему следует относиться с недоверием.
Прямоугольный треугольник ABC с гипотенузой BC. Обозначим AC = x и BC = y. Тогда, когда C движется вдоль линии AC, x изменяется, а также y. Предположим, что x изменилось на небольшую величину dx. Затем y изменилось на небольшую величину dy. Треугольник CDE приближенно можно считать прямоугольным. Если предположить, что это так, то он имеет общий угол (D) с треугольником ABD и, следовательно, подобен последнему. Это приводит к пропорции x/y = dy/dx, или (разделяемому) дифференциальному уравнению
y·dy — x·dx = 0,
, что после интегрирования дает y² — x² = const. Значение константы определяется из начального условия для x = 0. Поскольку y(0) = a, y² = x² + a² для всех x.
Значение константы определяется из начального условия для x = 0. Поскольку y(0) = a, y² = x² + a² для всех x.
С этим доказательством легко спорить. Что означает, что треугольник приблизительно правильный? Могу предложить следующее объяснение. Треугольники ABC и ABD прямоугольные по построению. Имеем AB² + AC² = BC², а также AB² + AD² = BD² по теореме Пифагора. В терминах x и y теорема выглядит как
| x² + a² = y² | |
| (x + dx)² + a² = (y + dy)² |
, что дает 9 после вычитания
, y·dy — x·dx = (dx² — dy²)/2.
Для малых dx и dy dx² и dy² еще меньше, и ими можно пренебречь, что приводит к приблизительному значению y·dy — x·dx = 0.
Хитрость в виньетке Майкла заключается в том, что он пропускает вопрос приближения. Но можно ли действительно обосновать вывод, не полагаясь в первую очередь на теорему Пифагора? Как бы то ни было, мне очень нравится, что вездесущее уравнение y·dy — x·dx = 0 помещено в этот геометрический контекст.
Расширенная, но явно независимая версия этого доказательства была опубликована Майком Старингом ( Mathematics Magazine , V. 69, n. 1 (Feb., 1996), 45-46).
Предполагая Δx > 0 и обнаруживая подобные треугольники,
Δf / Δx = CQ/CD > CP/CD = CA/CB = x/f(x).
А также,
Δf / Δx = SD/CD < RD/CD = AD/BD = (x + Δx) / (f(x) + Δf) < x/f(x) + Δx/f(x).
Переход к пределу при стремлении Δx к 0 + , получаем
df/dx = x/f(x).
Случай ∆x < 0 рассматривается аналогично. Теперь решая дифференциальное уравнение получаем
f 2 (x) = x² + c.
Константа c находится из граничного условия f(0) = b: c = b². И доказательство завершено.
Доказательство #41
Создайте 3 масштабированные копии треугольника со сторонами a, b, c, умножив их на a, b и c по очереди. Соедините вместе три подобных треугольника, полученных таким образом, чтобы сформировать прямоугольник, верхняя сторона которого равна a² + b², а нижняя сторона равна c².
Дополнительные сведения и модификации см. на отдельной странице.
Доказательство № 42
Доказательство основано на той же диаграмме, что и № 33 [Pritchard, p. 226-227].
Площадь треугольника, очевидно, равна rp, где r — внутренний радиус, а p = (a + b + c)/2 — полупериметр треугольника. Из диаграммы гипотенуза c = (a — r) + (b — r), или r = p — c. Затем площадь треугольника вычисляется двумя способами:
р(р — с) = ab/2,
, что эквивалентно
(а + b + с)(а + b — с) = 2ab,
или
(а + b)² — c² = 2ab.
И, наконец,
а² + b² — с² = 0.
Доказательство принадлежит Джеку Оливеру и первоначально было опубликовано в Mathematical Gazette 81 (март 1997 г.), стр. 117-118.
Мацей Мадерек сообщил мне, что такое же доказательство появилось в польском издании Sladami Pitagorasa 1988 года Щепана Еленского:
Еленски приписывает доказательство Меллманну, не указывая ни источника, ни даты.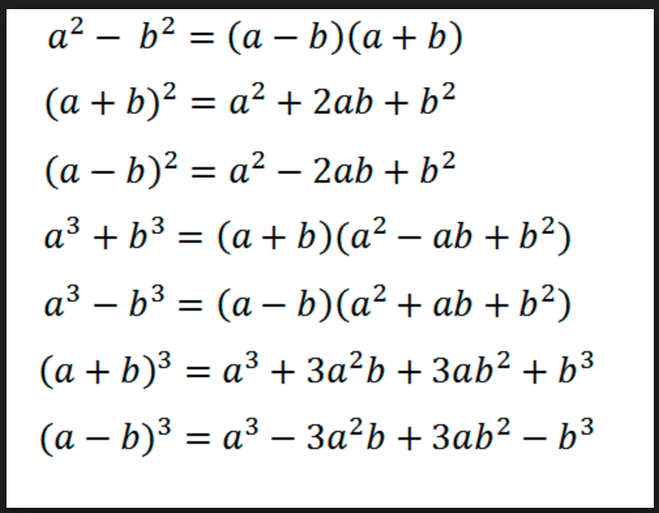
Джон Ф. Ригби сделал соответствующее наблюдение в 1996 г. (WALMATO Conference, University of Wales, Gergynog, 1996). Его обозначения ясны из диаграммы.
Вычисление площади треугольника двумя способами дает (r+x)(r+y)=r(2r+2x+2y), что можно упростить до
r² + rx + ry = ху
, который преобразуется в (r+x)² + (r+y)² = (x+y)² путем прибавления x² + y² к обеим сторонам.
Доказательство № 43
Ларри Хен [Pritchard, p. 229 и Math Gazette].
Примените теорему о силе точки к диаграмме выше, где сторона a служит касательной к окружности радиуса b: (c — b)(c + b) = a². Результат следует сразу.
(Конфигурация здесь, по сути, такая же, как и в доказательстве № 39. Вызов теоремы о силе точки можно рассматривать как кратчайший путь к аргументу в доказательстве № 39. Кроме того, это в точности доказательство XVI Б. Ф. Янни и Дж. А. Колдерхед, 9 лет0576 Am Math Monthly , т. 3, н. 12 (1896), 299-300. )
)
Джон Молокач предложил модификацию на основе следующей схемы:
Из подобия треугольников a/b = (b + c)/d, так что d = b(b + c)/a. Четырехугольник слева — воздушный змей со сторонами b и d и площадью 2bd/2 = bd. Прибавив к этому площадь маленького треугольника (ab/2), получим площадь большого треугольника — (b + c)d/2:
бд + аб/2 = (б + в)д/2
, что упрощается до
ab/2 = (c — b)d/2 или ab = (c — b)d.
Теперь используем формулу для d:
ab = (c — b)d = (c — b)(c + b)b/a.
Деление на b и умножение на a дает a² = c² — b². Этот вариант очень близок к Доказательству №82, но с другой мотивацией.
Наконец, рассуждение показывает, что площадь кольца (кольца), ограниченного окружностями радиусов b и c > b; равно πa², где a² = c² — b². а — половина длины касательной к внутренней окружности, заключенной внутри внешней окружности.
Доказательство #44
Следующее доказательство, относящееся к #39, было представлено Адамом Роузом (23 сентября 2004 г. )
)
Начните с двух одинаковых прямоугольных треугольников: ABC и AFE, БЭ и КФ. Отметьте D на AB и G на продолжении AF, так что
BC = BD = FG (= EF).
(Дальнейшие обозначения см. на диаграмме выше.) ΔBCD равнобедренный. Следовательно, ∠BCD = p/2 — α/2. Поскольку угол C прямой,
∠ACD = p/2 — (p/2 — α/2) = α/2.
Поскольку ∠AFE является внешним по отношению к ΔEFG, ∠AFE = ∠FEG + ∠FGE. Но ΔEFG тоже равнобедренный. Таким образом,
∠ВОЗРАСТ = ∠FGE = α/2.
Теперь у нас есть две прямые, CD и EG, пересекаемые CG с двумя чередующимися внутренними углами, ACD и AGE, равными. Следовательно, CD||EG. Треугольники ACD и AGE подобны, причем AD/AC = AE/AG:
b/(c — a) = (c + a)/b,
и следует теорема Пифагора.
Доказательство #45
Это доказательство принадлежит Дугласу Роджерсу, который наткнулся на него в ходе своего исследования истории китайской математики.
Доказательство представляет собой вариант №33, №34 и №42. Доказательство проводится в два этапа. Во-первых, как видно из
Доказательство проводится в два этапа. Во-первых, как видно из
тождество Лю Хуэй (см. также Математика в Китае)
а + b = с + d,
где d — диаметр окружности, вписанной в прямоугольный треугольник со сторонами a и b и гипотенузой c. Основываясь на этом и переставляя части двумя способами, мы получаем другое доказательство без слов теоремы Пифагора:
Доказательство #46
Это доказательство принадлежит Тао Тонгу ( Учитель математики , февраль 1994 г., Читательские размышления). Я узнал об этом благодаря добрым услугам Дугласа Роджерса, который также привлек мое внимание к Доказательствам № 47, № 48 и № 49. По духу доказательство напоминает доказательство №32.
Пусть ABC и BED равные прямоугольные треугольники, с E на AB. Мы собираемся оценить площадь ΔABD двумя способами:
Площадь (ΔABD) = BD·AF/2 = DE·AB/2.
Используя обозначения, указанные на диаграмме, получаем c(c — x)/2 = b·b/2. x = CF можно найти, заметив подобие (BD AC) треугольников BFC и ABC:
x = CF можно найти, заметив подобие (BD AC) треугольников BFC и ABC:
х = а²/с.
Две формулы легко объединяются в тождество Пифагора.
Доказательство #47
Это доказательство, принадлежащее старшекласснику Джону Кавамуре, было представлено Крисом Дэвисом, его учителем геометрии в школе Head-Rouce, Окленд, Калифорния (учитель математики , апрель 2005 г., с. 518.)
Конфигурация практически идентична Доказательству №46, но на этот раз нас интересует площадь четырехугольника ABCD. Обе его перпендикулярные диагонали имеют длину c, так что его площадь равна c²/2. С другой стороны,
| c²/2 | = Area(ABCD) |
| = Area(BCD) + Area(ABD) | |
| = a·a/2 + b·b/2 |
Умножение на 2 дает желаемый результат.
Доказательство #48
(WJ Dobbs, The Mathematical Gazette , 8 (1915-1916), стр. 268.)
268.)
На схеме два прямоугольных треугольника — ABC и ADE — равны и E расположен на AB. Как и в доказательстве президента Гарфилда, мы оцениваем площадь трапеции ABCD двумя способами:
| Площадь (ABCD) | = Площадь (AECD) + Площадь (BCE) |
| = c·c/2 + a(b — a)/2, |
, где, как и в доказательстве №47, c·c — произведение двух перпендикулярных диагоналей четырехугольника AECD. С другой стороны,
| Площадь(ABCD) | = AB·(BC + AD)/2 |
| = b(a + b)/2. |
Объединяя два числа, мы получаем c²/2 = a²/2 + b²/2, или, после умножения на 2, c² = a² + b².
Доказательство № 49
В предыдущем доказательстве мы можем поступить немного иначе. Заполните квадрат на сторонах AB и AD двух треугольников. Его площадь с одной стороны b², а с другой
| b² | = Площадь (ABMD) |
| = Площадь (AECD) + Площадь (CMD) + Площадь (BCE) | |
| 7 = b/b/) 2 + a(b — a)/2 | |
| = c²/2 + b²/2 — a²/2, |
, что соответствует той же идентичности, что и раньше.
Дуглас Роджерс, наблюдавший взаимосвязь между доказательствами 46-49, также заметил, что квадрат можно было бы нарисовать на меньших катетах двух треугольников, если бы второй треугольник был нарисован в «нижней» позиции, как в доказательствах 46 и 47. В этом случае мы снова будем оценивать площадь четырехугольника ABCD двумя способами. Со ссылкой на вторую из диаграмм выше,
| c²/2 | = Площадь (ABCD) |
| = Площадь (EBCG) + Площадь (CDG) + Площадь (AED) a)/2 | |
| = a²/2 + b²/2, |
, как хотелось бы.
Он также указал, что можно представить себе, что один из прямоугольных треугольников скользит из своего положения в доказательстве №46 в положение в доказательстве №48, так что его короткая сторона скользит вдоль длинной стороны другого треугольника. В любом промежуточном положении находится четырехугольник с равными и перпендикулярными диагоналями, так что для всех положений можно построить доказательства, аналогичные приведенным выше. Треугольник всегда остается внутри квадрата со стороной b — длиной длинной стороны двух треугольников. Теперь мы также можем представить, как треугольник ABC скользит внутри этого квадрата. Что приводит к доказательству, которое напрямую обобщает № 49.и включает конфигурации доказательств 46-48. Смотри ниже.
Треугольник всегда остается внутри квадрата со стороной b — длиной длинной стороны двух треугольников. Теперь мы также можем представить, как треугольник ABC скользит внутри этого квадрата. Что приводит к доказательству, которое напрямую обобщает № 49.и включает конфигурации доказательств 46-48. Смотри ниже.
Доказательство #50
Площадь большого квадрата KLMN равна b². Квадрат разбит на 4 треугольника и один четырехугольник:
| b² | = Площадь (KLMN) |
| = Площадь (AKF) + Площадь (FLC) + Площадь (CMD) + Площадь (ДНК) + Площадь (AFCD) | 9y|
| = [y(a+x) + b(a+y) — y(a+x) — x(b-y) — a·a + (b-a-y)b + x(b-y) + c²] /2 | |
| = [b(a+y) — a·a + b·b — (a+y)b + c²]/2 | |
| = b²/2 — a²/2 + с²/2. |
Это неинтересный вывод, но он показывает, что при столкновении с задачей упрощения алгебраических выражений умножение всех членов для удаления всех круглых скобок может быть не лучшей стратегией. В этом случае, однако, есть даже лучшая стратегия, которая полностью избегает длительных вычислений. По предложению Дугласа Роджерса дополните каждый из четырех треугольников соответствующим прямоугольником:
В этом случае, однако, есть даже лучшая стратегия, которая полностью избегает длительных вычислений. По предложению Дугласа Роджерса дополните каждый из четырех треугольников соответствующим прямоугольником:
Четыре прямоугольника всегда отсекают квадрат размера a, так что их общая площадь равна b² — a². Таким образом, мы можем закончить доказательство, как и в других доказательствах этой серии:
b² = c²/2 + (b² — a²)/2.
Доказательство #51
(W. J. Dobbs, The Mathematical Gazette , 7 (1913-1914), стр. 168.)
Этот любезно предоставлен Дугласом Роджерсом из его обширной коллекции. Как и в Доказательстве №2, треугольник повернут на 90 градусов вокруг одного из его углов, так что угол между гипотенузами в двух положениях прямой. Полученная форма площади b² затем разбивается на два прямоугольных треугольника с длинами сторон (c, c) и (b — a, a + b) и площадями c²/2 и (b — a)(a + b)/2 = (б² — а²)/2:
b² = c²/2 + (b² — a²)/2.
Дж. Эллиот добавляет морщинку в доказательство, переворачивая один из треугольников:
Опять же, площадь можно вычислить двумя способами:
ab/2 + ab/2 + b(b — a) = c²/2 + (b — a)(b + a)/2,
, что сокращается до
b² = c²/2 + (b² — a²)/2,
и, в конечном счете, к пифагорейской идентичности.
Доказательство #52
Это доказательство, обнаруженное старшеклассником Джейми де Лемосом ( Учитель математики , 88 (1995), стр. 79.), было процитировано Ларри Хеном ( Учитель математики , 90 (1997), стр. 438-441.)
С одной стороны площадь трапеции равна
(2а + 2б)/2·(а + б)
и с другой,
2a·b/2 + 2b·a/2 + 2·c²/2.
Приравнивание двух дает a² + b² = c².
Доказательство тесно связано с доказательством президента Гарфилда.
Доказательство #53
Ларри Хен также опубликовал следующее доказательство ( Учитель математики , 88 (1995), стр. 168.):
168.):
Продлите катет AC прямоугольного треугольника ABC до D так, чтобы AD = AB = c, как показано на рисунке. В точке D проведите перпендикуляр к CD. В точке А проведите биссектрису угла BAD. Пусть две прямые пересекаются в E. Наконец, пусть EF перпендикулярна CF.
По этой конструкции треугольники ABE и ADE имеют общую сторону AE, две другие стороны равны: AD = AB, а также углы, образованные этими сторонами: ∠BAE = ∠DAE. Следовательно, треугольники ABE и ADE равны по SAS. Отсюда угол АВЕ прямой.
Отсюда следует, что в прямоугольных треугольниках ABC и BEF углы ABC и EBF в сумме дают 90°. Таким образом,
∠ABC = ∠BEF и ∠BAC = ∠EBF.
Два треугольника подобны, поэтому
х/а = и/б = у/с.
Но, EF = CD, или x = b + c, что в сочетании с приведенной выше пропорцией дает
u = b(b + c)/a и y = c(b + c)/a.
С другой стороны, y = u + a, что приводит к
c(b + c)/a = b(b + c)/a + a,
, что легко упростить до c² = a² + b².
Доказательство #54k
Позже ( Учитель математики , 90 (1997), стр. 438-441.) семейство доказательств, которое для различных значений параметра включало его старое доказательство, а также № 41. Ниже я предлагаю упрощенный вариант, вдохновленный работой Ларри.
Чтобы воспроизвести существенный момент доказательства № 53, т. е. имея прямоугольный треугольник ABE и еще один BEF, подобный ΔABC, мы можем просто разместить ΔBEF со сторонами ka, kb, kc для некоторого k, как показано на рис. диаграмма. Чтобы диаграмма имела смысл, мы должны ограничить k так, чтобы ka ≥ b. (Это гарантирует, что D не опустится ниже A.)
Теперь площадь прямоугольника CDEF можно вычислить непосредственно как произведение его сторон ka и (kb + a) или как сумму площадей треугольников BEF, АВЕ, АВС и АДЭ. Таким образом, мы получаем
ka·(kb + a) = ka·kb/2 + kc·c/2 + ab/2 + (kb + a)·(ka — b)/2,
, который после упрощения сокращается до
а² = с²/2 + а²/2 — b²/2,
, что всего на один шаг меньше пифагорейского утверждения.
Доказательство работает для любого значения k, удовлетворяющего условию k ≥ b/a. В частности, при k = b/a мы получаем доказательство №41. Далее, k = (b + c)/a приводит к доказательству №53. Конечно, мы получили бы тот же результат, представив площадь трапеции AEFB двумя способами. Для k = 1 это привело бы к доказательству президента Гарфилда.
Очевидно, что работа с трапецией менее ограничительна и работает при любом положительном значении k.
Доказательство #55
Следующее обобщение теоремы Пифагора принадлежит У. Дж. Хазарду ( Am Math Monthly , v 36, n 1, 1929, 32-34). Доказательство представляет собой небольшое упрощение опубликованного.
Пусть слева изображен параллелограмм ABCD, вписанный в параллелограмм MNPQ. Нарисуйте BK||MQ и AS||MN. Пусть они пересекаются по Y. Тогда
Площадь (ABCD) = Площадь (QAYK) + Площадь (BNSY).
Ссылка на доказательство №9 показывает, что это верное обобщение теоремы Пифагора. Диаграмма доказательства № 9 получается, когда оба параллелограмма становятся квадратами.
Диаграмма доказательства № 9 получается, когда оба параллелограмма становятся квадратами.
Доказательство проходит в 4 этапа. Сначала вытяните линии, как показано ниже.
Тогда первым шагом будет отметить, что параллелограммы ABCD и ABFX имеют равные основания и высоты, а значит, и равные площади (Евклид I.35 На самом деле они хорошо равноразложимы). По той же причине параллелограммы ABFX и YBFW также имеют равные области. Это шаг 2. На шаге 3 обратите внимание, что параллелограммы SNFW и DTSP имеют равные площади. (Это связано с тем, что параллелограммы DUCP и TENS равны, а точки E, S, H лежат на одной прямой. Тогда Евклид I.43 подразумевает равные площади параллелограммов SNFW и DTSP). Наконец, параллелограммы DTSP и QAYK полностью равны.
(Есть динамическая версия доказательства.)
Доказательство № 56
Более ста лет назад Американский математический ежемесячник опубликовал серию коротких заметок, в которых перечислялось множество доказательств теоремы Пифагора. Авторы, Б. Ф. Янни и Дж. А. Колдерхед, приложили дополнительные усилия, подсчитывая и классифицируя доказательства различных вкусов. Это и следующее доказательство — числа V и VI из их коллекции ( Am Math Monthly , т. 3, № 4 (1896), 110-113) дают образец их основательности. Основываясь на диаграмме ниже, они насчитали целых 4864 различных доказательства. Образец их работы я разместил на отдельной странице.
Авторы, Б. Ф. Янни и Дж. А. Колдерхед, приложили дополнительные усилия, подсчитывая и классифицируя доказательства различных вкусов. Это и следующее доказательство — числа V и VI из их коллекции ( Am Math Monthly , т. 3, № 4 (1896), 110-113) дают образец их основательности. Основываясь на диаграмме ниже, они насчитали целых 4864 различных доказательства. Образец их работы я разместил на отдельной странице.
Доказательство #57
Немного по-другому рассматривая треугольник, теперь продолжая его стороны, а не пересекая их, Б. Ф. Янни и Дж. А. Колдерхед пришли к практически той же диаграмме:
Следуя методу, использованному в предыдущем доказательстве, они снова насчитали 4864 различных доказательства пифагорейского предложения.
Доказательство № 58
(Б. Ф. Янни и Дж. А. Колдерхед, Am Math Monthly , т. 3, № 6/7 (1896), 169–171, № VII)
Пусть ABC образует прямой угол с C. Произведите BC, получив BD = AB. Присоединяйтесь к АД. Из Е, середины CD, проведите перпендикуляр, пересекающий AD в точке F. Соедините BF. DADC похож на DBFE. Следовательно.
Произведите BC, получив BD = AB. Присоединяйтесь к АД. Из Е, середины CD, проведите перпендикуляр, пересекающий AD в точке F. Соедините BF. DADC похож на DBFE. Следовательно.
AC/BE = CD/EF.
Но CD = BD — BC = AB — BC. Используя этот
| БЭ | = БК + CD/2 |
| BE | = BC + (AB — BC)/2 |
| = (AB + BC)/2 |
и EF = AC/
. Так что
АС·АС/2 = (АВ — ВС)·(АВ + ВС)/2,
, что, конечно же, приводит к AB² = AC² + BC².
(Как мы видели в доказательстве 56, Янни и Колдерхед любят использовать конфигурацию всеми возможными способами. Что касается диаграммы настоящего доказательства, они отмечают, что треугольники BDF, BFE и FDE подобны, что позволяет им вывести множество пропорций между различными элементами конфигурации. Они ссылаются на свой подход в доказательстве 56, чтобы предположить, что и здесь существует множество доказательств, основанных на одной и той же диаграмме. Они предоставляют фактический подсчет читателю.)
Они предоставляют фактический подсчет читателю.)
Доказательство № 59
(Б. Ф. Янни и Дж. А. Колдерхед, Am Math Monthly , т. 3, № 12 (1896), 299-300, № XVII)
Пусть ABC образует прямой угол в точке C, а BC = a — кратчайшая из двух сторон. Используя C в качестве центра и a в качестве радиуса, опишите окружность. Пусть D будет пересечением AC с окружностью, а H — другим, полученным путем создания AC вне C, E — пересечением AB с окружностью. Проведите CL перпендикулярно AB. L — середина BE.
По теореме о пересекающихся хордах,
АХ·АД = АВ·АЕ.
Другими словами,
(b + а)(b — а) = с(с — 2·BL).
Теперь прямоугольные треугольники ABC и BCL имеют общий угол в точке B и, следовательно, подобны, откуда
БЛ/ВС = ВС/АВ,
, так что BL = a²/c. Объединив все вместе видим, что
b² — a² = c(c — 2a²/c)
и, в конечном счете, пифагорейское тождество.
Примечание
Обратите внимание, что доказательство не выполняется для равнобедренного прямоугольного треугольника. Для учета этого случая авторы предлагают использовать обычный метод теории пределов. Я совсем не уверен, что такое «обычный метод» имели в виду авторы. Может быть, лучше всего подвергнуть этот случай сократовским рассуждениям, которые просты и не требуют теории пределов. Если случай в любом случае исключительный, то почему бы и не относиться к нему как к таковому.
Для учета этого случая авторы предлагают использовать обычный метод теории пределов. Я совсем не уверен, что такое «обычный метод» имели в виду авторы. Может быть, лучше всего подвергнуть этот случай сократовским рассуждениям, которые просты и не требуют теории пределов. Если случай в любом случае исключительный, то почему бы и не относиться к нему как к таковому.
Доказательство № 60
(Б. Ф. Янни и Дж. А. Колдерхед, Am Math Monthly , т. 3, н. 12 (1896), 299-300, #XVIII)
Идея та же, что и раньше (доказательство №59), но теперь круг имеет радиус b, длину более длинного катета. Изготовив стороны как на схеме, получим
АВ·ВК = BJ·BF,
или
с·ВК = (b — а)(b + а).
BK, то есть AK — c, можно найти из подобия треугольников ABC и AKH: AK = 2b²/c.
Обратите внимание, что, как и предыдущее доказательство, это тоже не работает в случае равнобедренного треугольника.
Доказательство № 61
(Б. Ф. Янни и Дж. А. Колдерхед, Am Math Monthly , т. 3, № 12 (1896), 299-300, № XIX)
Ф. Янни и Дж. А. Колдерхед, Am Math Monthly , т. 3, № 12 (1896), 299-300, № XIX)
Это третье доказательство в семействе доказательств, использующих теорему о пересекающихся хордах. Радиус окружности теперь равен высоте от прямого угла C. В отличие от двух других доказательств здесь нет исключительных случаев. Ссылаясь на схему,
AD² = AH·AE = b² — CD²,
BD² = BK·BL = a² — CD²,
2AD·BD = 2CD².
Сложение трех дает тождество Пифагора.
Доказательство #62
В этом доказательстве, принадлежащем Флору ван Ламоэну, используются некоторые из многих свойств симедианной точки. Прежде всего известно, что в любом треугольнике ABC симедиана точки K имеет барицентрические координаты, пропорциональные квадратам длин сторон треугольника. Отсюда следует соотношение между площадями треугольников ABK, BCK и ACK:
Площадь (BCK) : Площадь (ACK) : Площадь (ABK) = a² : b² : c².
Далее, в прямоугольном треугольнике точка симедианы является серединой высоты гипотенузы. Следовательно, если угол при С прямой, а СН является рассматриваемой высотой (а также симедианой), то АК служит медианой ΔACH, а BK — медианой ΔBCH. Вспомните теперь, что медиана делит треугольник на две равные части. Таким образом,
Следовательно, если угол при С прямой, а СН является рассматриваемой высотой (а также симедианой), то АК служит медианой ΔACH, а BK — медианой ΔBCH. Вспомните теперь, что медиана делит треугольник на две равные части. Таким образом,
Площадь (ACK) = Площадь (AKH) и
Площадь (BCK) = Площадь (BKH).
Но
| Площадь (ABK) | = Площадь (AKH) + Площадь (BKH) |
| = Площадь (ACK) + Площадь (BCK), |
, так что действительно = k·c·c a² + k·b², для некоторого k > 0; и отсюда следует пифагорейское тождество.
Флор также предложил другой подход к использованию свойств симедианной точки. Обратите внимание, что симметричная точка является центром тяжести трех грузов на A, B и C величин a², b² и c² соответственно. В прямоугольном треугольнике основание высоты из C является центром тяжести весов на B и C. Тот факт, что точка симедианы является серединой этой высоты, теперь показывает, что a² + b² = c².
Доказательство #63
Это еще одно доказательство от Флор ван Ламоен; Флор пришел к доказательству с помощью теоремы Боттемы. Однако на самом деле теорема не нужна для проведения доказательства.
На рисунке M — центр квадрата ABA’B’. Треугольник AB’C’ является вращением треугольника ABC. Итак, мы видим, что B’ лежит на C’B». Точно так же A’ лежит на A»C». И AA», и BB» равны a + b. Таким образом, расстояние от M до A»C», а также до B’C’ равно (a + b)/2. Это дает
| Площадь (AMB’C’) | = Площадь (MAC’) + Площадь (MB’C’) |
| = (a + b)/2 · b/2 + (a + b) /2 · a/2 | |
| = a²/4 + ab/2 + b²/4. |
Но также:
| Площадь (AMB’C’) | = Площадь (AMB’) + Площадь (AB’C’) |
| = c²/4 + ab/2. |
Это дает a²/4 + b²/4 = c²/4 и теорему Пифагора.
Базовая конфигурация была использована Б. Ф. Янни и Дж. А. Колдерхедом ( Am Math Monthly , v.4, n 10, (1987), 250-251) для получения нескольких доказательств на основе следующих диаграмм
Ни одно из их доказательств не использовало центральность точки М.
Доказательство № 64
И еще одно доказательство Флор ван Ламоэн; в типично математическом духе, на этот раз Флор сводит общее утверждение к частному случаю, случаю прямоугольного равнобедренного треугольника. Последняя была рассмотрена Сократом и показана независимо от общей теоремы.
FH делит квадрат ABCD со стороной a + b на два равных четырехугольника, ABFH и CDHF. Первый состоит из двух равных треугольников с площадью ab/2 и равнобедренного прямоугольного треугольника с площадью c²/2. Последний составлен из двух равнобедренных прямоугольных треугольников: площади одного a²/2, другого b²/2, и прямоугольного треугольника, площадь которого (по вводному замечанию) равна ab! Удалив равные площади двух четырехугольников, мы получим тождество площадей: a²/2 + b²/2 = c²/2.
Идея доказательства Сократа о том, что площадь равнобедренного прямоугольного треугольника с гипотенузой k равна k²/4, использовалась и раньше, хотя и неявно. Например, Лумис, № 67 (со ссылкой на издание 1778 года Э. Форри Curiosities Geometrique [орфография Лумиса]) опирается на следующую диаграмму:
Треугольник ABC лежит прямо в точке C, а ABD равнобедренный. (Точка D — середина полуокружности с диаметром AB, так что CD — биссектриса прямого угла ACB.) AA’ и BB’ перпендикулярны CD, а AA’CE и BB’CF — квадраты; в частности, EF ⊥ CD.
Треугольники AA’D и DB’B (с равными гипотенузами и дополнительными углами при D) равны. Отсюда следует, что AA’ = B’D = A’C = CE = AE. И аналогично для отрезков, равных B’C. Далее, CD = B’C + B’D = CF + CE = EF.
| Площадь (ADBC) | = Площадь (ADC) + Площадь (DBC) |
| Площадь (ADBC) | = CD×AA’/2 + CD×BB’/2 |
| Площадь (ADBC) ) | = CD×EF/2.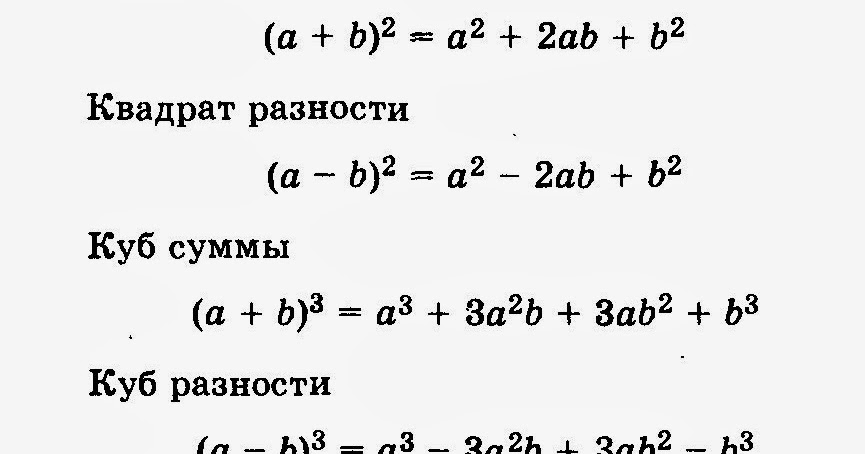 |
С другой стороны,
| Площадь (ABFE) | = EF×(AE + BF)/2 |
| Площадь (ADBC) | = CD×AA’/2 + CD×BB’/2 |
| Площадь (ADBC) ) | = CD×EF/2. |
Таким образом, два четырехугольника имеют ту же площадь и ΔABC, что и пересечение. Удалив ΔABC, мы видим, что
Площадь (ADB) = Площадь (ACE) + Площадь (BCF).
Доказательство сводится к случаю Сократа, поскольку последнее тождество эквивалентно c²/4 = a²/4 + b²/4.
Совсем недавно Буй Куанг Туан выдвинул другой аргумент:
Исходя из вышеизложенного, площадь (BA’D) = площадь (BB’C) и площадь (AA’D) = площадь (AB’C). Кроме того, площадь (AA’B) = площадь (AA’B’), для AA’||BB’. Отсюда следует, что площадь (ABD) = площадь (AA’C) + площадь (BB’C) с теми же последствиями.
Доказательство № 65
Это и следующее доказательство также принадлежат Флору ван Ламоэну. Оба основаны на следующей лемме, которая, по-видимому, обобщает теорему Пифагора: образуйте квадраты на сторонах ортогональный четырехугольник . Квадраты делятся на две пары противоположных квадратов. Тогда суммы площадей квадратов в двух парах равны.
Оба основаны на следующей лемме, которая, по-видимому, обобщает теорему Пифагора: образуйте квадраты на сторонах ортогональный четырехугольник . Квадраты делятся на две пары противоположных квадратов. Тогда суммы площадей квадратов в двух парах равны.
Доказательство основано на дружеской связи между треугольником и его боковыми треугольниками: высота треугольника через прямой угол, выходящий за вершину, является медианой бокового треугольника под прямым углом. Имея это в виду, обратите внимание, что два параллелограмма на левом рисунке имеют не только общее основание, но и равные высоты. Следовательно, они имеют равные площади. Используя сдвиг, мы видим, что квадраты под рукой разбиваются на пары прямоугольников одинаковой площади, которые можно комбинировать двумя способами, что доказывает лемму.
Теперь для доказательства представьте две смежные вершины четырехугольника, смыкающиеся к точке пересечения диагоналей. В пределе четырехугольник станет прямоугольным треугольником, а один из квадратов сожмется в точку. Из оставшихся трех квадратов два дадут в сумме третий.
Из оставшихся трех квадратов два дадут в сумме третий.
Доказательство № 66
(Флор Ван Ламоен). Лемму из доказательства 65 можно использовать по-другому:
Пусть будет два квадрата: APBM c и C 1 M c C 2 Q с общей вершиной M c . Поворот на 90° в положительном направлении вокруг M c перемещает C 1 M c в C 2 M c и BM c в AM c . Это означает, что ΔBM c C 1 вращается в ΔAM c C 2 , так что AC 2 и BC 1 ортогональны. Четырехугольник ABC 2 C Таким образом, число 1 является ортогональным, и применима лемма: красные и синие квадраты в сумме дают одинаковую площадь. Важно отметить, что сумма площадей исходных квадратов APBM c и C 1 M c C 2 Q составляет половину этой величины.
Теперь предположим, что конфигурации таковы, что M c совпадает с точкой пересечения диагоналей. Из-за получившейся симметрии красные квадраты равны. Поэтому площади APBM c и C 1 M c C 2 Q составляют красный квадрат!
(Есть динамическая иллюстрация этого аргумента.)
Доказательство №67
Это доказательство прислала мне 14-летняя Сина Шиян из Сабзевара, Иран. Помимо описанной окружности, комбинация треугольников точно такая же, как в подслучае С. Броди в VI.31 Евклида. Однако подход Броуди, если его сделать явным, потребует аргументации, отличной от той, которую использует Сина. Итак, я считаю, что ее вывод хорошо подходит в качестве индивидуального доказательства.
Из концов гипотенузы AB опущены перпендикуляры AP и BK к касательной к описанной окружности ΔABC в точке C. Поскольку OC также перпендикулярен касательной, C является серединой KP. Отсюда следует, что
| Площадь(ACP) + Площадь(BCK) | = CP·AP/2 + CK·BK/2 |
| = [KP·(AP + BK)/2]/2 | |
= Площадь (АБКП)/2. |
Следовательно, площадь(ABC) также равна площади(ABKP)/2. Так что
Площадь (ACP) + Площадь (BCK) = Площадь (ABC)
Теперь все три треугольника подобны (так как они прямоугольные и имеют равные углы), поэтому их площади связаны как квадраты их гипотенуз, равные b, a и c соответственно. Отсюда следует теорема.
Я поместил оригинальный вывод Сины на отдельную страницу.
Доказательство #68
Теорема Пифагора является прямым следствием закона параллелограмма. Я благодарен Флору ван Ламоэну за то, что он обратил мое внимание на доказательство последнего без слов. Есть второе доказательство, которое я люблю еще больше.
Доказательство #69
Несколько доказательств, использующих практически одинаковую конфигурацию
прекрасно используют разные инструменты для достижения цели. Это вопрос того, что мы видим на этой диаграмме. Ниже приведены несколько вариантов, которые различаются точкой зрения и, как таковые, приводят к разным выводам.
Некоторые из них я разместил на отдельной странице.
Доказательство #70
Продолжим высоту CH до гипотенузы до D: CD = AB и рассмотрим площадь ортогонального четырехугольника ACBD (аналогично доказательствам 47-49). С одной стороны, его площадь равна половине произведения его диагоналей: c²/2 . С другой стороны, это сумма площадей двух треугольников, ACD и BCD. Опустим перпендикуляры DE и DF на точки AC и BC. Прямоугольник CEDF имеет стороны, равные DE, и DF, равные AC и BC соответственно, потому что, например, ΔCDE = ΔABC, так как оба прямые, имеют равные гипотенузы и углы. Отсюда следует, что
Площадь (CDA) = b² и
Площадь (CDB) = а²
, так что действительно c²/2 = a²/2 + b²/2.
Это доказательство 20 из коллекции Лумиса. В доказательстве 29 CH продолжается вверх до D, так что снова CD = AB. Снова площадь четырехугольника ACBD вычисляется двумя способами точно таким же образом.
Доказательство #71
Пусть D и E — точки на гипотенузе AB такие, что BD = BC и AE = AC. Пусть AD = x,DE = y,BE = z. Тогда AC = x + y, BC = y + z, AB = x + y + z. Тогда теорема Пифагора эквивалентна алгебраическому тождеству
(у + г)² + (х + у)² = (х + у + г)².
Что упрощается до
у² = 2xz.
Чтобы убедиться, что последнее верно, вычислите мощность точки A по отношению к окружности B(C), т. е. окружности с центром в B и проходящей через C, двумя способами: сначала как квадрат касательной AC, а затем как продукт AD·AL:
(х + у)² = х (х + 2 (у + г)),
, что также упрощается до y² = 2xz.
Это алгебраическое доказательство 101 из коллекции Лумиса. Его динамическая версия доступна отдельно.
Доказательство #72
Это геометрическое доказательство № 25 из коллекции Э. С. Лумиса, за которое он ссылается на более раннюю публикацию Дж. Верслуйса (1914 г.). Доказательство практически не требует пояснений, и добавление нескольких строк показывает способ сделать его формальным.
Верслуйса (1914 г.). Доказательство практически не требует пояснений, и добавление нескольких строк показывает способ сделать его формальным.
Мишель Ласверньяс придумал еще более прозрачную перестановку (справа внизу):
Эти два получаются друг из друга путем поворота каждого из квадратов на 180° вокруг его центра.
Также доступна динамическая версия.
Доказательство #73
Это доказательство принадлежит weininjieda из Инкоу, Китай, который планирует стать учителем математики, китайского языка и истории. Оно было включено как алгебраическое доказательство № 50 в сборник Э. С. Лумиса, для чего он ссылается на более раннюю публикацию Дж. Верслуйса (1914 г.), где доказательство приписывается Сесилу Хокинсу (1909 г.) из Англии.
Пусть CE = BC = a, CD = AC = b, F — пересечение DE и AB.
ΔCED = ΔABC, следовательно, DE = AB = c. Так как AC BD и BE AD,ED AB, как третья высота в ΔABD. Сейчас с
Сейчас с
Площадь (ΔABD) = Площадь (ΔABE) + Площадь (ΔACD) + Площадь (ΔBCE)
получаем
c(c + EF) = EF·c + b² + a²,
, что подразумевает тождество Пифагора.
Доказательство #74
Следующее доказательство методом вскрытия принадлежит персидскому математику и астроному 10 -го -го века Абул Вафа (Абу’л-Вафа, а также Абу аль-Вафа) аль-Бузджани. Два равных квадрата легко соединяются в один больший квадрат способом, известным еще Сократу. Метод Абул Вафа работает, если квадраты разные. Квадраты размещены так, чтобы иметь общий угол и две боковые линии. Их разрезают и собирают, как показано на рисунке. Рассечение большого квадрата почти такое же, как у Лю Хуэя. Однако меньший квадрат разрезается совершенно по-другому. Разложение получившегося квадрата практически такое же, как и в Доказательстве №3.
Также доступна динамическая версия.
Доказательство #75
Это дополнительное применение формулы Герона к доказательству теоремы Пифагора. Хотя он намного короче первого, я тоже поместил его в отдельный файл, чтобы облегчить сравнение.
Хотя он намного короче первого, я тоже поместил его в отдельный файл, чтобы облегчить сравнение.
Идея достаточно проста: формула Герона применима к равнобедренному треугольнику, изображенному на рисунке ниже.
Доказательство #76
Это геометрическое доказательство № 27 из коллекции Э. С. Лумиса. Согласно Лумису, он получил доказательство в 1933 г. от Дж. Адамса, Гаага. Лумис делает замечание, указывающее на уникальность этого доказательства среди других рассечений тем, что все прямые либо параллельны, либо перпендикулярны сторонам данного треугольника. Что странно, так как, скажем, доказательство № 72 выполняет тот же подвиг, но с меньшим количеством строк. Что еще более удивительно, последний также включен в сборник Э. С. Лумиса как геометрическое доказательство № 25.
Необъяснимым образом Лумис делает ошибочное введение в построение, начиная с неправильного деления гипотенузы. Однако нетрудно догадаться, что точка, в которой построена работа, есть основание биссектрисы прямого угла.
Динамическая иллюстрация доступна на отдельной странице.
Доказательство #77
Это доказательство принадлежит знаменитому голландскому математику, астроному и физику Христиану Гюйгенсу (1629–169 гг.).5), опубликованный в 1657 году. Он был включен в сборник Лумиса как геометрическое доказательство № 31. Как и в Доказательстве № 69, основным инструментом в доказательстве является Евклидов I.41: если параллелограмм и треугольник имеют общее основание и находятся на одних и тех же параллелях (I.41), то площадь параллелограмма вдвое больше площади параллелограмма. треугольник.
Более конкретно,
| Площадь (ABML) | = 2 · Площадь (ΔABP) = Площадь (ACFG), и |
| Площадь (KMLS) | = 2·Площадь(ΔKPS), а |
| Площадь(BCED) | = 2·Площадь(ΔANB). |
Объединяя их с тем фактом, что ΔKPS = ΔANB, мы немедленно получаем утверждение Пифагора.
(Динамическая иллюстрация доступна на отдельной странице.)
Доказательство № 78
Это доказательство принадлежит выдающемуся голландскому математику Э. В. Дейкстре (1930–2002). Само доказательство, как и доказательство № 18, является обобщением доказательства № 6 и основано на той же диаграмме. Оба доказательства сводятся к варианту Евклида VI.31 для прямоугольных треугольников (с прямым углом C). Помимо доказательства, Дийкстра также нашел удивительно свежий взгляд на суть самой теоремы:
Если в треугольнике углы α, β, γ лежат против сторон длины a, b, c, то
знак (α + β — γ) = знак (a² + b² — c²),
где sign(t) — сигнум-функция.
Как и в Доказательстве №18, Дейкстра образует два треугольника ACL и BCN, подобных основанию ΔABC:
BCN = CAB и
ACL = CBA
, чтобы ACB = ALC = BNC. Детали и динамическая иллюстрация находятся на отдельной странице.
Доказательство № 79
На этой странице есть несколько доказательств, использующих теорему о пересекающихся хордах, особенно доказательства №№ 59, 60 и 61, где окружность, к хордам которой применяется теорема, имеет радиус, равный короткому катет ΔABC, длинный катет и высота от прямого угла соответственно. Книга Лумиса перечисляет их среди своего собрания алгебраических доказательств наряду с несколькими другими, которые выводят теорему Пифагора с помощью теоремы о пересекающихся хордах, примененной к хордам в причудливом разнообразии окружностей, добавленных к ΔABC. Александр Вайнберг из Unité de Recherches sur l’Enseignement des Mathématiques, Université Libre de Bruxelles, предложил вариант, который, кажется, заполняет упущение в этой серии доказательств. Конструкция также выглядит проще и естественнее, чем любая из перечисленных Лумисом. Какой сюрприз!
Книга Лумиса перечисляет их среди своего собрания алгебраических доказательств наряду с несколькими другими, которые выводят теорему Пифагора с помощью теоремы о пересекающихся хордах, примененной к хордам в причудливом разнообразии окружностей, добавленных к ΔABC. Александр Вайнберг из Unité de Recherches sur l’Enseignement des Mathématiques, Université Libre de Bruxelles, предложил вариант, который, кажется, заполняет упущение в этой серии доказательств. Конструкция также выглядит проще и естественнее, чем любая из перечисленных Лумисом. Какой сюрприз!
Подробнее см. на отдельной странице.
Доказательство #80
Доказательство, основанное на приведенной ниже диаграмме, было опубликовано в письме учителю математики (т. 87, № 1, январь 1994 г.) Дж. Гроссмана. Доказательство было обнаружено его учеником Дэвидом Хьюстоном, в то время восьмиклассником.
Я благодарен профессору Гроссману за то, что он обратил мое внимание на доказательство. Доказательство и обсуждение вынесены на отдельную страницу, но суть его такова.
Доказательство и обсуждение вынесены на отдельную страницу, но суть его такова.
Предположим, что две копии прямоугольного треугольника с катетами a и b и гипотенузой c расположены спиной к спине, как показано на левой диаграмме. Образованный таким образом равнобедренный треугольник имеет площадь S = c² sin(θ) / 2. На правой диаграмме две копии одного и того же треугольника соединены под прямым углом и вложены в прямоугольник с одной стороной, равной c. Каждый из треугольников имеет площадь, равную половине площади половины прямоугольника, из чего следует, что площади остальных равнобедренных треугольников также в сумме составляют половину площади прямоугольника, т. е. площадь равнобедренного треугольника на левой диаграмме. Сумма площадей двух меньших равнобедренных треугольников равна 9.0029
| S | = a² sin(π — θ) / 2 + b² sin(θ) / 2 | |||||||||||||
| = (a² + b²) sin(θ) / 2, | для 009048 грех (π — θ) = грех (θ). Поскольку две площади равны, а sin(θ) ≠ 0, для невырожденного треугольника a² + b² = c².
| Площадь (BCJK) | = BK × CA |
| = (b + a²/b) × b | |
| b² + | . |
Мы видим, что c² = Area(BCJK) = a² + b² завершая доказательство.
Доказательство № 82
Это доказательство было опубликовано в American Mathematical Monthly (v. 116, n. 8, 2009, October 2009, p. 687) с примечанием редактора: хотя это доказательство не кажутся широко известными, это новое открытие доказательства, которое впервые появилось в печати в [Loomis, стр. 26-27]. Доказательство было представлено Сан Ву Рю, учеником средней школы Карлайла, Карлайл, Пенсильвания.
Лумис берет на себя ответственность за доказательство, хотя редактор Monthly прослеживает его происхождение до статьи Б. Ф. Янни и Дж. А. Колдерхеда 1896 года ( Monthly , т. 3, стр. 65-67.)
Ф. Янни и Дж. А. Колдерхеда 1896 года ( Monthly , т. 3, стр. 65-67.)
Начертите AD, биссектрису угла A, и DE перпендикулярно AB. Пусть, как обычно, AB = c, BC = a и AC = b. Пусть CD = DE = х. Тогда BD = a — x и BE = c — b. Треугольники ABC и DBE подобны, что приводит к x/(a — x) = b/c или x = ab/(b + c). Но также (c — b)/x = a/b, что означает c — b = ax/b = a²/(b + c). Что приводит к (c — b)(c + b) = a² и тождеству Пифагора.
Доказательство #83
Это доказательство представляет собой небольшую модификацию доказательства, присланного мне Яном Стивенсом из Технологического университета Чалмерса и Гетеборгского университета. Доказательство на самом деле является обобщением Дейкстры и основано на расширении конструкции доказательства № 41.
| α + β > γ |
Подробную информацию можно найти на отдельной странице.
Доказательство #84
Элиша Лумис, я и, несомненно, многие другие считали и до сих пор считают, что никакое тригонометрическое доказательство теоремы Пифагора невозможно. Это убеждение проистекало из предположения, что любое такое доказательство будет основываться на самом фундаментальном из тригонометрических тождеств: sin²α + cos²α = 1 есть не что иное, как переформулировка собственно теоремы Пифагора. Теперь Джейсон Зимба показал, что теорему можно вывести из формул вычитания для 90 576 синуса 9.0577 и косинус без обращения к sin²α + cos²α = 1. Я с радостью признаю свою неправоту.
Доказательство Джейсона Зимбы находится на отдельной странице.
Доказательство #85
Буй Куанг Туан нашел способ вывести теорему Пифагора из теоремы о сломанной хорде.
Подробнее см. на отдельной странице.
Доказательство #86
Буй Куанг Туан также показал способ вывода теоремы Пифагора из теоремы Боттемы.
Подробнее см. на отдельной странице.
Доказательство #87
Джон Молокач предложил доказательство теоремы Пифагора, основанное на следующей диаграмме:
Если какое-либо доказательство заслуживает того, чтобы называться алгебраическим, то это доказательство. Подробности смотрите на отдельной странице.
Доказательство #88
Стюарт Андерсон дал еще один вывод теоремы Пифагора из теоремы о сломанной хорде. Доказательство иллюстрирует вписанная (и немного искаженная) Звезда Давида:
Подробнее см. на отдельной странице. Рассуждение примерно такое же, как и в Доказательстве № 79, но полученное с помощью теоремы о сломанной хорде.
Доказательство #89
Джон Молокач, преданный пифагорейец, нашел то, что он назвал Параллелограмм доказательством теоремы. Он основан на следующей схеме:
Подробнее см. на отдельной странице.
Доказательство #90
Джон также совершил ужасную ересь, придумав доказательство, основанное на решении дифференциального уравнения. После продолжительного обсуждения между Александром Гивенталем из Беркли, Уэйном Бишопом из Калифорнийского государственного университета, Джоном и мной было решено, что доказательство не содержит порочного круга, как все изначально ожидали.
После продолжительного обсуждения между Александром Гивенталем из Беркли, Уэйном Бишопом из Калифорнийского государственного университета, Джоном и мной было решено, что доказательство не содержит порочного круга, как все изначально ожидали.
Подробнее см. на отдельной странице.
Доказательство #91
Джон Молоках также заметил, что теорема Пифагора следует из формулы Гаусса о шнурках:
Подробнее см. на отдельной странице.
Доказательство #92
Доказательство Гаэтано Сперанца основано на следующей диаграмме
Подробную информацию и интерактивную иллюстрацию см. на отдельной странице.
Доказательство #93
Джорджио Феррарезе из Университета Турина, Италия, заметил, что доказательство Перигала, получившее высокую оценку за симметрию сечения квадрата на более длинном катете прямоугольного треугольника, допускает дальнейшую симметричную обработку. Его доказательство основано на следующей диаграмме
Его доказательство основано на следующей диаграмме
.
Подробнее см. на отдельной странице.
Доказательство #94
Так получилось, что производная правой части формулы Герона по одной из сторон равна нулю, когда две другие стороны перпендикулярны. Более того, приравнивая производную к нулю, сразу приходим к формуле Пифагора.
Подробности можно найти на отдельной странице.
Доказательство #95
Доказательство Буй Куанг Туана основано на конструкции, показанной ниже:
Подробности можно найти на отдельной странице.
Доказательство #96
Джон Молокач начал со следующей диаграммы
, из которых он вывел два доказательства. Подробности можно найти на отдельной странице.
Доказательство №97
Когда я уже начал думать, что принципиально новых доказательств не будет; к моему удивлению, Эдгардо Аландете из Колумбии предложил довольно простое и прямое доказательство путем вскрытия. Добавляю как «доказательство без слов»:
Добавляю как «доказательство без слов»:
У Эдгардо было несколько взглядов на свой подход, которые он резюмировал в двух файлах PDF: файл № 1 и файл № 2.
Доказательство #98
Джон Молокач придумал другое доказательство, доказательство без слов, основанное на следующей диаграмме:
Краткое пояснение см. на отдельной странице.
Джону также удалось вывести теорему из тождества с биномиальными коэффициентами, возведя в квадрат ряды синуса и косинуса Маклорена.
Доказательство № 99
Даниэль Хардиски опубликовал следующее доказательство в виде головоломки вскрытия. Вот как я передаю это:
Вы можете распечатать графику, вырезать части и попытаться сложить их вместе, чтобы сформировать больший квадрат. Решение находится на отдельной странице.
Доказательство #100
Джон Ариони опубликовал доказательство, в котором пифагорейское тождество возникает на пределе сходящегося геометрического ряда. Вот подсказка:
Вот подсказка:
Подробную информацию можно найти на отдельной странице.
Доказательство №101
На самом деле это обобщение теоремы Пифагора. Его опубликовал Дао Тхань Оай (Вьетнам).
Пусть CH c и BH b — две высоты nn ΔABC.
Тогда
BC 2 =AB×BH b + AC×CH c .
Теорема Пифагора получается, когда угол при А равен 90°. Я поместил простое доказательство в отдельный файл.
Доказательство №102
Это доказательство было сообщено мне Марсело Брафманом (Израиль). Э. Лумис, возможно, охарактеризовал его как алгебраическую разновидность, но я не нашел ничего подобного во всей его книге.
Доказательство основано на следующей схеме:
Вы можете сами разобраться, о чем идет речь. Объяснение можно найти в другом месте.
Доказательство #103
Тони Фостер, III, представил ряд доказательств, в которых использовалось свойство трапеций, установленное при доказательстве теоремы о коврах.
Одно из доказательств, например, основано на следующей диаграмме:
Важно отметить, что два синих треугольника на схеме имеют одинаковую площадь. Немного больше деталей, наряду с другими доказательствами, можно найти на отдельной странице.
Доказательство №104
Вот доказательство элегантного препарирования, принадлежащее А. Г. Самосвату.
Динамическая иллюстрация доступна на отдельной странице.
Доказательство #105
Несколько раз ранее (доказательства 22, 43, 71) теорема Пифагора выводилась из теоремы о силе точки. Вот еще один пример силы этой теоремы, придуманной Буй Куанг Туаном. Подход Буи иллюстрируется следующей диаграммой
Полный вывод можно найти на отдельной странице.
Доказательство #106
Буй Куанг Туан открыл элегантную лемму, из которой легко вывести теорему Пифагора: )$ и $AC$ перпендикулярны $BD.$ Обозначим через $[X]$ площадь формы $X.$ Тогда $\displaystyle\frac{[AED] + [BEC]}{2} = [AOB]. $
$
Доказательство леммы и вывод теоремы Пифагора можно найти на отдельной странице.
Доказательство #107
Тран Куанг Хунг нашел расширение теоремы Пифагора:
В $\Delta ABC $$AD,$$$BE,$$CF$ — высоты. Треугольники $BCX,$ $CEY,$ и $BFZ$ вне $\Delta ABC.$
Обозначим через $[X]$ площадь формы $X.$ Тогда $[\Delta BCX]=[\Delta ACY]+[\Delta ABZ].$
Это истинное обобщение теоремы Пифагора, которое получается, когда угол при $A$ прямой. Доказательство утверждения можно найти на отдельной странице.
Конструкция Тран Куанг Хунга вдохновила на создание двух ответвлений: Доказательства 107′ и 107»:
Доказательство #107′
В остром $\Delta ABC,$ $AD,$ $BE,$ $CF$ — высоты, $r$ произвольное действительное число. Вне $\Delta ABC$ провести прямую $aa$, параллельную $BC$, на расстоянии $rBC;$ прямую $bb$, параллельную $AC$, на расстоянии $rCE;$ прямую $cc$, параллельную $AB$, на расстоянии $rBF .$ Пусть $X\in aa,$ $Y\in bb,$ $Z\in cc. $
$
Обозначим через $[X]$ площадь фигуры $X.$ Тогда $[\Delta BCX]=[\Delta ACY]+[\Delta ABZ].$
Доказательство #107»
В остром $\Delta ABC,$ $AD,$ $BE,$ $CF$ — высоты. Постройте квадраты $BCX_{1}X_{2},$ $BFZZ_1,$ и $CEYY_1$ вне $\Delta ABC.$ Пусть прямоугольники $ABZ_{1}Z_2$ и $ACY_{1}Y_{2}$ описывают последние два.
Обозначим через $[X]$ площадь фигуры $X.$ Тогда $[BCX_{1}X_{2}]=[ACY_{1}Y_{2}]+[ABZ_{1}Z_2].$
Доказательство утверждения можно найти на отдельной странице.
Доказательство #108
Еще более любопытно другое обобщение Тран Куанг Хунга. Это иллюстрируется следующей диаграммой: 92 \ гидроразрыва {\ тета} {2}. $
, которое он выводит, не прибегая к теореме Пифагора. Еще два тригонометрических доказательства. Подробности на отдельной странице.
Доказательства #111
Нуно Лусия также нашел доказательство, использующее аналитическую геометрию. На схеме
$h$ находится как длина серединного перпендикуляра к гипотенузе до его пересечения с осью $x$. Подробности на отдельной странице.
Подробности на отдельной странице.
Пробы #112
Джон Молоках вывел тождество Пифагора в тригономатрической форме, искусно манипулируя формулами с двойным аргументом. Подробности можно найти в отдельном файле.
Доказательства #113
Джон также придумал простое доказательство теоремы Пифагора, основанное на следующей диаграмме:
Некоторые детали вынесены на отдельную страницу.
Доказательства #114
Буи Куанг Туан, чтобы получить теорему Пифагора, вычислил площадь особого равностороннего треугольника двумя способами:
Это напоминает доказательства 46, 47, 48, 49, 50. Простой вывод вынесен на отдельную страницу.
Доказательства #115
Доказательство выполнено Нилеоном М. Дималалуаном-младшим и основано на следующей диаграмме
Подробная информация находится в отдельном файле.
Доказательства #116
Вот доказательство без слов из последней книги Роджера Нельсена. Доказательство принадлежит Нам Го Хо.
Доказательство принадлежит Нам Го Хо.
Пробы #117
Доказательство Андреса Наваса основано на следующей диаграмме
Подробная информация находится в отдельном файле.
Доказательство #118
Доказательство выполнено Буркардом Полстером и Марти Россом и основано на следующей диаграмме
Подробная информация находится в отдельном файле.
Доказательства #119
Доказательство без слов Джона Молокача начинается со следующей диаграммы
Подробная информация находится в отдельном файле.
Доказательства #120
Доказательство без слов Тони Фостера начинается со следующей диаграммы
Подробная информация находится в отдельном файле.
Доказательства #121
Это нетрадиционное доказательство может быть выполнено с небольшим количеством математических вычислений или без них; Я нахожу это поразительно очаровательным. Доказательство (автор Эндрю Стейси) основано на следующей диаграмме
.
Подробная информация находится в отдельном файле.
Доказательство #122
Доказательство от противного.
Подробности в отдельном файле.
Ссылки
- Дж. Д. Биркхофф и Р. Битли, Базовая геометрия , паб AMS Chelsea, 2000 г.
- В. Данэм, Математическая Вселенная , John Wiley & Sons, Нью-Йорк, 1994.
- У. Данхэм, Путешествие через Genius , Penguin Books, 1 991
- Х. Ивс, Великие моменты в математике до 1650 года , MAA, 1983
- Г. Н. Фредериксон, Рассечения: Plane & Fancy , Cambridge University Press, 1997.
- Г. Н. Фредериксон, Шарнирные рассечения: раскачивание и скручивание , Cambridge University Press, 2002
- Э. С. Лумис, Предложение Пифагора , NCTM, 1 968
- Р. Б. Нельсен, Доказательства без слов , MAA, 1993
- Р. Б. Нельсен, Доказательства без слов II , MAA, 2000
- Р.




 — 240 с. : ил. — ISBN 978-5-09-019315-3.
— 240 с. : ил. — ISBN 978-5-09-019315-3. Кожевникова. Высшая сатематика в задачах и упражнениях. T.: “Узбек файласуфлари миллий жамияти” – 2007. – 53 с.
Кожевникова. Высшая сатематика в задачах и упражнениях. T.: “Узбек файласуфлари миллий жамияти” – 2007. – 53 с.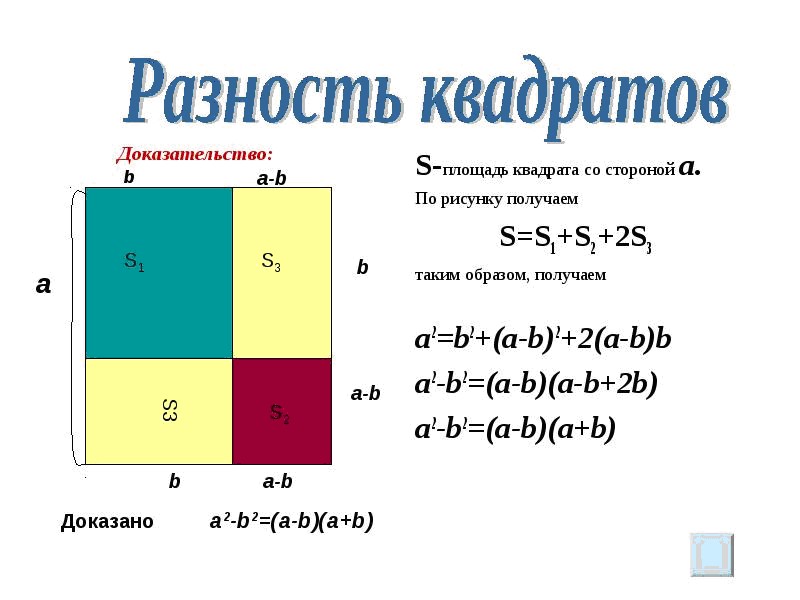

 Книга представляет собой сборник из 367 доказательств теоремы Пифагора и была переиздана NCTM в 1968. В предисловии автор справедливо утверждает, что число алгебраических доказательств безгранично, как и число геометрических доказательств, но что это предложение не допускает тригонометрического доказательства. Любопытно, что нигде в книге Лумис не упоминает VI.31 Евклида, даже когда предлагает его и варианты в качестве алгебраических доказательств 1 и 93 или геометрических доказательств 230.
Книга представляет собой сборник из 367 доказательств теоремы Пифагора и была переиздана NCTM в 1968. В предисловии автор справедливо утверждает, что число алгебраических доказательств безгранично, как и число геометрических доказательств, но что это предложение не допускает тригонометрического доказательства. Любопытно, что нигде в книге Лумис не упоминает VI.31 Евклида, даже когда предлагает его и варианты в качестве алгебраических доказательств 1 и 93 или геометрических доказательств 230. (Всего было 100 «стенографических» доказательств.)
(Всего было 100 «стенографических» доказательств.) Некоторые обобщения далеко не очевидны. Теорема Пифагора служит основой формулы Евклидова расстояния.
Некоторые обобщения далеко не очевидны. Теорема Пифагора служит основой формулы Евклидова расстояния.
 Дейкстра заслуженно считает (EWD) более симметричным и информативным. Дополнительным преимуществом считается отсутствие трансцендентных величин (р). Доказательство Дейкстры включено в Доказательство 78 и более подробно описано на отдельной странице.
Дейкстра заслуженно считает (EWD) более симметричным и информативным. Дополнительным преимуществом считается отсутствие трансцендентных величин (р). Доказательство Дейкстры включено в Доказательство 78 и более подробно описано на отдельной странице. Он погиб в окопах во Франции в 1914 году. Так писал Дж. Адамс в августе 1933 года.
Он погиб в окопах во Франции в 1914 году. Так писал Дж. Адамс в августе 1933 года.
 В прямоугольных треугольниках BIK и BIL BI = BC = c и ∠IBL = ∠ACB = β, что делает их соответственно подобными и равными ΔABC. Тогда ΔIKL также подобен ΔABC, и мы находим BL = b и LK = a²/b. Так что
В прямоугольных треугольниках BIK и BIL BI = BC = c и ∠IBL = ∠ACB = β, что делает их соответственно подобными и равными ΔABC. Тогда ΔIKL также подобен ΔABC, и мы находим BL = b и LK = a²/b. Так что