|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного… Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является. Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 136 из 296Следующая ⇒ Объект исследования: формула комбинаторики для числа сочетаний с повторениями. Результаты, полученные лично автором: рассмотрен способ построения форумы числа сочетаний с повторениями. Решены задачи, использующие данную формулу.
Сочетания с повторениями – это сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз. Таким образом, сочетание с повторениями из n элементов по k элементов (при этом допускается, что m>n) может содержать любой элемент сколько угодно раз от 1 до Существует специальная формула для вычисления числа сочетаний с повторениями. Выведем эту формулу, используя пример. Пусть в кондитерском магазине продаются пирожные 4 видов: корзиночки, наполеоны, песочные и эклеры. Если куплено 3 корзиночки (к), 1 наполеон (н), 2 песочных (п) и 1 эклер (э), то получим такую запись:111|1|11|1. В этой записи палочки отделяют одну группу пирожных от другой. Если же куплено 2 корзиночки и 5 песочных, то получим запись 11||11111|. Ясно, что разным покупкам соответствуют при этом разные комбинации из 7 единиц и 3 палочек. Обратно, каждой комбинации единиц и палочек соответствует какая-то покупка. Например, комбинации |111|1111| соответствует покупка 3 наполеонов и 4 песочных (крайние группы отсутствуют). В результате мы получим столько единиц, сколько предметов входит в комбинацию, т. е. k, а число палочек будет на 1 меньше, чем число типов предметов, т. е. n–1. Таким образом, мы получим перестановки с повторениями из k единиц и n–1 палочек. Различным комбинациям при этом соответствуют различные перестановки с повторениями, а каждой перестановке с повторениями соответствует своя комбинация. Итак, число сочетаний с повторениями из элементов n типов по k равно числу P(k, n–1) перестановок с повторениями из n–1 палочек и k единиц, то есть , поэтому Рассмотрим задачу. Материал поступил в редколлегию 24.04.2017 УДК 519.253 Е.В. Киселёва Научный руководитель: доцент кафедры «Высшая математика», к.т.н. А.Г. Белоусов Анализ качества результатов социологических Опросов Объект исследования: результаты социологических опросов. Результаты, полученные лично автором: проанализированы данные реальных социологических исследований, на основе которых предложена методика выявления недостоверности результатов опросов, опирающаяся на методы теории вероятности и математической статистики. Результаты социологических опросов, как правило, представляют собой не только информацию, но и средство влияния на принятие решений, также они могут влиять на общественное мнение. Сфальсифицированные результаты опросов можно условно разделить на три уровня: 1) фальсификация выявляется с помощью комбинирования арифметики и методов теории вероятностей и математической статистики, 2) выявление фальсификации требует существенного опыта в сфере теории вероятностей и математической статистики, 3) соблюдение требований предыдущего уровня, а также сбор дополнительных эмпирических данных. При этом анализ, как правило, не предоставляет строгого доказательства, что результаты опроса недостоверные, но он может позволить выявить данные, являющиеся недостоверными с высокой вероятностью. К признакам потенциально сфальсифицированных результатов опросов, по нашему мнению, относятся: общее кратное процентов голосов, круглые величины в процентах, погрешности при суммировании процентов. В анкетных листах нередко встречаются вопросы, где можно выбрать несколько вариантов ответа, всего не более k, при этом вариант вида «затрудняюсь ответить» не предусматривается. Любой респондент может выбрать число вариантов от 1 до k. Допустим, выбор варианта респондентом – случайная величина. Таким образом, количество процентов, набираемых всеми вариантами по всей выборке, – случайная величина, являющаяся суммой большого числа n одинаково распределённых независимых случайных величин (никакой респондент не знает, какие варианты выбирают другие респонденты), где n – размер выборки. Согласно ЦПТ распределение суммарного процента должно быть близко к нормальному. Следовательно, если суммарный процент оказался близок к 100 или 100k, это может быть вызвано наличием сфабрикованных данных, поскольку такое случайное событие маловероятно. Так, в нескольких найденных источниках приводятся случаи при k=3, когда суммарный процент составлял более 260, что требует дополнительных исследований на предмет причин таких показателей. Особенно важна проверка близости к верхней границе (300% для k=3). Естественно, постоянная близость суммы процентов к одному и тому же значению, включая «идеальное» 50(k+1), также должна являться аргументом для расследования. Ещё одним примером возможного низкого качества результатов опроса может являться следующая ситуация. Так, в публикациях, касающихся опросов проводимых среди студентов вузов, насчитывающих 5-10 тыс. чел., часто фигурирует размер выборки порядка 100-200. Допустим, в некотором вузе есть 5 тыс. студентов, и по данным было опрошено 200 студентов, то есть 0,04=4% от контингента. Преимущества математических методов анализа заключаются в том, что большинство из них достаточно быстры в применении и не требуют детальных данных об опросе. Кроме того, большинство из них могут быть использованы «здесь и сейчас», на основе компьютерных технологий и интернет-ресурсов. Положительные результаты применения математических методов свидетельствуют о высокой вероятности некачественных данных, однако не гарантируют, что не имеет место случайности, или что результаты вызваны не преднамеренной подтасовкой, а ошибками при обеспечении репрезентативности данных и подсчётах результатов организаторами опроса. Материал поступил в редколлегию 27.04.2017
УДК 519.2 Е.В. Минаков Научный руководитель: ассистент кафедры «Высшая математика», А.О. Алейникова
⇐ Предыдущая131132133134135136137138139140Следующая ⇒ Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
29.
 Комбинаторные формулы
Комбинаторные формулыПусть имеется множество, состоящее из N Элементов. Обозначим его Un. Перестановкой из N Элементов называется заданный порядок во множестве Un.
Примеры перестановок:
1)распределение N различных должностей среди N человек;
2)расположение N различных предметов в одном ряду.
Сколько различных перестановок можно образовать во множестве Un? Число перестановок обозначается Pn (читается Р из N).
Чтобы вывести формулу числа перестановок, представим себе N Ячеек, пронумерованных числами 1,2,…N. Все перестановки будем образовывать, располагая элементы Un В этих ячейках. В первую ячейку можно занести любой из N Элементов (иначе: первую ячейку можно заполнить N различными способами). Заполнив первую ячейку, можно N-1 способом заполнить вторую ячейку (иначе: при каждом способе заполнения первой ячейки находится N-1 способов заполнения второй ячейки). Таким образом существует N(N-1) способов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти N-2 способов заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить N(N-1)(N-2) способами. Продолжая этот процесс, получим, что число способов заполнения N ячеек равно . Отсюда
Таким образом существует N(N-1) способов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти N-2 способов заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить N(N-1)(N-2) способами. Продолжая этот процесс, получим, что число способов заполнения N ячеек равно . Отсюда
Pn = N(N — 1)(N — 2)…×3×2×1
Число n(N — 1)(N — 2)…×3×2×1, то есть произведение всех натуральных чисел от 1 до N, называется «N-факториал» и обозначается N!. Отсюда Pn =N!
Пример. .
По определению считается: 1!=1; 0!=1.
Размещениями из N элементов по K элементов будем называть упорядоченные подмножества, состоящие из K элементов, множества Un — (множества, состоящего из N элементов). Число размещений из N элементов по K элементов обозначается (читается «А из N по K«).
Примеры задач, приводящих к необходимости подсчета
1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?
2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?
В задачах о размещениях полагается K<N. В случае, если K=N, то легко получить
Для подсчета используем тот же метод, что использовался для подсчета Pn ,только здесь возьмем лишь K ячеек. Первую ячейку можно заполнить N способами, вторую, при заполненной первой, можно заполнить N-1 способами. Можно продолжать этот процесс до заполнения последней K-й ячейки. Эту ячейку при заполненных первых K-1 ячейках можно заполнить N-(K-1) способами (или N—K+1). Таким образом все K ячеек заполняются числом способов, равным
Отсюда получаем:
Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Сочетаниями из N элементов по K элементов называются подмножества, состоящие из K элементов множества Un (множества, состоящего из N элементов).
Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из N элементов по K элементов обозначается (читается «C из N по K«).
Примеры задач, приводящих к необходимости подсчета числа сочетаний:
1) Сколькими способами можно из 15 человек выбрать 6 кандидатов для назначения на работу в одинаковых должностях?
2) Сколькими способами можно из 20 книг отобрать 12 книг?
Выведем формулу для подсчета числа сочетаний. Пусть имеется множество Un И нужно образовать упорядоченное подмножество множества Un, содержащее K элементов (то есть образовать размещение). Делаем это так:
1) выделим какие-либо K элементов из N элементов множества Un Это, согласно сказанному выше, можно сделать способами;
2) упорядочим выделенные K элементов, что можно сделать способами. Всего можно получить вариантов (упорядоченных подмножеств), откуда следует: ,то есть
Пример: 6 человек из 15 можно выбрать числом способов, равным
Задачи на подсчет числа подмножеств конечного множества называются комбинаторными. Рассмотрим некоторые комбинаторные задачи.
Рассмотрим некоторые комбинаторные задачи.
1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы?
Так как все заводы различны, и из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, здесь нужно считать число размещений
2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний.
3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на несколько заводов).
В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один — седьмому.
Задача решается так. Первый заказ может быть размещен семью различными способами (на первом заводе, на втором и т. д.). Разместив первый заказ, имеем семь вариантов размещения второго (иначе, каждый способ размещения первого заказа может сопровождаться семью способами размещения второго). Таким образом, существует 7×7=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов размещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами распределения третьего заказа). Следовательно, существуют 49×7=73 способов размещения трех заказов. (Если бы заказов было N, то получилось бы 7N способов размещения).
4.Как решать задачу 3, если в ее тексте вместо слов «различных производственных заказа» поставить «одинаковых производственных заказа»?
5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?
Сколькими способами могут быть распределены все заказы?
Каждый из способов распределения заказов на заводах может сопровождаться способами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно
| < Предыдущая | Следующая > |
|---|
§8. Число сочетаний с повторениями
Пусть − число всех –сочетаний с повторениями.
Теорема 9. .
Доказательство. Пусть
,
–сочетание
с повторениями, в котором элемент встречается раз для
всех
,
причем
.
Сочетанию поставим в соответствие двоичный набор,
в котором единиц и нулей, следующим образом:
.
Между множеством двоичных наборов с единицами и k нулями и множеством
–сочетаний
с повторениями существует взаимно-однозначное
соответствие. Отсюда получаем, что Теорема доказана.
Задача 11. Сколькими способами можно купить букет из 9 роз, если в продаже имеются розы 3 цветов: белые, розовые и красные.
Решение. Число всех букетов совпадает с числом всех сочетаний из трех элементов по 9 с повторениями, тогда
Пусть заданы множества А и В, найдем число элементов в . Если , то в силу следствия теоремы 7.
Если , построим диаграмму Венна 2-го порядка.
Рис.2
Множество А пометим горизонтальной штриховкой, а В – вертикальной, тогда в входят все элементы универса, которые находятся в заштрихованной области, причем элементы множества находятся в дважды заштрихованной области, так как они входят и в множество А, и в множество В. Отсюда получаем, что . (1)
Очевидно, что формула (1) верна и в случае, если .
Из формулы (1) можно получить формулу для мощности объединения трех множеств:
=.
Отсюда получаем, что
. (2)
Аналогично из формул (1) и (2) можно получить формулы для мощности объединения четырех множеств и т.д.
Теорема 10. (3)
Доказательство. Утверждение докажем индукцией по n.
Для утверждение очевидно. Справедливость теоремы для вытекает согласно формуле (1).
Допустим, что теорема выполнена для множеств.
Пусть . Тогда , следовательно, в силу формулы (1).
Согласно предположению индукции,
. (4)
Рассмотрим . Обозначим через , тогда
.
Таким образом, получаем, что =
Теорема доказана.
Задачи
Студенты изучают 7 предметов. Сколькими способами можно составить расписание на один день, если в день следует устанавливать не менее двух и не более четырех предметов?
Сколько существует семизначных чисел, делящихся на 5? Сколько среди них четных?
Сколько существует девятизначных чисел, которые одинаково читаются как слева направо, так и справа налево? Сколько среди них четных?
В скольких точках пересекаются диагонали выпуклого n-угольника, если никакие три из них не пересекаются в одной точке?
В комнате n лампочек.
 Сколькими способами можно
зажечь k лампочек?
Сколько существует способов освещения
комнаты?
Сколькими способами можно
зажечь k лампочек?
Сколько существует способов освещения
комнаты?Сколько существует пятизначных чисел, у которых каждая следующая цифра больше предыдущей?
Сколько существует шестизначных чисел, у которых цифры расположены в неубывающем порядке?
Имеется n черных и m белых шаров. Сколькими способами можно их выложить в ряд так, чтобы никакие два черных шара не лежали рядом?
Студенту необходимо сдать 4 экзамена в течение 10 дней, причем известно, что в последний день он сдает экзамен. Сколькими способами он может это сделать?
Сколькими способами можно рассадить n гостей за круглым столом?
Имеется 4 типа открыток. Сколькими способами можно выбрать 10 открыток?
Сколькими способами n различных (одинаковых) предметов можно разложить в k одинаковых ящиков (разных ящиков)?
Сколько существует чисел не больше 100, которые не делятся ни на 2, ни на 3, ни на 5?
На полке стоят n книг.
 Сколькими способами можно взять
из них m так, чтобы никакие две не стояли рядом?
Сколькими способами можно взять
из них m так, чтобы никакие две не стояли рядом?Сколькими способами можно выбрать три различных карандаша из имеющихся пяти карандашей разных цветов?
В группе 5 девочек и 7 мальчиков. Сколькими способами их можно разделить на 2 группы по 6 человек? Сколькими способами это можно сделать при условии, что в каждой группе должно быть хотя бы по одной девочке?
Сколькими способами можно рассадить за круглым столом m юношей и n девушек так, чтобы никакие две девушки не сидели рядом?
Имеется n абонентов телефонной сети. Сколькими способами можно одновременно соединить три пары?
Три студента сдают экзамен. Сколькими способами они могут сдать экзамен по пятибалльной системе? По семибалльной?
Сколько различных слов можно составить из букв слова «комбинаторика»?
Сколькими способами 12 одинаковых монет можно разложить по пяти пакетам так, чтобы ни один из пакетов не был пуст?
В конструкторском бюро все сотрудники знают хотя бы один из трех языков.
 Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.
Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.
Убийственная математика: Неизвестная формула!
Убийственная математика: Неизвестная формула! Для комбинаций, когда выбор может повторяться и порядок НЕ имеет значения В книге ММ «Идеальная колбаса и другие фундаментальные формулы» мы встречаем «Неизвестную формулу».Чего НЕ делает Неизвестная Формула…
Если вы выберете четыре карты из стопки из шести разных карт, сколько различных комбинаций карт вы можете получить? Ответ дается в формуле комбинаций:
Количество возможных комбинаций выбора S объектов из D различных объектов = D!/S!(D-S)!
В этом случае вы получаете D=6 и S=4, поэтому сумма становится 6!/4!x2! = 6x5x4x3x2x1/(4x3x2x1)x(2×1), что сокращается до 6×5/2 = 15. Если вы этого не понимаете, все это объясняется в разделе «Повезло ли вам?»
Если вы этого не понимаете, все это объясняется в разделе «Повезло ли вам?»
| Вот только три из 15 возможных способов выбрать четыре карты из шести, показанных выше. |
Неважно, в каком порядке выбираются карты, но важно то, что каждую карту можно выбрать только один раз, поэтому все четыре карты будут разными .
Та же самая формула и числа применимы к шести монетам, выложенным в ряд, все перевернутым орлом вверх, и посмотреть, сколькими способами можно перевернуть четыре разные монеты. Вы можете получить HHTTTT, или HTTHTT, или TTTHHT, или… Всего вы найдете 15 различных способов.
| Сколькими способами вы можете перевернуть ЧЕТЫРЕ разные монеты из шести рядов? | |||||
| Вот один из способов… | |||||
. ..и вот еще… ..и вот еще… | |||||
| … и другой… | |||||
| …всего вы найдете 15 различных способов. | |||||
S= количество предметов, которые вы можете выбрать N = общее количество элементов на выбор |
| Вы не можете сделать это: | |
| Но вы МОЖЕТЕ сделать это: |
Чтобы получить количество различных комбинаций для костей, вам нужна «Неизвестная формула».
При бросании четырех шестигранных костей N=6 и S=4, поэтому количество возможных комбинаций равно
(С+Н-1)!/С!(Н-1)! = (4+6-1)!/4!(6-1)! = 9!/4!x5!
= 9x8x7x6x5x4x3x2x1/(4x3x2x1)x(5x4x3x2x1) = 9x8x7x6/(4x3x2)= 126
Что такое «разные» комбинации?Хотя бросать четыре кубика гораздо интереснее, легче увидеть, что именно происходит с двумя кубиками. Если вы думаете, что существует 6 x 6 = 36 способов, которыми могут выпасть две кости, то вы правы: | |||
| |||
| Неизвестной Формуле удается игнорировать все повторяющиеся комбинации,
поэтому эта комбинация будет учитываться только один раз. Итак, сколько существует различных комбинаций двух игральных костей? Подставьте N=6 и S=2 в формулу Unknown, и вы получите ответ 21 . |
Откуда взялась Неизвестная Формула?
Предположим, вы бросаете свои четыре кости и получаете 1,3,3,5.
Хитрость заключается в том, что вам даже не нужно отмечать отдельные числа, поэтому 2345 может быть 00*0*0*0*0, а 1335 — 0*00**00*0. Таким образом, ЛЮБУЮ комбинацию из четырех игральных костей можно изобразить линией, состоящей из нулей и звездочек. Что делает это еще более странным, так это то, что строка всегда будет начинаться с 0, и поэтому вам не нужно ее записывать! Поэтому 2345 будет 0*0*0*0*0 или 1335 будет *00**00*0.
Вы заметите, что какую бы комбинацию из четырех кубиков вы ни бросили, она может быть представлена в общей сложности девятью 0 и * в строке. Вы также заметите, что строка теперь содержит такое же количество звездочек, как и количество задействованных кубиков. Также на один 0 меньше, чем набор чисел, которые могут показать кости. (Поскольку у обычного игрального кубика 6 граней, в ряду всего пять нулей.)
Вы также заметите, что строка теперь содержит такое же количество звездочек, как и количество задействованных кубиков. Также на один 0 меньше, чем набор чисел, которые могут показать кости. (Поскольку у обычного игрального кубика 6 граней, в ряду всего пять нулей.)
Предположим, вам нужно бросить шесть восьмигранных костей! Если вы получили 144467, то строка будет *000***00*0*0. Обратите внимание, что на шести кубиках есть шесть * и семь нулей, что на единицу меньше, чем восемь возможных чисел на каждом кубике.
Внезапно мы вернулись к простым комбинациям. С нашими четырьмя кубиками можно составить любую возможную комбинацию, расположив ****00000 в любом порядке. Кроме того, каждый другой заказ ****00000 представляет собой другую комбинацию. Поэтому вопрос в том, сколько способов мы можем упорядочить ****00000? Это то же самое, что начать с девяти пустых ячеек и выбрать, в какие из четырех поставить *. Это даже то же самое, что начать с девяти монет, перевернутых решкой вверх, и увидеть, сколько разных способов мы можем перевернуть четыре из них! Поэтому мы можем адаптировать простую формулу комбинации (оглянитесь на начало страницы!). Вместо общего количества монет D представляет собой общее количество символов * и 0, что в данном случае равно 9.. S представляет количество игральных костей, поэтому здесь S=4. Если мы подставим эти значения в формулу, то получим ответ 126.
Вместо общего количества монет D представляет собой общее количество символов * и 0, что в данном случае равно 9.. S представляет количество игральных костей, поэтому здесь S=4. Если мы подставим эти значения в формулу, то получим ответ 126.
Для шести восьмигранных костей линия будет состоять из шести символов * и семи нулей. Следовательно, D=13 и S=6, и получается 1716 комбинаций.
В более общем случае, когда мы бросаем кости и представляем комбинацию в строке, такой как 00***000*, количество звездочек совпадает с количеством игральных костей = S. Количество нулей в строке равно единице. меньше, чем количество разных граней на каждом кубике (т. е. наше количество вариантов), поэтому количество 0 = (N-1). Следовательно, количество элементов в строке равно количеству * плюс количество нулей = (S+N-1). Итак, все, что нам нужно знать, это сколькими способами мы можем выбрать N элементов из (S+N-1) элементов. Получаем исходную формулу комбинации, заменяем N=S и (N+D-1)=D. Поэтому Д!/С!(Д-С)! становится (N+D-1)!/N!(N+D-1-N)! и заканчиваем (Н+Д-1)!/Н!(Д-1)! .
Поэтому Д!/С!(Д-С)! становится (N+D-1)!/N!(N+D-1-N)! и заканчиваем (Н+Д-1)!/Н!(Д-1)! .
Если вы поняли это, побалуйте себя вечеринкой.
Посмотрите, как получить результаты для Неизвестной формулы из треугольника Паскаля!
Многие компании нашли успешную формулу найма сотрудников, используя программа для набора текста. Недавний HR статистика показывает, что 60% работодателей использовали текстовый рекрутинг в той или иной форме.
Большое спасибо РИЧАРД ГЕРТИН Стэнфордского университета, Калифорния , кто связался с нами с полезным обновление на эту страницу! |
Вы чувствуете себя счастливым?
Идеальная колбаса и другие фундаментальные формулы
Главная страница индекса убийственной математики
Дополнительные перестановки и комбинации
- Вопрос о перестановке и комбинировании, который мы задавали до сих пор, в основном касался выбора объектов.

- У вас есть \(n\) объектов и выберите \(r\) из них. Сколькими способами, если порядок имеет/не имеет значения?
- Ответы: \(P(n,r)\) и \(C(n,r)\).
- … и мы нашли проблемы там, где они были полезны, но не были очевидны. (например, сколько битовых строк с единицами \(r\)?) 9г\) различных \(г\)-перестановок \(п\) элементов с повторением.
- Доказательство: правило произведения применено \(r\) раз.
- Есть много задач, похожих на базовые комбинации/перестановки.
- Основной подход таков: как сделать так, чтобы это выглядело как проблема, которую вы знаете, как решить? Когда вы это сделаете, на сколько вы переоценили/занизили?
- Пример: Сколько существует способов переставить буквы в слове \(\mathrm{HAPPY}\)?
- Было бы \(5!\) способов перестановки \(\mathrm{HAPQY}\), так как все буквы разные.
- Что делать с повторяющимся P? Давайте представим, что они разные: \(\mathrm{HAP_1P_2Y}\).

- Теперь есть \(5!\) способов, но мы посчитали оба, а в исходной задаче их надо было посчитать только один раз: \[\mathrm{P_1AHP_2Y}\\\mathrm{P_2AHP_1Y}\]
- На самом деле мы считали каждую перестановку дважды: при каждом возможном порядке Ps.
- Действительное решение: \(5!/2!=60\).
- Пример (снова): Сколько существует способов переставить буквы в слове \(\mathrm{HAPPY}\)?
- Давайте сначала решим, куда поместить Ps, \(C(5,2)\) способами.
- Затем в оставшихся 3 позициях переставить оставшиеся 3 элемента.
- Окончательный ответ: \[C(5,2)\cdot P(3,3) = \frac{5!}{2!3!}\frac{3!}{0!} = 5!/2!\,.\]
- Теорема: Существует \(n!/k!\) способов перестановки \(n\) объектов, где \(k\) идентичны (но другие \(n-k\) различны).
Доказательство идеи: То же, что и в предыдущем примере, с \(n=5\) и \(k=2\). [Второе решение больше похоже на доказательство.
 Первое слишком небрежно, чтобы быть «доказательством», но это хороший способ подумать об этом.]
Первое слишком небрежно, чтобы быть «доказательством», но это хороший способ подумать об этом.] - Теорема: Предположим, у нас есть \(n\) элементов, где есть \(n_1,n_2,\ldots,n_k\), которые идентичны. Количество способов их перестановки равно
\[\frac{n!}{n_1!n_2!\cdots n_k!}\,.\]
Мы потребуем, чтобы \(\sum n_i = n\) для доказательства, но, очевидно, нам не нужно считать единственные в своем роде элементы, чтобы получить правильный ответ, поскольку \(1!=1\) .
Доказательство: Как и раньше, сначала выберите позиции для \(n_1\) одинаковых элементов \(C(n,n_1)\) способов. Затем разместите \(n_2\) элементов \(C(n-n_1,n_2)\) способами и так далее. Общее количество способов упорядочить предметы равно \[\начать{выравнивать*} &\mbox{} C(n,n_1) C(n-n_1,n_2) C(n-n_1-n_2,n_3) \cdots C(n-n_1-\cdots -n_{k-1},n_k) \ \ &= \tfrac{n!}{n_1!(n-n_1)!} \tfrac{(n-n_1)!}{n_2!(n-n_1-n_2)!} \tfrac{(n-n_1-n_2) !}{n_3!(n-n_1-n_2-n_3)!}\cdots \tfrac{(n-n_1-\cdots -n_{k-1})}{n_k!0!}\\ &= \frac{n!}{n_1!n_2!\cdots n_k!}\,.
 \quad∎
\конец{выравнивание*}\]
9{51}\) протоны+нейтроны, составляющие массу Земли.]
\quad∎
\конец{выравнивание*}\]
9{51}\) протоны+нейтроны, составляющие массу Земли.]
- Букв 11, но четыре Is, четыре Ss, два Ps.
- Есть \(\frac{11!}{4!4!2!}=34650\) способы.
- Ваша свекровь покупает 1000 маленьких подарков для родственников на Рождество по причинам, которые вы не понимаете. Каждая из 1000 вещей отличается, потому что она тратит слишком много времени на покупки. Есть 25 родственников, которым нужно подарить подарки. Сколько существует способов распределить подарки?
- Примечание: вопрос допускает возможность того, что один человек получит 1000 вещей, а все остальные ничего не получат. В этой семье нет справедливости
- В приведенном выше сценарии сколькими способами можно распределить подарки, чтобы каждый человек получил по 40 предметов?
- В следующем году вас отправляют в подвал, чтобы разложить 1000 подарков на 25 стопок, по одной на человека.
 {139{1369}\,.\]
{139{1369}\,.\] - Это на удивление сложно. См. обсуждение в учебнике «различимых объектов и неразличимых ящиков» на с. 337 или найдите Числа Стирлинга второго рода .
- Чтобы раздать подарки, мы должны выбрать людей, которые получат каждый из них. Порядок здесь не имеет значения, так как ручки идентичны. Это комбинация с проблемой повторения: комбинации 1000 25 членов семьи с повторением. Итак, есть \(C(1024,25)\) способов распространения.
- Попытка №1: подсчитайте все \(C(1024,25)\) способов распределения ручек, затем вычтите число, в котором кто-то получает 2 или меньше ручек. Сколько из них есть? Эммм…
Попытка №2: Сначала раздайте всем по три ручки, используя 75 из них. Затем распределите оставшиеся 925 \(C(949,25)\) способами.
- Один из способов: дать каждому по 40 ручек.
Определение перестановки
Оглавление
Содержание
Что такое перестановка?
Понимание перестановок
Перестановки и комбинации
Типы
Примеры
Часто задаваемые вопросы о перестановках
Итог
По
Раджив Дхир
Полная биография
Раджив Дхир — писатель с более чем 10-летним опытом работы в качестве журналиста с опытом работы в вещательных, печатных и цифровых отделах новостей.
Узнайте о нашем редакционная политика
Обновлено 27 июля 2022 г.
Рассмотрено
Хадиджа Хартит
Рассмотрено Хадиджа Хартит
Полная биография
Хадиджа Хартит — эксперт по стратегии, инвестициям и финансированию, а также преподаватель финансовых технологий и стратегических финансов в ведущих университетах. Она была инвестором, предпринимателем и консультантом более 25 лет. Она является держателем лицензий FINRA Series 7, 63 и 66.
Узнайте о нашем Совет по финансовому обзору
Факт проверен
Сюзанна Квилхауг
Факт проверен Сюзанна Квилхауг
Полная биография
Сюзанна — исследователь, писатель и специалист по проверке фактов. Она имеет степень бакалавра финансов в Государственном университете Бриджуотер и работала над печатным контентом для владельцев бизнеса, национальных брендов и крупных изданий.
Узнайте о нашем редакционная политика
Что такое перестановка?
Термин перестановка относится к математическому расчету количества способов, которыми можно упорядочить конкретный набор. Проще говоря, перестановка — это слово, описывающее количество способов упорядочения или расположения вещей. При перестановках порядок расположения имеет значение. Существует три разных типа перестановок, в том числе один без повторения и один с повторением. Перестановки отличаются от комбинаций, где данные выбираются из группы и порядок не имеет значения.
Ключевые выводы
- Перестановка — это количество способов упорядочить набор или количество способов упорядочить вещи.
- При перестановке важен порядок чисел.
- Основными типами перестановок являются перестановки с повторением и без повторения, хотя к другим менее распространенным типам относятся перестановки с множественными наборами и круговые перестановки.
- Из одной комбинации можно получить несколько перестановок.

- Перестановки отличаются от комбинаций, которые представляют собой выборку данных из группы, где порядок не имеет значения.
Понимание перестановок
Перестановки — это понятия, используемые в математике. Они представляют различные договоренности, которые могут быть возможны в группе. Порядок очень важен, когда дело доходит до перестановок. Это отличает его от комбинации, в которой порядок не имеет значения. В какой-то степени перестановки представляют собой форму упорядоченных комбинаций. Мы обсудим комбинации более подробно ниже.
Есть способ вычислить перестановки по формуле. Эта формула:
Р(п, г) = п! ÷ (н-р)!
куда
- n = общее количество предметов в наборе;
- r = элементы, взятые для перестановки;
- «!» обозначает взятие факториала
Обобщенное выражение формулы таково: «Сколькими способами можно расположить r из набора n, если порядок имеет значение?»
Перестановку также можно рассчитать вручную, выписав все возможные перестановки. В комбинации, которую иногда путают с перестановкой, может быть любой порядок элементов.
В комбинации, которую иногда путают с перестановкой, может быть любой порядок элементов.
Простой подход к визуализации перестановки — это количество способов, которыми можно упорядочить последовательность трехзначной клавиатуры. Используя цифры от нуля (0) до девяти (9) и используя определенную цифру только один раз на клавиатуре, количество перестановок равно:
Р(10,3) = 10! ÷ (10-3)! = 10! ÷ 7! = 10 х 9 х 8 = 720
Порядок здесь имеет значение, потому что перестановка дает количество входов цифр, а не комбинацию.
Перестановки и комбинации
И перестановки, и комбинации включают группу элементов. Для перестановок важен порядок данных. Рассмотрим порядок комбинации для сейфа. У вас должен быть правильный ордер, чтобы открыть его. Таким образом, он должен быть введен точно в соответствии со сценарием, иначе он не будет работать.
Однако пример сбивает с толку, поскольку безопасные комбинации на самом деле не являются комбинациями. Комбинации не зависят от порядка или последовательности, что означает, что данные в группе могут быть упорядочены любым способом, даже случайным образом. Сказав это, нет никакого намерения, когда дело доходит до установки комбинаций. Они совершенно случайны. Подумайте о том, чтобы выбрать блюда из обеденного меню в местной закусочной.
Комбинации не зависят от порядка или последовательности, что означает, что данные в группе могут быть упорядочены любым способом, даже случайным образом. Сказав это, нет никакого намерения, когда дело доходит до установки комбинаций. Они совершенно случайны. Подумайте о том, чтобы выбрать блюда из обеденного меню в местной закусочной.
Другое ключевое различие между перестановками и комбинациями заключается в типе данных. Перестановки опираются на список вещей, поэтому порядок имеет значение. Это могут быть цифры, буквы или люди. Комбинации, с другой стороны, полагаются на группу вещей, таких как меню в вашей любимой закусочной. Поэтому порядок вообще не имеет значения. Так что это может означать подбор людей из спортивной команды или выбор блюд из меню ресторана.
| Различия между перестановками и комбинациями | |
|---|---|
| Перестановки | Комбинации |
| Данные выбираются из списка | Данные выбираются из группы |
| Есть расположение данных | Идет выборка данных |
| Порядок имеет значение | Порядок не имеет значения |
| Из одной комбинации возможны множественные перестановки | Из одной перестановки возможна одна комбинация |
Типы перестановок
Существуют различные виды перестановок. Два основных типа перестановок:
Два основных типа перестановок:
- Перестановки с повторением. При повторении можно составлять разные комбинации с разными предметами. Данные не ограничены тем, сколько раз они могут появляться, поэтому вы можете использовать данные более одного раза.
- Перестановки без повторения. В этом случае один элемент удаляется из списка каждый раз, когда вам приходится придумывать новую перестановку. Проще говоря, доступные варианты перестановок истощаются по мере продвижения.
Существуют и некоторые другие, менее распространенные типы перестановок, в том числе перестановки с использованием мультимножеств (которые включают элементы в списке, которые не являются отдельными), а также циклические или круговые перестановки или количество способов, которыми ряд элементов может быть расположен по кругу.
Примеры перестановок
Вот несколько примеров, показывающих, как работают перестановки. Первые два относятся к финансам и бизнесу. Предположим, управляющий портфелем отобрал 100 компаний для нового фонда, который будет состоять из 25 акций. Эти 25 холдингов не будут иметь равного веса, а значит, произойдет упорядочение. Количество способов заказа фонда будет:
Эти 25 холдингов не будут иметь равного веса, а значит, произойдет упорядочение. Количество способов заказа фонда будет:
Р(100,25) = 100! ÷ (100-25)! = 100! ÷ 75! = 3,76E + 48
Это оставляет портфельному управляющему много работы по созданию своего фонда.
Более простым примером может быть ситуация, когда компания хочет построить свою складскую сеть по всей стране. Компания возьмет на себя обязательства по трем локациям из пяти возможных. Порядок имеет значение, потому что они будут построены последовательно. Количество перестановок равно:
Р(5,3) = 5! ÷ (5-3)! = 5! ÷ 2! = 60
В реальном мире существует множество примеров перестановок.
- Как отмечалось выше, безопасные комбинации на самом деле являются перестановками. Это потому, что порядок чисел имеет значение. Вы не можете открыть сейф или шкафчик, если у вас нет правильного заказа.
- Другим распространенным примером является анаграмма, в которой вы составляете разные слова из одного и того же корневого слова.
 Опять же, порядок имеет значение, потому что вы должны быть в состоянии составить реальное слово, а не просто случайную последовательность букв.
Опять же, порядок имеет значение, потому что вы должны быть в состоянии составить реальное слово, а не просто случайную последовательность букв. - Выбор порядка, в котором люди финишируют в гонке. Вы можете использовать факториалы, чтобы определить, кто займет первое, второе и третье место, не говоря уже о порядке остальных участников.
Что означает перестановка?
Перестановка — это понятие в математике, которое описывает количество способов, которыми можно упорядочить определенный набор данных. Проще говоря, это количество способов упорядочения данных. Эти данные обычно берутся из списка. При перестановках порядок набора данных имеет значение, как в случае с комбинацией сейфа или шкафчика.
Какие существуют 4 типа перестановок?
Четыре типа перестановок: перестановки с повторением, перестановки без повторения, перестановки с множественными наборами и круговые перестановки.
В чем разница между перестановкой и комбинацией?
Существует несколько ключевых различий между перестановками и комбинациями.




 Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10? Ответ:
Сколько можно построить различных прямоугольных параллелепипедов, длина каждого ребра которых является целым числом от 1 до 10? Ответ:


 Вероятность неучастия в опросе составит 0,96 для взятого наугад студента, для каждого последующего она медленно убывает, если все предыдущие ответили отрицательно. Если есть разнообразие по курсам и специальностям среди студентов (гарантированная случайность выборки), то для 50 человек вероятность отсутствия среди них участника опроса составит менее 13%. Уже для 60 студентов она составит менее 9%. При увеличении числа потенциальных «неучастников» с высокой долей вероятности можно утверждать, что: имел место несуществующий опрос, или репрезентативность выборки оказалась крайне низкая (например, посещено 2-3 поточных лекции, где и было отобрано 200 респондентов).
Вероятность неучастия в опросе составит 0,96 для взятого наугад студента, для каждого последующего она медленно убывает, если все предыдущие ответили отрицательно. Если есть разнообразие по курсам и специальностям среди студентов (гарантированная случайность выборки), то для 50 человек вероятность отсутствия среди них участника опроса составит менее 13%. Уже для 60 студентов она составит менее 9%. При увеличении числа потенциальных «неучастников» с высокой долей вероятности можно утверждать, что: имел место несуществующий опрос, или репрезентативность выборки оказалась крайне низкая (например, посещено 2-3 поточных лекции, где и было отобрано 200 респондентов). Вследствие этого целесообразно использовать математические методы как дополнение к нематематическим способам выявления подтасовок.
Вследствие этого целесообразно использовать математические методы как дополнение к нематематическим способам выявления подтасовок.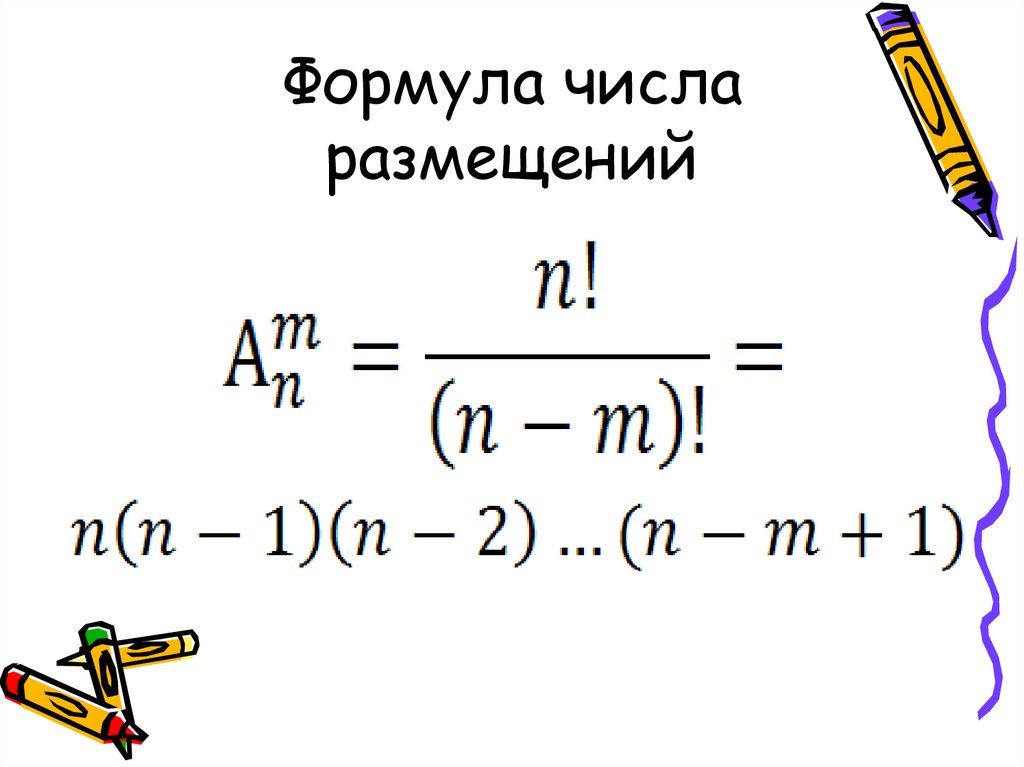 Сколькими способами можно
зажечь k лампочек?
Сколько существует способов освещения
комнаты?
Сколькими способами можно
зажечь k лампочек?
Сколько существует способов освещения
комнаты? Сколькими способами можно взять
из них m так, чтобы никакие две не стояли рядом?
Сколькими способами можно взять
из них m так, чтобы никакие две не стояли рядом? Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.
Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.


 Первое слишком небрежно, чтобы быть «доказательством», но это хороший способ подумать об этом.]
Первое слишком небрежно, чтобы быть «доказательством», но это хороший способ подумать об этом.] \quad∎
\конец{выравнивание*}\]
9{51}\) протоны+нейтроны, составляющие массу Земли.]
\quad∎
\конец{выравнивание*}\]
9{51}\) протоны+нейтроны, составляющие массу Земли.] {139{1369}\,.\]
{139{1369}\,.\]
 Опять же, порядок имеет значение, потому что вы должны быть в состоянии составить реальное слово, а не просто случайную последовательность букв.
Опять же, порядок имеет значение, потому что вы должны быть в состоянии составить реальное слово, а не просто случайную последовательность букв.