Вычислить используя полярные координаты двойной интеграл: Двойной интеграл в полярных координатах

Двойной интеграл в полярных координатах

Алгоритм вычисления двойных интегралов при переходе к полярным координатам детально приведен как в настоящей статье, так и предыдущих публикациях с теорией. Для перехода к полярным координатам нужно найти якобиан, который несколько раз здесь повторим. Дальше сами уравнения кривых, которые ограничивают область интегрирования следует также перевести в полярные координаты. В теории все хорошо описано и выглядит понятным, однако на практике во многих студентов возникают трудности и немало вопросов, поэтому внимательно пересмотрите приведенные дальше решения.

Пример 2.1 Вычислить двойной интеграл, используя полярные координаты:

Решение: Построим область интегрирования ограниченную кривыми
-3≤x≤3
Эти кривые записываем из пределов интегрирования, внимательно пересмотрите в каких пределах изменяются «икс» и «игрек».
Нижний предел по оси «игреков» приведем к каноническому виду

x²+y²=9.
Получили уравнение круга с центром в точке O(0;0) и радиусом 3 (нижняя половина).

Перейдем к полярной системе координат с помощью превращения координат:

найдем якобиан перехода:

Найдем подынтегральную функцию в полярных координатах:

Внимательно пересмотрите формулы двойного синуса, косинуса и им подобных.
Они достаточно часто встречаются при упрощении подынтегральных функций, все сделано умышленно для того, чтобы Вы без проблем могли интегрировать.
Запишем пределы интегрирования в полярной системе координат:
0≤r≤3, π≤φ≤2 π.
Вычислим двойной интеграл:

Поскольку переменные разделены, то интегрирование не тяжелое, достаточно воспользоваться табличными интегралами и подставить пределы.

 

Пример 2.2 Найти двойной интеграл, используя полярные координаты:

Решение: Из интеграла выписываем область интегрирования
0≤x≤1
Она ограничена прямыми, которые совпадают с-осями координат  
, y²=12-x²,x²+y²=1² — дуга круга в I четверти.

Получили круг с центром в точке O(0;0) и радиусом r=1 (верхняя половина).
Якобиан перехода к ПСК I=r.
Запишем подынтегральную функцию в полярной системе координат:

Для круговых областей не трудно записать пределы интегрирования при переходе к полярной системе координат:
0≤r≤1, 0≤φ≤π/2.
Находим двойной интеграл:

В результате интегрирования в ответе получили выражение которое содержит логарифм двойки, и число Пи.

 

Пример 2.3 Вычислить значение двойного интеграла, перейдя к полярным координатам:

Решение: Выпишем область интегрирования, которая ограничена кривыми
— 2≤x≤2,
По «игреку» имеем ограничения ветками круга , y²=4-x², x²+y²=2² с центром в начале координат O(0;0) и радиусом 2.

Перейдем к полярной системе координат:
якобиан переходу: I=r.
С учетом формул перехода подынтегральная функция в полярной системе координат примет вид корневой зависимости:

Пределы интегрирования в ПСК следующие:
0≤r≤2, 0≤φ≤2π.
Переходим от двойного интеграла в декартовых координатах к двойному в полярных координатах и находим его значение:

Интеграл равен 16π/3.

 

Пример 2.4 Найти двойной интеграл, используя полярные координаты:

D: {x²+y²=π²/9; x²+y²=π²/4}.
Решение: Выпишем область интегрирования ограниченную кривыми
Первая кривая x²+y²=π²/9 — круг с центром в начале координат O(0;0) и радиусом π/3;
второе уравнение описывает x²+y²=π²/4 — больший круг с центром в той же точке O(0;0) и радиусом π/2.
Область между кругами образует кольцо, по которому выполняем интегрирование.

Найдем подынтегральную функцию в полярной СК:

Круги в полярной системе координат можно задать радиусами и центрами:
, отсюда r= π/3;
, имеем r= π/2.
Пределы интегрирования в полярной системе координат следующие:
π/3≤r≤π/2, 0≤φ≤2π.
Выполняем вычисление двойного интеграла:

Переход к полярной СК значительно упрощает вычисление интегралов для круговых и кольцевых областей.

 

Пример 2.5 Найти двойной интеграл, используя полярные координаты:

D: {x²+y²— 2y=0; x²+y²— 4y=0}.
Решение: На основе предыдущих примеров делаем вывод, что область интегрирования, ограниченная x²+(y-1)²=1 — кругом с центром в точке O(0;1) и радиусом 1;
Вторая кривая x²+(y-2)²=2- круг с центром в точке O(0;2) и радиусом 2.
Графически они формируют следующую область интегрирования.

Переходим к полярной системе координат с помощью якобиана перехода I=r.
Дальше записываем кривые в полярной системе координат:


расставляем корректные пределы интегрирования:
2sin(φ)≤r≤4sin(φ), 0≤φ≤2π.
Вычисляем двойной интеграл в полярной СК:

Нахождение двойных интегралов не тяжелое занятие, если часто самостоятельно практиковать и иметь перед собой таблицу основных интегралов.
Все остальные манипуляции не тяжелые и их Вы повсюду в математике выполняете.
Дальше рассмотрим еще несколько примеров на вычисление двойных интегралов в полярных координатах.

Двойные интегралы в полярных координатах: теория и примеры

• Что значит вычислить двойной интеграл полярных координатах?
• Пределы интегрирования в повторных интегралах
• Решения двойных интегралов в полярных координатах: примеры

Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ:

.

Что представляет собой элемент площади dxdy, выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const.

Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr. Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ. Поэтому элемент площади в полярных координатах выражается следующим образом:

dxdy = rdrdφ,

а двойной интеграл в полярных координатах записывается так:

.

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ, а внутренний — по радиусу

r.

Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D.

При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.

Случай первый

Полюс O является внутренней точкой области интегрирования D, область ограничена линией r = r(φ).

Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

.

Случай второй

Полюс O находится на границе области интегрирования D, ограниченного линией r = r(φ), но не является угловой точкой.

Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

.

Случай третий

Полюс O находится на границе области интегрирования D, ограниченного линией r = r(φ), и является угловой точкой.

Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы

α и β. Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β, а внутреннего интеграла — 0 и r(φ). Переход к повторным интегралам осуществляется следующим образом:

.

Случай четвёртый

Полюс O находится вне области интегрирования D.

Из полюса O проведём лучи, которые будут ограничивать область D. Пусть эти лучи образуют с полярной осью углы α и β, а область D ограничивают линии r = r1(φ) и r = r2(φ). Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β, а внутреннего интеграла —

r1(φ) и r2(φ). Переход к повторным интегралам осуществляется следующим образом:

.

Пример 1. Вычислить в полярных координатах двойной интеграл

,

где область D ограничена линиями , , .

Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.

Выразим подынтегральную функцию как функцию полярных переменных:

.

Данные в условии линии, ограничивающие D, приводим к полярным координатам:

Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

.

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):

Пример 2. В повторном интеграле

перейти к полярной системе координат.

Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x², а сверху — прямой y = 1. Область интегирования изображена на следующем чертеже.

При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой

y = 1, в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1). В первой точке полярный угол составляет , во второй точке он составляет . Поэтому в первой области φ меняется от от 0 до , во второй области — от 0 до , в третьей области — от до π.

Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1: или . Найдём уравнение параболы y = x² в полярной системе координат:

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Пример 3. Вычислить в полярных координатах двойной интеграл

,

где область D ограничена линией окружности .

Решение. Строим на чертеже область интегрирования.

Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a. В этом легко убедиться, преобразовав её уравнение следующим образом:

.

Линия окружности касается оси Oy, поэтому полярный угол в области интегрирования меняется от до . Подставим и в уравнение окружности и получим

Напишем подынтегральную функцию в полярных координатах:

.

Теперь можем перейти в данном двойном интеграле к полярным координатам:

Наконец, находим двойной интеграл в полярных координатах:

В полученном выражении второе слагаемое равно нулю, так как и sinπ, и sin(−π) равны нулю. Продолжая, получаем:

Пример 4. Вычислить плоской фигуры, которую ограничивают линии , , , .

Решение. Построим заданную фигуру на следующем рисунке.

Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:

Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:

Пример 5. Вычислить в полярных координатах двойной интеграл

,

где область D ограничена линиями и .

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

.

Строим на чертеже область интегрирования.

В данных уравнениях линий перейдём к полярным координатам:

.

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Кратные и криволинейные интегралы

Кратные и криволинейные интегралы

• Вычисление двойных интегралов
• Двойные интегралы в полярных координатах
• Вычисление тройных интегралов
• Вычисление криволинейных интегралов
• Интегралы по замкнутому контуру, формула Грина
• Вычисление поверхностных интегралов

Поделиться с друзьями

Как переходить к полярным координатам в двойном интеграле

1.5. Как вычислить двойной интеграл в полярных координатах?

Типовое задание формулируется примерно так: «Вычислить двойной интеграл, используя полярную систему координат». После чего для решения предлагается… обычный двойной интеграл в декартовых координатах по области .
Сначала рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных и двойной интеграл численно равен площади области интегрирования. Разберём алгоритм решения на бесхитростной демо-задаче:

Пример 23

Вычислить площадь плоской фигуры, ограниченную линиями , с помощью двойного интеграла, используя полярную систему координат

На первом этапе решения ничего нового. Выполняем чертёж области в прямоугольной системе координат. Линейное неравенство определяет правую полуплоскость, включая ось , а уравнение , очевидно, задаёт какую-то линию 2-го порядка. Чтобы выяснить, какую – выделим полный квадрат:

– окружность единичного радиуса с центром в точке .
Таким образом, нам нужно вычислить площадь половинки круга:

Не упустим возможность сразу узнать ответ. По школьной формуле площади круга, должно получиться:

Площадь фигуры стандартно рассчитывается по формуле , однако по условию нужно воспользоваться полярными координатами. При переходе к полярной системе координат произведение дифференциалов ВСЕГДА превращается в следующую вещь:

То есть, от интегрирования по декартовым «иксу» и «игреку» мы перешли к интегрированию по полярному радиусу «эр» и полярному углу «фи». Обратите внимание на появившийся множитель , образно говоря, это «плата за переход», любители вышмата могут погуглить якобиан перехода к полярным координатам. Практическая же сторона вопроса состоит в том, что этот множитель «эр» терять нельзя.

Таким образом:
Но это ещё не всё – ведь границы области тоже заданы в декартовой системе. Используем формулы перехода к полярным координатам . Ось ординат не трогаем, а вот окружность потревожим:

, основное тригонометрическое тождество:
и сокращаем на «эр»:

– что и говорить, гораздо более приятное уравнение окружности.

Сведём двойной интеграл к повторным интегралам. Для этого нужно выяснить порядок обхода области. Недавно мы орудовали лазерной указкой, а сейчас будет удачна другая ассоциация – просвечивание области радаром. Представьте, что из полюса исходит красный луч света и вращается против часовой стрелки:
Когда луч радара поворачивается от полярной оси до угла (зелёная стрелка), то он входит в область непосредственно из полюса (начиная со значения ) и выходит из неё через окружность (красная стрелка). Таким образом, на промежутке полярный радиус изменяется в пределах , и область интегрирования полностью «просканирована».
В результате: – множитель , разумеется, уходит во внутренний интеграл, где осуществляется интегрирование по «эр».

И здесь я вновь рекомендую оформлять решение в два пункта:

1) Сначала возьмём внутренний интеграл:

2) Подставляем трофей во внешний интеграл и используем популярную формулу понижения степени :
что и требовалось получить (вспоминаем вычисления по школьной формуле).

Ответ:

В простых случаях, как этот, вычисления можно оформить и «одной строкой»:

К слову, совсем забыл привести такое решение для случая декартовых координат, решим «быстрым» способом, скажем, простенький Пример 13:

Но злоупотреблять короткой дорожкой не советую – повышается риск запутаться.

В разобранной задаче жёстко требовалось использовать полярную систему координат, и это очень хорошо! Я не иронизирую. Как ни странно, более свободная формулировка условия может здОрово осложнить жизнь. Отрубим ящерице хвост:

«Вычислить площадь плоской фигуры, ограниченную линиями , с помощью двойного интеграла»

Дело в том, что площадь данной фигуры рассчитывается и с помощью двойного интеграла в прямоугольной системе координат. Но решение получается длительным и громоздим, и если человек не знает о возможности перехода к полярным координатам, то будет загружен трудной работой. А по условию, никто ведь не запрещает решать через декартовы координаты 😉

Давайте ещё укоротим условие:

«Вычислить площадь плоской фигуры, ограниченную линиями »

Здесь появилась новая степень свободы, и площадь фигуры помимо прочих способов можно рассчитать с помощью однократного интеграла (решение будет почти совпадать с решением через двойной интеграл).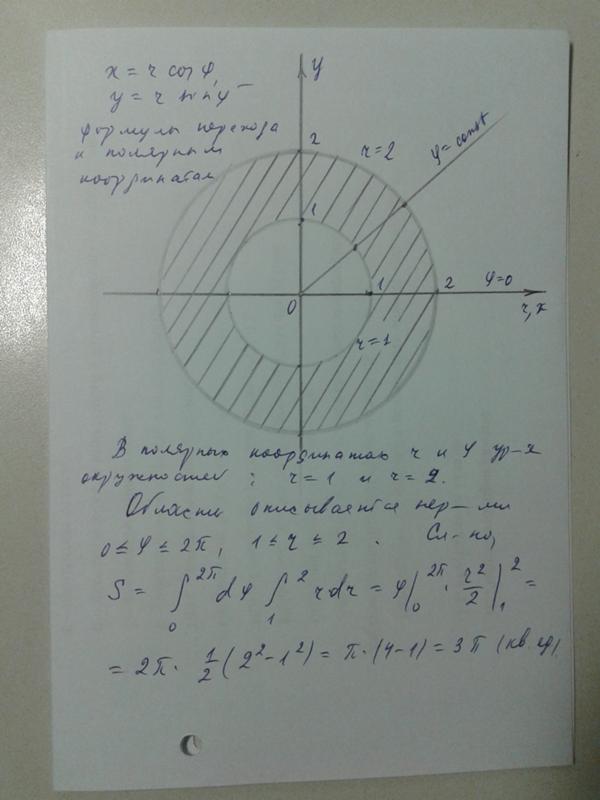 Впрочем, рецензент может не оценить такую вольность :). Чуть позже я коснусь ещё одной важной разновидности условия, а пока рассмотрим более содержательный пример:

Пример 24

С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями

Решение: изобразим данную фигуру на чертеже. С прямыми всё понятно, осталось прояснить вид линий 2-го порядка. Выделяем полные квадраты:

– окружность единичного радиуса с центром в точке .

– окружность с центром в точке радиуса 2.

Таким образом:

В условии задачи ничего не сказано о полярной системе координат, и поэтому площадь фигуры можно рассчитать «обычным» двойным интегралом в декартовых координатах. Но что-то не хочется :).

Итак, площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:

По формулам перехода найдём полярные уравнения окружностей:

Теперь выясним порядок обхода области. Луч радара (см. рис. выше) входит в область через окружность и выходит из неё через окружность (красная стрелка), при этом он осуществляет поворот от полярной оси до угла (зелёная стрелка).

Напомню также, что «альфа» и «бета» – это не просто формальные значения углов: полярное уравнение непосредственно задаёт полярную ось (положительное направление оси абсцисс), а уравнение – луч, исходящий из полюса и совпадающий с верхней частью прямой . В нашей задаче дана «хорошая» прямая и значение угла понятно «с ходу». Но как найти угол в общем случае? Вспоминаем, что угловой коэффициент прямой равен тангенсу угла наклона данной прямой к положительному направлению оси абсцисс: . В данном случае , откуда следует, что .

И после такой шикарной справки возвращаемся к решению. По результатам «сканирования» области мы выяснили, что на промежутке полярный радиус изменяется в пределах .

Перейдём к повторным интегралам:

Остальное – дело техники:

1) Раскрутим внутренний интеграл:

2) И внешний, с помощью формулы :

Ответ:

Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен. Теперь ответим на следующий важный вопрос:

Каковы предпосылки для перехода к полярным координатам?

Основной предпосылкой является наличие окружности (ей). Подчёркиваю, что это лишь предпосылка, а не обязательное правило! То есть, область интегрирования может быть ограничена окружностью (ями), но переход к полярным координатам только усложнит решение, а то и вообще заведёт его в тупик. Поэтому другим важным условием является удачное «сканирование» области «радаром». Впрочем, в каждом случае нужно смотреть индивидуально.

Следующие два примера для самостоятельного решения:

Пример 25

С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями

Пример 26

Вычислить двойной интеграл, используя полярные координаты

И в Примере 26 мы встретили ещё одну распространённую формулировку условия, в которой предложено непосредственно вычислить двойной интеграл. Да, он численно равен площади области , но, коль скоро, о площади изначально молчок, то и в решении об этом не нужно упоминать 😉 Подумайте, как грамотно записать ответ задания.
Примерные образцы решений и чертежи в конце книги. Я их оформил в разном стиле, выбирайте, что больше нравится.

Разумеется, в двойном интеграле может оказаться и «настоящая» функция с «живым» «иксом» и / или «игреком»:

Пример 27

Вычислить двойной интеграл, используя полярные координаты

Решение: область интегрирования здесь очень простая – это часть кольца между концентрическими окружностями , которая располагается в 4-й координатной четверти (о чём нам сообщают неравенства ). И коль скоро так всё просто, можно сразу заняться переходом к полярной системе координат по формулам .

Найдём уравнения окружностей в полярных координатах:

ну, прямо чудо получилось – всегда бы такие уравнения J

Выполним чертёж:

Порядок обхода области предельно понятен:

Можно было взять промежуток , но работать с табличным значением гораздо привычнее.

Отличие от предыдущих примеров состоит в дополнительном шаге – преобразовании подынтегральной функции . Используем те же стандартные формулы перехода . Если совсем просто, то в функцию двух переменных вместо «икс» подставляем и вместо «игрек» :

После подстановки полученное выражение максимально упрощают, но здесь этого особо не потребовалось.

Фишка последнего шага должна быть вам хорошо знакома: когда проводится интегрирование по переменной «эр», то переменная «фи» считается константой (и наоборот). Поэтому константу целесообразно сразу вынести из внутреннего интеграла, чтобы она не мешалась под ногами.

1) Вычислим незамысловатый внутренний интеграл:

2) И внешний, сразу вынося полученную выше константу за пределы интеграла:

Ответ:

Повторим геометрический смысл полученного результата. Так как и , то поверхность расположена над плоскостью (в 4-й координатной четверти). Полученный в задаче результат – это в точности объём цилиндрического бруса, который ограничен (представляем мысленно) плоскостью снизу, поверхностью – сверху и множеством перпендикулярных лучей, исходящих из границы области – сбоку. С задачей нахождения объёма тела мы вплотную столкнёмся при изучении тройных интегралов.

Аналогичный пример для самостоятельного решения:

Пример 28

Вычислить двойной интеграл, используя полярные координаты

Примерный образец чистового оформления задания в конце книги.

В соответствующей статье сайта я также разбираю более редкие интегралы, где можно обойтись даже без чертежа, но это уже углублённый курс. Напомню заодно, что если условие задачи того не требует – то чертёж можно и не выполнять. Правда, область интегрирования всё равно придётся представить мысленно. Но даже если у вас есть такие способности, то демонстрировать их совсем не обязательно, ибо что тяжелА жизнь вундеркинда 😉 Исключение составляют какие-то совсем простые области .

Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

Вычисление двойного интеграла в полярных координатах

Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.

Определим преобразование независимых переменных и (замену переменных) как

Если функции (53.9) имеют в некоторой области плоскости не прерывные частные производные первого порядка и отличный от нуля определитель

а функция непрерывна в области , то справедлива формула замены переменных в двойном интеграле:

Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.

Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат и полярными координатами и .

В качестве и возьмем полярные координаты и . Они связаны с декартовыми координатами формулами (см п. 9.1).

Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как

Формула замены переменных (53.11) принимает вид:

где — область в полярной системе координат, соответствующая области в декартовой системе координат.

Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если область имеет вид, изображенный на рисунке 221 (ограничена лучами и , где , и кривыми и , где , т. е. область правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде

Внутренний интеграл берется при постоянном .

1. Переход к полярным координатам полезен, когда подынтегральная функция имеет вид , область есть круг, кольцо или часть таковых.
2. На практике переход к полярным координатам осуществляется путем замены , ; уравнения линий, ограничивающих область , также преобразуются к полярным координатам. Преобразование области в область не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по и (исследуя закон изменения и точки при ее отождествлении с точкой области ).

Пример №53.2.

Вычислить , где область — круг .

Решение:

Применив формулу (53.12), перейдем к полярным координатам:

Область в полярной системе координат определяется неравенствами (см. рис. 222) . Заметим: область — круг — преобразуется в область — прямоугольник. Поэтому, согласно формуле (53.13), имеем:

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www. lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Двойные интегралы. Определение двойных интегралов. Повторные интегралы. Тройные интегралы , страница 2

.

б) Построим область интегрирования D (см. рис.1.3). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем – по y. В этом случае при изменении x от –1 до 1 изменения переменной y сверху будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y=0 до ; на отрезке [0;1] переменная y изменяется от y=0 до y=1–x. Таким образом,

.

Пусть теперь во внешнем интеграле интегрирование производится по y, а во внутреннем – по x. В этом случае y будет изменяться от 0 до 1, а переменная x – от дуги окружности до прямой x=1–y. В результате получим

.

Данные примеры показывают, как важно правильно выбирать порядок интегрирования.

1.4. Вычисление двойных интегралов в декартовой системе координат

Пример 1.3. Вычислить двойной интеграл

Решение. Построим область интегрирования (см. рис.1.4). Расставим пределы в соответствующих повторных интегралах и произведем вычисления. В результате, получим

.

Пример 1.4. Вычислить площадь фигуры ограниченной линиями x 2 =y, x 2 =4y, y=4.

Решение. Изобразим данную фигуру (рис. 1.5). Видно, что полученная фигура состоит из двух одинаковых областей: D₁ и D₂. следовательно

.

Интегрирование во внешнем интеграле будем производить по переменной y (в противном случае область интегрирования пришлось бы разбивать на две части). Тогда переменная y будет изменяться от 0 до 4, а переменная x, соответственно, от параболы до параболы . В результате получаем

.

1.5. Вычисление двойных интегралов в полярной системе координат

Наиболее употребительная система координат на плоскости – это полярные координаты. Они связаны с декартовыми координатами x и y равенствами:

(1.8)

При переходе от декартовых координат к полярным, двойной интеграл преобразуется следующим образом

. (1.9)

Если область интегрирования D является простой в осевом направлении, т.е. любой луч, выходящий из центра координат, пересекает границу области интегрирования не более чем в двух точках, то двойной интеграл можно записать в виде повторного:

. (1.10)

Пример 1.5. Вычислить интеграл

где .

Решение. Перейдем в полярную систему координат x=rsinj, y=rcosj, x 2 +y 2 =r 2 . Тогда уравнение границы области D примет вид r=2cosj. Это есть уравнение окружности
(рис. 1.6). Здесь j изменяется от –p/2 до p/2, а r от 0 до окружности r=2cosj. Таким образом, получаем

Пример 1.6. Вычислить площадь фигуры, ограниченной линией .

Решение. Запишем уравнение линии в полярной системе координат

,

т.е.

.

Построим эту линию (рис. 1.7). Поскольку полученная формула симметрична относительно осей Ox и Oy, то достаточно вычислить площадь четвертой части этой фигуры, а затем умножить полученный результат на 4:

.

2. ТРОЙНЫЕ ИНТЕГРАЛЫ

2.1. Определение и вычисление тройных интегралов в декартовой системе координат

По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть в некоторой замкнутой ограниченной области T трехмерного пространства задана ограниченная функция трех переменных f(x,y,z). Разобьем эту область на n произвольных частей с объемами Dv_i. В каждой частичной области возьмем произвольную точку M(x_i,y_i,z_i) и составим сумму:

,

которая называется интегральной суммой для функции f(x,y,z) по области T. Если интегральная сумма при n®¥ (при этом диаметры всех областей должны стремится к нулю: ) имеет предел, то этот предел называется тройным интегралом:

. (2.1)

Отметим, что тройные интегралы обладают свойствами, аналогичные свойствам двойных интегралов.

Предположим, что область T является простой в направлении оси Oz, т.е. любая прямая, проведенная параллельно оси Oz, пересекает границу области T не более чем в двух точках. Это означает, что область T ограничена снизу поверхностью z=z₁(x,y), сверху поверхностью z=z₂(x,y) и с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. Тогда тройной интеграл можно записать в виде

. (2.2)

Отметим, что здесь внешний интеграл обязательно (!) должен иметь постоянные пределы (т.е. числа), пределы во втором интеграле могут зависеть только от той переменной, которая стоит во внешнем интеграле.

Если в тройном интеграле подынтегральная функция f(x,y,z)º1, то тройной интеграл будет равен объему области интегрирования T, т.е.

. (2.3)

При вычислении тройных интегралов следует:

1) сделать чертеж области интегрирования T;

2) изобразить проекцию области T на выбранную координатную плоскость;

3) расставить пределы интегрирования.

Пример 2.1. Вычислить

, если

5.3 Двойные интегралы в полярных координатах. Расчет, том 3

Цели обучения

• 5.3.1 Распознать формат двойного интеграла по полярной прямоугольной области.
• 5.3.2 Вычислите двойной интеграл в полярных координатах с помощью повторного интеграла.
• 5.3.3 Распознать формат двойного интеграла по общей полярной области.
• 5.3.4 Используйте двойные интегралы в полярных координатах для вычисления площадей и объемов.

Двойные интегралы иногда гораздо проще вычислить, если мы заменим прямоугольные координаты на полярные. Однако, прежде чем мы опишем, как сделать это изменение, нам нужно установить понятие двойного интеграла в полярной прямоугольной области.

Полярные прямоугольные области интегрирования

Когда мы определили двойной интеграл для непрерывной функции в прямоугольных координатах — скажем, gg по области RR в плоскости xyxy — мы разделили RR на подпрямоугольники со сторонами, параллельными осям координат. Эти стороны имеют либо постоянные значения xx, либо постоянные значения yy. В полярных координатах фигура, с которой мы работаем, представляет собой полярный прямоугольник, стороны которого имеют постоянные значения rr и/или постоянные значения θθ. Это означает, что мы можем описать полярный прямоугольник, как показано на рис. 5.28(а), где R={(r,θ)|a≤r≤b,α≤θ≤β}.R={(r,θ)|a≤ r≤b,α≤θ≤β}.

В этом разделе мы рассматриваем возможность интегрирования по полярным прямоугольникам. Рассмотрим функцию f(r,θ)f(r,θ) над полярным прямоугольником R.R. Разобьем интервал [a,b][a,b] на мм подинтервалы [ri−1,ri][ri−1,ri ] длины Δr=(b−a)/mΔr=(b−a)/m и разобьем интервал [α,β][α,β] на nn подинтервалов [θj−1,θj][θj−1,θj ] ширины Δθ=(β−α)/n. Δθ=(β−α)/n. Это означает, что окружности r=rir=ri и лучи θ=θjθ=θj для 1≤i≤m1≤i≤m и 1≤j≤n1≤j≤n делят полярный прямоугольник RR на меньшие полярные подпрямоугольники RijRij (рис. 5.28). (б)).

Рисунок 5,28 (а) Полярный прямоугольник RR (б), разделенный на подпрямоугольники Rij.Rij. (c) Крупный план подпрямоугольника.

Как и ранее, нужно найти площадь ΔAΔA полярного подпрямоугольника RijRij и «полярный» объем тонкого прямоугольника над Rij.Rij. Напомним, что в окружности радиуса r,r длина дуги ss, опирающейся на центральный угол θθ радиан, равна s=rθ.s=rθ. Обратите внимание, что полярный прямоугольник RijRij очень похож на трапецию с параллельными сторонами ri−1Δθri−1Δθ и riΔθriΔθ и шириной Δr.Δr. Следовательно, площадь полярного подпрямоугольника RijRij равна

ΔA=12Δr(ri-1Δθ+r1Δθ).ΔA=12Δr(ri-1Δθ+r1Δθ).

Упрощая и полагая rij*=12(ri−1+ri),rij*=12(ri−1+ri), мы имеем ΔA=rij*ΔrΔθ.ΔA=rij*ΔrΔθ. Следовательно, полярный объем тонкого ящика над RijRij (рис. 5.29) равен

f(rij*,θij*)ΔA=f(rij*,θij*)rij*ΔrΔθ.f(rij*,θij*)ΔA=f(rij*,θij*)rij*ΔrΔθ.

Рисунок 5.29 Нахождение объема тонкого ящика над полярным прямоугольником Rij.Rij.

Используя ту же идею для всех подпрямоугольников и суммируя объемы прямоугольных ящиков, мы получаем двойную сумму Римана как

∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.

Как мы видели ранее, мы получаем лучшее приближение к полярному объему твердого тела над областью RR, когда мы позволяем mm и nn увеличиваться. Следовательно, мы определяем полярный объем как предел двойной суммы Римана,

V=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.V=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij *ΔrΔθ.

Это становится выражением для двойного интеграла.

Определение

Двойной интеграл функции f(r,θ)f(r,θ) по полярной прямоугольной области RR в плоскости rθrθ определяется как

∬Rf(r,θ)dA=limm,n→∞ ∑i=1m∑j=1nf(rij*,θij*)ΔA=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ. ∬Rf(r,θ)dA= limm,n→∞∑i=1m∑j=1nf(rij*,θij*)ΔA=limm,n→∞∑i=1m∑j=1nf(rij*,θij*)rij*ΔrΔθ.

(5.8)

Опять же, как и в случае с двойными интегралами по прямоугольным областям, двойной интеграл по полярной прямоугольной области может быть выражен как повторный интеграл в полярных координатах. Следовательно,

∬Rf(r,θ)dA=∬Rf(r,θ)rdrdθ=∫θ=αθ=β∫r=ar=bf(r,θ)rdrdθ.∬Rf(r,θ)dA=∬Rf( r,θ)rdrdθ=∫θ=αθ=β∫r=ar=bf(r,θ)rdrdθ.

Обратите внимание, что выражение для dAdA заменяется на rdrdθrdrdθ при работе в полярных координатах. Другой способ взглянуть на двойной полярный интеграл — изменить двойной интеграл в прямоугольных координатах подстановкой. Когда функция ff задана через xx и y, y, использование x=rcosθ,y=rsinθ и dA=rdrdθx=rcosθ,y=rsinθ и dA=rdrdθ изменяет ее на

.

∬Rf(x,y)dA=∬Rf(rcosθ,rsinθ)rdrdθ.∬Rf(x,y)dA=∬Rf(rcosθ,rsinθ)rdrdθ.

Обратите внимание, что все свойства, перечисленные в разделе Двойные интегралы по прямоугольным областям для двойного интеграла в прямоугольных координатах, справедливы и для двойного интеграла в полярных координатах, так что мы можем использовать их без колебаний.

Пример 5.24

Эскиз полярной прямоугольной области

Эскиз полярной прямоугольной области R={(r,θ)|1≤r≤3,0≤θ≤π}.R={(r,θ)|1≤r≤3 ,0≤θ≤π}.

Решение

Как видно из рис. 5.30, r=1r=1 и r=3r=3 — это окружности радиусов 1, 31 и 3, а 0≤θ≤π0≤θ≤π покрывает всю верхнюю половину плоскости. Следовательно, область RR выглядит как полукруглая полоса.

Рисунок 5.30 Полярная область RR лежит между двумя полуокружностями.

Теперь, когда мы нарисовали полярную прямоугольную область, давайте продемонстрируем, как вычислить двойной интеграл по этой области, используя полярные координаты.

Пример 5,25

Вычисление двойного интеграла по полярной прямоугольной области

Вычисление интеграла ∬R3xdA∬R3xdA по области R={(r,θ)|1≤r≤2,0≤θ≤π}.R={(r ,θ)|1≤r≤2,0≤θ≤π}.

Решение

Сначала нарисуем фигуру, аналогичную рисунку 5. 30, но с внешним радиусом 2.2. Из рисунка видно, что имеем

∬R3xdA=∫θ=0θ=π∫r=1r=23rcosθrdrdθИспользуем повторный интеграл с правильными пределами интегрирования.=∫θ=0θ=πcosθ[r3|r=1r=2] dθПроинтегрировать сначала по tor.=∫θ=0θ=π7cosθdθ=7sinθ|θ=0θ=π=0.∬R3xdA=∫θ=0θ=π∫r=1r=23rcosθrdrdθИспользовать повторный интеграл с правильными пределами интегрирования.=∫θ =0θ=πcosθ[r3|r=1r=2]dθПроинтегрируем сначала по tor.=∫θ=0θ=π7cosθdθ=7sinθ|θ=0θ=π=0.

Контрольно-пропускной пункт 5.17

Зарисовать область R={(r,θ)|1≤r≤2,−π2≤θ≤π2},R={(r,θ)|1≤r≤2,−π2≤θ≤π2} , и вычислить ∬RxdA.∬RxdA.

Пример 5.26

Вычисление двойного интеграла путем преобразования прямоугольных координат

Вычисление интеграла ∬R(1−x2−y2)dA∬R(1−x2−y2)dA, где RR — единичная окружность на плоскости xyxy.

Решение

Область RR представляет собой единичную окружность, поэтому мы можем описать ее как R={(r,θ)|0≤r≤1,0≤θ≤2π}. R={(r,θ)|0≤r≤ 1,0≤θ≤2π}.

Используя преобразование x=rcosθ,y=rsinθ,x=rcosθ,y=rsinθ и dA=rdrdθ,dA=rdrdθ, получаем

∬R(1−x2−y2)dA=∫02π∫01( 1−r2)rdrdθ=∫02π∫01(r−r3)drdθ=∫02π[r22−r44]01dθ=∫02π14dθ=π2.∬R(1−x2−y2)dA=∫02π∫01(1−r2 )rdrdθ=∫02π∫01(r−r3)drdθ=∫02π[r22−r44]01dθ=∫02π14dθ=π2.

Пример 5.27

Вычисление двойного интеграла путем преобразования прямоугольных координат

Вычисление интеграла ∬R(x+y)dA∬R(x+y)dA, где R={(x,y)|1≤x2+y2≤4, x≤0}.R={(x,y)|1≤x2+y2≤4,x≤0}.

Решение

Мы видим, что RR представляет собой кольцевую область, которую можно преобразовать в полярные координаты и описать как R={(r,θ)|1≤r≤2,π2≤θ≤3π2}R={(r,θ)| 1≤r≤2,π2≤θ≤3π2} (см. следующий график).

Рисунок 5.31 Кольцевая область интегрирования R.R.

Отсюда, используя преобразование x=rcosθ,y=rsinθ,x=rcosθ,y=rsinθ и dA=rdrdθ,dA=rdrdθ, имеем

∬R(x+y)dA =∫θ=π/2θ=3π/2∫r=1r=2(rcosθ+rsinθ)rdrdθ=(∫r=1r=2r2dr)(∫π/23π/2(cosθ+sinθ)dθ)=[r33] 12[sinθ−cosθ]|π/23π/2=−143. ∬R(x+y)dA=∫θ=π/2θ=3π/2∫r=1r=2(rcosθ+rsinθ)rdrdθ=(∫ r=1r=2r2dr)(∫π/23π/2(cosθ+sinθ)dθ)=[r33]12[sinθ−cosθ]|π/23π/2=−143.

Контрольно-пропускной пункт 5.18

Вычислите интеграл ∬R(4−x2−y2)dA∬R(4−x2−y2)dA, где RR — окружность радиуса 22 на плоскости xyxy.

Общие полярные регионы интеграции

Чтобы вычислить двойной интеграл непрерывной функции с помощью повторных интегралов по общим полярным областям, мы рассмотрим два типа областей, аналогичных типам I и II, как обсуждалось для прямоугольных координат в Двойных интегралах по общим областям. Чаще записывают полярные уравнения как r=f(θ)r=f(θ), чем θ=f(r),θ=f(r), поэтому мы описываем общую полярную область как R={(r, θ)|α≤θ≤β,h2(θ)≤r≤h3(θ)}R={(r,θ)|α≤θ≤β,h2(θ)≤r≤h3(θ)} (см. следующий рисунок).

Рисунок 5.32 Общая полярная область между α<θ<βα<θ<β и h2(θ)

Теорема 5,8

Двойные интегралы по общим полярным областям

Если f(r,θ)f(r,θ) непрерывна на общей полярной области DD, как описано выше, то

∬Df(r,θ)rdrdθ=∫θ=αθ=β∫r=h2( θ)r=h3(θ)f(r,θ)rdrdθ∬Df(r,θ)rdrdθ=∫θ=αθ=β∫r=h2(θ)r=h3(θ)f(r,θ)rdrdθ

(5,9)

Пример 5,28

Вычисление двойного интеграла по общей полярной области

Вычислите интеграл ∬Dr2sinθrdrdθ∬Dr2sinθrdrdθ, где DD — область, ограниченная полярной осью и верхней половиной кардиоиды r=1+cosθ. r=1+cosθ.

Решение

Мы можем описать область DD как {(r, θ)|0≤θ≤π,0≤r≤1+cosθ}{(r,θ)|0≤θ≤π,0≤r≤1+cosθ} как показано на следующем рисунке.

Рисунок 5.33 Область DD — это верхняя половина кардиоиды.

Следовательно, имеем

∬Dr2sinθrdrdθ=∫θ=0θ=π∫r=0r=1+cosθ(r2sinθ)rdrdθ=14∫θ=0θ=π[r4]r=0r=1+cosθsinθdθ=14∫θ=0θ=π( 1+cosθ)4sinθdθ=−14[(1+cosθ)55]0π=85.∬Dr2sinθrdrdθ=∫θ=0θ=π∫r=0r=1+cosθ(r2sinθ)rdrdθ=14∫θ=0θ=π[ r4]r=0r=1+cosθsinθdθ=14∫θ=0θ=π(1+cosθ)4sinθdθ=−14[(1+cosθ)55]0π=85.

Контрольно-пропускной пункт 5.19

Вычислить интеграл

∬Dr2sin22θrdrdθwhereD={(r,θ)|-π4≤θ≤π4, 0≤r≤2cos2θ}. r≤2cos2θ}.

Полярные районы и объемы

Как и в прямоугольных координатах, если твердое СС ограничено поверхностью z=f(r,θ),z=f(r,θ), а также поверхностями r=a,r=b,θ=α ,r=a,r=b,θ=α и θ=β,θ=β, можно найти объем VV СС путем двойного интегрирования, как

V=∬Rf(r,θ)rdrdθ=∫θ=αθ=β∫r=ar=bf(r,θ)rdrdθ. V=∬Rf(r,θ)rdrdθ=∫θ=αθ=β∫r =ar=bf(r,θ)rdrdθ.

Если основание твердого тела можно описать как D={(r,θ)|α≤θ≤β,h2(θ)≤r≤h3(θ)},D={(r,θ)|α≤ θ≤β,h2(θ)≤r≤h3(θ)}, то двойной интеграл для объема становится равным

V=∬Df(r,θ)rdrdθ=∫θ=αθ=β∫r=h2(θ)r=h3(θ)f(r,θ)rdrdθ.V=∬Df(r,θ)rdrdθ= ∫θ=αθ=β∫r=h2(θ)r=h3(θ)f(r,θ)rdrdθ.

Проиллюстрируем эту мысль несколькими примерами.

Пример 5.29

Нахождение объема с помощью двойного интеграла

Найдите объем твердого тела, лежащего под параболоидом z=1−x2−y2z=1−x2−y2 и над единичной окружностью на плоскости xyxy (см. следующий рисунок ).

Рисунок 5,34 Параболоид z=1−x2−y2z=1−x2−y2.

Решение

Методом двойного интегрирования видим, что объем есть повторный интеграл вида ∬R(1−x2−y2)dA∬R(1−x2−y2)dA, где R={(r,θ) |0≤r≤1,0≤θ≤2π}.R={(r,θ)|0≤r≤1,0≤θ≤2π}.

Это интегрирование было показано ранее в примере 5.26, поэтому объем равен π2π2 кубических единиц.

Пример 5.30

Нахождение объема с помощью двойного интегрирования

Найдите объем твердого тела, лежащего под параболоидом z=4−x2−y2z=4−x2−y2 и над диском (x−1)2+y2=1(x −1)2+y2=1 на плоскости xyxy. См. параболоид на рис. 5.35, пересекающий цилиндр (x−1)2+y2=1(x−1)2+y2=1 над плоскостью xyxy.

Рисунок 5,35 Нахождение объема тела с параболоидной шапкой и круглым основанием.

Решение

Сначала измените диск (x−1)2+y2=1(x−1)2+y2=1 на полярные координаты. Расширяя квадратный член, мы имеем x2−2x+1+y2=1.x2−2x+1+y2=1. Затем упростите, чтобы получить x2+y2=2x,x2+y2=2x, что в полярных координатах становится r2=2rcosθr2=2rcosθ, а затем либо r=0r=0, либо r=2cosθ.r=2cosθ. Точно так же уравнение параболоида меняется на z=4−r2.z=4−r2. Поэтому мы можем описать круг (x−1)2+y2=1(x−1)2+y2=1 на плоскости xyxy как область

D={(r,θ)|0≤θ≤π ,0≤r≤2cosθ}.D={(r,θ)|0≤θ≤π,0≤r≤2cosθ}.

Отсюда объем твердого тела, ограниченного сверху параболоидом z=4−x2−y2z=4−x2−y2 и снизу r=2cosθr=2cosθ, равен

V=∬Df(r,θ)rdrdθ=∫θ =0θ=π∫r=0r=2cosθ(4−r2)rdrdθ=∫θ=0θ=π[4r22−r44|02cosθ]dθ=∫0π[8cos2θ−4cos2θ]dθ=[52θ+52sinθcosθ−sinθcos3θ]0π= 52π.V=∬Df(r,θ)rdrdθ=∫θ=0θ=π∫r=0r=2cosθ(4−r2)rdrdθ=∫θ=0θ=π[4r22−r44|02cosθ]dθ=∫0π[ 8cos2θ−4cos2θ]dθ=[52θ+52sinθcosθ−sinθcos3θ]0π=52π.

Обратите внимание, что в следующем примере интегрирование с полярными координатами не всегда просто. Сложность интеграции зависит от функции, а также от региона, по которому нам нужно выполнить интеграцию. Если область имеет более естественное выражение в полярных координатах или если ff имеет более простую первообразную в полярных координатах, то изменение полярных координат уместно; в противном случае используйте прямоугольные координаты.

Пример 5.31

Нахождение объема с помощью двойного интеграла

Нахождение объема области, лежащей под параболоидом z=x2+y2z=x2+y2 и над треугольником, заключенным линиями y=x,x=0,y=x ,x=0 и x+y=2x+y=2 в плоскости xyxy (рис. 5.36).

Решение

Сначала исследуем область, по которой нам нужно установить двойной интеграл и сопутствующий ему параболоид.

Рисунок 5,36 Нахождение объема тела под параболоидом и над данным треугольником.

Область DD равна {(x,y)|0≤x≤1,x≤y≤2−x}.{(x,y)|0≤x≤1,x≤y≤2−x}. Преобразуя линии y=x,x=0,y=x,x=0 и x+y=2x+y=2 в плоскости xyxy в функции от rr и θ,θ, мы имеем θ=π/4 ,θ=π/4,θ=π/2,θ=π/2 и r=2/(cosθ+sinθ),r=2/(cosθ+sinθ) соответственно. Нарисовав область на плоскости xyxy, мы видим, что она имеет вид D={(r,θ)|π/4≤θ≤π/2,0≤r≤2/(cosθ+sinθ)}.D={ (r,θ)|π/4≤θ≤π/2,0≤r≤2/(cosθ+sinθ)}. Теперь преобразование уравнения поверхности дает z=x2+y2=r2.z=x2+y2=r2. Следовательно, объем твердого тела определяется двойным интегралом

V=∬Df(r,θ)rdrdθ=∫θ=π/4θ=π/2∫r=0r=2/(cosθ+sinθ)r2rdrdθ=∫π/4π/2[r44]02/(cosθ +sinθ)dθ=14∫π/4π/2(2cosθ+sinθ)4dθ=164∫π/4π/2(1cosθ+sinθ)4dθ=4∫π/4π/2(1cosθ+sinθ)4dθ.V=∬ Df(r,θ)rdrdθ=∫θ=π/4θ=π/2∫r=0r=2/(cosθ+sinθ)r2rdrdθ=∫π/4π/2[r44]02/(cosθ+sinθ)dθ= 14∫π/4π/2(2cosθ+sinθ)4dθ=164∫π/4π/2(1cosθ+sinθ)4dθ=4∫π/4π/2(1cosθ+sinθ)4dθ.

Как видите, этот интеграл очень сложен. Таким образом, мы можем вместо этого вычислить этот двойной интеграл в прямоугольных координатах как

V=∫01∫x2−x(x2+y2)dydx.V=∫01∫x2−x(x2+y2)dydx.

Оценка дает

V=∫01∫x2−x(x2+y2)dydx=∫01[x2y+y33]|x2−xdx=∫0183−4x+4×2−8x33dx=[8×3−2×2+4×33−2×43 ]|01=43.V=∫01∫x2−x(x2+y2)dydx=∫01[x2y+y33]|x2−xdx=∫0183−4x+4×2−8x33dx=[8×3−2×2+4×33−2×43 ]|01=43.

Чтобы ответить на вопрос, как находятся формулы объемов различных стандартных тел, таких как сфера, конус или цилиндр, мы хотим продемонстрировать пример и найти объем произвольного конуса.

Пример 5.32

Нахождение объема с помощью двойного интеграла

Используйте полярные координаты, чтобы найти объем внутри конуса z=2−x2+y2z=2−x2+y2 и выше xy-plane.xy-plane.

Решение

Область DD для интегрирования является основанием конуса, который выглядит как окружность на плоскости xy-xy (см. следующий рисунок).

Рисунок 5,37 Нахождение объема твердого тела внутри конуса над плоскостью xyxy.

Находим уравнение окружности, полагая z=0:z=0:

0=2−x2+y22=x2+y2x2+y2=4.0=2−x2+y22=x2+y2x2+y2=4 .

Это означает, что радиус окружности равен 2,2, поэтому для интегрирования мы имеем 0≤θ≤2π0≤θ≤2π и 0≤r≤2.0≤r≤2. Подставив x=rcosθx=rcosθ и y=rsinθy=rsinθ в уравнение z=2−x2+y2z=2−x2+y2, мы получим z=2−r.z=2−r. Следовательно, объем конуса равен

∫θ=0θ=2π∫r=0r=2(2−r)rdrdθ=2π43=8π3∫θ=0θ=2π∫r=0r=2(2−r)rdrdθ =2π43=8π3 кубических единиц.

Анализ

Обратите внимание, что если бы нам нужно было найти объем произвольного конуса с радиусом aa единиц и высотой hh единиц, то уравнение конуса было бы z=h−hax2+y2.z=h−hax2+y2.

Мы по-прежнему можем использовать рис. 5.37 и представить интеграл как rdrdθ.

Вычисляя интеграл, получаем 13πa2h.13πa2h.

Контрольно-пропускной пункт 5.

20

Используйте полярные координаты, чтобы найти повторный интеграл для нахождения объема твердого тела, заключенного в параболоиды z=x2+y2z=x2+y2 и z=16−x2−y2.z=16−x2−y2.

Как и в случае с прямоугольными координатами, мы также можем использовать полярные координаты для нахождения площадей определенных регионов с помощью двойного интеграла. Как и прежде, нам нужно понять область, площадь которой мы хотим вычислить. Набросок графика и определение области может помочь понять пределы интегрирования. В общем случае формула площади при двойном интегрировании будет иметь вид 9.0015

AreaA=∫αβ∫h2(θ)h3(θ)1rdrdθ. AreaA=∫αβ∫h2(θ)h3(θ)1rdrdθ.

Пример 5.33

Нахождение площади с помощью двойного интеграла в полярных координатах

Оценить площадь, ограниченную кривой r=cos4θ.r=cos4θ.

Решение

Набросав график функции r=cos4θr=cos4θ, можно увидеть, что это полярная роза с восемью лепестками (см. следующий рисунок).

Рисунок 5,38 Нахождение площади полярной розы с восемью лепестками.

Используя симметрию, мы видим, что нам нужно найти площадь одного лепестка, а затем умножить ее на 8,8. Обратите внимание, что значения θθ, при которых график проходит через начало координат, являются нулями функции cos4θ, cos4θ и являются нечетными кратными π/8.π/8. Таким образом, один из лепестков соответствует значениям θθ в интервале [−π/8,π/8].[−π/8,π/8]. Следовательно, площадь, ограниченная кривой r=cos4θr=cos4θ, равна

A=8∫θ=−π/8θ=π/8∫r=0r=cos4θ1rdrdθ=8∫−π/8π/8[12r2|0cos4θ] dθ=8∫−π/8π/812cos24θdθ=8[14θ+116sin4θcos4θ|−π/8π/8]=8[π16]=π2.A=8∫θ=−π/8θ=π/8∫r=0r =cos4θ1rdrdθ=8∫−π/8π/8[12r2|0cos4θ]dθ=8∫−π/8π/812cos24θdθ=8[14θ+116sin4θcos4θ|−π/8π/8]=8[π16]=π2.

Пример 5,34

Нахождение площади между двумя полярными кривыми

Найдите площадь, заключенную в окружность r=3cosθr=3cosθ и кардиоиду r=1+cosθ.r=1+cosθ.

Решение

Прежде всего нарисуйте графы области (рис. 5.39).

Рисунок 5,39 Нахождение площади, ограниченной как кругом, так и кардиоидой.

Из симметрии графа видно, что нам нужно найти точки пересечения. Приравнивание двух уравнений друг к другу дает

3cosθ=1+cosθ.3cosθ=1+cosθ.

Одна из точек пересечения θ=π/3.θ=π/3. Область над полярной осью состоит из двух частей: одна часть определяется кардиоидой от θ=0θ=0 до θ=π/3θ=π/3, а другая часть определяется окружностью от θ=π/3θ=π /3 к θ=π/2.θ=π/2. По симметрии общая площадь в два раза больше площади над полярной осью. Таким образом, имеем

A=2[∫θ=0θ=π/3∫r=0r=1+cosθ1rdrdθ+∫θ=π/3θ=π/2∫r=0r=3cosθ1rdrdθ].A=2[∫ θ=0θ=π/3∫r=0r=1+cosθ1rdrdθ+∫θ=π/3θ=π/2∫r=0r=3cosθ1rdrdθ].

Оценивая каждую часть отдельно, получаем, что площадь равна

A=2(14π+9163+38π−9163)=2(58π)=54πквадратных единиц.A=2(14π+9163+38π−9163)=2 (58π)=54πквадратных единиц.

Контрольно-пропускной пункт 5.21

Найдите площадь, заключенную внутри кардиоиды r=3−3sinθr=3−3sinθ и вне кардиоиды r=1+sinθ.r=1+sinθ.

Пример 5,35

Вычисление неправильного двойного интеграла в полярных координатах

Вычисление интеграла ∬R2e−10(x2+y2)dxdy.∬R2e−10(x2+y2)dxdy.

Решение

Это неправильный интеграл, потому что мы интегрируем по неограниченной области R2.R2. В полярных координатах всю плоскость R2R2 можно рассматривать как 0≤θ≤2π,0≤θ≤2π,0≤r≤∞.0≤r≤∞.

Используя замену прямоугольных координат на полярные, получаем 2π(лима→∞∫r=0r=ae−10r2rdr)dθ=(∫θ=0θ=2πdθ)(lima→∞∫r=0r=ae−10r2rdr)=2π(lima→∞∫r=0r=ae− 10r2rdr)=2πlima→∞(−120)(e−10r2|0a)=2π(−120)lima→∞(e−10a2−1)=π10.∬R2e−10(x2+y2)dxdy=∫θ= 0θ=2π∫r=0r=∞e−10r2rdrdθ=∫θ=0θ=2π(лима→∞∫r=0r=ae−10r2rdr)dθ=(∫θ=0θ=2πdθ)(lima→∞∫r=0r =ae−10r2rdr)=2π(lima→∞∫r=0r=ae−10r2rdr)=2πlima→∞(−120)(e−10r2|0a)=2π(−120)lima→∞(e−10a2−1 )=π10.

Контрольно-пропускной пункт 5.22

Вычислить интеграл ∬R2e−4(x2+y2)dxdy.∬R2e−4(x2+y2)dxdy.

Раздел 5.3 Упражнения

В следующих упражнениях выразите область DD в полярных координатах.

122.

DD — это область диска радиусом 22 с центром в начале координат, которая находится в первом квадранте.

123.

DD — это область между окружностями радиусом 44 и радиусом 55 с центром в начале координат, который находится во втором квадранте.

124.

DD — область, ограниченная осью yy и x=1−y2.x=1−y2.

125.

DD — область, ограниченная осью xx и y=2−x2.y=2−x2.

126.

D={(x,y)|x2+y2≤4x}D={(x,y)|x2+y2≤4x}

127.

D={(x,y)|x2+y2≤4y}D={(x,y)|x2+y2≤4y}

В следующих упражнениях дан график полярной прямоугольной области DD. Выразите ДД в полярных координатах.

128.

129.

130.

131.

132.

На следующем графике область DD расположена ниже точки y=xy=x и ограничена точками x=1,x=5,x=1,x=5 и y=0.y=0.

133.

На следующем графике область DD ограничена y=xy=x и y=x2.y=x2.

В следующих упражнениях вычислите двойной интеграл ∬Rf(x,y)dA∬Rf(x,y)dA по полярной прямоугольной области D.D.

134.

f(x,y)=x2+y2,D={(r,θ)|3≤r≤5,0≤θ≤2π}f(x,y)=x2+y2,D={(r,θ) )|3≤r≤5,0≤θ≤2π}

135.

f(x,y)=x+y,D={(r,θ)|3≤r≤5,0≤θ≤2π}f(x,y)=x+y,D={(r,θ) )|3≤r≤5,0≤θ≤2π}

136.

f(x,y)=x2+xy,D={(r,θ)|1≤r≤2,π≤θ≤2π}f(x,y)=x2+xy,D={(r,θ) )|1≤r≤2,π≤θ≤2π}

137.

f(x,y)=x4+y4,D={(r,θ)|1≤r≤2,3π2≤θ≤2π}f(x,y)=x4+y4,D={(r,θ) )|1≤r≤2,3π2≤θ≤2π}

138.

f(x,y)=x2+y23,f(x,y)=x2+y23, где D={(r,θ)|0≤r≤1,π2≤θ≤π}.D={ (r,θ)|0≤r≤1,π2≤θ≤π}.

139.

f(x,y)=x4+2x2y2+y4,f(x,y)=x4+2x2y2+y4, где D={(r,θ)|3≤r≤4,π3≤θ≤2π3} .D={(r,θ)|3≤r≤4,π3≤θ≤2π3}.

140.

f(x,y)=sin(arctanyx),f(x,y)=sin(arctanyx), где D={(r,θ)|1≤r≤2,π6≤θ≤π3}D= {(r,θ)|1≤r≤2,π6≤θ≤π3}

141.

f(x,y)=arctan(yx),f(x,y)=arctan(yx), где D={(r,θ)|2≤r≤3,π4≤θ≤π3}D= {(r,θ)|2≤r≤3,π4≤θ≤π3}

142.

∬Dex2+y2[1+2arctan(yx)]dA,D={(r,θ)|1≤r≤2,π6≤θ≤π3}∬Dex2+y2[1+2arctan(yx)]dA,D ={(r,θ)|1≤r≤2,π6≤θ≤π3}

143.

∬D(ex2+y2+x4+2x2y2+y4)arctan(yx)dA,D={(r,θ)|1≤r≤2,π4≤θ≤π3}∬D(ex2+y2+x4+2x2y2 +y4)arctan(yx)dA,D={(r,θ)|1≤r≤2,π4≤θ≤π3}

В следующих упражнениях интегралы были преобразованы в полярные координаты. Убедитесь, что тождества верны, и выберите самый простой способ вычисления интегралов в прямоугольных или полярных координатах.

144.

∫12∫0x(x2+y2)dydx=∫0π4∫secθ2secθr3drdθ∫12∫0x(x2+y2)dydx=∫0π4∫secθ2secθr3drdθ

145.

∫23∫0xxx2+y2dydx=∫0π/4∫2secθ3secθrcosθdrdθ∫23∫0xxx2+y2dydx=∫0π/4∫2secθ3secθrcosθdrdθ

146.

∫01∫x2x1x2+y2dydx=∫0π/4∫0tanθsecθdrdθ∫01∫x2x1x2+y2dydx=∫0π/4∫0tanθsecθdrdθ

147.

∫01∫x2xyx2+y2dydx=∫0π/4∫0tanθsecθrsinθdrdθ∫01∫x2xyx2+y2dydx=∫0π/4∫0tanθsecθrsinθdrdθ

В следующих упражнениях преобразуйте интегралы в полярные координаты и оцените их.

148.

∫03∫09−y2(x2+y2)dxdy∫03∫09−y2(x2+y2)dxdy

149.

∫02∫−4−y24−y2(x2+y2)2dxdy∫02∫−4−y24−y2(x2+y2)2dxdy

150.

∫01∫01−x2(x+y)dydx∫01∫01−x2(x+y)dydx

151.

∫04∫−16−x216−x2sin(x2+y2)dydx∫04∫−16−x216−x2sin(x2+y2)dydx

152.

Вычислите интеграл ∬DrdA∬DrdA, где DD — область, ограниченная полярной осью и верхней половиной кардиоиды r=1+cosθ.r=1+cosθ.

153.

Найти площадь области DD, ограниченной полярной осью и верхней половиной кардиоиды r=1+cosθ.r=1+cosθ.

154.

Вычислить интеграл ∬DrdA,∬DrdA, где DD — область, ограниченная частью четырехлепестковой розы r=sin2θr=sin2θ, расположенной в первом квадранте (см. следующий рисунок).

155.

Найдите общую площадь области, ограниченной четырехлепестковой розой r=sin2θr=sin2θ (см. рисунок в предыдущем упражнении).

156.

Найдите площадь области D,D, которая является областью, ограниченной y=4−x2,y=4−x2,x=3,x=3,x=2,x=2 и y=0 . у=0.

157.

Найдите площадь области D,D, которая является областью внутри круга x2+y2≤4×2+y2≤4 и справа от линии x=1.x=1.

158.

Определить среднее значение функции f(x,y)=x2+y2f(x,y)=x2+y2 по области DD, ограниченной полярной кривой r=cos2θ,r=cos2θ, где −π4≤θ ≤π4−π4≤θ≤π4 (см. следующий график).

159.

Определить среднее значение функции f(x,y)=x2+y2f(x,y)=x2+y2 по области DD, ограниченной полярной кривой r=3sin2θ,r=3sin2θ, где 0≤θ≤ π20≤θ≤π2 (см. следующий график).

160.

Найти объем тела, расположенного в первой октанте и ограниченного параболоидом z=1−4×2−4y2z=1−4×2−4y2 и плоскостями x=0,y=0,x=0,y=0, и z=0.z=0.

161.

Найти объем твердого тела, ограниченного параболоидом z=2−9×2−9y2z=2−9×2−9y2 и плоскость z=1.z=1.

162.

1. Найдите объем твердого тела S1S1, ограниченного цилиндром x2+y2=1×2+y2=1 и плоскостями z=0z=0 и z=1.z=1.
2. Найти объем твердого тела S2S2 вне двойного конуса z2=x2+y2,z2=x2+y2, внутри цилиндра x2+y2=1,x2+y2=1 и над плоскостью z=0.z=0 .
3. Найдите объем тела внутри конуса z2=x2+y2z2=x2+y2 и ниже плоскости z=1z=1, вычитая объемы тел S1S1 и S2.S2.

163.

1. Найдите объем твердого тела S1S1 внутри единичной сферы x2+y2+z2=1×2+y2+z2=1 и над плоскостью z=0.z=0.
2. Найдите объем твердого тела S2S2 внутри двойного конуса (z−1)2=x2+y2(z−1)2=x2+y2 и над плоскостью z=0.z=0.
3. Найдите объем твердого тела вне двойного конуса (z−1)2=x2+y2(z−1)2=x2+y2 и внутри сферы x2+y2+z2=1.x2+y2+z2=1 .

В следующих двух упражнениях рассмотрим сферическое кольцо, представляющее собой сферу с цилиндрическим отверстием, вырезанным так, что ось цилиндра проходит через центр сферы (см. следующий рисунок).

164.

Если сфера имеет радиус 44, а цилиндр имеет радиус 2,2, найдите объем сферического кольца.

165.

Цилиндрическое отверстие диаметром 66 см просверлено в сфере радиусом 55 см так, что ось цилиндра проходит через центр сферы. Найдите объем получившегося сферического кольца.

166.

Найдите объем тела, лежащего под двойным конусом z2=4×2+4y2,z2=4×2+4y2, внутри цилиндра x2+y2=x,x2+y2=x и над плоскостью z=0.z =0.

167.

Найдите объем тела, лежащего под параболоидом z=x2+y2,z=x2+y2, внутри цилиндра x2+y2=x,x2+y2=x и над плоскостью z=0.z= 0.

168.

Найдите объем твердого тела, лежащего под плоскостью x+y+z=10x+y+z=10 и над диском x2+y2=4x.x2+y2=4x.

169.

Найдите объем твердого тела, лежащего под плоскостью 2x+y+2z=82x+y+2z=8 и над единичным кругом x2+y2=1. x2+y2=1.

170.

Радиальная функция ff — это функция, значение которой в каждой точке зависит только от расстояния между этой точкой и началом системы координат; то есть f(x,y)=g(r),f(x,y)=g(r), где r=x2+y2.r=x2+y2. Покажите, что если ff — непрерывная радиальная функция, то ∬Df(x,y)dA=(θ2−θ1)[G(R2)−G(R1)], ∬Df(x,y)dA=(θ2−θ1 )[G(R2)−G(R1)], где G′(r)=rg(r)G′(r)=rg(r) и (x,y)∈D={(r,θ)| R1≤r≤R2,0≤θ≤2π},(x,y)∈D={(r,θ)|R1≤r≤R2,0≤θ≤2π}, где 0≤R1

171.

Используйте информацию из предыдущего упражнения для вычисления интеграла ∬D(x2+y2)3dA,∬D(x2+y2)3dA, где DD — единичный круг.

172.

Пусть f(x,y)=F′(r)rf(x,y)=F′(r)r — непрерывная радиальная функция, определенная на кольцевой области D={(r,θ)|R1≤r ≤R2,0≤θ≤2π},D={(r,θ)|R1≤r≤R2,0≤θ≤2π}, где r=x2+y2,r=x2+y2,0 ∬Df(x,y)dA=2π[F(R2)−F(R1)].

173.

Примените предыдущее упражнение для вычисления интеграла ∬Dex2+y2x2+y2dxdy,∬Dex2+y2x2+y2dxdy, где DD — кольцевая область между окружностями радиусов 11 и 22, расположенными в третьем квадранте.

174.

Пусть ff — непрерывная функция, которая может быть выражена в полярных координатах как функция только от θθ; то есть f(x,y)=h(θ),f(x,y)=h(θ), где (x,y)∈D={(r,θ)|R1≤r≤R2,θ1 ≤θ≤θ2},(x,y)∈D={(r,θ)|R1≤r≤R2,θ1≤θ≤θ2}, где 0≤R1

175.

Примените предыдущее упражнение для вычисления интеграла ∬Dy2x2dA,∬Dy2x2dA, где D={(r,θ)|1≤r≤2,π6≤θ≤π3}.D={(r,θ)|1≤ r≤2,π6≤θ≤π3}.

176.

Пусть ff — непрерывная функция, которая может быть выражена в полярных координатах как функция только от θθ; то есть f(x,y)=g(r)h(θ),f(x,y)=g(r)h(θ), где (x,y)∈D={(r,θ) |R1≤r≤R2,θ1≤θ≤θ2}(x,y)∈D={(r,θ)|R1≤r≤R2,θ1≤θ≤θ2} с 0≤R1 0≤θ1<θ2≤2π. Покажите, что ∬Df(x,y)dA=[G(R2)−G(R1)][H(θ2)−H(θ1)], ∬Df(x,y)dA=[G(R2)−G (R1)][H(θ2)−H(θ1)], где GG и HH — первообразные gg и h,h соответственно.

177.

Вычислить ∬Darctan(yx)x2+y2dA,∬Darctan(yx)x2+y2dA, где D={(r,θ)|2≤r≤3,π4≤θ≤π3}.D={(r, θ)|2≤r≤3,π4≤θ≤π3}.

178.

Сферическая шапка — это область сферы, расположенная выше или ниже заданной плоскости.

1. Покажите, что объем сферической крышки на рисунке ниже равен 16πh(3a2+h3).16πh(3a2+h3).
   
2. Сферический сегмент – это твердое тело, определяемое пересечением сферы двумя параллельными плоскостями. Если расстояние между плоскостями равно h,h, покажите, что объем сферического сегмента на рисунке ниже равен 16πh(3a2+3b2+h3).16πh(3a2+3b2+h3).
   б.»>

179.

В статистике совместная плотность для двух независимых нормально распределенных событий со средним значением μ=0μ=0 и стандартным распределением σσ определяется как p(x,y)=12πσ2e−x2+y22σ2. p(x,y) =12πσ2e−x2+y22σ2. Рассмотрим (X, Y), (X, Y) декартовы координаты шара в положении покоя после того, как он был выпущен из положения на оси z по направлению к плоскости xyxy. Предположим, что координаты мяча независимо распределены нормально со средним значением μ=0μ=0 и стандартным отклонением σσ (в футах). Вероятность того, что мяч остановится на расстоянии не более чем aa футов от начала координат, определяется как P[X2+Y2≤a2]=∬Dp(x,y)dydx,P[X2+Y2≤a2]=∬Dp(x, y)dydx, где DD — диск радиуса a с центром в начале координат. Покажите, что P[X2+Y2≤a2]=1−e−a2/2σ2.P[X2+Y2≤a2]=1−e−a2/2σ2.

180.

Двойной несобственный интеграл ∫−∞∞∫−∞∞e−(x2+y2)/2dydx∫−∞∞∫−∞∞e−(x2+y2)/2dydx может быть определен как предельное значение двойного интегралы ∬Dae−(x2+y2)/2dA∬Dae−(x2+y2)/2dA по кругам DaDa радиусов a с центром в начале координат, при a неограниченно возрастают; то есть ∫−∞∞∫−∞∞e−(x2+y2)/2dydx=lima→∞∬Dae−(x2+y2)/2dA. ∫−∞∞∫−∞∞e−(x2+y2) /2dydx=lima→∞∬Dae−(x2+y2)/2dA.

1. Используйте полярные координаты, чтобы показать, что ∫−∞∞∫−∞∞e−(x2+y2)/2dydx=2π.∫−∞∞∫−∞∞e−(x2+y2)/2dydx=2π.
2. Покажите, что ∫−∞∞e−x2/2dx=2π,∫−∞∞e−x2/2dx=2π, используя соотношение ∫−∞∞∫−∞∞e−(x2+y2)/2dydx=( ∫−∞∞e−x2/2dx)(∫−∞∞e−y2/2dy).∫−∞∞∫−∞∞e−(x2+y2)/2dydx=(∫−∞∞e−x2/2dx )(∫−∞∞e−y2/2dy).

Двойные интегралы в полярных координатах

Одним из частных случаев замены переменных является переход от декартовой к полярной системе координат (рис. 1):

\[x = r\cos \theta ,\;\;y = r\sin \theta .\]

Рис. 1.

Определитель Якоби для этого преобразования равен

.

\[ \ frac {{\ парциальное \ влево ( {x, y} \ right)}} {{\ парциальное \ влево ( {r, \ theta} \ right)}} = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное х}} {{\ парциальное г}}} & {\ гидроразрыва {{\ парциальное х}} {{\ парциальное \ тета}}} \\ {\ гидроразрыва {{\ парциальное у}} {{\ парциальное г}}} & {\ гидроразрыва {{\ парциальное у}} {{\ парциальное \ тета}}} \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} {\ гидроразрыва {{\ парциальное \ влево ( {г \ соз \ тета} \ вправо)}} {{\ парциальное г}}} & {\ гидроразрыва {{\ парциальное \ влево ( {г \ соз \ тета} \ вправо )}}{{\partial \theta}}}\\ {\ гидроразрыва {{\ парциальное \ влево ({г \ грех \ тета} \ вправо)}}} {{\ парциальное г}}} & {\ гидроразрыва {{\ парциальное \ влево ( {г \ грех \ тета} \ вправо )}}{{\partial \theta}}} \end{массив}} \right| = \ влево | {\начать{массив}{*{20}{с}} {\ соз \ тета} & { — г \ грех \ тета} \\ {\ грех \ тета} & {г \ соз \ тета} \end{массив}} \right| = \cos \theta \cdot r\cos \theta — \left( { — r\sin \theta } \right) \cdot \sin \theta знак равно г \, {\ соз ^ 2} \ тета + г \, {\ грех ^ 2} \ тета = r \ left ( {{{\ cos } ^ 2} \ theta + {{\ sin } ^ 2} \ theta } \ right) = r. {b} {f\left( { r\cos\theta ,r\sin\theta } \right)rdrd\theta } } .\] 92}} \right)dydx}\] путем преобразования в полярные координаты. Областью интегрирования \(R\) является сектор \(0 \le \theta \le {\frac{\pi }{2}}\) окружности с радиусом \(r = \sqrt 3.\)

Раствор.

Область \(R\) представляет собой полярный прямоугольник \(\left({\text{Рисунок}4}\right)\) и описывается набором

\[R = \Big\{ {\left( {r,\theta} \right)|\;0 \le r \le \sqrt 3 ,\; 0 \le \theta \le {\ frac{\pi }{2}}} \Big\} .\]

Рисунок 4.

Использование формулы 9{\ sqrt 5 } = \ frac {1} {4} \ left ( { — \ cos \ pi + \ cos 0} \ right) \ cdot \ frac {1} {4} \ left ( {25 — 1} \ справа) = \frac{1}{4}\left( { 1 + 1} \right) \cdot 6 = 3.\]

Дополнительные проблемы см. на стр. 2.

15.2 Двойные интегралы в цилиндрических координатах

Этот пример очень похож на простой в прямоугольных координатах: область интерес может быть точно описан постоянным диапазоном для каждой из переменных. Как и в случае с прямоугольными координатами, мы можем адаптировать способ работы с более сложными областями. 9{\пи/2}\кр &={8\over3}\pi-{32\over9}.\cr }$$ $\квадрат$

Рисунок 15.2.2. Объем по области с непостоянными ограничениями.

Возможно, вы выучили формулу вычисления площадей в полярных широтах. координаты. можно вычисляйте области как объемы, так что вам нужно запомнить только один техника. Рассмотрим поверхность $z=1$, горизонтальную плоскость. Громкость под этой поверхностью и над ней находится область в плоскости $x$-$y$. просто $1\cdot(\hbox{площадь области})$, поэтому вычисление объема на самом деле просто вычисляет площадь региона. 92=г$. (отвечать)

Пример 15.2.7 Найдите площадь внутри $r=1+\sin\theta$ и снаружи $r=2\sin\тета$. (отвечать)

Пример 15.2.8 Найдите площадь внутри обоих $r=2\sin\theta$ и $r=2\cos\theta$. (отвечать)

Пример 15.2.9 Найдите площадь внутри четырехлистной розы $r=\cos(2\theta)$ и вне $r=1/2$.