Log 2 корень из 7 49: Вычислить: log^2 корень из 7 49

2

Информатика — B5 математика с ege.yandex.ru

B5.1        B5.2      B5.3     B5.4      B5.5        B5.6       B5.7          B5.8       B5.9          B5.10

B5.11      B5.12      B5.13     B5.14     B5.15      B5.16     B5.17    B5.18      B5.19        B5.20

B5.21      B5.22     B5.23      B5.24    B5.25       B5.26    B5.27    B5.28     B5.29        B5.30

B5.31     B5.32        B5.33

 

Справочные материалы от Д.

Гущина 

 

 

 

№1
Найдите sinα, если cosα=−\(\) и π<α<\(\)

Решение

\(\)

=> \(\)

из условия: π<α<\(\), или третья четверть, где и синус и косинус отрицательны.

=>\(\)

Ответ -0,8

 

 

№2
Найдите значение выражения: \(\)

Решение

\(\)

Ответ 16807

 

 

№3
Найдите значение выражения: \(\).
Решение
\(\)

Ответ 54

 

 

№4
Найдите значение выражения \(\)
Решение  
log₁₁(12,1) + log₁₁10 = log₁₁(12,1*10) =  log₁₁(121) = log₁₁(11²

) = 2

Ответ 2

 

 

№5
Найдите значение выражения \(\).
Решение
\(\).

Ответ 5

 

 

№6

Найдите значение выражения

\[\]

.

Решение 

(4x²−25) / (2x+5) −2x= ((4x²−25) – 2x*(2x+5) ) / (2x+5) = (4x²−25 — 4x²−10x) / (2x+5) = — (10x+25)/ (2x+5) = -5

Ответ -5

 

 

№7

Найдите 25cos2α, если sinα=−0,7.

Решение 

cos(2α) = 1 – 2sin²α = 1 – 2*(-0,7)

2 = 1 – 2*0,49 = 1 – 0,98 = 0,02

25* cos(2α) = 25*0,02 = 0,5

Ответ 0,5

 

 

№8

Найдите значение выражения

\[\]

.

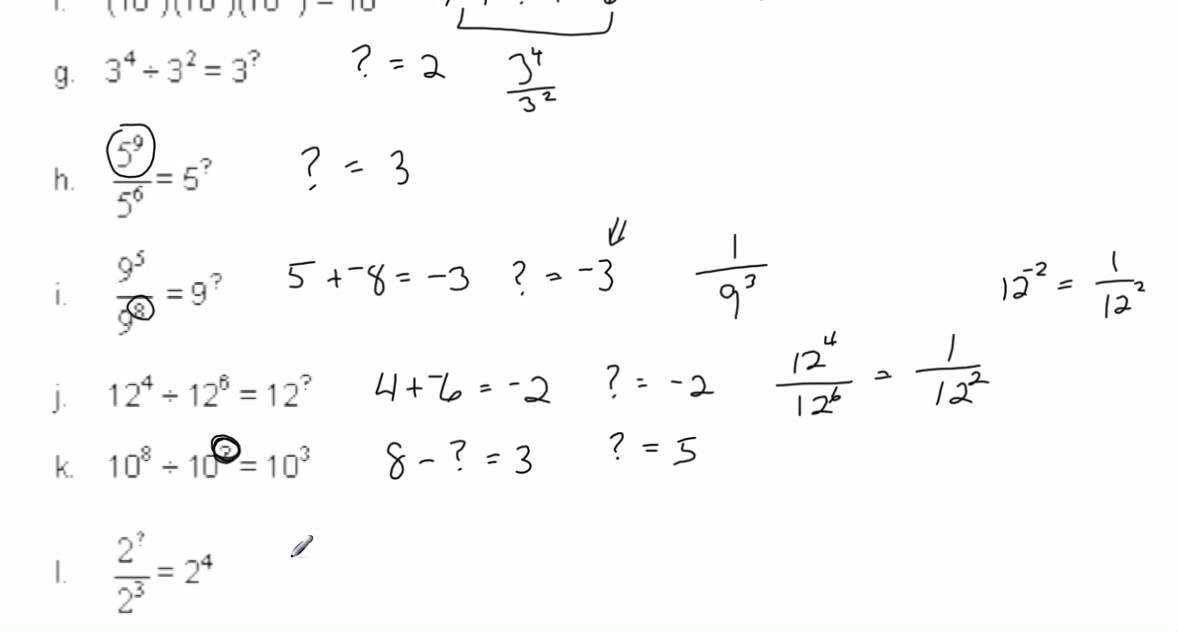
Решение 

(6sin27°cos27°)  / sin54° = 3*(2sin27°cos27°) / sin54°  = 3*sin54° / sin54° = 3

Ответ 3

 

 

№9

 

 

Решение.  

Имеем:                                                            

\[\]

\[\]

\[\]

 

Ответ -0,5

 

 

№10

Найдите значение выражения \(\), если tga=\(\).

Решение 

cos²α = 1/(1+tg²α) = 1/(1+11) = 1/12

36*cos²α = 36*(1/12) = 3

Ответ 3

 

 

№11

Найдите значение выражения \(\).

Решение 

39⋅:65 = 39*26: (3⁵ *2⁵) = 3^9-5 * 2^6-5 = 81*2 = 162

Ответ 162

 

 

№12

Найдите значение выражения \(\).

Решение

\(\).

Ответ 9

 

 

№13

Найдите значение выражения \(\).

Решение

\(\)

\(\).

 

Ответ -10

 

 

№14

Найдите значение выражения: \(\).

Решение

\(\).

 

Ответ 81

 

 

№15

Найдите значение выражения \(\).

Решение

\(\)
Ответ 16

 

 

№16  Найдите значение выражения: log₄9 /  log₆₄9.

Решение. Имеем: log₄9 = log₄64 * log₆₄9.    (см. Примечание после ответа) Поэтому

log₄9 /  log₆₄9 = (log₄64 * log₆₄9) / log₆₄9 = log₄64 = 3

Ответ. 3

Примечание. Докажем формулу

  log_ax = log_ab * log_bx

Пусть (a^p)^q=x. Обозначим a^pчерез b. Имеем:

                                                         x= (a^p)^q= a^pq

                                                           b = a^p

                                                           x = b^q

Поэтому

log_ax   = pq                            (1)

log_ab   = p                              (2)

log_bx   = q                               (3)

 

Из (1), (2) и (3) следует:

log_ax = log_ab * log_bx

 

 

№17

Найдите значение выражения \(\).

Решение
(9+√77) /(√11+√7)2 = (9+√77) /(11+2*√11*√7 + 7) = (9+√77) /(18+2*√77) = ½ = 0,5
Ответ 0,5

 

 

№18

Вычислите:

\[\]

.

Решение

\(\)

=>\(\)

Ответ 31

 

 

№19

Найдите значение выражения \(\).

Решение 

log₇ (⁴√24) / log₇ (24) = log₇ (24^1/4 ) / log₇ (24) = ¼ *log₇ (24) / log₇ (24) = ¼

Ответ 0,25

 

 

№20

Вычислите: \(\).

Решение 

log7log₂128 = log7log₂(2⁷) = log77 = 1

Ответ 1

 

№21

 

 

Вычислите: \(\).

Решение 

30*cos33^∘/sin57^∘ = 30*cos(90^∘ — 57^∘)/sin57^∘ = 30*sin57^∘/sin57^∘ = 30

Ответ 30

 

 

№22

 

Решение.Обозначим

квадратный корень из 13 через r. Имеем:

(7^r)*(2^r)/(14^r-3) = (14³) )/(14^r-3) = 14^r-(r—3)= 14³=2744

 Ответ   2744

 

 

№23 

Вычислите log_0,52

Решение. Имеем:

0,5 = ½

2 = (½)^-1

Поэтому log_0,52 = -1 

Ответ  -1

 

 

№24

Вычислите \(\).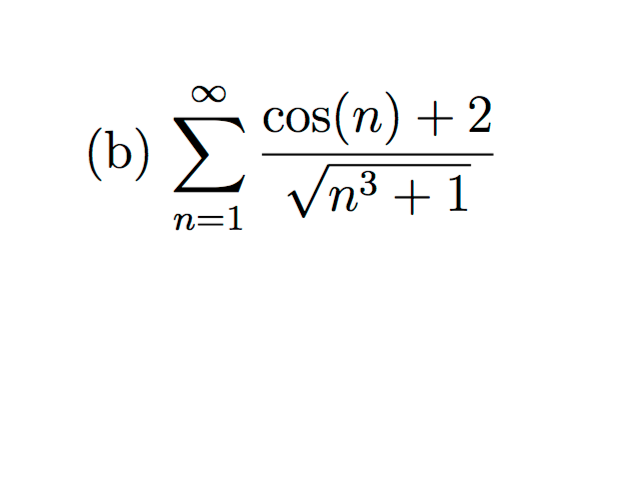

Решение

см №2 №23

 

Ответ 25

 

 

№25

Вычислите \(\).

Решение Имеем: 216 = 6³ = ( (√6)²)³ =(√6)^2*3= (√6)⁶  . Поэтому log_√6 (216)  = 6 и log²_√6 (216) = 6² = 36.

Ответ 36

 

 

№26

 

 

Решение

Обозначим значение, которое нужно вычислить, через Z.

Имеем:                           5+3/5 = 28/5;  12+3/5 = 63/5;

Z = ( √(28/5) — √(63/5) ) / √(7/45) =

=  ( √(28/5) / √(7/45) ) – (√(63/5) / √(7/45))

Вычислим отдельно уменьшаемое и вычитаемое.

√(28/5) / √(7/45) = √(28/5  : 7/45) =

= √(28*45/(5*7) = √( (4 *9 )= 2*3 =6

 

√(63/5) / √(7/45) = √(63/5  : 7/45) =

= √ (63*45/(5*7) = √( 9* 9 )= 9

Таким образом,

Z = 6 – 9 = -3

 Ответ   -3

 

 

№27

 

 

 

Решение

Ответ

 

 

№28

 

 

 

Решение .  Кубический корень из x обозначается: rt(x).

Имеем:

( rt(6)*rt(4) ) / rt(3) = rt(6*4/3) = rt(4*2) = rt (2³) = 2

 Ответ  3

 

 

 

 

№29  

 

 

Решение 

(8+2/11) : (9/11) = (90/11) : (9/11) = (90*11) /(11*9)   = 90 / 9 = 10

Ответ

 

 

 

№30

Найдите значение выражения

3^2z+1:9^z:z

при z=1/12.

Решение     9^z = (3² ) ^z     =  3^2z .  Поэтому:

3^2z+1:9^z:z  = 3^2z+1:3^2z:z = 3^(2z+1)-2z:z = 3^2z+1-2z:z = 3:z

При z =  1/12 это равно 3:1/12 = 3*12 = 36

Ответ:  36

 

 

№31   

 

 

Решение.  

(√200)* cos²(5π/8) — (√50) = (√50) * ((√4)*cos²(5π/8) – 1) =

= (√50) * (2*cos²(5π/8) – 1) = (√50) * (cos²(5π/8) – sin²(5π/8)) = (√50) * (cos(2*5π/8) = (√50) * (cos(5π/4) = (√50) * (-(√2)/2) = — (√100)/2 = -10/2 = -5

Ответ 

 

 

№32

 

 

 

 

Решение.

 

Ответ 1

 

 

№33 

 

 

Решение.

log₂ (4√2) + log₃12 — log₃4 = log₂ (2^2+1/2) + log₃(12/4) = 2+1/2 + 1 = 3,5

Ответ 

 

АЛГЕБРА И НАЧАЛА АНАЛИЗА

АЛГЕБРА  И НАЧАЛА АНАЛИЗА

 

А. Смоляков,
г. Нефтекумск

АЛГЕБРА  И НАЧАЛА АНАЛИЗА

Вариант N 4-98

1. Решить уравнение

.

Решение. Данное уравнение равносильно системе

Решим уравнение системы:

3x + 7 = x² — 14x + 49,  x² – 17x + 42 = 0,

D = 289 — 168 = 121 > 0,

x_1,2 = , откуда x1 = 14, x2 = 3.

Условию x і 7 удовлетворяет первый корень, второй корень не удовлетворяет условию x і 7 и является посторонним для исходного уравнения.

Ответ: 14.

Замечание 1. Покажем еще один способ решения данного уравнения. Пусть t, где t  і 0, тогда
x = и данное уравнение примет вид

t = – 7,  t² – 3t – 28 = 0, D = 9 + 112 = 121 > 0,

t_{1,2 =}  , t₁ = 7, t₂ < 0.

Следовательно, остается решить уравнение7, откуда 3x + 7 = 49, откуда x = 14.

Замечание 2. Оформление решения данного уравнения можно представить и в таком виде:

x — 7 Ы  Ы

Ы Ы откуда x = 14.

Замечание 3. Укажем и самый стандартный прием решения рассматриваемого уравнения. Возведем обе части уравнения в квадрат, получим 3x + 7 = (x — 7)², откуда x² — 14x + 49 = 3x + 7, x² — 17x + 42 = 0. По теореме Виета (x₁ + x₂ = 17, x₁x₂ = 42) находим, что x₁ = 14, x₂ = 3.

Проверка.

x = 14, = 7 — равенство верное, 14 — корень данного уравнения.

x = 3, = — 4 — равенство ложное, 3 — не корень данного уравнения.

Ответ: 14.

2. Решить уравнение 14sin² x + cos 4x — 10 = 0.

Решение. Так как

sin² x = и cos 4x = 2cos² 2x — 1,

то данное уравнение равносильно уравнению

7(1 — cos 2x) + 2cos² 2x — 1 — 10 = 0,

2cos² 2x — 7 cos 2x — 4 = 0.

Положим cos 2x = y, где | y | Ј 1, тогда 2y² — 7y — 4 = 0.
D = 49 + 32 = 81 > 0, y_1,2 = , y₁ = 4, y₂ = — . Условию | y | Ј 1 удовлетворяет только второй корень, поэтому необходимо решить уравнение cos 2x = — , откуда

Замечание. Наметим и другой вариант решения уравнения. Так как cos 4x = 1 — 2sin² 2x, то данное уравнение примет вид

14sin² x — 8sin² x cos² x — 9 = 0

или

14sin² x — 8sin² x + 8sin⁴ x — 9 = 0,

8sin⁴ x + 6sin² x — 9 = 0.

Далее остается ввести новое неизвестное: sin² x = y, где yО (0; 1).

3. Вычислить .

Решение. Функция f(x) = (2x — 3)⁷ непрерывна и интегрируема на отрезке [1; 2] как многочлен. Применяя формулу Ньютона–Лейбница, получим

=.

Ответ: 0.

4. Решить неравенство  .

Решение. Так как D(log_a) = R₊, где a > 0, a № 1, то
x² — 2x — 9 > 0, x + 1 > 0. Так как > 1, то функция

возрастающая и x² — 2x — 9 і x + 1. Следовательно, данное неравенство равносильно системе

которая равносильна системе

откуда x і 5.

Замечание 1. Решая систему можно дать ее подробное решение. Решим второе неравенство методом интервалов. f(x) = x² — 3x — 10, D(f) = R, так как f — многочлен. Найдем нули функции: x² — 3x — 10 = 0,
D = 9 + 40 = 49 > 0.

Находим общее решение системы:

Ответ: [5; +Ґ ).

Замечание 2. При выполнении этого задания иногда решавшие его находили так называемую ОДЗ, что в данном примере приводит к усложнению решения: ведь необходимо тогда решить и неравенство x² — 2x — 9 > 0.

Замечание 3. Данное неравенство можно решить методом интервалов. Пусть

f(x) = log_p/3(x² — 2x — 9) — log_p/3(x + 1).

Необходимо найти все x, при которых f(x) і 0. Находим D(f):

Итак, D(f) = . Находим нули f: x² — 3x — 10 = 0, откуда x = — 2 — не нуль функции, так как
— 2П , x = 5 — нуль функции.

f(6) =  log_p/315 —  log_p/37 > 0,

f(4,5) =  log_p/32,25 — log_p/35,5 < 0.

5. Найти наибольшее и наименьшее значения функции f(x) = tg x — x на отрезке .

Решение. Заданная функция определена и непрерывна на отрезке и дифференцируема на интервале . Найдем производную функции f(x):

f ‘(x) = 1/cos² x — 1 = 1 + tg² x — 1 = tg² x.

Так как f ‘(x) і 0 при всех x из промежутка , f(x) = 0 лишь при x = p и f(x) непрерывна на , то функция монотонно возрастает на и свое наименьшее значение принимает на левом конце отрезка, а наибольшее — на правом. Далее имеем:

— наименьшее значение функции,
— наибольшее значение функции.

Ответ:  на   min f(x) == ,   max  f(x) == .

Замечание. Задачу можно решить, применив алгоритм нахождения наибольшего и наименьшего значений функции на отрезке. Мы нашли, что f ‘(x) = tg² x. Найдем критические точки: tg² x = 0, x =pn, nОZ. Выберем из них те, которые принадлежат отрезку . Для этого решим неравенство 3p/4< pn <5p/4 , nОZ.
Имеем 3/4< n <5/4 , откуда n = 1 и x = p. Вычисляем значение функции на концах отрезка и в полученной критической точке:

=, f(p)=-p , =.

Дальнейшие рассуждения очевидны:

4 > p Ю 4 + 3p > 4p Ю   < – p,

p < 4 Ю 5p < 4 + 4p Ю 5p – 4 < 4p Ю > – p.

6. При каком значении a графики функций

y = ln (3x – 4) и y = 3x – 4 + a

имеют единственную общую точку?

Решение. Введем новую переменную, положив 3x – 4 = t, где t > 0. Тогда необходимо выяснить, при каком значении a графики функций y₁ = ln t и y₂ = t + a имеют единственную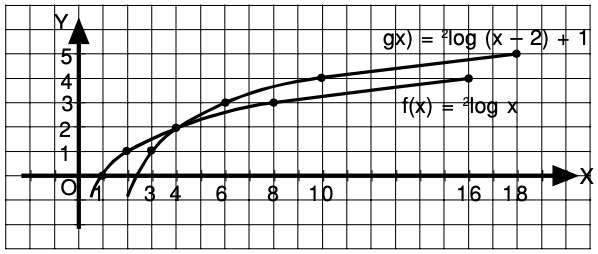 общую точку. Обозначив абсциссу общей точки через x0, получим ln t₀ = t₀ + a. Так как графики имеют единственную общую точку, то прямая y₁ = t + a является касательной к графику функции y₂ = ln t в точке с абсциссой t₀, а поэтому y₁‘ = y₂‘ и при t=t₀ ln’ t = 1, откуда 1/t₀= 1, t₀ = 1, a = ln t₀ – t0 = – 1. Покажем, что прямая y = t – 1 не имеет других общих точек с графиком функции y = ln t, отличных от точки (1; 0). С этой целью докажем неравенство t – 1 > ln t (при t > 0, t № 1). Введем функцию f(t) = t – 1 – ln t;  f ‘(t) = 1 –1/t . f ‘(t) > 0 при t > 1 и функция f(t) на промежутке [1; +Ґ) возрастает, а поэтому f(t) > f(1). f ‘(t) < 0 при 0 < t < 1 и функция на промежутке (0; 1] убывает, а поэтому f(t) > f(1). Итак, при t > 0 f(t) = t – 1 – ln t > f(1) = 0, т. е. t – 1 > ln t. Следовательно, при a = – 1 и графики данных функций имеют только одну общую точку.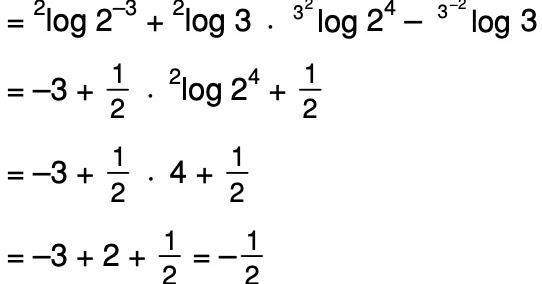

Ответ: a = – 1.

Замечание 1. Анализ решенной задачи позволяет ее обобщить. Вместо функции 3x — 4 можно взять любую другую линейную функцию вида y = kx + b, где k № 0. Будут меняться только координаты общей точки, при этом ее ордината всегда равна 0.

Замечание 2. При решении задачи рассмотренным способом мы показали, что при найденном значении a действительно существует только одна общая точка. Это важно. Мы подробно остановимся на решении задачи N 6, так как практически во всех работах, которые мы увидели в медальной комиссии, рассматривался вариант приведенного нами решения с некоторыми усложнениями. При этом утверждалось, что функции y = 3x — 4 + a
и y = ln (3x — 4) — возрастающие, каждая в своей области определения, а поэтому их графики могут иметь две общие точки, одну или ни одной. Во втором случае y = 3x — 4 + a — касательная. На наш взгляд, решение верное, но потому, что y = ln (3x — 4) — функция выпуклая, возрастающая и не имеющая точек перегиба.

Замечание 3. Задача решается просто, если вновь ввести новое неизвестное t = 3x — 4, где t > 0, и сформулировать задачу так: «При каких значениях a уравнение ln t = t + a имеет единственный корень»? Перепишем уравнение: ln t — t = a и построим график функции f(t) = ln t — t, проведя исследования.

1. D(f) = R₊.

2. f ‘(t) =1/t — t. Критическая точка t = 1.

3. На промежутке (0; 1] функция возрастает, а на промежутке [1; +Ґ) функция убывает.

4. При x_max = 1 y_max = — 1.

Ясно, что при a = — 1 уравнение ln t — t = — 1 имеет единственный корень t = 1.

Теперь делаем вывод, что графики функций

y = ln (3x — 4) и y = 3x — 4 + a

имеют единственную общую точку при a = — 1. Ее координаты .(5/3;0)

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Квадратный корень из 49 — Как найти квадратный корень из 49?

LearnPracticeDownload

49 — это число в совершенном квадрате, которое можно получить путем возведения в квадрат числа 7, а также составное число. Следовательно, квадратный корень из 49 является рациональным числом. В этом уроке мы изучим понятие квадратного корня из 49. В этом уроке также объясняется квадратный корень из 49 в радикальной форме вместе с решенными примерами.

• Квадратный корень из 49 : √49  = 7
• Квадрат 49: 49 ² = 2401

1.	Чему равен квадратный корень из 49?
2.	Является ли квадратный корень из 49 рациональным или иррациональным?
3.	Как найти квадратный корень из 49?
4.	Важные примечания
5.	сложные вопросы
6.	Часто задаваемые вопросы о квадратном корне из 49

Чему равен квадратный корень из 49?

Квадратный корень из 49 получается из числа, квадрат которого дает исходное число.

√ 49 = 7

Ответ, полученный при возведении 7 в квадрат, равен 49. Следовательно, 49 — полный квадрат.

Является ли квадратный корень из 49 рациональным или иррациональным?

Рациональное число — это число, которое может быть выражено в виде p/q, где p и q — целые числа, а q не равно 0. Мы уже выяснили, что √ 49 = 7. 7 – это целое число, которое легко выражается в форме p/q. Число 7 является рациональным числом. Итак, квадратный корень из 49 – рациональное число.

Как найти квадратный корень из 49?

Мы обсудим два метода нахождения квадратного корня из 49

• Факторизация простых чисел
• Длинное деление

Факторизация простых чисел — это способ представления числа в виде произведения его простых множителей.
Простая факторизация 49равно 49 = 7 × 7 
Чтобы найти квадратный корень из 49, мы берем по одному числу из каждой пары одинаковых чисел и перемножаем их.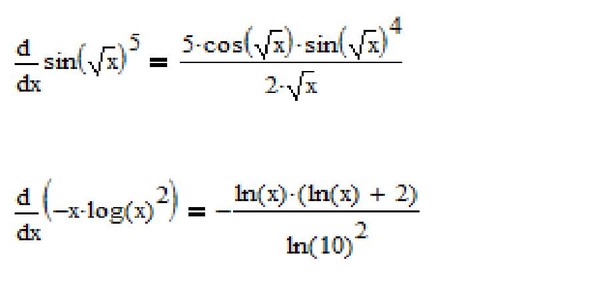
49 = 7 × 7
√ 49 = 7

Квадратный корень из 49 путем деления в длину

Значение квадратного корня из 49 методом деления в длину состоит из следующих шагов:

• справа мы соединим цифры, поставив над ними черту.
• Шаг 2 : Найдите число, которое при умножении на себя дает произведение, меньшее или равное 49. Итак, число 7. Подставив делитель 7, мы получим частное 7 и остаток 0.
• Шаг 3 : Число 49 — правильный квадрат.

Изучение квадратных корней с помощью иллюстраций и интерактивных примеров

• Квадратный корень из 64
• Квадратный корень из 144
• Квадратный корень из 16
• Квадратный корень из 169
• Квадратный корень из 14

Важные примечания:

• Квадратный корень — это операция, обратная возведению в квадрат.
• 49 — это полный квадрат, так как ответ, полученный после квадратного корня, является рациональным числом.
• Квадратный корень из 49 можно упростить до 7 либо с помощью разложения 49 на простые множители, либо путем выражения 49 в виде квадрата 7.

Наводящие вопросы:

• Мы знаем, что (-7) × (-7) =49. Итак, можем ли мы сказать, что -7 – это квадратный корень из 49?
• Сможете ли вы определить квадратное уравнение, корни которого равны 49?а -49?

 

1. Пример 1 : Томас говорит, что значение -( √ 49) такое же, как (- √ 12). Что вы думаете?

   Решение

   Отрицательный квадратный корень не может иметь действительных корней.
   -( √ 49) имеет действительные корни но (- √ 49) имеет только мнимые корни.
   Следовательно, они не одинаковы. -( √ 49) не совпадает с (- √ 49).

г.

2. Пример 2 : Помогите Райану упростить квадратный корень из 49 до наименьшей радикальной формы.

   No related posts.