Изменение графика параболы по мере увеличения и уменьшения числового коэффициента:
Если мы прибаляем к функции \(f(x)=|x|\) число \(f(x)=|x|+3\) , то график смещается по оси \(0Y\) на \(+3\) еденицы вверх, а если мы вычитаем число \(-4\)
\(f(x)=|x|-4\), то график сместиться вниз на 4 вниз:
То же самое с графиком \(f(x)=\sqrt{x}\):
\(f(-x)-\)отражение относительно \(OY\):
\(-f(x)- \)отражение относительно \(OX\) :
Изменение графиков функций
\(f(x)+c-\) сдвиг \(f(x)\) вверх относительно \(OY\)
\(f(x)-c-\) сдвиг \(f(x)\) вниз относительно \(OY\)
\(f(x+c)-\)сдвиг \(f(x)\) влево относительно \(OX\)
\(f(x-c)-\)сдвин \(f(x)\) вправо относительно \(OX\)
\(f(-x)-\) отражение относительно \(OY\)
\(-f(x)- \)отражение относительно \(OX\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Елена Ивановна Качанова
Репетитор по математике
Стаж (лет)
Образование:
Витебский государственный педагогический институт им. С.М. Кирова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях!
На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях!
Михаил Николаевич Макеев
Репетитор по математике
Стаж (лет)
Образование:
Московский энергетический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Учитель по физике 7-11 классов, подготовка к ЕГЭ и ОГЭ. Физика в рамках школьной программы. Буду вашим гидом в онлайн режиме. Помогу с домашним заданием по программе 7-11 классов. Подготовлю по любым темам для сдачи ЕГЭ. Основой успешного обучения считаю доверительный и комфортный контакт между преподавателем и учеником.
Физика в рамках школьной программы. Буду вашим гидом в онлайн режиме. Помогу с домашним заданием по программе 7-11 классов. Подготовлю по любым темам для сдачи ЕГЭ. Основой успешного обучения считаю доверительный и комфортный контакт между преподавателем и учеником.
Азамат Муллашаехович Калимуллин
Репетитор по математике
Стаж (лет)
Образование:
Башкирский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по физике 9-11 классы. Стараюсь преподавать доступно, интересно. Большое внимание уделяю решению задач. Готовлю к ОГЭ, ЕГЭ и всевозможным олимпиадам.Также оказываю помощь при выполнении домашних заданий.
Стараюсь преподавать доступно, интересно. Большое внимание уделяю решению задач. Готовлю к ОГЭ, ЕГЭ и всевозможным олимпиадам.Также оказываю помощь при выполнении домашних заданий.
Похожие статьи
- Возведение смешанных дробей в натуральную степень
- Как перевести м/мин в км/час
- Движение в противоположных направлениях
- Сочетательное свойство умножения
- МИФИ: Бизнес-Информатика
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 4)
- Интересные факты об устройстве Вселенной
- Плюсы и минусы группового обучения + пара игр на сближение участников
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Функции и графики | Cubens
Ниже приведен список всех тем из раздела функции и графики.
- Функция, область определения и множество значений функции
- Область определения функции
- График функции
- Четные функции, нечетные функции
- Свойства функций
- Возрастающие функции, убывающие функции
- Непрерывность функции
- Периодичность функции
- Обратная функция
- Асимптоты графика функции
- Элементарные преобразования графика функции
- Линейная функция, график линейной функции
- Дробно-линейная функция
- Квадратичная функция, график квадратичной функции
- Функция корня, график функции корня
- Степенная функция
- Показательная функция, график показательной функции
- Логарифмическая функция, график логарифмической функции
Справочник
- Числа и выражения
- Делимость целых чисел, признаки делимости
- Простые и составные числа простые делители
- Наибольший общий делитель и наименьшее общее кратное
- Проценты, процент от числа
- Действительные числа, числовые множества
- Пропорции и отношения, прямая и обратная пропорциональность
- Модуль числа и свойства модуля
- Среднее арифметическое и среднее геометрическое
- Алгебраические выражения, одночлен и многочлен
- Формулы сокращенного умножения
- Многочлен.
 Деление многочлена на многочлен
Деление многочлена на многочлен - Формулы Виета и корни многочлена
- Корень n-го степеня, свойства корней n-ой степени
- Логарифм числа, свойства логарифмов
- Последовательности чисел, метод математической индукции
- Арифметическая прогрессия, сумма арифметической прогрессии
- Геометрическая прогрессия, сумма геометрической прогрессии
- Уравнения и неравенства
- Уравнения с одной переменной, область допустимых значений уравнения
- Неравенство с одной переменной ОДЗ неравенства
- Схема решению уравнений, замена переменных
- Решению неравенств, метод интервалов
- Системы уравнений, решению систем линейных уравнений
- Системы неравенств, решению систем линейных неравенств
- Линейные уравнения и неравенства
- Квадратное уравнение, теорема Виета
- Квадратное неравенство
- Дробные уравнения, как розвязати дробное уравнение
- Дробные неравенства, как розвязати дробное неравенство
- Уравнения и неравенства с модулями, геометрический смысл модуля
- Иррациональные уравнения
- Иррациональные неравенства
- Показательные уравнения
- Показательные неравенства
- Показниково-степенные уравнения
- Логарифмические уравнения
- Логарифмические неравенства
- Системы линейных уравнений
- Функции и графики
- Функция, область определения и множество значений функции
- Область определения функции
- График функции
- Четные функции, нечетные функции
- Свойства функций
- Возрастающие функции, убывающие функции
- Непрерывность функции
- Периодичность функции
- Обратная функция
- Асимптоты графика функции
- Элементарные преобразования графика функции
- Линейная функция, график линейной функции
- Дробно-линейная функция
- Квадратичная функция, график квадратичной функции
- Функция корня, график функции корня
- Степенная функция
- Показательная функция, график показательной функции
- Логарифмическая функция, график логарифмической функции
- Алгебра и начала анализа
- Предел функции
- Предел функции в бесконечности
- Вычисление предела функции
- Производная функции, найти производную функции
- Таблица производных
- Применение производной к исследованию функции
- Дифференциал функции, нахождение дифференциала
- Вторая производная, точка перегиба
- Исследование функции, построение графика функции
- Первообразная и интеграл
- Определенный интеграл
- Вычисление площадей и объемов с помощью определенного интеграла
- Тригонометрия
- Тригонометрия.
 Измерение углов
Измерение углов
- Тригонометрия.
- Комбинаторика
- Перестановки
- Дробные числа
- Обыкновенные дроби, виды дробей
- Десятичные дроби
- Деление десятичных дробей, умножения десятичных дробей
- Сокращение дробей, возведение дробей к общему знаменателю
- Умножение дробей
- Сложение и вычитание дробей
- Деление дробей
- Преобразование неправильной дроби в смешанное число
- Преобразование смешанного числа в неправильную дробь
- Преобразование десятичных дробей в обыкновенные дроби
- Среднее арифметическое
- Обучение по скайпу
- Математика по скайпу с репетитором
- 5 советов программистам на успешное собеседование
- Что такое ГДЗ и для чего оно нужно?
- База «Библиофонд» — лучшие рефераты и сочинения для студентов
- Курсы QA\QC, тестирование Львов
- Рабочие тетради для дошкольников Федиенко: учитесь легко и с удовольствием
- Почему стоит выбрать Logos QA Academy?
Таблицы и формулы
- Таблица умножения, таблица квадратов, таблица кубов, таблица степеней
- Таблица умножения
- Таблица квадратов
- Таблица кубов
- Таблица степеней
- Таблица факторіалів
- Таблица чисел
- Таблица деления
- Таблица значений тригонометрических функций
- Таблица Брадиса косинусов, синусов, тангенсов, котангенсів
- Таблица косинусов
- Таблица синусов
- Таблица тангенсов
- Таблица котангенсів
- Таблица производных функций
- Таблица производных элементарных функций, производная функции
- Формулы сокращенного умножения
- Формулы сокращенного умножения
Классы
- 1 Класс
- 2 Класс
- 3 Класс
- 4 Класс
- 5 Класс
- 6 Класс
- 7 Класс
- 8 Класс
- 9 Класс
- 10 Класс
- 11 Класс
Использование Cookies
Если Вы будете продолжать использовать данный веб-сайт, мы предполагаем, что Вы согласны получать все файлы cookie на всех сайтах Cubens. Получить подробную информацию можно здесь.
Получить подробную информацию можно здесь.
в любое время
Спасибо, я уже оформил подписку
§ Как решать задачи на функцию
Что такое функция в математике
Как решать задачи на функцию
Функция «y = kx» и её график
Линейная функция
«y = kx + b» и её график
Как построить график функции вида
«y = 7» или «x = 2»
Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».
После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание. Функция задана формулой «y = 2x − 1»
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором значение «y» равно «−19».
Для того, чтобы вычислить «y» при «x = 15» достаточно подставить в функцию вместо «x» необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x» по известному «y», необходимо подставить вместо «y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x» мы подставляем в функцию «y = 2x − 1» вместо «y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x», которое решается по правилам решения линейных уравнений.
Запомните!
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание. Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство «f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x» числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!
Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18» для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси «Ox» вместо «x» и координату по оси «Oy» вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6» координаты точки (1; 2).
Вместо «x» подставим «1». Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0». Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции «y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.
Рассмотрим функцию «y(x) = −2x + 1». Её график мы уже строили в предыдущем уроке.
Найдем на графике функции «y(x) = −2x + 1», чему равен «y» при x = 2.
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции «y(x) = −2x + 1». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!
Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Что такое функция в математике
Как решать задачи на функцию
Функция «y = kx» и её график
Линейная функция
«y = kx + b» и её график
Как построить график функции вида
«y = 7» или «x = 2»
АннотацияЭтот урок предназначен для ознакомления учащихся с графическими функциями. ЦелиПо окончании данного занятия учащиеся будут:
СтандартыУпражнения и обсуждения на этом уроке касаются следующих Стандарты НКТМ: Алгебра Понимание закономерностей, взаимосвязей и функций
Требования для учащихся
Подготовка учителяСтудентам понадобятся:
Основные терминыЭтот урок знакомит учащихся со следующими терминами посредством обсуждений:
План урока Эти действия могут быть выполнены индивидуально или в группах до четырех студентов.
y = _____ x + ____ с использованием
Инструмент графического эскиза для определения
какие функции исходят от этой формы, и что меняется каждая
константа делает с функцией. Убедитесь, что они следят за тем, что они
попробуйте и запишите свои гипотезы и наблюдения.
92 + ____ .
Альтернативные контуры Этот урок можно перестроить несколькими способами.
Предлагаемое продолжениеПосле этих обсуждений и занятий у студентов будет больше опыта с функциями и графикой. Следующий урок, Чтение графиков, показывает студентам что графики могут быть использованы для передачи большого количества информации о заданная ситуация. |
Как построить график функции
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
ACT Math Help » Алгебра » Координатная плоскость » График » Как построить график функции
Ось Y представляет собой _______________ функции Y = 1/X
Возможные ответы:
Asymptote
Уравнение
нулевой раствор
Вертикальный наклон
Правильный ответ:
Asymptote
. Объяснение:
Объяснение:Линия является асимптотой на графике, если график функции приближается к линии по мере увеличения абсолютного значения X или Y.
Сообщить об ошибке
Какая из данных функций изображена ниже?
Возможные ответы:
Правильный ответ:
33 Объяснение:
На графике есть точки пересечения x = 0 и x = 8. Это указывает на то, что 0 и 8 являются корнями функции.
Функция должна иметь форму y = x(x — 8), чтобы эти корни были истинными.
Парабола направлена вниз, что указывает на отрицательный старший коэффициент. Разверните уравнение, чтобы получить наш ответ.
y = -x(x — 8)
y = -x 2 + 8x
y = 8x — x 2
Следовательно, ответ должен быть y = 8x — x 9006
2 70006 2 2 2 Отчет о ошибке Каков домен следующей функции: Возможные ответы: x ≠ 2 x ≠ —2 и x ón. x ≠ –1 x ≠ 5 Правильный ответ: x ≠ –2 и x ≠ –3 Объяснение: Знаменатель не может быть равен нулю, иначе функция будет неопределенной. Поэтому 90 254 x 90 255 не может быть –2 или –3. Сообщить об ошибке На рисунке выше показан график зависимости y = f(x). Что из следующего является графиком y = |f(x)|? Возможные ответы: Правильный ответ: Объяснение: Одним из свойств получения абсолютного значения функции является то, что все значения становятся положительными. Сами значения не меняются; только их знаки. На этом графике ни одно из значений y не является отрицательным, поэтому ни одно из них не изменится. Таким образом, два графика должны быть идентичными. Сообщить об ошибке Ниже приведен график функции: Какое из следующего может быть уравнением для ? Возможные ответы: Правильный ответ: Объяснение: Во-первых, поскольку график состоит из частей, являющихся прямыми линиями, функция должна включать абсолютное значение, функции которого обычно имеют характерную форму буквы «V». Таким образом, мы можем исключить f(x) = x 2 – 4x + 3 из нашего выбора. Кроме того, функции с членами x 2 представляют собой изогнутые параболы и не имеют прямых отрезков. Это означает, что f(x) = |x 2 – 4x| – 3 – неправильный выбор. Далее рассмотрим f(x) = |2x – 6|. Поскольку эта функция сама по себе состоит из абсолютного значения, на ее графике не будет отрицательных значений. Абсолютное значение само по себе будет давать только неотрицательные числа. Далее мы можем проанализировать f(x) = |x – 1| – 2. Примем x равным 1 и посмотрим, какое значение мы получим из f(1). f(1) = | 1 – 1 | – 2 = 0 – 2 = –2 Однако на приведенном выше графике показано, что f(1) = –4. В результате f(x) = |x – 1| – 2 не может быть правильным уравнением для функции. Методом исключения ответ должен быть f(x) = |2x – 2| – 4. Мы можем проверить это, подставив несколько значений x в это уравнение. Например, f(1) = |2 – 2| – 4 = –4, что соответствует точке (1, –4) на графике выше. Аналогичным образом, если мы подставим 3 или –1 в уравнение f(x) = |2x – 2| – 4, получаем ноль, а это означает, что график должен пересекать ось x в точках 3 и –1. Судя по графику выше, именно так и происходит. Ответ: f(x) = |2x – 2| – 4. Сообщить об ошибке Какое из следующих значений может быть значением для ? Возможные ответы: Правильный ответ: Объяснение: График представляет собой ниспадающую параболу с максимумом . Сообщить об ошибке Какое уравнение для линии, изображенной выше? Возможные ответы: Правильный ответ: Объяснение: Линия имеет уравнение , где это точка пересечения, а это наклон. Пересечение можно найти, отметив точку пересечения линии и оси Y, в данном случае в точке so . Наклон можно найти, выбрав две точки, например точку пересечения с осью y и следующую точку, пересекающую четную точку, например . Теперь применим формулу наклона что дает . Следовательно, уравнение прямой принимает вид: Сообщить об ошибке Какой из следующих графиков представляет точку пересечения этой функции по оси y? Возможные ответы: Правильный ответ: Объяснение: Графически точка пересечения с осью Y — это точка, в которой график касается оси Y. Здесь нам дана функция . Чтобы вычислить точку пересечения по оси Y, установите равным нулю и найдите . Таким образом, точка пересечения по оси y находится в точке . Сообщить об ошибке Какой из следующих графиков представляет точку пересечения этой функции по оси x? Возможные ответы: Правильный ответ: Объяснение: Графически точка пересечения с абсциссой – это точка, в которой график касается оси х. Алгебраически это значение для которого . Здесь нам дана функция . Чтобы рассчитать точку пересечения по оси x, установите равным нулю и найдите . Таким образом, точка пересечения с х находится в . Сообщить об ошибке Что из следующего представляет ? Возможные ответы: Правильный ответ: Объяснение: Линия определяется любыми двумя точками на линии. Пусть. Затем Таким образом, наш первый набор точек (который также является точкой пересечения по оси Y) равен Пусть . Затем Итак, наш второй набор точек (который также является точкой пересечения по оси X) равен . Сообщить об ошибке ← Назад 1 2 Далее → Уведомление об авторских правах 14 Диагностические тесты
767 практических тестов
Вопрос дня
Карточки
Учитесь по концепции Онлайн-заметки Пола Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т. Теперь нам нужно обсудить графические функции. Если вспомнить из предыдущего раздела, мы говорили, что \(f\left( x \right)\) — не что иное, как причудливый способ записи \(y\). Это означает, что мы уже знаем, как строить графики функций. Мы рисуем функции точно так же, как мы рисуем уравнения. Если мы заранее знаем, что функция является графиком, мы можем использовать эту информацию, чтобы помочь нам с графиком, и если мы не знаем, что представляет собой функция заранее, тогда все, что нам нужно сделать, это подключить некоторые \( x\) вычисляют значение функции (которое на самом деле является значением \(y\)) и затем наносят точки. Показать решение Теперь, как мы говорили ранее в этой главе, когда впервые рассматривали построение графиков, нам нужно выбрать значения \(x\) для подстановки, а знание значений для выбора на самом деле приходит только с опытом. Поэтому не беспокойтесь так о значениях \(x\), которые мы здесь используем. К концу этой главы вы также сможете правильно выбирать эти значения. Вот оценки функций. Вот набросок графика. Итак, построение графиков функций очень похоже на построение графиков уравнений. 92} + 4 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 дюйма} x < 1 \\ 2x - 1 \ hspace {0,25 дюйма} & {\ mbox {on}} \ hspace {0,25 in}x \ge 1\end{align*}\] Нам нужно быть немного осторожными с тем, что происходит прямо в точке \(x = 1\), так как технически это справедливо только для нижней функции. Однако мы займемся этим в самом конце, когда будем строить график. Сейчас мы будем использовать \(x = 1\) в обеих функциях. Первое, что нужно сделать здесь, это получить таблицу значений для каждой функции в указанном диапазоне, и снова мы будем использовать \(x = 1\) в обоих случаях, хотя технически его следует использовать только с нижней функцией. 92} + 4\) Вот набросок графика и обратите внимание, как мы обозначили точки \(x = 1\). Обратите внимание: поскольку два графика не пересекались в точке \(x = 1\), мы оставили на графике пустое место. НЕ соединяйте эти две точки линией. Там действительно должен быть разрыв, чтобы показать, что две части не встречаются в точке \(x = 1\). Иногда две части встречаются в этих точках, а иногда нет. Мы не должны ожидать, что они встретятся или не встретятся, пока мы не набросаем график. Давайте рассмотрим еще один пример кусочной функции. 92}}&{{\mbox{if}} — 2 \le x < 1}\\{ - x + 2}&{{\mbox{if}}\,x \ge 1}\end{массив}} \Правильно.\] Показать решение В этом случае мы будем строить графики трех функций в диапазонах, указанных выше. Итак, как и в предыдущем примере, мы будем получать значения функций для каждой функции в указанном диапазоне и будем включать конечные точки каждого диапазона в каждое вычисление. действительные числа
действительные числа
 Следовательно, поскольку график опускается ниже оси x (что означает, что f(x) имеет отрицательные значения), f(x) = |2x – 6| не может быть правильным ответом.
Следовательно, поскольку график опускается ниже оси x (что означает, что f(x) имеет отрицательные значения), f(x) = |2x – 6| не может быть правильным ответом. Следовательно, для этой функции нет значений y, превышающих это значение.
Следовательно, для этой функции нет значений y, превышающих это значение. Алгебраически это значение когда .
Алгебраически это значение когда . Часто проще всего вычислить две точки, подставив ноль вместо x и решив для y, и подставив ноль вместо y и решив для x.
Часто проще всего вычислить две точки, подставив ноль вместо x и решив для y, и подставив ноль вместо y и решив для x. Все математические ресурсы ACT
Алгебра — Графические функции
Главная
/
Алгебра
/
Графики и функции
/ Графические функции е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Раздел 3-5: Графические функции
 93} + 1\).
93} + 1\). \(х\) \(f(x)\) \(\влево({х,у}\вправо)\) -1 -7 \(\слева( { — 1, — 7} \справа)\) 0 0 \(\влево({0,0} \вправо)\) 1 1 \(\влево({1,1} \вправо)\) 2 2 \(\влево( {2,2} \вправо)\) 3 9 \(\влево( {3,9} \вправо)\) 
\(\влево({х,у}\вправо)\) -2 0 \(\влево( { — 2,0} \вправо)\) -1 3 \(\влево( { — 1,3} \вправо)\) 0 4 \(\влево( {0,4} \вправо)\) 1 3 \(\влево({1,3} \вправо)\) \(х\) \(2x — 1\) \(\влево({х,у}\вправо)\) 1 1 \(\влево({1,1} \вправо)\) 2 3 \(\слева({2,3} \справа)\) 3 5 \(\влево( {3,5} \вправо)\) 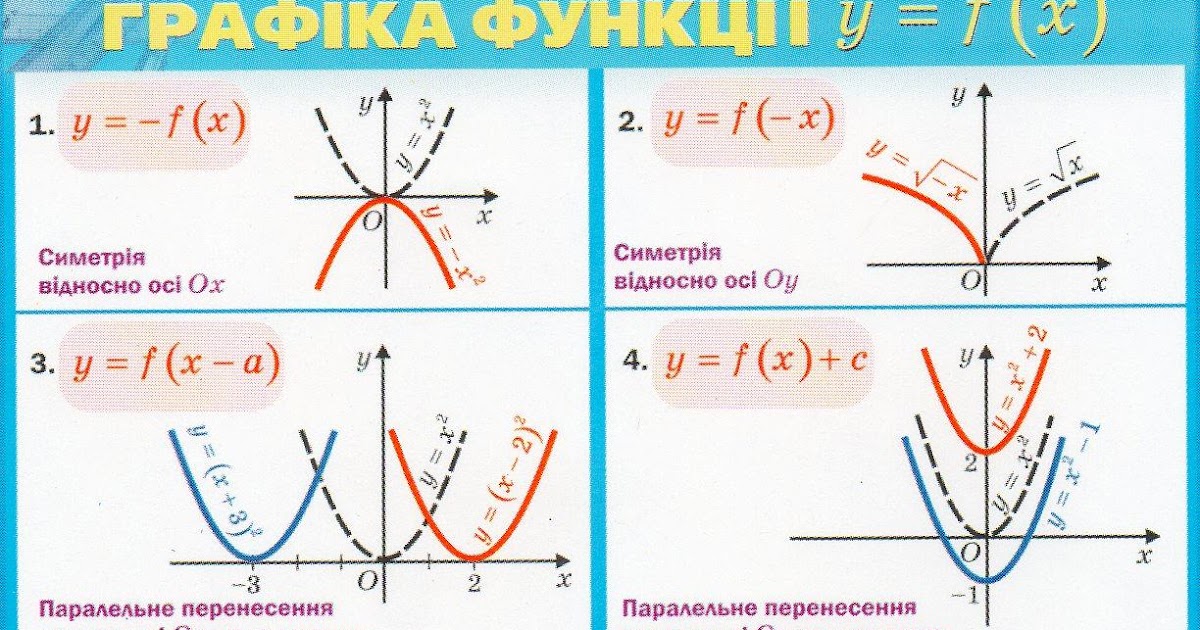 Для верхней функции мы использовали открытую точку для точки \(x = 1\), а для нижней функции мы использовали закрытую точку для \(x = 1\). Таким образом, на графике становится ясно, что только нижняя функция действительно имеет точку \(x = 1\).
Для верхней функции мы использовали открытую точку для точки \(x = 1\), а для нижней функции мы использовали закрытую точку для \(x = 1\). Таким образом, на графике становится ясно, что только нижняя функция действительно имеет точку \(x = 1\).

 Деление многочлена на многочлен
Деление многочлена на многочлен Измерение углов
Измерение углов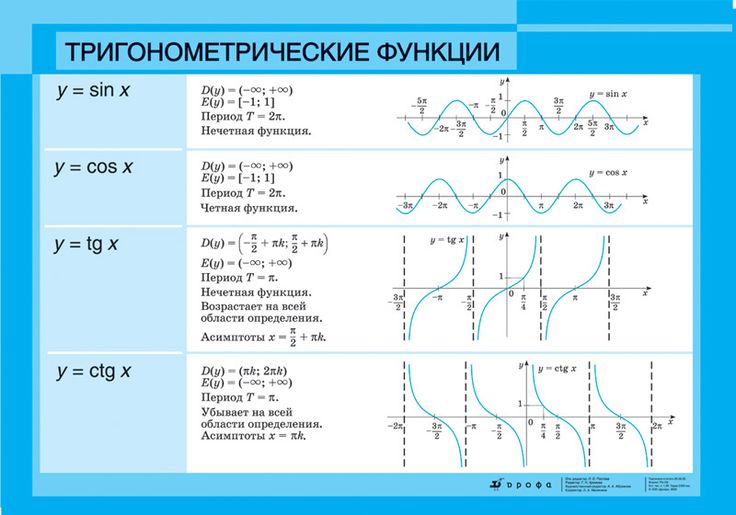

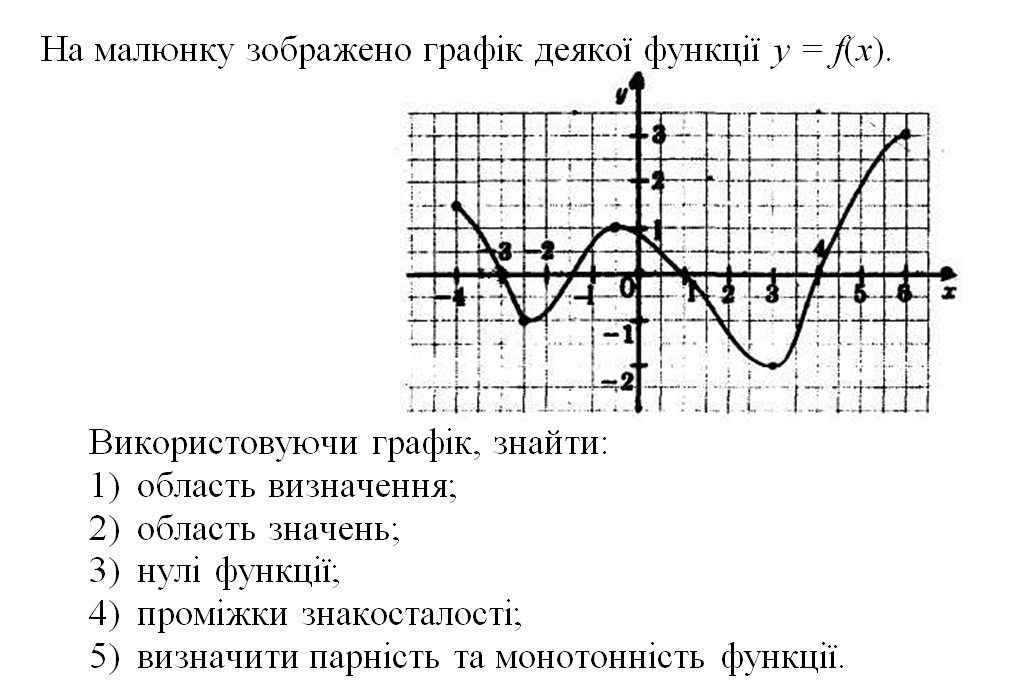 Выделите 2-3 часа учебного времени на весь урок, если все части
делается в классе
Выделите 2-3 часа учебного времени на весь урок, если все части
делается в классе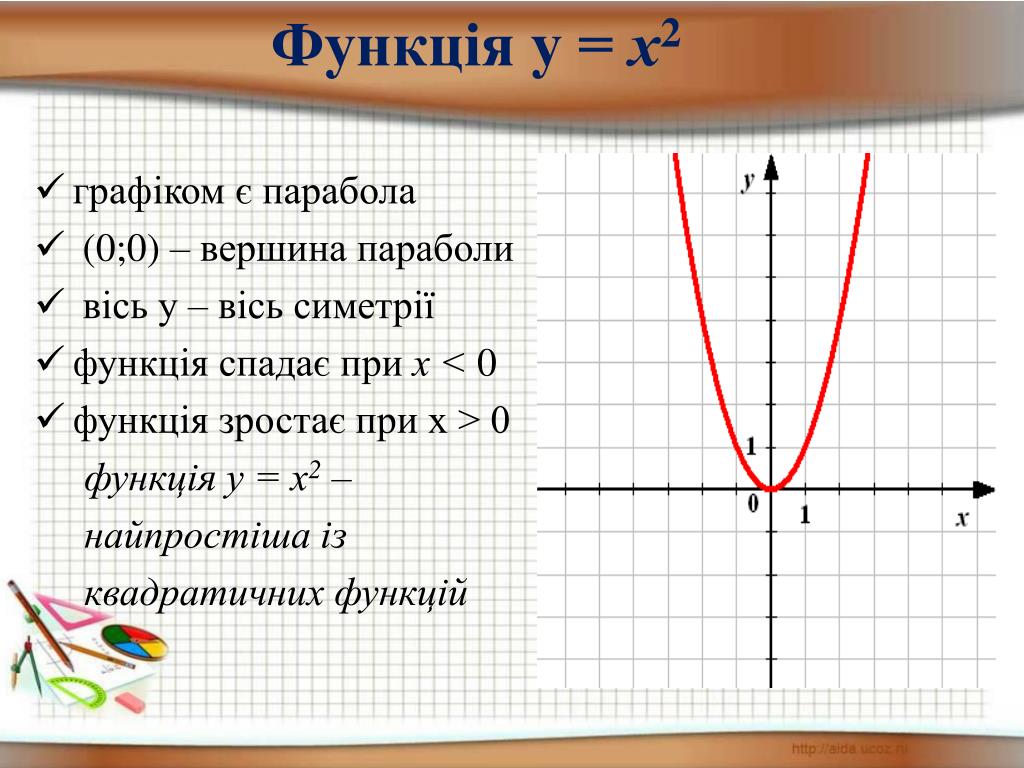 Даже если доступны графические калькуляторы, пусть учащиеся начертят
точки на миллиметровой бумаге — это навык, который важен для
потренироваться руками. Вот несколько функций, которые могут быть назначены:
92
Даже если доступны графические калькуляторы, пусть учащиеся начертят
точки на миллиметровой бумаге — это навык, который важен для
потренироваться руками. Вот несколько функций, которые могут быть назначены:
92 