Ответ:
Одной пачки семян травы недостаточно, чтобы заново засеять центральный круг футбольного поля.
Пример 2
Подрядчика муниципального образования попросили покрасить 20 мини-кольцевых развязок диаметром 4 метра каждая. Менеджер по закупкам подрядчиков связывается с 3 поставщиками, чтобы проверить уровень цен на складе и расход на банку краски, как показано в таблице ниже. У какого поставщика подрядчик должен покупать краску?
Поставщик | Блин, нет качества | Мальчики и Боден | Ужасно дорого |
Стоимость за банку | 5,00 фунтов стерлингов | 5,30 фунтов стерлингов | 5,10 фунтов стерлингов |
Расход на банку | 10 м 2 | 10 м | 8 м 2 |
Жестяные банки в наличии | 20 | 35 | 35 |
92`
Этап 2.
Теперь подсчитайте, сколько банок потребуется от каждого поставщика, чтобы покрасить все мини-кольца.
Черт возьми Нет качества
`251,4/10=25,14` Таким образом, потребуется 26 банок
Значит, у этого поставщика недостаточно банок для покраски всех каруселей.
Boys & Boden
`251,4/10=25,14` Следовательно, потребуется 26 банок
Ужасно дорого
`251,4/8=231,43` Следовательно, потребуется 32 банки
Этап 3 – Выясните стоимость необходимого количества банок краски у поставщиков.
Boys & Boden
`26times £ 5,30 = £ 137,80`
ужасно дорогие
`32Times £ 5,10 = 163,20`
Ответ:
Следовательно, подрядчик должен купить рисование для Mini Roundabouts. от Мальчики и Боден.
Подробнее
Уравнение окружности | Brilliant Math & Science Wiki
Праншу Габа, Эндрю Эллинор, Тарун Сингх, и
способствовал
Содержимое
- Общее уравнение окружности
- Стандартное уравнение окружности
92 + 2gx + 2fy + c = 0.
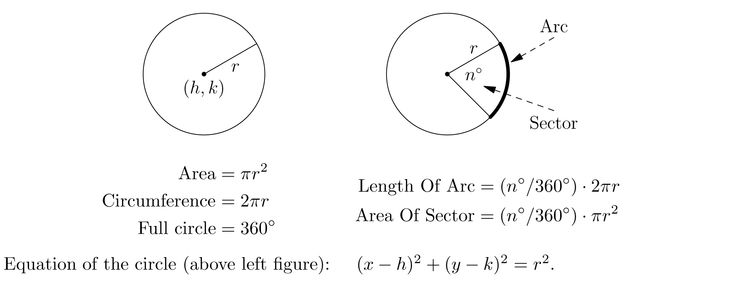
2\) .Если у нас есть точка \(O=(a,b)\) на плоскости и радиус \(r\), то мы можем построить единственный круг.
Мы находим геометрическое место точки, которая движется таким образом, что ее расстояние \(r\) от другой точки (\(a,b\)) всегда постоянно. Теперь, если \(P=(h,k)\) является любой точкой уникальной окружности с центром \(O\) и радиусом \(r\), расстояние от \(O=(a,b)\) до \(P=(h,k)\) должно быть \(r\).
Локус P 92. \]
Сравнивая со стандартным уравнением, мы видим, что \(a=b=0.\) Таким образом, центр круга является началом координат , а его радиус равен \(5\)! \(_\квадрат\)
Каково значение \(k\) на рисунке ниже?
Рисунок
Поскольку это круг и он касается как оси \(x\), так и оси \(y\), его расстояние от обеих осей должно быть одинаковым.
Поскольку он находится в \(3\) единицах от оси \(x\), он должен быть в \(3\)-единицах от оси \(y\). Следовательно,\[k = 3.\ _\квадрат\]
Другим способом выражения уравнения окружности является диаметральная форма.
Предположим, что на окружности есть две точки \((x_1, y_1)\) и \((x_2, y_2)\), такие, что они лежат на противоположных концах одного и того же диаметра, тогда уравнение окружности можно записывается как
\[(x-x_1)(x-x_2) + (y-y_1)(y — y_2) = 0.\]
Предположим, что 2 точки на окружности \(A= (x_1, y_1)\) и \(B= (x_2, y_2)\) диаметрально противоположны, тогда для любой точки \(C= (x, y)\) на круг, \(\треугольник ABC\) будет прямоугольным треугольником с прямым углом в \(C\). Отсюда следует
\[\begin{выравнивание} AC &\perp BC\\ (m_{AC}) \cdot (m_{BC}) &= -1\\ \left(\dfrac{y — y_1}{x — x_1}\right) \cdot \left( \dfrac{y — y_2}{x — x_2}\right)&= -1. \конец{выравнивание}\]
Так как \(x\) может быть равно \(x_1\) и \(x_2\),
\[\begin{выравнивание} (y-y_1)(y — y_2 ) &= — (x — x_1) (x- x_2)\\ (x-x_1)(x-x_2) + (y-y_1)(y — y_2) &= 0.
2\) .
