Формула Тейлора с остаточным членом в форме Лагранжа
22.1Приближение значений функций с помощью тейлоровских многочленов
Формула Тейлора с остаточным членом в форме Пеано, которую мы обсуждали на прошлой лекции — мощный результат про локальное поведение функций. Однако, он записывается в терминах o-малых, то есть утверждает что-то про поведение функции при x→x0. Если мы зафиксируем конкретный x, эта формула не говорит ничего. В частности, она не позволяет сделать никакого утверждения о том, что тейлоровские многочлены приближают значения соответствующих функций с ростом степени. Однако зачастую это является правдой.
22.1.1Хорошее приближение: синус
Пример 1. Рассмотрим функцию f(x)=sinx. Найдём её производные:
f′(x)=cosx,f′′(x)=−sinx,f′′′(x)=−cosx,f(4)(x)=sinx,f(5)(x)=cosx,
дальше процесс зацикливается. Пусть x0=0. Тогда производные в точке x0
образуют периодическую последовательность (начиная с нулевой производной, то
есть со значения функции): 0,1,0,−1,0,1,0,−1,….
Тейлоровский
многочлен степени n=2k+1 в окрестности точки 0 для синуса имеет вид:
T2k+1(x)=x−x33!+x55!−x77!+…+(−1)kx2k+1(2k+1)!.
T2k+1(x)=x−x33!+x55!−x77!+…++(−1)kx2k+1(2k+1)!.
Возьмём несколько тейлоровских многочленов разных степеней и построим их графики вместе с графиком синуса, см. рис. 22.1.
Рис. 22.1: Приближение sinx тейлоровскими многочленами
На графике мы видим, что каждый следующий тейлоровский многочлен приближает синус всё лучше и лучше, причём на всё большем и большем промежутке. Например, если бы я захотел посчитать значение sin(π/2) (мы знаем, что это 1, но вдруг забыли), используя для этого тейлоровские многочлены, многочлен первой степени (линейное приближение) никуда бы не годился, многочлен третьей степени дал бы ощутимую погрешность, пятой — погрешность, не видимую на графике, а девятый — ошибку в шестом знаке после запятой.
n T_n(pi/2) 1 1.5707963 3 0.9248322 5 1.0045249 7 0.9998431 9 1.0000035
9248322
5 1.0045249
7 0.9998431
9 1.0000035
Итак, в случае синуса, логично было бы предположить, что верно утверждение:
limn→∞Tn(x)=sinx
для любых x. Заметим, что это утверждение никак не следует из формулы Тейлора с остаточным членом в форме Пеано — там речь про предел при x→x0, а здесь мы взяли конкретный x, зафиксировали его и рассматриваем предел при n→∞.
22.1.2Приближение работает не везде: ln(1+x)
Пример 2. Повторим предыдущий пример для функции f(x)=ln(x). Будем записывать тейлоровские многочлены в окрестности точки 1. Имеем: f′(x)=1/x=x−1,f′′(x)=−x−2,f′′′(x)=2x−3,f(4)(x)=−6x−4. При каждом дифференцировании степень уменьшается на 1 и сносится в виде коэффициента. Значит, f(n)(x)=(−1)n+1(n−1)!x−n и тейлоровский многочлен степени n имеет вид:
Tn(x)=(x−1)−(x−1)22+(x−1)33−(x−1)44+…+(−1)n(x−1)nn.
Tn(x)=(x−1)−(x−1)22++(x−1)33−(x−1)44++…+(−1)n(x−1)nn.
Построим график логарифма и его тейлоровских многочленов. Для наглядности используем анимацию, см. рис. 22.2.
Рис. 22.2: Приближение lnx тейлоровскими многочленами
Мы видим, что с ростом n приближение становится всё лучше и лучше — но только на множестве (0,2]. Если x>2, приближение становится, наоборот, всё хуже и хуже!
22.1.3Примерчик посложнее: e−1/x2
Пример 3. Рассмотрим функцию
f(x)={e−1/x2,x≠00,x=0
Докажем, что она дифференцируема сколько угодно раз в нуле и найдём её тейлоровские многочлены в окрестности нуля.
Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, т.к. функция по-разному опрделена в нуле и вне нуля.
f′(0)=limΔx→0e−1/Δx2−0Δx.
Когда Δx→0 выражение 1/Δx2→+∞ и можно сделать замену t=1/Δx2:
f′(0)=limt→+∞e−t√1/t=limt→+∞√tet.
(На самом деле, если Δx→0−, перед корнем будет минус, но это ни на что не влияет.) Мы знаем, что экспонента стремится к бесконечности быстрее, чем любая степенная функция, и значит этот предел равен нулю. (Можно воспользоваться, например, правилом Лопиталя.)
Вторую производную тоже нужно находить по определению:
f′′(0)=limΔx→0f′(Δx)−f′(0)Δx.(22.1)
Мы знаем, что f′(0)=0. Однако чтобы найти этот предел, нам нужно знать, чему равняется f′ и в точках, отличных от нуля. Для этих точек мы можем найти f′ по стандартным правилам — если x≠0, то f(x)=e−1/x2 и эту функцию можно просто продифферецировать:
f′(x)=e−1/x2(−1×2)′=e−1/x2(−x−2)′=−e−1/x2⋅(−2x−3).
f′(x)=e−1/x2(−1×2)′==e−1/x2(−x−2)′==−e−1/x2⋅(−2x−3).
Подставляя это в (22.1), имеем:
f′′(0)=limΔx→02Δx−3e−1/Δx2Δx=limΔx→02Δx−4e−1/Δx2.
f′′(0)=limΔx→02Δx−3e−1/Δx2Δx==limΔx→02Δx−4e−1/Δx2.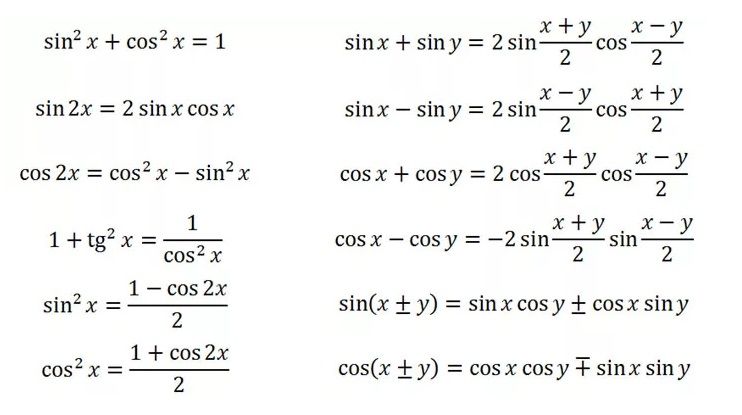
Аналогично предыдущему, экспонента стремится к нулю быстрее любой степени, и значит этот предел тоже равен нулю.
Дальше можно продолжать в том же духе. Каждый раз будет получаться 0. (Докажите, что это действительно так!)
Итак, мы получаем, что все производные f в нуле равны нулю. Это означает, что тейлоровский многочлен этой функции тождественно нулевой: для всякого n, Tn(x)=0 для всех x.
Функция f при этом принимает ненулевые значения при всех x≠0. То есть о стремлении Tn(x) к f(x) при n→∞ нет и речи.
Рис. 22.3: Функция с нулевыми производными. Кажется, что вблизи нуля у неё целый отрезок нулевых значений, но это иллюзия: f(x)≠0 при x≠0. Просто она стремится к нулю о-о-очень быстро.
Подведём промежуточный итог. Тейлоровские многочлены приближают функцию, по
которой они построены, вблизи точки x0, то есть когда x→x0. Но это не
означает, что для фиксированного значения x, Tn(x) будет приближаться к
f(x) при больших значениях n.
Хотя часто это верно. Когда именно? Об этом —
следующая теорема.
22.2Остаточный член в форме Лагранжа
Мы сформулируем теорему, которая позволяет доказывать оценки на остаточный член, то есть разницу между значением функции и значением её тейлоровского многочлена, при фиксированных x.
Теорема 1. Пусть функция f определена в окрестности точки a. Пусть точка b принадлежит этой окрестности и для определенности b>a. Предположим также, что функция f имеет (n+1) производную на интервале (a,b) и n производных на отрезке [a,b], причём f(n) непрерывна на [a,b]. Обозначим через Tn тейлоровский многочлен функции f в окрестности точки a. Тогда найдётся такая точка c∈(a,b), что
f(b)=Tn(b)+f(n+1)(c)(n+1)!(b−a)n+1.(22.2)
f(b)=Tn(b)++f(n+1)(c)(n+1)!(b−a)n+1.(22.2)
Доказательство. Теперь можно перейти к доказательству. Оно будет очень похоже на
доказательство теоремы Лагранжа о конечных приращениях.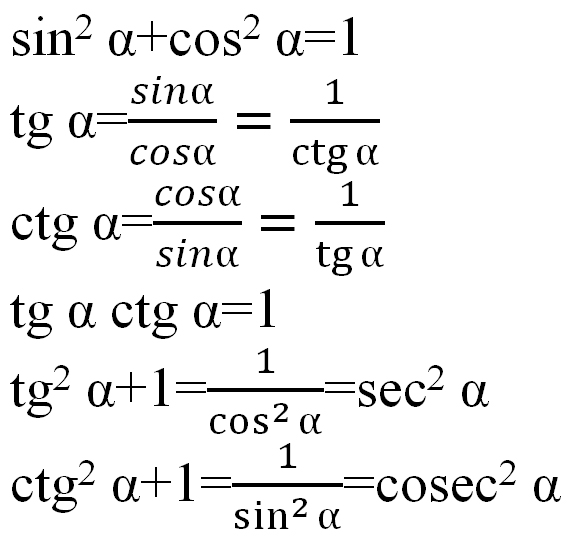
Для начала, обозначим остаточный член (каким бы он ни был) через Rn(x):
Rn(x):=f(x)−Tn(x).
Заметим, что для всех k=0,…,n:
R(k)n(a)=0,
поскольку многочлен Тейлора Tn(x) строился по функции f в окрестности точки a, и значит его значение, а также первые n производных в точке a совпадают со значениями и производными функции f.
Рассмотрим функцию
H(x):=Rn(x)−q⋅(x−a)n+1,
где q — некоторая константа, которую мы выберем позже. Заметим, что для всех k=0,…,n
H(k)(a)=0.
Действительно, для Rn это верно, а первые n производных добавки q(x−a)n+1 в точке x=a равны нулю (продифференцируйте и подставьте!).
Выберем теперь q таким образом, чтобы H(b)=0. В этом случае
Rn(b)−q(b−a)n+1=0,
то есть
q=Rn(b)(b−a)n+1.(22.3)
Теперь заметим, что функция H удовлетворяет условиям теоремы
Ролля на отрезке [a,b].
H′(c1)=0.
Теперь рассмотрим функцию H′(x) на отрезке [a,c1]. Она снова удовлетворяет условию теоремы Ролля! Действительно, H′(a)=0 и H′(c1)=0. Функция H′ непрерывна на отрезке [a,b] и значит на [a,c1]. (Если n=1, непрерывность первой производной f на всём отрезке [a,b] явно сформулирована в условии теоремы, а если n>1, то она следует из существования второй производной на всём отрезке, и значит дифференцируемости первой производной.)
Значит существует такая точка c2∈(a,c1), что H′′(c2)=0.
Продолжая в том же духе, мы будем строить последовательность точек ck, удовлетворяющих условиям ck∈(a,ck−1) и H(k)(ck)=0.
Сколько шагов так можно сделать? Заметим, что условия теоремы Ролля будут
выполняться для всех производных функции H вплоть до H(n).
В
частности, мы явно потребовали, чтобы f(n) была непрерывна на
отрезке [a,b], а значит и H(n) тоже будет непрерывной на этом
отрезке, и, следовательно, и на отрезке [a,cn]. Значит в нашем
алгоритме мы дойдём до k=n+1, то есть найдётся такая точка cn+1∈(a,cn)⊂(a,b), что
H(n+1)(cn+1)=0.
Покажем, что cn+1 — это и есть искомая точка c, существование которой утверждается в теореме. Для этого нужно найти (n+1)-ю произодную H:
H(n+1)(x)=f(n+1)(x)−T(n+1)n(x)−q⋅(n+1)!=f(n+1)(x)−q⋅(n+1)!.
H(n+1)(x)=f(n+1)(x)−T(n+1)n(x)−−q⋅(n+1)!=f(n+1)(x)−q⋅(n+1)!.
Значит в точке x=cn+1 имеем:
0=H(n+1)(cn+1)=f(n+1)(cn+1)−q⋅(n+1)!.
Теперь нужно вспомнить, чему равняется q, см. (22.3). Получается такая штука:
Rn(b)(b−a)n+1(n+1)!=f(n+1)(cn+1)
или
Rn(b)=f(n+1)(cn+1)(n+1)!(b−a)n+1.
То есть если положить c:=cn+1, получится ровно то, что мы обещали. Доказательство завершено.∎
22.2.1Бонус: формула Тейлора и равноускоренное движение
Приведенное выше доказательство — самое простое из всех, что я знаю. Но у меня всегда есть ощущение, что я достаю кролика из шляпы, когда я его завершаю, и после его прочтения всё равно нет ощущения, что становится понятно, почему формула именно такая. Возможно, следующая интерпретация прольёт на неё чуть больше света.
Рассмотрим движение с постоянным ускорением. Пусть в момент времени x=a мы находились в точке y0 и в этот момент скорость движения составляла v0. Пусть также на всём промежутке времени, который нас интересует, ускорение равнялось A. Тогда закон движения задаётся следующим образом:
y=y0+v0(x−a)+A2(x−a)2.(22.4)
Действительно, если продифференцировать правую часть и подставить x=a,
получим, что положение и скорость в начальный момент времени совпадают с
искомыми, а если продифференцировать дважды, то мы получим константу A.
Слагаемое A2(x−a)2 показывает, насколько сильно мы отклоняемся от движения с постоянной скоростью v0 к моменту времени x.
Рассмотрим теперь некоторый другой закон движения y=f(x), уже не обязательно происходящий с равномерным ускорением. Мы приближаем его движением с постоянной скоростью:
y=T1(x)=f(a)+f′(a)(x−a)
и интересуемся, насколько сильно реальное движение уходит от этого движения с постоянной скоростью к моменту времени x=b. Это и есть остаточный член f(b)−T1(b).
Пусть ускорение непрерывно, то есть f′′ непрерывно на всём отрезке [a,b]. В каких-то точках оно достигает своего максимума Amax и минимума Amin, а также принимает все значения из отрезка [Amax,Amin].
Если я стартую в точке f(a) с начальной скоростью f′(a) и всю дорогу буду двигаться с максимально возможным ускорением Amax, к моменту b я попаду в точку
fmax(b):=T1(b)+Amax2(b−a)2,
а если с минимально возможным ускорением Amin — то в точку
fmin(b):=T1(b)+Amin2(b−a)2.
Реальное положение f(b) находится где-то между этими двумя крайностями. (Это утверждение кажется очевидным; его аккуратное обоснование несложно и опирается на теорему Лагранжа.)
T1(x)+Amin2(b−a)2≤f(b)≤T1(x)+Amax2(b−a)2.
T1(x)+Amin2(b−a)2≤f(b)≤≤T1(x)+Amax2(b−a)2.
Пусть A непрерывно меняется от Amin до Amax. Тогда для какого-то значения A=A∗,
f(b)=T1(b)+A∗2(b−a)2.
Но с другой стороны если A∗∈[Amin,Amax], это какое-то значение ускорения между минимальным и максимальным. Из непрерывности ускорения, найдётся момент времени x=c, при котором f′′(c)=A∗. В этом случае
f(b)=T1(b)+f′′(c)2(b−a)2,
а это и есть формула Тейлора с остаточным членом в форме Лагранжа (для n=1).
Аналогичным образом можно доказать эту формулу для любого n — только вместо ускорения нужно будет брать (n+1)-ю производную f. Заметим, что наше доказательство использует схожие идеи: функцию H можно записать в виде
H(x)=f(x)−(Tn(x)+q(x−a)n)
и из такого представления видно, что она показывает, насколько движение по
закону y=f(x) отличается от движения с постоянной (n+1)-й производной, и мы
специально так подбираем эту производную (константу q), чтобы оказаться в той
же точке, в которой мы оказались при движении по закону y=f(x).
Это
соответствует выбору A∗ в рассуждении выше.
22.3Заключение
Формула Тейлора с остаточным членом в форме Лагранжа позволяет доказывать, что некоторые функции представляются в виде бесконечных сумм — рядов Тейлора. Трудно переоценить значение этого факта для развития математики: ведь что может быть проще, чем степенной ряд — прямое обобщение многочлена, простейшего класса математических функций? Анализ функций, представимых в виде своих рядов Тейлора (они называюется аналитическими) — большая и красивая область математики. Однако, как показывает пример 3, не все функции являются аналитическими. И у этого факта есть важные следствия — в частности, можно склеивать гладкие функции из кусочков, сохраняя их гладкость.
← Предыдущая глава Следующая глава →
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
ca.
классический анализ и оды — Как решить $f(f(x)) = \cos(x)$? 9{k-m} \binom{m}{k} \phi_{1/2}(k-1,z)$$Интерполируем от первой целочисленной точки, где значение действительно, т.е. от x=-1.
Теперь мы получаем аппроксимацию другого полупотока cos x, беря arccos по приведенной выше функции:
$$\phi_{2}(x,z)=\arccos(\phi_{1}(x+ 1,z))$$
Мы знаем, что поток cos(x) должен совпадать с первой функцией в четных числах и со второй функцией в нечетных числах.
Итак, мы делаем заглушку потока, следующего за этим знанием (мы также хотим, чтобы его абсолютное значение было монотонным). 9{[n]} (\phi(x+n,z))$$
Численно этот предел сходится довольно быстро. Если предел существует, то он по определению удовлетворяет уравнению
$$ \cos(\Phi(x,z))=\Phi(x+1,z)$$
, так что это истинный поток.
Вышеизложенное можно проиллюстрировать графиком:
Здесь верхний полупоток (поток cos(cos z)) выделен синим цветом, нижний полупоток — красным, реальная часть потока — желтым, воображаемая часть потока зеленый.
Все потоки принимаются за точку z=1.
Следуя этому, мы можем построить график полуитерации косинуса $\Phi(1/2,z)$:
Здесь синий — действительная часть, а красный — мнимая часть.
Мы можем убедиться, что повторенная дважды полуитерация $\Phi(1/2,\Phi(1/2,z))$ (синяя) достаточно хорошо следует косинусу (красная) на положительных полупериодах и везде, где конус положителен (то есть также на мнимой оси):
Я думаю, что это совпадает с ответом Джеральда Эдгара выше. Модифицированная функция, повторенная дважды, дает косинус по всем действительным осям:
Это истинная половинная итерация косинуса, которая работает на всей действительной оси, производя точно косинус:
из которых работают для целых комплексных чисел.
Эту функцию можно рассматривать как истинное решение на комплексной плоскости, если интерпретировать ее как многозначную функцию. Для этого возьмем функцию на каждом интервале и аналитически продолжим ее на всю комплексную плоскость.