Вопросы по теме «Подобие»
Вопросы по теме ПОДОБИЕ и его применение
1.Что называют отношением отрезков?
2.Каким свойством обладают площади треугольников, имеющих по одному равному углу?
3.Когда отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1?
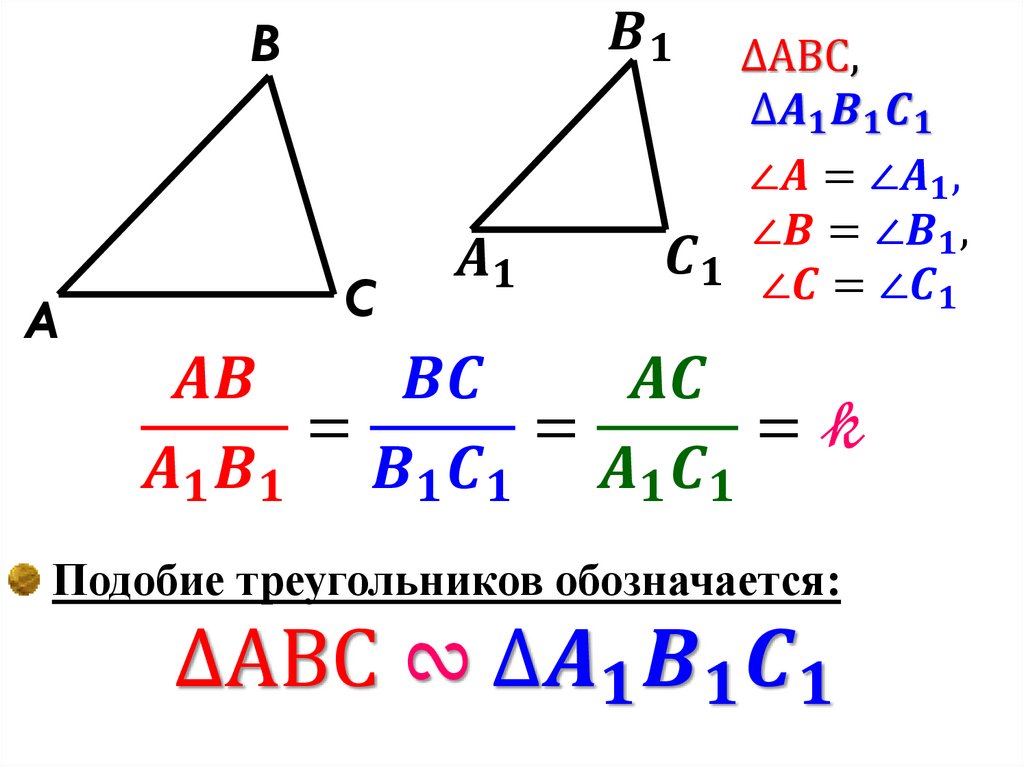
4.Какие два треугольника называют подобными?
5.Что называют коэффициентом подобия?
6.Как относятся площади подобных треугольников?
7.Каким свойством обладает биссектриса треугольника?
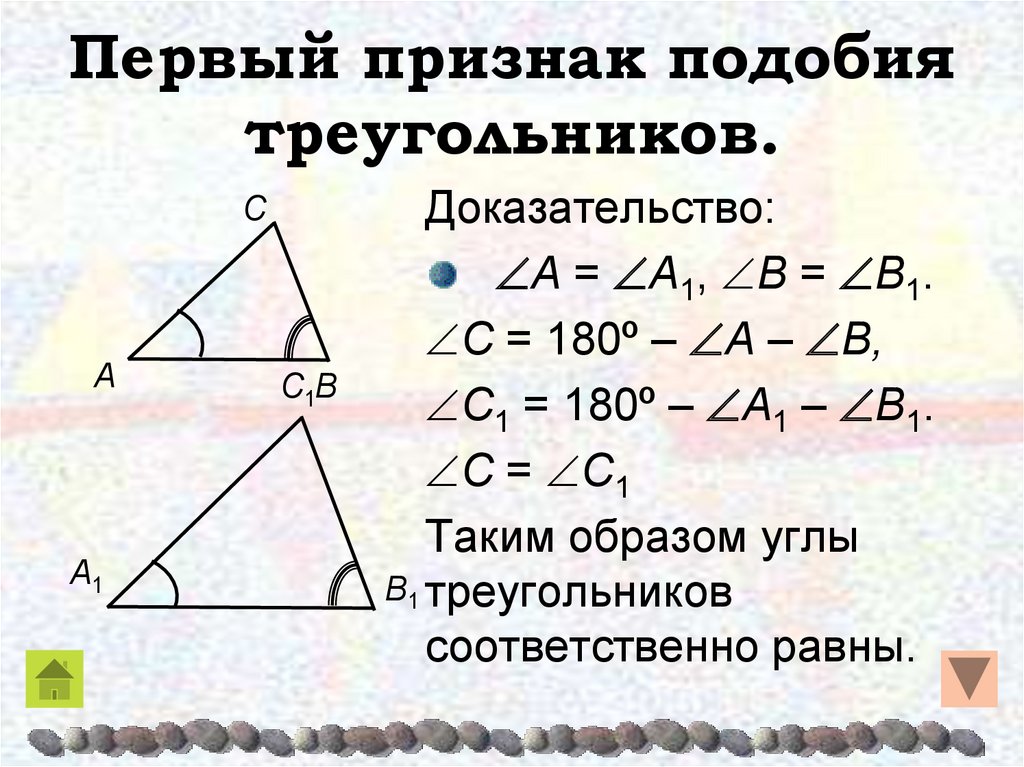
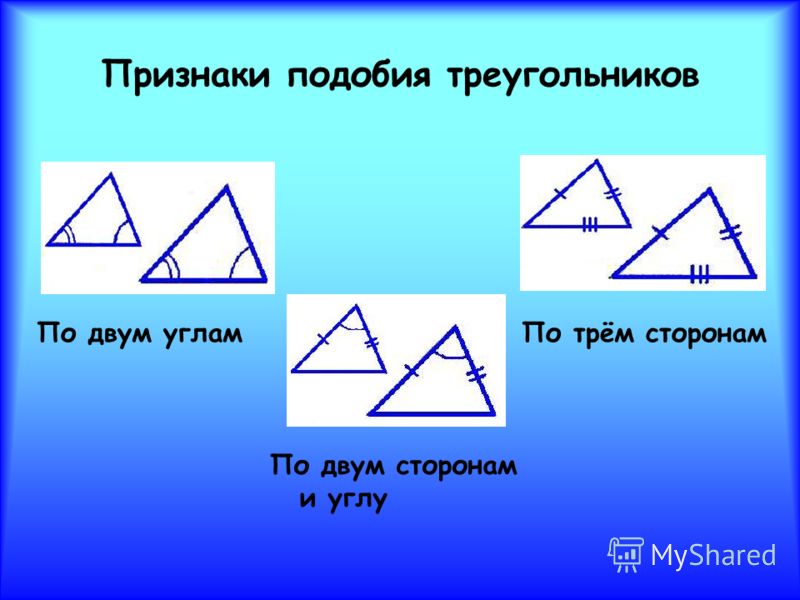
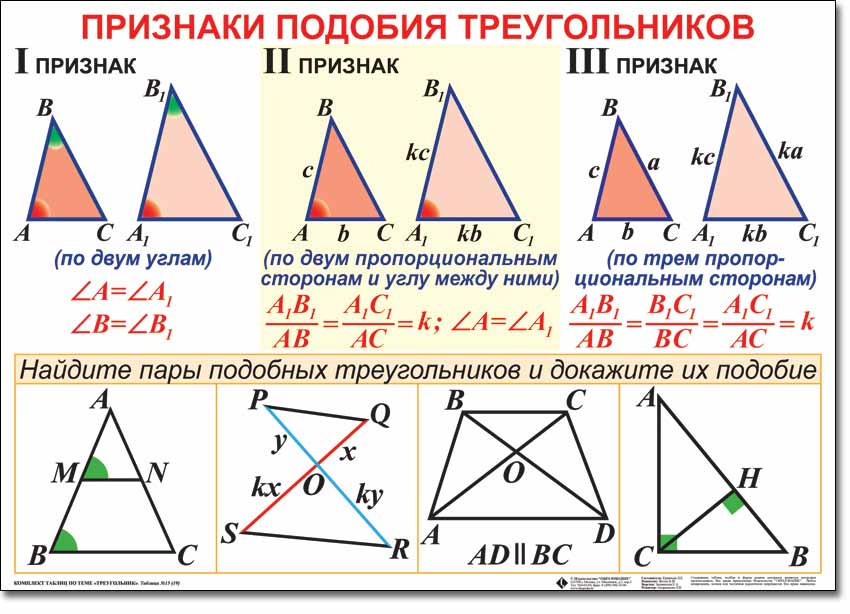
8.Сформулируйте первый признак подобия треугольников.
9. Сформулируйте второй признак подобия треугольников.
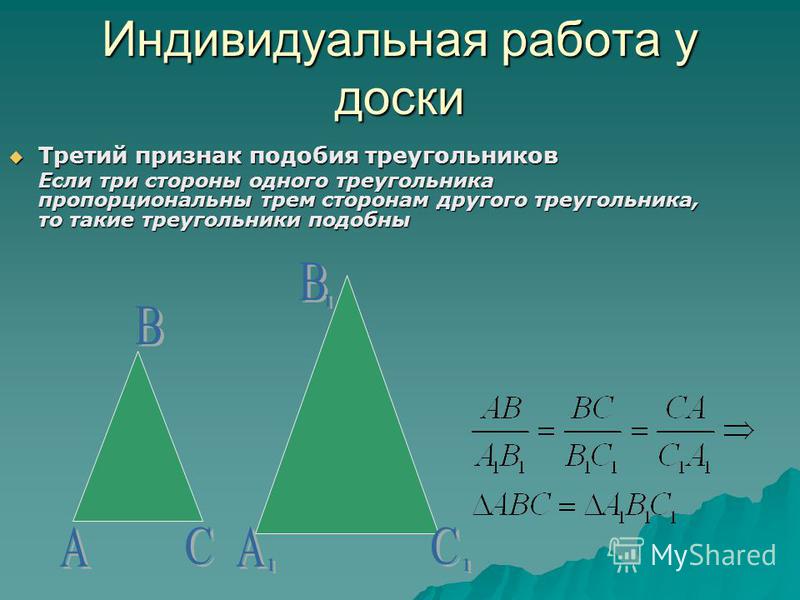
10. Сформулируйте третий признак подобия треугольников.
11.Что называют средней линией треугольника?
12.Каково свойство средней линии треугольника?
13.Каким свойством обладают медианы треугольника?
14.Когда отрезок XY называется средним пропорциональным (средним геометрическим) для отрезков АВ и CD?
15.
Каким свойством обладает высота прямоугольного треугольника, проведенная к гипотенузе?
16.Каким свойством обладает каждый катет прямоугольного треугольника?
17.Что называют синусом острого угла прямоугольного треугольника?
18.Что называют косинусом острого угла прямоугольного треугольника?
19.Что называют тангенсом острого угла прямоугольного треугольника?
20.Как записывается основное тригонометрическое тождество?
21.Назовите значения синуса, косинуса и тангенса угла в 30º.
22. Назовите значения синуса, косинуса и тангенса угла в 60º.
23. Назовите значения синуса, косинуса и тангенса угла в 45º.
Вопросы по теме ПОДОБИЕ и его применение
1.Что называют отношением отрезков?
2.Каким свойством обладают площади треугольников, имеющих по одному равному углу?
3.Когда отрезки АВ и СD пропорциональны отрезкам А1В1 и С1D1?
4.Какие два треугольника называют подобными?
5.
Что называют коэффициентом подобия?
6.Как относятся площади подобных треугольников?
7.Каким свойством обладает биссектриса треугольника?
8.Сформулируйте первый признак подобия треугольников.
9. Сформулируйте второй признак подобия треугольников.
10. Сформулируйте третий признак подобия треугольников.
11.Что называют средней линией треугольника?
12.Каково свойство средней линии треугольника?
13.Каким свойством обладают медианы треугольника?
14.Когда отрезок XY называется средним пропорциональным (средним геометрическим) для отрезков АВ и CD?
15.Каким свойством обладает высота прямоугольного треугольника, проведенная к гипотенузе?
16.Каким свойством обладает каждый катет прямоугольного треугольника?
17.Что называют синусом острого угла прямоугольного треугольника?
18.Что называют косинусом острого угла прямоугольного треугольника?
19.Что называют тангенсом острого угла прямоугольного треугольника?
20.
Как записывается основное тригонометрическое тождество?
21.Назовите значения синуса, косинуса и тангенса угла в 30º.
22. Назовите значения синуса, косинуса и тангенса угла в 60º.
23. Назовите значения синуса, косинуса и тангенса угла в 45º.
Теоретический зачет по геометрии. Тема: «Подобие треугольников»
- Бузецкая Татьяна Валерьевна
Рейтинг: 5 / 5
Пожалуйста, оцените Оценка 1Оценка 2Оценка 3Оценка 4Оценка 5Урок по геометрии.
Тема: «Теоретический зачет по теме Подобие треугольников»
Цели:
· Систематизировать и обобщить знания учащихся по данной теме
· Проконтролировать усвоение теоретического материала.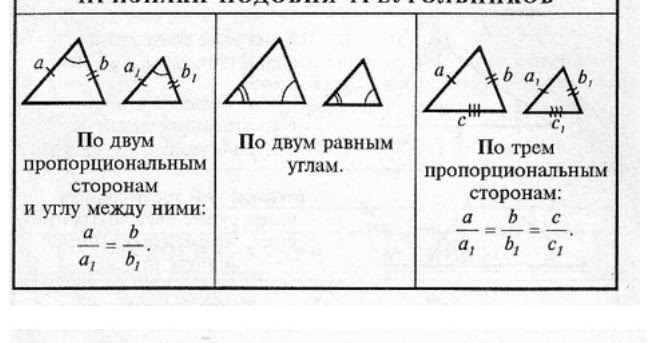
План:
1). Актуализация знаний (15 минут)
Организована, в виде работы в парах. На парте лежат вопросы, учащиеся друг другу рассказывают ответы на них. После чего результаты своей работы заносят в таблицу:
|
Моя оценка ответов товарища (оцениваются ответы 1 человека) |
Оценка мне моего товарища (оцениваются ответы 2 человека) |
|
|
|
Вопросы:
1). Признаки подобия треугольников
2). Определение подобных треугольников
3). Теорема об отношении периметров подобных треугольников
4). Теорема об отношении площадей подобных треугольников
5).
Определение средней линии треугольника
6). Теорема о средней линии треугольника
7). Определение среднего геометрического двух отрезков
8). Определение проекции катета на гипотенузу
9). Теоремы о высоте прямоугольного треугольника, проведенного из вершины прямого угла
10). Определение основных тригонометрических функций острого угла прямоугольного треугольника
11).Таблица значений тригонометрических функций углов в .
2). Проверка знаний теоретического материала (30 минут)
Самостоятельная работа учащихся, составлены задания в 2 вариантах
• первая часть предполагает определение истинности утверждения.
Эти задания развивают память, критическое мышление, формируют метопредметные умения анализировать, сравнивать. Такие зачеты позволяют учащимся подготовиться к сдаче ГИА.
• вторая часть направлена на реализацию навыков письменного изложения знаний и мыслей.
Умение говорить на языке проверяемого предмета. Возможно изображение конкретных фактов.
Важным при написании теста является умение работать в темпе. Однако учитель имеет возможность самостоятельно определять время выполнения заданий, критерии оценивания, способы проверки заданий (например, взаимопроверка на тренировочных уроках).
• третья часть направлена на умение грамотно изложить доказательство определенных фактов, или умение применить весь свой «багаж знаний» по данной теме для применения при решении нестандартной задачи.
Зачет по геометрии. Тема: «Подобие треугольников».
1 вариант.Часть 1.
Определить являются ли ниже приведенные утверждения верными (да -+, нет-)
|
№ |
Утверждение |
+/- |
|
1 |
Любые два прямоугольных треугольника подобны |
|
|
2 |
Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны. |
|
|
3 |
Два треугольника называются подобными, если их углы соответственно равны |
|
|
4 |
Если два треугольника подобны, то их соответствующие стороны равны |
|
|
5 |
Отношение периметров двух подобных треугольников равно коэффициенту подобия |
|
|
6 |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. |
|
|
7 |
Любые два прямоугольных и равнобедренных треугольника подобны. |
|
|
8 |
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны |
|
|
9 |
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны |
|
|
10 |
Любые два равнобедренных треугольника подобны. |
|
|
11 |
Высота прямоугольного треугольника равна среднему геометрическому между проекциями катетов на гипотенузу |
|
|
12 |
Синус острого угла прямоугольного треугольника это отношение катетов треугольника |
|
|
13 |
Косинус 45° не существует |
|
|
14 |
Диагонали трапеции при пересечении образуют четыре подобных треугольника. |
|
Часть 2.
Необходимо ответить на вопросы и записать формулировку геометрического утверждения
|
№ |
Вопрос |
Ответ |
|
1 |
Что такое средняя линия треугольника? |
|
|
2 |
Дать определение проекции катета на гипотенузу?
|
|
|
3. |
Какие треугольники называются подобными?
|
|
|
4. |
Сформулируйте признаки подобия треугольников:
|
1.
2.
3.
|
|
5 |
Запишите теорему об отношении площадей подобных треугольников.
|
|
|
6 |
Сформулируйте утверждение о пропорциональных отрезках в прямоугольном треугольнике.
|
|
|
7. |
Что такое косинус острого угла прямоугольного треугольника?
|
|
|
8. |
Записать основное тригонометрическое тождество.
|
|
|
9. |
Косинус 45º, синус 30º,тангенс 90º
|
|
|
10. |
Сформулировать теорему о точке пересечения медиан треугольника
|
|
Часть 3. (выполнить любое из предложенных заданий)
1). Доказать любой признак подобия треугольников
2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла есть среднее геометрическое между проекциями катетов на гипотенузу.
3). Решить задачу: Найдите высоту ракеты, по данным рисунка
Зачет по геометрии. Тема: «Подобие треугольников».
2 вариант.
Часть 1.
Определить являются ли ниже приведенные утверждения верными (да -+, нет-)
|
№ |
Утверждения |
+/- |
|
1 |
Любые два равнобедренных треугольника подобны. |
|
|
2 |
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. |
|
|
3 |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. |
|
|
4 |
Любые два равнобедренных прямоугольных треугольника подобны. |
|
|
5 |
Два треугольника называются подобными, если их углы соответственно пропорциональны |
|
|
6 |
Если два треугольника подобны, то их соответствующие стороны равны. |
|
|
7 |
Отношение площадей двух подобных треугольников равно коэффициенту подобия |
|
|
8 |
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны. |
|
|
9 |
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны |
|
|
10 |
Любой прямоугольный и равнобедренный треугольники подобны |
|
|
11 |
Косинус это отношение противолежащего катета и гипотенузы |
|
|
12 |
Тангенс прямого угла не существует |
|
|
13 |
Проекция катета на гипотенузу, это отрезок гипотенузы треугольника, заключенный между основанием высоты, проведенный к гипотенузе и катетом |
|
|
14 |
Диагонали трапеции при пересечении образуют два подобных треугольника. |
|
Часть 2.
Необходимо ответить на вопросы и записать формулировку геометрического утверждения
|
№ |
Вопрос |
Ответ |
|
1 |
Сформулируйте теорему о средней линии треугольника? |
|
|
2 |
Запишите определение подобных треугольников
|
|
|
3. |
Что называют коэффициентом подобия?
|
|
|
4. |
Чему равен квадрат коэффициента подобия
|
|
|
5 |
Сформулируйте признаки подобия треугольников:
|
1.
2.
3.
|
|
6 |
Что такое тангенс острого угла прямоугольного треугольника
|
|
|
7. |
Что такое синус острого угла прямоугольного треугольника
|
|
|
8. |
Запишите значения синус , косинус 45º, тангенс 90º |
|
|
9. |
Определение среднего геометрического двух отрезков
|
|
|
10. |
Теорема о высоте прямоугольного треугольника
|
|
Часть 3. (выполнить любое из данных заданий)
1). Доказать любой признак подобия треугольников
2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла разбивает этот треугольник на два подобных между собой треугольника.
3). Решить задачу:
Высота Эйфелевой башни в Париже 300м, а её тени 510 м. В это же время длина тени часов Биг Бен в Лондоне составляет 164,9 м. Определите высоту часов.
Литература и интернет ресурсы.
1). Фароков А.В. Теоретические тесты по геометрии 8 класс. 2012 год
2).Кукарцева Г.И. Сборник задач по геометрии в рисунках и тестах 7-9 класс, 2000 год
3). http://imteacher.ru (теоретические зачеты)
4). http://www.uchportal.ru (подобие треугольников)
5).Белицкая О.В. Геометрия 8 класс. Тесты в 2-х частях. 2012 год
- Назад
- Вперед
You have no rights to post comments
Авторизация
Запомнить меня
Регистрация
- Забыли данные входа?
- Регистрация
Перевод сайта
Отличное объяснение утверждения о сходстве в геометрии с примерами
Понятие подобия очень важно в геометрии и помогает доказать многие теоремы и следствия. В статье ScienceStruck дается объяснение утверждения о сходстве в геометрии с примерами.
Краткие советы для запоминания
- Два подобных треугольника не обязательно должны быть конгруэнтными, но два конгруэнтных треугольника подобны.
- Если острый угол прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.
- Все равносторонние треугольники подобны.
В заявлении о сходстве упоминается, что для того, чтобы две фигуры были похожи, они должны иметь одинаковые углы, а их стороны должны быть пропорциональны. При написании заявления о сходстве в геометрии объясняются причины, по которым две формы похожи. Эта концепция используется для доказательства многих теорем, как упоминалось ранее.
Также используется для нахождения значения неизвестной стороны геометрической фигуры, при этом предоставляются значения других сторон. В следующих абзацах вы узнаете, как писать утверждения о сходстве для различных геометрических фигур.
Как написать заявление о сходстве
Шаг I
Для начала определите похожие формы. Затем нарисуйте их на бумаге. Фигуры, которые вам будут предоставлены, будут иметь разную ориентацию, поэтому, даже если они похожи, они могут выглядеть по-разному. Не раскачивайтесь.
Шаг II
Нарисуйте фигуры так, чтобы равные углы выстраивались подобно друг другу, т. е. вам либо будут заданы значения углов, либо конгруэнтные углы уже будут отмечены. Таким образом, вы можете определить угол и начать рисовать их соответственно. Например, если в треугольниках ABC и PQR угол ABC равен углу PQR, сначала обведите эти углы на бумаге. Назовите вершины правильно.
Шаг III
Затем перейдите к следующему набору конгруэнтных треугольников и пометьте их соответствующим образом. Повторите то же самое с третьим набором конгруэнтных углов.
Шаг IV
Теперь, когда вы поняли сходство, запишите подобные углы. Укажите, что угол ABC равен углу PQR, угол BCA равен углу QRC и так далее.
Шаг V
Рассчитайте длины сторон и убедитесь, что они пропорциональны. Теперь напишите утверждение о сходстве. Вы должны написать треугольник ABC ~ треугольник PQR. Знак «~» — это знак конгруэнтности в геометрии.
Заявление о сходстве и соотношение
- У подобных фигур стороны пропорциональны. Это отношение длин двух соответствующих сторон называется масштабным коэффициентом. Это необходимо указать при написании заявления о сходстве.
- Например, на приведенном выше рисунке AB/PQ = BC/QR = AC/PR = 1/2.
- В подобных треугольниках отношение их площадей равно квадрату отношения их сторон.
- Масштабный коэффициент используется для определения значения неизвестной стороны в геометрических задачах. Это особенно полезно в случае полигонов.
Примеры утверждений о сходстве
Для трех треугольников
На приведенных выше рисунках показаны три подобных треугольника. В приведенных выше треугольниках
угол A = угол P = угол X
угол B = угол Q = угол Y
угол C = угол R = угол Z
Утверждение подобия: треугольник ABC ~ треугольник PQR ~ треугольник XYZ
Для a Четырехугольник
угол A = угол P
угол B = угол Q
угол C = угол R
угол D = угол S
AB/PQ = BC/QR = CD/RS = AD/PS = ½
Утверждение подобия: четырехугольник ABCD ~ четырехугольник PQRS
Для прямоугольников
угол A = угол P
угол B = угол Q
угол C = угол R
угол D = угол S
AB/PQ = BC/QR = CD/RS = AD/PS = 2/1
Утверждение подобия: прямоугольник ABCD ~ прямоугольник PQRS
Для полигонов
угол A = угол P
угол B = угол Q
угол C = угол R
угол D = угол S
угол E = угол T
угол F = угол U
AB/PQ = BC/QR = CD/RS = DE/ST = EF/TU = ½
Предположим, что на приведенном выше рисунке угол BAC = 30°, а угол ACB = 60°. Тогда по теореме угол ABD = 60°, а угол DBC = 30°.
Итак,
угол ABC = угол ADB = угол BDC
угол BAC = угол DAB = угол DBC
угол ACB = угол ABD = угол BCD
Утверждение подобия: треугольник ABC ~ треугольник ADB ~ треугольник BDC
Эта теорема может использоваться для решения «x» на приведенном выше рисунке. Поскольку они подобны, их стороны также будут пропорциональны. Для начала разделите треугольники и обведите их по отдельности. Затем по теореме подобия рассмотрим любой из двух вписанных треугольников и главный прямоугольный треугольник, чтобы найти значение неизвестного. Рассмотрим треугольник ABC и треугольник BDC. Таким образом,
AB/BD = AC/BC
3/x = 5/4
5x = 12
x = 2,4
Подобные геометрические фигуры имеют одинаковый порядок и направление. Какой бы набор вершин вы ни выбрали при трассировке, остальные будут соединяться соответствующим образом.
Подобные треугольники
| ||||||||||||
| Домашняя страница | Заказать программное обеспечение по математике | О сериале | Учебники по математическому программному обеспечению |
| Программное обеспечение по математике для 7 класса | Программное обеспечение по математике для 8 класса | Программное обеспечение по математике для 9 классов | Программное обеспечение по математике для 10 класса |
| Программное обеспечение для домашних заданий | Программное обеспечение для репетиторов | Математическая программная платформа | Пробное математическое программное обеспечение |
| Обратная связь | О mathsteacher.com.au | Условия | Наша политика | Ссылки | Контакты |
Copyright 2000-2022 mathsteacher.