Формула длины окружности расчет: Длина окружности. Площадь круга — урок. Математика, 6 класс.

Содержание

Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Оглавление:
Характеристики фигуры
Основные термины окружности
Основные формулы для вычислений
Диаметр в формулах вычисления
Расчёты по радиусу
Подручные способы вычисления
Круглые предметы в истории человеческой жизни

Содержание

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

Это интересно: как переводить градусы в радианы?

В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.

Это интересно: какой четырёхугольник называется квадратом?

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.

Это интересно: что такое горизонтально, что означает слово горизонталь?

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Это интересно: формулировка и доказательство признаков параллелограмма.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Длина окружности круга через радиус — онлайн калькулятор

Справочник
Онлайн-калькуляторы
Тесты с ответами

Длину окружности можно рассчитать самостоятельно. Но если требуется производить конвертацию из одних величин в другие, использовать громоздкие числа и при этом уложиться в короткий срок, лучше автоматизировать вычисления. Онлайн-калькуляторы на сайте охватывают все темы по алгебре и геометрии.

Наш сервис дает возможность рассчитать искомое значение несколькими способами в зависимости от условий задания. В этой программе используется радиус. Если у вас другие данные, ищите подходящий вариант в разделе сайта.

Введите длину радиуса окружности в соответствующее окно.
Установите единицы измерения для радиуса и искомой площади. Отправьте задание на расчет кнопкой «Найти».
Получите решение и ответ.

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Длина окружности круга (По диаметру)

Периметр квадрата
Периметр треугольника
Периметр трапеции
Периметр прямоугольника
Периметр ромба
Периметр параллелограмма
Периметр квадрата по диагонали

Расчет длины окружности по формуле через радиус происходит так:

После ввода условий программа сразу выдает пошаговое решение и ответ. Это позволяет школьникам овладеть непонятным материалом или закрепить тему, свериться с самостоятельно решенным заданием, подготовиться к экзамену. Также программой пользуются студенты, преподаватели, родители учеников. Точные расчеты пригодятся инженерам, специалистам строительной сферы при вычислении нужного количества материалов.

Чем полезен сервис:

Не надо тратить время на регистрацию. На зачете или контрольной особенно важна скорость получения решения.
Сервис работает бесплатно и доступен круглосуточно. Свериться с решением можно в любое время.

Количество запросов не лимитируется. Тренироваться в вычислениях можно столько, сколько требуется для усвоения материала.

Если после использования программы все равно остались вопросы, свяжитесь с консультантом. Опишите подробно свою проблему, чтобы мы смогли подобрать под ваш запрос преподавателя из своего штата для объяснения темы, решения контрольной или онлайн-сопровождения.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Процент
Решение матриц
Точка, прямая, плоскость

Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами
Периметр фигур

Поможем с любой работой

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Решение задач
Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Вычислите длину окружности / Хабр

«Пожалуйста, напишите на C++ функцию, которая получает диаметр круга как float и возвращает длину окружности как float».

Звучит как задание на первой неделе курса по C++. Но это только на первый взгляд. Сложности возникают уже на первых этапах решения задачи. Предлагаю рассмотреть несколько подходов.

Студент: Как вам такой вариант?

#include <math.h>
float CalcCircumference1(float d)
{
    return d * M_PI;
}

Преподаватель: Да, этот код может нормально откомпилироваться. А может и нет. M_PI не определена в стандартах C или C++. С компилятором в VC++ 2005 это сработает, но для более поздних версий придется использовать #define _USE_MATH_DEFINES перед включением math.h, чтобы получить доступ к этой нестандартной константе. Причем в результате вы напишете код, с которым могут не справиться другие компиляторы.

Сцена вторая

Студент: Благодарю за мудрость, учитель. Я убрал зависимость от нестандартной константы M_PI. Так лучше?

float CalcCircumference2(float d)
{
    return d * 3.14159265358979323846;
}

Преподаватель: Да, так лучше.

Этот код будет скомпилирован, и вы получите искомый результат. Но ваш код неэффективен. Вы умножаете число с одинарной точностью на константу с двойной точностью. Компилятору придется привести параметр функции типа float к типу double, а затем выполнить обратное преобразование для получения возвращаемого значения. Если вы компилируете код для SSE2, то это добавляет две инструкции в цепочку зависимостей и вычисления могут выполняться втрое дольше! В большинстве случаев такие задержки вполне допустимы, но во внутреннем цикле негативный эффект может быть весьма значительным.

Если вы компилируете для платформы x87, то преобразование в тип double ничего не стоит, а вот обратное преобразование затратно – настолько затратно, что некоторые оптимизирующие компиляторы выбрасывают это преобразование, а в результате можно получить КРАЙНЕ НЕОЖИДАННЫЕ результаты – например, CalcCircumference( r ) == CalcCircumference( r ) вернет false!

Сцена третья

Студент: Спасибо, учитель. Честно говоря, я не знаю, что такое SSE2 и x87, но я вижу, насколько элегантным становится код, когда типы согласованы. Это настоящая поэзия. Я буду использовать константу одинарной точности. Как вам вот это?

float CalcCircumference3(float d)
{
    return d * 3.14159265358979323846f;
}

Преподаватель: Да, превосходно! Символ «f» в конце константы все меняет. Если бы вы посмотрели на сгенерированный машинный код, вы бы поняли, что этот вариант намного компактнее и эффективнее. Однако у меня есть замечания к стилю. Не кажется ли вам, что этой загадочной константе не место внутри функции? Даже если это число Пи, значение которого вряд ли изменится, лучше присвоить константе имя и поместить в заголовочный файл.

Сцена четвертая

Студент: Спасибо. Вы объясняете все очень доходчиво. Я помещу строку кода ниже в общий файл заголовка и буду использовать ее в своей функции. Так нормально?

const float pi = 3. 14159265358979323846f;

Преподаватель: Да, отлично! С помощью ключевого слова «const» вы указали, что переменная не должна и не может быть изменена, кроме того, ее теперь можно поместить в заголовочный файл. Но, боюсь, теперь нам придется углубиться в некоторые тонкости определения областей видимости в C++.

Объявив pi с ключевым словом const, вы получите в качестве бонуса эффект ключевого слова static. Для целочисленных типов это нормально, но если вы имеете дело с другим типом данных (число с плавающей точкой, массив, класс, структура), память под вашу переменную может быть выделена отдельно в каждой единице трансляции, которая включает в себя ваш заголовочный файл. В некоторых случаях у вас в итоге будет несколько десятков или даже сотен экземпляров переменной типа float и ваш исполняемый файл будет неоправданно большим.

Сцена пятая

Студент: Вы шутите? И что делать?

Преподаватель: Да, мы пока далеки от идеала. Вы можете повесить на объявление константы атрибут __declspec(selectany) или __attribute __(weak), для того чтобы VC++ и GCC, соответственно, поняли, что достаточно сохранить одну из многочисленных копий этой константы. Но поскольку мы с вами находимся в идеалистическом мире науки, я настаиваю на применении стандартных конструкций C++.

Сцена шестая

Студент: То есть примерно так? С помощью constexpr из C++11?

constexpr float pi = 3.14159265358979323846f;

Преподаватель: Да. Теперь ваш код идеален. Конечно, VS 2013 не сможет его откомпилировать, потому что не знает, что делать с constexpr. Но вы всегда можете воспользоваться набором инструментов Visual C++ Compiler Nov 2013 CTP либо последней версией GCC или Clang.

Студент: А #define можно использовать?

Преподаватель: Нет!

Студент: А, к черту все это! Лучше я стану бариста.

Сцена седьмая

Студент: Стоп, я кое-что припоминаю. Это же просто! Вот как будет выглядеть код:

mymath.h:
extern const float pi;
mymath.cpp:
extern const float pi = 3.14159265358979323846f;

Преподаватель: Точно, в большинстве случаев это будет верное решение. Но что если вы работаете над DLL, как внешние функции будут обращаться к mymath.h в вашей DLL? В таком случае вам придется обеспечить экспорт и импорт этого символа.

Проблема в том, что правила для целочисленных типов абсолютно другие. Целесообразно и рекомендуется добавить в заголовочный файл C++ следующее:

const int pi_i = 3;

Число Пи здесь указано недостаточно точно, но дело в том, что целочисленные константы в заголовочных файлах не требуют выделения памяти в отличие от остальных констант. Чем такое отличие обусловлено, не совсем понятно, но чаще всего это и не важно.

О том, что значит «static» в «const», я узнал несколько лет назад, когда меня попросили выяснить, почему одна из наших ключевых библиотек DLL вдруг прибавила в весе 2 МБ. Оказывается, в заголовочном файле был массив констант, и мы получили тридцать копий этого массива в DLL. То есть иногда это все же имеет значение.

И да, я по-прежнему считаю, что #define — ужасный выбор в данном случае. Может быть, это еще не самое худшее решение, но мне оно совершенно не нравится. Однажды я столкнулся с ошибками компиляции, вызванными объявлением pi с помощью #define. Приятного мало, скажу я вам! Замусоривание пространства имен — вот главная причина, почему следует избегать #define, насколько это возможно.

Заключение

Не знаю точно, какой урок мы извлекли из всего этого. Суть проблемы, которая возникает, когда мы объявляем в заголовочных файлах константу типа float или double либо структуру или массив констант, ясна далеко не всем. В большинстве серьезных программ из-за этого возникают дубликаты статических констант, и иногда они неоправданно большого размера. Полагаю, constexpr может избавить нас от этой проблемы, но у меня нет достаточного опыта его использования, чтобы знать наверняка.

Я сталкивался с программами, которые были на сотни килобайт больше своего «реального» размера — и все из-за массива констант в заголовочном файле. Я также видел программу, в которой в конечном счете оказалось 50 копий объекта класса (плюс еще по 50 вызовов конструкторов и деструкторов), потому что этот объект класса был определен как тип const в заголовочном файле. Иначе говоря, тут есть над чем подумать.

Вы можете увидеть, как это происходит с GCC, загрузив тестовую программу отсюда. Соберите её с помощью команды make, а затем выполните команду objdump -d constfloat | grep flds, чтобы найти четыре инструкции чтения со смежных адресов в сегменте данных. Если вы хотите занять больше пространства, добавьте в header.h следующее:

const float sinTable[1024] = { 0.0, 0.1, };

В случае с GCC прирост составит 4 КБ на одну запись преобразования (исходный файл), то есть исполняемый файл вырастет на 20 КиБ, даже если к таблице ни разу никто не обращается.

Как обычно, операции над числами с плавающей точкой связаны со значительными трудностями, но в данном случае, как мне кажется, в этом виновата слишком медленная эволюция языка С++.

Что еще почитать по теме:

VC++: как избежать дублирования и как понять, что дублирования не избежать

У компилятора в VC++ 2013 Update 2 появился параметр /Gw, который помещает каждую глобальную переменную в отдельный контейнер COMDAT, позволяя компоновщику выявлять и избавляться от дубликатов. Иногда такой подход помогает избежать негативных последствий объявления констант и статических переменных в заголовочных файлах. В Chrome такие изменения помогли сэкономить около 600 КБ (подробности). Частично такой экономии удалось добиться (сюрприз!) путем удаления тысячи экземпляров twoPiDouble и piDouble (а также twoPiFloat и piFloat).

Однако в VC++ 2013 STL есть несколько объектов, объявленных как static или const в объявлении класса, которые /Gw не может удалить. Все эти объекты занимают по одному байту, но в итоге набегает свыше 45 килобайт. Я сообщил разработчикам об этой ошибке и получил ответ, что в VC++ 2015 она была исправлена.

По просьбе автора делимся ссылкой на оригинал здесь

Окружность круга, Информация, Уравнение, Формула, Расчет

Окружность круга, Информация, Уравнение, Формула, Расчет | Окружность круга

Окружность фигуры в математике относится к пределу или расстоянию, которое окружает фигуру. Периметры и длина окружности равны. Это длина окружности в целом. Круг существует столько же, сколько существует Земля. Мы можем видеть естественные круги, наблюдая за луной, солнцем и другими природными круглыми формами. Окружность состоит из нескольких точек, равноудаленных от одной центральной точки, называемой центром окружности. Линия, проходящая через центр окружности, разделенной на две равные части, называется диаметром. Диаметр представлен d. Радиус – это линия, проходящая через центр окружности и половину диаметра. Радиус обозначается буквой r.

Длина окружности — важное понятие в геометрии, которое мы можем изучить в этой статье. Когда мы видим круглые часы, окружность круглых часов — это внешняя граница часов, которая кажется нам видимой, и мы ее видим. Общая длина границы круглых часов называется окружностью круглых часов.

Какова длина окружности

Расстояние по периметру окружности известно как окружность круга. Длина ребра по окружности называется окружностью круга. Для дальнейшего понимания этого понятие, рассмотрим следующую схему. Рассмотрим на примере циркулярки. детская площадка на схеме ниже.

Маршрут пройден игроком, если он бежит из пункта А в точка B после полного круга игровой площадки. Расстояние, пройденное а. игрок называется окружностью игровой площадки. Окружность представлен буквой C в математике. Есть единицы измерения такие как сантиметры (см), миллиметры (мм) и дюймы (дюймы).

Длина окружности формула

Длина окружности – это ее периметр. Уравнение для определения длины окружности

Окружность круга = π×d

C = π×d

C = 2πr

Следующие уравнения связывают его с диаметром, радиус и пи. «С» обозначает длину окружности, «d» — длину окружности. диаметр окружности. «π» является постоянным и специальное число равно 3,14519…. или 22/7. Диаметр круга равен наибольшее расстояние по нему можно измерить из любой точки окружности, проходящей через ее центр, до точки соединения на противоположной конец. Радиус равен половине диаметра.

Какова формула длины окружности

радиус «r» круга и значение «пи» используются в формуле для расчет длины окружности. Длина окружности формула = 2r — это один из способов выразить это. Если мы не знаем значение радиуса, мы можем использовать диаметр, чтобы найти его, используя эту формулу окружности. Поскольку диаметр а круг равен двум радиусам, если известен диаметр, то его можно разделить на два, чтобы получить значение радиуса. Окружность = диаметр — еще одна формула для вычисление длины окружности. Когда длина окружности Учитывая, мы применяем формулу Радиус = Окружность/2 для определения радиуса или диаметр окружности.

Как найти длину окружности

Длина окружности равна длине ее граница, ее нельзя определить с помощью шкалы-линии. Это объясняется тем, что круг — фигура изогнутая. Поэтому мы вычислить длину окружности с помощью окружности формула.

Окружность круга=πдиаметр

C=π×d

Пример : Какова длина окружности, диаметр 13 единиц?

Решение : заданный диаметр = 13 единиц

Воспользуемся формулой для длины окружности и подставим значение диаметра в нем.

Формула длины окружности=π×d

C=π×d

C=3,14×13

C=40,82 единицы

Следовательно, длина окружности равна 40,82 единицы.

Проблема : Лорен планирует поездку в Лондон и хочет прокатитесь на Лондонском глазе, самом известном в мире колесе обозрения. Она обнаруживает радиус круга составляет около 78 метров при исследовании деталей об огромном колесе обозрения. Сколько стоит колесо обозрения длина окружности? В качестве грубой оценки числа пи используйте 3,14.

Решение :

Колесо обозрения имеет радиус = 78 м

Окружность колеса обозрения = ?

Используя формулу окружности

Окружность колесо парома = 2 π r

C =3,14

C= 489 м

Как вычислить длину окружности

Хотя длина окружности пропорциональна длине ее границы, это не может быть рассчитан с использованием линейки (шкалы), как другие полигоны. Это объясняется тем, что круг — фигура изогнутая. В результате мы используйте формулу, которая использует радиус или диаметр круга и значение Пи () для расчета длины окружности.

приведенное ниже уравнение объясняет взаимосвязь между окружностью и радиус окружности

c=2πr

Где является константой и имеет фиксированное значение, равное 3,14159265….. Точный цифру рассчитать невозможно. Обычно мы используем приближения вроде 3,14 или 22/7, потому что это иррациональное число.

Метод для вычисления длины окружности

Метод 1. Использование диаметр для расчета длины окружности:

Использование формула

C=π×d

Если мы знаем диаметр, мы можем определить окружность. В этом отношении «С» символизирует длину окружности, а «d» символизирует его диаметр. То есть мы можем найти длину окружности. круг, просто умножив число пи на диаметр. Подставив значение числовое значение 3,14 или 22/7. вставьте заданное значение диаметра в длину окружности формулу и решить. Для дальнейших практических примеров задачи ниже:

Пример : Круглое велосипедное колесо диаметром 10 футов. Вычислите длину окружности круглого велосипеда. рулевое колесо.

Кому рассчитать окружность круглого велосипедного колеса. Диаметр круглого велосипедное колесо 10 футов. Теперь подставим значения в формулу

C=πd

C=π×10

C=31,42 фута

Метод 2. Использование радиус для вычисления длины окружности:

Используйте формулу

C=2πr

Это отношение представляет собой радиус окружности.

А радиус — это длина отрезка от центра окружности до ее другой конец на границе круга.

Это формула аналогична C=π d. Это потому, что радиус составляет половину его диаметр, поэтому диаметр можно записать как d=2r.

Заменитель заданное значение радиуса в приведенное выше соотношение и решить его. Для дальнейшего практические примеры задач ниже:

Проблема: Вы вырезаете лента, чтобы обернуть вокруг края браслета. Радиус браслета 2 дюймы.

Решение: для вычисления длины окружности что вам нужно просто, подставив значения радиуса в данное уравнение

C=2πr

C=2π2

C=12,57 дюймов

Как получить длину окружности

Мы знать либо диаметр, либо радиус окружности, чтобы рассчитать ее длина окружности. Затем в этом уравнении мы используем правильное значение: C=2πr (из конечно, «r» означает радиус).

Как мы знаем, что формула нахождения длины окружности равна пи времени диаметр.

C=πd

Просто например, больше формул мы используем сокращения: C для окружности и d для диаметры. Это довольно простая формула. Он говорит нам, что если мы знаем диаметр круга, все, что нам нужно сделать, это умножить диаметр.

Проблема : Круглый ковер имеет диаметр 46 м. Какова окружность круглого ковра?

Решение :

Диаметр круглого коврика = 42 м

Окружность круглого ковер=?

По по формуле длины окружности

Длина окружности коврик = π

Окружность круга ковер = π

окружность круглый ковер = 132 м

Проблема: Йохан водил машину. Его автомобильное колесо имеет диаметр 4 м. Найдите пройденное расстояние когда он сделает 50 оборотов?

Решение:

Во-первых, чтобы найти путь, пройденный за 1 оборот, надо найти длину окружности колеса.

радиус колеса = диаметр колеса/2

=4/2=2 м

Расстояние

=50

=616 м

Как измерить длину окружности

Эратосфен был первым человеком, измерившим окружность Земли. Он был греком математик, в 240 г. до н.э. Он обнаружил, что объекты в городе на севере Тропики не отбрасывают тень в полдень летнего солнцестояния, но в более северное расположение. Зная это и расстояние между точками, он удалось измерить окружность Земли. Расстояние между двумя Города были измерены Эратосфеном в 800 километров. Он умножил 800 километров на 50, чтобы получить цифру 40 000 километров для Земли. диаметр.

Четный хотя окружность круга является его длиной, ее нельзя измерить используя масштаб, как и другие фигуры, такие как квадраты, треугольники и прямоугольники, можно Обоснованием этого является изогнутая форма круга.

стратегии ниже могут быть использованы для измерения длины окружности

Метод 1. Мы будет использовать эту нить, чтобы проследить ход круга и обозначить места на тренде можно использовать обычную линейку для проверки длины нити потом. Изучите возможность, когда нам дана круглая тарелка с окружность круга.

Шаг 1.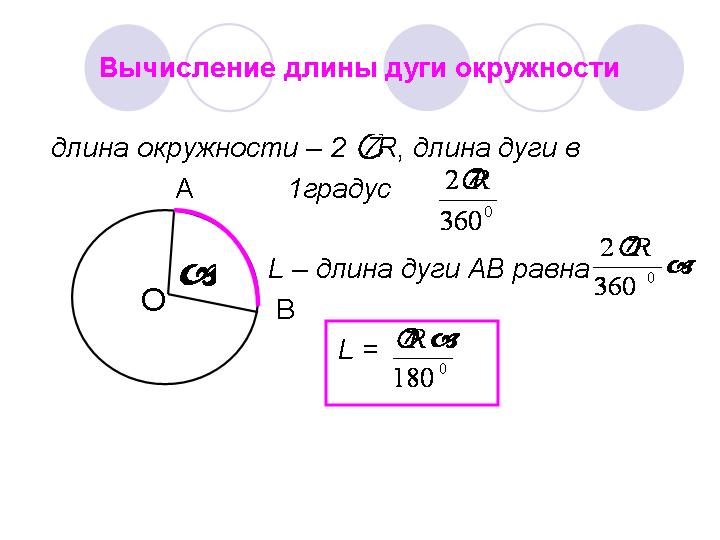 Используя метод, описанный выше, теперь мы можем взять нить и обернуть ее к круглой пластине.

Шаг 2. Далее на резьбе сделать стартовую и конечная точка.

Шаг 3. Наконец, используя измерение периметра, измерьте длину нити. от точки старта до финиша.

Метод 2. Измерение длины окружности – это точный способ ее вычисления в геометрия. В результате применяем формулу, в которой участвуют радиус, диаметр круг, и значение Pi(π) для определения длины окружности. К начало, если нам дан радиус и длину окружности надо вычислить, следующие шаги:

Если радиус любого случайного круга равен 7 см, мы может определить длину окружности, используя следующие шаги:

Шаг 1. Проверьте данные, которые были предоставленный нам; в этом случае радиус был предоставлен.

Шаг 2. Используйте следующую формулу:

C=2πr

Здесь C = длины окружностей, r = радиус и π = 22/7.

Шаг 3. Получаем желаемые результаты подстановкой значений в формулу

Шаг 4:

С=2π r=222/77=44см

Аналогично, если указан диаметр, мы можем следовать следующей процедуре:

Пример : Если диаметр круглого компакт-диска равен 14 см, а длина окружности Требуется следующее решение:

Шаг 1. Проверьте предоставленную информацию, в данном случае указан диаметр.

Шаг 2. Используйте следующую формулу

C=πd

(Здесь, C обозначает длину окружности, d обозначает диаметр, а π=22/7 или 3,14)

Шаг 3. Получаем требуемый результат подстановкой значений в формулу.

C=π=22/714=44см

Как найти длину окружности с диаметром

Окружность окружности — это расстояние вокруг окружности, а диаметр по окружности равен отрезок круга — это используемый отрезок линии, а точка лежит на круг и которые проходят через центр круга, поэтому желтые линии в диаграмме будет диаметр круга, потому что дает и точки лежат на и он проходит через центр круга, поэтому отрезок, подобный этому, называется диаметром окружности.

Окружность диаметру:

отношение окружности к диаметру получено из общепринятого определения числа Пи (π).

C=π d

Исключить d с обеих сторон

C/ d=π

Мы можем получить значение, приблизительно равное сравнимо с обеими частями уравнения

(C=π г) по диаметру d. C представляет окружность, а d представляет диаметр.

Это указывает, что

d=C/π

Мы можем использовать его, чтобы найти диаметр если мы знаем окружность, так как окружность и диаметр связаны числом Пи (π). Чтобы выделить диаметр d в одной части уравнения, проведем некоторые математические вычисления:

C=π d

C/π = d

Затем определяется диаметр путем деления длины окружности на число Пи (π).

мы понимаем это понятие как пример:

Пример: Купол здание окружено кругом окружностью 63 фута. Купол здание имеет диаметр чего?

Решение

Окружность купола = 63 фута

Диаметр купола =?

Используя формулу окружности

C=π d

d=C/π

d= 20,06 футов

Круг насыпи питчера имеет диаметр 20,06 футов.

Если мы знаем диаметр, мы можем использовать вышеуказанное отношение, чтобы получить окружность.

Понять эта концепция с некоторыми проблемами:

Проблема: расстояние вокруг экватора Урана составляет около 160,535 км.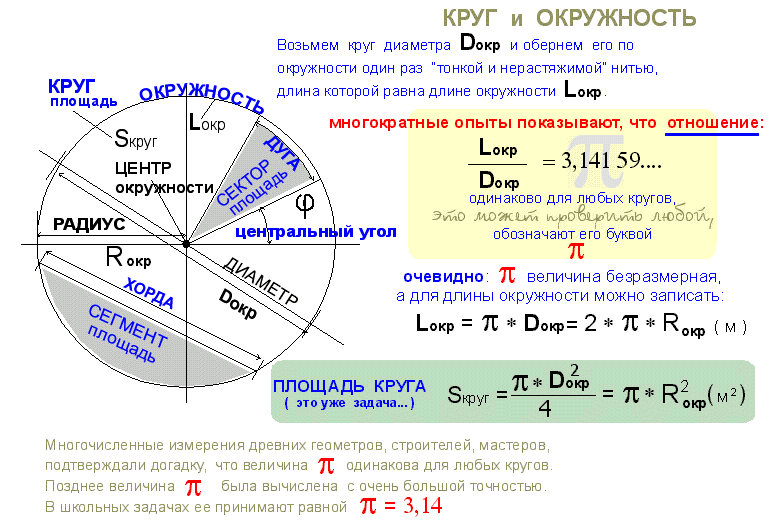 Что это экваториальный диаметр Урана?

Решение:

Шаг 1. Согласно приведенным данным,

окружности Урана=160,535км

Экваториальный диаметр Урана =?

Шаг 2: Формула, используемая в этой задаче:

d=C/π

Шаг 3: Подстановка значений в формулу

d=160,535/π=51100 км

Шаг 4: в результате экваториальный диаметр Урана составляет 51100 км.

Проблема: А Круглый бассейн имеет диаметр 7 ярдов. Выработайте окружность круглый бассейн?

Решение:

Шаг 1: Запишите данные

Циркуляр диаметр бассейна =7 ярдов

Окружность круглого бассейна =?

Шаг 2: Формула, используемая в этой задаче:

C = π d

Шаг 3:Подстановка значений в формулу

C=22/7

C=22 ярда

Шаг 4:

Следовательно, окружность круглого бассейна составляет 22 ярда при диаметре 7 ярдов.

Окружность окружности диаметром

Мы можем найти радиус окружности, измерив расстояние от его центра до внешнего края. Рассмотрим часы: если один из стрелки были достаточно длинными, чтобы достать до края циферблата, эту стрелку можно было учитывал радиус часов – независимо от времени!

Диаметр круга измеряется от края до края и проходит через центр, тогда как радиус измеряется от центра к край. Диаметр круга делит фигуру пополам. Радиус круг равен половине длины его диаметра (или диаметр круга в два раза меньше его диаметра). радиус).

Радиус окружности определяется как длина от центр окружности в любую точку на линии границы окружности.

Поскольку мы знаем, что диаметр в два раза больше длины радиус. Математически это записывается как

Диаметр=2×радиус

D=2r

Длина окружности также записывается как

Длина окружности=πd

Путем подстановки

C=9πr

3 Пример: это длина окружности, имеющая радиус 10 юнитов?

Решение: Дан радиус=10 единиц

Используя формулу

Длина окружности формула=2πr

C=2πr

C=23,1410

C=62,8 единиц

Следовательно, длина окружности равна 62,8 единиц.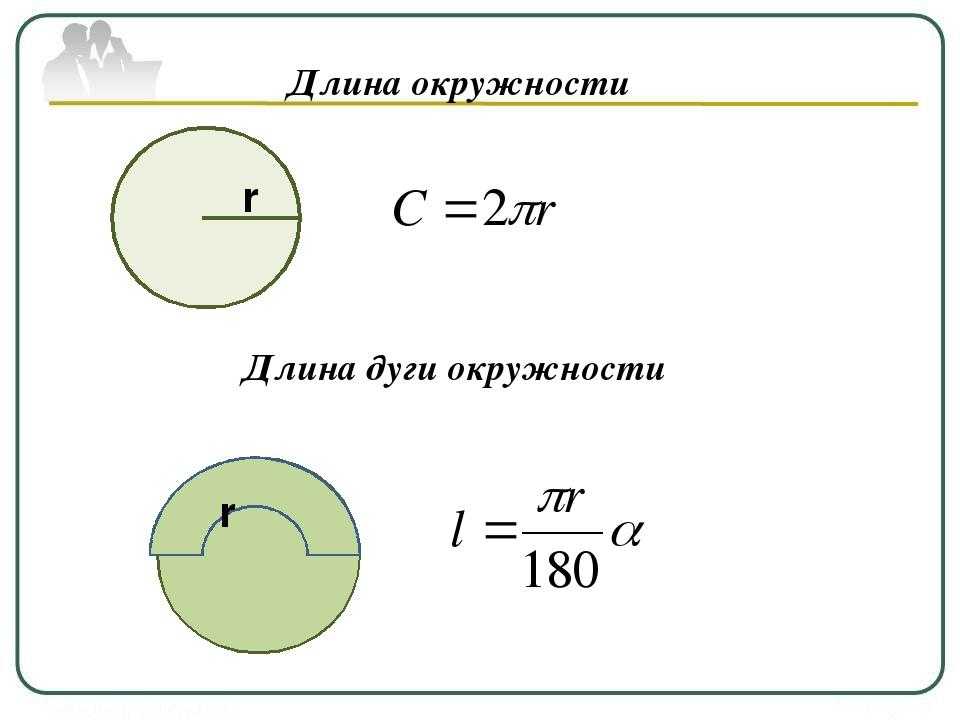

Радиус окружности от окружности

Другой важное соотношение радиуса к диаметру также можно использовать для расчета длина окружности. Половину диаметра окружности называют радиусом. Как В результате мы можем использовать заменяющий атрибут равенства, чтобы заменить радиус, r, в наших формулах. Мы можем заменить диаметр на 2r, если два радиуса эквивалентны на один диаметр.

Переместительное свойство умножение также позволяет нам передавать значения. Следующие четыре уравнения взаимозаменяемы:

C= π d

C = π (2r)

C = 2 πr

потренироваться на примере.

Пример: национальная команда ударный круг поля представляет собой четверть круга с радиусом 32 ярда, за которым следует четыре ярда по прямой и еще четверть круга. Два из этих привлекательных круги можно найти на поле. У вас осталось только достаточно мела, чтобы сформировать 222-ярдовая линия после отметки всех прямых линий мелом.

Решение:

Добавьте прямую в два, четыре ярда отрезков к окружности круга, чтобы получить общую длину.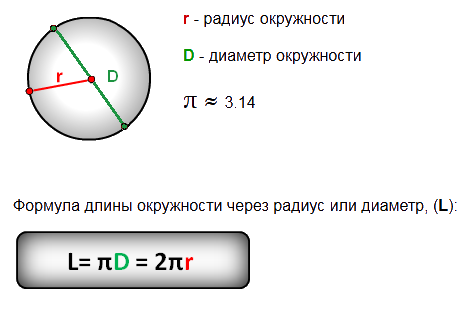

Рассмотрите свои варианты перед взглянув!

Четыре четверти окружности равны единице Круг радиусом 32 ярда. Затем для двух прямых участков прибавьте шестнадцать ярдов.

C=πd

C=2πr

C=2 x 3,14159 x 32 ярда

C = 2 x 3,14159 x 32 ярда

C = 200,96 ярда

Объедините два следующих: 200,96 ярда+ 16 ярдов=216,96 ярда

Как найти площадь и длину окружности

фиксированное расстояние от фиксированной точки, называемой центром, и разделены фиксированное расстояние, называемое радиусом. Периметр круга или расстояние вокруг него, это его окружность (С). Площадь круга (А) – это пространство, которое он занимает или площадь, которую он охватывает.

Рассчитайте площадь круга по формуле:

Шаг 1. Площадь круга можно определить с помощью двух различных формул, основанных на диаметре или радиус:

A =π или A = π, где – математическое постоянная около 3,14». r — это радиус, а «d» — диаметр.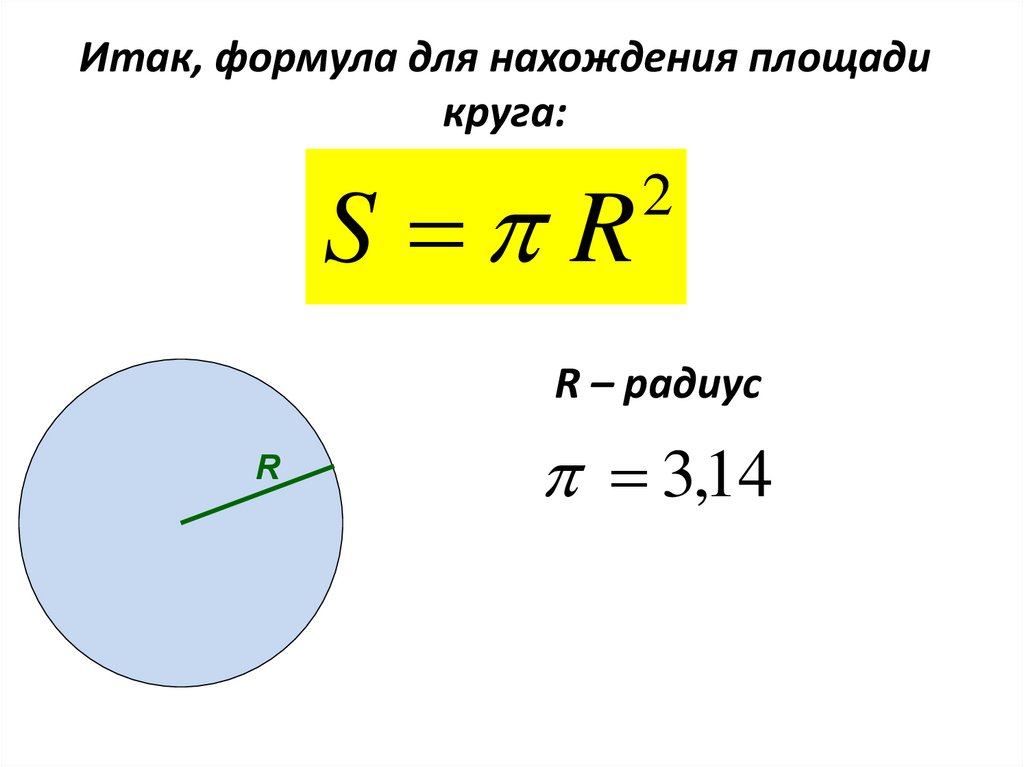

Эти уравнения по существу одинаковы, потому что радиус окружности равен половине своего диаметра. Площадь может быть измерена в квадратных футах (), квадратных метрах (), квадратных сантиметрах () и других единицах измерения. длина в квадрате.

Шаг 2. Распознавать различные компоненты формула. Радиус, диаметр и длина окружности – это три компоненты, необходимые для вычисления его окружности. Радиус и диаметр равны пропорциональна: радиус равен половине диаметра, а диаметр в два раза больше радиус.

Круг радиус (r) — это расстояние между одной точкой окружности и ее центром.

Круг диаметр (d) — это расстояние между одной точкой окружности и другой точно напротив него, измеренного через центр.

число 3,14159265…, иррациональное число, не имеющее ни последней цифры, ни распознанный образец повторяющихся цифр, показывает отношение длины окружности к по диаметру.

Шаг 3. Рассчитайте радиус окружности или диаметр. Поместите один конец линейки на одну сторону круга, а другой конец на другой стороне круга, проходящей через центральную точку. Радиус — это расстояние от центра круга, а диаметр — это расстояние от одного конца к другому.

указывается радиус или диаметр радиус=4м диаметр=6м

Шаг 4. Решите проблему, вставив переменные. Вы можете ввести радиус и/или диаметр окружности в соответствующее уравнение после того, как мы определили радиус и/или диаметр.

Используйте A =π , если известен радиус, и A = π , если известен диаметр.

Пример: Что площадь круга радиусом 4 метра?

По ввод значений:

А =π – это формула, описывающая отношение между двумя переменными.

Переменные к плагину: A=π

Радиус в квадрате: значение равно шестнадцати.

Умножение на пи (π), если мы хотим получить более сложный ответ

A=π 16 =

Пример:

площадь круга диаметром 8 м?

По ввод значений

A =π – это формула, описывающая отношение между двумя переменными.

Переменные к плагину: A=π

умножив диаметр на два, можно получить следующий результат: 2=8

= 64 — это квадрат результат.

Умножение на число пи (π), если мы хотим получить более сложный ответ круга с переменными:

Шаг 1. Рассчитайте радиус круга или диаметр. Некоторые выпуски предложат вам переменный радиус или диаметр, например г = (у + 2) или d = (у + 4). Вы все еще можете найти площадь или окружность в этот сценарий, но ваше окончательное решение будет включать эту переменную. Как указано в задаче запишите радиус или диаметр.

Например: Определите окружность круга с (y = 2) радиусом.

Шаг 2. С информацией при условии, напишите формулу.

Независимо от того, решаете ли вы для площади или окружности основные шаги заполнения того, что вы знаете, оставаться прежним. Запишите формулу площади или окружности, а затем поставьте в переменных.

В качестве иллюстрации: вычисление длины окружности. с радиусом (y +2) и диаметр (у + 4).

Напишите формулу: C =2πr

Заполните данные предоставленными данными: C=2π(y+2)

Шаг 4. Решите задачу, как если бы переменная была числом.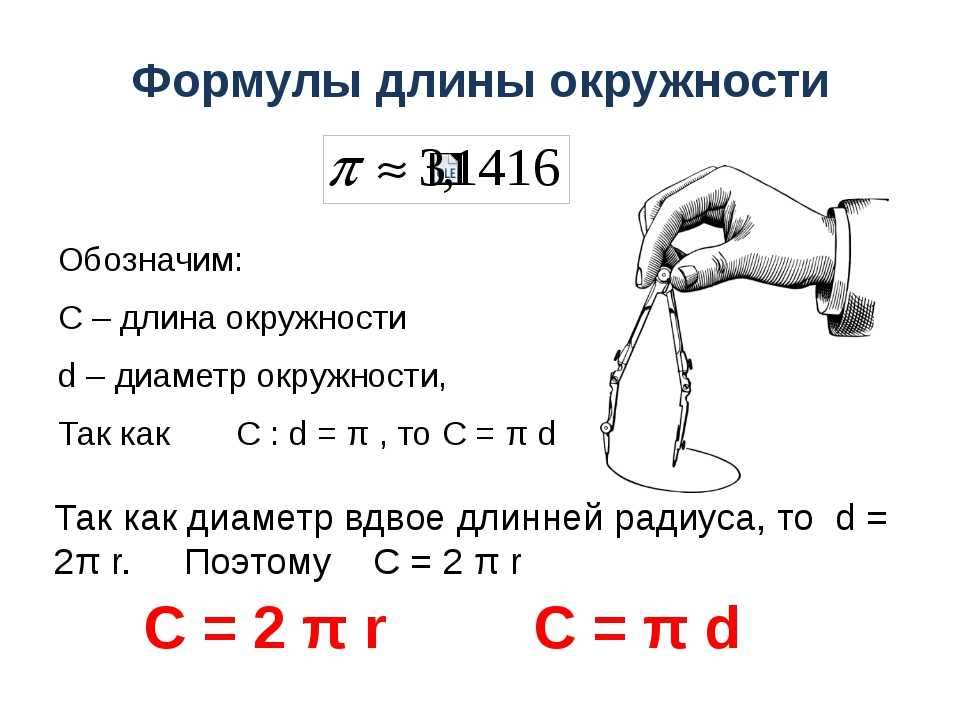 Теперь вы можете ответить на задачу как обычно, используя переменная, как если бы это было число. Чтобы упростить окончательный ответ, вам может понадобиться применять распределительное свойство.

В качестве иллюстрации: Расчет длины окружности. с радиусом y=1

C = 2πr=2π(y +2) = 2πy +2π(2) = 6,28y + 12,56

Вы можете вставить значение «y» в вышеуказанное уравнение для получения целочисленного решения.

C = 6,28 (1) + 12,56 = 18,84 ед. покрытая кругом, называется площадью круга. Площадь круга на двумерная поверхность — это площадь, занимаемая кругом. Площадь круг можно рассчитать по следующей формуле:

A=π

Эта формула применима ко всем кругам различного радиуса, где r — радиус окружности. Квадратная единица, такая как и т. д., является единицей площади.

Формулу площади круга можно использовать для вычисления сколько места обычно занимает круглое поле или участок. Если у вас есть сюжет и хотите огородить его, формула площади может помочь вам вычислить, сколько ограждения вы понадобится.

Если мы знаем радиус круга, найти его площадь простое вычисление. Если мы не знаем радиуса, мы все равно можем определить площадь, если мы знаем длину окружности или периметра круга. Мы можно сначала найти радиус, а затем длину окружности по формуле

Окружность = 2πr

Затем площадь можно рассчитать по формуле

Площадь круга = π

Мы также можем использовать формулу его площадь, а затем извлечение положительного квадратного корня, как показано в формуле

A = π

A/π =

= r

Не зная длины радиуса, это выражение выражает длину окружности как функцию ее площади.

Понять, что площадь это количество пространства, покрываемого двумерной фигурой, и выражается в единицах в квадрате. Площадь большинства форм, включая круги, должна быть рассчитана с использованием формула. Используйте следующую формулу, чтобы найти площадь круга:

A = π

Радиус круга показан на зеленым, а диаметр круга показан красным.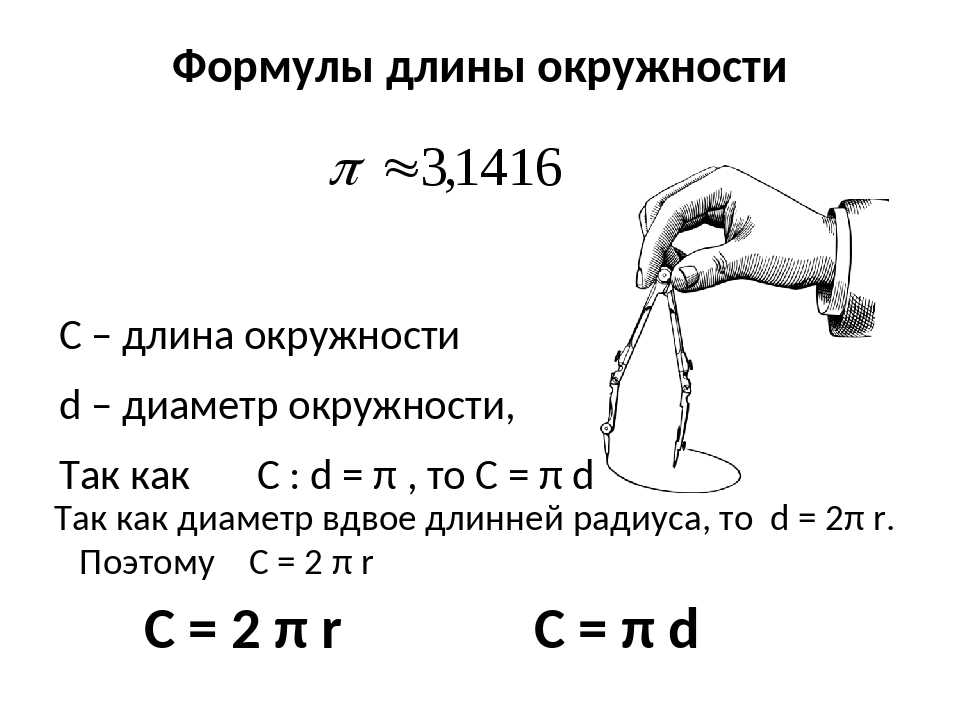 Они необходимы для вычисление площади круга.

Диаметр и радиус окружности используются для вычисления его площади.

Радиус или сегмент от центра круга к точке на краю круга, обозначается буквой r в этой формуле. Он вдвое меньше диаметра, и каждый радиус внутри круг одинакового размера. Давайте узнаем, как найти площадь круга в более деталь.

Определение площади круга Задача:

Рассмотрим теперь круг М:

Радиус М равен половине его длина окружности. Площадь М рассчитывается с использованием его диаметра и радиуса.

Диаметр 24 дюйма, как можно увидеть выше. Чтобы найти радиус и вычислить площадь круга M, мы должен разделить диаметр пополам. Мы видим, что радиус составляет 12 дюймов в длину. когда мы делим 24 на два.

Радиус=диаметр/2

r=d/2

r=24/2

r=12 дюймов = 12 к уравнению сейчас:

А=π

А = π144 = 452,16

— это формула, которую можно использовать для расчета нескольких вещи.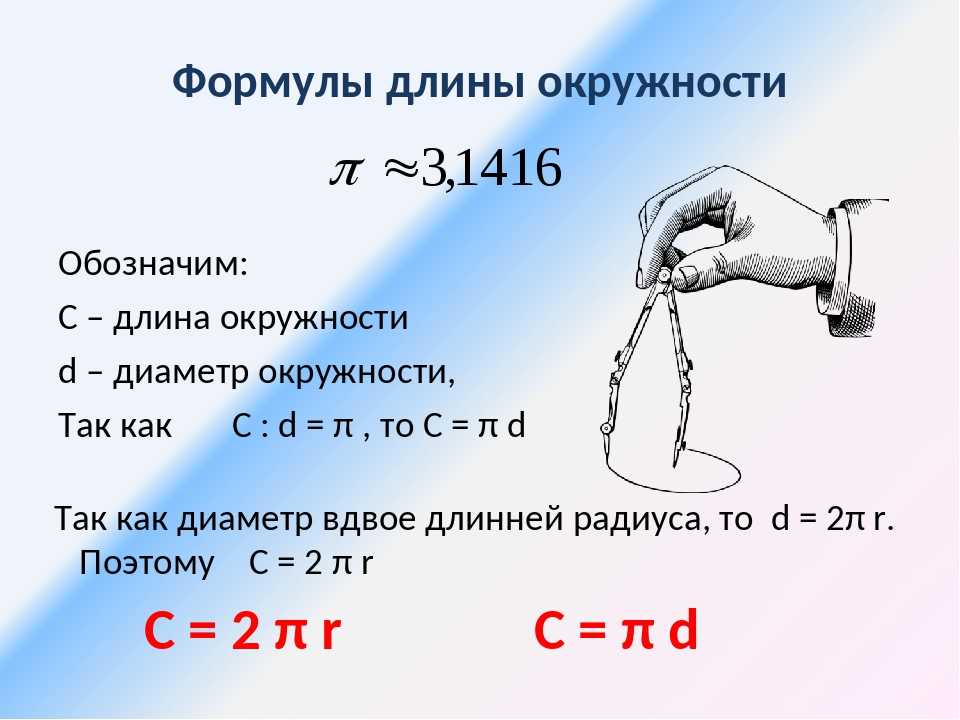

Рассмотрим пример из настоящая жизнь.

Площадь этого обеденного стола может быть определяется с помощью красной линии, проходящей через центр.

Используется диаметр обеденного стола чтобы вычислить площадь круга, который он символизирует.

Джон покупает материалы, которые он нужно создать свой первый обеденный стол. Сколько дерева ему нужно будет приобрести, если он хочет, чтобы диаметр стола был 28 футов в длину?

Решение:

Чтобы определить радиус, мы еще раз уменьшить диаметр вдвое.

Радиус= диаметр/2

r=d/2

r=28/2

r=14 футов

Радиус стола будет 14 футов когда вы закончите. После этого подставляем этот радиус в уравнение:

A=π

A=π =196 π

A=616

Общая площадь обеденного стола равно 196π, или 616 футов в квадрате, как только мы завершим наши вычисления, используя порядок операций.

Изучение взаимосвязи между площадь и окружность:

Начните с окружности радиусом r.

Формула для определения Длина окружности и площадь круга радиусом r хорошо известны.

C = 2πr в окружности

Площадь

A = π

1-й шаг:

Для r решить уравнение C = 2πr

Обе стороны разделить на 2π

C/2 /2π =r — математическое выражение которая выражает связь между двумя переменными

2-й шаг:

В формуле площади круга замените r = C/2π

A = π

В скобках возведите в квадрат условия.

A = π

Упрощение

A =

A = это формула для расчета площади круг.

3-й шаг:

Для, решить заданное уравнение.

Добавьте 4π к обеим сторонам уравнение.

4πA = 4π

4πA =

Упростить

= 4πA

В результате радиус окружности квадрат равен четырехкратной площади.

Соблюдать

Применима ли эта формула к окружность радиусом 14 дюймов? Выставьте свою работу на обозрение.

Мы можем применить формулу = 3,14 потому что радиус 14 дюймов – это кратно 7.

Сначала мы должны выполнить следующие шаги.

Вычислите площадь поверхности круга.

есть формула, описывающая связь между двумя переменными.

Положим r = 14

A = π

π заменить на

A= 196

A = 616

2-й шаг:

Измерьте длину окружности.

C = 2π r

Положим r = 14

C = 2 π 14

C = 2

C=88 дюймов

Шаг 3:

Сделайте длину окружности площадь.

= =7744 ————— (1)

Умножая площадь на 4π, вы можно получить более точную оценку размера региона.

A = 616

4π A = 4π

4π A = 4

4π A = 7744 ——————— (2)

Из (1) и (2) можно сделать вывод =

2
В результате площадь в четыре раза длина окружности в квадрате.
Примеры длины окружности
Пример: Прямоугольный провод имеет длину 132 метра. периметр. Круг образуется путем скручивания той же проволоки. Окружность формулу можно использовать для вычисления радиуса окружности.
Решение:
Периметр прямоугольника равна общей длине используемой проволоки, которая равна окружности круг получился.
В результате образовавшийся круг имеет Окружность 132 метра.
Формула расчета длина окружности = 2 πr
132 — длина окружности.
Чтобы найти радиус, мы можем заменить известные значения.
132 = 2r
132 = 2 (22/7) r
132 = 44/7 r
= r
r = 21 метр
Таким образом, радиус окружности равен 21 метров.
Чтобы понять эту концепцию, используйте пример:
Пример: Умар проехал четыре круга круговая дорожка. Каковы диаметр и радиус поля, если он пробежал всего расстояние 500 м?
Решение:
Умар прошел один круг по кругу поле = 500 / 4 = 125
Окружность круга поле 125 метров.
Диаметр круглого поля = длина окружности / π
Диаметр круглого поля = 125/3,14= 39,81 метра
Радиус кругового поля = окружность / 2π
Радиус круглого поля = = = 19,905 метра
Пример : Круглые парки имеют 70-метровую диаметр. По 2 доллара США за метр посчитайте стоимость его ограждения.
Решение:
Диаметр парка 70 метров.
Радиус круга равен
r= 70/2 = 35 метров
Метр ограждения стоит 2 доллара.
Окружность круглая парк — это длина, покрытая ограждением.
Окружность парка
= 2 π r
= 2 (22/7) x 35 = 220 метров
Стоимость ограждения = 220 2 = 440 долларов
Пример: На стене одной из его новых квартир , Жасмин рисует большой круг. Круг будет 49футов в диаметре самая широкая точка. Какова примерная площадь, которую будет занимать круг на стена?
Решение:
Мы находим область, если вы попросили подсчитать количество квадратных футов, покрытых чем-либо. Вычислять площадь круга Жасмин, мы должны сначала определить, является ли радиус или указан диаметр. Диаметр окружности определяется как наибольшая расстояние через него, следовательно, диаметр равен 49стопы в этом случае. Радиус 7 стопы в этом случае. Следовательно:
A= π = 154
В результате круг Жасмин будет окружить около 154 квадратных футов его собственности.
Пример: В круговой салон. Диаметр круглого зала составляет 14 ярдов. Что это площадь круглого салона?
Решение:
Диаметр круглого зала = 14 ярдов
Мы хотим найти площадь круговая гостиная
Сначала найдем радиус круговой зал от диаметра, как мы знаем
Радиус = диаметр/2
r = 14/2 = 7 ярдов
Применяя площадь круга формула
= 154 ярда
В результате площадь круговая гостиная составляет 154 ярда.
Вычисление с числом Пи ｜ Хацуди
В начальной школе учащимся предлагается решить задачи, связанные с кругами. Круг – это фигура круглой формы. В форме круга вас просят найти длину окружности и площадь круга. Чтобы выполнить эти вычисления, нам нужно использовать число Пи. Изучая круги, важно понимать, что такое число пи.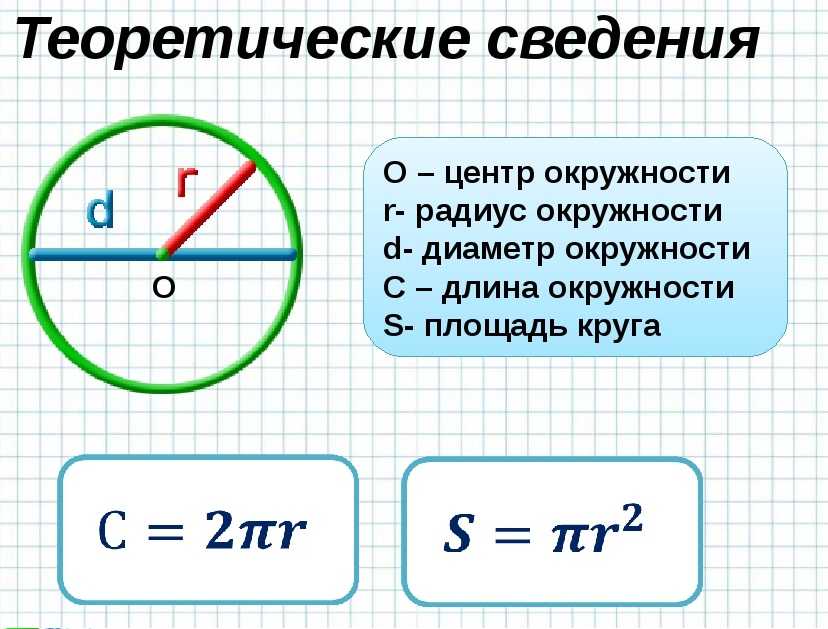
Круги бывают разной длины, и одним из них является радиус. Зная радиус, можно вычислить длину окружности и площадь круга.
При расчете длины окружности или площади круга необходимо использовать формулу. Другими словами, если вы не помните формулу, вы не сможете решить задачу.
Поэтому мы объясним, как думать и вычислять длину окружности и площадь круга, и что такое число пи.
Соглашение о таблице
1 Понимание важных терминов в кругах
1.1 Что такое PI: число 3.14
2 Использование диаметра и PI для расчета окружности
2.1 Расчет диаметра
9549950
950
9509509509509950
9509950
509509950
2.1. 3 Использование радиуса и числа Пи для вычисления площади круга
3.1 Вычисление радиуса круга из его площади
3.2 Почему мы можем вычислить площадь круга с помощью радиуса и числа Пи?
4 Вычисление длины окружности и площади круга
Понимание важных терминов в кругах
Существует несколько типов круглых фигур. Все нижеперечисленные имеют круглую форму.
Круглая форма, которую мы изучаем в начальной школе по математике, — это круг. Из фигур, показанных на рисунке выше, фигура слева называется кругом. Также при решении задач с кругами постарайтесь запомнить следующие важные термины.
Окружность: по кругу.
Центр: Точка в середине круга.
Радиус: линия, проведенная от центра к окружности.
Диаметр: Линия, проведенная от окружности к окружности через центр
Эти термины часто используются. Радиус и диаметр также являются терминами, которые часто используются в нашей повседневной жизни. Итак, постарайтесь вспомнить, что они означают.
Что такое Пи: число 3.14
В дополнение к предыдущим терминам нам нужно узнать число пи при решении задач с кругами. Что такое пи? Пи – это значение, полученное путем деления длины окружности на ее диаметр.
Древнеегипетские математики уже знали, что существует зависимость между длиной окружности и диаметром круга. Они измерили длину окружности следующим образом.
На этот раз мы использовали мягкую розовую нить для измерения длины окружности. Далее мы рассмотрим диаметр круга. Изучите длину линии, проходящей через центр круга, как показано ниже.
Затем разделите длину окружности на диаметр окружности.
Длина окружности ÷ диаметр
Полученное таким образом значение равно пи. Значение числа Пи одинаково для всех кругов. Значение числа пи следующее.
Пи = 3,14159…
Пи — это число, которое продолжается вечно. Итак, в геометрии начальной школы мы думаем и вычисляем «Пи = 3,14».
Когда мы делим длину окружности на диаметр окружности, получается число пи. Кроме того, как упоминалось выше, все круги имеют одинаковое значение числа пи. Пи — свойство круга.
Использование диаметра и числа «пи» для вычисления окружности
Как только вы поймете число «пи», вы сможете вычислить длину окружности, используя диаметр.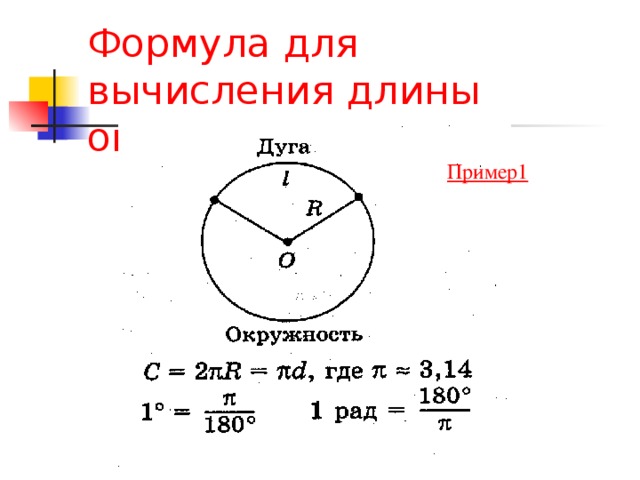 Мы объяснили, что, используя длину окружности и диаметр окружности, мы можем вычислить число Пи. Это означает, что мы можем вычислить длину окружности, используя диаметр и число Пи.
При расчете длины окружности мы используем следующую формулу.
Окружность = Диаметр × 3,14 (Пи)
Таким образом, умножая диаметр на число пи, мы можем найти длину окружности.
Обратите внимание: если вы удвоите радиус, вы получите диаметр. Следовательно, зная радиус, можно вычислить длину окружности. После удвоения радиуса умножьте его на 3,14 (пи), чтобы получить длину окружности.
Окружность = Радиус × 2 × 3,14 (Пи)
В любом случае помните, что если вы знаете диаметр или радиус, вы можете рассчитать длину окружности.
Вычисление диаметра по окружности
Тот факт, что мы можем вычислить длину окружности, используя диаметр и число пи, также означает, что мы можем использовать длину окружности для вычисления диаметра.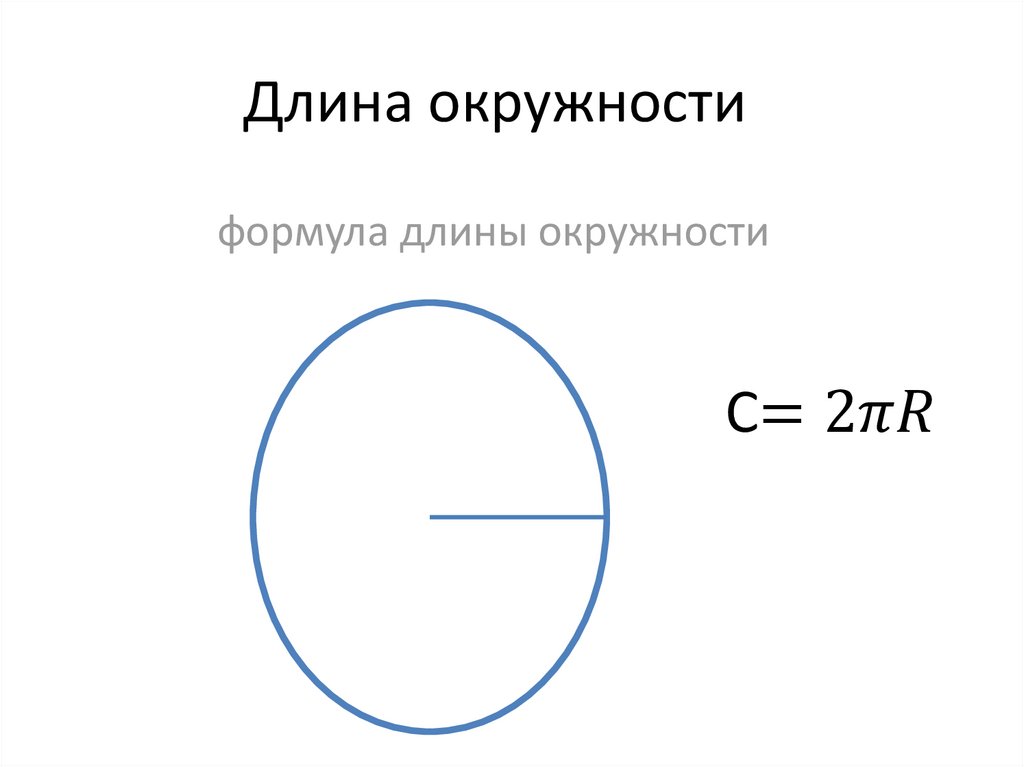 Умножение имеет тот же смысл, что и деление. Например, $□×2=6$ можно изменить следующим образом.
$□=6÷2$.
Таким же образом изменим формулу вычисления длины окружности. Если диаметр равен $□$, формула выглядит следующим образом.
Окружность = $□$ × 3,14 (Пи)
Если мы изменим эту формулу, мы получим следующее.
$□$ = Окружность ÷ 3,14 (Пи)
Другими словами, если вы помните формулу для нахождения длины окружности, вы можете вычислить диаметр по окружности. Кроме того, если вы разделите диаметр пополам, вы получите радиус, так что вы также можете вычислить радиус из длины окружности.
Формула со знаком равенства обладает тем свойством, что обе части можно умножать или делить, используя одно и то же число. Итак, для формулы длины окружности разделим обе стороны на 3,14. Таким образом, мы можем заменить формулу длины окружности на формулу диаметра.
Использование радиуса и числа Пи для вычисления площади круга
Существует еще одна важная формула, в которой используется число Пи. Это формула нахождения площади круга. Используя число пи, мы можем вычислить площадь круга.
Формула для вычисления площади круга выглядит следующим образом.
Площадь круга = Радиус × Радиус × 3,14 (Пи)
Используя радиус и число Пи, мы можем вычислить площадь круга. Обязательно запомните формулу вычисления площади круга.
Вычисление радиуса круга из его площади
Тот факт, что мы можем вычислить площадь круга, используя его радиус, означает, что мы можем вычислить радиус, используя его площадь. Если радиус равен $□$, площадь круга можно рассчитать по следующей формуле.
Площадь круга = $□$ × $□$ × 3,14
Затем изменим эту формулу следующим образом.
$□$ × $□$ = площадь круга ÷ 3,14
Например, если площадь круга равна 50,24 см ² , какой радиус? 50,24$÷3,14=16$. Кроме того, при умножении двух равных чисел найдите значение, которое дает 16. Тогда мы знаем, что ответом является 4. Итак, если площадь круга 50,24 см ² , радиус равен 4 см.
Почему мы можем вычислить площадь круга, используя радиус и число Пи?
Почему можно вычислить площадь круга, используя радиус и число пи? Чтобы понять причину, давайте разделим круг на более мелкие части следующим образом.
После этого расположим части круга следующим образом.
В результате мы можем построить параллелограмм, как показано ниже.
Строго говоря, это не параллелограмм, потому что он неровный. Однако, если разделить круг на очень маленькие части, неровности почти исчезают и становятся незначительными, что позволяет создать параллелограмм. Кроме того, если вы используете интегралы, которые вы изучаете в средней школе по математике, вы можете использовать это понятие, чтобы найти площадь круга.
Итак, длина параллелограмма по вертикали — это радиус. С другой стороны, длина стороны равна «радиус х 3,14». Сверяясь с рисунком, окружность оранжевого круга (полукруга) выглядит следующим образом.
Длина окружности полукруга = диаметр × 3,14 ÷ 2
Умножьте радиус на 2, чтобы получить диаметр. Следовательно, длина окружности полукруга равна «радиус × 3,14».
Длина окружности полукруга = Радиус × 2 × 3,14 ÷ 2 = Радиус × 3,14
Также, если вы посмотрите на предыдущий рисунок, вы увидите, что длина окружности оранжевого круга (полукруга) — это длина стороны параллелограмма. Итак, умножая вертикаль (радиус) на горизонталь (радиус × 3,14) параллелограмма, мы можем получить площадь. Результат аналогичен формуле нахождения площади круга.
Таким образом, мы можем получить формулу для нахождения площади круга. Если вы хотите разобраться в причине более подробно, давайте попробуем доказать это, выучив интеграл.
Вычисление длины окружности и площади круга
Геометрические задачи, связанные с кругами, являются общими. Используя отношение пи, мы можем вычислить длину окружности и площадь круга.
Для того, чтобы вычислить длину окружности, нужно знать формулу вычисления длины окружности. И если вы понимаете формулу, вы можете использовать длину окружности для расчета диаметра и радиуса.
Кроме того, вам нужно выучить формулу для вычисления площади круга. Используя радиус и число Пи, вы можете вычислить площадь круга. Кроме того, узнайте, почему верна формула вычисления площади круга.
Часто используются формулы для длины окружности и площади круга. Кроме того, есть много проблем с вычислениями, связанными с кругами. Итак, давайте выучим две формулы и сможем их использовать.
Калькулятор окружности эллипса
Преобразователь Кайла >
Калькуляторы >
Геометрия >
org/ListItem»> Окружность эллипса
Расчет окружности эллипса:
Пожалуйста, поделитесь, если вы нашли этот инструмент полезным:
Формула окружности эллипса
Эллипс – это окружность, вытянутая вдоль одной оси; эта длинная ось называется большой осью, а кратчайшее расстояние поперек эллипса называется малой осью. Чтобы вычислить длину окружности эллипса, мы можем использовать радиус вдоль каждой оси. Этот конкретный метод не является точным расчетом, но обеспечивает хорошую оценку, если большая ось не намного длиннее малой оси.
C = 2π * √((r ₁ ² + r ₂ ² ) / 2)
Формула окружности эллипса
Переменные окружности эллипса
Радиус по большой оси и радиус по малой оси — это две переменные, которые можно использовать для вычисления длины окружности эллипса.
Радиус 1 (r ₁ )
Максимальный радиус эллипса вдоль большой оси.
Радиус 2 (r ₂ )
Кратчайший радиус эллипса вдоль малой оси.
Окружность (c)
Расстояние полностью по периметру эллипса.
Решение для определения окружности эллипса
Как найти длину окружности эллипса с радиусом 7 по большой оси и радиусом 5 по малой оси.
C = 2π * √((r ₁ ² + r ₂ ² ) / 2)
Формула для нахождения длины окружности эллипса
C = 2π * √((7 ² + 5 ² ) / 2)
Подставить в значения радиусов
org/HowToStep»>
C = 2π * √((49 + 25) / 2)
Возведение значений радиусов в квадрат
C = 2π * √(74 / 2)
Дополнение в скобках
C = 2π * √37
Деление внутри скобок
C = 2π * 6,083
Квадратный корень, округленный до трех знаков после запятой
No related posts.