Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
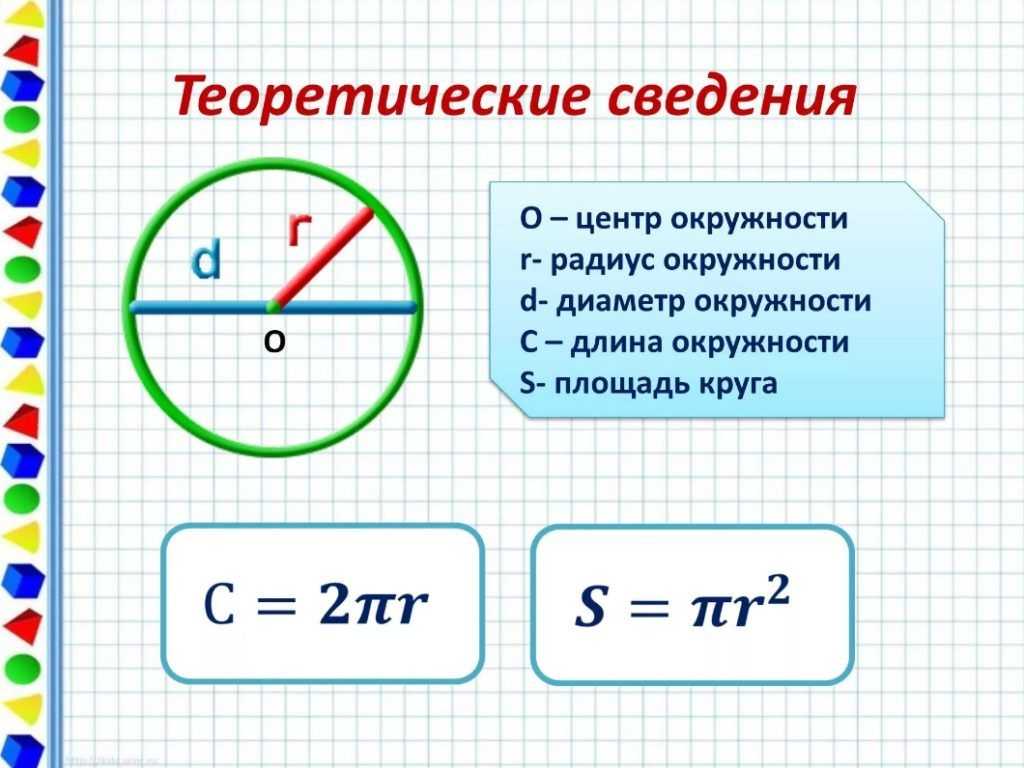
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926.
Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.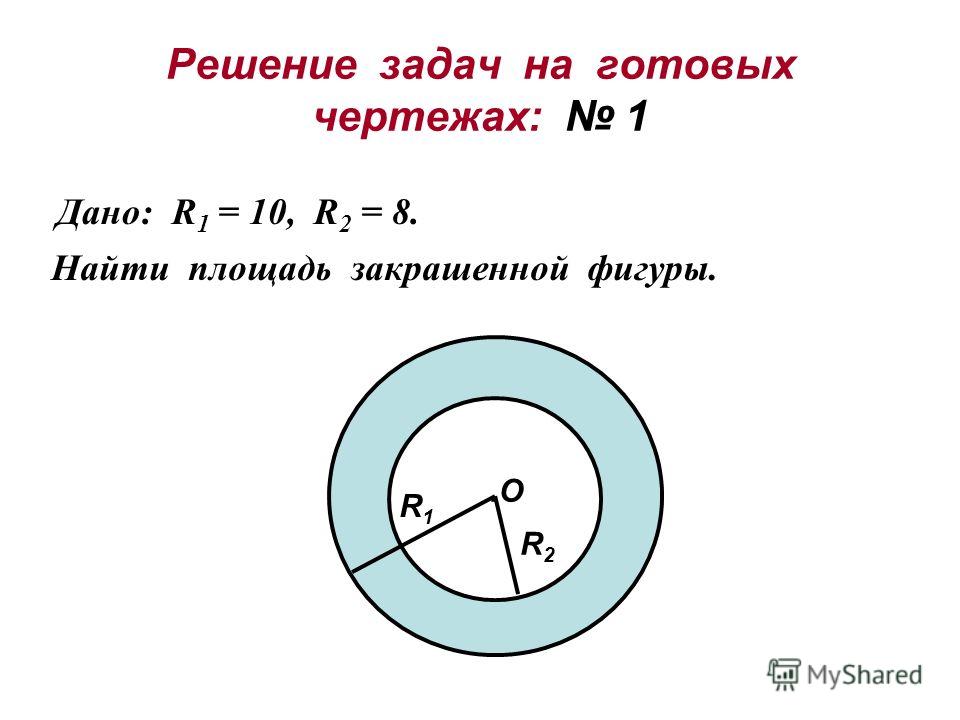
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение.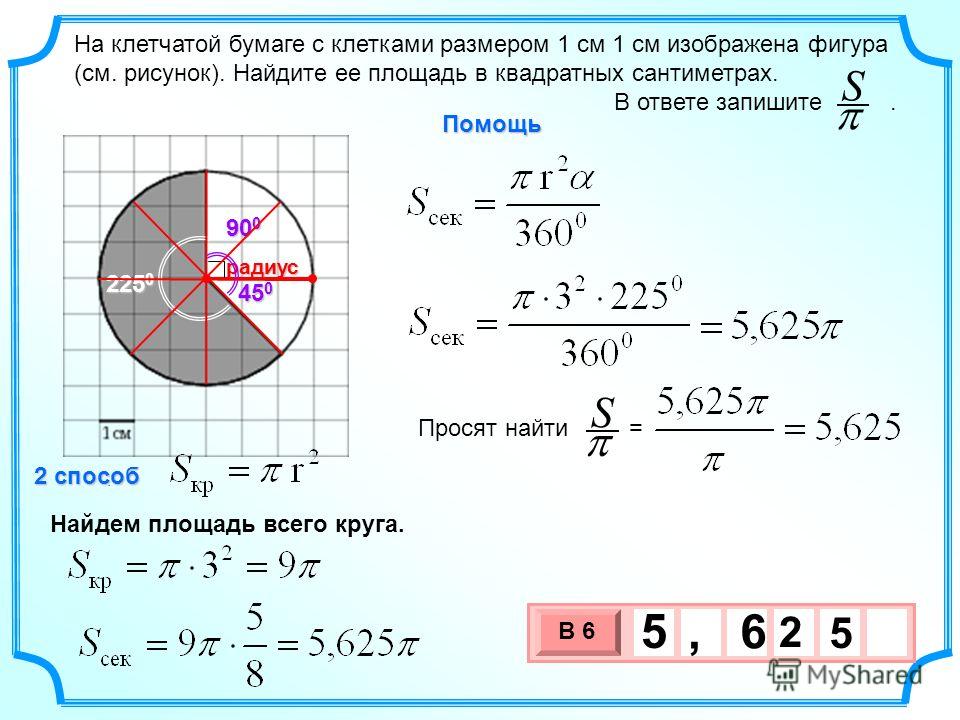 Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
| Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур). | |||
| Площади фигур | |||
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула | |
| 1 | радиус | ||
| 2 | диаметр | ||
| 3 | длина окружности | ||
| 4 | сторона квадрата вписанного в круг | ||
| 5 | сторона квадрата, в который вписан круг | ||
| 6 | стороны треугольника | где | |
| 7 | сторона равностороннего треугольника | ||
| 8 | высота равностороннего треугольника | ||
| 9 | боковая сторона и основание равнобедренного треугольника | ||
| 10 | стороны при прямом угле треугольника | ||
| 11 | боковая сторона и основание равнобедренного треугольника | ||
| 12 | боковые стороны равнобедренного треугольника и угол между ними | ||
| 13 | стороны прямоугольного треугольника | ||
| 14 | сторона и угол при основании треугольника | ||
| 15 | сторона равностороннего треугольника | ||
| 16 | сторона и угол при основании трапеции | ||
| 17 | боковые стороны и диагональ трапеции | где | |
| 18 | стороны прямоугольника | ||
| 19 | сторона и количество сторон многоугольника | ||
| 20 | сторона шестиугольника |
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π, как отношение длины окружности C к двум ее радиусам r. Исходя из этого, выводится формула длины окружности C, которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r.
Отношение длины любой окружности C к ее диаметру d всегда будет равно одному и тому же числу. Это число – всем известное число π («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числа π, как отношение длины окружности C к двум ее радиусам r. Исходя из этого, выводится формула длины окружности C, которая равна произведения числа π и диаметра d окружности или 2-м ее радиусам r.
С=2πr
С= πd
π=C/d
Для примера решим простую задачу, где нужно найти длину окружности, у которой известен радиус r=2 см.
C= πd
d=2r=4 см
С=4*3,14=12,56
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки.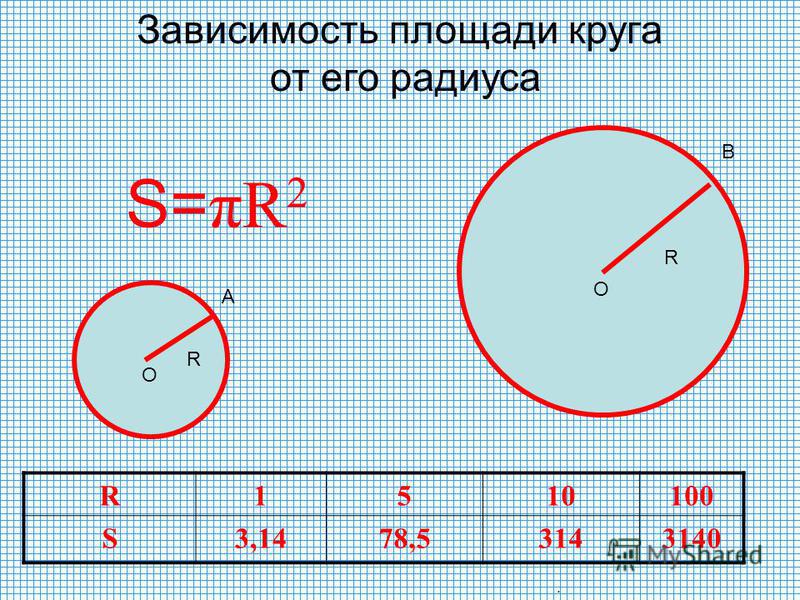 Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Источники
- https://tokar.guru/hochu-vse-znat/raschet-ploschadi-poperechnogo-secheniya-kruga.html
- https://mnogoformul.ru/formuly-ploshhadi-kruga-i-raschet-onlayn
- https://www.calc.ru/ploshchad-kruga.html
- https://ru.onlinemschool.com/math/formula/circle/
- https://allcalc.ru/node/18
- https://minus-procentov-online.ru/krug/diametr/
- https://doza.pro/art/math/geometry/area-circle
- https://zen.yandex.ru/media/studystudent/dlina-okrujnosti-i-ploscad-kruga-formuly-i-primery-5e9d7c122517bd2ed0b40460
- https://2mb.ru/matematika/geometriya/ploshhad-kruga/
формула. Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапецию
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².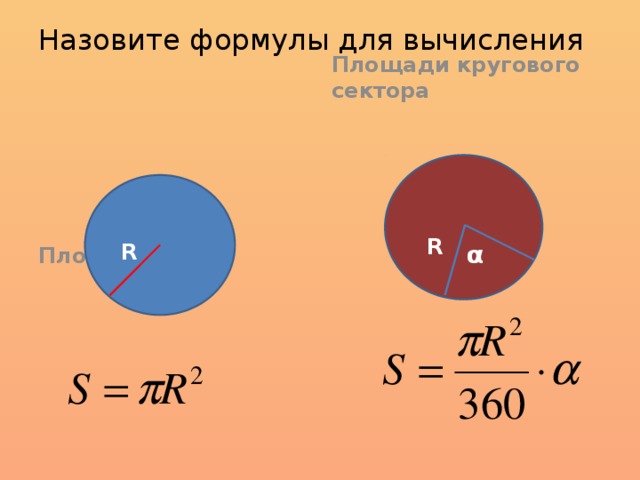
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус.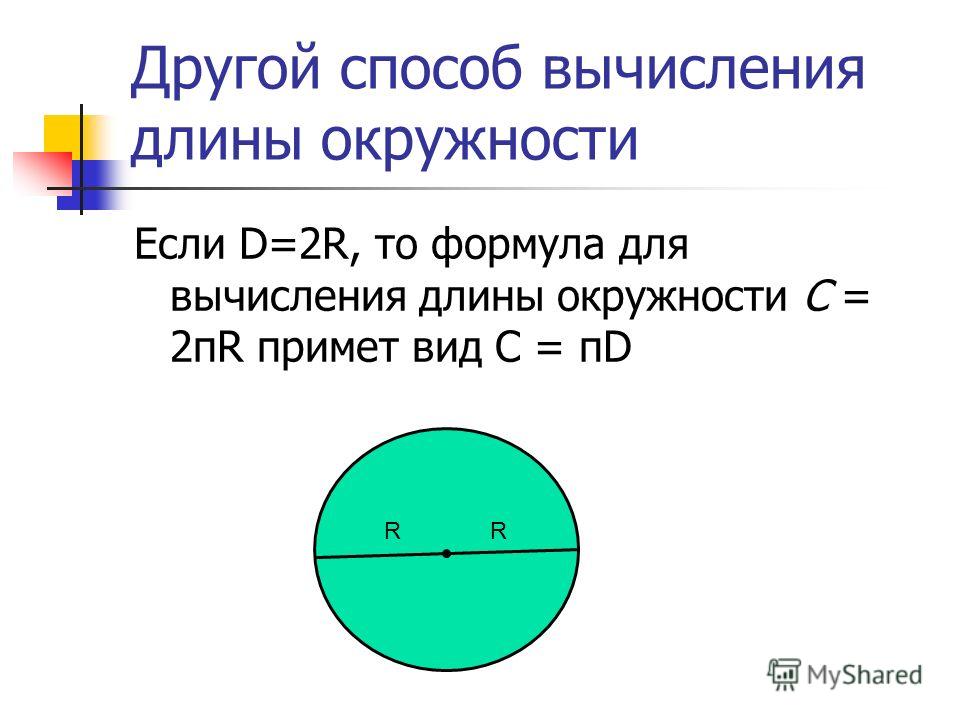 Формулу смотрите выше по тексту.
Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца.
 При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью.
 Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.
Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.
Величины, участвующие в расчете площади круга
Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях — это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC
в первой окружности. По теореме Пифагора: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга — площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S
/π
= 2.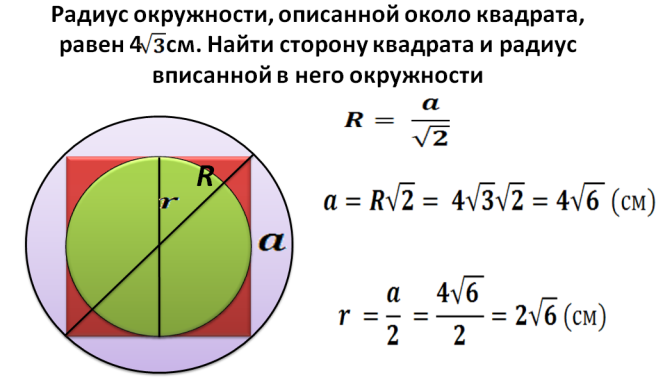
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков».
 Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;
Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30; - Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
Площадь круга диаметром 6 метров. Площадь круга в задаче B5
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
Как найти площадь круга? Сначала найдите радиус.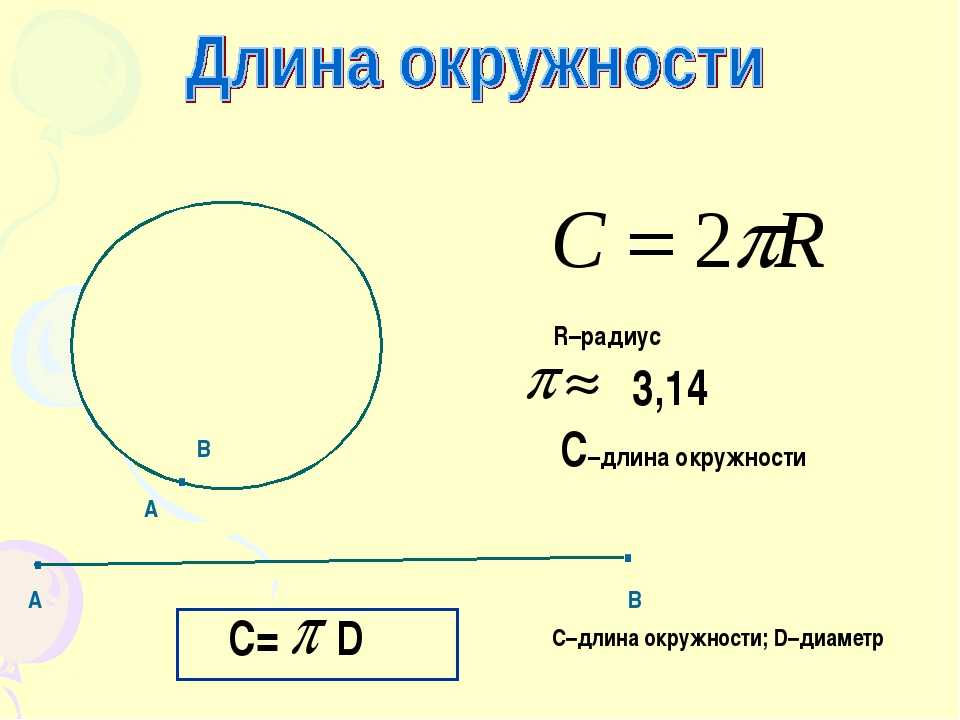 Учитесь решать простые и сложные задачи.
Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.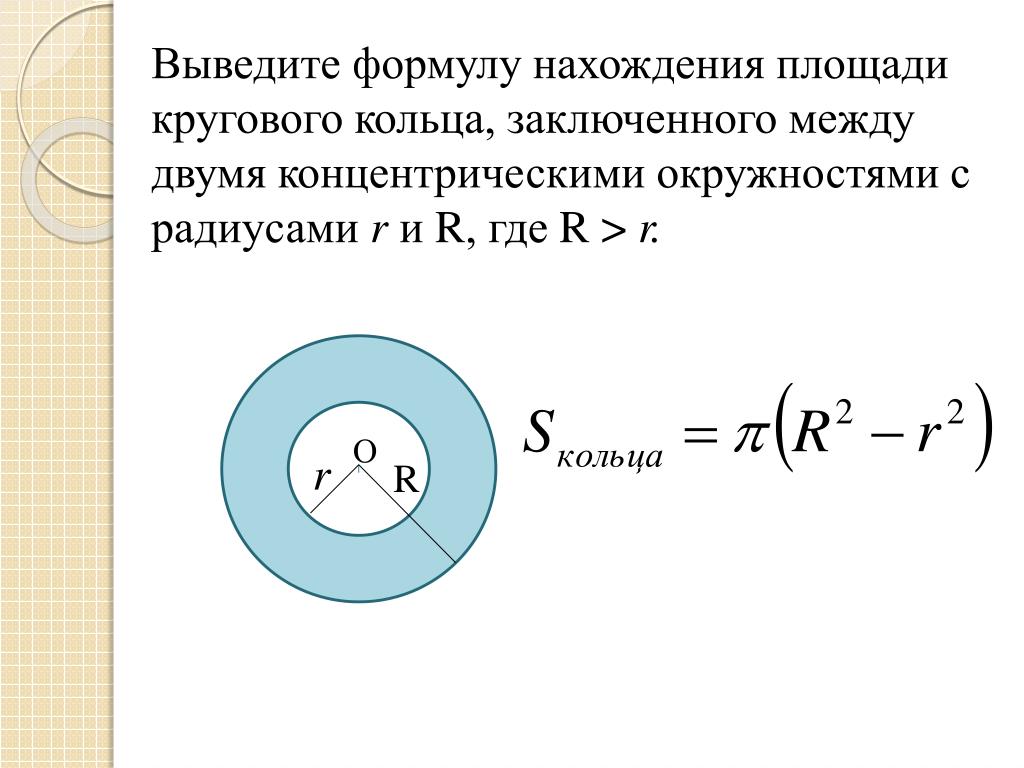
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция.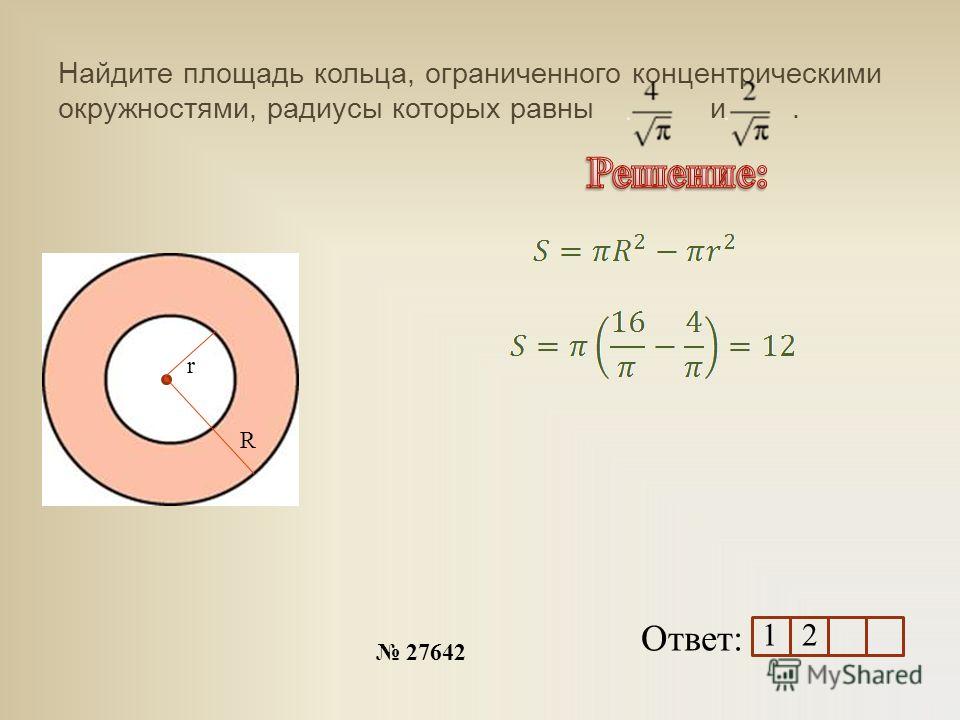 Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3. 14
14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна.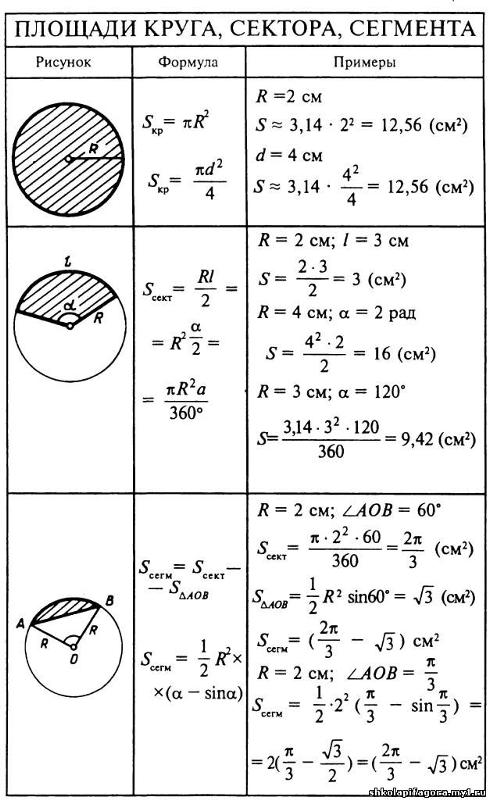 Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Как нам известно из школьной программы, кругом принято называть плоскую геометрическую фигуру, которая состоит из множества точек, равноудалённых от центра фигуры. Так как все они находятся на одинаковом расстоянии, они формируют окружность.
Удобная навигация по статье:
Отрезок, соединяющий центр круга и точки его окружности называют радиусом. 2}/{4*3,14}=64/{12,56}=5. И получаем площадь круга равную пяти квадратным сантиметрам.
2}/{4*3,14}=64/{12,56}=5. И получаем площадь круга равную пяти квадратным сантиметрам.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Площадь круга определяется по формуле. Площадь круга: формула
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы.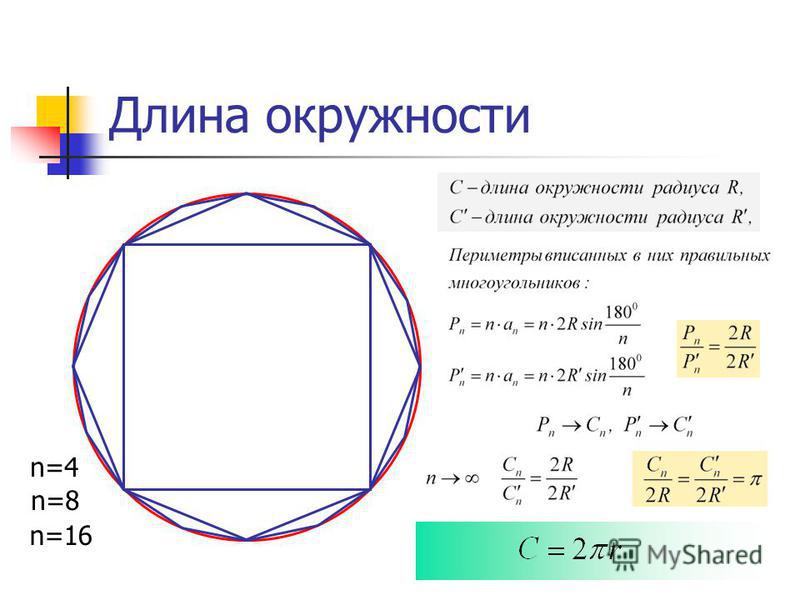 Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².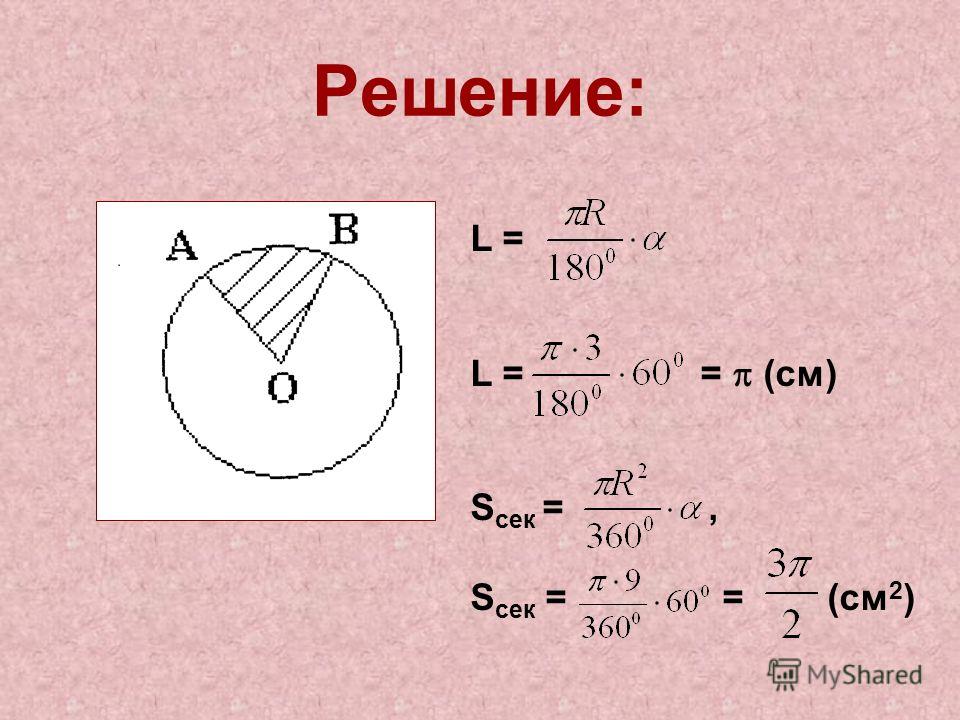
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже.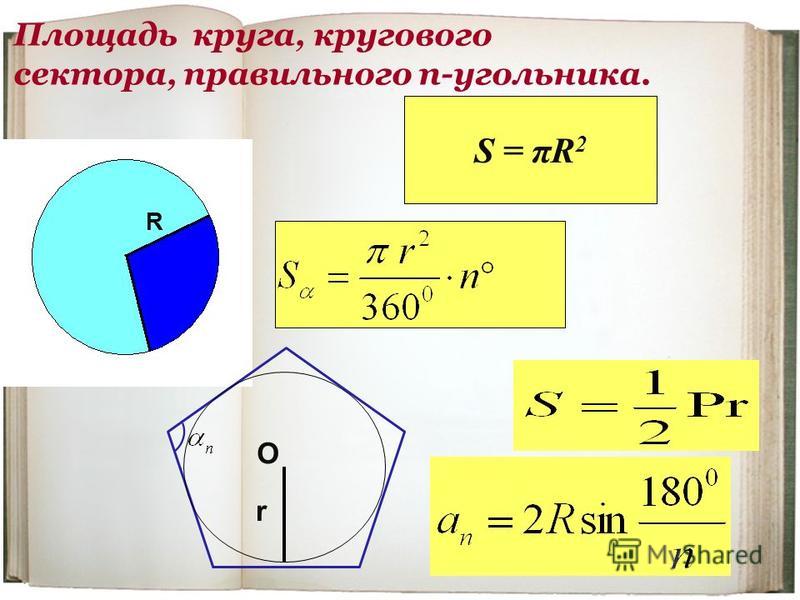 Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях — это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC
в первой окружности. По теореме Пифагора: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга — площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S
/π
= 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
Пусть исходный круг имеет площадь S круга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков».
 Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;
Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30; - Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Площадь круга – формула, вывод, определение, примеры
Площадь круга – это пространство, занимаемое кругом на двумерной плоскости. В качестве альтернативы пространство, занимаемое в пределах границы/окружности круга, называется площадью круга. Формула площади круга: A = πr 2 , где r — радиус круга. Единицей площади является квадратная единица, например, м 2 , см 2 , 2 дюйма и т. д. Площадь круга = πr 2 или πd 2 /4 в квадратных единицах, где (Pi) π = 22/7 или 3,14. Пи (π) — это отношение длины окружности к диаметру любого круга. Это специальная математическая константа.
В качестве альтернативы пространство, занимаемое в пределах границы/окружности круга, называется площадью круга. Формула площади круга: A = πr 2 , где r — радиус круга. Единицей площади является квадратная единица, например, м 2 , см 2 , 2 дюйма и т. д. Площадь круга = πr 2 или πd 2 /4 в квадратных единицах, где (Pi) π = 22/7 или 3,14. Пи (π) — это отношение длины окружности к диаметру любого круга. Это специальная математическая константа.
Формула площади круга полезна для измерения области, занимаемой круглым полем или графиком. Предположим, если у вас есть круглый стол, то формула площади поможет нам узнать, сколько ткани нужно, чтобы полностью его покрыть. Формула площади также поможет нам узнать длину границы, то есть длину окружности. Имеет ли круг объем? Нет, у круга нет объема. Круг — это двумерная фигура, у него нет объема. У круга есть только площадь и периметр/окружность.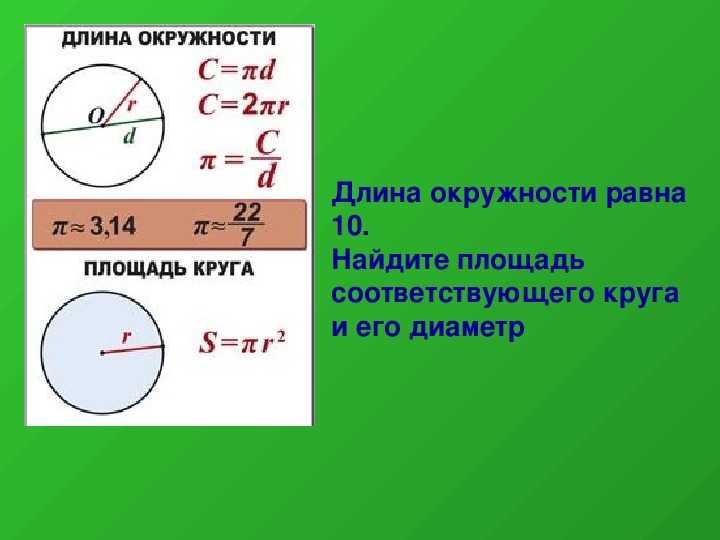 Давайте подробно узнаем о площади круга, площади поверхности и его окружности на примерах.
Давайте подробно узнаем о площади круга, площади поверхности и его окружности на примерах.
| 1. | Круг и части круга |
| 2. | Какова площадь круга? |
| 3. | Формулы площади круга |
| 4. | Вывод формулы площади круга |
| 5. | Площадь поверхности круга Формула |
| 6. | Реальный пример площади круга |
| 7. | Часто задаваемые вопросы по площади круга |
Круг и части круга
Окружность — это совокупность точек, находящихся на фиксированном расстоянии от центра окружности. Круг представляет собой замкнутую геометрическую фигуру. Мы видим круги в повседневной жизни, такие как колесо, пицца, круглая площадка и т. Д. Мера пространства или области, заключенной внутри круга, известна как площадь круга.
Радиус: Расстояние от центра до точки на границе называется радиусом окружности. Обозначается буквой «р» или «р». Радиус играет важную роль в формуле площади и длины окружности, которую мы изучим позже.
Диаметр: Линия, которая проходит через центр и ее концы лежат на окружности, называется диаметром окружности. Обозначается буквой «d» или «D».
Формула диаметра: Формула диаметра круга равна удвоенному его радиусу. Диаметр = 2 × Радиус
d = 2r или D = 2R
Если диаметр круга известен, его радиус можно рассчитать как:
r = d/2 или R = D/2
Окружность: Длина окружности равна длине ее границы. Это означает, что периметр круга равен его окружности. Длина веревки, идеально обвивающей границу круга, будет равна его длине окружности. Приведенный ниже рисунок поможет вам визуализировать то же самое. Окружность можно измерить, используя данную формулу:
, где «r» — радиус окружности, а π — математическая константа, значение которой приблизительно равно 3,14 или 22/7. Окружность круга может быть использована для нахождения площади этого круга.
Окружность круга может быть использована для нахождения площади этого круга.
Для круга с радиусом «r» и длиной окружности «C»:
- π = длина окружности/диаметр
- π = C/2r = C/d
- С = 2πr
Давайте разберемся с различными частями круга на следующем примере из реальной жизни.
Рассмотрим парк круглой формы, как показано на рисунке ниже. Мы можем определить различные части круга с помощью рисунка и таблицы, приведенных ниже.
| По кругу | В нашем парке | Назван буквой |
|---|---|---|
| Центр | Фонтан | Ф |
| Окружность | Граница | |
| Хорд | Вход в игровую зону | ПК |
| Радиус | Расстояние от фонтана до Въездных ворот | ФА |
| Диаметр | Расстояние по прямой линии между входными и выходными воротами через фонтан | Авиабаза |
| Малый сегмент | Меньшая часть парка, обозначенная как игровая площадка | |
| Основной сегмент | Большая площадь парка, кроме игровой площадки | |
| Внутренняя часть круга | Зеленая зона всего парка | |
| Внешняя часть круга | Территория за пределами парка | |
| Дуга | Любая изогнутая часть по окружности. |
Какова площадь круга?
Площадь круга — это пространство, ограниченное границами круга. Область внутри границы круга — это площадь, занимаемая кругом. Его также можно назвать общим количеством квадратных единиц внутри этого круга.
Формулы площади круга
Площадь круга можно вычислить промежуточными шагами, исходя из диаметра и длины окружности. Из диаметра и окружности мы можем найти радиус, а затем найти площадь круга. Но эти формулы обеспечивают кратчайший способ найти площадь круга. Предположим, что круг имеет радиус «r», тогда площадь круга = πr 2 или πd 2 /4 в квадратных единицах, где π = 22/7 или 3,14, а d — диаметр.
Площадь круга, A = πr 2 квадратных единиц
Окружность / периметр = 2πr единиц
Площадь круга можно рассчитать по формуле:
- Площадь = π × r 2 , где ‘r’ — радиус.
- Площадь = (π/4) × d 2 , где d — диаметр.

- Площадь = C 2 /4π, где C — длина окружности.
Примеры использования формулы площади круга
Рассмотрим следующие иллюстрации на основе формулы площади круга.
Пример 1: Если длина радиуса окружности равна 4 единицам. Вычислите его площадь.
Решение:
Радиус (r) = 4 единицы (данные)
Используя формулу площади круга,
Площадь круга = πr 2
Поставьте значения,
А = π4 2
А =π × 16
A = 16π ≈ 50,27
Ответ: Площадь круга равна 50,27 квадратных единиц.
Пример 2: Длина наибольшей хорды окружности 12 единиц. Найдите площадь круга.
Решение:
Диаметр (d) = 12 единиц (данные)
Используя формулу площади круга,
Площадь круга = (π/4)×d 2
Поставьте значения,
А = (π/4) × 12 2
А = (π/4) × 144
A = 36π ≈ 113,1
Ответ: Площадь круга равна 113,1 квадратных единиц.
Площадь круга с использованием диаметра
Формула площади круга через диаметр: Площадь круга = πd 2 /4. Здесь d — диаметр окружности. Диаметр круга в два раза больше радиуса круга. д = 2р. Как правило, из диаметра нам нужно сначала найти радиус круга, а затем найти площадь круга. С помощью этой формулы мы можем напрямую найти площадь круга, исходя из меры диаметра круга.
Площадь круга с использованием длины окружности 92}{4\пи}\). Есть два простых шага, чтобы найти площадь круга по заданной окружности круга. Длина окружности сначала используется для нахождения радиуса окружности. Этот радиус также полезен для нахождения площади круга. Но в этой формуле мы сможем напрямую найти площадь круга из длины окружности круга.
Площадь круга-Вычисление
Площадь круга удобно вычислять по радиусу, диаметру или длине окружности. Константа, используемая при вычислении площади круга, равна пи и имеет дробное числовое значение 22/7 или десятичное значение 3,14. Любое из значений pi может быть использовано в зависимости от требований и необходимости уравнений. В приведенной ниже таблице показан список формул, если мы знаем радиус, диаметр или длину окружности.
Любое из значений pi может быть использовано в зависимости от требований и необходимости уравнений. В приведенной ниже таблице показан список формул, если мы знаем радиус, диаметр или длину окружности.
| Площадь круга, когда известен радиус. | πr 2 |
| Площадь круга, когда известен диаметр. | πd 2 /4 |
| Площадь круга, когда известна длина окружности. | С 2 / 4π |
Вывод площади круга
Почему площадь круга πr 2 ? Чтобы понять это, давайте сначала разберемся, как выводится формула площади круга.
Внимательно посмотрите на приведенный выше рисунок, если мы разделим круг на более мелкие части и расположим их систематически, он образует форму параллелограмма. Когда круг делится на еще более мелкие сектора, он постепенно принимает форму прямоугольника. Чем больше у него секций, тем больше он имеет форму прямоугольника, как показано выше.
Когда круг делится на еще более мелкие сектора, он постепенно принимает форму прямоугольника. Чем больше у него секций, тем больше он имеет форму прямоугольника, как показано выше.
Площадь прямоугольника = длина × ширина
Ширина прямоугольника = радиус окружности (r)
Сравнив длину прямоугольника и длину окружности, мы увидим, что длина равна = ½ окружности круга
Площадь круга = Площадь образовавшегося прямоугольника = ½ (2πr) × r
Следовательно, площадь круга равна πr 2 , где r — радиус круга, а значение π равно 22/7 или 3,14.
Площадь поверхности круга Формула
Площадь поверхности круга равна площади круга. На самом деле, когда мы говорим о площади круга, мы имеем в виду не что иное, как общую площадь его поверхности. Площадь поверхности — это площадь, занимаемая поверхностью трехмерной формы. Поверхность сферы будет иметь сферическую форму, но круг — это простая плоская двумерная форма.
Если дана длина радиуса или диаметр или даже длина окружности, то мы можем узнать площадь поверхности. Он представлен в квадратных единицах. Площадь поверхности круга по формуле = πr 2 где ‘r’ — радиус окружности, а значение π приблизительно равно 3,14 или 22/7.
Он представлен в квадратных единицах. Площадь поверхности круга по формуле = πr 2 где ‘r’ — радиус окружности, а значение π приблизительно равно 3,14 или 22/7.
Реальный пример площади круга
Рон и его друзья заказали пиццу в пятницу вечером. Длина каждого кусочка была 15 см.
Вычислите площадь пиццы, которую заказал Рон. Можно считать, что длина куска пиццы равна радиусу пиццы.
Решение:
Пицца имеет круглую форму. Таким образом, мы можем использовать формулу площади круга для вычисления площади пиццы.
Радиус равен 15 см
Формула площади круга = πr 2 = 3,14 × 15 × 15 = 706,5
Площадь пиццы = 706,5 кв.см.
Примеры площади круга
Пример 1: Найдите длину окружности и площадь круга, радиус которого равен 14 см.
Решение:
Дано: Радиус круга = 14 см
Длина окружности = 2πr
= 2 × 22/7 × 14
= 2 × 22 × 2
= 88 см
Используя формулу площади круга = πr 2
= 22/7 × 14 × 14
= 22 см × 2 × 7 кв.
 .
.Площадь круга = 616 кв. см.
Пример 2: Соотношение площадей двух кругов составляет 4:9. С помощью формулы площади круга найдите отношение их радиусов.
Решение:
Предположим следующее:
Радиус 1-го круга = R1
Площадь 1-го круга = A1
Радиус 2-го круга = R2
Площадь 2-го круга = A2
Дано, что A1:A2 = 4: 9
Площадь круга = πr 2
π\(R_1\) 2 : π\(R_2\) 2 = 4 : 9
R 9001 9001 R2 = 2 : 3
Следовательно, отношение радиусов = 2:3
Пример 3: Гоночная трасса имеет форму круглого кольца. Внутренний радиус гусеницы составляет 58 ярдов, а внешний радиус — 63 ярда. Найдите площадь гоночной трассы.
Решение:
Дано: R = 63 ярда, r = 56 ярдов.
Пусть площадь внешнего круга равна A 1 , а площадь внутреннего круга равна A 2
Площадь гоночной трассы = A 1 — A 2 = πR 2
0
2
= π(63 2 — 56 2 ) = 22/7 × 833 = 2618 квадратных ярдов.
Таким образом, площадь гоночной трассы составляет 2618 квадратных метров.
Пример 4: Провод имеет форму равностороннего треугольника. Каждая сторона треугольника составляет 7 дюймов. Проволока согнута в форме круга. Найдите площадь образовавшегося круга.
Решение:
Периметр равностороннего треугольника: Периметр треугольника = 3 × сторона = 3 × 7 = 21 дюйм.
Так как периметр равностороннего треугольника = длина окружности образовавшегося круга.
Таким образом, периметр треугольника равен 21 дюйму.
Длина окружности = 2πr = 2 × 22/7 × r = 21. r = (21 × 7)/(44) = 3,34.
Следовательно, радиус окружности равен 3,34 см. Площадь круга = πr 2 = 22/7 × (3,34) 2 = 35,042 квадратных дюйма.
Следовательно, площадь круга равна 35,042 квадратных дюйма.
Пример 5: Время, показанное на круглых часах, равно 15:00.
 Длина минутной стрелки составляет 21 единицу. Найдите расстояние, пройденное кончиком минутной стрелки в 15:30.
Длина минутной стрелки составляет 21 единицу. Найдите расстояние, пройденное кончиком минутной стрелки в 15:30.Решение:
Когда минутная стрелка находится в 15:30, она покрывает половину круга. Таким образом, расстояние, пройденное минутной стрелкой, на самом деле составляет половину окружности. Расстояние \(= \pi\) (где r — длина минутной стрелки). Отсюда пройденное расстояние = 22/7 × 21 = 22 × 3 = 66 единиц. Следовательно, пройденный путь равен 66 единицам.
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Пусть ваш ребенок решит задачи из реальной жизни, используя математику
Пусть ваш ребенок применит понятия, полученные в школе, в реальном мире с помощью наших экспертов.
Записаться на бесплатный пробный урок
Практические вопросы по площади круга
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по площади круга
Как вычислить площадь круга?
Площадь круга рассчитывается с использованием следующих перечисленных формул:
- Площадь = π × r 2 , где ‘r’ — радиус.

- Площадь = (π/4) × d 2 , где d — диаметр.
- Площадь = C 2 /4π, где C — длина окружности.
Что такое формула площади круга?
Формула площади круга = π × r 2 . Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга при заданном радиусе r равна πr 2 . Площадь круга, если известен диаметр d, равна πd 2 /4. π составляет примерно 3,14 или 22/7. Площадь (A) также можно найти по формуле A = (π/4) × d 2 , где d — радиус, а A = C 2 /4π, где C — длина окружности.
Что такое периметр и площадь круга?
Длина окружности равна длине ее границы. Это означает, что периметр круга равен его окружности. Площадь круга πr 2 , а периметр (окружность) равен 2πr, когда радиус равен r единицам, π составляет приблизительно 3,14 или 22/7. Длина окружности и длина радиуса круга являются важными параметрами для определения площади этого круга. Для круга с радиусом «r» и окружностью «C»:
Для круга с радиусом «r» и окружностью «C»:
- π = длина окружности ÷ диаметр
- π = С/2r
- Следовательно, C = 2πr
Почему формула площади круга равна πr
2 ?Круг можно разделить на множество маленьких секторов, которые затем можно переставить соответствующим образом, чтобы сформировать параллелограмм. Когда круг делится на еще более мелкие сектора, он постепенно принимает форму прямоугольника. Мы можем ясно видеть, что одна из сторон прямоугольника будет радиусом, а другая будет половиной длины окружности, т. е. π. Как мы знаем, площадь прямоугольника равна его длине, умноженной на ширину, которая равна π, умноженному на «r». Следовательно, площадь круга равна πr 2 .
Чему равна формула площади круга, выраженная числом π?
Значение числа пи (π) приблизительно равно 3,14. Пи — иррациональное число. Это означает, что его десятичная форма не заканчивается (например, 1/5 = 0,2) и не повторяется (например, 1/3 = 0,3333. ..). Пи равно 3,141592653589793238… (всего до 18 знаков после запятой). Следовательно, формула площади круга, выраженная в числах пи, равна πr 2 квадратных единиц.
..). Пи равно 3,141592653589793238… (всего до 18 знаков после запятой). Следовательно, формула площади круга, выраженная в числах пи, равна πr 2 квадратных единиц.
Как найти длину окружности и площадь круга?
Площадь и длину окружности можно рассчитать по следующим формулам. Окружность = 2πr; Площадь = πr 2 . Окружность круга можно взять как π, умноженное на диаметр круга. А площадь круга в π раз больше квадрата радиуса круга.
Как рассчитать площадь круга с диаметром?
Диаметр круга в два раза больше радиуса круга. Следовательно, формула площади круга с использованием диаметра равна π/4, умноженному на квадрат диаметра круга. Формула площади круга с использованием диаметра круга π/4 × диаметр 2 .
Как найти площадь круга, зная длину окружности?
Площадь круга также можно найти, используя длину окружности круга. Радиус круга можно найти из длины окружности круга, и это значение можно использовать для нахождения площади круга.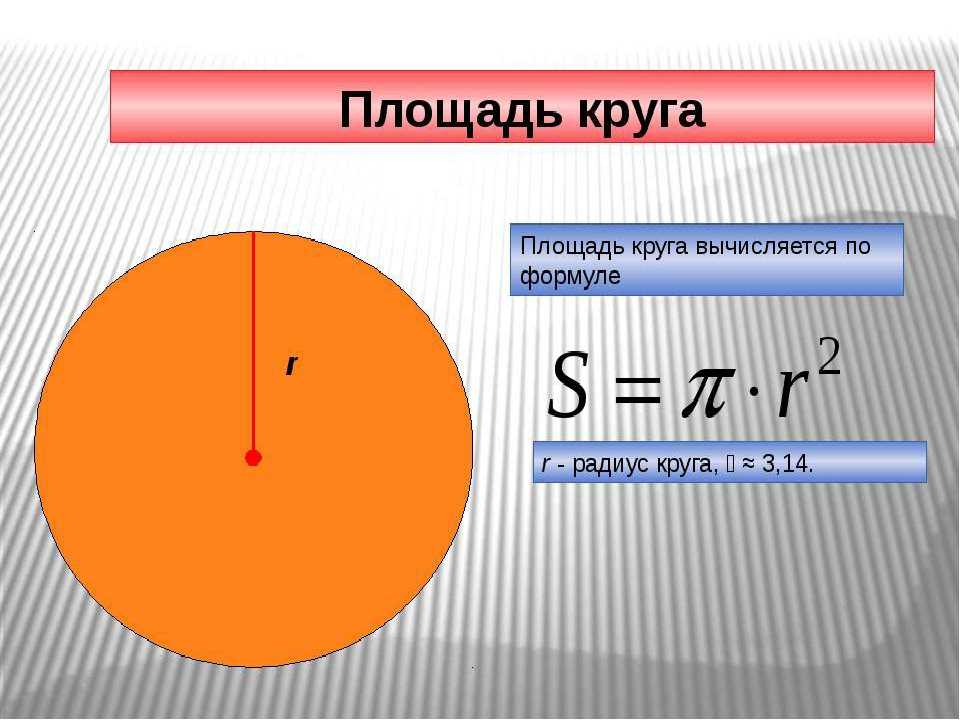 Предположим, что длина окружности равна «С». Имеем C = 2πr или r = C/2π. Теперь, применяя это значение «C» к формуле площади, мы получаем A = πr 2 = π × (C/2π) 2 = C 2 /4π.
Предположим, что длина окружности равна «С». Имеем C = 2πr или r = C/2π. Теперь, применяя это значение «C» к формуле площади, мы получаем A = πr 2 = π × (C/2π) 2 = C 2 /4π.
Какова площадь круга с радиусом 3 м?
Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга (A) при заданном радиусе r составляет πr 2 . π составляет примерно 3,14 или 22/7. Следовательно, площадь = 3,14 × 3 × 3 = 28,26 кв.м.
Длина окружности данного круга равна 16 см. Какова будет его площадь?
Длина окружности = 16 см
Мы знаем формулу длины окружности, C =2πr
Итак,
2πr = 16
или r = 16/2π = 8/π
Подставляя значение ‘r’ в формулу площади окружности, получаем:
А = πr 2
А = π(8/π) 2 = 64/π
При решении,
Площадь = 20,38 кв.см.
Площадь круга – формула и примеры
Окружности можно увидеть от микро до макрообъектов вокруг нас. Например, наша Земля представляет собой плоский круг; луна — гигантский круг; ваша собака может играть с круглым мячом и многое другое. Окружность — это двумерная фигура, геометрическое место которой равноудалено от центра окружности. Граница круга называется его периметром или окружностью, а площадь, ограниченная его границами, называется площадью. Знаете ли вы о частях круга? И как область связана с ними?
Например, наша Земля представляет собой плоский круг; луна — гигантский круг; ваша собака может играть с круглым мячом и многое другое. Окружность — это двумерная фигура, геометрическое место которой равноудалено от центра окружности. Граница круга называется его периметром или окружностью, а площадь, ограниченная его границами, называется площадью. Знаете ли вы о частях круга? И как область связана с ними?
Середина любого круга является его центром. Линия, проведенная от одного конца круга, касающегося периферии, к другому краю через центр круга, называется диаметром круга. Половина этого диаметра называется радиусом. Что мы говорим, если диаметр не проходит через центр? Тогда диаметр уже не будет диаметром. Вместо этого он будет называться аккордом. Хорда – это линия, проведенная от одной периферии к другой периферии круга, не пересекая центр. Отсюда можно сделать вывод, что более длинная хорда, присутствующая в окружности, будет диаметром окружности.
Окружность может иметь бесконечное количество хорд, диаметров и радиусов. Вы когда-нибудь ели кусок пиццы? Что вы заметили? Этот кусочек является частью круглой пиццы, разделенной по центру. Следовательно, часть круга проходит через центр, образуя с центром определенный угол, известный как сектор. Как площадь круга связана с этими частями круга? Какая формула площади круга?
Вы когда-нибудь ели кусок пиццы? Что вы заметили? Этот кусочек является частью круглой пиццы, разделенной по центру. Следовательно, часть круга проходит через центр, образуя с центром определенный угол, известный как сектор. Как площадь круга связана с этими частями круга? Какая формула площади круга?
Формула площади круга: универсальная форма
Формула площади круга: 𝜋r 2 , где r — радиус круга. Значение 𝜋, произносится как пи, равно 22/7 или 3,14. Пи — это отношение длины окружности к диаметру круга. Это одна из широко используемых математических констант. Площадь круга измеряется в квадратных единицах. Каковы бы ни были единицы измерения радиуса, диаметра или длины окружности, то же самое будет и с площадью круга, но в квадратах. Обозначается единицами².
Круглый стол будет иметь площадь, круглая тарелка будет иметь площадь, шар будет иметь площадь, и, подобно этому, многие другие объекты будут иметь круглую площадь. Площадь определяет пространство, необходимое для удержания объекта в определенном месте. Итак, если нам нужно поместить круглый диск в шкаф, нам нужно найти площадь, т. е. сколько места потребуется. После площади круг имеет объем? Поскольку круг — двумерная фигура, он не имеет объема. А как насчет площади его поверхности?
Итак, если нам нужно поместить круглый диск в шкаф, нам нужно найти площадь, т. е. сколько места потребуется. После площади круг имеет объем? Поскольку круг — двумерная фигура, он не имеет объема. А как насчет площади его поверхности?
Площадь поверхности круга формула: 2D-версия круга
Поскольку площадь поверхности является свойством трехмерной фигуры, двумерный круг не имеет такой площади поверхности, как у сферы. Однако найти площадь сферы, которую нужно куда-то поместить, можно найти по площади поверхности. И эта площадь поверхности такая же, как площадь круга. Следовательно, площадь поверхности любого круга будет равна площади круга, т. е. 𝜋r 2 .
Формула площади круга через диаметр
Диаметр равен удвоенному радиусу, т. е. мы можем записать диаметр = 2 x радиус. Следовательно, радиус будет d/2. Из площади круга 𝜋r 2 , переводя значение r через d, получаем
A = 𝜋 (d/2) 2 = 𝜋/4 d 2 . Это площадь круга по диаметру.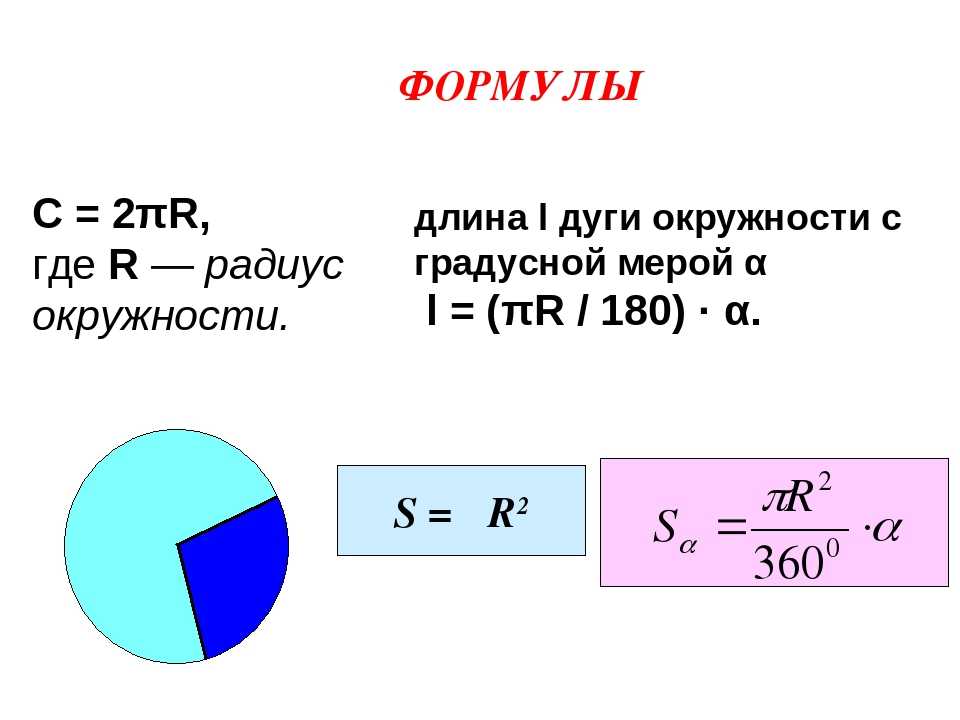
Формула площади круга в терминах длины окружности
Длина окружности — это граница окружности, обозначаемая 2𝜋r, где r — радиус окружности. Следовательно, C = 2𝜋r. Вынимая отсюда значение r и подставляя формулу площади круга, получаем
А = 𝜋 (С/2𝜋)2 = С 2 / 4𝜋. Это формула площади круга в пересчете на длину окружности.
Площадь сектора круга формула
Зная площадь круга, зная радиус, диаметр и длину окружности, пришло время найти площадь круга, зная сектор. Сектор — это часть круга, иногда называемая клином. Когда два радиуса проведены от центра круга к краю круга, область, ограниченная этими двумя радиусами и окружностью, называется сектором. Прямо как кусок пиццы? Да, кусок пиццы является примером сектора, если кусок разрезается по центру круга, а не по окружности.
Как измерить центральный угол, образуемый окружностью? Ну, используйте транспортир. Поместите транспортир между двумя радиусами и измерьте центральный угол. Во многих вопросах угол дается в самом вопросе. Таким образом, никто не должен беспокоиться об измерении угла.
Таким образом, никто не должен беспокоиться об измерении угла.
Площадь сектора, когда заданы угол и радиус сектора, обозначается как
A сектор = 𝜃/360° 𝜋r², где 𝜃 будет в градусах.
Сектор = ½ r² 𝜃, где 𝜃 в радианах.
Соотношение между радианами и градусами определяется как радиан = градус x 𝜋/180
После нахождения площади сектора ее можно использовать для нахождения площади круга.
Площадь круга = Площадь сектора x 360 / Центральный угол, здесь центральный угол в градусах.
Мы узнали обо всех способах нахождения площади круга, но откуда берется универсальная формула?
Вычисление площади круга по формуле
Почему формула для нахождения площади круга 𝜋r²? Чтобы вывести формулу площади круга, разделите круг на различные треугольники так, чтобы эти треугольники можно было соединить в виде прямоугольника, как показано на рисунке. Чем больше количество секций, тем четче будет форма прямоугольника.
Мы знаем, что площадь прямоугольника равна произведению его длины на ширину. Из приведенной схемы длина прямоугольника равна половине длины окружности, которую обозначают 𝜋r. Ширина прямоугольника — это радиус.
Из приведенной схемы длина прямоугольника равна половине длины окружности, которую обозначают 𝜋r. Ширина прямоугольника — это радиус.
Следовательно, площадь прямоугольника равна длине x ширине = 𝜋r x r = 𝜋r², что является площадью по формуле круга.
Узнайте больше о формуле площади круга, решив примеры
Пример 1: Какова площадь круга, если радиус равен 60 м?
Решение: Согласно формуле площади круга,
A = 𝜋 r², где r — радиус
Подставляя значения в формулу, получаем, A = 𝜋 60².= 11304 м².
Пример 2: Найдите площадь круга, наибольшая хорда которого равна 32 см.
Решение: Мы знаем, что наибольшая хорда в окружности — это ее диаметр. Следовательно, используя формулу площади круга,
A = 𝜋/4 d², где d — диаметр круга.
Подставляя значения в формулу, получаем, A = 𝜋/4 32²= 803,84 см².
Пример 3. Найдите площадь круга, площадь сектора которого равна 6𝜋 единиц, а угол, образуемый в центре, равен 45 градусам.
Решение: Из формулы площади сектора мы знаем, что
A окружность = A сектор (360/C), где C — центральный угол в градусах.
Следовательно, площадь круга будет равна
A = 6𝜋 (360/45) = 48𝜋 = 150,72 единицы.
Пример 4: Найдите чистую площадь данного круга.
Решение: На данном рисунке видны два круга. Больший имеет диаметр 11 см, а меньший имеет диаметр 3,5 см. Согласно формуле площади круга, A = 𝜋/4 d², где d — диаметр круга.
Подставляя значения в формулу, получаем,
Площадь большего круга = A B = 𝜋/4 11² = 94,985 см²
Площадь меньшего круга = A C = 𝜋/4 3,52 = 9,616 см²
Чтобы найти чистую площадь круга, вычтя площадь меньшего круга из большего круга, мы получим 94,985 – 9,616 = 85,369 см².
Площадь круга Формула и примеры
Площадь круга — это общее пространство, ограниченное его границей или окружностью. В круге нет объема, потому что это плоская двухмерная форма. Зная радиус круга, легко найти его площадь. Как видите, радиус круга — это просто отрезок линии от центра до любой точки на границе круга.
В круге нет объема, потому что это плоская двухмерная форма. Зная радиус круга, легко найти его площадь. Как видите, радиус круга — это просто отрезок линии от центра до любой точки на границе круга.
Площадь круга 92}. Кстати, иррациональное число \большое\пи — это отношение длины окружности к ее диаметру, которое при округлении до четвертого знака после запятой примерно равно 3,1416.
Мы предпочитаем использовать радиус, потому что это удобно, т. е. формула выражается через радиус. Но также полезно знать, что мы можем использовать другие входные данные для нахождения площади круга, такие как диаметр и окружность .
Во-первых, давайте изменим исходную формулу, чтобы изменить входную переменную с радиуса \large{r} на диаметр \large{d}. 92}} \over 4}}}
Теперь мы продолжим вывод другой формулы, где входной переменной является длина окружности {C}.
Начнем с формулы длины окружности.
\large{C = 2\pi r}
Перепишем r в терминах C.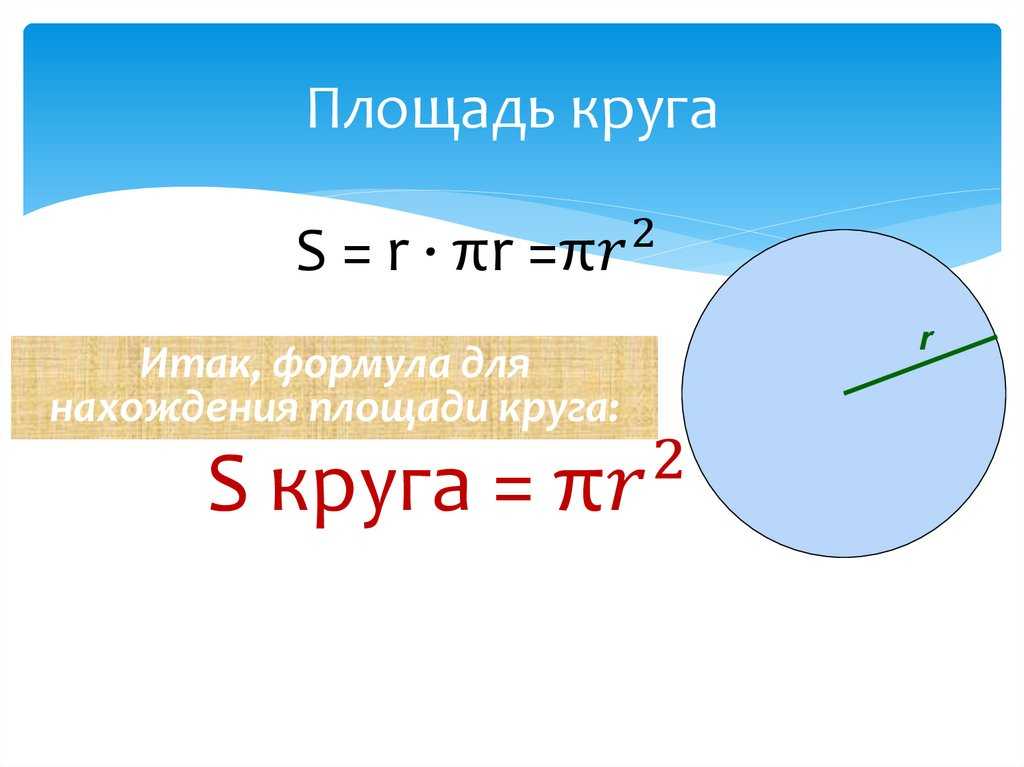 Мы можем сделать это, разделив обе части на 2\pi .
Мы можем сделать это, разделив обе части на 2\pi .
\large{r = \Large{{C \over {2\pi }}}}
Вернемся к формуле площади круга, подставим выражение для r через C.
92}} \over {4\pi }}}}Итак, это все формулы для нахождения площади круга.
Формула площади кругаПримеры нахождения площади круга по его радиусу
Пример 1: Какова площадь круга с радиусом 4 дюйма?
Как вы могли догадаться, это очень простая задача. Нам дана мера радиуса, равная \color{red}4 дюймам. Единственное, что нам нужно сделать, это подставить значение радиуса в формулу, а затем упростить.
Обратите внимание, что в нашем ответе выше мы просто сохранили площадь с точки зрения \pi. Мы не умножали число 16 на приблизительное числовое значение \pi, т.е. \pi = 3,14.
Если вы оставите свой ответ как 16\,\pi , вы правильно поняли, поскольку это точное значение площади. Однако, если вы хотите, чтобы ваш ответ был приблизительным, вы можете умножить его на оценочное значение \pi, которое в этом случае мы использовали \color{blue}3,14, округленное до двух знаков после запятой.
Следовательно, площадь круга составляет около 50,24 квадратных дюйма. 9 .
Теперь, округлив результат до двух знаков после запятой, мы получим 50,27 квадратных дюйма.
Пример 2: Найдите площадь круга диаметром 10 сантиметров.
Вот в чем дело. Предполагается, что вы даете свой ответ в терминах \pi, если только вам явно не сказали указать площадь в качестве приблизительного значения. Если ваш учитель хочет, чтобы это было приблизительно, здесь вы заменяете \pi некоторым числовым значением.
Теперь нарисуем круг диаметром 10 см.
Чтобы вычислить площадь круга, нам понадобится радиус. Однако мы можем легко вычислить, что такое радиус, если мы знаем диаметр. Радиус окружности равен половине диаметра. Таким образом, {\Large{{10} \over 2}} = 5.
Подставьте значение радиуса в формулу и упростите.
Следовательно, площадь круга равна 25\pi квадратных сантиметров.
Пример 3: Найдите точную площадь круга, диаметр которого имеет концы \left( { — 7,2} \right) и \left( {5,2} \right).
Построим конечные точки диаметра. Нарисуйте отрезок, соединяющий их, и убедитесь, что он проходит через центр.
Теперь нам нужно найти диаметр окружности, а затем разделить его на 2, чтобы получить радиус. В этой ситуации диаметр можно легко определить путем осмотра. Поскольку конечные точки диаметра лежат на горизонтальной линии y=2, длина диаметра есть абсолютная величина разности координат x.
\левый| { — 7 -5 } \право| = \ влево | { — 12} \право| = 12
Поскольку диаметр равен 12 единицам, его радиус должен быть равен 6 единицам. Единственное, что нам нужно сделать, это подставить значение радиуса в формулу.
Следовательно, площадь круга равна 36\,\pi квадратных единиц.
Примеры нахождения площади круга по его диаметру
В следующих примерах мы будем использовать версию формулы, в которой площадь круга выражается через диаметр d.
Напоминаю, что вот еще раз формула, которую вы можете использовать, чтобы найти площадь, когда известен диаметр. 92}.
92}.
Пример 5 : Вычислите площадь круга ниже, используя радиус r и диаметр d. Сравните свои ответы.
Примечание. Используйте \pi = 3.14. Округлите ответ до сотых.
В этой задаче мы вычислим площадь круга двумя способами, а затем сравним их, чтобы проверить, совпадают ли оба ответа.
Давайте сначала найдем площадь, используя формулу, которая включает в себя диаметр d в качестве входного значения.
Указан диаметр d = 2,75. Обязательно используйте \pi = 3.14, потому что это инструкция проблемы.
Теперь найдем площадь круга по стандартной формуле, то есть входное значение — радиус r. Не забудьте разделить диаметр на 2, чтобы получить радиус окружности.
Два решения дают один и тот же ответ, который составляет около 5,94 квадратных ярда.
Примеры нахождения площади круга по его длине окружности
В предыдущих примерах площадь круга вычислялась по его радиусу или диаметру. На этот раз мы вычислим площадь круга, используя его длину окружности.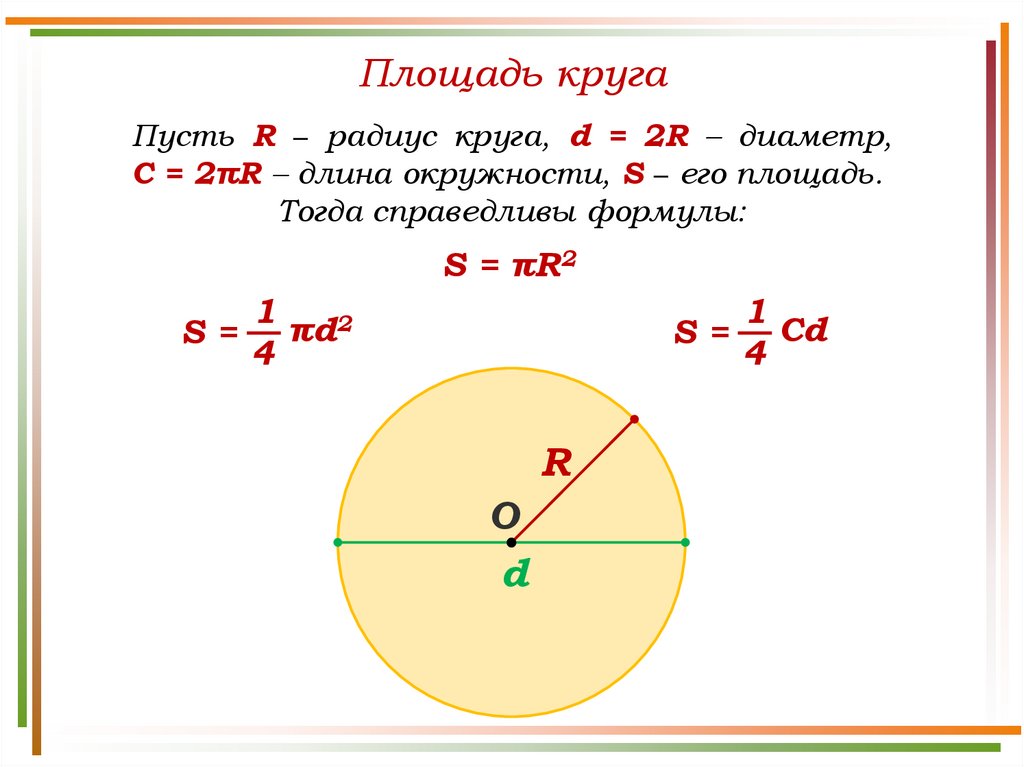 2}. 92}} \над {4\пи }}}.
2}. 92}} \над {4\пи }}}.
Обычная процедура:
Формула для длины окружности:
C = 2\pi r
Поскольку длина окружности равна 10, значение радиуса равно
Теперь, подставив значение радиуса в формула площади
Прямой маршрут:
Подставим значение длины окружности прямо в формулу.
Один и тот же ответ мы получаем разными методами. Площадь около 7,92}. Используйте коэффициент преобразования 1 мили. = 1,6 км.
Примечание. Используйте \pi = 3.14. Округлите ответ до сотых.
Поскольку мы хотим, чтобы наш ответ был в квадратных километрах, давайте сначала преобразуем нашу окружность из миль в километры.
Теперь мы готовы подставить известные значения в формулу для вычисления площади круга.
C = 1,696
\pi = 3,14
Не забудьте округлить площадь до двух знаков после запятой.
Площадь круга составляет около 0,23 квадратных километра. 92}?
Примечание. Используйте \pi = 3,1416 и округлите окончательный ответ до десятых.
Используйте \pi = 3,1416 и округлите окончательный ответ до десятых.
Поскольку мы знаем площадь, мы можем легко найти радиус, используя формулу площади, которая содержит радиус.
Подставляем значения площади и \pi. Чтобы найти \large{r}, мы разделим обе части на \pi, а затем возьмем квадратные корни обеих частей уравнения. Следите за тем, чтобы мы не округляли промежуточные вычисления. Только окончательный ответ.
Таким образом, радиус составляет примерно 8,6 дюйма. 92}.
Примечание. Используйте \pi = 3,1416 и округлите ответ до двух знаков после запятой.
Мы можем использовать формулу площади круга, где входным значением является диаметр.
Подставьте значение площади, затем определите диаметр.
Таким образом, диаметр круга составляет около 4,82 метра.
Вас также может заинтересовать:
Площадь круга Практические задачи с ответами
Площадь треугольника
Как найти уравнение окружности
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
ACT Math Help » Алгебра » Координатная плоскость » Круги » Как найти уравнение окружности
В стандартной координатной плоскости каковы радиус и центр окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
При нахождении центра и радиуса круга центр равен , а радиус равен . Обратите внимание, что они не отрицательны, хотя в уравнении перед ними стоят отрицательные знаки. Это становится важным при работе с действительными числами. Также обратите внимание на квадрат .
Обратите внимание, что они не отрицательны, хотя в уравнении перед ними стоят отрицательные знаки. Это становится важным при работе с действительными числами. Также обратите внимание на квадрат .
В нашем круге применяются те же принципы, что и в предыдущем принципе, поэтому он является нашим центром. Обратите внимание, как поменялись местами знаки чисел. Это относится ко всем кругам из-за отрицательного значения в основном уравнении выше.
Чтобы найти радиус окружности, нужно взять число, которому равно уравнение, и извлечь из него квадратный корень. Это связано с упомянутым выше квадратом. . Используйте наименьшее общее кратное 27, чтобы найти, что три тройки составляют 27. Вычтите две тройки, так как квадратный корень из числа, умноженного на самого себя, равен самому себе. Это оставляет один 3 под радикалом. Поэтому наш радиус равен .
Центр: Радиус:
Сообщить об ошибке
Какова площадь круга в стандартной координатной плоскости?
Возможные ответы:
Правильный ответ:
Объяснение:
Общее уравнение окружности .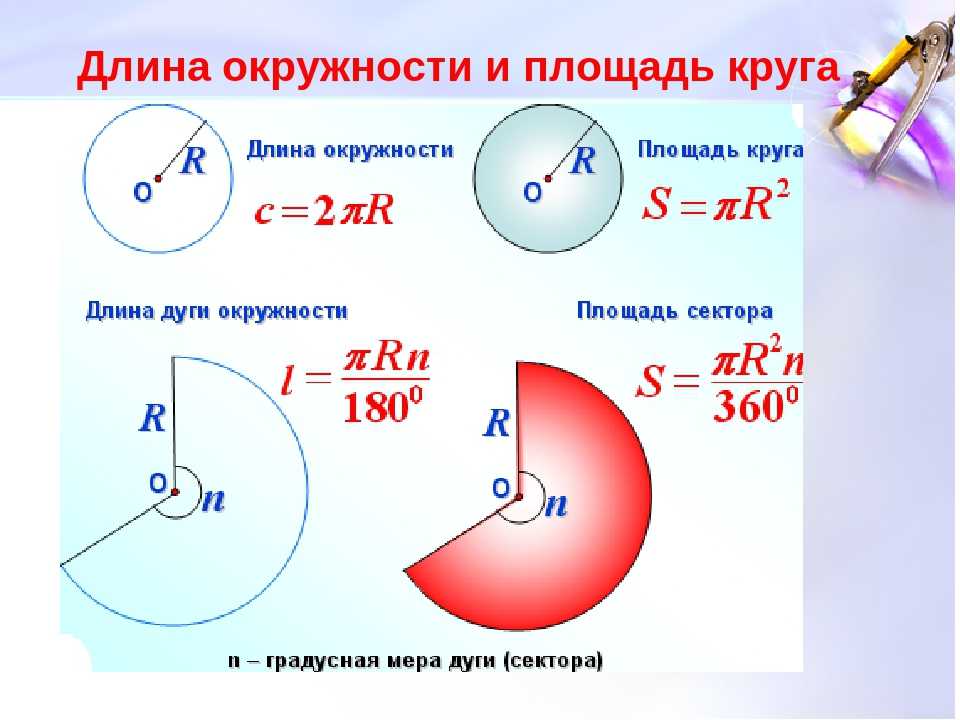
Согласно вопросу, . Таким образом, .
Общее уравнение площади круга.
Когда мы подставляем 13 вместо , наша площадь становится равной .
Сообщить об ошибке
Окружность в стандартной координатной плоскости касается оси X в точке (3,0) и оси Y в точке (0,3). Что такое уравнение окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула уравнения окружности: (x – h) 2 + (y – k) 2 = r 2 , где (h, k) представляет собой координаты центра круг, а r представляет радиус круга.
Если окружность касается оси x в точке (3,0), это означает, что она касается оси x в этой точке. Если окружность касается оси y в точке (0,3), это означает, что она касается оси y в этой точке. Зная эти две точки, мы можем определить центр и радиус окружности. Центр круга должен быть равноудален от любой из точек на окружности. Это означает, что и (0,3), и (3,0) находятся на одинаковом расстоянии от центра. Если мы нарисуем эти точки на координатной плоскости, станет очевидным, что центр окружности должен быть (3,3). Эта точка находится ровно в трех единицах от каждой из заданных точек, что указывает на то, что радиус окружности равен 3,9.0017
Центр круга должен быть равноудален от любой из точек на окружности. Это означает, что и (0,3), и (3,0) находятся на одинаковом расстоянии от центра. Если мы нарисуем эти точки на координатной плоскости, станет очевидным, что центр окружности должен быть (3,3). Эта точка находится ровно в трех единицах от каждой из заданных точек, что указывает на то, что радиус окружности равен 3,9.0017
Когда мы вводим эту информацию в формулу для окружности, мы получаем (x – 3) 2 + (y – 3) 2 = 9.
Сообщить об ошибке
Найти уравнение окружности с координаты центра и радиус .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение окружности
Центр равен или, записанному по-другому . Заменив для и для , наша формула становится
Наконец, формула круга
Сообщить об ошибке
На плоскости xy, какова площадь круга со следующим уравнением:
Верные ответы:
ответ:Объяснение:
Уравнение стандартной формы окружности , где – центр окружности, – радиус. Таким образом, поскольку у нас уже есть стандартное уравнение формы окружности, мы можем игнорировать и , поскольку все, что нам нужно, это .
Таким образом, поскольку у нас уже есть стандартное уравнение формы окружности, мы можем игнорировать и , поскольку все, что нам нужно, это .
Площадь круга равна , что равно .
Сообщить об ошибке
Окружность имеет центр в точке (5,5) и радиус 2. Если формат уравнения для окружности (x-A) 2 + (y-B) 2 =C, что такое С?
Возможные ответы:
Правильный ответ:
4
Пояснение:
Центр окружности находится в точке (5,5) и имеет радиус 2. Следовательно, уравнение (x-5) 2 +(y-5) 2 =2 2 , или (x-5) 2 +(y-5) 2 =4.
Сообщить об ошибке
Если центр окружности находится в точке (0,4), а диаметр окружности равен 6, каково уравнение этой окружности?
Возможные ответы:
x 2 + Y 2 =
x 2 + (Y-4) 2 =
(x-4) 2 + Y =
(x-4) 2 + Y 2 = 9
(х-4) 2 + у 2 = 36
x 2 + (Y-4) 2 = 36
Правильный ответ:
x 2 + (Y-4) 2 =
. Объяснение:
Объяснение:
Формула уравнения окружности:
(x-h) 2 + (y-k) 2 = r 2
Где (h,k) — центр окружности.
h = 0 и k = 4
и диаметр = 6, поэтому радиус = 3
(x-0) 2 + (y-4) 2 = 3 2
x 2 + (y-4) 2 = 9
Сообщить об ошибке 9000 – 4) 2 + (y + 3) 2 = 29. Окружность A сдвинута вверх на пять единиц и влево на шесть единиц. Затем его радиус удваивается. Какое новое уравнение для окружности A?
Возможные ответы:
(x – 10) 2 + (y + 8) 2 = 58
(x + 2) 2 + (y – 2) 2 = 58
(x + 2) 2 + (y – 2) 2 = 116
(x – 10)
0 8 2 ) 2 = 116
(x – 2) 2 + (y + 2) 2 = 58
Правильный ответ:
(9y +
) 2 (x0 + 2) 2 = 116
Пояснение:
Общее уравнение окружности: (x – h) 2 + (y – k) 2 = r 2 , где (h, k) представляет собой положение центра круга, а r представляет собой длину его радиуса.
Окружность A сначала имеет уравнение (x – 4) 2 + (y + 3) 2 = 29. Это означает, что ее центр должен находиться в точке (4, –3), а ее радиус равен √ 29.
Затем нам сообщают, что круг А сдвинут вверх на пять единиц, а затем влево на шесть единиц. Это означает, что координата y центра увеличится на пять, а координата x центра уменьшится на 6. Таким образом, новый центр будет расположен в точке (4 – 6, –3 + 5), или ( –2, 2).
Затем нам сообщают, что радиус круга A увеличился вдвое, что означает, что его новый радиус равен 2√29.
Теперь, когда у нас есть новый центр и радиус окружности A, мы можем написать ее общее уравнение, используя (x – h) 2 + (y – k) 2 = r 2 . 11
(x + 2) 2 + (y – 2) 2 = 116.
Ответ: (x + 2) 2 + (y – 2) 2 = 116.
Сообщить об ошибке
Какое из следующих уравнений описывает все точки (x, y) на координатной плоскости, которые находятся на расстоянии пяти единиц от точки (– 3, 6)?
Возможные ответы:
(x — 3) 2 + (Y + 6) 2 = 25
(x + 3) 2 + (Y — 6) 2 = 25
(x – 3) 2 + (y + 6) 2 = 5
(x – 3) 2 – (y + 6) 2 = 25
y + 6 = 5 — (x — 3) 2
Правильный ответ:
(x + 3) 2 + (y — 6) 2 = 25
Объяснение:
Мы пытаемся найти уравнение для всех точек, находящихся на одинаковом расстоянии (5 единиц) от (–3, 6). Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5.
Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5.
Стандартная форма окружности приведена ниже:
(x – h) 2 + (y – k) 2 = r 2 , где центр расположен в точках (h, k) и r это длина радиуса.
В этом случае h будет равно –3, k будет равно 6, а r будет равно 5.
(x + 3) 2 + (y – 6) 2 = 25
Ответ: (x + 3) 2 + (y – 6) 2 = 25.
Сообщить об ошибке
Уравнение для окружности радиусом 12 с центром на пересечении двух прямых:
y 1 = 4 x и 7
0 + 3 9001у 2 = 5 х + 44?
Возможные ответы:
(x — 22) 2 + (Y — 3) 2 = 12
(x — 3) 2 + (Y — 44) 2 = 144
(х — 41) 2 + (Y — 161) 2 = 144
(x + 41) 2 + (Y + 161) 2 = 144
Ни один из других ответов
Правильный ответ:
(х + 41) 2 + (у + 161) 2 = 144
Объяснение:
Для начала определим точку пересечения этих двух линий, установив равенства между собой:
4 x + 3 = 5 x + 44; 3 = х + 44; –41 = x
Чтобы найти координату y , подставьте в одно из уравнений. Возьмем y 1 :
Возьмем y 1 :
y = 4 * –41 + 3 = –164 + 3 = –161
Таким образом, центр нашей окружности: (–41, –161).
Теперь вспомним, что общая форма круга с центром в ( x 0 , y 0 ) такова:
( x — x00494)
2 + ( Y — Y 0 ) 2 = R 2
Для наших данных это означает, что наше уравнение:
( x + 41 + 41 + 41 + 41 + 41 + 41 + 41 + 41 + 41 + 41 + 41 + 41. 2 + ( Y + 161) 2 = 12 2 или ( x + 41) 2 + ( y + 161) 2 = 144
Отчет о ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
Площадь круга (Формула определения, Практическая реализация и примеры)
Поверхность Площадь круга сильно отличается от всех других форм из-за круглой природы. Однако в повседневной жизни есть много практических приложений, где нужно вычислить площадь круга. Калькулятор площади круга не сложный. Все, что вам нужно знать, это формулу, и вы сможете быстро понять размер любого круглого объекта. Узнайте больше об идентификаторах Trig на нашем веб-сайте.
Однако в повседневной жизни есть много практических приложений, где нужно вычислить площадь круга. Калькулятор площади круга не сложный. Все, что вам нужно знать, это формулу, и вы сможете быстро понять размер любого круглого объекта. Узнайте больше об идентификаторах Trig на нашем веб-сайте.
Какова площадь круга?
Площадь круга — это любое пространство, которое круг занимает на плоской поверхности. Когда мы говорим о площади поверхности круга, мы имеем в виду двухмерные объекты. При нахождении площади круга мы учитываем еще три измерения, включая длину окружности, диаметр и радиус. Все три вычисления также помогают нам уточнить площадь круга.
Вы также можете узнать о
БЛОК ЦИКЛ
ДИАГРАММА ОБОРУДОВАНИЯ
Практические приложения для вычисления площади круга
Только математик может по-настоящему понять практическую важность формул для вычисления площади, радиуса, диаметра или длины окружности. Хотя большинство людей считают, что формулы не имеют практического применения, они являются критически важными факторами во многих повседневных делах.
Хотя большинство людей считают, что формулы не имеют практического применения, они являются критически важными факторами во многих повседневных делах.
Архитекторы используют симметричные свойства круга для проектирования колес обозрения, зданий, спортивных дорожек, кольцевых развязок и т. д. Эти круговые измерения также важны для инженеров при проектировании самолетов, велосипедов, ракет и т. д.
Круг незаменим. Короче говоря, от проектирования простой машины, такой как часы, до разработки сложного ядерного реактора, круговые вычисления играют значительную роль.
Как найти площадь круга или по какой формуле найти площадь круга
Многие студенты задаются вопросом, по какой формуле находят площадь круга? Итак, ответ очень прост: формула для площади круга: A = πr2 . Число, которое используется для уравновешивания уравнения любого круга, представлено как π. Это бесконечное число впервые открыли египтяне при вычислении площади круга.
«R» используется для обозначения радиуса окружности. Это расстояние любой линии от центра круга до края круга. Вы также можете рассчитать радиус, разделив диаметр на 2.
Это расстояние любой линии от центра круга до края круга. Вы также можете рассчитать радиус, разделив диаметр на 2.
Чтобы запомнить формулу площади круга, используйте фразу « кругов в квадрате, но они круглые ».
Методы вычисления площади круга:
Два метода доказывают формулу площади круга, известную как:
- Вычисление площади круга с использованием прямоугольников
- Вычисление площади круга с помощью треугольников
Давайте рассмотрим эти два метода, чтобы лучше понять площадь круга.
Расчет площади круга с использованием прямоугольников
В этом методе мы делим круг на 16 равных секторов. Сектора расположены таким образом, что образуют прямоугольник. Все сектора одинаковы по площади, поэтому длина дуги всех секторов будет одинаковой. Площадь круга будет такой же, как площадь фигуры параллелограмма или прямоугольника.
Взгляните на рисунок выше. На этом изображении вы видите 16 секторов, в том числе 8 зеленых и 8 синих. Секторы, выделенные зеленым цветом, представляют собой половину окружности круга, а другая половина окружности представлена выделенными размытием секторами. При увеличении количества секторов, вырезанных из круга, параллелограмм превратится в прямоугольник. Длина прямоугольника будет равна πr, а ширина равна r.
На этом изображении вы видите 16 секторов, в том числе 8 зеленых и 8 синих. Секторы, выделенные зеленым цветом, представляют собой половину окружности круга, а другая половина окружности представлена выделенными размытием секторами. При увеличении количества секторов, вырезанных из круга, параллелограмм превратится в прямоугольник. Длина прямоугольника будет равна πr, а ширина равна r.
Это означает, что площадь круга равна площади прямоугольника. Итак, у нас
A = πr×r (прямоугольник)
A = πr2 (окружность)
Вычисление площади круга с использованием треугольников
Этот метод требует, чтобы мы создали концентрические круги внутри круга с радиусом r. Когда мы разрезаем круг по прямой линии от центра круга и распространяем концентрические линии круга, он образует треугольник. Это описано на изображении ниже
Теперь высота треугольника равна радиусу окружности, а основание треугольника равно его окружности. Все это указывает на то, что и треугольники, и круги имеют одинаковую площадь. Таким образом, формулы будут выглядеть примерно так:
Таким образом, формулы будут выглядеть примерно так:
A = 1/2×основание×высота
A = 1/2×(2πr)×r
A = πr2
Как найти площадь круга с радиусом?
Если дан радиус круга, то найти площадь довольно просто. Все, что вам нужно сделать, это возвести радиус в квадрат и умножить его на символ Пи. Хотя значение π можно упростить до 3,14 для конкретных расчетов, лучше использовать точную сумму на калькуляторе.
Пример
Например, если радиус круга равен 6 см, то квадрат радиуса будет равен 36 см. Если вы умножите это число на π, вы получите общую площадь поверхности 113,04 см в квадрате. Если у вас нет значения π, вы можете представить площадь как 36 π см в квадрате.
A= πr2
A=113,04
Как найти длину окружности?
Окружность окружности представляет собой периметр эллиптической или круглой формы. Другими словами, это длина дуги или длина границы окружности; если мы выпрямим его или раскроем в отрезке.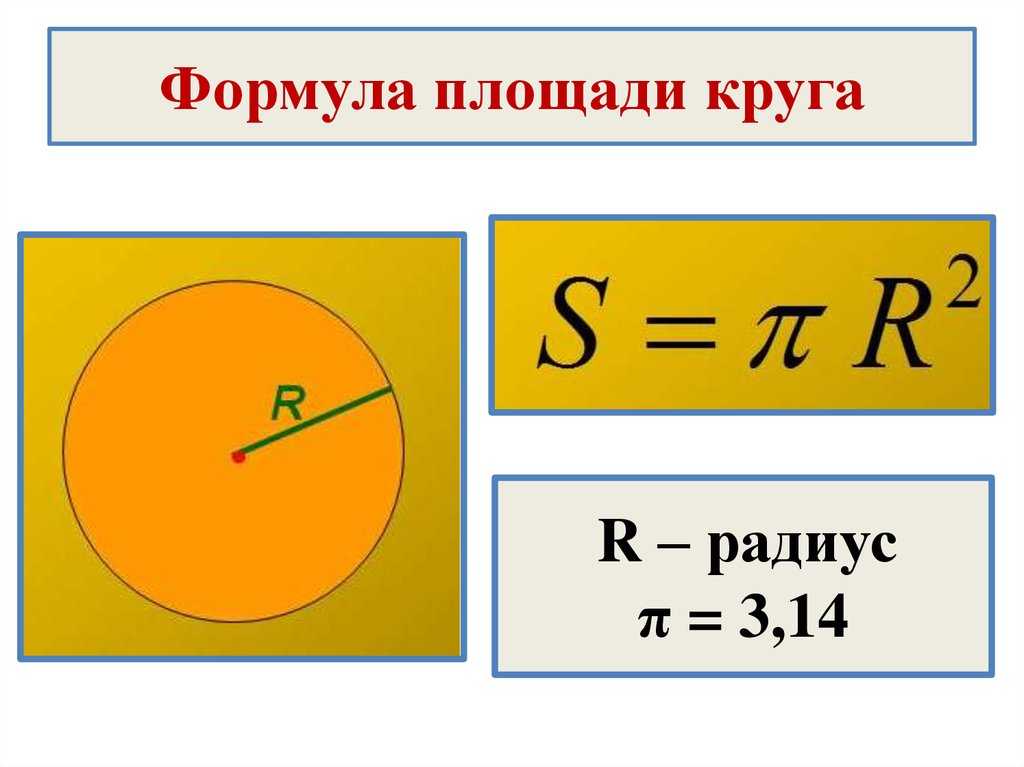
Чтобы лучше понять это, взгляните на рисунок ниже:
Есть кусок веревки и круг. o — центр окружности, r — радиус. Теперь длина окружности или периметра круга будет равна длине веревки, обернутой вокруг круга.
На приведенном выше рисунке вы видите две формулы. C представляет длину окружности в первой формуле, также обозначаемую как P.
Как найти площадь круга с диаметром?
Найти радиус не всегда просто, особенно если у вас нет центра круга. Вместо этого вы можете рассчитать площадь, используя диаметр. Применяется та же формула, что и выше, но сначала вам нужно рассчитать радиус окружности. Просто разделите диаметр на 2, чтобы получить радиус.
Пример
Например, если диаметр 12 см, то радиус будет 6 см. Получив радиус, вы можете использовать ту же формулу, что и выше.
Эта формула применима к любому кругу для получения площади поверхности. Также помните, что значение π будет одинаковым, независимо от размера круга.
Объяснение формулы окружности на примере из «реального мира»
Теперь, когда мы знаем всю формулу окружности и три основных элемента — диаметр, радиус и длину окружности, — давайте применим эти формулы на примере из реальной жизни. Таким образом, мы можем более четко понять формулы и их важность:
Пример: Мистер Смит строит дом для Брэндона. Чтобы построить дом, ему нужно сначала создать основу; ему нужно просверлить несколько отверстий и залить бетоном. Но вы думаете, что он может просверлить отверстия любого размера? Нет! Все ямы должны быть шириной 0,5 м и глубиной 1,5 м. Итак, сколько бетона должен заказать мистер Смит, чтобы заполнить все отверстия?
Вот как он может узнать:
Поскольку отверстия имеют ширину 0,5 м и круглую форму, диаметр круга будет 0,5 м. Таким образом, площадь круга будет рассчитана как:
A=1/4πD2
A= ¼*π*(0,5)2
A=0,785 м2
Теперь глубина отверстий составляет 1,5 м. Таким образом, используя это, мы можем легко рассчитать объем каждой дыры, используя формулу объема площадь x глубина.
Таким образом, используя это, мы можем легко рассчитать объем каждой дыры, используя формулу объема площадь x глубина.
Объем = площадь круга x глубина
Объем = 0,785*1,5
Объем = 1,177 м3
Площадь круга – определение, формула, вывод, примеры, часто задаваемые вопросы окружность в двумерной плоскости. Его легко определить по формуле A = πr
2 , где r — радиус окружности. Площадь круга измеряется в квадратных единицах, например, м 2 , см 2 и т. д.Площадь круга = πr 2 или πd 2 /4, квадратные единицы
, где π = 22/7 или 3.14
Формула площади круга полезна для измерения площадей круглых полей или участков. Также полезно измерить площадь, покрытую круглой мебелью и другими круглыми предметами.
Что такое круг?
Окружность — это набор точек, находящихся на фиксированном расстоянии от определенной точки. Каждая линия, проходящая через окружность, образует линию симметрии отражения. В дополнение к этому, он имеет вращательную симметрию вокруг центра для каждого угла. Некоторыми примерами кругов являются колеса, пицца, круглая площадка и т. д. Расстояние от центра до круга называется радиусом.
В дополнение к этому, он имеет вращательную симметрию вокруг центра для каждого угла. Некоторыми примерами кругов являются колеса, пицца, круглая площадка и т. д. Расстояние от центра до круга называется радиусом.
Какова площадь круга?
Площадь круга определяется как пространство, охватываемое границей круга. Измеряется в квадратных единицах. Площадь круга измеряется с помощью радиуса круга. Он равен π, умноженному на квадрат радиуса. Формулы, используемые для расчета площади круга, приведены ниже.
Формулы площади круга
Формула для нахождения площади круга прямо пропорциональна квадрату его радиуса. Также можно узнать, если задан диаметр или длина окружности. Площадь круга вычисляется путем умножения квадрата радиуса на π. Формулы для нахождения площади круга
- Площадь = πr 2
- Площадь = (π /4) × D 2
- Площадь = C 2 /4π
, где
π — Значение
π — состоит.
3,14 (приблизительно),
r — радиус круга,
d — диаметр круга,
C — длина окружности.
Длина окружности находится по формуле C = 2πr . Подробнее об окружности можно прочитать здесь.
Область круга с использованием RADIUS19. круга составляет 3 единицы. Вычислите его площадь.Площадь = πr 2
, где,
R — это радиус, а π — это константное значение
Решение:
Площадь круга с использованием диаметраМы знаем, что радиус r = 3 единицы
Таким образом, используя приведенные выше формулы:0017
3,14 × 3 × 3 = 28,26
Следовательно, площадь круга равна 28,26 квадратных единиц.
Диаметр круга равен удвоенной длине радиуса круга, т. е.
е.
d диаметр окружности.
Пример: Если длина диаметра круга равна 8 единицам. Вычислите его площадь.
Решение:
Площадь круга с использованием окружностиМы знаем, что диаметр = 8 ед. × 8 × 8 = 28,26
Следовательно, площадь круга равна 50,24 квадрата.
Окружность определяется как длина полной дуги окружности.
Площадь = C 2 /4π
, где
C — длина окружности
Пример: если длина окружности равна 4 единицам. Вычислите его площадь.
Решение:
Мы знаем, что длина окружности = 4 единицы (дано)
поэтому, используя приведенные выше формулы:
4 × 4/(4 × 3,14) = 28,26
Следовательно, площадь круга равна 1,273 квадратных единиц.
Шаги для нахождения площади круга
Ниже приведены различные шаги, необходимые для нахождения площади круга:
Шаг 1: Отметьте радиус круга.
Шаг 2: Подставьте значение радиуса в формулу
Шаг 3: Полученный ответ на шаге 2 — это искомая площадь круга. Измеряется в квадратных единицах.
Если задан диаметр круга, то сначала его преобразуют в радиус, используя соотношение Диаметр = радиус/2
Решенный пример площади круга круглая форма. Его радиус составляет 5 единиц. Что такое площадь?Решение:
Большая веревка имеет круглую форму, что означает, что она похожа на круг, поэтому мы можем использовать формулы окружности для расчета площади большой веревки.
Мы знаем, что радиус r = 5 единиц
Итак, используя приведенные выше формулы:
подставим r = 5.
Поскольку мы знаем, что значение π = 3,14
3,14 × 3 × 3 = 28,26
площадь круга 78,50 кв.
Пример 2: Если длина веревки в форме круга составляет 4 единицы. Вычислите его площадь.
Решение:
Мы знаем, что длина веревки равна окружности. поэтому его диаметр = 4 единицы (данные)
, поэтому, используя приведенные выше формулы:
подставьте d = 4.
Поскольку мы знаем, что значение π = 3,14
(3,14 /4) × 4 × 4 = 28,26
Следовательно, площадь веревки равна 12,56 квадратные единицы.
Пример 3: Если длина окружности равна 8 единицам. Вычислите его площадь.
Решение:
Мы знаем, что длина окружности = 8 единиц (дано)
, поэтому, используя приведенные выше формулы:
замените C = 8.
Поскольку мы знаем, что значение π = 3,14
8 × 8/(4 × 3,14) = 28,26
Следовательно, площадь круга равна 5,09 квадратных единиц.
Пример 4: Найдите длину окружности и площадь круга, если его радиус равен 21 см.
Решение:
Радиус, r = 21 см
Диаметр окружности равен 2πr см.
Теперь, подставив значение, получим
C = 2 × (22/7)× 21
C = 2×22×3
C = 132 см
Таким образом, длина окружности равна 132 см.
Теперь площадь круга равна πr 2 см 2
A = (22/7) × 21 × 21
A = 22 × 63
A = 1386 CM 2
Таким площадь круга 1386 см 2
Часто задаваемые вопросы о площади круга
Вопрос 1: Напишите формулу длины окружности.
Ответ:
Окружность круга – это граница круга. Окружность можно рассчитать, умножив радиус круга на удвоенное число π. т. е. Окружность = 2πr.
Вопрос 2: Как вычислить площадь круга?
Ответ:
Площадь круга можно определить по формулам:
Площадь = π x r 2 , где r радиус круга
Площадь = (π/90) x 3 d 2 , где d — диаметр круга
Площадь = C 2 /4π, где C — длина окружности
Вопрос 3: Что понимается под площадью круга? Также найдите его формулу.

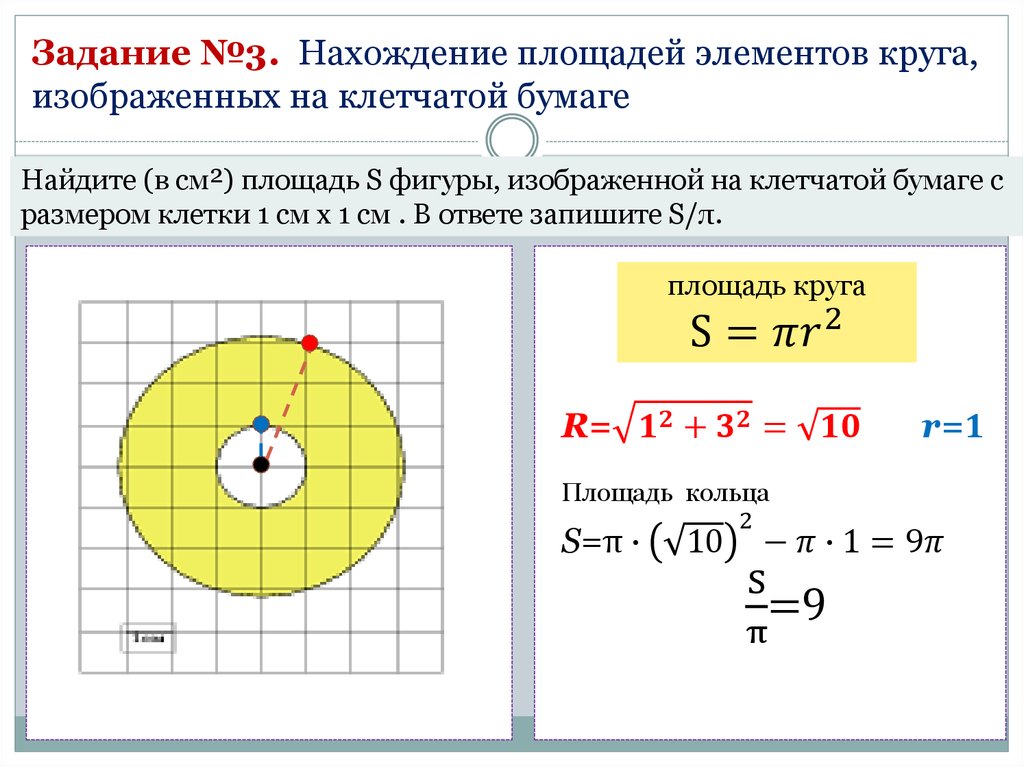
 Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги. 2}
2}
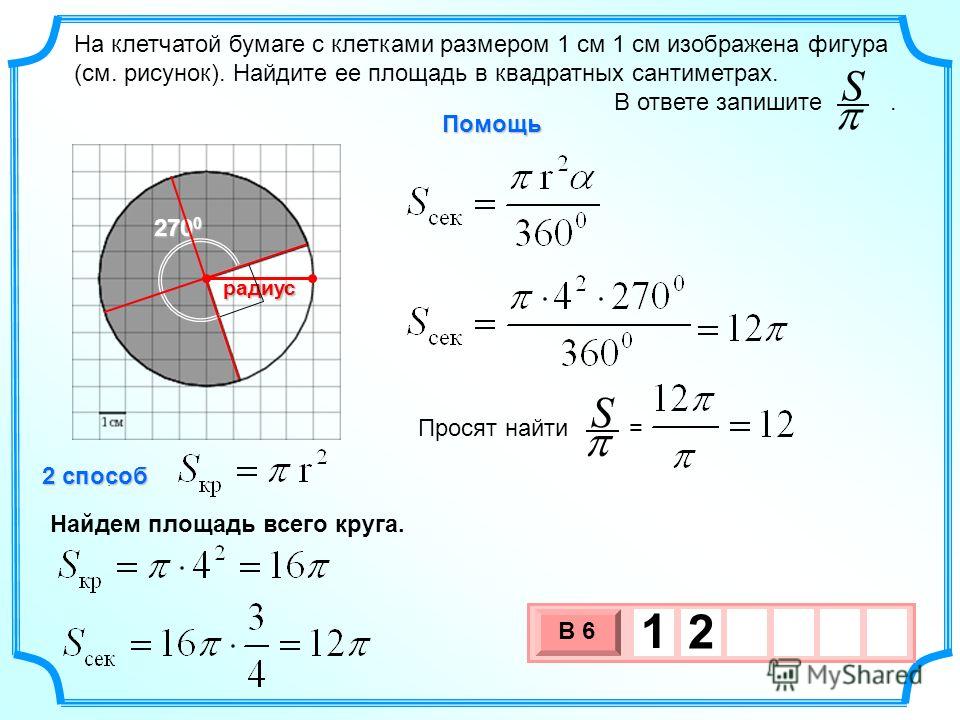 При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ; Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;
Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;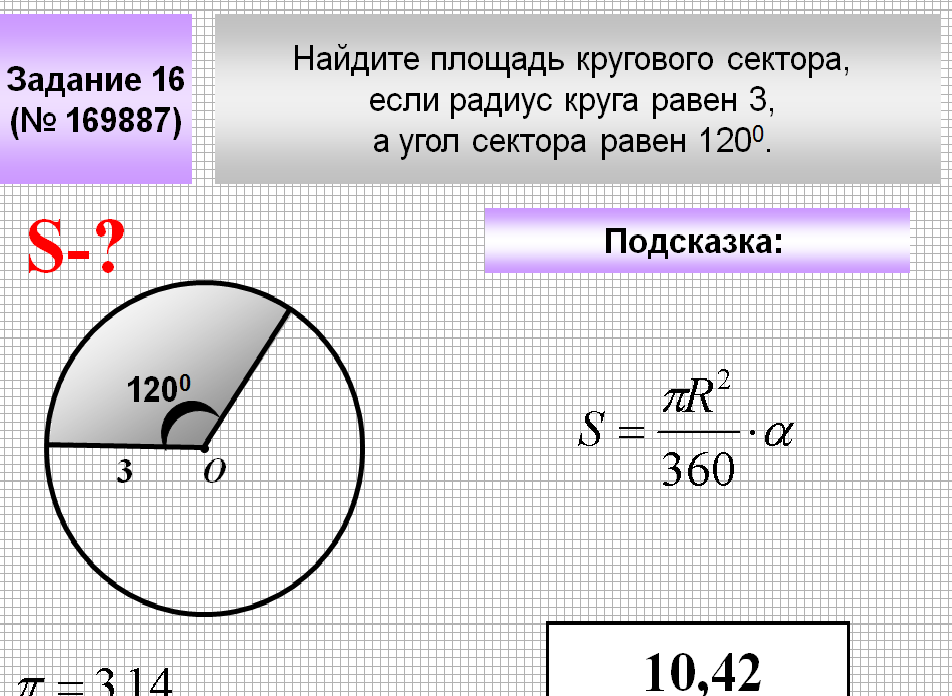 Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;
Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S
круга = 240, то «ошметки» имеют площадь S
= 240: 8 = 30;
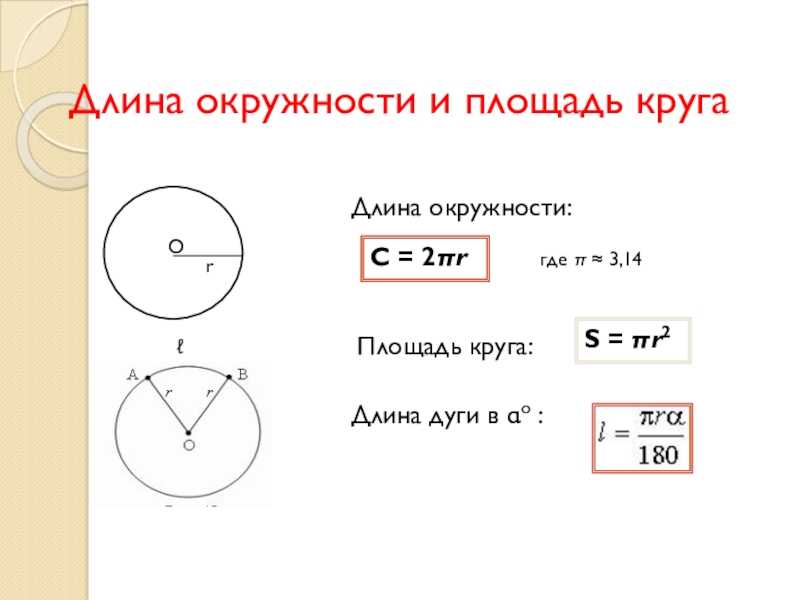 .
.
 Длина минутной стрелки составляет 21 единицу. Найдите расстояние, пройденное кончиком минутной стрелки в 15:30.
Длина минутной стрелки составляет 21 единицу. Найдите расстояние, пройденное кончиком минутной стрелки в 15:30.