НЕПРЕРЫВНАЯ ФУНКЦИЯ • Большая российская энциклопедия
НЕПРЕРЫ́ВНАЯ ФУ́НКЦИЯ, функция, значения которой мало изменяются при малых изменениях аргумента. Точнее, функция $f(x)$, определённая на интервале $(a, b)$, называется непрерывной в точке $x_0∈ (a, b)$, если для любого $ε>0$ существует $δ>0$ такое, что $|f(x)-f(x_0)|<ε$ для всех $x$ таких, что $|x-x_0|<δ$. В этом определении число $δ$, зависящее от $ε$, может зависеть и от $x_0$. Это определение равносильно следующему: для любой последовательности $x_1, x_2,\dots$ такой, что $x_n→x_0$ при $n→∞$, последовательность $f(x_1), f(x_2),\dots$ такова, что $f(x_n)→f(x_0)$ при $n→∞$. Иначе говоря, $\lim_{n\rightarrow\infty}f(x_n)=f(\lim_{n\rightarrow \infty}x_n)$ для всех последовательностей, сходящихся к $x_0$.
Если условие, указанное в определении Н. ф., выполняется лишь при $x⩾x_0$ или лишь при $x⩽x_0$, то функция $f(x)$ называется соответственно непрерывной справа или слева в точке $x_0$. {–1}(y)$ существует, строго возрастает и непрерывна на $[f(a), f(b)]$; аналогичное утверждение справедливо для строго убывающих функций.
{–1}(y)$ существует, строго возрастает и непрерывна на $[f(a), f(b)]$; аналогичное утверждение справедливо для строго убывающих функций.
Н. ф. обладают многими важными свойствами, которыми объясняется значение этих функций в математике и её приложениях. Функция, непрерывная на отрезке, ограничена на нём и достигает на нём наибольшего и наименьшего значений, кроме того, она принимает на этом отрезке все промежуточные значения, лежащие между её наименьшим и наибольшим значениями. Для любой функции, непрерывной на отрезке $[a, b]$, существует многочлен, значения которого отличаются на этом отрезке от значений функции менее, чем на произвольное сколь угодно малое, наперёд заданное число (теорема Вейерштрасса о приближении Н. ф. многочленами). Функции, непрерывные на отрезке, обладают свойством равномерной непрерывности.
Рис. 3.
3.
Рис. 2.
Любая функция, непрерывная на некотором отрезке, интегрируема на нём. Однако не всякая Н. ф. имеет производную. Геометрически это означает, что график Н. ф. не обязательно обладает касательной в каждой точке; это может быть связано с тем, что график имеет угловую точку (рис. 2, функция $y= |x|$), или с тем, что он совершает в окрестности к.-л. точки бесконечно много колебаний между двумя пересекающимися прямыми (рис. 3, функция $y=x\sin{|1/x|}$ при $x≠0$ и $y=0$ при $x=0$). Существуют Н. ф., не имеющие производной ни в одной точке, первый пример такого рода был предложен Б. Больцано в 1830.
Функция $f(x, y, z,\dots)$ нескольких переменных, определённая в некоторой окрестности точки $(x_0, y_0, z_0,\dots)$, называется непрерывной (по совокупности переменных $x, y, z, \dots$) в этой точке, если для любого $ε>0$ можно указать такое $δ> 0$, что при одновременном выполнении неравенств$$|x-x_0|<δ,\: |y-y_0|<δ, \:|z-z_0|<δ, \:\dots$$выполняется также и неравенство$$|f(x, y, z, \dots)-f(x_0, y_0, z_0, \dots)|<ε.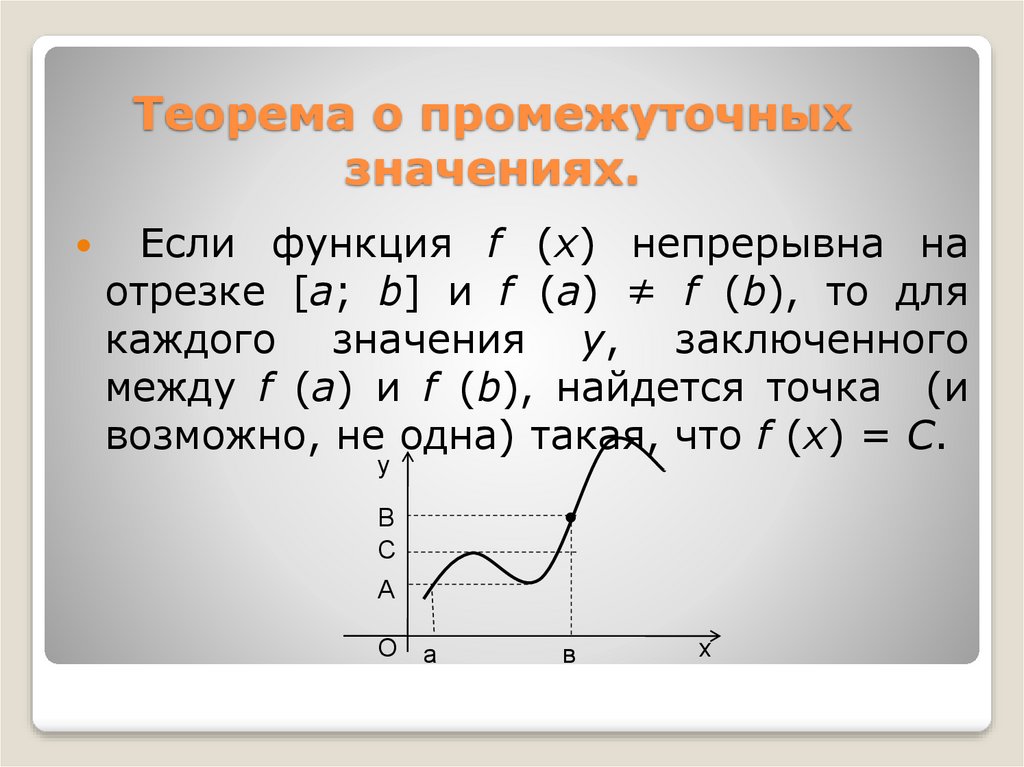 2}\bigg|<ε$. На Н. ф. нескольких переменных распространяются все осн. теоремы, относящиеся к Н. ф. одного переменного.
2}\bigg|<ε$. На Н. ф. нескольких переменных распространяются все осн. теоремы, относящиеся к Н. ф. одного переменного.
Непрерывная функция | это… Что такое Непрерывная функция?
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Содержание
|
Определения
ε-δ определение
Пусть и .
Функция непрерывна в точке , если для любого существует такое, что для любого
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции .

- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).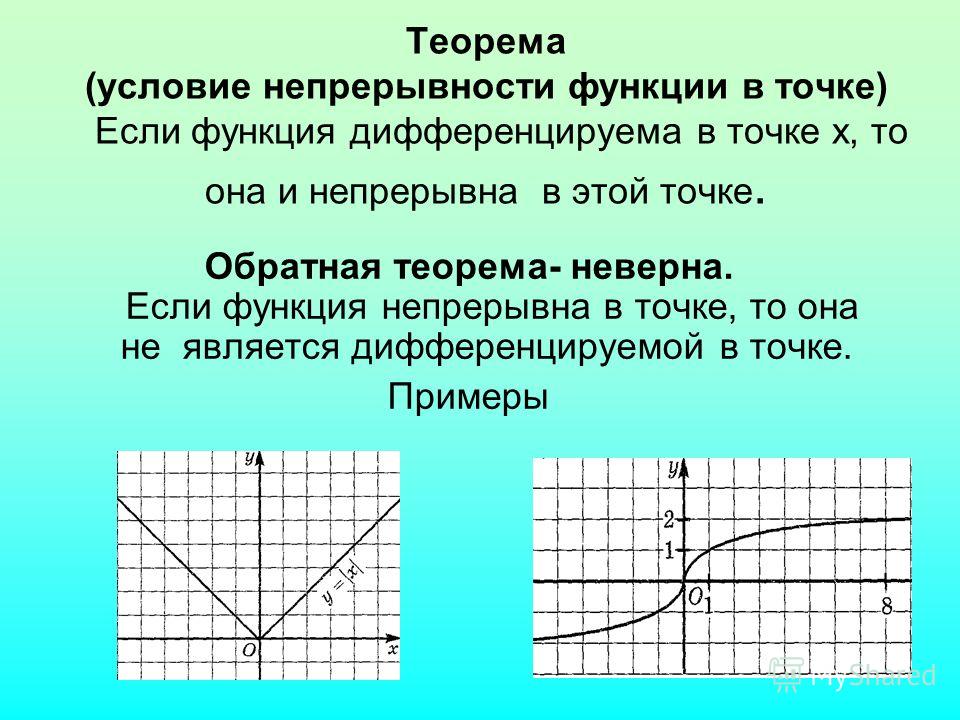
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Свойства
Локальные
- Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.

- Если функция непрерывна в точке и (или ), то (или ) для всех , достаточно близких к .
- Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .
- Если функции и непрерывны в точке и при этом , то функция тоже непрерывна в точке .
- Если функция непрерывна в точке и функция непрерывна в точке , то их композиция непрерывна в точке .
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .
- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .

- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
- ,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Основная статья: Функция Дирихле
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
называется функцией Римана.
Эта функция является непрерывной всюду в множестве иррациональных чисел (), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Основная статья: Равномерная непрерывность
Функция называется равномерно непрерывной на , если для любого существует такое, для любых двух точек и таких, что выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция называется полунепрерывной снизу в точке , если для любого существует такая окрестность , что для всякого ;
- функция называется полунепрерывной сверху в точке , если для любого существует такая окрестность , что для всякого .

Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию , непрерывную в точке , и уменьшить её значение (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ;
- если взять функцию , непрерывную в точке , и увеличить её значение (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке .
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если , то будем считать такую функцию полунепрерывной снизу в точке ;
- если , то будем считать такую функцию полунепрерывной сверху в точке .
Односторонняя непрерывность
Функция называется односторонне непрерывной слева (справа) в каждой точке её области определения, если для одностороннего предела выполняется равенство: ()
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Непрерывная функция | это… Что такое Непрерывная функция?
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Содержание
|
Определения
ε-δ определение
Пусть и .
Функция непрерывна в точке , если для любого существует такое, что для любого
Функция непрерывна на множестве
, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции .
- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Свойства
Локальные
- Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
- Если функция непрерывна в точке и (или ), то (или ) для всех , достаточно близких к .
- Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .
- Если функции и непрерывны в точке и при этом , то функция тоже непрерывна в точке .
- Если функция непрерывна в точке и функция непрерывна в точке , то их композиция непрерывна в точке .
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .

- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
- ,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Основная статья: Функция Дирихле
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
называется функцией Римана.
Эта функция является непрерывной всюду в множестве иррациональных чисел (), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Основная статья: Равномерная непрерывность
Функция называется равномерно непрерывной на , если для любого существует такое, для любых двух точек и таких, что выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция называется полунепрерывной снизу в точке , если для любого существует такая окрестность , что для всякого ;
- функция называется полунепрерывной сверху в точке , если для любого существует такая окрестность , что для всякого .

Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию , непрерывную в точке , и уменьшить её значение (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ;
- если взять функцию , непрерывную в точке , и увеличить её значение (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке .
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если , то будем считать такую функцию полунепрерывной снизу в точке ;
- если , то будем считать такую функцию полунепрерывной сверху в точке .
Односторонняя непрерывность
Функция называется односторонне непрерывной слева (справа) в каждой точке её области определения, если для одностороннего предела выполняется равенство: ()
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Непрерывная функция | это… Что такое Непрерывная функция?
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Содержание
|
Определения
ε-δ определение
Пусть и .
Функция непрерывна в точке , если для любого существует такое, что для любого
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции .
- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .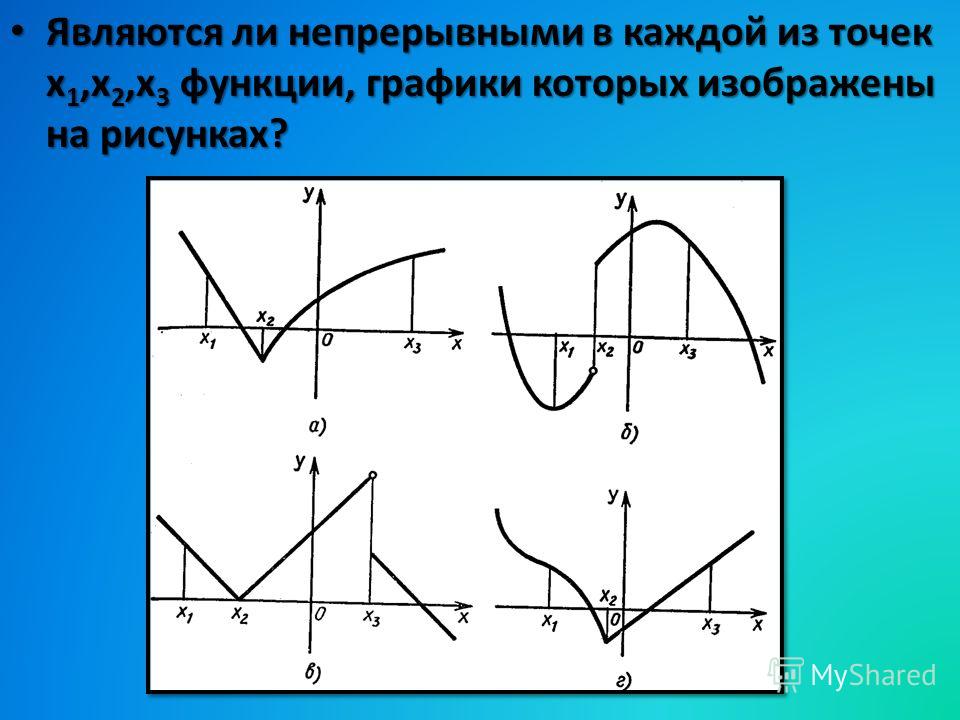
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Свойства
Локальные
- Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
- Если функция непрерывна в точке и (или ), то (или ) для всех , достаточно близких к .
- Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .
- Если функции и непрерывны в точке и при этом , то функция тоже непрерывна в точке .
- Если функция непрерывна в точке и функция непрерывна в точке , то их композиция непрерывна в точке .
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .

- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
- ,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Основная статья: Функция Дирихле
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
называется функцией Римана.
Эта функция является непрерывной всюду в множестве иррациональных чисел (), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Основная статья: Равномерная непрерывность
Функция называется равномерно непрерывной на , если для любого существует такое, для любых двух точек и таких, что выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция называется полунепрерывной снизу в точке , если для любого существует такая окрестность , что для всякого ;
- функция называется полунепрерывной сверху в точке , если для любого существует такая окрестность , что для всякого .

Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию , непрерывную в точке , и уменьшить её значение (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ;
- если взять функцию , непрерывную в точке , и увеличить её значение (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке .
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если , то будем считать такую функцию полунепрерывной снизу в точке ;
- если , то будем считать такую функцию полунепрерывной сверху в точке .
Односторонняя непрерывность
Функция называется односторонне непрерывной слева (справа) в каждой точке её области определения, если для одностороннего предела выполняется равенство: ()
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Непрерывная функция | это… Что такое Непрерывная функция?
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.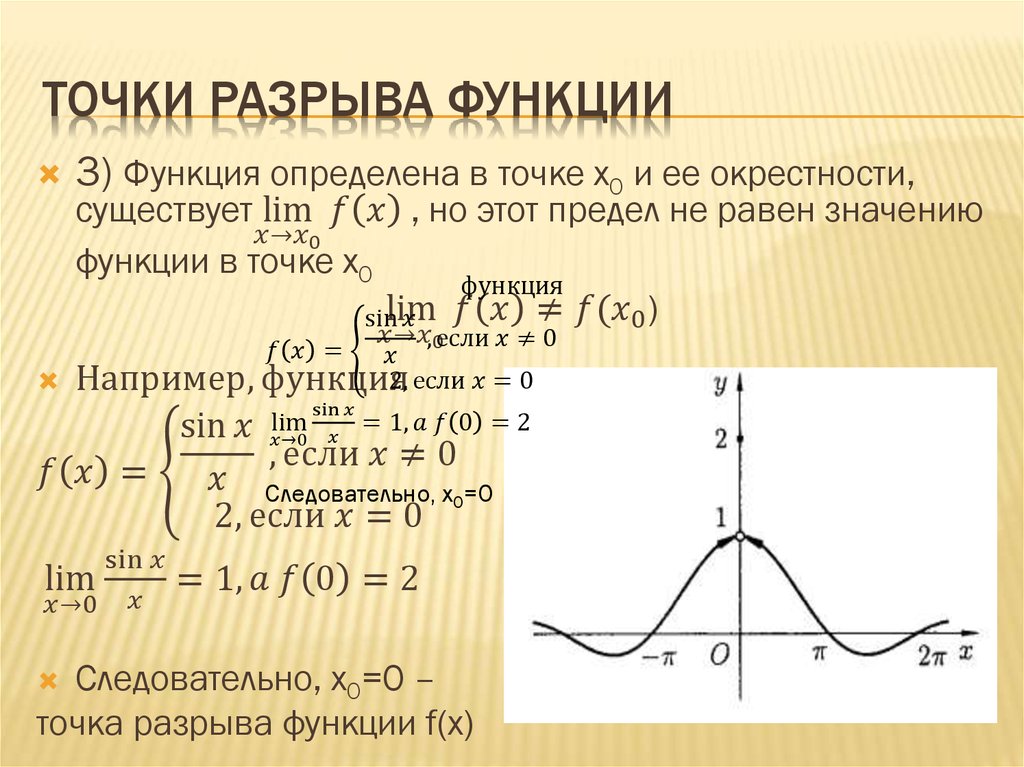
Содержание
|
Определения
ε-δ определение
Пусть и .
Функция непрерывна в точке , если для любого существует такое, что для любого
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции .
- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Свойства
Локальные
- Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
- Если функция непрерывна в точке и (или ), то (или ) для всех , достаточно близких к .
- Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .
- Если функции и непрерывны в точке и при этом , то функция тоже непрерывна в точке .
- Если функция непрерывна в точке и функция непрерывна в точке , то их композиция непрерывна в точке .
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .

- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
- ,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Основная статья: Функция Дирихле
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
называется функцией Римана.
Эта функция является непрерывной всюду в множестве иррациональных чисел (), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Основная статья: Равномерная непрерывность
Функция называется равномерно непрерывной на , если для любого существует такое, для любых двух точек и таких, что выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция называется полунепрерывной снизу в точке , если для любого существует такая окрестность , что для всякого ;
- функция называется полунепрерывной сверху в точке , если для любого существует такая окрестность , что для всякого .

Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию , непрерывную в точке , и уменьшить её значение (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ;
- если взять функцию , непрерывную в точке , и увеличить её значение (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке .
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если , то будем считать такую функцию полунепрерывной снизу в точке ;
- если , то будем считать такую функцию полунепрерывной сверху в точке .
Односторонняя непрерывность
Функция называется односторонне непрерывной слева (справа) в каждой точке её области определения, если для одностороннего предела выполняется равенство: ()
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Непрерывная функция | это… Что такое Непрерывная функция?
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Содержание
|
Определения
ε-δ определение
Пусть и .
Функция непрерывна в точке , если для любого существует такое, что для любого
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции .
- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Свойства
Локальные
- Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.
- Если функция непрерывна в точке и (или ), то (или ) для всех , достаточно близких к .
- Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .
- Если функции и непрерывны в точке и при этом , то функция тоже непрерывна в точке .
- Если функция непрерывна в точке и функция непрерывна в точке , то их композиция непрерывна в точке .
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .

- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область ее значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
- ,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Основная статья: Функция Дирихле
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
называется функцией Римана.
Эта функция является непрерывной всюду в множестве иррациональных чисел (), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Основная статья: Равномерная непрерывность
Функция называется равномерно непрерывной на , если для любого существует такое, для любых двух точек и таких, что выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция называется полунепрерывной снизу в точке , если для любого существует такая окрестность , что для всякого ;
- функция называется полунепрерывной сверху в точке , если для любого существует такая окрестность , что для всякого .

Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию , непрерывную в точке , и уменьшить её значение (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке ;
- если взять функцию , непрерывную в точке , и увеличить её значение (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке .
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если , то будем считать такую функцию полунепрерывной снизу в точке ;
- если , то будем считать такую функцию полунепрерывной сверху в точке .
Односторонняя непрерывность
Функция называется односторонне непрерывной слева (справа) в каждой точке её области определения, если для одностороннего предела выполняется равенство: ()
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Исчисление I — Непрерывность
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-9: Непрерывность
В последних нескольких разделах мы использовали термин «достаточно хороший» для определения тех функций, пределы которых мы могли бы оценить, просто оценивая функцию в рассматриваемой точке. Пришло время формально определить, что мы подразумеваем под «достаточно хорошим».
Определение
Функция \(f\left( x \right)\) называется непрерывной в точке \(x = a\), если
\[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\]
Функция называется непрерывной на отрезке \(\left[ {a,b} \right]\), если она непрерывна в каждой точке отрезка.
Обратите внимание, что это определение также неявно предполагает, что как \(f\left( a \right)\), так и \(\mathop {\lim }\limits_{x \to a} f\left( x \right)\ ) существует. Если любой из них не существует, функция не будет непрерывной в \(х = а\). 9+ }} f\left( x \right) = f\left( a \right)\]
Это точно такой же факт, который мы впервые записали, когда начали рассматривать пределы, за исключением того, что мы заменили фразу «достаточно приятно» на «непрерывно».
Приятно, наконец, узнать, что мы подразумеваем под «достаточно хорошим», однако это определение на самом деле не говорит нам, что именно означает, что функция должна быть непрерывной. Давайте рассмотрим пример, который поможет нам понять, что означает непрерывность функции.
Пример 1. Учитывая график \(f\left( x \right)\), показанный ниже, определите, является ли \(f\left( x \right)\) непрерывным в \(x = — 2\), \( х = 0\) и \(х = 3\).
Показать решение
Чтобы ответить на вопрос для каждой точки, нам нужно получить как предел в этой точке, так и значение функции в этой точке. Если они равны, то функция в этой точке непрерывна, а если не равны, то функция в этой точке непрерывна.
Если они равны, то функция в этой точке непрерывна, а если не равны, то функция в этой точке непрерывна.
Первый \(x = — 2\).
\[f\left( {- 2} \right) = 2\hspace{0.5in}\mathop {\lim }\limits_{x \to — 2} f\left(x \right)\,\,\, {\mbox{не существует}}\]
Значение функции и предел не совпадают, поэтому в этой точке функция не является непрерывной. Такой разрыв в графе называется разрывом скачков . Разрывы скачков возникают там, где на графике есть разрыв, как на этом графике, и значения функции по обе стороны от разрыва конечны ( т.е. функция не уходит в бесконечность).
Теперь \(х = 0\).
\ [f \ влево ( 0 \ вправо) = 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 0} f \ влево ( x \ вправо) = 1 \]
В этой точке функция непрерывна, так как функция и предел имеют одно и то же значение.
Наконец \(x = 3\).
\ [f \ влево ( 3 \ вправо) = — 1 \ hspace {0,5 дюйма} \ mathop {\ lim } \ limit_ {x \ to 3} f \ влево ( x \ вправо) = 0 \]
В этот момент функция не является непрерывной. Этот вид разрыва называется устранимым разрывом . Устранимые разрывы — это те, где в графе есть дыра, как в данном случае.
Из этого примера мы можем быстро получить «рабочее» определение непрерывности. Функция непрерывна на отрезке, если мы можем нарисовать график от начала до конца, ни разу не взяв в руки карандаш. Граф в последнем примере имеет только два разрыва, так как есть только два места, где мы должны были бы взяться за карандаш, рисуя его.
Другими словами, функция непрерывна, если на ее графике нет дыр или разрывов.
Для многих функций легко определить, где они не будут непрерывными. Функции не будут непрерывными там, где есть такие вещи, как деление на ноль или логарифмирование нуля. Давайте быстро рассмотрим пример определения того, где функция не является непрерывной. 2} — 2t — 15}}\]
92} — 2t — 15 = \left( {t — 5} \right)\left( {t + 3} \right) = 0\]
2} — 2t — 15}}\]
92} — 2t — 15 = \left( {t — 5} \right)\left( {t + 3} \right) = 0\]
Значит, функция не будет непрерывной в точках \(t=-3\) и \(t=5\).
Приятным следствием преемственности является следующий факт.
Факт 2
Если \(f\left( x \right)\) непрерывно в \(x = b\) и \(\mathop {\lim }\limits_{x \to a} g\left( х \справа) = б\) тогда
\[\ mathop {\lim }\limits_{x \to a} f\left({g\left(x\right)} \right) = f\left( {\mathop {\lim }\limits_{x \ к } г\влево( х \вправо)} \вправо)\] 90} = 1\]
Другим очень хорошим следствием непрерывности является теорема о промежуточном значении.
Теорема о промежуточном значении
Предположим, что \(f\left( x \right)\) непрерывно на \(\left[ {a,b} \right]\) и пусть \(M\) будет любым числом между \(f\left( a \right)\) и \(f\left( b \right)\). Тогда существует число \(c\) такое, что
- \(a < c < b\)
- \(е\влево(с\вправо) = М\)
Теорема о промежуточном значении на самом деле говорит о том, что непрерывная функция будет принимать все значения между \(f\left( a \right)\) и \(f\left( b \right)\). Ниже приведен график непрерывной функции, иллюстрирующий теорему о промежуточном значении.
Ниже приведен график непрерывной функции, иллюстрирующий теорему о промежуточном значении.
Как видно из этого изображения, если мы выберем любое значение \(M\), то есть между значением \(f\left( a \right)\) и значением \(f\left( b \right)\) и проведите из этой точки прямую линию, которая будет пересекаться с графиком хотя бы в одной точке. Другими словами, где-то между \(a\) и \(b\) функция примет значение \(M\). Кроме того, как показано на рисунке, функция может принимать значение более чем в одном месте.
Также важно отметить, что теорема о промежуточном значении говорит только о том, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\). Не сказано, каким именно будет это значение. Это только говорит о том, что он существует.
Итак, теорема о промежуточном значении говорит нам, что функция будет принимать значение \(M\) где-то между \(a\) и \(b\), но она не говорит нам, где она примет значение или говорит ли он нам, сколько раз он будет принимать значение. 2} — 10x + 5\) имеет корень где-то в интервале \(\left[ { — 1, 2} \справа]\).
2} — 10x + 5\) имеет корень где-то в интервале \(\left[ { — 1, 2} \справа]\).
Показать решение
На самом деле мы спрашиваем здесь, примет ли функция значение
или нет. \[р\влево( х \вправо) = 0\]
где-то между -1 и 2. Другими словами, мы хотим показать, что существует число \(c\) такое, что \(- 1 < c < 2\) и \(p\left( c \right) = 0\). Однако если мы определим \(M = 0\) и признаем, что \(a = -1\) и \(b = 2\), мы увидим, что эти два условия на \(c\) являются в точности выводами промежуточного Теорема о ценности.
Итак, эта задача построена на использовании теоремы о промежуточном значении, и на самом деле все, что нам нужно сделать, это показать, что функция непрерывна и что \(M = 0\) находится между \(p\left( { — 1} \right)\) и \(p\left( 2 \right)\) ( т.е. \(p\left( { — 1} \right) < 0 < p\left( 2 \right)\ ) или \(p\left( 2 \right) < 0 < p\left( { - 1} \right)\) и мы закончим.
Для этого все, что нам нужно сделать, это вычислить,
\[p\left( { — 1} \right) = 8\hspace{0.5in}\hspace{0.25in}p\left( 2 \right) = — 19\]
Итак, имеем
\[ — 19 = p\влево( 2 \вправо) < 0 < p\влево( { - 1} \вправо) = 8\]
Следовательно, \(M = 0\) находится между \(p\left( { — 1} \right)\) и \(p\left( 2 \right)\), а поскольку \(p\left( x \ right)\) — полином, он непрерывен везде и, в частности, непрерывен на отрезке \([-1,2]\). Таким образом, по теореме о промежуточном значении должно существовать число \(-1 \[р\влево( с \вправо) = 0\] Следовательно, у многочлена есть корень между -1 и 2. Для полноты картины вот график, показывающий корень, существование которого мы только что доказали. Обратите внимание, что мы использовали компьютерную программу, чтобы фактически найти корень, и что теорема о промежуточном значении не сказала нам, что это за значение. Давайте рассмотрим еще один пример теоремы о промежуточном значении.
- Соответствует ли \(f\left( x \right) = 10\)?
- Соответствует ли \(f\left( x \right) = — 10\)?
Показать все решения Скрыть все решения
Показать обсуждение
Итак, как и в предыдущем примере, нас просят определить, если возможно, принимает ли функция одно из двух значений выше в интервале [0,5]. Во-первых, давайте заметим, что это непрерывная функция, и поэтому мы знаем, что можем использовать теорему о промежуточном значении для решения этой проблемы.
Теперь для каждой части мы допустим, что \(M\) будет заданным значением для этой части, а затем нам нужно будет показать, что \(M\) находится между \(f\left( 0 \right)\) и \(f\left( 5 \right)\). Если это так, то мы можем использовать теорему о промежуточном значении, чтобы доказать, что функция будет принимать заданное значение.
Итак, поскольку нам понадобятся две оценки функций для каждой части, давайте приведем их здесь,
\[f\влево( 0 \вправо) = 2,8224\hspace{0,5 дюйма}\hspace{0,25 дюйма}f\влево( 5 \вправо) = 19.7436\]
Теперь давайте рассмотрим каждую часть.
a Соответствует ли \(f\left( x \right) = 10\)? Показать решение
Хорошо, в этом случае мы определим \(M = 10\) и увидим, что
\[f\влево( 0 \вправо) = 2,8224 < 10 < 19,7436 = f\влево( 5 \вправо)\]
Итак, по теореме о промежуточном значении должно быть число \(0 \le c \le 5\) такое, что
\[е\влево(с\вправо) = 10\]
b Соответствует ли \(f\left( x \right) = — 10\)? Показать решение
В этой части мы определим \(M = — 10\). Теперь у нас есть проблема. В этой части \(M\) не живет между \(f\left( 0 \right)\) и \(f\left( 5 \right)\).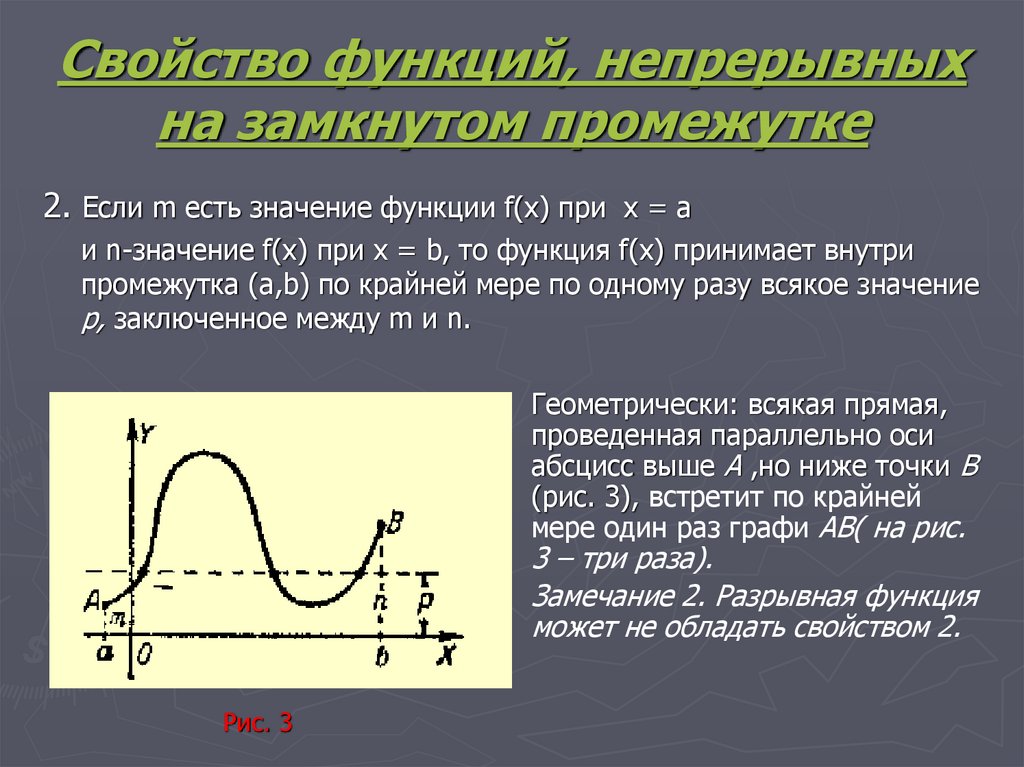 2}) }}{2}} \right)\) в интервале [0,5].
2}) }}{2}} \right)\) в интервале [0,5].
Из этого графика видно, что не только \(f\left( x \right) = — 10\) в [0,5], но и всего 4 раза! Также обратите внимание, что, как мы проверили в первой части предыдущего примера, \(f\left( x \right) = 10\) в [0,5], и на самом деле это происходит всего 3 раза.
Итак, помните, что теорема о промежуточном значении проверяет только то, что функция принимает заданное значение. Он никогда не будет исключать получение значения функцией. Кроме того, если мы можем использовать теорему о промежуточном значении для проверки того, что функция будет принимать значение, она никогда не скажет нам, сколько раз функция будет принимать значение, она только говорит нам, что она действительно принимает значение.
Нежное введение в непрерывные функции
By Mehreen Saeed on 14 июля 2021 in Calculus
Многие области исчисления требуют понимания непрерывных функций. Характеристики непрерывных функций и изучение точек разрыва представляют большой интерес для математического сообщества. Благодаря своим важным свойствам непрерывные функции имеют практическое применение в алгоритмах машинного обучения и методах оптимизации.
Благодаря своим важным свойствам непрерывные функции имеют практическое применение в алгоритмах машинного обучения и методах оптимизации.
В этом руководстве вы узнаете, что такое непрерывные функции, их свойства и две важные теоремы при изучении алгоритмов оптимизации, т. е. теорему о промежуточном значении и теорему об экстремальном значении.
После завершения этого урока вы будете знать:
- Определение непрерывных функций
- Теорема о промежуточном значении
- Теорема об экстремальных значениях
Начнем.
Нежное введение в непрерывные функции Фото Джини Кхала, некоторые права защищены.
Обзор учебника
Этот туториал разделен на 2 части; они:
- Определение непрерывных функций
- Неформальное определение
- Формальное определение
- Теоремы
- Теорема о промежуточном значении
- Теорема об экстремальных значениях
Предпосылки
Этот учебник требует понимания концепции пределов. Чтобы освежить вашу память, вы можете взглянуть на пределы и непрерывность, где также кратко определены непрерывные функции. В этом уроке мы углубимся в детали.
Чтобы освежить вашу память, вы можете взглянуть на пределы и непрерывность, где также кратко определены непрерывные функции. В этом уроке мы углубимся в детали.
Мы также будем использовать интервалы. Таким образом, квадратные скобки означают закрытые интервалы (включая граничные точки), а круглые скобки означают открытые интервалы (не включая граничные точки), например,
.- [a,b] означает a<=x<=b
- (a,b) означает a
- [a,b) означает a<=x
- [a,b) означает a<=x
Из вышеизложенного видно, что интервал может быть открытым с одной стороны и закрытым с другой.
И наконец, мы будем обсуждать только реальные функции, определенные над действительными числами. Мы не будем обсуждать комплексные числа или функции, определенные на комплексной плоскости.
Предположим, у нас есть функция f(x). Мы можем легко проверить, непрерывна ли она между двумя точками a и b, если мы можем построить график функции f(x), не поднимая руки. В качестве примера рассмотрим прямую линию, заданную как:
.
f(x)=2x+1
Мы можем провести прямую линию между [0,1], не поднимая руки. На самом деле мы можем провести эту линию между любыми двумя значениями x, и нам не придется поднимать руку (см. рисунок ниже). Следовательно, эта функция непрерывна во всей области действительных чисел. Теперь давайте посмотрим, что произойдет, когда мы построим график функции ceil:
Непрерывная функция (слева) и не непрерывная функция (справа)
Функция ceil имеет значение 1 на интервале (0,1), например, ceil(0,5)= 1, ceil(0,7) = 1 и т. д. В результате функция непрерывна в области определения (0,1]. Если мы настроим интервал на (0,2], ceil(x) подскочит до 2, как только x>1. Чтобы построить ceil(x) для области (0,2], мы должны теперь Поднимите руку и снова начните рисовать при x = 2. В результате функция ceil не является непрерывной функцией.
Если функция непрерывна во всей области действительных чисел, то она является непрерывной функцией в целом, в противном случае она не является непрерывной в целом. Для более позднего типа функций мы можем проверить, на каком интервале они непрерывны.
Для более позднего типа функций мы можем проверить, на каком интервале они непрерывны.
Формальное определение
Функция f(x) непрерывна в точке a, если значение функции приближается к f(a), когда x приближается к a. Следовательно, чтобы проверить непрерывность функции в точке x=a, проверьте следующее:
- f(a) должен существовать
- f(x) имеет предел, когда x приближается к
- Предел f(x) при x->a равен f(a)
Если все вышеперечисленное верно, то функция непрерывна в точке a.
Примеры
Некоторые примеры перечислены ниже, а также показаны на рисунке:
- f(x) = 1/x не является непрерывным, поскольку оно не определено при x=0. Однако функция непрерывна для области x>0.
- Все полиномиальные функции являются непрерывными функциями.
- Тригонометрические функции sin(x) и cos(x) непрерывны и колеблются между значениями -1 и 1.
- Тригонометрическая функция tan(x) не является непрерывной, поскольку она не определена при x=𝜋/2, x=-𝜋/2 и т.
 д.
д. - sqrt(x) не является непрерывным, так как не определено для x<0.
- |х| непрерывна всюду.
Примеры непрерывных функций и функций с разрывами
Связь непрерывности с функциональными производными
Из определения непрерывности в терминах пределов у нас есть альтернативное определение. f(x) непрерывна в точке x, если:
f(x+h)-f(x)→ 0, когда (h→0)
Давайте посмотрим на определение производной:
f'(x) = lim(h→0) (f(x+h)-f(x))/ч
Следовательно, если f'(x) существует в точке a, то функция непрерывна в точке a. Обратное не всегда верно. Функция может быть непрерывной в точке a, но f'(a) может не существовать. Например, на приведенном выше графике |x| непрерывна всюду. Мы можем нарисовать ее, не поднимая руки, однако при x=0 ее производной не существует из-за крутого поворота кривой.
Теорема о промежуточном значении
Теорема о промежуточном значении утверждает, что:
Если:
- функция f(x) непрерывна на [a,b]
- и f(a) <= K <= f(b)
затем:
- Существует точка c между a и b, т.
 е. a<=c<=b такая, что f(c) = K
е. a<=c<=b такая, что f(c) = K
Проще говоря, эта теорема гласит, что если функция непрерывна на [a,b], то все значения функции между f(a) и f(b) будут существовать в пределах этого интервала, как показано на рисунке ниже. .
Иллюстрация теоремы о промежуточном значении (слева) и теоремы об экстремальном значении (справа)
Теорема об экстремальных значениях
Эта теорема утверждает, что:
Если:
- функция f(x) непрерывна на [a,b]
затем:
- Внутри интервала [a,b] есть точки x_min и x_max, т. е.
- а<=х_мин<=б
- а<=x_max<=b
- , а функция f(x) имеет минимальное значение f(x_min) и максимальное значение f(x_max), т.е.
- f(x_min)<=f(x)<=f(x_max), когда a<=x<=b
Проще говоря, непрерывная функция всегда имеет минимальное и максимальное значение в пределах интервала, как показано на рисунке выше.
Непрерывные функции и оптимизация
Непрерывные функции очень важны при изучении задач оптимизации. Мы видим, что теорема об экстремальном значении гарантирует, что внутри интервала всегда будет точка, в которой функция имеет максимальное значение. То же самое можно сказать и о минимальном значении. Многие алгоритмы оптимизации основаны на этом фундаментальном свойстве и могут выполнять удивительные задачи.
Мы видим, что теорема об экстремальном значении гарантирует, что внутри интервала всегда будет точка, в которой функция имеет максимальное значение. То же самое можно сказать и о минимальном значении. Многие алгоритмы оптимизации основаны на этом фундаментальном свойстве и могут выполнять удивительные задачи.
Расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
- Сходящиеся и расходящиеся последовательности
- Определения Вейерштрасса и Жордана непрерывных функций, основанные на бесконечно малых константах
Если вы изучите какое-либо из этих расширений, я хотел бы знать. Опубликуйте свои выводы в комментариях ниже.
Дополнительное чтение
В этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.
Учебники
- Пределы и непрерывность
- Оценка пределов
- Производные
Ресурсы
- Дополнительные ресурсы в книгах по математическому анализу для машинного обучения
Книги
- Исчисление Томаса, 14-е издание, 2017 г.
 (на основе оригинальных работ Джорджа Б. Томаса в редакции Джоэла Хасса, Кристофера Хейла, Мориса Вейра)
(на основе оригинальных работ Джорджа Б. Томаса в редакции Джоэла Хасса, Кристофера Хейла, Мориса Вейра) - Исчисление, 3-е издание, 2017 г. (Гилберт Стрэнг)
- Исчисление, 8-е издание, 2015 г. (Джеймс Стюарт)
Резюме
В этом руководстве вы познакомились с концепцией непрерывных функций.
В частности, вы узнали:
- Что такое непрерывные функции
- Формальные и неформальные определения непрерывных функций
- Точки разрыва
- Теорема о промежуточном значении
- Теорема об экстремальных значениях
- Почему важны непрерывные функции
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Получите доступ к вычислениям для машинного обучения!
Почувствуйте себя умнее с концепциями исчисления
…путем лучшего понимания символов и терминов исчисления
Узнайте, как это сделать в моей новой электронной книге:
Исчисление для машинного обучения
В нем содержится учебных пособий для самостоятельного изучения с полными рабочий код на:
дифференциация , градиент , Подход множителя Лагранжа , Матрица Якоби ,
и многое другое. ..
..
Привнесите достаточно знаний в области исчисления для
ваших проектов машинного обучения
Посмотрите, что внутри
О Мехрин Саид
Просмотреть все сообщения Мехрин Саид →
Нежное введение в неопределенные формы и правило Лопиталя
Применение производных
Непрерывные функции — Подход к исчислению
Подход
к
C A L C U L U S
Содержание | Дом
3
Непрерывное движение
Непрерывная функция
Определение «функция непрерывна при значении x »
Пределы непрерывных функций
Съемная несплошность
НЕПРЕРЫВНОЕ ДВИЖЕНИЕ — это движение, которое продолжается без перерыва. Его прототипом является прямая линия. Нет предела малости пройденных расстояний.
Исчисление хочет описать это движение математически, как пройденное расстояние, так и скорость в любой момент времени, особенно когда скорость непостоянна. Решение этой математической задачи — одно из первых применений исчисления.
Решение этой математической задачи — одно из первых применений исчисления.
В любой реальной задаче о непрерывном движении пройденное расстояние будет представлено как «непрерывная функция» пройденного времени, потому что мы всегда рассматриваем время как непрерывное. Поэтому мы должны выяснить, что мы понимаем под непрерывной функцией.
Непрерывная функция
В предыдущем уроке мы видели, что предел многочлена при x приближается к любому значению c , это просто значение многочлена при x = c .
Если P ( x ) полином, то
Сравните пример 1 и задачу 2 урока 2.
Мы скоро увидим, что это определение функции, которая «непрерывна при значении 9».0506 c .» «Но почему?
График помогает увидеть взаимосвязь между числами. Поэтому рассмотрим график функции f ( x ) слева. Этот график представляет собой непрерывную непрерывную линию. Поэтому мы хотим сказать, что f ( x ) является непрерывной функцией . Но функция — это отношение между числами. (Тема 3 Precalculus.) Поэтому любое определение непрерывной функции должно быть выражено только в терминах чисел. Для этого мы должны увидеть, что делает график — линию — непрерывной, и попытаться найти то же свойство в числах.
Поэтому мы хотим сказать, что f ( x ) является непрерывной функцией . Но функция — это отношение между числами. (Тема 3 Precalculus.) Поэтому любое определение непрерывной функции должно быть выражено только в терминах чисел. Для этого мы должны увидеть, что делает график — линию — непрерывной, и попытаться найти то же свойство в числах.
(Чтобы избежать прокрутки, рисунок выше повторяется.)
Если представить каждый граф f ( x ) и g ( x ) как имеющий две ветви, две части — одну слева от x = c , а другой вправо — тогда график f ( x ) остается связным при x = c . На графике г ( x ) справа нет.
На графике f ( x ) между двумя частями нет разрыва. Эти части имеют общую границу, точку ( c , f ( c )). Мы видели в уроке 1, что
— это то, что характеризует любую непрерывную величину. Именно поэтому граф
Именно поэтому граф
из f ( x ) является непрерывным при x = c.
Как мы можем математически определить предложение «9Функция 0506 f ( x ) непрерывна при x = c «?
Давайте подумаем, что значения x состоят из двух частей: одна меньше x = c , а другая больше. Затем, когда x приближается к c , как слева, так и справа, если соответствующие значения f ( x ) — эти числа — приближаются к f ( c ), эти значения будет иметь общую границу, а именно одно число, ф ( с ). Заимствуя слово «непрерывный» из геометрии, мы будем говорить, что функция непрерывна при x = c .
Например, если y = x 2 и c = 4, то
(Урок 2.)
Предел x 2 по мере приближения x к 4 равен 4 2 .
y = x 2 непрерывно в x = 4.
Однако в функции 90 506 г ( x ) предел г ( x ), поскольку x приближается к c , не существует. Если бы левосторонним пределом было значение 90 506 г 90 507 ( 90 506 c 90 507 ), правый предел не был бы равен 90 506 г 90 507 ( 90 506 c 90 507 ). Эта функция разрывна в x = c .
Вот определение:
ОПРЕДЕЛЕНИЕ 3. Функция, непрерывная при значении x .
Мы говорим, что функция F ( x ) определяется на x = C IS Непрерывная при x = C
IF LILIT F ( ( x50507 ( ( x50507 ( x50507 ( x50507 ( x50507 ( ( x50507 ( x (. ) при приближении x к c
равно значению f ( x ) в x = c .
Символами, если
, затем f ( x ) равно непрерывному при x = c .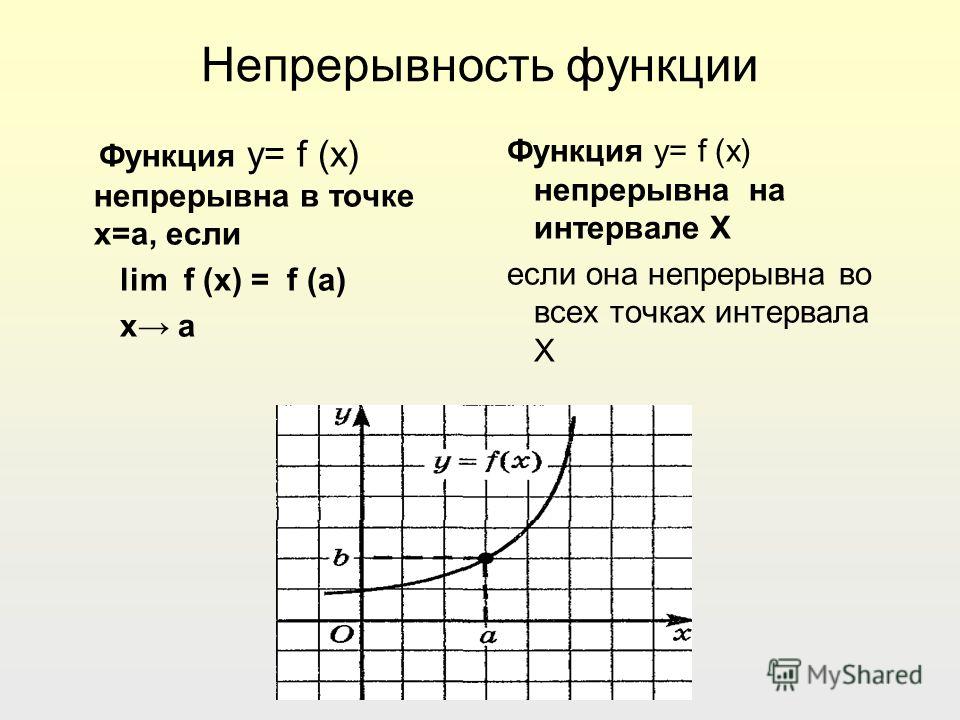
Итак, чтобы функция была непрерывной при x = c , должен существовать предел, когда x приближается к c , то есть левый и правый пределы — эти числа — должны быть равный. (Определение 2.2)
Если функция непрерывна при каждом значении в интервале, то мы говорим, что функция непрерывна в этом интервале. А если функция непрерывна на каком-либо интервале, то мы просто называем ее непрерывной функцией.
Под «каждым» значением мы подразумеваем каждого, кого мы назовем; любое другое значение, кроме этого, не нужно.
Исчисление в основном касается функций, которые непрерывны при каждом значении в своих областях. Яркими примерами непрерывных функций являются многочлены (Урок 2).
Задача 1.
а) Докажите, что этот полином
f ( х ) = 2 х 2 — 3 х + 5,
а) непрерывно при 90 506 x 90 507 = 1,
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
Мы должны применить определение «непрерывный при значении х .»
Определение 3.
То есть мы должны показать, что когда x приближается к 1 как предел, f ( x ) приближается к f (1), что равно 4.
(Согласно теоремам о пределах, это верно.)
f ( x ) поэтому является непрерывным при x = 1.
b) Можете ли вы придумать любое значение 90 506 x 90 507, где этот многочлен — или любое
б) многочлен — не будет непрерывным?
Вы не должны быть в состоянии. Многочлены непрерывны всюду. Поскольку x приближается к любому пределу c , любой многочлен
P ( x ) приближается к P ( c ).
(Урок 2)
Задачи 4, 5, 6 и 7 урока 2 являются примерами функций — многочленов — которые непрерывны при каждом заданном значении.
Помимо полиномов, следующие функции также непрерывны при каждом значении в своих областях определения.
Рациональные функции
Основные функции
Тригонометрические функции
Обратные тригонометрические функции
Логарифмические функции
Экспоненциальные функции
Это функции, которые встречаются в исчислении.
Пределы непрерывных функций
Как и любое определение, определение непрерывной функции обратимо. Это означает, что если
, то мы можем сказать, что f ( x ) непрерывно. И наоборот, если мы скажем, что f ( x ) непрерывно, то
Следовательно:
Чтобы оценить предел любой непрерывной функции как x приближается к значению, просто вычислите функцию по этому значению.
Определение 3.
| Пример 2. Оценить |
Решение . |
Студент должен хорошо понимать основные значения тригонометрических функций. В расчетах они незаменимы. См. темы 15 и 16 тригонометрии.
| Задача 2. Оценить |
грех 0 = 0,
| Задача 3. Оценить |
Задача 4. Скорость v ( t ) является непрерывной функцией времени t . Пусть
v ( t ) = 2 t 2 + 1.
Если расстояние измеряется в метрах, а функция определена как
t = 5 сек, то объясните, почему
Поскольку v ( t ) является непрерывной функцией, то предел при приближении t к 5 равен значению v ( t ) при t = 5,
Если функция не является непрерывной при каком-то значении, то она разрывна при этом значении. Вот график функции, которая разрывна при 90 506 x 90 507 = 0,
Вот график функции, которая разрывна при 90 506 x 90 507 = 0,
| Это график y = | 1 х | . При x = 0 функция не определена , |
, потому что деление на 0 является исключенной операцией. (Навык алгебры, урок 5.) х = 0 — точка разрыва. На самом деле, поскольку 90 506 x 90 507 приближается к 0 — будь то справа или слева, — 90 506 y 90 507 не приближается ни к одному числу.
Тем не менее, поскольку x непрерывно увеличивается в интервале, не включающем 0, то y будет непрерывно уменьшаться в этом интервале. Мы говорим,
| «Функция y = | 1 х | непрерывно для всех значений 90 506 x 90 507, кроме 90 506 x 90 507 = 0″. |
Эквивалентно
| «Функция y = | 1 х | непрерывно для всех значений 90 506 x 90 507 в своем домене». |
Пример 3. Рассмотрите эту функцию:
.| f ( x ) | = | x 2 − 4 x − 2 |
Эта функция не определена при x = 2 и, следовательно, там она разрывна; однако мы вернемся к этому ниже.
Тем не менее, функция определена при всех других значениях x и непрерывна при всех других значениях.
Например, поскольку 90 506 x 90 507 приближается к 8, то, согласно теоремам Урока 2, 90 506 f 90 507 ( 90 506 x 90 507 ) приближается к 90 506 f 90 507 (8).
| f (8) = | 60 6 | = 10, |
f ( x ) поэтому является непрерывным при x = 8. (Определение 3.)
Таким же образом мы могли бы показать, что функция непрерывна при всех значениях х , кроме х = 2.
Это пример неправильной функции, в которой функции преднамеренно присваивается значение, отличное от предела, когда x приближается к 1. Этот предел равен 5. Но значение функции при x = 1 равно −17. . f ( x ) не является непрерывным при x = 1.
На уроках по непрерывным функциям такие задачи (логические шутки?) обычно встречаются. Они построены, чтобы проверить понимание учащимся определения непрерывности. Однако такие функции имеют очень короткое время жизни. После урока непрерывных функций ученик больше никогда не увидит себе подобных.
Съемный разрыв
Чтобы функция была непрерывной при x = c , она должна существовать при x = c . Однако, когда функция не существует в 90 506 x 90 507 = 90 506 c 90 507 , иногда можно 90 506 присвоить 90 507 значение, чтобы оно 90 506 было 90 507 непрерывным.
Эта функция
| f ( x ) | = | x 2 − 4 x − 2 |
не существует при x = 2. Но для каждого значения x 2:
Но для каждого значения x 2:
| x 2 − 4 x − 2 | = | ( x + 2)( x − 2) x − 2 | = | х + 2. |
Следовательно, поскольку x приближается к 2,
(Сравните пример 2 из урока 2.) То есть
.Теперь f ( x ) не определено как x = 2, но мы можем его определить. Мы могли бы определить его как значение этого предела. Мы могли бы сказать,
«При x = 2 пусть f ( x ) имеет значение 4.»
Если мы это сделаем, то f ( x ) будет непрерывным при x = 2 — потому что предел при этом значении будет значением функции.
(Определение 3.)
Когда мы можем определить функцию со значением, при котором она не определена или ее значение не является пределом, мы говорим, что функция имеет устранимый разрыв.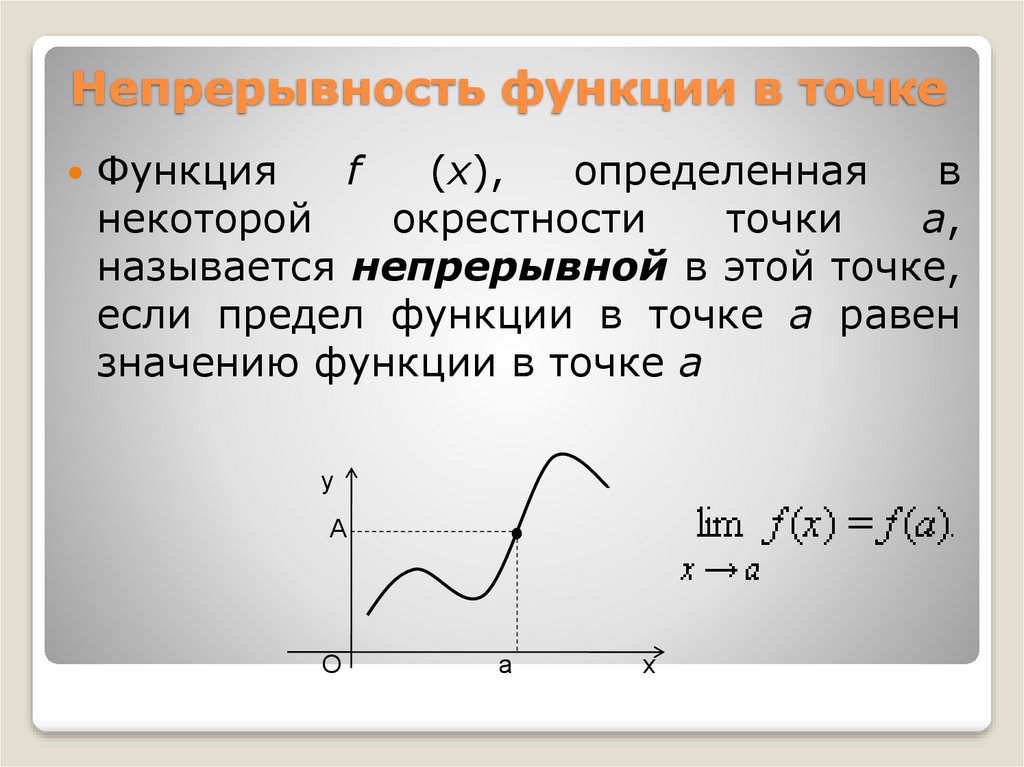
Примечание: с
, то при определении f (2) как 4, тогда фактически было определено как 1.
Задача 5. Рассмотрите эту функцию:
а) Для какого значения 90 506 x 90 507 эта функция является прерывистой? х = 3,
б) Определите там функцию так, чтобы она была непрерывной.
Поскольку предел f ( x ) при приближении x к 3 равен 8, то если мы определим f (3) = 8, а не 7, то мы устраним разрыв.
Следующий урок: «Предел» бесконечности (∞)
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Continuous Functions and Discontinuities
Continuous Functions and Discontinuities- About
- Statistics
- Number Theory
- Java
- Data Structures
- Cornerstones
- Calculus
Интуитивные понятия и терминология
Возвращаясь к нашему интуитивному понятию предела, вспомним, что мы говорили, что если не знать, что делает функция при определенном значении $x$ (как показано на графике ниже, когда $x=2$), можно считать предел в качестве «ожидания» высоты функции при этом значении $x$ — в предположении, что вблизи этого значения $x$ график функции можно нарисовать одним непрерывным росчерком пера.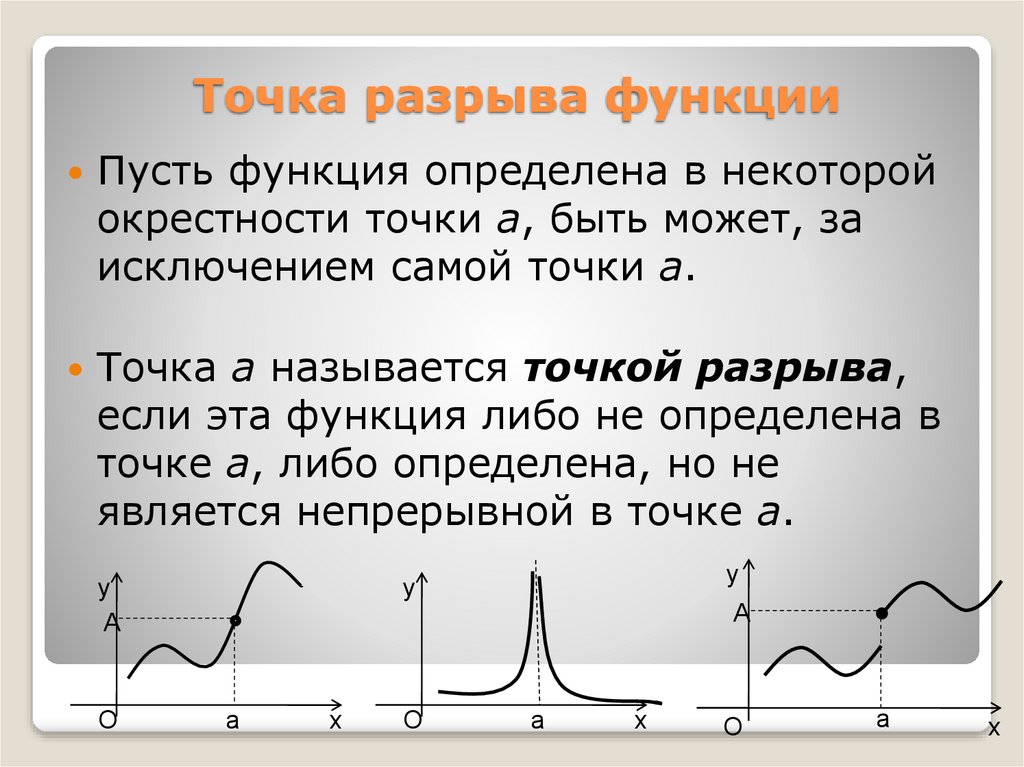
Как мы видели, это ожидание, даже если оно существует, не обязательно должно согласовываться с фактическим поведением функции при рассматриваемом значении $x$. То есть не обязательно, чтобы $\lim_{x \rightarrow c} f(x) = f(c)$. Рассмотрим еще раз следующие три функции. 92-1 &\textrm{if} x \neq 2\\ 1 & \textrm{если} х = 2 \end{массив} \right.$$
В первом примере фактическое значение $f(2)$ совпадает с нашим «ожидаемым значением», $\lim_{x \rightarrow 2} f(x)$. Также обратите внимание, что в первом примере функция может быть нарисована одним непрерывным росчерком пера (во всяком случае, около $x=2$).
Во втором случае $f(2)$ даже не существует ($x=2$ не находится в области определения второй функции), поэтому она никак не может совпадать с нашим «ожидаемым значением», $\lim_{ х \rightarrow 2} f(x)$. Кроме того, может показаться, что рисование этой функции требует, чтобы мы на мгновение оторвали перо от бумаги в точке $x=2$, учитывая наличие там «дыры». Таким образом, мы не можем нарисовать эту функцию одним непрерывным штрихом.
Таким образом, мы не можем нарисовать эту функцию одним непрерывным штрихом.
Аналогично, в третьем примере $f(2)$ существует, но отличается по значению от $\lim_{x \rightarrow 2} f(x)$. Это снова приводит к «дыре» в функции, из-за которой мы поднимаем перо, когда пытаемся нарисовать эту функцию. Следовательно, мы не можем нарисовать эту функцию вблизи $x=2$ одним непрерывным штрихом.
Точно так же, если мы посмотрим на три функции, где $\lim_{x \rightarrow c} f(x)$ не существует, мы увидим в каждом случае функции, которые нельзя нарисовать одним непрерывным росчерком пера вокруг $х=с$. ( По общему признанию, за последней функцией может быть сложнее следить, но, конечно, вы должны согласиться с тем, что рисовать эту функцию вокруг $x=0$ сложно! )
| $$y=f(x), \quad c=2$$ | $$y=g(x), \quad c=1$$ | $$y=h(x), \quad c=0$$ |
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, мы не можем иметь $\lim_{x \rightarrow c} f(x) = f(c)$.
Таким образом, из этих примеров может показаться, что мы можем нарисовать график $y=f(x)$ около некоторого $x=c$ одним непрерывным штрихом только в том случае, если происходят три вещи:
$\lim_{x \rightarrow c} f(x)$ существует,
$f(c)$ существует (т. е. $c$ находится в области определения $f(x)$), и
- +} f(x)$ ВСЕ существуют и совпадают по значению.
Существует множество вариаций на тему, когда речь заходит о словоблудии, используемой в разговоре о непрерывных функциях. Например:
Мы говорим, что функция непрерывна всюду , если она непрерывна при каждом действительном значении $c$.
Мы также можем сказать, что функция непрерывна в своей области определения , если она непрерывна при каждом действительном значении $c$, попадающем в область определения рассматриваемой функции. 9-} f(x) = f(c)}$.
Обратите внимание, что функции могут быть прерывистыми различными способами (все, кроме одного из приведенных выше маленьких рисунков, в какой-то момент были прерывистыми).

Если $\lim_{x \rightarrow c} f(x)$ существует, но по какой-то другой причине не является непрерывным в точке $x=c$ (т. е. либо $f(c)$ не существует, либо не равно значение этого предела), мы говорим, что $f(x)$ имеет устранимых разрывов при $x=c$ .
Можно думать о функциях с устранимыми разрывами как о функциях, непрерывность которых легко «починить» в определенном смысле. То есть, если просто определить (или переопределить) значение функции при $x=c$, разрыв можно устранить. Следующие два графика имеют устранимые разрывы при $x=2$. 92-1 &\textrm{if} x \neq 2\\ 1 & \textrm{если} х = 2 \end{массив} \right.$$
Как видно выше, устранимые разрывы представляются графически как « отверстий » в функциях.
Конечно, если $\lim_{x \rightarrow c} f(x)$ не существует, то определения или переопределения значения $f(x)$ при $x=c$ будет недостаточно для устранения разрыва. Мы говорим в этой ситуации, что $f(x)$ имеет неустранимых разрывов в точке $x=c$}.
 9+} f(x)$ (см. график D ниже)
9+} f(x)$ (см. график D ниже) Мы говорим, что имеем вертикальную асимптоту , когда $\lim_{x \rightarrow c} f(x)$ или один из связанных с ней односторонних пределов не существует, поскольку он бесконечен. (см. диаграмму E ниже)
полиномиальные функции
рациональные функции (т. е. отношения двух многочленов)
нечетные корневые функции (т. е. $\sqrt[n]{x}$ для нечетных $n>1$)
Примечание: четные корневые функции (т. е. функции того же вида, что и выше, но с указанным выше индексом $ n$ четно, а не нечетно) непрерывны на $(0,\infty)$ и непрерывны справа в точке $x=0$.тригонометрические функции
обратные тригонометрические функции
экспоненциальные функции
логарифмические функции
$f+g$
$f-g$
$fg$
$kf$, где $k$ — некоторая константа
$\displaystyle{\frac{f}{g}}$ при условии $g(c) \neq 0$
Предел должен существовать в этой точке.
В этот момент функция должна быть определена, и 90 455
Предел и функция должны иметь равные значения в этой точке.

Полиномы
грех и кос
Рациональные функции, где знаменатель не равен нулю
Суммы, разности и произведения непрерывных функций
Частные непрерывных функций, где функция знаменателя отлична от нуля
Композиции непрерывных функций
у = х 2 + 3х — 4
у = х грех х
1
у =
1+ х 2х — 1
у =
х + 1
х
у =
х 2 + 3х — 4у = { 2x + 3 вместо x < 1 3x — 2 для x > 1 у = { x 2 для x < 2 5x — 6 для x > 2 При каком значении k функция непрерывна?
f(x) = { 3x 2 -5 для x < 1 5x + k вместо x > 1 - Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Какие функции являются непрерывными?
Примеров непрерывных функций множество. Например, рассмотрим полиномиальную функцию $p(x)$. Мы знаем, что область определения $p(x)$ — это множество всех вещественных чисел. Это в сочетании с одним из наших предельных законов, «$\lim_{x \rightarrow c} p(x) = p(c)$ всякий раз, когда $p(x)$ является полиномиальной функцией», говорит нам, что $\lim_{ x \rightarrow c} p(x)$ и $p(x)$ существуют и совпадают по значению для каждого действительного числа $c$. Таким образом, все полиномиальные функции непрерывны всюду (т. е. при любом действительном значении $c$).
е. при любом действительном значении $c$).
С такими аргументами (которые ссылаются на предельные законы для простых функций и комбинаций функций) мы можем аналогичным образом вывести, что следующие функции непрерывны в своих областях определения:
Мы также можем обратиться к предельным законам, чтобы обнаружить, что если функции $f$ и $g$ непрерывны при некотором $x=c$, то следующие комбинации также непрерывны:

Непрерывность
Преемственность
Непрерывность
Если граф не имеет дырок, асимптот или разрывов, то функция непрерывный . Или если вы можете нарисовать функцию, не поднимая ваш карандаш, то он непрерывен. Ниже приведено формальное определение.
Определение непрерывности Функция непрерывна в х = с если |
Обратите внимание, что для того, чтобы функция была непрерывной в точке, должны быть выполнены три вещи.
быть правдой:
Обратите внимание, что функция, представленная на графике выше, не является непрерывной. в
х = -2, х = -1,
х = 0 и х = 2
Ниже приведен список функций, которые являются непрерывными.
Непрерывные функции:
Примеры:
Следующие являются непрерывными:
Упражнения:
Определите, являются ли следующие непрерывными. Если
они не непрерывны, в каких точках они разрывны?
Если
они не непрерывны, в каких точках они разрывны?
Односторонние ограничители
Для функции с изломом предела не существует, однако он все же
интересно рассмотреть, куда ведет дорога с левой стороны
и где это направление справа. Например, если
Например, если
|х|
е(х)
=
Икс
тогда для отрицательного x
f (х) =
-1
в то время как для положительного x
е (х) = 1
Мы пишем
и
Теорема о промежуточном значении
Предположим, что непрерывная функция начинается слева внизу xy-плоскости и заканчивается в правом верхнем углу xy-плоскости. Теперь нарисуйте горизонтальная линия где-то посередине страницы. Можешь нарисовать непрерывная функция (то есть без отрыва карандаша от бумаги) от из левого нижнего угла в правый верхний без пересечения линии? Ответ конечно нет. Попытайся! Теорема о промежуточном значении формализует эту мысль.
| Теорема о промежуточном значении Если ф непрерывен на [а, б] и f(a) < k < f(b) , то существует хотя бы одно число c в отрезке [a,b], для которых f(c) = k |
В частности, если f(a) и f(b)
имеют разные знаки, то f имеет корень между а и б.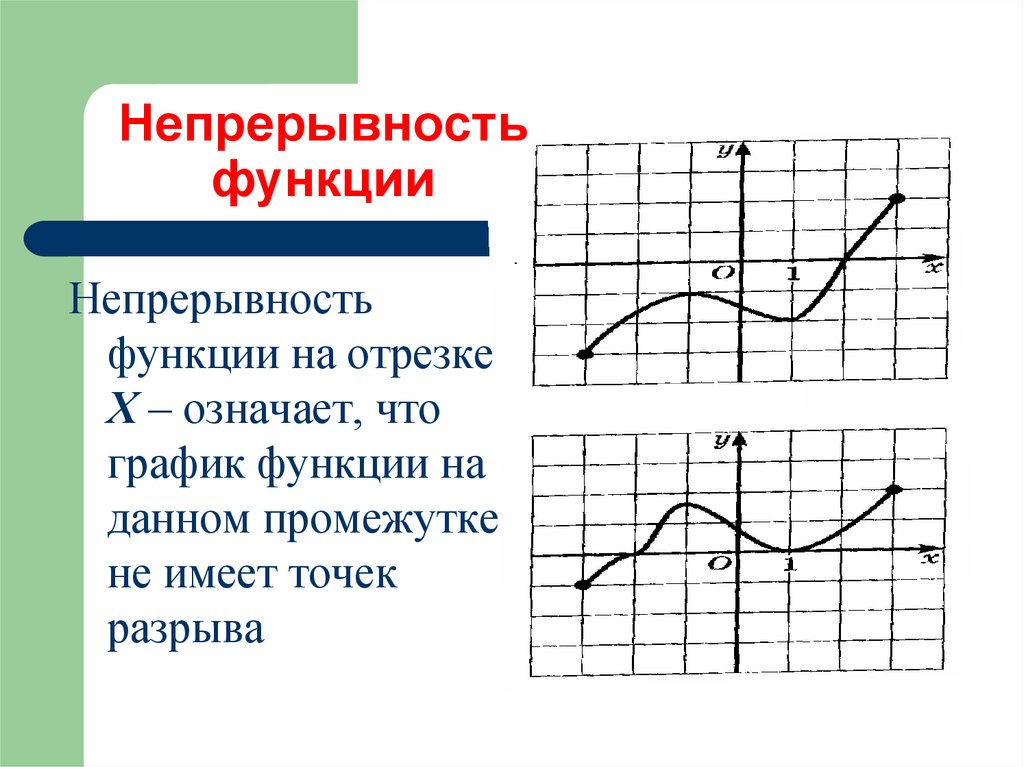
Пример
Покажите, что кривая, заданная
у =
8x 7 + x 4 — 2x 3 + x — 3
имеет корень между -1 и 1.
Решение
Применим теорему о промежуточном значении. функция
е(х)
= 8x 7 + x 4 — 2x 3 + x — 3
непрерывен между -1 и 1, так как это многочлен. Мы
есть
f(-1) = -8
+ 1 + 2 — 1 — 3 = -9
и
f(1) = 8 +
1 — 2 + 1 — 3 = 5
С
f(-1) <
0 < f(1) Здесь
к = 0
По теореме о промежуточном значении между
-1 и 1
с
f(с) = 0
Упражнение:
Напишите псевдокод, чтобы найти корень функции
Исчисление Карла
Визуальный Исчисление
Огайо Государственный расчет
Вайсштейн Мир математики
Интерактивный Расчет
UC Исчисление Дэвиса
Назад к домашней странице Math 105
электронная почта Вопросы и Предложения
Определить, является ли функция непрерывной, используя пределы
Определить, является ли функция непрерывной, используя пределы — предварительное исчисление—>
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы Precalculus
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Помощь » Вводный расчет » Ограничения » Определите, является ли функция непрерывной, используя пределы
Найдите область, в которой следующая функция непрерывна:
Возможные ответы:
Правильный ответ:
Объяснение:
Функция в числителе размножается на:
поэтому, если мы сократим x+3 в числителе и знаменателе, мы получим ту же функцию, но она непрерывна. дает нам дыру в точке x=-3, поэтому наша функция не является непрерывной при x=-3.
дает нам дыру в точке x=-3, поэтому наша функция не является непрерывной при x=-3.
Сообщить об ошибке
Какие существуют разрывы в следующей функции и каковы их виды?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку множитель находится в числителе и знаменателе, существует устранимый разрыв в точке . Функция не определена в , но функция будет двигаться к той же точке для результирующей функции .
Поскольку множитель нельзя вынести за скобки, существует бесконечный разрыв в точке . Знаменатель станет очень маленьким, а числитель приблизится к фиксированному значению.
В . В этот момент функция просто возвращает ноль.
Сообщить об ошибке
Определить, является ли функция непрерывной при использовании пределов.
Возможные ответы:
Нет, оно не является непрерывным, потому что левосторонний предел не совпадает с правым пределом.
Нет, она не непрерывна, потому что левый и правый пределы не равны значению функции в 0.
Да, она непрерывна, потому что правый и левый пределы равны фактическому значению функции.
Да, непрерывно, потому что левый и правый пределы равны.
Правильный ответ:
Да, непрерывно, потому что правый и левый пределы равны фактическому значению функции.
Объяснение:
Чтобы определить, является ли функция непрерывной в какой-либо точке, должны произойти три вещи.
1) Существует предел от левой части функции к определенной точке.
2) Существует предел от правой части функции к определенной точке.
3) Пределы из 1) и 2) равны и равны значению исходной функции в конкретной рассматриваемой точке.
В нашем случае
1)
2)
3)
Поскольку все эти условия выполняются, функция непрерывна в 0.
Сообщить об ошибке его домен.
Возможные ответы:
Нет, она не непрерывна, потому что левый и правый пределы не равны значению функции в 0.
Да, она непрерывна, потому что правый и левый пределы равны фактическому значения функции.
Да, он непрерывен, потому что левый и правый пределы равны.
Нет, он не является непрерывным, поскольку левый предел не совпадает с правым пределом.
Правильный ответ:
Да, она непрерывна, потому что правый и левый пределы равны фактическим значениям функции.
Объяснение:
Сначала найдите, что в любой точке, где , .
Затем найдите, что
и .
Поскольку все они равны, можно определить, что функция непрерывна во всех точках своей области определения.
Сообщить об ошибке
Let . Определите, является ли функция непрерывной, используя ограничения.
Возможные ответы:
Правильный ответ:
Объяснение:
По мере приближения функция приближается, что не определено. Однако, если мы разложим, мы получим:
Множители в числителе и знаменателе сокращаются, остается .
Следовательно, наша функция непрерывна при всех значениях от .
Сообщить об ошибке
Уведомление об авторских правах
Просмотр репетиторов по предварительному исчислению
Хайди
Сертифицированный преподаватель
Главный кампус Университета Нью-Мексико, бакалавр наук, математика.
Посмотреть репетиторов по математике
Франциско
Сертифицированный репетитор
Техасский университет в Браунсвилле, бакалавриат, математика. Техасский университет в Браунсвилле, магистр, математика.
View Pre-Calculus Tutors
Justin
Сертифицированный преподаватель
Кампус Вашингтонского университета в Сиэтле, нынешний студент бакалавриата, биомедицинская инженерия.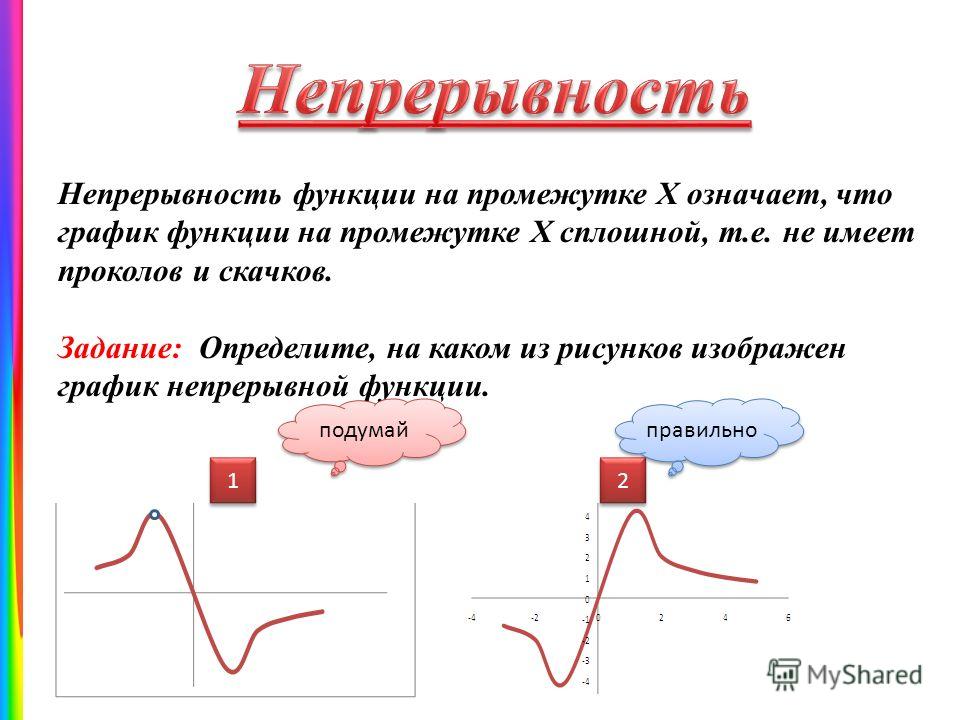

 1 Локальные
1 Локальные















 д.
д. е. a<=c<=b такая, что f(c) = K
е. a<=c<=b такая, что f(c) = K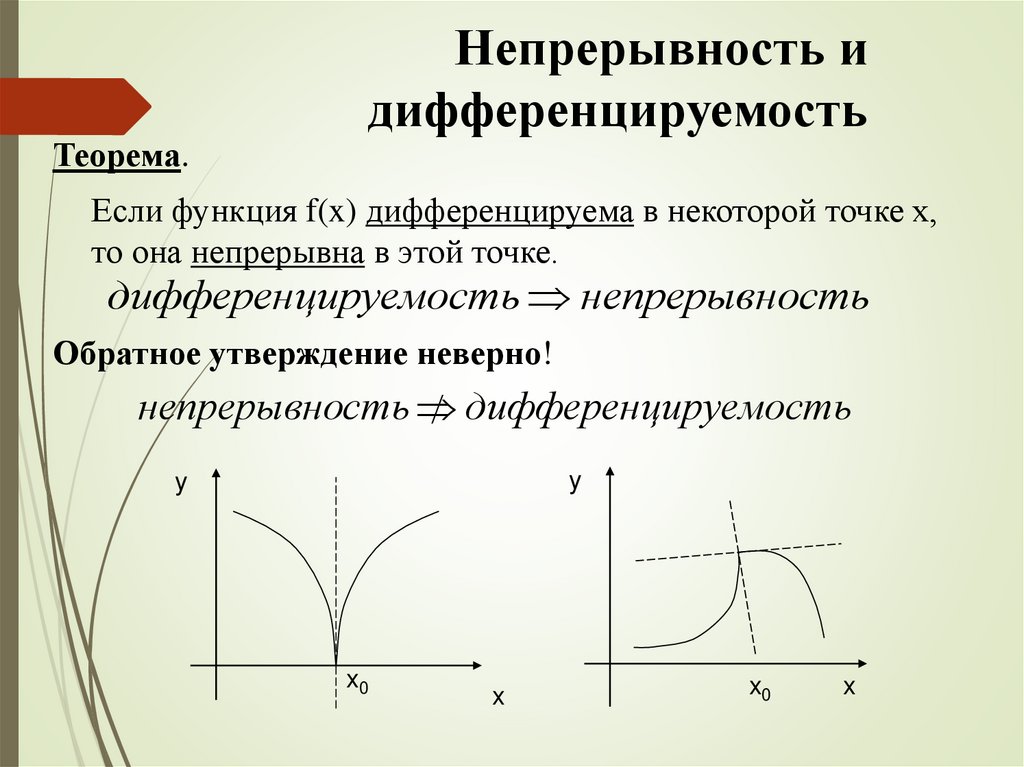 (на основе оригинальных работ Джорджа Б. Томаса в редакции Джоэла Хасса, Кристофера Хейла, Мориса Вейра)
(на основе оригинальных работ Джорджа Б. Томаса в редакции Джоэла Хасса, Кристофера Хейла, Мориса Вейра)
 9+} f(x)$ (см. график D ниже)
9+} f(x)$ (см. график D ниже)