- Как рассчитать объем куба?
- Как найти площадь и объем куба?
- Какая формула объема?
- Как найти объем куба Зная диаметр?
- Как вычислить 1 кубический метр?
- Чему равен объем?
- Какая формула площадь куба?
- Как найти объем через площадь?
- Как вычислить объем прямоугольника?
- Как искать объем?
- Как определить объем бруска?
- Как найти объем воды?
- Как найти объем куба если ребро 4 см?
- Как найти массу куба 5 класс?
- Как найти объем куба со стороной 2 1 см?
- В чем измеряется объем куба?
- Чему равен объем куба с ребром 12 см?
- Как рассчитать объем в трубе?
- Как найти сторону куба из объема?
- Как найти площадь куба если известен объем 5 класс?
- Как найти площадь и периметр куба?
Как рассчитать объем куба?
Формула для вычисления объема куба: V=a^3=a*a*a — то есть сторона куба, возведенная в третью степень.
Как найти площадь и объем куба?
Объём куба равен произведению его ширины, на длину и на высоту. У куба все ребра равны. V = 4 * 4 * 4 = 4³ = 64 дм³; Площадь поверхности куба равна сумме площадей его граней.
Какая формула объема?
Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра. Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус — 1,5 метра, в квадрате будет 2,25.
Как найти объем куба Зная диаметр?
Для того, чтобы найти объём куба нам надо прежде всего найти значение стороны куба. Для этого существует формула: d = a√3, где d — диагональ куба, а a — сторона куба.
Как вычислить 1 кубический метр?
При помощи формулы нахождения объема прямоугольного параллелепипеда, мы можем рассчитать ее объем: V = a * b * h, где V — это объем в метрах кубических, a — длина в метрах, b — ширина в метрах, h — высота в метрах.
Чему равен объем?
Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность, то есть объём любого тела равен сумме объёмов его (непересекающихся) частей.
Объём | |
|---|---|
Размерность | L3 |
Единицы измерения | |
СИ | м3 |
СГС | см3 |
Какая формула площадь куба?
Площадь поверхности куба можно вычислить через ребро куба по формуле: S = 6 * h3. h3 = площадь одной грани куба, а у куба всего 6 граней.
Как найти объем через площадь?
V = a * b * h. В то же время произведение длины и ширины основания параллелепипеда есть не что иное как площадь его основания (S).
Как вычислить объем прямоугольника?
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Как искать объем?
Объем параллелепипеда равен произведению площади основания на высоту.
V = a × b × h.
A | длина параллелепипеда |
|---|---|
H | высота параллелепипеда |
P (осн) | периметр основания |
S (осн) | площадь основания |
S (бок) | площадь боковой поверхности |
Как определить объем бруска?
Объем взятого прямоугольного бруска можно вычислить по формуле: V = L * S * h.
Как найти объем воды?
V — обьем воды, S — скорость наполнения, t — время:
- Чтобы найти обьем воды V, перемножим скорость наполнения (л/ч) — d на время t. V = d * t.
- Для нахождения времени t, необходимо разделить обьем воды на скорость наполнения p.
- Чтобы вычислить скорость наполнения S, разделим обьем V на скорость наполнения t.
Как найти объем куба если ребро 4 см?
У куба они равны также. Объем куба вычисляется как произведение значений всех трех его измерений: 4 * 4 * 4 = 4 ^ 3 = 64 м³.
2.
Как найти площадь и периметр куба?
Для того чтобы найти периметр, площадь и объём куба воспользуемся формулами: Периметр куба = 12 * a; Объем куба = a × a × a = a³; Площадь куба = 6 × a².
Вычисление объёма прямоугольного параллелепипеда: как найти, формула нахождения
Школа — это необъятная чаша знаний, которая включает в себя множество дисциплин, которые могут заинтересовать любого ребенка. Математика — царица точных наук. Строгая и дисциплинированная, она не терпит неточностей. Даже повзрослев, в обычной жизни мы можем столкнуться с разными математическими проблемами: вычисление квадратных метров для укладки плитки в ванной, кубических метров для определения объема бака и т. д., чего уж говорить о школьниках, которые только-только начинают свой математический путь.
Очень часто, начав изучать математику, точнее, геометрию, ученики путают плоские фигуры с объемными. Куб называют квадратом, шар — кругом, параллелепипед обычным прямоугольником. И здесь есть свои тонкости.
Сложно помочь ребенку в выполнении домашнего задания, не зная точно, объем или площадь какой фигуры — плоской или же объемной, нужно найти. Невозможно найти объем плоских фигур, таких как квадрат, круг, прямоугольник. В их случае можно найти лишь площадь. Прежде чем переходить к выполнению задачи, следует подготовить нужные атрибуты:
- Линейка, для того чтобы измерить необходимые нам данные.
- Калькулятор, для того чтобы в дальнейшем подсчитать расчеты.
Содержание:
- Вычисление объема прямоугольного параллелепипеда
- Пример первый
- Пример второй
- Пример третий
Итак, вы знаете, что нужно рассчитать объем, но не забывайте, что обязательно нужно уточнить о какой именно фигуре идет речь: объем куба, или же объемного прямоугольника. Ведь расчет этих, казалось бы, одинаковых фигур, абсолютно разный.
Для начала рассмотрим само понятие объемного прямоугольника. Это параллелепипед. В его основании находится параллелограмм.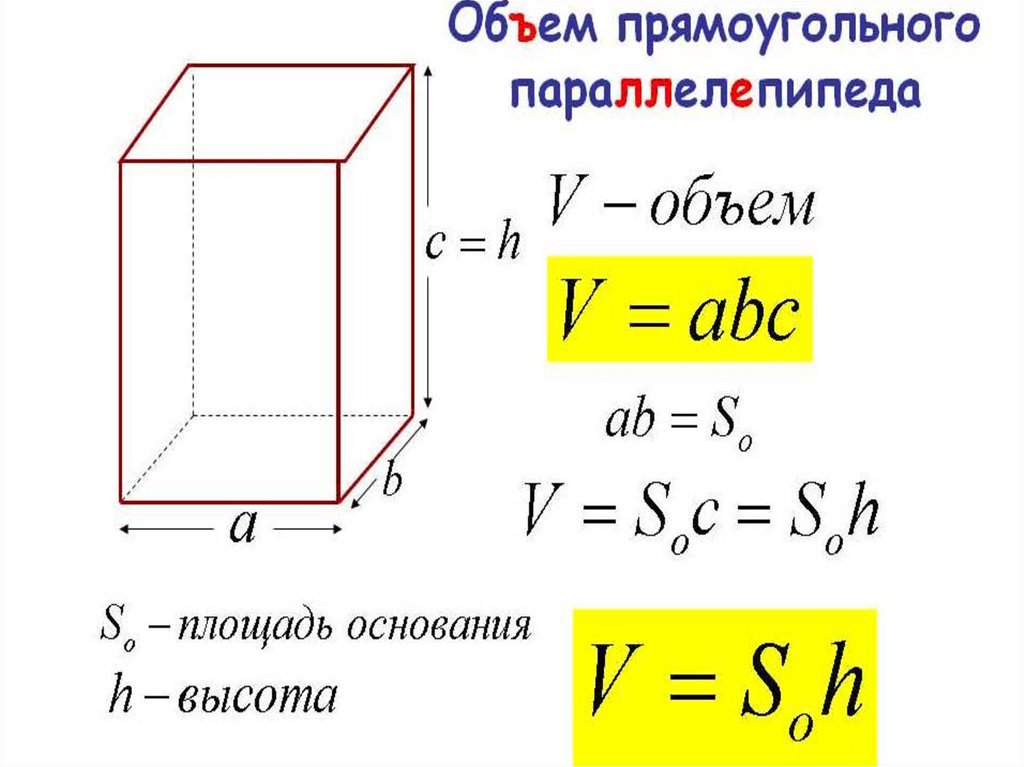
Так как таковых у него шесть, следовательно все параллелограммы являются гранями параллелепипеда.
Что касается его граней, они могут отличаться, то есть, если прямые боковые грани представляют собой прямоугольники, тогда это прямой параллелепипед, ну, а если все шесть граней являются прямоугольниками, то перед нами прямоугольный параллелепипед.
- После прочтения задачи, нужно определить что именно следует найти; длину фигуры, объем или же площадь.
- Какая именно часть фигуры рассматривается в задаче — ребро, вершина, грань, сторона, а может быть, вся фигура целиком?
Определив все поставленные задачи, можно переходить непосредственно к вычислениям. Для этого нам понадобятся специальные формулы. Итак, для того чтобы найти объем прямоугольного параллелепипеда перемножается между собой длина, ширина и высота (то есть толщина фигуры). Формула вычисления объема прямоугольного параллелепипеда следующая:
V=a*b*h,
V является объемом параллелепипеда, где a — его длина b — ширина и h — высота соответственно.
Важно! Перед началом перевести все измерения в одну единицу исчисления. Ответ должен получится непременно в кубических единицах.
Пример первый
Определим объем бака для спирта, при следующих размерах:
- длина три метра;
- ширина два метра пятьдесят сантиметров;
- высота триста сантиметров.
Для начала обязательно согласовываем единицы измерения и перемножаем их:
3*2.5*3.
Перемножив данные, мы получим ответ в кубических метрах, то есть 3*2.5*3= 22.5 метра в кубе.
Пример второй
Шкаф имеет высоту четыре метра, ширину семьдесят сантиметров и глубину 80 сантиметров.
Зная формулу вычисления можно произвести умножение. Но не стоит торопиться, как и было сказано вначале, следует согласовать между собой единицы, то есть при желании вычислять в сантиметрах перевести все исчисления в сантиметры, ежели в метрах, то в метры. Сделаем оба варианта.
Итак, начнем с сантиметров. Переводим метры в сантиметры:
V = 400 * 70 * 80;
V = 2240000 сантиметров в кубе.
Теперь метры:
V = 4* 0.7 * 0.8;
V = 2.24 метра в кубе.
Исходя из вышеперечисленных манипуляции, очевидно, что работа с кубическими метрами более легка и понятна.
Пример третий
Дана комната, объем которой должен быть вычислен. Длина этой комнаты равна пяти метрам, ширина — трем, а высота потолка 2,5. Опять используем известную нам формулу:
V = a * b * h;
где, а длина комната и равна 5, b- ширина и равна 3 и h высота, которая равна 2.5
Так как все единицы даны в метрах, можно сразу приступать к вычислениям. Перемножая между собой a, b и h:
V = 5 * 3 * 2.5;
V = 37.5 метра в кубе.
Итак, в качестве заключения, можно сказать, что зная основные математические правила для вычисления объема или же площади фигур, а также правильно определив фигуры (плоские или же объемные), умея переводить сантиметры в метры и наоборот — можно облегчить изучение геометрии вашему ребенку, что не может не сделать этот процесс более интересным и привлекательным, ведь все накопленные знания в школе, могут быть успешно использованы в самой обычной бытовой жизни в будущем.
Нахождение объема куба
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
All Common Core: математические ресурсы для 7-го класса
7 диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
Common Core: справка по математике для 7-го класса »
Геометрия »
Решение задач на площадь, объем и площадь поверхности двух- и трехмерных объектов: CCSS.
Math.Content.7.GB.6 »
Нахождение объема куба
Если куб имеет высоту в дюймах, каков его объем?
Возможные ответы:
Недостаточно информации.
Правильный ответ:
Объяснение:
Чтобы найти объем куба, мы умножаем длину на ширину на высоту, что может быть представлено с помощью forumla. Поскольку у куба равные стороны, мы можем использовать для всех трех значений.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Объем куба (или прямоугольной призмы) можно определить с помощью следующего уравнения:
Сообщить об ошибке
Определите объем куба с площадью поверхности 150 квадратных дюймов.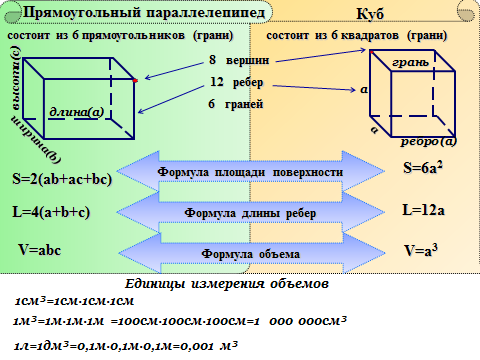
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть это будет длина одного ребра куба. Поскольку площадь его поверхности составляет 150 квадратных дюймов, на одну грань приходится одна шестая этой площади, или квадратных дюймов. Следовательно, и .
Объем равен кубу этого или кубическим дюймам.
Сообщить об ошибке
Укажите объем куба с площадью поверхности 240 квадратных дюймов.
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть это будет длина одного ребра куба. Поскольку площадь его поверхности составляет 240 квадратных дюймов, на одну грань приходится одна шестая этой площади, или квадратных дюймов.
Следовательно, и .
Объем равен кубу этого или кубическим дюймам.
Сообщить об ошибке
Рассчитайте объем указанной цифры.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно вспомнить формулу объема для куба:
Теперь, когда у нас есть правильная формула, мы можем заменить в наши известные значения и решить:
Сообщить об ошибке
Рассчитайте объем указанной фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно вспомнить формулу объема для куба:
Теперь, когда у нас есть правильная формула, мы можем заменить в наши известные значения и решить:
Сообщить об ошибке
Рассчитайте объем указанной фигуры.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно вспомнить формулу объема для куба:
Теперь, когда у нас есть правильная формула, мы можем заменить в наши известные значения и решить:
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов
Дэвид
Сертифицированный репетитор
Кентский государственный университет, бакалавриат, маркетинг. Кентский государственный университет в Кенте, магистр педагогических наук, специальное образование.
Посмотреть репетиторов
Аманда
Сертифицированный репетитор
Сиэтлский университет, нынешний студент бакалавриата, факультет прикладной математики.
Посмотреть репетиторов
Оскар
Сертифицированный репетитор
Гаванский университет, бакалавриат, физика.
All Common Core: математические ресурсы для 7-го класса
7 диагностических тестов 110 практических тестов Вопрос дня Карточки Learn by Concept
Volume of A Cube — GCSE Maths
Введение
Каков объем куба?
Как рассчитать объем куба
Объем рабочего листа куба
Как вычислить недостающую длину, учитывая объем
Распространенные заблуждения
Практика объем куба вопросы
Объем куба GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Каков объем куба?
Как рассчитать объем куба
Объем рабочего листа куба
Как вычислить недостающую длину, учитывая объем
Распространенные заблуждения
Практика объем куба вопросы
Объем куба GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем об объеме куба, в том числе о том, как вычислить объем куба и как найти недостающие длины куба, зная его объем.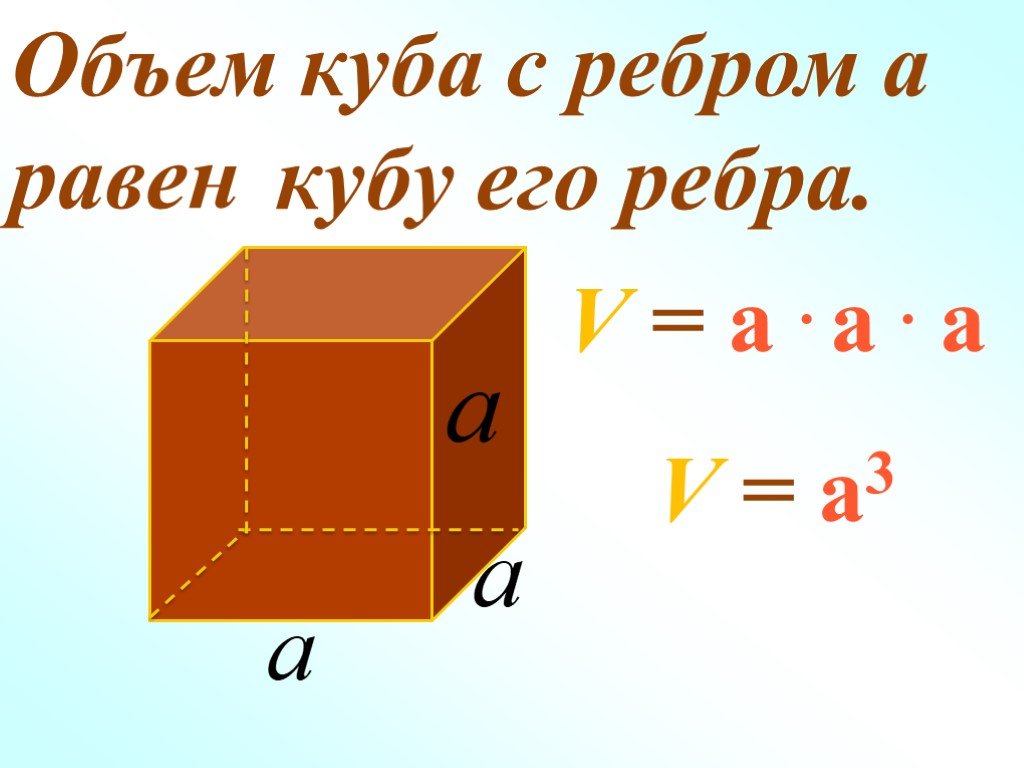
Также есть рабочие листы объемом куба, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли. 9{3}
Объясните, как вычислить объем куба
Объем рабочей таблицы куба
Получите бесплатный объем рабочей таблицы куба из 20+ вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО 93 и др.).
- Расчет в других единицах измерения
Перед расчетом объема необходимо убедиться, что все измерения указаны в одних и тех же единицах измерения.
Например, у вас не может быть что-то в см, а что-то в м.
- Деление на три, а не кубический корень
Если вам известен объем куба и вам нужно найти длину стороны, помните, что обратным значением куба является кубический корень, а не деление на 3.