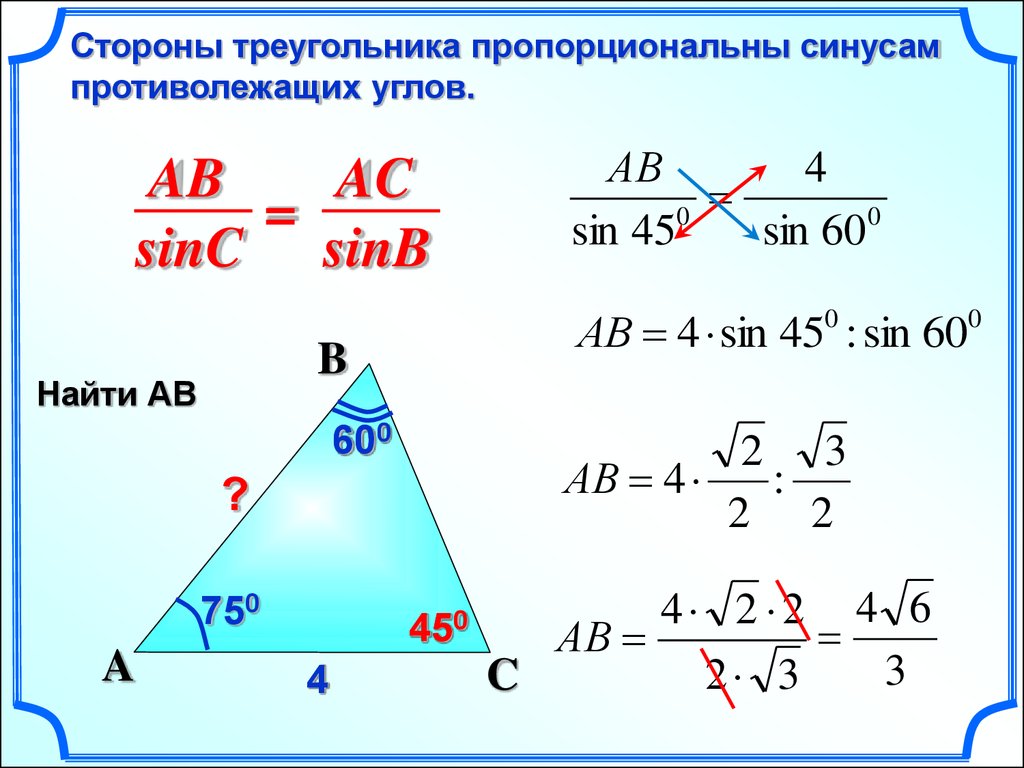
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формула стороны через диагонали, ( a ):
Формулы стороны через диагональ и угол, ( a ):
Формулы стороны через диагональ и половинный угол, ( a ):
Формулы стороны через диагонали и угол, ( a ):
Формулы стороны через площадь ромба ( S ) и угол, ( a
Формулы стороны через периметр ромба ( P ) и угол, ( a ):
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Свойства ромба:
1.
Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S
и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Свойства ромба:
1.
Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы диагоналей через сторону и угол, ( D d):
Формулы диагоналей через сторону и половинный угол, (D d):
Формулы диагоналей через сторону и другую диагональ, (D d):
Формулы диагоналей через угол и другую диагональ, (D d):
Формулы диагоналей через площадь (D d):
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
Косинус суммы двух углов
Докажем следующие две формулы:
cos (α + β) = cos α cos β — sin α sin β, (1)
cos (α — β) = cos α cos β + sin α sin β.
(2)
Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2π:
0 < α < 2π, 0 < β < 2π;
2) α > β .
Пусть положительная часть оси 0х является общей начальной стороной углов α и β.
Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α — β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.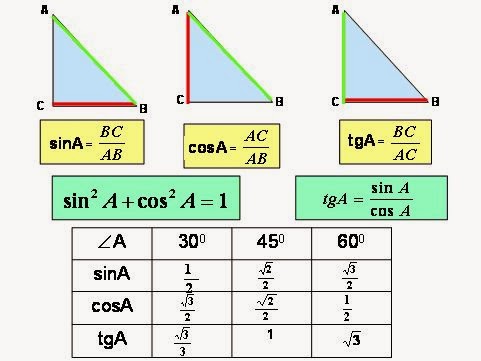
В системе координат х0у точка М имеет координаты (cos α, sin α), а точка N — координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:
d12 = (cos α — cos β)2 + (sin α — sin β)2 = cos2 α — 2 cos α cos β +
+ cos2β + sin2 α — 2sin α sin β + sin2 β = 2 (1 — cos α cos β — sin α sin β).
При вычислениях мы воспользовались тождеством
sin2 φ + cos2 φ = 1.
Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β.
В этой системе координат точка М имеет координаты (cos (α — β), sin (α
— β)), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:d22 = [cos (α — β) — 1] 2 + [sin (α — β) — 0]2 = cos2 (α — β) — 2 cos (α — β) + 1 +
+ sin2 (α — β) = 2 [1- cos(α — β)].
Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому
d12 = d22
или
2 (1 — cos α cos β — sin α sin β) = 2 [1- cos(α — β)].
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β.
Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2r, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный
Не существенным оказывается и условие α > β. Действительно, если α < β, то β >α; поэтому, учитывая четность функции cos х, получаем:
cos (α — β) = cos (β — α) = cos β cos α + sin β sin α,
что по существу совпадает с формулой (2).
Таким образом, формула
cos (α — β) = cos α cos β + sin α sin β
верна для любых углов α и β. В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin
х нечетной, получаем:cos (α + β) = cos [α — ( — β)] =cos α cos (-β) + sin α sin (-β) =
= cos α cos β — sin α sin β,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
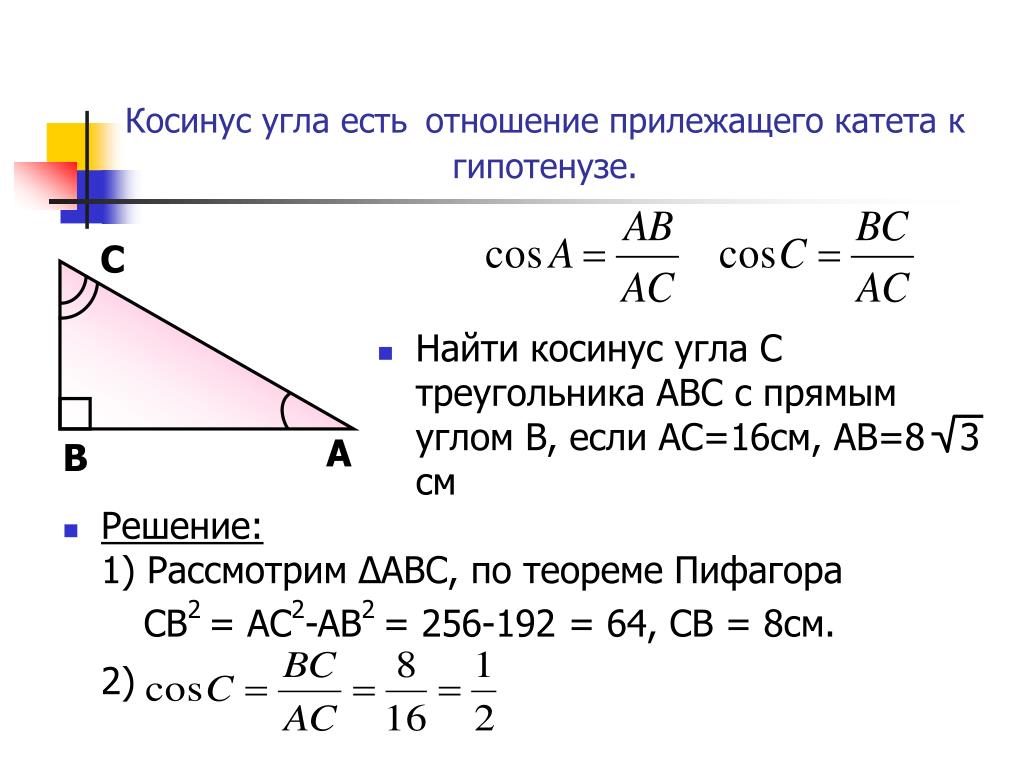
1) cos 75° = cos (30° + 45°) = cos 30° • cos 45°-sin 30°-sin 45° =
\( \frac{\sqrt3}{2}\cdot\frac{\sqrt2}{2} — \frac{1}{2}\cdot\frac{\sqrt2}{2}=\frac{\sqrt6 — \sqrt2}{4} \)
2) cos 15° = cos (45° — 30°) = cos 45° • cos 30° + sin 45°• sin 30° =
\( \frac{\sqrt2}{2}\cdot\frac{\sqrt3}{2} + \frac{\sqrt2}{2}\cdot\frac{1}{2}=\frac{\sqrt6 + \sqrt2}{4} \)
2-2\text{ab}\cos(\text{C})}\] Правило косинуса можно использовать с любым треугольником; нет необходимости, чтобы он был под прямым углом как с
СОХ КАХ ТОА.
{-1}\left(\frac{-1}{56}\right)
\\[8pt] \text{C}&=92-2\times19\times17\cos(37)}
\\[6pt] \text{c}&=\sqrt{650-646\cos(37)}
\\[6pt] \text{c}&=11.58\hspace{12pt}\text{[2dp]}
\\[14pt] \text{x}&=11.58\hspace{12pt}\text{[2dp]}
\конец{выравнивание}\]
Неограниченное количество примеров правила косинуса можно найти в интерактивном инструменте тригонометрии.
Закон косинусов – формула, доказательство и примеры
Закон косинусов, также называемый правилом косинусов или законом косинусов, гласит, что квадрат стороны треугольника равен на сумму квадратов двух других сторон минус удвоенное их произведение, умноженное на косинус прилежащего к ним угла.
Формула закона косинусов
Если a, b и c — длины сторон треугольника, а A, B и C — меры углов, противолежащих этим сторонам, то
a 2 = b 2 + c 2 — 2bc cos(A)
b 2 = a 2 + c 2 — 2ac cos(B)
6 09 9c 2
55 2
+ B 2 — 2AB COS (C)Обратите внимание, что происходит, когда C = 90 градусов
C 2 = A 2 + B 2 — 2AB COS (90)
C 5 2 2 = a 2 + b 2 , поскольку cos(90) = 0
Правило косинуса является обобщением теоремы Пифагора, так что формула работает для любого треугольника.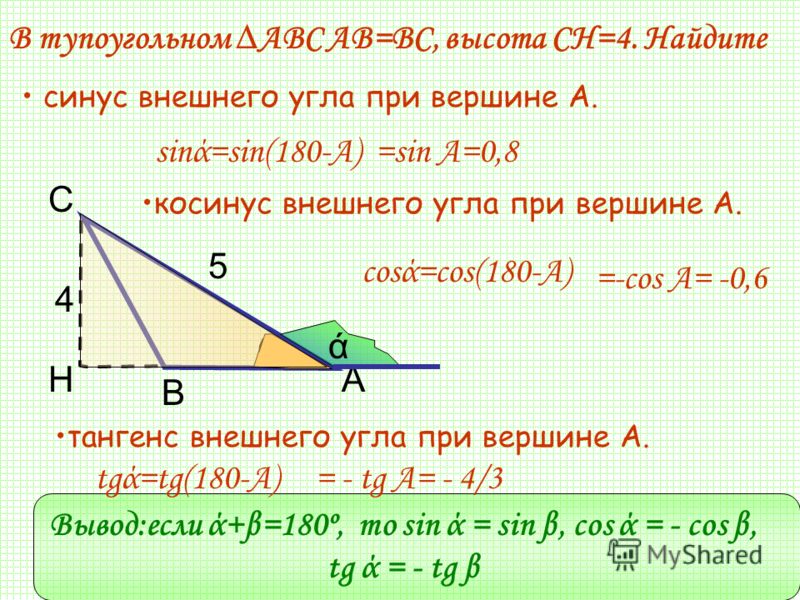
Когда следует использовать закон косинусов?
Мы используем закон косинусов для решения косоугольного треугольника или любого треугольника, который не является прямоугольным. Решая косоугольный треугольник, вы пытаетесь найти длины трех сторон и меры трех углов косоугольного треугольника.
Решение треугольника SAS или треугольника Сторона-Угол-Сторона
Если известны две стороны и угол между ними ( SAS ) косоугольного треугольника, то ни одно из трех соотношений закона синусов неизвестно. Поэтому вы должны сначала использовать закон косинусов, чтобы найти третью сторону или сторону, противоположную данному углу. Выполните три шага ниже, чтобы решить косой треугольник.
- Используйте закон косинусов, чтобы найти сторону, противоположную заданному углу
- Снова используйте закон синусов или закон косинусов, чтобы найти другой угол
- Найдите третий угол, вычитая величину заданного угла и угол, найденный в шаге 2, из 180 градусов.
Решение треугольника SSS или треугольника Side-Side-Side
Если известны три стороны ( SSS ), решение треугольника означает нахождение трех углов. Выполните следующие три шага, чтобы решить косой треугольник.
- Используйте закон косинусов, чтобы найти наибольший угол, противолежащий самой длинной стороне
- Снова используйте закон синусов или закон косинусов, чтобы найти другой угол.
- Найдите третий угол, вычитая величину углов, найденных в шагах 1 и 2, из 180 градусов.
Примеры, показывающие, как использовать закон косинусов
Пример №1:
Решите показанный ниже треугольник с A = 120 градусов, b = 7 и c = 8.
a 2 = b 2 + c 2 — 2bc cos(A)
a 2 = 7 2 + 8 2 — 2(7)(8) cos(120)
а 2 = 49 + 64 — 2(56)(-0,5) =
1 3а 2 90 + 1 (56)
A 2 = 113 + 56
A 2 = 169
A = √169 = 13
= sin A / a
sin C / 8 = sin 120 / 13
sin C / 8 = 0,866 / 13
sin C / 8 = 0,0666
Умножить обе части на 8
sin C = 0.
0666(8)
sin C = 0.536
C = arcsin(0.5328)
C = 32.19
Angle B = 180 — 120 — 32.19
Angle B = 27.81
The lengths стороны треугольника равны 7, 8 и 13. Меры углов треугольника равны 27,81, 32,19 и 120 градусов.
Пример №2:
Решите треугольник ABC, если a = 9, b = 12 и c = 10.
Нет недостающих сторон. Нам просто нужно найти недостающие углы. Поскольку угол, противоположный самой длинной стороне, равен углу B, используйте b 2 = a 2 + c 2 — 2ac cos(B), чтобы найти cos(B).
B 2 = A 2 + C 2 — 2AC COS (B)
12 2 = 9 2 + 10 2 — 2 (9) (10) COS (B)
144 = 81 + 100 — 2(90) cos(B)
144 = 181 — 180 cos(B)
144 — 181 = -180 cos(B)
-37 = -180 cos(B)
Разделите обе части на -180
cos(B) = -37 / -180 = 0,205
B = arccos(0,205)
B = 78,17 градуса
Используйте закон синусов, чтобы найти угол A
sin(A) / 9 = 0,97876 / 12
sin(A) / 9 = 0,081563
Умножить обе части на 9 = arcsin(0,734)
A = 47,22 градуса
Угол C = 180 — 78,17 — 47,22
Угол C = 54,61
Доказательство закона косинусов
Чтобы доказать закон косинусов, поместите треугольник ABC в прямоугольную систему координат, как показано на рисунке ниже.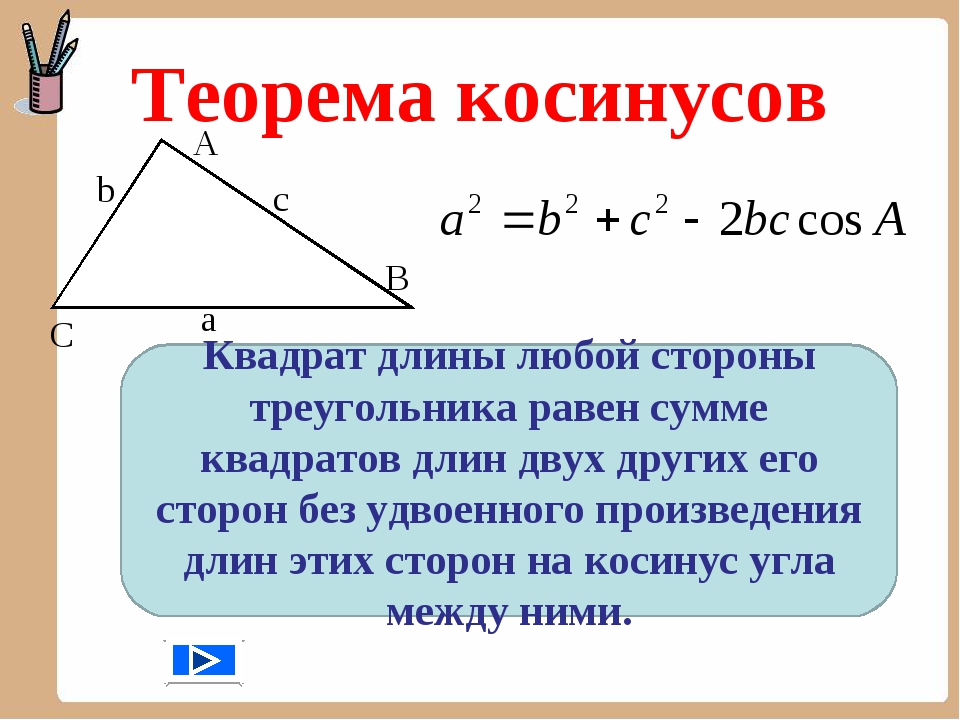
Обратите внимание, что вершина A находится в начале координат, а сторона c лежит вдоль положительной оси x.
Используйте формулу расстояния и точки (x,y) и (c,0), чтобы найти длину a.
а = √[(х — с) 2 + (у — 0) 2 ]
а = √[(х — с) 2 + у 2 ]
Квадрат обе части уравнения
a 2 = (x — c) 2 + y 2
Теперь нам нужно найти их 5 в 20 90 и y0 = (x — c) 2 + y 2
Используя треугольник, напишите выражения для sin A и cos A, а затем найдите x и y.
sin(A) = y / b, поэтому y = bsin(A)
cos(A) = x / b, поэтому x = bcos(A)
a 2 = (bcos A — c) 2 + (bsin A) 2
a 2 = b 2 cos 2 A — 2bc cos A + c 2 + b 2 sin 2 A
Rearrange Термины
A 2 = B 2 COS 2 A + B 2 SIN 2 A + C 2 — 2bc 2 А + sin 2 А) + c 2 — 2bc cos A
а 2 = B 2 (1) + C 2 — 2BC COS A С момента COS 2 A + SIN 2 A = 1
A 2 = B 2 + C 2 = B 2 + C 2 6 2 6 2 = B 2 + C 2 6 2 2 = B 2 + C 2 2 