Формула критерий гурвица: Обычный критерий Гурвица

Обычный критерий Гурвица

• ◄
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• ►

Глава 2. Принятие решений в условиях неопределенности

Обычный (или простой) критерий Гурвица учитывает только крайние исходы x_i max и x_i min каждой альтернативы:

x_i max = max(x_ij), x_i min = min(x_ij), j = 1..M

Он позволяет учесть субъективное отношение применяющего данный критерий ЛПР за счет придания этим исходам разных «весов». Для этого в расчет критерия введен «коэффициент оптимизма» λ, 0 ≤ λ ≤ 1. Формула для расчета критерия Гурвица для i-й альтернативы с коэффициентом оптимизма λ выглядит следующим образом:

H_i (λ) = λ x_i max + (1 — λ) x_i min

Если исходы представляют возможные выигрыши, то оптимальной признается альтернатива с максимальным значением критерия Гурвица:

Х* = Х_k , H_k (λ) = max(H_i (λ)), i = 1. .N

Как видно из формулы, правильный выбор коэффициента оптимизма λ оказывает существенное влияние на результат применения критерия. Остановимся подробнее на логике подбора λ.

Если ЛПР настроен пессимистически, то для него важнее меньше потерять при плохом развитии событий, пусть даже это означает не такой большой выигрыш при удачном состоянии. Значит, удельный вес наихудшего исхода x_imin в оценке альтернативы должен быть выше, чем для x_imах. Это обеспечивается, когда λ находится в пределах от 0 до 0.5, исключая последнее значение.

При λ = 0 критерий Гурвица «вырождается» в критерий Вальда и подходит только для очень пессимистично настроенных ЛПР.

Оптимистичный ЛПР, напротив, ориентируется на лучшие исходы, так как для него важнее больше выиграть, а не меньше проиграть. Больший удельный вес в оценке наилучшего исхода достигается при λ больше 0.5 и до 1 включительно. При λ = 1 критерий Гурвица становится критерием «максимакса», который учитывает исключительно наибольший исход каждой альтернативы.

Если у ЛПР нет ярко выраженного уклона ни в сторону пессимизма, ни оптимизма, коэффициент λ принимается равным 0.5.

Пример применения критерия Гурвица

В условиях задачи из п.2.7 (табл.2.2) рассмотрим принятие решения по критерию Гурвица для ЛПР, настроенного оптимистически (λ = 0.8), и ЛПР-пессимиста (λ = 0.3). Порядок действий таков:

1. Найдем максимальные x_i max и минимальные x_i min исходы для каждого проекта:

x_1 max

= max(45, 25, 50) = 50 x_1 min = min(45, 25, 50) = 25

x_2 max = max(20, 60, 25) = 60 x_2 min = min(20, 60, 25) = 20

2. Рассчитаем величину критерия Гурвица при заданных значениях коэффициента оптимизма:

ЛПР-оптимист (λ=0.8):

H₁ (0.8) = λ x_1max + (1 — λ) x_1min = 0.8×50 + (1 — 0.8)×25 = 45

H₂ (0.8) = λ x_2max + (1 — λ) x_2min = 0.8×60 + (1 — 0. 8)×20 = 52

ЛПР-пессимист (λ=0.3):

H₁ (0.3) = λ x_1max + (1- λ) x_1min = 0.3×50 + (1 — 0.3)×25 = 32.5

H₂ (0.3) = λ x_2max + (1- λ) x_2min = 0.3×60 + (1 — 0.3)×20 = 32

3. Сравним полученные величины. Оптимальными для каждого ЛПР будут альтернативы с максимальным значением критерия Гурвица:

ЛПР-оптимист (λ = 0.8):

45 < 52 => H₁(0.8) < H₂(0.8) => X* = X₂

ЛПР-пессимист (λ = 0.3):

32.5 < 32 => H₁(0.3) > H₂(0.3) => X* = X₁

Как мы видим, выбор оптимальной альтернативы в одних и тех же условиях существенным образом зависит от отношения ЛПР к риску. Если для пессимиста оба проекта примерно равноценны, то оптимист, который надеется на лучшее, выберет второй проект. Его высокая наилучшая прибыль (60) при больших значениях коэффициента λ значительно повышает ценность данного проекта по критерию Гурвица.

Недостатком обычного критерия Гурвица является его «нечувствительность» к распределению исходов между крайними значениями. Это может приводить к неправильным решениям. Например, альтернатива А{100; 150; 200; 1000} по критерию Гурвица с «оптимистичным» коэффициентом λ = 0.7 лучше альтернативы В{100; 750; 850; 950}, так как:

H_А (0.7) = 0.7×1000 + (1 — 0.7)×100 = 730

H_В (0.7) = 0.7×950 + (1 — 0.7)× 100 = 695

Однако, если посмотреть внимательнее на возможности, которые предоставляет В, то становится заметно, что она выгоднее. Ее «внутренние» исходы (750 и 850) существенно лучше, чем у А (150 и 200), а максимальный выигрыш лишь немногим хуже (950 против 1000). В реальной жизни логичнее было бы выбрать В.

Наверх

• ◄
• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• ►

Дата обновления: 25.

09.2014

Критерий Вальда, Сэвиджа, Гурвица, Лапласа, максимакса

Основные критерии применяемые в процессе принятия решений в условиях неопределённости и риска, а также в игре с природой 

Формула критерия среднего выигрыша

Формула оптимального решения

Пример

Пусть даны вероятности, p₁=0.2 p₂=0.1 p₃=0.3 p₄=0.2, тогда получаем

K(a₁)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.4=0.3
K(a₂)=0.2*0.3+0.1*0.2+0.3*0.3+0.2*0.5=0.27
K(a₃)=0.2*0.6+0.1*0.3+0.3*0.3+0.2*0.2=0.28
K(a₄)=0.2*0.4+0.1*0.5+0.3*0.2+0.2*0.3=0.25
K_опт=max{0.27; 0.48; 0. 43; 0.51}=0.51

В итоги оптимальным вариантом выбора программы по критерию среднего выигрыша является вариант первой программы.

Формула критерия Вальда или максимина

Формула оптимального решения по критерию Лапласа

Пример

K(a₁)=min(0.4;0.5;0.3;0.4)=0.3
K(a₂)=min(0.3;0.2;0.3;0.5)=0.2
K(a₃)=min(0.6;0.3;0.3;0.2)=0.2
K(a₄)=min(0.4;0.5;0.2;0.3)=0.2
K_опт=max{0.3; 0.2; 0.2; 0.2}=0.3

По критерию Вальда оптимальным решением является выбор первой программы.

Формула критерия максимакса

Формула оптимального решения по критерию максимакса

Пример

K(a₁)=max(0. 4;0.5;0.3;0.4)=0.5
K(a₂)= max (0.3;0.2;0.3;0.5)=0.5
K(a₃)= max (0.6;0.3;0.3;0.2)=0.6
K(a₄)= max (0.4;0.5;0.2;0.3)=0.5
K_опт=max{0.5; 0.5; 0.6; 0.5}=0.6

По критерию максимакса оптимальным решением является выбор третьей программы.

Формула критерия Лапласа

Формула оптимального решения по критерию Лапласа

Пример

Решение
K(a₁)=0.25*(0.4+0.5+0.3+0.4)=0.4
K(a₂)=0.25*(0.3+0.2+0.3+0.5)=0.325
K(a₃)=0.25*(0.6+0.3+0.3+0.2)=0.35
K(a₄)=0.25*(0.4+0.5+0.2+0.3)=0.35
K_опт=max{0.4; 0.325; 0.35; 0.35}=0.4

По критерию Лапласа оптимальным решением является выбор первой программы.

Пример

Формула критерия Гурвица

Формула оптимального решения по Гурвица критерию

Коэффициент α принимает значения от 0 до 1. Если α стремится к 1, то критерий Гурвица приближается к критерию Вальда, а при α стремящемуся к 0, то критерий Гурвица приближается к критерию максимакса.

Пусть α=0.7

K(a₁)= 0.7* 0.5+(1-0.7)*0.3=0.44
K(a₂)= 0.7* 0.5+(1-0.7)*0.2=0.41
K(a₃)= 0.7* 0.6+(1-0.7)*0.2=0.48
K(a₄)= 0.7* 0.5+(1-0.7)*0.2=0.41
K_опт=max{0.44; 0.41; 0.48; 0.41}=0.48

По критерию Гурвица оптимальным решением является выбор третьей программы.

Формула критерия Сэвиджа для построения матрицы потерь

Формула для выбора максимального значения из матрицы потерь

Формула оптимального решения по критерию Сэвиджа

Для примера

Строим матрицу потерь по столбцам выбираем максимальное значение и поочередно вычитаем значения каждой ячейки соответствующего столбца согласно формуле, в итоге получим матрицу вида

K(a₁)= max{0. 2; 0; 0; 0.1}=0.2
K(a₂)= max{0.3; 0.3; 0; 0}=0.3
K(a₃)= max{0; 0.2; 0; 0.3}=0.3
K(a₄)= max{0.2; 0; 0.1; 0.2}=0.2
K_опт=min{0.2; 0.3; 0.3; 0.2}=0.2

По критерию Сэвиджа оптимальным решением является выбор первой или четвёртой программы.

Таким образом, в соответствии со всеми приведёнными критериями большинство решений указывает на выбор первой программы.

Критерий Рауса-Гурвица для стабильности Часть 1 — 3.2 -…

Опубликовано 15 апреля 2021 г.

На основе информации, полученной в предыдущем руководстве по стабильности, мы начнем это руководство с критерия Рауса-Гурвица (критерий RH для короткий).

Во-первых, давайте разберемся, зачем нам нужен RH-критерий!

Мы знаем, что для устойчивости системы ее полюса должны лежать в левой половине s-плоскости. Кажется прямолинейным, не так ли? Для любой системы просто найдите расположение полюсов, решив полином знаменателя (также называемый характеристическим уравнением) передаточной функции, а затем, если все полюса лежат в левой половине s-плоскости, вы называете эту систему устойчивой. Теперь вы, вероятно, легко можете решить квадратное уравнение. Вы также можете быть в состоянии решить кубическое уравнение с некоторыми трудностями. Но по мере увеличения порядка характеристического уравнения нам становится все труднее решать и находить расположение полюсов. Следовательно, критерий RH — это то, где мы можем определить устойчивость, не решая для полюсов.

Прежде чем двигаться дальше, давайте обсудим несколько моментов.

Рассмотрим систему с характеристическим уравнением уравнение q ( s ) должно иметь тот же знак,
Основная причина, по которой мы получаем коэффициенты с другим знаком, заключается в том, что полюс находится в правой полуплоскости. Попробуйте!

Не должно быть пропущенных терминов. Это означает, что не должно быть никакого коэффициента с нулевым значением между самой высокой степенью s и самой низкой степенью

s в уравнении q ( s ).

Вы можете подумать, что если я проверю все коэффициенты и обнаружу, что все они имеют одинаковый знак и если ни один из них не пропущен, я могу объявить систему стабильной. Зачем нам что-то еще?

Возьмем пример.

Пусть q ( s ) будет

Уравнение имеет все положительные коэффициенты и нет пропущенных членов. Итак, он стабилен?

При решении получаем корни уравнения в виде

Два из трех полюсов лежат в правой половине s-плоскости и, следовательно, система неустойчива.

Как уже упоминалось, эти два условия необходимы для стабильной работы системы. Их недостаточно, чтобы объявить систему стабильной. Другими словами, если все коэффициенты имеют одинаковый знак и нет пропущенных членов, у нас нет гарантии, что система будет стабильной. Но если эти условия НЕ выполняются, мы можем сразу объявить систему нестабильной. Итак, это еще одна необходимость для RH Критерий

Итак, давайте начнем с критерия Рауса-Гурвица для стабильности.

Во-первых, этот метод является и необходимым, и достаточным условием стабильности. Этот метод обычно состоит из двух шагов. Во-первых, нужно сгенерировать массив маршрутов. Далее следует интерпретировать массив Рауса, чтобы найти, есть ли какие-либо полюса в правой половине s-плоскости, и определить стабильность.

Итак, давайте сгенерируем массив маршрутов.

Рассмотрим характеристическое уравнение

Сначала мы упорядочим коэффициенты приведенного выше уравнения в массиве, как показано на рисунке.

Как видите, это просто запись коэффициентов попеременно в первую и вторую строку массива, начиная с первой строки.

Далее мы сформируем третий ряд следующим образом. Внимательно наблюдайте.

Аналогично, для следующего ряда повторяем так же.

Мы будем продолжать делать это до s ⁰ и закончим создание полного массива Route, как показано на рисунке

Итак, теперь у нас есть массив Route. Очевидно, что это утомительная задача, и с более сложными уравнениями ее можно значительно ускорить с помощью некоторой компьютерной логики. Однако теперь мы поймем, как мы можем интерпретировать стабильность этого массива.

Согласно критерию Рауса-Гурвица, для устойчивости системы достаточно, чтобы все элементы первого столбца массива Рауса были положительными. Если это условие не выполняется, то можно сразу объявить систему неустойчивой, а количество перемен знака в первом столбце массива Рауса даст количество полюсов, лежащих в правой половине s-плоскости. Иллюстрация ниже сделает это еще более ясным.

Давайте рассмотрим пример.

Рассмотрим систему с характеристическим уравнением

Корни этого уравнения лежат в

Система устойчива, так как все полюса лежат в левой половине s-плоскости.

Проверим этот результат с помощью критерия Рауса-Гурвица

Поскольку все элементы первого столбца массива Рауса положительны, система устойчива.

Теперь давайте рассмотрим другой пример.

Так как это уравнение имеет один отрицательный коэффициент, то сразу можно сказать, что система неустойчива. Но мы проверим то же самое с критерием Рауса-Гурвица.

Поскольку не все элементы первого столбца положительны, система неустойчива, а так как происходит одна смена знака, то в правой половине s-плоскости имеется один полюс.

Подводя итог, в этом уроке мы изучили основные условия, необходимые для стабильности системы, а затем поняли необходимость критерия Рауса-Гурвица.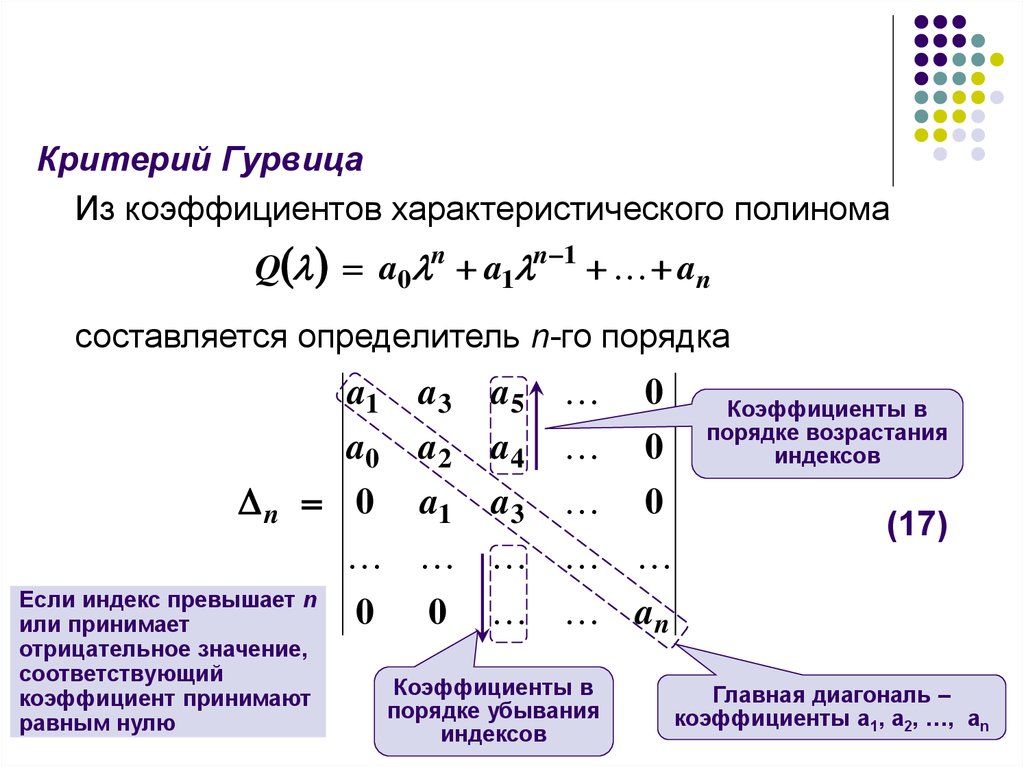 Мы перешли к изучению критерия Рауса-Гурвица, в котором мы сначала научились генерировать массив Рауса, а затем научились его интерпретировать.

Возьмите несколько случайных характеристических уравнений и проверьте их устойчивость. После этого попробуйте сформировать массив Рауса для характеристических уравнений ниже

Вы застрянете здесь и не сможете заполнить массив Рауса. Но не волнуйтесь, приведенные выше уравнения являются примерами двух особых случаев, которые мы обсудим в следующем уроке. Мы также обсудим, как мы можем сравнивать устойчивость систем, используя критерий Рауса-Гурвица.

• Системы управления (18)
• Теория управления (17)

Автор:

Кушал Гауда

Инженер-электрик и электронщик. Любит играть в настольный теннис, крикет и бадминтон. Всегда готов учиться и учить. В сферу его интересов входят силовая электроника, электронные приводы, теория управления и аккумуляторные системы.

Получите новейшие инструменты и учебные пособия, только что из тостера.

Критерий Рауса-Гурвица, часть 2 — 3.3 — Электроника…

Опубликовано 02 июня 2021 г.

В предыдущем уроке мы начали с критерия Рауса-Гурвица для проверки стабильности систем управления. Мы закончили предыдущий урок двумя характеристическими уравнениями. Как уже упоминалось, есть уравнения, на которых мы застрянем, формируя массив маршрута, и мы использовали два уравнения в качестве примеров. Это частные случаи критерия Рауса-Гурвица. В этом уроке мы начнем с понимания особых случаев, затем мы увидим, как использовать критерий RH для проектирования систем управления, и, наконец, мы узнаем, как можно избежать всех этих вычислений с помощью Scilab с помощью нескольких строк кода.

Возьмем первое характеристическое уравнение, упомянутое в конце прошлого урока.

Особый случай 1

Теперь мы сформируем массив routh для приведенного выше характеристического уравнения, используя шаги, которые мы изучили в предыдущем уроке.

Как видно, первый элемент третьей строки становится равным 0, поэтому первый элемент следующей строки не определен. Так что же нам делать?

Вот решение: если первый элемент любой строки в массиве Рауса становится нулем, то ноль заменяется небольшим положительным числом, которое обычно представляется как ϵ (произносится как эпсилон).

Теперь, чтобы оценить устойчивость, находим знак первого элемента соответствующих строк, приближая ϵ к нулю. Затем, как обычно, ищут изменения знака для анализа устойчивости. Пример ниже прояснит это.

Как видите, при ϵ → 0 первый элемент четвертой строки положителен, а пятой — отрицателен. Так как один из элементов первого столбца отрицательный, то система неустойчива, а так как перемены знака две, то в правой половине s-плоскости два полюса.

Особый случай 2

Теперь возьмем второе характеристическое уравнение, упомянутое в конце предыдущего урока.

Формирование его массива Рауса,

Вся третья строка становится нулевой и из-за этого мы не можем пройти дальше и сформировать четвертую строку.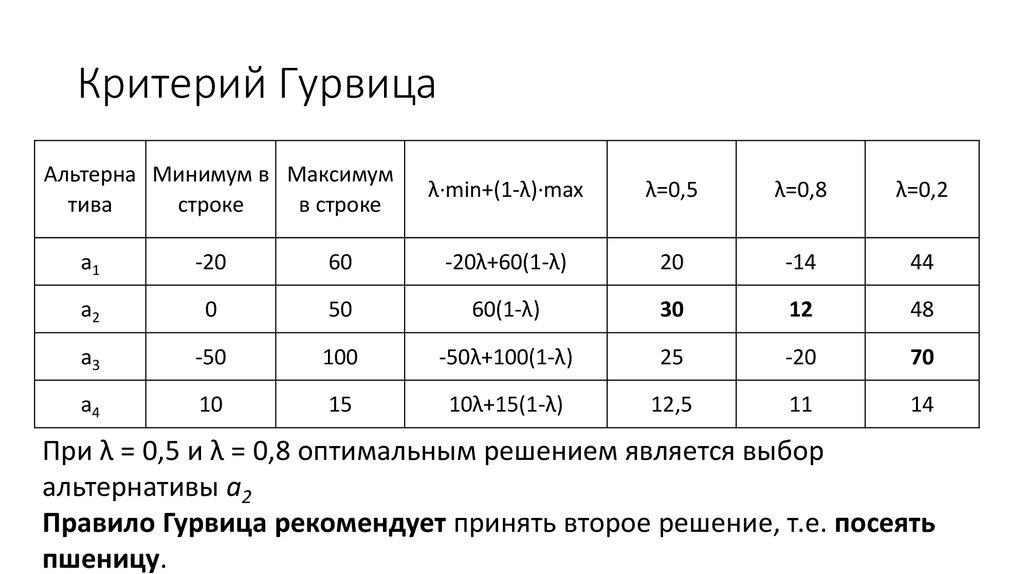 Итак, что нам теперь делать?

В этом случае мы берем многочлен, образованный строкой над строкой нулей (этот многочлен известен как вспомогательный многочлен), и затем дифференцируем по s. Затем ряд нулей заменяется коэффициентами многочлена, полученного после дифференцирования. На примере будет понятно.

Вторая строка берется для формирования вспомогательного многочлена.

Теперь замените нули третьей строки на 10 и 0 и действуйте как обычно.

Поскольку все элементы в первом столбце положительны, система устойчива. Чтобы быть более точным, система маргинально устойчива из-за появления ряда нулей. Вот почему.

Вспомогательный многочлен — это многочлен, корни которого симметричны относительно начала координат в s-плоскости.

Это происходит при трех условиях.

Решив вспомогательный многочлен, полученный в предыдущем примере,

А так как на мнимой оси есть корни, мы заключаем, что система маргинально устойчива.

Попробуйте сами,

Проверьте устойчивость системы, характеристическое уравнение которой задается выражением,

Решение:

Массив Рауса

Поскольку вся 3 ^rd строка равна нулю, вспомогательный полином равен

Заменив нули в третьей строке на 4, 4 и 0 и продолжая как обычно, массив Рауса становится равным

Теперь опять весь 5 ^й ряд равен нулю, поэтому снова составим вспомогательное уравнение.

Заменив нули в пятой строке на 2 и 0 и действуя как обычно, получим массив Рауса следующим образом.

Вы можете подумать, что, поскольку все элементы в первом столбце массива Рауса положительны, система стабильна. Но это неправильно. Вот почему.

Решив первое вспомогательное уравнение, получим

А теперь решив второе вспомогательное уравнение, получим

На воображаемой оси повторяются полюса. Если вы помните из урока 3.1, система становится нестабильной, если на воображаемой оси есть повторяющиеся полюса. Следовательно, система, описанная в приведенном выше примере, неустойчива.

Практический пример создания стабильных систем

Рассмотрев эти особые случаи, мы можем двигаться вперед и узнать, как мы можем проектировать стабильные системы. Для этого возьмем пример.

Рассмотрим систему с передаточной функцией без обратной связи

, где K положительный.

Найдем его передаточную функцию с обратной связью.

Характеристическое уравнение

Массив Рауса для вышеуказанной системы становится

Чтобы система была стабильной, элементы первого столбца массива Рауса должны быть положительными. Следовательно,

и

, то есть

. Чтобы система была стабильной, дизайн должен быть таким, что

Если

, то первый элемент третьей строки становится отрицательным, а первый элемент четвертой строки остается положительным. Следовательно, система становится неустойчивой с двумя полюсами справа от s-плоскости, что следует из двух изменений знака.

Если

, то третья строка становится нулевой, и система маргинально устойчива.

С Scilab жизнь намного проще.

Рассмотрим большое характеристическое уравнение:

Давайте воспользуемся Scilab для получения массива routh.

И на выходе

Как видите, две смены знака, поэтому система нестабильна. Но это гораздо проще, чем делать расчеты вручную.

Резюме

Подводя итог, в этом руководстве мы обсудили два особых случая критерия Рауса-Гурвица. Затем мы узнали, как критерий RH можно применять при проектировании систем управления, и, наконец, мы использовали Scilab для вычисления массива Рауса большого характеристического уравнения.