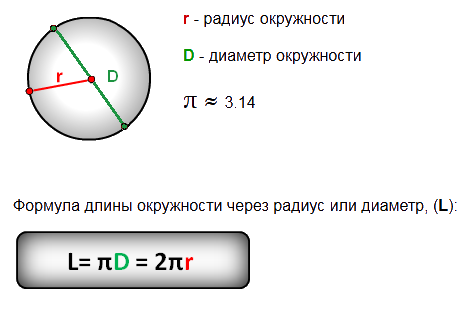Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Анна Игоревна Нестерук
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им. А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях!
Люблю математику за то, что она дисциплинирует человека, систематизирует мысли, помогает другим наукам, без неё никуда! Помогу ученикам закрепить знания, которые имеются, восполню «пробелы» и научу новому. Также помогу с домашним заданием. Индивидуальный подход к каждому ученику. Жду Вас на своих занятиях!
Эмма Акоповна Акопян
Репетитор по математике
Стаж (лет)
Образование:
Пятигорский государственный институт иностранных языков
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку 6-11 классы. Готовлю к ОГЭ. Имею большой опыт как преподавательской, так и репетиторской деятельности, доступно объясняю темы, помогаю преодолеть языковой барьер. На занятиях применяю методику развития критического мышления, коммуникативную методику. Занятия включают упражнения на развитие всех речевых видов деятельности. Использую индивидуальный подход к каждому конкретному ученику.
Готовлю к ОГЭ. Имею большой опыт как преподавательской, так и репетиторской деятельности, доступно объясняю темы, помогаю преодолеть языковой барьер. На занятиях применяю методику развития критического мышления, коммуникативную методику. Занятия включают упражнения на развитие всех речевых видов деятельности. Использую индивидуальный подход к каждому конкретному ученику.
Елена Васильевна Латышевич
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им. А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-5 классов. Математику невозможно не любить! Она открывает дверь в удивительный мир чисел. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Со мной ребенок полюбит учить математику и будет с удовольствием спешить на мои уроки!
Математику невозможно не любить! Она открывает дверь в удивительный мир чисел. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Со мной ребенок полюбит учить математику и будет с удовольствием спешить на мои уроки!
Похожие статьи
- Формула площади эллипса
- Примеры решения уравнений: логарифм с переменным основанием
- Формула пути
- Как перевести граммы в миллиграммы?
- ОГЭ по математике, базовый уровень. Квадратные уравнения
- Задачи с прикладным содержанием (вариант 1)
- Как вернуть веру в Деда Мороза и подарить сказку на зимних каникулах
- Как организовать режим школьника на каникулах, чтобы потом было легче снова идти в школу
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
Основные определения и свойства. Число π Число π |
| Формулы для площади круга и его частей |
| Формулы для длины окружности и ее дуг |
| Площадь круга |
| Длина окружности |
| Длина дуги |
| Площадь сектора |
| Площадь сегмента |
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
Около любого правильного многоугольника можно описать окружность |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
Часть окружности, расположенная между двумя точками окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |
Часть круга, ограниченная двумя радиусами |
| Сегмент |
Часть круга, ограниченная хордой |
| Правильный многоугольник |
Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность |
Определение 1.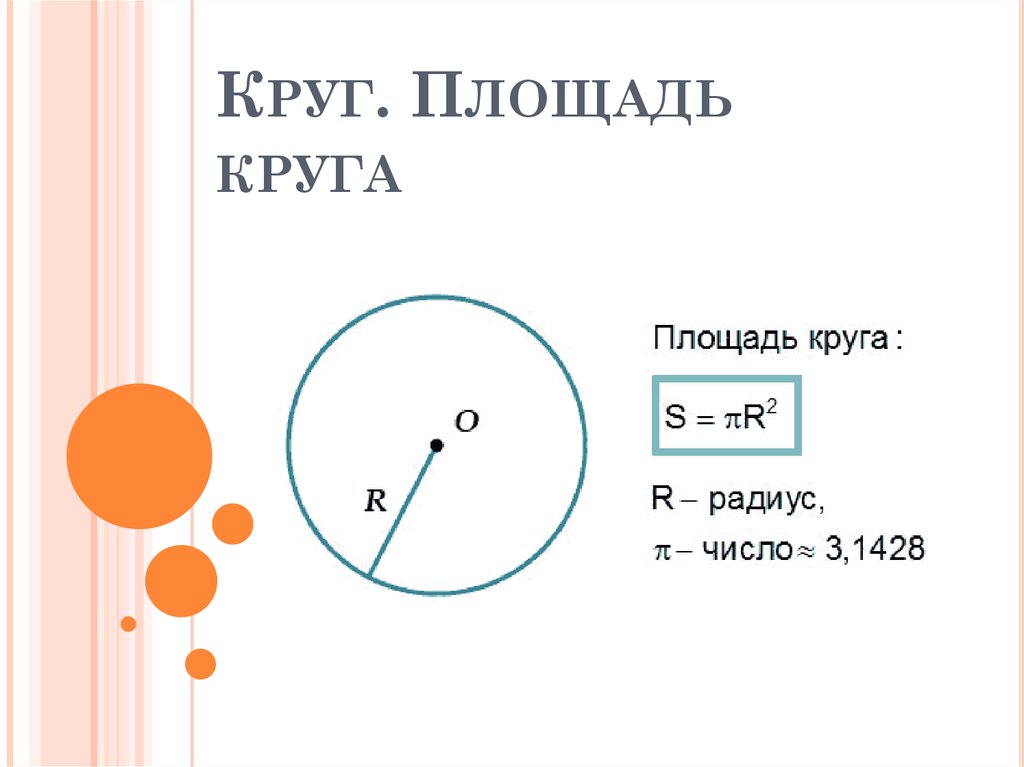 Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга | , где R – радиус круга, D – диаметр круга Посмотреть доказательство | |
| Площадь сектора | , если величина угла α выражена в радианах Посмотреть доказательство | |
, если величина угла α выражена в градусах Посмотреть доказательство | ||
| Площадь сегмента | , если величина угла α выражена в радианах Посмотреть доказательство | |
, если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь круга |
, где R – радиус круга, D – диаметр круга Посмотреть доказательство |
| Площадь сектора |
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
| Площадь сегмента |
, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула |
| Длина окружности | C = 2πR = π D, где R – радиус круга, D – диаметр круга Посмотреть доказательство | |
| Длина дуги | L(α) = αR, если величина угла α выражена в радианах Посмотреть доказательство | |
, если величина угла α выражена в градусах Посмотреть доказательство |
| Длина окружности |
C = 2πR = π D, где R – радиус круга, D – диаметр круга Посмотреть доказательство |
| Длина дуги |
L(α) = αR, если величина угла α выражена в радианах Посмотреть доказательство * * * , если величина угла α выражена в градусах Посмотреть доказательство |
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис.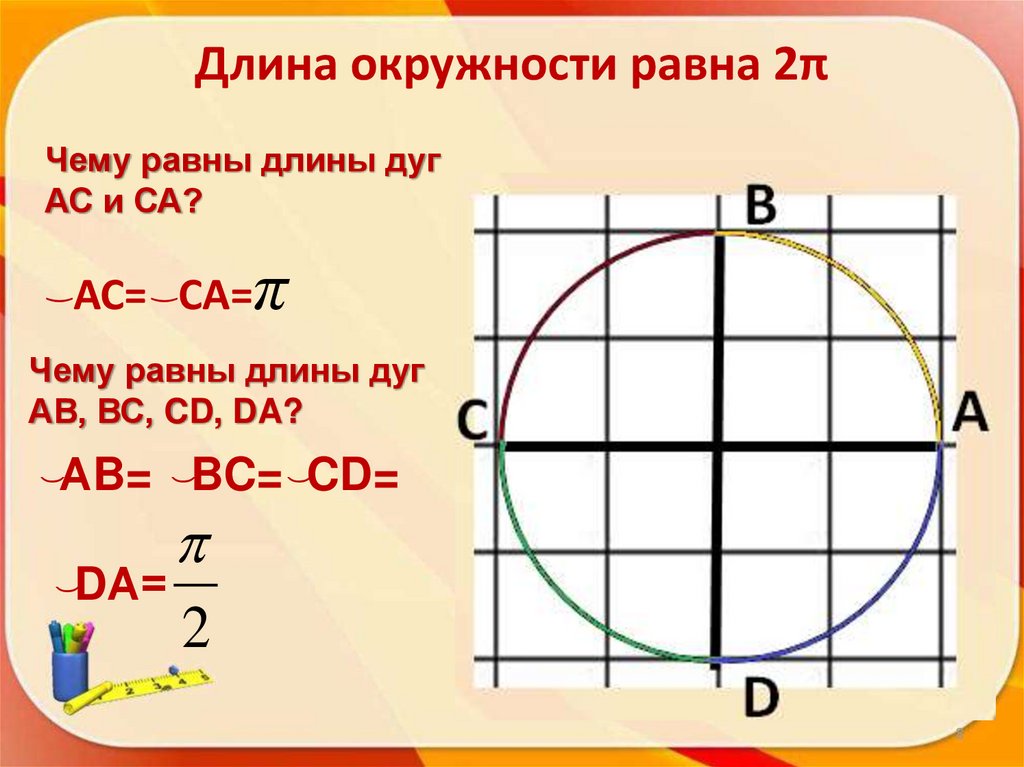 1).
1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
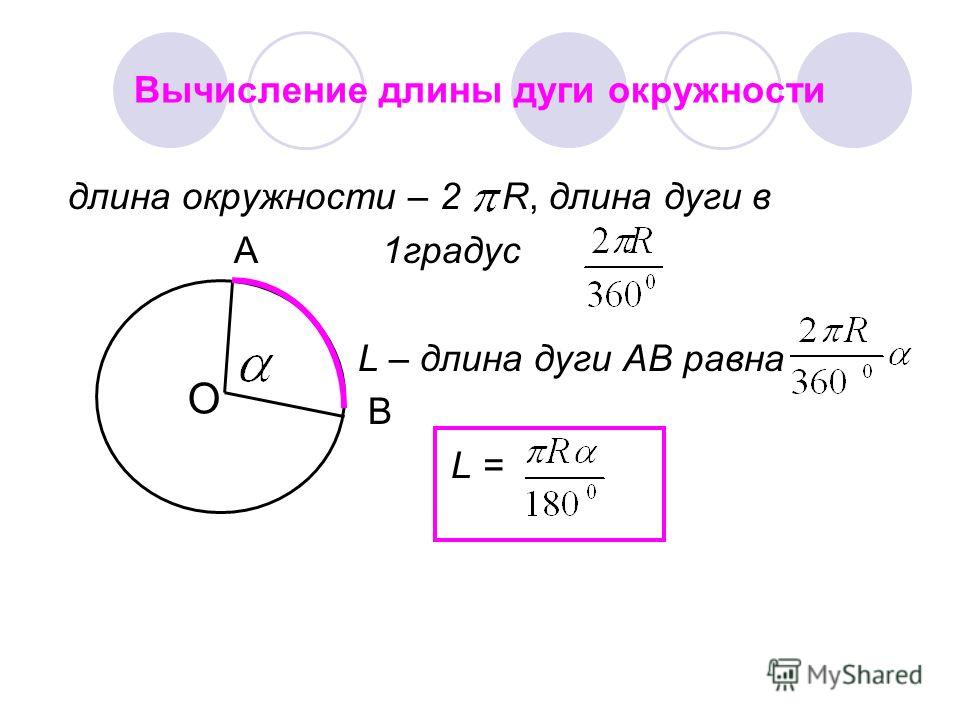
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.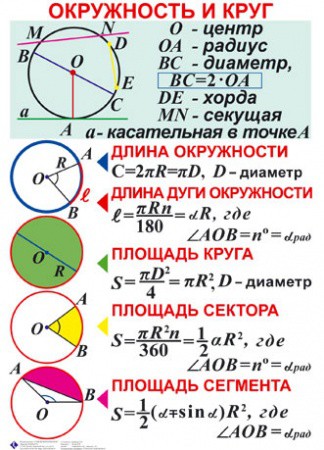
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
Следовательно,
В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
ДЛИНА ОКРУЖНОСТИ И ПЛОЩАДЬ КРУГА
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Крутько И.В. 1
1
Легович М.В. 1
1
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Надо только постараться и запомнить
Всё, как есть: 3, 14, 15, 92 и 6.
Введение
Данная тема представляет определенный интерес, поскольку её истоки относятся к древности:с давних пор люди пытались решать задачи, связанные с кругом – измерять длину окружности, находить площадь круга.
Любой школьник сегодня должен уметь находить длину окружности и площадь круга, первый опыт вычислений происходит в 6 классе. Но, к сожалению, эти знания остаются для многих формальными, и уже через годмало кто помнит не только то, что отношение длины окружности к её диаметру одно и то число, но даже с трудом вспоминают численное значение числа π, равное 3,14.
В ходе работы над проектом появляется возможность не только усвоить формулы для нахождения длины окружности и площади круга, нои приподнять завесу богатейшей истории числа π, которым человечество пользуется уже много веков.
Актуальность проекта заключается в том, что появляется возможность не только усвоить формулы для нахождения длины окружности и площади круга, но и создать информационный продукт в виде буклета, который будет содержать не только основные понятия и формулы по теме «Длина окружности и площадь круга», но и интересные факты и исторические сведения.
Гипотеза: Длина окружности, её радиус и площадь связаны между собой посредством формул.
Цель работы: Исследование числа π и выявление его роли в окружающей среде . Задачи работы: 1. Познакомиться подробнее с числом π. 2. Провести практическую работу нахождения числа π. 3. Найти занимательные факты и правила для запоминания числа π.
4.Изучить формулу площади круга.
5.Научится создавать буклеты с помощью текстового процессора MicrosoftWord.Предмет исследования:
окружность.Объект исследования: отношение длины окружности к диаметру.
Методы исследования: эксперимент, наблюдение, анализ.
Ожидаемые результаты: Некоторые данные и формулы достаточно трудно запоминаются, но с помощью открытия интересных фактов о числах или понятиях, можно лучше запомнить формулы, правила. Создание буклета с помощью MicrosoftOffice.
Создание буклета с помощью MicrosoftOffice.
У круга есть одна подруга.
Известна всем её наружность.
Она идёт по краю круга
Окружность – это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром окружности.
Точка О – центр окружности. R –радиус окружности (это отрезок, соединяющий центр окружности с любой ее точкой). По-латыни radius – это спица колеса.
1.2. Длина окружности.
Если разрезать окружность в какой-либо точке и распрямить её, то получим отрезок, длина которого и есть длина окружности.
Отношение длины окружности к её диаметру есть одно и то же число для всех окружностей. Установлено, что какой бы ни была окружность, отношение ее длины к диаметру является постоянным числом. Это число принято обозначать буквой π.
Более точное его значение 3,1415926535897932… [1, стр.189]
Обозначим длину окружности буквой С, а ее диаметр буквой d , то, тогда формулы для вычисления длины окружности С = πd.
Если известен радиус окружности, то формула длины окружности будет выглядеть следующим образомC = 2πr.
1.3. Круг. Площадь круга
Круг – это часть плоскости, ограниченная окружностью.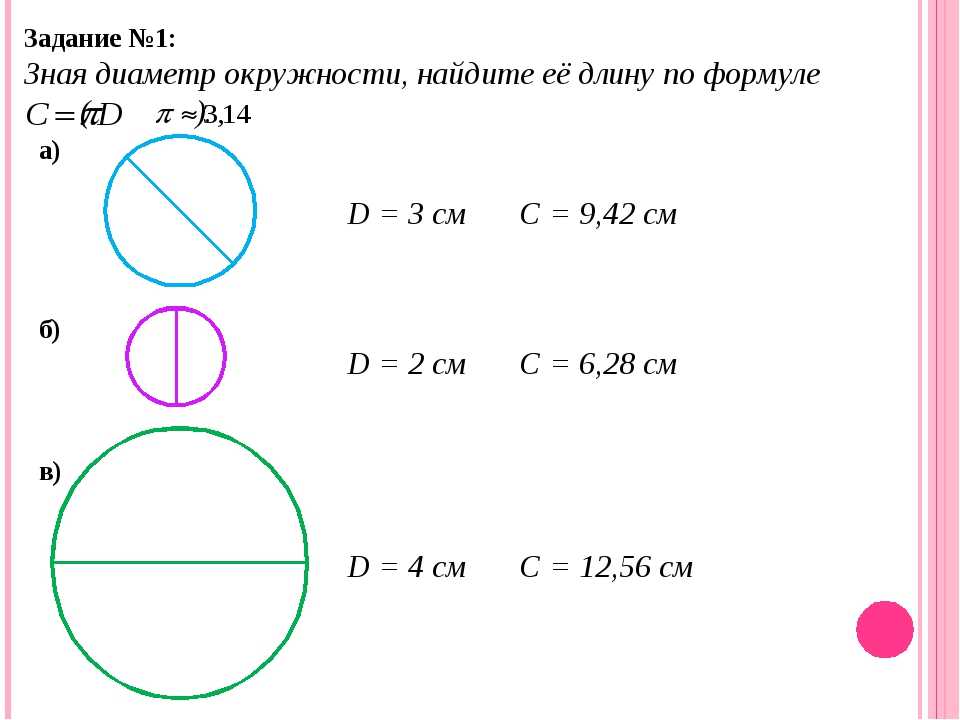
Площадь круга вычисляется по формуле: S
Ещё в древности пытались решать задачи связанные с кругом. Измерение длины окружности имеет чисто «практическое» решение: можно уложить вдоль окружности нить, а потом развернут её и приложить к линейке ил же отметить на окружности точку и «прокатить» её вдоль линейки (можно, наоборот, «обкатить» линейкой окружность). Так или иначе измерения показывали, что отношение длины окружности к её диаметру одно и то же для всех окружностей. Древние египтяне считали, что длиннее диаметра в 3,16 раза, а римляне – в 3,12 раза. Однако древнегреческих математиков такой опытный подход к определению длины окружности не удовлетворял. К тому же такой подход не позволял определить площадь круга. Выход был найден, впервые известным учёным Архимед предложил первый математический метод вычисления числа π, с помощью расчета вписанных в круг многоугольников.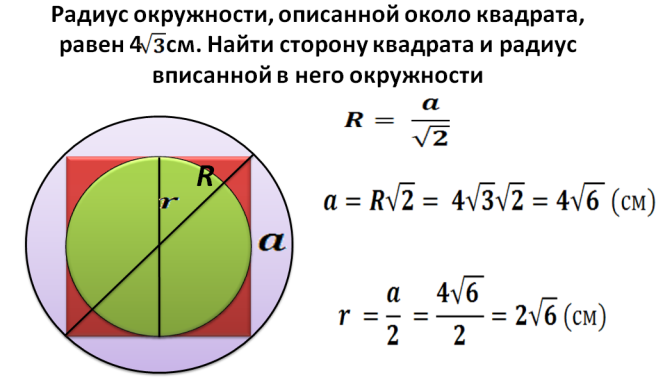
Это позволяло вычислять значение π не практически – ниткой и линейкой, а математически, что обеспечивало гораздо большую точность. [3, стр. 65-72]
Известный ученый Архимед нашел значение π =, что дает величину 3.1428. В Древней Греции вскоре после Архимеда было получено более точное приближение к числу π = .
В V веке н.э. китайским математиком Цзу Чунчжи было найдено более точное значение π =3,1416927… .
Спустя полтора столетия в Европе нашли число π только с 9 правильными десятичными знаками, сделав 16 удвоений числа сторон многоугольников, но при этом Ф.Виету принадлежит первенство в открывшейся возможности отыскания π. Это открытие имело огромное значение, так как позволило вычислять число π с какой угодно точностью. [4]
Вначале XVII в. Голландский математик из Кельна (Кейлен) Лудольф ван Цейлен затратил 10 лет на вычисление числа Пи и нашел 32 правильных знака после запятой. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: « У кого есть охота, пусть идёт дальше». С тех пор (1615г.) значение числа π с 32 десятичными знаками получило название числа Лудольфа. [5]
Голландский математик из Кельна (Кейлен) Лудольф ван Цейлен затратил 10 лет на вычисление числа Пи и нашел 32 правильных знака после запятой. Изложив свои результаты в сочинении «Об окружности», Лудольф закончил его словами: « У кого есть охота, пусть идёт дальше». С тех пор (1615г.) значение числа π с 32 десятичными знаками получило название числа Лудольфа. [5]
В настоящее время число Пи вычислено с точностью до 10 триллионов знаков после запятой.
-
- Интересные факты
-
Первый миллион знаков после запятой в числе Пи состоит из: 99959 нулей, 99758 единиц, 100026 двоек, 100229 троек, 100230 четвёрок, 100359 пятёрок, 99548 шестёрок, 99800 семёрок, 99985 восьмёрок и 100106 девяток.
-
Если рассчитать длину экватора с точностью до 1 см – предполагая, что мы знаем длину его диаметра вполне точно – нам достаточно было бы взять π всего с 9 цифрами после запятой.
 А взяв вдвое больше цифр (18) , мы могли бы вычислить длину окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0003 мм (волос в 100 раз толще этой возможной ошибки!)
А взяв вдвое больше цифр (18) , мы могли бы вычислить длину окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0003 мм (волос в 100 раз толще этой возможной ошибки!)
-
В штате Иллинойс (США) официально принят закон о том, чтобы чисто Пи считать равным 4! [6]
-
Многие математики утверждают, что правильным будет такая формулировка: «круг – фигура с бесконечным количеством углов». Здорово, правда?!
-
Есть такая поговорка английского математика Моргана: «Число π лезет в дверь, в окно и через крышу».
-
14 марта объявлено Всемирным днем числа π. [7]
Вывод: Число π захватывает умы гениев всего мира.
(приложение 1. Портрет числа π)
Портрет числа π)
Практическая работа состояла в том, чтобы найти отношение длины окружности к её диаметру.
-
Берём шесть круглых предметов, в частности вазу, несколько стаканов и чашек разных размеров.
-
С помощью нити измеряем длину окружности.
-
Поставив предмет на лист бумаги, обводим его карандашом, вырезаем бумажный круг, сгибаем пополам и линейкой измеряем длины диаметров.(приложение 2)
Составим таблицу с измеренными данными, последний столбец таблицы вычислительного характера: вычислим с помощью калькулятора отношение длины окружности (столбец 2) к диаметру (столбец 3) .
|
Длина окружности (длина нити в см) |
Диаметр окружности |
Отношение длины окружности к диаметру |
|
|
1 |
2 |
3 |
4 |
|
Измерение №1 |
30,2 |
9,5 |
3,17894 |
|
Измерение №2 |
26,5 |
8,4 |
3,15476 |
|
Измерение №3 |
24 |
7,6 |
3,15795 |
|
Измерение№4 |
37,7 |
12,5 |
3,11362 |
|
Измерение №5 |
20,5 |
6,3 |
3,15068 |
|
Измерение № 6 |
66,7 |
33,1 |
3,12035 |
Вывод: Результаты оказались близки к числу 3,14 но с числом 3,14 ни одно измерение не совпало.
Я представила, что если бы мне попалась, например, ваза с круглым дном, диаметром в 100 мм, а длиной окружности 314мм, то при измерении ниткой длины окружности ошибка хотя бы в 1 мм весьма вероятна, тогда число π окажется равным 3,13 или 3,15, а если принять во внимание, что и диаметр вазы нельзя измерить вполне точно, для «пи» получаются довольно широкие пределы : от . В десятичных дробях число от 3,09 до 3,18. И это измерение с погрешностью всего в 1 мм.
2.2. Эксперимент 2. «Ищем взаимосвязь величин» с помощью робота NXT
Для следующего эксперимента нам потребуется три вида колёс конструктора EducationMindstormsNXT (перворобот NXT). На них есть маркировки «56», «43,2», «74» – это указан диаметр колеса в миллиметрах. По форме колесо нашего робота является окружностью. Поэтому, если запрограммировать робот на «вращение» колеса один раз, то расстояние, которое пройдёт робот будет равно длине окружности (в данном случае колеса).
Эксперимент «Ищем взаимосвязь величин» заключается в том, что необходимо измерить путь, пройденный роботом за один оборот колеса, используя при этом колёса разного диаметра. [8, стр. 163-165]Приложение 3
-
Программируем робота NXT следующим образом: движение вперёд, ровно на один оборот мотора (в этом случае одно полное вращение колеса).
-
Располагаем на столе рулетку.
-
Ставим робота, чтобы его движение было параллельно расположению измерительной части рулетки.
-
Измерение перемещения робота проводим точно по оси колеса.
-
Результаты записываем в таблицу.
|
Диаметр колеса, мм |
Пройденное расстояние роботом NXT, мм |
Отношение пройденного расстояния к диаметру колеса |
Вывод: min max |
Округление до двух знаков |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
56 |
177 |
3,160714 |
3,16 |
|
|
2 |
56 |
176 |
3,142857 |
min |
3,14 |
|
3 |
43,2 |
136 |
3,148148 |
3,15 |
|
|
4 |
43,2 |
137 |
3,171296 |
max |
3,15 |
|
5 |
74 |
233 |
3,148649 |
3,15 |
|
|
6 |
74 |
234 |
3,162162 |
3,16 |
Вывод: Минимальный результат вычислений после проведения эксперимента 3,142857, а максимальный 3,171296. Если данные ответы отношений округлить до сотых, то число 3,14 будет ответом второго опыта-заезда робота.
Если данные ответы отношений округлить до сотых, то число 3,14 будет ответом второго опыта-заезда робота.
Теперь понятно, почему Древний мир не знал правильного отношения длины окружности к диаметру и понадобился гений Архимед, который нашёл значение «пи» без всяких измерений, а одним лишь геометрическим рассуждением.
2.3. Немного истории. Число π и ЭВМВ настоящее время с помощью компьютеров число π вычислено с точностью до миллионов знаков. Эпоха цифровой техники в ХХ веке привела к увеличению скорости появления рекордов вычисления количества цифр числа π. Например, Джон фон Нейман в 1949 году, используя первую ЭВМ «ЭНИАК» за 70 часов вычислил 2037 цифр числа π. В 1973 году было вычислено более миллиона цифр. Таков прогресс имел место благодаря более быстрым компьютерам (аппаратное обеспечение) и новым алгоритмам вычислений (программное обеспечение).
Заключение
В ходе работы над проектом я узнала, что длина окружности и диаметр связаны между собой посредством числа π. Зная формулы, я смогу применять их при решении практических задач, а если понадобится, то и в повседневной жизни. Кроме того, я узнала много интересных фактов о числе π, а также прочла об учёных, которых раньше не знала.
Зная формулы, я смогу применять их при решении практических задач, а если понадобится, то и в повседневной жизни. Кроме того, я узнала много интересных фактов о числе π, а также прочла об учёных, которых раньше не знала.
Познакомившись с темой длина окружности и площадь круга, я создала информационный продукт в виде буклета, который может быть использован в дальнейшем на уроках математики, при решении задач. Кроме того, в нем содержатся интересные факты о числе π, и исторические сведения. Поскольку, следующий раз с темой «Длина окружности и площадь» круга мы встретимся в 9 классе, этот буклет можно использовать как памятку.
Литература-
Энциклопедический словарь юного математика. А. П. Савин, М: 1989 г
-
Виленки Н.Я., Жохов В.И., Чесноков А.С., Шварцбург С.И. Математика, 6 класс. Учебник для учащихся общеобразовательных организаций.
 М.: Мнемозина, 2014г.
М.: Мнемозина, 2014г.
-
Занимательная геометрия на вольном воздухе и дома. М: 2011 г.
-
http://i-fakt.ru/interesnye-fakty-o-chisle-pi/
-
http://school-assistant.ru/?predmet=matematika&theme=dlina_okruznosti_i_ploshad_kruga
-
http://sitefaktov.ru/index.php/home/515-chislopi
-
http://ppt4web.ru/matematika/dlina-okruzhnosti-i-ploshhad-kruga0.html
-
Колосов Д.Г. Первый шаг в робототехнику. Практикум для 5-6 кл. М.: БИНОМ, Лаборатория знаний, 2015.
-
Епифанов Е. «Портрет» числа π. Коллекция головоломок // Квант, научно-популярный журнал . №4, 2014г.
Приложение
Приложение 1
Портрет числа π
Таким необычным способом изобразил первые 10000 знаков числа π румынский художник Кристиан Василе. Принцип простой: дуги соединяют сектора, соответствующие последовательным цифрам в десятичной записи числа π. Например, так как π≈3,1415…, то первая дуга идёь из сектора 3 в сектор 1, вторая – из 1 в 4 и так далее. Цвет дуги совпадает с цветом сектора, из которого она стартует. Этот «портрет» был получен при помощи программы Circos (www.circos.ca), разработанной специально для построения круговых диаграмм. [9, обложка журнала, стр. 31]
Принцип простой: дуги соединяют сектора, соответствующие последовательным цифрам в десятичной записи числа π. Например, так как π≈3,1415…, то первая дуга идёь из сектора 3 в сектор 1, вторая – из 1 в 4 и так далее. Цвет дуги совпадает с цветом сектора, из которого она стартует. Этот «портрет» был получен при помощи программы Circos (www.circos.ca), разработанной специально для построения круговых диаграмм. [9, обложка журнала, стр. 31]
Приложение 2
Исследование 1. Практическая работаПриложение 3
Исследование 2. Практическая работаПросмотров работы: 6529
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Математики празднуют «пи» | Телеграф
Телеграф
Металлическая скульптура числа π установлена на ступенях перед зданием Музея искусств в Сиэтле в начале пешеходной зоны.
- Фото
- (Creative Commons license): Rex Sorgatz
14 марта этого года вот уже в двадцатый раз будет отмечаться День пи — неформальный праздник математиков, посвященный этому странному и загадочному числу. «Отцом» праздника стал Ларри Шоу (Larry Shaw), обративший внимание на то, что этот день (3.14 в американской системе записи дат) приходится кроме всего прочего на день рождения Эйнштейна . И, наверное, это самый подходящий момент для того, чтобы напомнить тем, кто далек от математики, о замечательных и странных свойствах этой математической константы.
1. Интерес к значению числа π, выражающему отношение длины окружности к диаметру, появился еще в незапамятные времена. Известная формула длины окружности L = 2 π R одновременно является определением числа π. В глубокой древности считалось, что π = 3. Например, об этом упоминается в Библии. В эллинистическую эпоху считалось, что
,
и этим значением пользовались и Леонардо да Винчи, и Галилео Галилей . Однако оба приближения очень грубы. Геометрический рисунок, изображающий окружность, описанную около правильного шестиугольника и вписанную в квадрат, сразу дает простейшие оценки для π: 3 William Jones, 1675–1749) в 1706 году. Это первая буква греческого слова περιφέρεια (окружность, периферия).
2. Первый шаг в изучении свойств числа π сделал Архимед (Άρχιμήδης, Archimedes, 287–212 до н. э.). В сочинении «Измерение круга» он вывел знаменитое неравенство
Это означает, что π лежит в интервале длиной 1/497. В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14…. Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней.
В десятичной системе счисления получаются три правильных значащих цифры: π = 3,14…. Зная периметр правильного шестиугольника и последовательно удваивая число его сторон, Архимед вычислил периметр правильного 96-угольника, откуда и следует неравенство. 96-угольник визуально мало отличается от окружности и является хорошим приближением к ней.
В том же сочинении, последовательно удваивая число сторон квадрата, Архимед нашел формулу площади круга S = π R 2 . Позднее он дополнил ее также формулами площади сферы S = 4 π R 2 и объема шара V = 4 /3 π R 3 .
Автомобиль «Мазда π» был обнаружен в американском штате Массачусетс.
- Фото com/photos/chrisdag/1254600248/">ChrisDag</a></noindex>» data-v-0136fa76=»»>(Creative Commons license): ChrisDag
3. Дальнейшая история числа π связана в первую очередь с его вычислением. Уточнялись нижняя и верхняя оценки числа и предпринимались неудачные попытки представить π в виде дроби и, таким образом, окончательно найти его значение.
Китаец Цзу Чунчжи (Zu Chongzhi, 430–501) нашел восемь правильных знаков: π = 3,1415926… и предложил приближение π ≈ 355/113. Голландец Людольф ван Цейлен (Ludolph van Ceulen, 1540–1610) вычислил 35 знаков π. И, наконец, в 1706 году англичанин Джон Мечин (John Machin, 1680–1751) впервые смог найти сто знаков π. Сегодня находят миллионы знаков π с помощью суперкомпьютеров. Чуть ли не каждый год устанавливаются новые рекорды знаков π, но, в отличие от ста знаков Мечина, вопрос о достоверности таких вычислений всегда остается открытым.
4. Формула длины окружности и три формулы Архимеда (для площади круга, площади сферы и объема шара) не являются конструктивными — они не содержат способа вычисления входящего в эти формулы числа π. Если применить известные в интегральном исчислении методы нахождения длины кривой, площади поверхности и объема тела к формулам для окружности, круга, сферы и шара, то можно доказать, что в каждой из этих формул π задается интегралом
Если применить известные в интегральном исчислении методы нахождения длины кривой, площади поверхности и объема тела к формулам для окружности, круга, сферы и шара, то можно доказать, что в каждой из этих формул π задается интегралом
Существующие методы вычисления интегралов позволяют таким образом находить π. (Заметим в скобках, что полученная для π интегральная формула служит исходным пунктом для вывода так называемого распределения вероятностей Коши–Лоренца (Cauchy-Lorentz distribution), хорошо известного в теории вероятностей и имеющего важные приложения в теоретической физике.)
Портрет Джона Валлиса, выполненный художником Джованни Баттистом Чиприани (Giovanni Battista Cipriani, 1727–1785).
5. Преобразуя то же самое интегральное выражение, несложно получить представление π в виде либо бесконечной суммы (ряда)
либо бесконечного произведения
Первую формулу нашли независимо шотландец Джеймс Грегори (James Gregory, 1638–1675) и немец Готфрид Вильгельм Лейбниц (Gottfried Wilhelm Leibniz, 1646–1716). Вторую формулу получил знаменитый криптограф Кромвеля (Oliver Cromwell, 1599–1658) англичанин Джон Валлис (John Wallis, 1616–1703). К сожалению, пользы от этих формул было немного: чтобы вычислить десять знаков π, необходимо сложить или умножить миллиарды слагаемых или перемножить миллиарды сомножителей, в чем легко убедиться, попытавшись вычислить π таким образом. Такая работа трудна даже для современного мощного компьютера.
Вторую формулу получил знаменитый криптограф Кромвеля (Oliver Cromwell, 1599–1658) англичанин Джон Валлис (John Wallis, 1616–1703). К сожалению, пользы от этих формул было немного: чтобы вычислить десять знаков π, необходимо сложить или умножить миллиарды слагаемых или перемножить миллиарды сомножителей, в чем легко убедиться, попытавшись вычислить π таким образом. Такая работа трудна даже для современного мощного компьютера.
6. Однако процесс вычисления можно ускорить, и тогда использование этих формул приобретает совсем другой смысл. Например, Мечин существенно ускорил вычисления по формуле Грегори–Лейбница, приведя формулу
к виду
и разложив арктангенс по формуле:
В этом случае десять знаков π находятся быстро. Именно эта формула помогла Мечину найти 100 знаков π. Сегодня открыто много аналогов формулы Мечина, по которым π вычисляется еще быстрее. Приведем только два примера:
Чем меньше аргументы арктангенсов, тем быстрее вычисляется π. Чем меньше максимальный аргумент арктангенсов в аналоге формулы Мечина, тем выше скорость сходимости этого аналога.
Чем меньше максимальный аргумент арктангенсов в аналоге формулы Мечина, тем выше скорость сходимости этого аналога.
Этот портрет выдающегося математика «японского Ренессанса» Секи Такакадзу (Секи Кова) был обнаружен современным исследователем Фудживара Масахико (Fujiwara Masahiko) и опубликован только в 2002 году. Если бы о достижениях Секи Такакадзу было известно в современной ему Европе, ее интеллектуальная история сложилось бы, вероятно, иначе.
7. Современник Исаака Ньютона (Sir Isaac Newton, 1643–1727) японский математик Секи Такакадзу (Takakazu Shinsuke Seki, 1642–1708) придумал метод ускорения медленно сходящихся последовательностей. Например, известные последовательности правильных многоугольников сходятся к окружности медленно, из-за этого медленно сходятся к числу π последовательности его приближений, рассчитанные с помощью этих многоугольников. Такакадзу ускорил сходимость последовательностей приближений и нашел десять знаков числа π. Прошло более двух столетий, когда английский математик Александр Крэг Эйткен (Alexander Craig Aitken, 1895–1967) переоткрыл метод ускорения сходимости последовательностей, известный сегодня как метод Эйткена. Метод Такакадзу-Эйткена творит чудеса. Если в формуле Грегори–Лейбница сложить семь слагаемых, то мы найдем только один правильный знак: π = 3,…. Если же к этим семи слагаемым применить метод ускорения, то получим шесть правильных знаков: π = 3,14159….
Метод Такакадзу-Эйткена творит чудеса. Если в формуле Грегори–Лейбница сложить семь слагаемых, то мы найдем только один правильный знак: π = 3,…. Если же к этим семи слагаемым применить метод ускорения, то получим шесть правильных знаков: π = 3,14159….
Попутно Такакадзу независимо от Ньютона открыл метод касательных для решения уравнений, первым в мире изучал определители второго и третьего порядка, а также открыл числа Бернулли раньше самого Якоба Бернулли (Jacob Bernoulli, 1654–1705), именем которого они названы.
8. Два голландских ученых Виллеброрд Снеллиус (Willebrord van Royen Snell, 1580–1626) и Христиан Гюйгенс (Christiaan Huygens, 1629–1695) предложили методы ускорения вычислений для выведенного Архимедом алгоритма нахождения числа π путем аппроксимации окружности правильными многоугольниками.
Снеллиус показал, что там, где правильный шестиугольник дает один знак числа π – тройку, на самом деле можно получить три знака: π = 3,14… . Взяв 96-угольник, Снеллиус нашел семь знаков π вместо трех знаков, соответствующих неравенству Архимеда. Для любого данного многоугольника Снеллиус увеличивал количество правильных знаков числа π более чем вдвое по отношению к количеству правильных знаков, полученных методом Архимеда. К сожалению, Снеллиусу не удалось доказать две теоремы, лежащие в основе его метода. Позднее Гюйгенс в своей работе «О найденной величине круга», написанной им в возрасте 25 лет, не только доказал теоремы Снеллиуса и развил его метод, но также смог создать новый, более мощный метод, в котором применяются некоторые свойства центра масс. Для данного многоугольника Гюйгенс увеличивал число правильных знаков π более чем втрое по отношению к знакам Архимеда. Для получения неравенства Архимеда он использовал всего лишь правильный треугольник! Взяв шестидесятиугольник, Гюйгенс нашел для π десять знаков: 3,141592653… .
Для любого данного многоугольника Снеллиус увеличивал количество правильных знаков числа π более чем вдвое по отношению к количеству правильных знаков, полученных методом Архимеда. К сожалению, Снеллиусу не удалось доказать две теоремы, лежащие в основе его метода. Позднее Гюйгенс в своей работе «О найденной величине круга», написанной им в возрасте 25 лет, не только доказал теоремы Снеллиуса и развил его метод, но также смог создать новый, более мощный метод, в котором применяются некоторые свойства центра масс. Для данного многоугольника Гюйгенс увеличивал число правильных знаков π более чем втрое по отношению к знакам Архимеда. Для получения неравенства Архимеда он использовал всего лишь правильный треугольник! Взяв шестидесятиугольник, Гюйгенс нашел для π десять знаков: 3,141592653… .
Посвященные кругу работы Архимеда и Гюйгенса написаны на геометрическом языке. Сегодня было бы полезно интерпретировать эти работы в рамках дифференциального и интегрального исчисления.
9. Важным достижением в изучении числа π было выяснение его теоретико-числовой природы. В 1766 году немецкий математик, физик и астроном Иоганн Генрих Ламберт (Johann Heinrich Lambert, 1728–1777) доказал иррациональность числа π. Это означает, что π нельзя представить в виде дроби. Но можно найти бесконечную последовательность дробей приближающих π, в определенном смысле, наилучшим образом. Такие дроби называются подходящими и строятся в рамках теории цепных или, что то же самое, непрерывных дробей. Ламберт нашел для π первые двадцать семь подходящих дробей. Выпишем здесь только первые семь из них:
Важным достижением в изучении числа π было выяснение его теоретико-числовой природы. В 1766 году немецкий математик, физик и астроном Иоганн Генрих Ламберт (Johann Heinrich Lambert, 1728–1777) доказал иррациональность числа π. Это означает, что π нельзя представить в виде дроби. Но можно найти бесконечную последовательность дробей приближающих π, в определенном смысле, наилучшим образом. Такие дроби называются подходящими и строятся в рамках теории цепных или, что то же самое, непрерывных дробей. Ламберт нашел для π первые двадцать семь подходящих дробей. Выпишем здесь только первые семь из них:
.
Первая, вторая и четвертая дроби нами уже рассматривались (и это не случайно).
Наконец, в 1882 году немецкий математик Карл Луис Фердинанд Линдеман (Ferdinand von Lindemann, 1852–1939) доказал, что π – трансцендентное число. Это означает, что π не может быть корнем какого-либо многочлена с целыми коэффициентами — то есть не является алгебраическим числом.
|
В год доказательства иррациональности π немецкий астроном Иоганн Даниель Тициус (Johann Daniel Titius, 1729–1796) опубликовал закон планетных расстояний, в котором неожиданно появляется последовательность Архимеда, сыгравшая важную роль в доказательстве знаменитого неравенства для π. Приняв расстояние Сатурна от Солнца за 100 единиц, Тициус представил расстояния планет от Солнца следующим образом:
Приняв расстояние Сатурна от Солнца за 100 единиц, Тициус представил расстояния планет от Солнца следующим образом:
Знаком вопроса отмечено место, где, как предполагал Тициус, предстоит что-то открыть. В XIX веке в этом месте открыли кольцо астероидов. Интересно, что Ламберт в 1761 году поставил следующий вопрос: «Кто знает, нет ли недостающих планет в обширном пространстве между Марсом и Юпитером, которые будут когда-нибудь обнаружены?». Мы видим, что последовательность Тициуса для планетных расстояний получается в результате суммирования последовательности Архимеда с постоянной последовательностью четверок. Позднее этот закон стали называть законом Тициуса–Боде, несмотря на то, что открыл его только один человек — Тициус.
10. В заключение укажем на связь числа π с многомерными сферами и шарами. Сферой в n -мерном евклидовом пространстве называется множество точек этого пространства, удаленных от данной точки на расстояние R . Шаром в n -мерном евклидовом пространстве называется множество точек этого пространства, удаленных от данной точки на расстояние, не превышающее R . Объем n- мерной сферы и объем n- мерного шара пропорциональны R n . Объем одномерной сферы – это длина окружности, а объем двумерной сферы – это площадь обычной сферы. Объем одномерного шара – это длина отрезка, объем двумерного шара – это площадь круга, а объем трехмерного шара – это объем обычного шара. В формулы объемов многомерных сфер и шаров, которые можно найти в математических справочниках, входит число π.
Объем n- мерной сферы и объем n- мерного шара пропорциональны R n . Объем одномерной сферы – это длина окружности, а объем двумерной сферы – это площадь обычной сферы. Объем одномерного шара – это длина отрезка, объем двумерного шара – это площадь круга, а объем трехмерного шара – это объем обычного шара. В формулы объемов многомерных сфер и шаров, которые можно найти в математических справочниках, входит число π.
Известные формулы для окружности, круга, сферы и шара не содержат способа вычисления входящего в эти формулы числа π. Поэтому при работе с этими формулами необходимо каким-то образом дополнительно задать π. Но вот что интересно. Если мы рассмотрим все множество формул для многомерных сфер и шаров, позволяющих находить их объемы, то при работе с этими формулами нет необходимости задавать π дополнительно. Дело в том, что, при естественном условии монотонности последовательности отношений объемов n –мерных шаров и n –мерных сфер для всех натуральных значений n , сами формулы однозначно определяют числовое значение π.
π символизирует связь круглого с прямолинейным.
- Фото
- (Creative Commons license): fdecomite
В настоящее время с числом π связано труднообозримое множество формул, математических и физических фактов. Их количество продолжает стремительно расти. Всё это говорит о возрастающем интересе к важнейшей математической константе, изучение которой насчитывает уже более двадцати двух веков.
Павел Антонюк
Теги
- Теория
Формула для вычисления длины окружности. Касательная к окружности
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.

Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.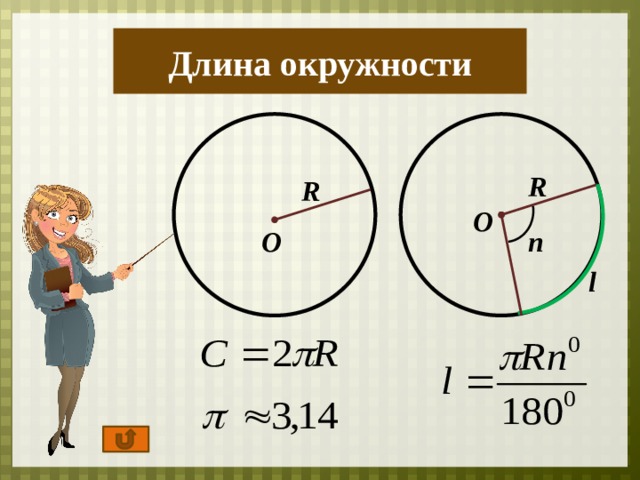
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ.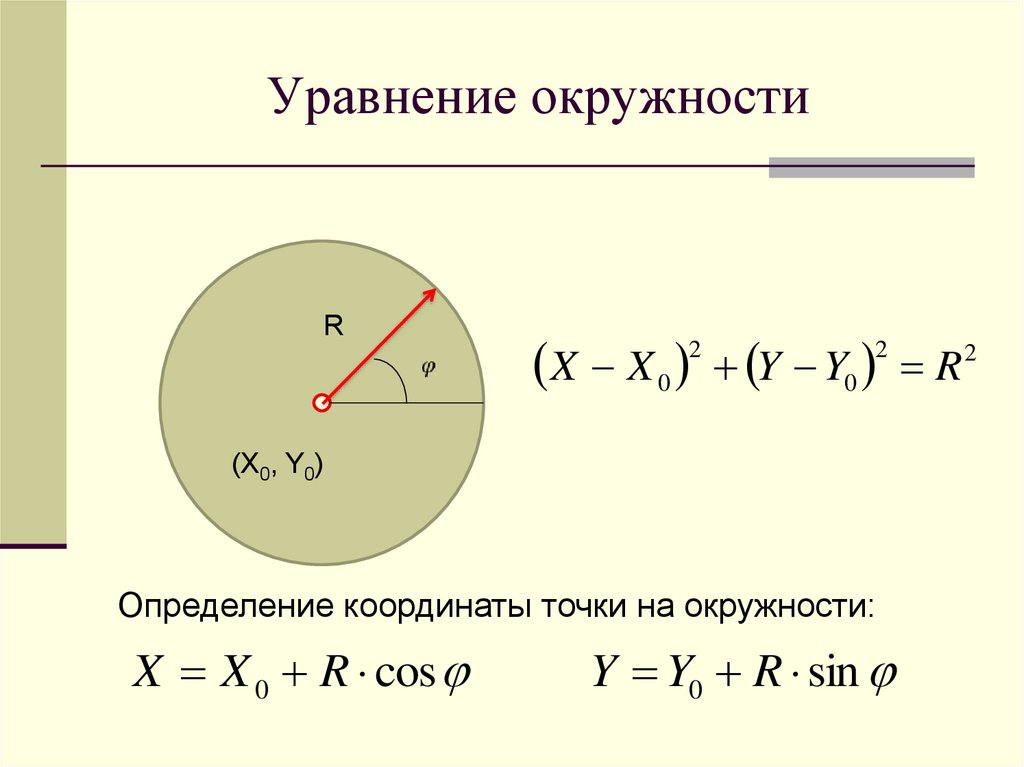 В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы.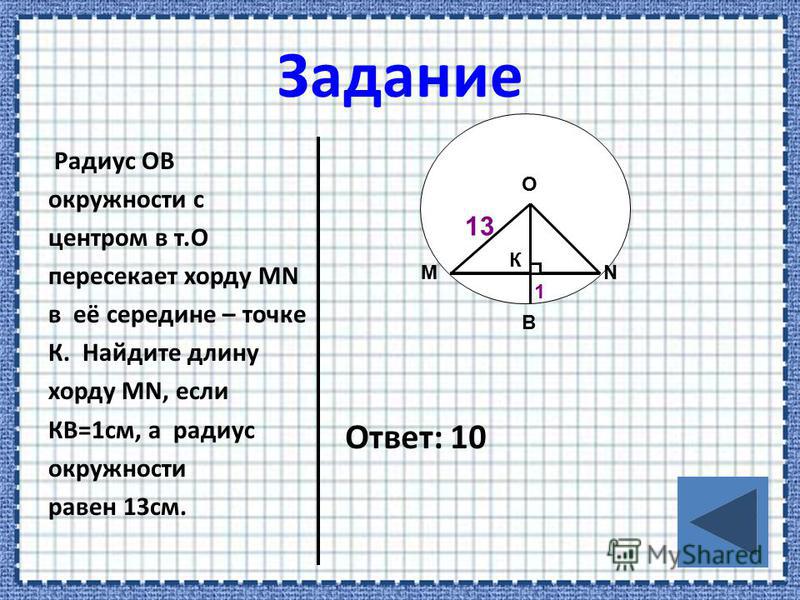 Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Что такое Круг и его свойства? (определение, формулы, примеры)
Окружность – это замкнутая форма, образованная путем отслеживания точки, которая движется в плоскости таким образом, что ее расстояние от данной точки постоянно.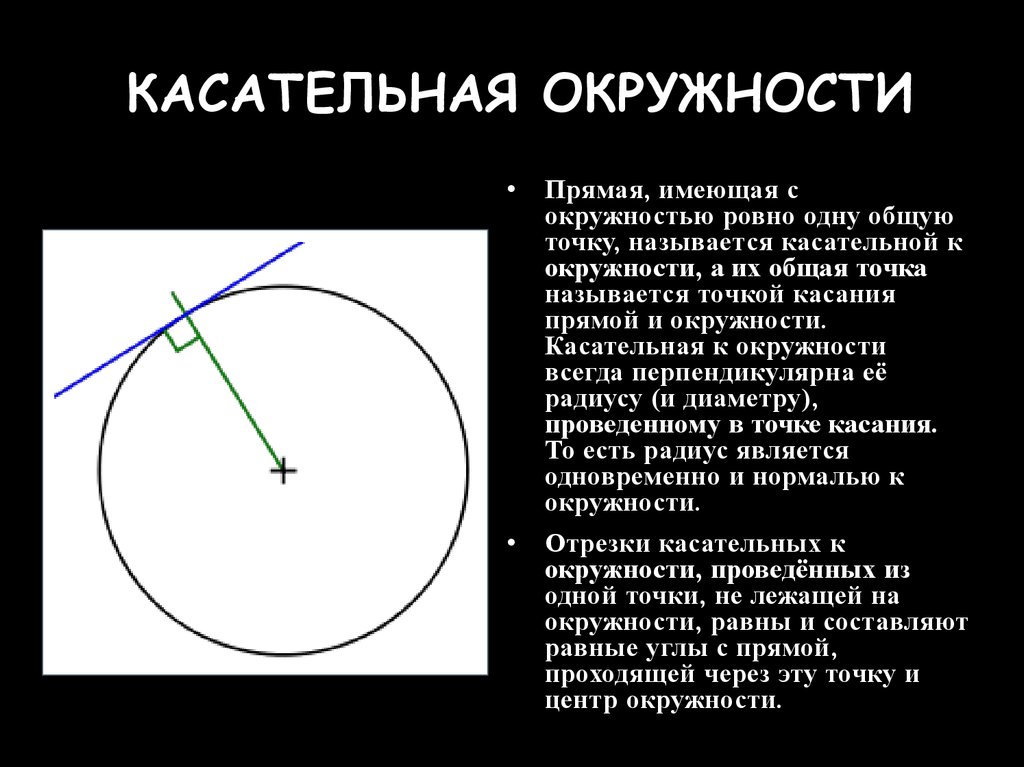 Слово «круг» происходит от греческого слова «киркос», что означает обруч или кольцо. в этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов.
Слово «круг» происходит от греческого слова «киркос», что означает обруч или кольцо. в этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов.
Ниже приводится краткое описание тем, которые мы рассмотрим в этой статье:
- Определение окружности
- Важные термины, связанные с Кругами
- Центр
- Радиус
- Диаметр
- Окружность
- Арка
- Сектор
- Полукруг
- Важные свойства кругов — связанные с линиями
- Аккорд
- Касательная
- Важные свойства круга – связанные с углами и кругами
- Вписанный угол
- Центральный угол
- Важные формулы круга
- Периметр – Формула окружности
- Площадь – Формула круга
Определение окружности
Когда набор всех точек , находящихся на фиксированном расстоянии от фиксированной точки , соединяется, то полученная геометрическая фигура называется окружностью.
Давайте теперь немного узнаем о терминологии, используемой в кругах.
Термины, относящиеся к окружностям
Центр
Фиксированная точка окружности называется центром.
- Итак, набор точек находится на фиксированном расстоянии от центра круга.
Радиус
Радиус — это фиксированное расстояние между центром и набором точек. Обозначается «R» .
Диаметр
Диаметр – это отрезок, имеющий в качестве концов граничные точки окружностей и проходящий через центр.
- Итак, логически диаметр можно разбить на две части:
- Одна часть от одной граничной точки круга до центра
- А, другая часть от центра до другой пограничной точки.
- Следовательно, диаметр = удвоенная длина радиуса или «D = 2R»
Окружность
Это мера внешней границы круга.
Итак, длина окружности или периметр окружности называется Окружность.
Дуга окружности
Дуга окружности является частью окружности.
Из любых двух точек, лежащих на границе круга, можно создать две дуги: Малую и Большую дуги.
- Малая дуга: Более короткая дуга, созданная двумя точками.
- Большая дуга: Более длинная дуга, созданная двумя точками.
Сектор круга:
Сектор образован соединением концов дуги с центром.
- При соединении концов с центром получится два сектора: Малый и Большой.
- По умолчанию мы рассматриваем только Малый сектор, если не указано иное.
Полукруг
Полукруг составляет половину круга или,
- Полукруг получается, когда круг делится на две равные части.
Теперь, когда мы знаем все термины, связанные с кругами, давайте узнаем о свойствах круга.
Геометрия — важная тема для первоклассников, если вы планируете набрать 700+ баллов на GMAT.
Позвольте нам помочь вам достичь мастерства в геометрии GMAT. Начните с регистрации на бесплатную пробную версию и учитесь у лучших в отрасли. В конце концов, мы самая популярная компания на gmatclub.
Кэрри Лоу, Гильермо, Сириш и Рагхав — лишь немногие из студентов, получивших оценку Q50+ в разделе GMAT Quant с помощью e-GMAT.
Важные свойства круга – линии
Свойства, относящиеся к линиям окружности
Хорда
Хорда — это отрезок прямой, концы которого лежат на границе окружности.
Свойства хорды
- Перпендикуляр, опущенный из центра, делит хорду на две равные части.
Касательная
Касательная — это линия, которая касается окружности в любой точке.
Свойства касательной
- Радиус всегда перпендикулярен касательной в точке, где она касается окружности.
Важные свойства окружности – относящиеся к углам
Свойства, относящиеся к углам окружности
Вписанный угол
Вписанный угол – это угол, образованный между двумя хордами, когда они пересекаются на границе круга.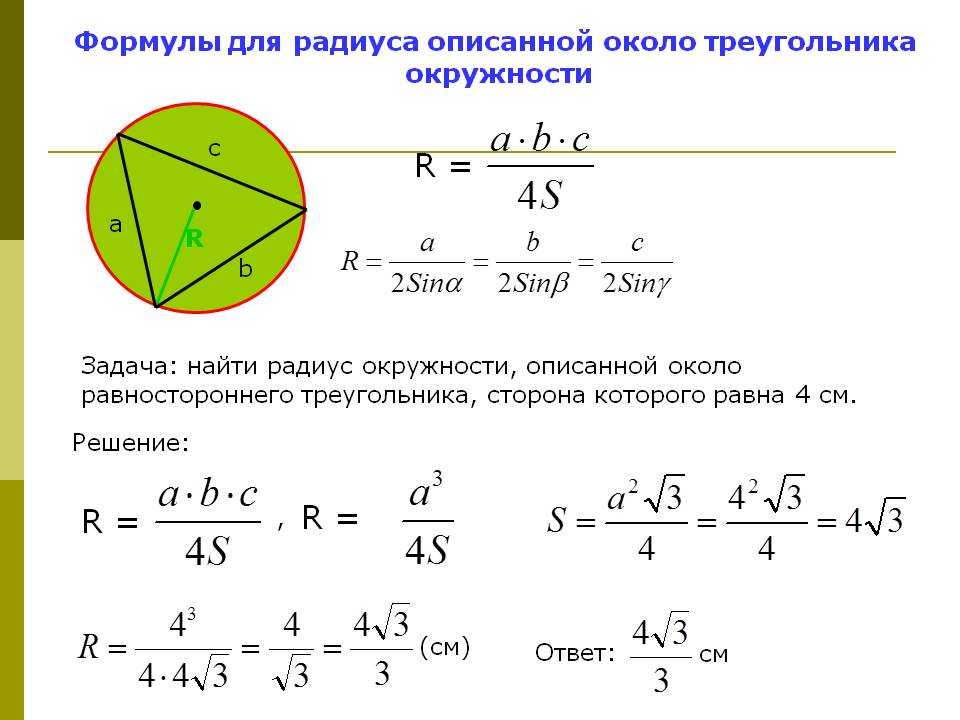
Свойства вписанных углов
1. Углы, образованные одной дугой на окружности, всегда равны.
2. Угол в полуокружности всегда равен 90°. Центральный угол
Центральный угол — это угол, образованный при пересечении двух отрезков, так что одна из конечных точек обоих отрезков находится в центре а другой находится на границе круга.
Свойство центральных углов
- Угол, образованный дугой в центре, в два раза больше вписанного угла , образованного той же дугой.
Важные формулы окружности: площадь и периметр
Ниже приведены некоторые математические формулы, которые помогут вам рассчитать площадь и периметр/длину окружности.
Периметр:
- Периметр или длина окружности = 2 × π × R.
- Длина дуги = (центральный угол дуги/360°) × 2 × π × R.
Площадь:
- Площадь круга = π × R²
- Площадь сектора = (центральный угол сектора/360°) × π × R².

Сводка всех свойств круга
Вот краткий список всех свойств, которые мы узнали в статье до этого момента. Важные свойства
2. Угол в полуокружности всегда равен 90.
| (Центральный угол дуги/360°) × 2 × π × R |
| (Центральный угол дуги/360°) × π × R² |
Применение свойств в вопросах
Вопрос 1
Длины двух сторон в прямоугольном треугольнике, кроме гипотенузы, равны 6 см и 8 см. Если этот прямоугольный треугольник вписан в окружность, то какова площадь этой окружности?
Если этот прямоугольный треугольник вписан в окружность, то какова площадь этой окружности?
- 5 №
- 10 №
- 15 №
- 20 №
- 25 №
Решение
Шаг 1: Дано
- Длины двух сторон прямоугольного треугольника, кроме гипотенузы, равны 6 см и 8 см.
- Этот треугольник вписан в окружность.
Шаг 2: Найти
- Площадь круга.
Шаг 3: Подход и разработка
Нарисуем схематическое изображение.
Применяя свойство, что угол в полуокружности равен 90º, мы можем сказать, что AB является диаметром окружности.
- И, как только мы найдем длину диаметра, мы можем найти радиус, а затем мы также можем найти площадь круга.
Применение теоремы Пифагора в △ ABC,
- AB² = AC² + BC²
- AB² = 6² + 8² = 36 + 64 = 100
- АВ = 10 см
Поскольку AB — это диаметр, AB = 2R = 10
- Следовательно, R = 5 см.

Площадь круга = π × R²= π × 5² = 25 π.
Следовательно, правильный ответ – вариант E.
Вопрос 2
На приведенной выше диаграмме O является центром круга. Если OB = 5 см и ∠ABC = 30 0 , то какова длина дуги AC?
- 5π/6
- 5π/3
- 5π/2
- 5π
- 10π
Решение
Шаг 1: Дано
- ОВ = 5 см
- ∠ABC = 30°
Шаг 2: Найти
- Длина дуги
Этап 3: Подход и отработка
- Длина дуги = (центральный угол дуги/360°) × 2 × π × R.
Чтобы найти длину дуги, нам нужно значение двух переменных: центральный угол дуги и радиус.
- Нам уже дан радиус OB = 5см
- Нам нужно найти ∠AOC
При визуализации диаграммы вписанный угол дугой AC равен ∠ABC, а центральный угол дугой AC равен ∠AOC.
- Следовательно, мы можем применить свойство, согласно которому угол, образованный дугой в центре, вдвое больше вписанного угла, образованного той же дугой.

- Таким образом, ∠AOC = 2 × ∠ABC = 2 × 30° = 60°
Теперь мы знаем и центральный угол, образованный дугой.
- Следовательно, длина дуги AC = (центральный угол дуги/360°) × 2 × π × R.
- =(60°/360°) × 2 × π × 5.
- = (1/6) × 2 × π × 5.
- =(5π/3) см
Таким образом, правильный ответ – вариант Б.
Если вам понравилась эта статья, вот еще несколько статей, связанных с геометрией:
- Треугольник – формулы и понятия (часть 1)
- Треугольник – Формулы и понятия (часть 2)
- Треугольник – Формулы и понятия (часть 3)
- Наиболее распространенные ошибки в вопросах по геометрии — GMAT Quant
Круговые уравнения
Круг сделать легко:
Нарисуйте кривую на расстоянии
«радиуса» от центральной точки.
И так:
Все точки находятся на одинаковом расстоянии
от центра.
На самом деле определение круга равно
Окружность: Набор всех точек на плоскости, находящихся на фиксированном расстоянии от центра.
Круг на графике
Нанесем на график окружность радиусом 5:
Теперь давайте вычислим ровно , где находятся все точки.
Делаем прямоугольный треугольник:
А затем используйте Пифагор:
x 2 + у 2 = 5 2
Таких точек бесконечное количество, вот несколько примеров:
| х | г | x 2 + у 2 |
|---|---|---|
| 5 | 0 | 5 2 + 0 2 = 25 + 0 = 25 |
| 3 | 4 | 3 2 + 4 2 = 9 + 16 = 25 |
| 0 | 5 | 0 2 + 5 2 = 0 + 25 = 25 |
| −4 | −3 | (-4) 2 + (-3) 2 = 16 + 9 = 25 |
| 0 | −5 | 0 2 + (−5) 2 = 0 + 25 = 25 |
Во всех случаях точка на окружности следует правилу x 2 + y 2 = радиус 2
Мы можем использовать эту идею, чтобы найти пропущенное значение
Пример:
x Значение 2, и A RADIUS из 5Начало с: x 2 + y 2 = R 2
Значения Мы знаем: 2 2 + y 2 2 2 2 2 2 2 2 2 2 2 . Перестановка: Y 2 = 5 2 — 2 2 квадратный корень с обеих сторон: y = ± √ (5 2 — 2 2 ) 2 — 2 2 ) 9000VE √21 y ≈ ±4,58… ( ± означает, что есть два возможных значения: одно с + другой с − ) А вот и две точки: Теперь поместим центр в (a,b) Таким образом, круг равен всем точкам (x,y) , которые находятся на расстоянии «r» от центра (a,b) . Теперь давайте выясним, где находятся точки (используя прямоугольный треугольник и Пифагор): Это та же идея, что и раньше, но нам нужно вычесть a и b : (х-а) 2 + (у-б) 2 = г 2 И это «Стандартная форма» для уравнения окружности! Сразу показывает всю важную информацию: центр (a,b) и радиус r . Начните с: (x-a) 2 + (y-b) 2 = r 2 Вставьте (a,b) и r: (x-7 3) 2 Затем мы можем использовать наши навыки алгебры, чтобы упростить и изменить это уравнение в зависимости от того, для чего оно нам нужно. изображения/circle-equn.js Но вы можете видеть уравнение окружности и не знать его ! Потому что это может не быть в аккуратной «Стандартной форме» выше. В качестве примера давайте присвоим несколько значений a, b и r, а затем расширим их Начните с: (x−a) 2 + (y−b) 2 = r 2 Пример: a=1, b=2, r=3:(x−1) 2 + (y−2) 2 = 3 2 Развернуть: x 2 − 2x + 1 + y 2 − 4y + 4 = 9 Собрать подобные члены: x 2 2 — 2х — 4у + 1 + 4 — 9 = 0 И получаем вот это: х 2 + у 2 — 2х — 4у — 4 = 0 Это уравнение окружности, но «замаскированное»! Так что, когда вы видите что-то подобное, подумайте «хм. На самом деле мы можем записать это в «Общая форма» , поставив константы вместо чисел: х 2 + у 2 + Ax + By + C = 0 Примечание. Общая форма всегда имеет x 2 + y 2 для первых двух членов . Теперь представьте, что у нас есть уравнение в общей форме : x 2 + y 2 + Ax + By + C = 0 Как мы можем ввести его в стандартную форму вот так? (х-а) 2 + (у-б) 2 = г 2 Ответ: Завершить квадрат (читайте об этом) дважды… один раз для x и один раз для y : Начните с: x 2 + y 2 — 2x — 4y — 4 = 0 и y s вместе: (x 2 − 2x) + (y 2 − 4y) − 4 = 0 Константа справа: (x 2 − 2x) + (y 2 − 4y) = 4 Теперь заполните квадрат для x (возьмите половину −2, возведите в квадрат и прибавьте к обеим сторонам): (x 2 − 2x + (−1) 2 ) + (y 2 − 4y) = 4 + (−1) 2 И завершите квадрат для y (взять половину −4, возвести в квадрат и прибавить к обеим сторонам) : (x 2 — 2x + (-1) 2 ) + (y 2 — 4y + (-2) 2 ) = 4 + (-1) 2 + (-2 ) 2 Убрать: Упростить:(x 2 − 2x + 1) + (y 2 − 4y + 4) = 9 Наконец: (x − 1) 2 + (y) − 2) 2 = 3 2 И это у нас есть в стандартной форме! (Примечание: здесь использовался предыдущий пример a=1, b=2, r=3, так что мы поняли правильно!) Если мы поместим центр круга в (0,0) и установим радиус равным 1, мы получим: (х-а) 2 + (у-б) 2 = г 2 (х-0) 2 + (у-0) 2 = 1 2 х 2 + у 2 = 1 1. 2. Нанесите 4 точки «радиуса» от центра вверх, вниз, влево и вправо 3. Зарисуйте! Формула для окружности: (x−a) 2 + (y−b) 2 = r 2 Таким образом, центр составляет (4,2) и R 2 IS 25 , так что радиус √25 = 5 Итак, мы можем сюжет: Итак, мы можем. Центр: (4,2) А теперь просто нарисуйте круг как можно лучше! Нам нужно изменить формулу, чтобы мы получили «y=». У нас должно получиться два уравнения (вверху и внизу круга), которые затем можно построить. Таким образом, центр находится в точке (4,2), а радиус равен √25 = 5 Переставить, чтобы получить «y=»: Начать с: (x−4) 2 + (y−2) 2 = 25 Переместить (x−4) 2 вправо: ( y−2) 2 = 25 − (x−4) 2 Извлечем квадратный корень: (y−2) = ± √[25 − (x−4) 2 ] (замечание ± «плюс/минус» … Переместите «-2» вправо: y = 2 ± √[25 — (x-4) 2 ] Итак, когда мы построим эти два уравнения, у нас должен быть круг: Попробуйте изобразить эти функции на графике функций. Также можно использовать Equation Grapher, чтобы сделать все за один раз. 8526, 8527, 8539, 8540, 8515, 8516, 569, 8544, 8559, 8560, 570, 1209 ОкружностьОкружность — это набор точек на плоскости, которые лежат на фиксированном расстоянии от заданной точки, называемой центром. В прямоугольной координатной плоскости, где центром круга с радиусом r является (h,k), мы имеем Рассчитаем расстояние между (h,k) и (x,y), используя формулу расстояния, (x−h)2+(y−k)2=r Возведение обеих сторон в квадрат приводит к уравнению окружности в стандартной формеУравнение окружности записывается в виде (x−h)2+(y −k)2=r2, где (h,k) — центр, а r — радиус., (x−h)2+(y−k)2=r2 В этой форме центр и радиус очевиден. Например, учитывая уравнение (x−2)2+ (y + 5)2=16, мы имеем, (x−h)2+ (x−k)2=r2↓↓↓(x−2)2+[y−(−5)]2=42 В этом случае центр равен (2, −5) и r=4. График круга полностью определяется его центром и радиусом. График: (x−2)2+(y+5)2=16. Решение: Записав эту форму, мы увидим, что центр равен (2,−5) и что радиус r=4 единицы. От центра отметьте точки на 4 единицы вверх и вниз, а также на 4 единицы влево и вправо. Затем нарисуйте круг через эти четыре точки. Ответ: Как и на любом графике, нас интересует нахождение точек пересечения x и y . Найдите точки пересечения: (x−2)2+(y+5)2=16. Решение: Чтобы найти y -отрезков, установите x=0: (x−2)2+(y+5)2=16(0−2)2+(y+5)2= 164+(y+5)2=16 Это уравнение можно решить, извлекая квадратные корни. (y+5)2=12y+5=±12y+5=±23y=−5±23 Следовательно, y -перехваты равны (0,−5−23) и (0,−5+23). Чтобы найти x -отрезков, установите y=0: (x−2)2+(y+5)2=16(x−2)2+(0+5)2=16(x−2) 2+25=16(x−2)2=−9x−2=±−9x=2±3i И поскольку решения сложные, мы заключаем, что не существует реальных x -отрезков. Ответ: x -перехваты: нет; y -пересечения: (0,−5−23) и (0,−5+23) Зная центр и радиус окружности, мы можем найти ее уравнение. Нарисуйте окружность радиусом r=3 единицы с центром в точке (−1,0). Приведите его уравнение в стандартной форме и определите точки пересечения. Решение: Учитывая, что центр равен (−1,0) и радиус равен r=3, нарисуем график следующим образом: в стандартной форме. Поскольку (h,k)=(−1,0) и r=3, имеем (x−h)2+(y−k)2=r2[x−(−1)]2+(y− 0)2=32(х+1)2+у2=9 Уравнение окружности (x+1)2+y2=9, используйте его для определения y -пересечений. (x+1)2+y2=9 Приложить x=0 к и решить для y.(0+1)2+y2=91+y2=9y2=8y=±8y=±22 Следовательно, y -пересечения равны (0,−22) и (0,22). Чтобы алгебраически найти x -перехватов, установите y=0 и найдите x ; это оставлено читателю в качестве упражнения. Ответ: Уравнение: (x+1)2+y2=9; y — точки пересечения: (0,−22) и (0,22); х — точки пересечения: (−4,0) и (2,0) Особое значение имеет единичный круг. Окружность с центром в начале координат и радиусом 1; его уравнение x2+y2=1., x2+y2=1 Или, (x−0)2+(y−0)2=12 В этой форме должно быть ясно, что центр равен (0,0), а радиус равен 1 единице. Кроме того, если мы найдем y , мы получим две функции: x2+y2=1y2=1−x2y=±1−x2 функция, определяемая выражением y=−1−x2, является нижней половиной единичного круга: Попробуйте! Постройте график и обозначьте точки пересечения: x2+(y+2)2=25. Ответ: (щелкните, чтобы посмотреть видео) Мы видели, что график окружности полностью определяется центром и радиусом, которые можно прочитать из уравнения в стандартной форме. Однако уравнение не всегда дается в стандартной форме. x2+y2+cx+dy+e=0 Здесь c , d и e — действительные числа. Ниже приведены шаги для построения графика окружности с учетом ее уравнения в общем виде. График: x2+y2+6x−8y+13=0. Решение: Начните с переписывания уравнения в стандартной форме. Шаг 1: Сгруппируйте члены с одинаковыми переменными и переместите константу в правую сторону. В этом случае вычтите по 13 с обеих сторон и сгруппируйте члены, содержащие x и термины, включающие y , следующим образом. x2+y2+6x−8y+13=0(x2+6x+___)+(y2−8y+___)=−13 Шаг 2: Заполните квадрат для каждой группы. Идея состоит в том, чтобы добавить значение, которое завершает квадрат, (b2)2, к обеим сторонам для обеих группировок, а затем разложить на множители. (x2+6x +9)+(y2−8y+16)=−13 +9+16(x+3)2+(y−4)2=12 Ответ: Определить центр и радиус: 4×2+4y2-8x+12y-3=0. Решение: Мы можем получить общий вид, разделив сначала обе части на 4. 4×2+4y2−8x+12y−34=04×2+y2−2x+3y−34=0 общий вид для круга, где оба члена степени два имеют старший коэффициент 1, мы можем использовать шаги для переписывания его в стандартной форме. Начните с добавления 34 к обеим сторонам и сгруппируйте одинаковые переменные. (x2−2x+___)+(y2+3y+___)=34 Затем заполните квадрат для обеих групп. Используйте (−22)2=(−1)2=1 для первой группы и (32)2=94 для второй группы. (x2−2x +1)+(y2+3y+94)=34 +1+94(x−1)2+(y+32)2=164(x−1)2+(y+32) 2=4 Ответ: Центр: (1,−32); радиус: r=2 Таким образом, чтобы преобразовать из стандартной формы в общую форму, мы умножаем, и чтобы преобразовать из общей формы в стандартную форму, мы завершаем квадрат. Попробуйте! График: x2+y2−10x+2y+21=0. Ответ: (нажмите, чтобы посмотреть видео) Определите центр и радиус по уравнению окружности в стандартной форме. (х-5)2+(у+4)2=64 (х+9)2+(у-7)2=121 х2+(у+6)2=4 (х-1)2+у2=1 (х+1)2+(у+1)2=7 (х+2)2+(у-7)2=8 Определите стандартную форму уравнения окружности с учетом ее центра и радиуса. Центр (5,7) с радиусом r=7. Центр (−2,8) с радиусом r=5. Центр (6,−11) с радиусом r=2. Центр (−4,−5) с радиусом r=6. Центр (0,−1) с радиусом r=25. Центр (0,0) с радиусом r=310. График. (х-1)2+(у-2)2=9 (х+3)2+(у-3)2=25 (х−2)2+(у+6)2=4 (х+6)2+(у+4)2=36 х2+(у-4)2=1 (х-3)2+у2=4 х2+у2=12 х2+у2=8 (х-7)2+(у-6)2=2 (х+2)2+(у-5)2=5 (х+3)2+(у-1)2=18 (х-3)2+(у-2)2=15 Найдите точки пересечения x и y . (х-1)2+(у-2)2=9 (х+5)2+(у-3)2=25 х2+(у-4)2=1 (х-3)2+у2=18 х2+у2=50 х2+(у+9)2=20 (х-4)2+(у+5)2=10 (х+10)2+(у-20)2=400 Найдите уравнение окружности. Окружность с центром (1,−2), проходящая через (3,−4). Окружность с центром (−4,−1), проходящая через (0,−3). Окружность, диаметр которой определяется (5,1) и (−1,7). Окружность, диаметр которой определяется (−5,7) и (−1,−5). Круг с центром (5,−2) и площадью 9π квадратных единиц. Круг с центром (−8,−3) и окружностью 12π квадратных единиц. Найдите площадь круга с помощью уравнения (x+12)2+(x−5)2=7. Найдите длину окружности с помощью уравнения (x+1)2+(y+5)2=8. Переписать в стандартной форме и графике. х2+у2+4х-2у-4=0 х2+у2-10х+2у+10=0 х2+у2+2х+12у+36=0 х2+у2-14х-8у+40=0 х2+у2+6у+5=0 х2+у2-12х+20=0 х2+у2+8х+12у+16=0 х2+у2-20х-18у+172=0 4×2+4y2−4x+8y+1=0 9×2+9y2+18x+6y+1=0 х2+у2+4х+8у+14=0 х2+у2-2х-4у-15=0 х2+у2-х-2у+1=0 х2+у2-х+у-12=0 4×2+4y2+8x−12y+5=0 9×2+9y2+12x−36y+4=0 2×2+2y2+6x+10y+9=0 9×2+9y2−6x+12y+4=0 Дана окружность общего вида, определить пересечения. х2+у2-5х+3у+6=0 х2+у2+х-2у-7=0 х2+у2-6у+2=2 х2+у2-6х-8у+5=0 2×2+2y2-3x-9=0 3×2+3y2+8y−16=0 Определите площадь круга, уравнение которого x2+y2-2x-6y-35=0. Определите площадь круга, уравнение которого 4×2+4y2-12x-8y-59=0. Определите длину окружности, уравнение которой x2+y2−5x+1=0. Определите длину окружности, уравнение которой x2+y2+5x−2y+3=0. Найдите общий вид уравнения окружности с центром в (−3,5), проходящей через (1,−2). Найдите общий вид уравнения окружности с центром в (−2,−3), проходящей через (−1,3). По графику окружности определите ее уравнение в общем виде. Является ли центр круга частью графика? Объяснять. Составьте свой собственный круг, напишите его в общем виде и начертите. Объясните, как можно отличить уравнение параболы в общем виде от уравнения окружности в общем виде. Приведите пример. Все ли круги имеют точки пересечения? Каково возможное количество перехватов? Проиллюстрируйте свое объяснение графиками. Центр: (5,−4); радиус: r=8 Центр: (0,−6); радиус: r=2 Центр: (−1,−1); радиус: r=7 (х-5)2+(у-7)2=49 (х-6)2+(у+11)2=2 х2+(у+1)2=20 х — отрезки: (1±5,0); г — отрезки: (0,2±22) x -перехваты: нет; г — точки пересечения: (0,3), (0,5) х -отсечки: (±52,0); г — точки пересечения: (0,±52) x -перехваты: нет; г -перехваты: нет (х-1)2+(у+2)2=8 (х-2)2+(у-4)2=18 (х-5)2+(у+2)2=9 7π квадратных единиц (х+2)2+(у-1)2=9; (х+1)2+(у+6)2=1; х2+(у+3)2=4; (х+4)2+(у+6)2=36; (х-12)2+(у+1)2=1; (х+2)2+(у-4)2=6; (х-12)2+(у-1)2=14; (х+1)2+(у-32)2=2; (х+32)2+(у+52)2=4; х -точки пересечения: (2,0), (3,0); г -перехваты: нет x -пересечения: (0,0); г — точки пересечения: (0,0), (0,6) х — точки пересечения: (−32,0), (3,0); г — точки пересечения: (0,±322) 45π квадратных блоков №21 шт. х2+у2+6х-10у-31=0 х2+у2-6х+10у+18=0 х2+у2+2у=0 Ответ может отличаться Ответ может отличаться Можете ли вы определить круглые объекты в вашем окружении? Более того, если эти круглые предметы положить на стол, можете ли вы описать местонахождение этого круглого предмета? Здесь вступает в игру уравнение окружности. Уравнение окружности не представляет площадь уравнения окружности. Вместо этого он обеспечивает алгебраический способ описания положения окружности или семейства окружностей на декартовой плоскости. Он содержит только координаты центра, фиксированную точку внутри круга и радиус, который представляет собой расстояние от центра до границы круга. При этом уравнение окружности обозначает все точки, лежащие на ее окружности. Так что же такое уравнение окружности? Изучив уравнение окружности, давайте узнаем, как вывести стандартное уравнение окружности. Координаты центра окружности обозначены (a, b), как показано на рисунке, а радиус представлен r, а (h, k) — произвольные точки, расположенные на окружности окружности. Общие обозначения для представления окружности используют x и y в качестве произвольных точек. Таким образом, уравнение окружности принимает вид (x – a)² + (x – y)² = r². Знаете ли вы, что уравнение окружности можно представить несколькими способами? Уравнение окружности может быть выражено в различных формах в зависимости от положения окружности в декартовой плоскости. Несколько форм представления круга: Общая форма Стандартная форма (x – x1)² + (y – y1)²= r², где (x, y) – произвольные координаты на окружности окружности, r – радиус окружности, а (x1, y1) — координаты центра окружности. Стандартная форма уравнения окружности выводится из формулы расстояния. Параметрическая форма Полярная форма Мы видели различные способы представления уравнения окружности в зависимости от положения центра окружности на декартовой плоскости. Следовательно, чтобы написать уравнение окружности, когда заданы координаты центра, можно выполнить следующие шаги: Шаг 1: Определите координаты центра круга (x 1 , y 1 ) и радиус круга. Пример 1: Найдите уравнение окружности, центр которой проходит через начало координат. Пример 2: Каким будет общее уравнение окружности, радиус которой равен 6 единицам, а центр лежит на (4, 2)? Пример 3. Найдите радиус стандартного уравнения путем преобразования следующего стандартного уравнения окружности в полярную форму: x² + y²= 25. Пример 4: Каково значение центра и радиуса окружности, если стандартное уравнение окружности (x + 7)² + (y – 9)² = 529? x 1 = -7, y 1 = 9 и r = 23. Уравнение апплета круга
92 =100 $$ — это окружность с центром в точке (9, 6) и радиусом 10 Диаграмма 1 Диаграмма 2 2
2 Более общий случай

Пример: Окружность с центром в точке (3,4) и радиусом 6:
Попробуйте сами
«Общая форма»
 .. что может быть кругом!»
.. что может быть кругом!» Переход от общей формы к стандартной форме
Пример: x
2 + y 2 — 2x — 4y — 4 = 0 Единичный круг
Как нарисовать круг вручную
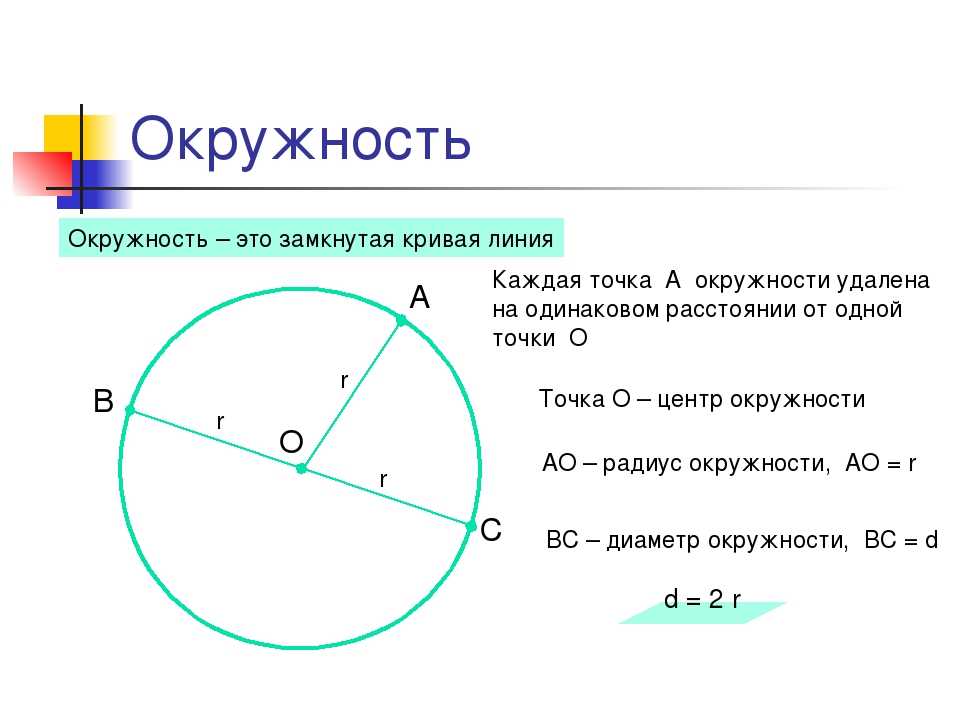 Участок центра (a,b)
Участок центра (a,b) Пример: График (x−4)
2 + (y−2) 2 = 25 Как нарисовать круг на компьютере

Пример: График (x−4)
2 + (y−2) 2 = 25
может быть два квадратных корня!) Окружности
Окружность в стандартной форме
 это множество точек на плоскости, которые лежат на фиксированном расстоянии, называемом радиусомФиксированное расстояние от центра круга до любой точки на круге., от любой точки, называемой центром. ДиаметрДлина отрезка, проходящего через центр окружности, концы которой лежат на окружности. длина отрезка, проходящего через центр, концы которого лежат на окружности. Кроме того, окружность может быть образована пересечением конуса и плоскости, перпендикулярной оси конуса:
это множество точек на плоскости, которые лежат на фиксированном расстоянии, называемом радиусомФиксированное расстояние от центра круга до любой точки на круге., от любой точки, называемой центром. ДиаметрДлина отрезка, проходящего через центр окружности, концы которой лежат на окружности. длина отрезка, проходящего через центр, концы которого лежат на окружности. Кроме того, окружность может быть образована пересечением конуса и плоскости, перпендикулярной оси конуса: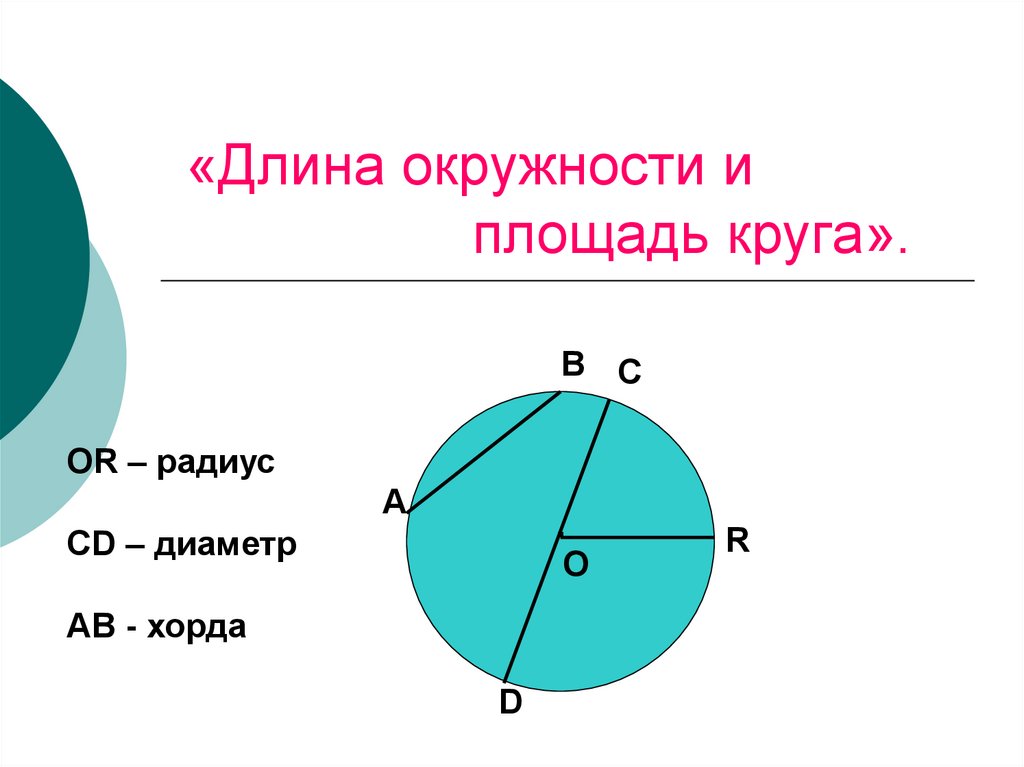 Далее следуют другие примеры:
Далее следуют другие примеры: Пример 1
Пример 2
 Обратите внимание, что это имеет смысл, учитывая график.
Обратите внимание, что это имеет смысл, учитывая график. Пример 3

Окружность в общем виде
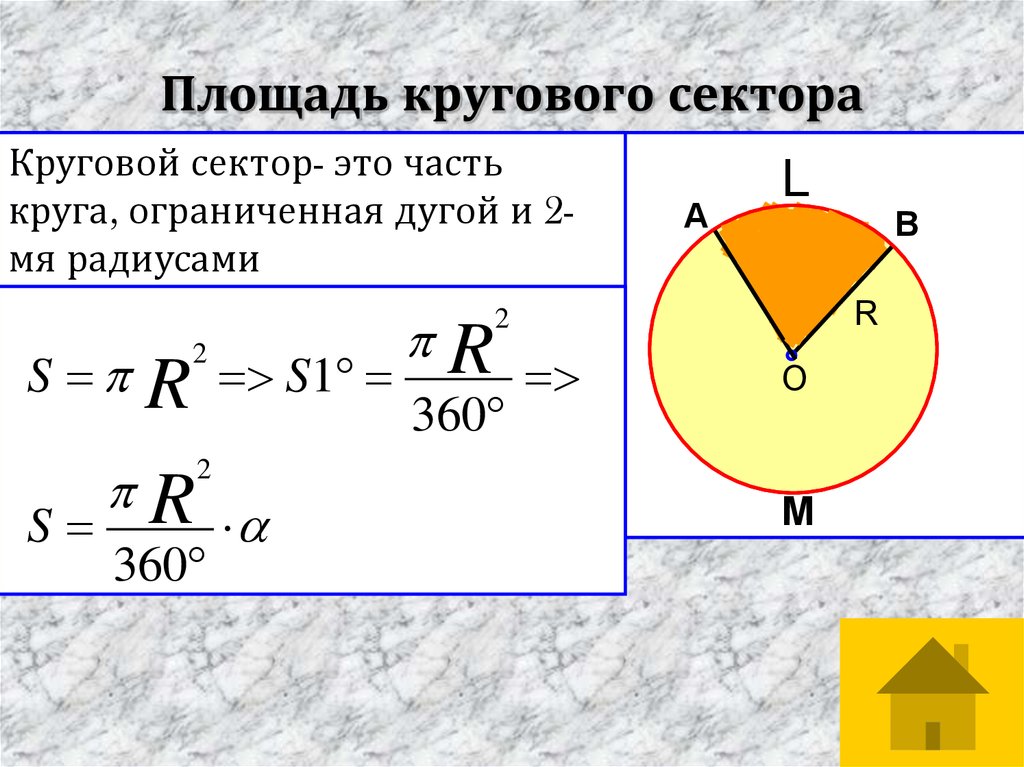 Уравнение окружности в общем видеУравнение окружности записывается в виде x2+y2+cx+dy+e=0. следует:
Уравнение окружности в общем видеУравнение окружности записывается в виде x2+y2+cx+dy+e=0. следует: Пример 4
 Для членов, включающих x , используйте (62)2=32=9, а для членов, включающих y , используйте (-82)2=(-4)2=16.
Для членов, включающих x , используйте (62)2=32=9, а для членов, включающих y , используйте (-82)2=(-4)2=16. Пример 5

Ключевые выводы
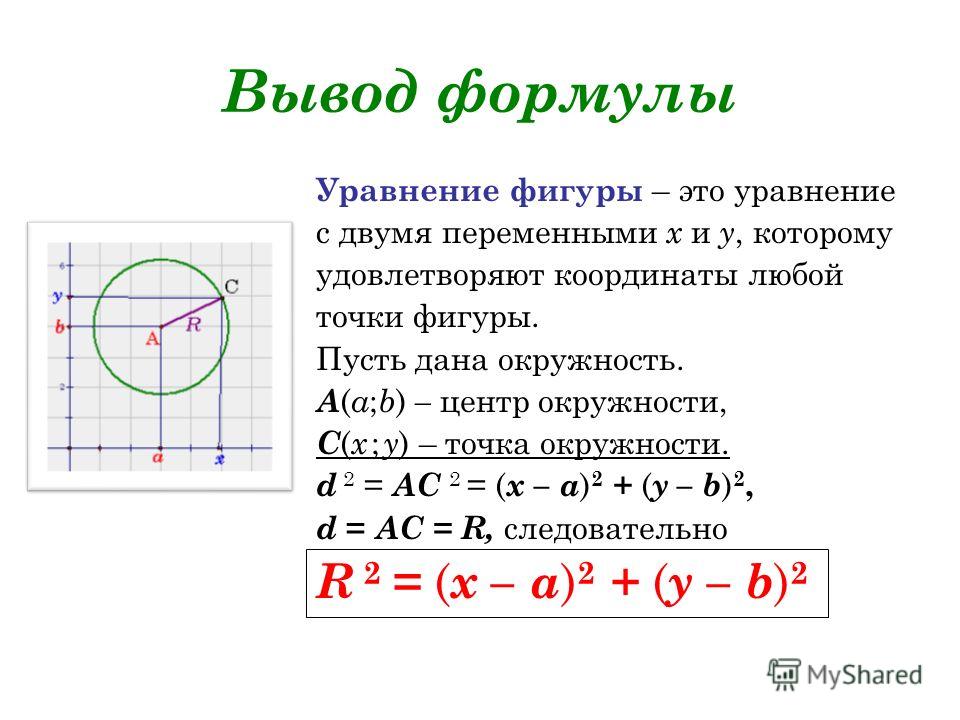
Тематические упражнения
Часть A: Круг в стандартной форме
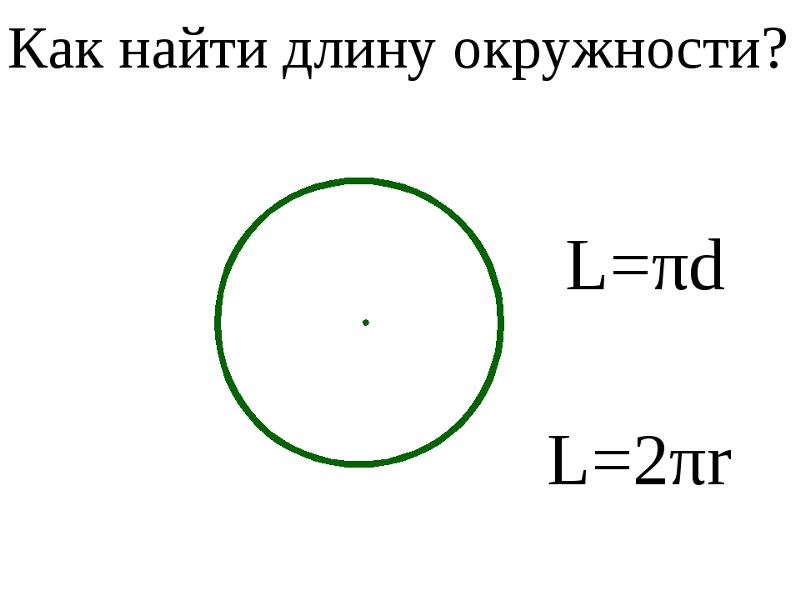


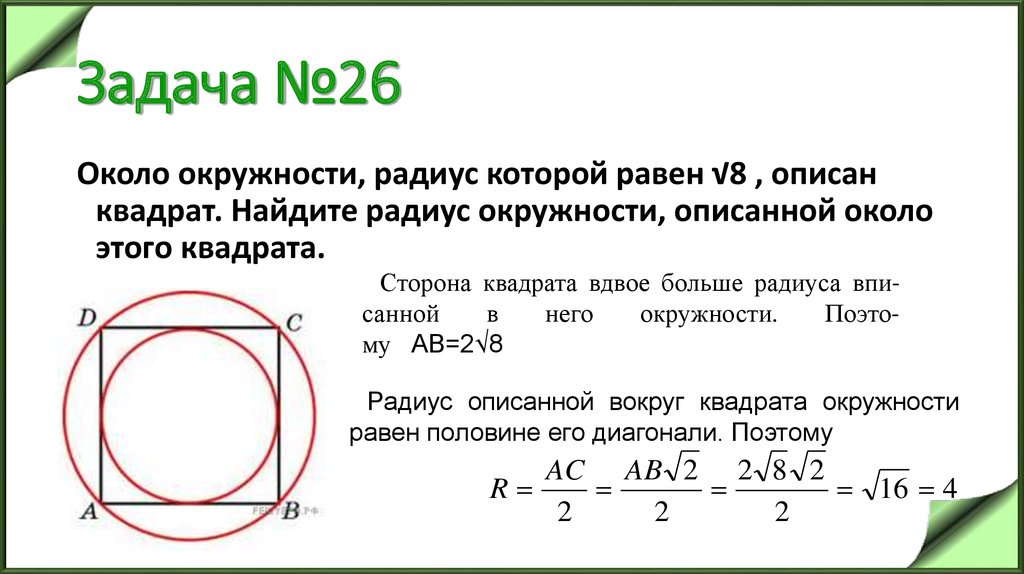
Часть B: Круг в общей форме
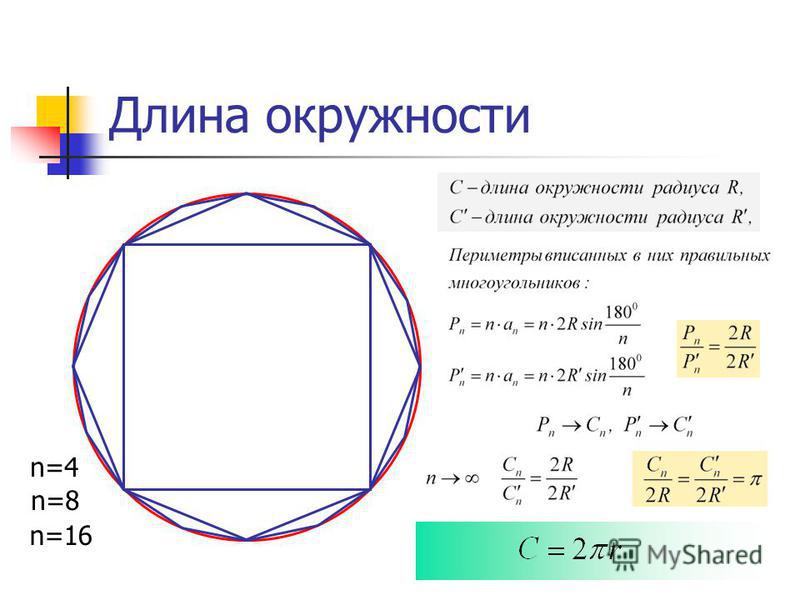
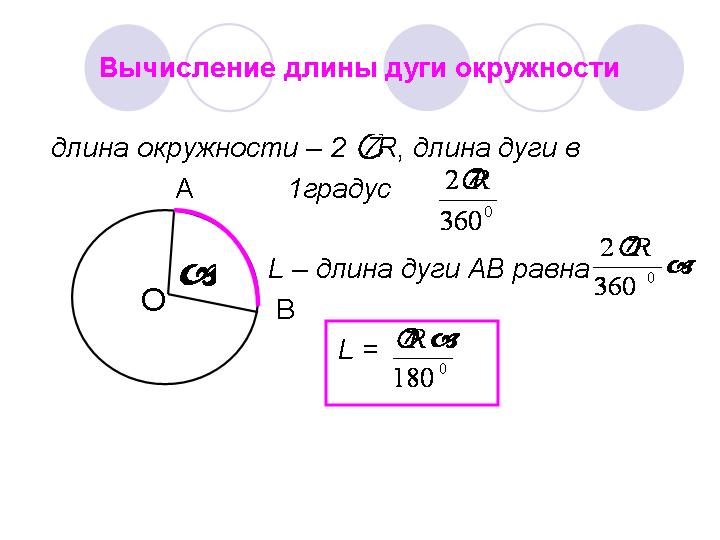
Часть C: Дискуссионная доска
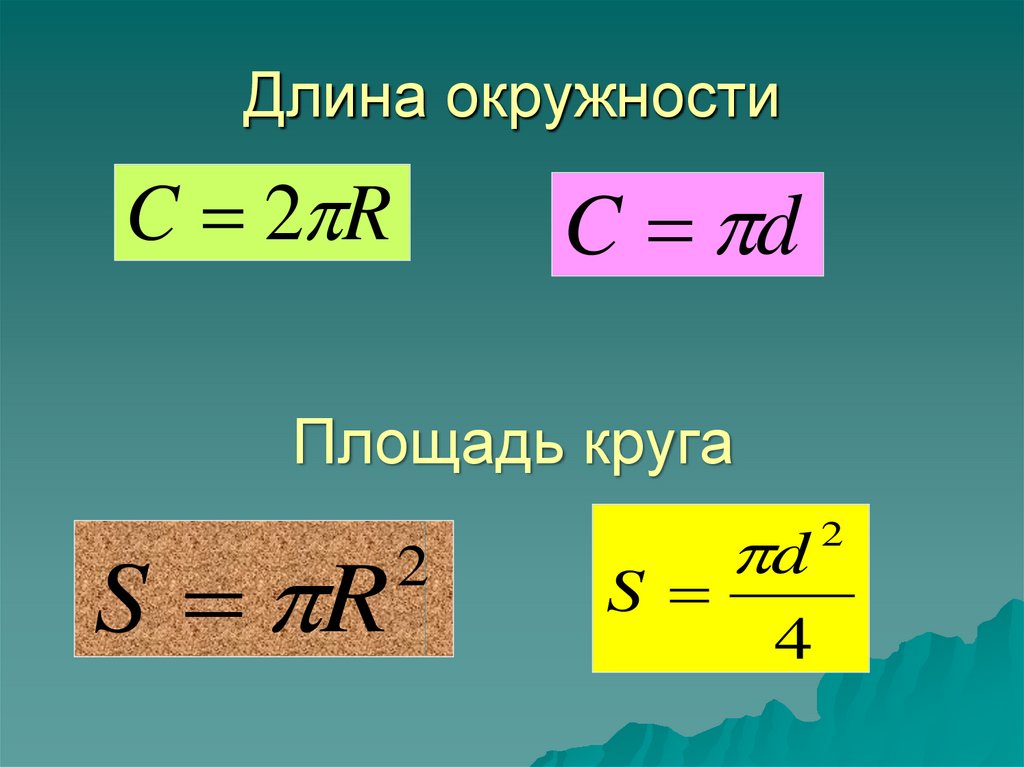
Ответы



Уравнение окружности с примерами

Расстояние между произвольной точкой и центром окружности равно радиусу окружности. Из формулы расстояния получаем
√(h-a)²+(k-b)²=r
Возводя в квадрат обе стороны, получаем
(h – a)²+ (k – b)² = r², что является стандартным уравнением окружности.
Однако это представление уравнения окружности не единственное, которое используется во всем мире. Есть также несколько других форм обозначения. Различные формы представления уравнения окружности
x2 + y2 + 2gx + 2fy + c = 0 — это общая форма уравнения окружности. x и y — произвольные точки на окружности, а g, f и c — константы. Эта общая форма уравнения используется для определения радиуса и координат центра окружности. В отличие от стандартной формы уравнения окружности, общая форма сложна для понимания и поиска некоторых значимых свойств окружности.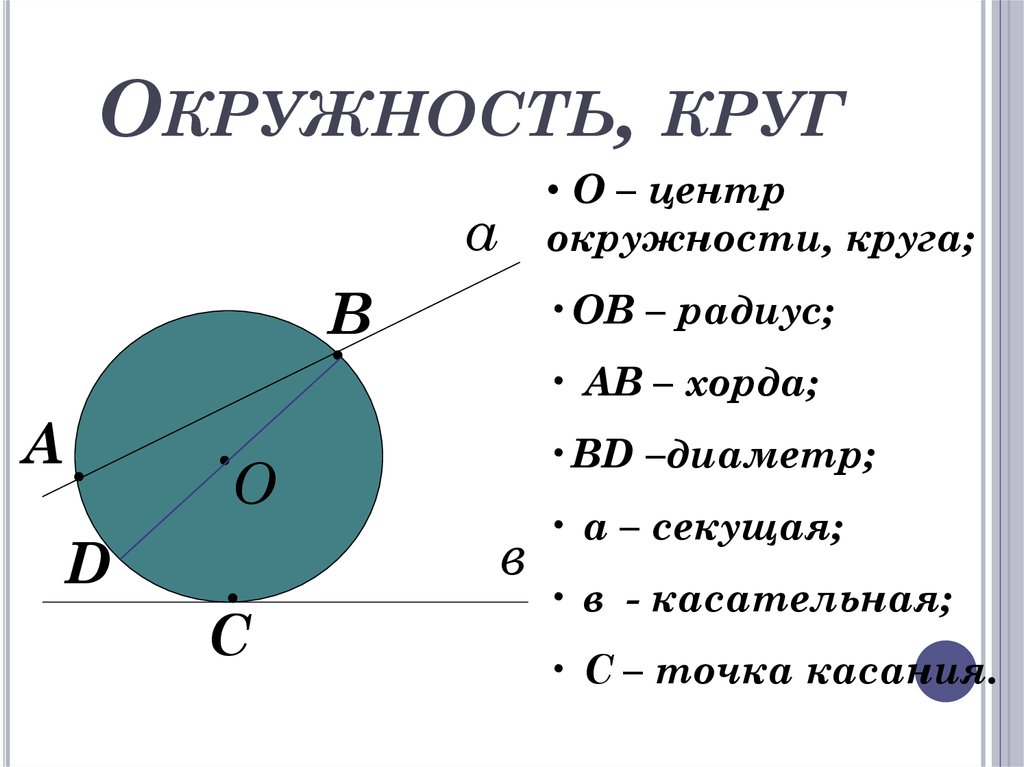 Однако общая форма уравнения окружности помогает найти семейство окружностей на декартовой плоскости.
Однако общая форма уравнения окружности помогает найти семейство окружностей на декартовой плоскости.
Большинство ученых и математиков используют уравнение стандартной формы окружности, потому что оно дает точную информацию о центре и радиусе окружности. Более того, уравнение окружности стандартной формы легче понять и прочитать. Уравнение стандартной формы окружности имеет вид:
Чтобы найти параметрическую форму уравнения окружности, выведите общую форму окружности x² + y² + 2hx + 2ky + C = 0. Для этого возьмите общую точку на границе окружности, например, (x, y), и соедините эту общую точку с центром окружности (-h. -k). Когда эти точки соединяются, они образуют угол 𝜃. Поэтому параметрическое уравнение окружности можно записать так: x²+ y²+ 2hx + 2ky + C = 0, где x = -h + r cos𝜃 и y =k + r sin𝜃.
Поэтому параметрическое уравнение окружности можно записать так: x²+ y²+ 2hx + 2ky + C = 0, где x = -h + r cos𝜃 и y =k + r sin𝜃.
Представление полярной формы аналогично параметрической форме уравнения окружности. Полярная форма в основном используется для представления уравнения окружности, центр которой находится в начале координат. Для этого возьмем произвольную точку A с координатами (r cos𝜃, r sin𝜃) на периферии окружности и радиусом r — расстоянием между случайной точкой и началом координат. Уравнение окружности с радиусом A и центром в начале координат будет иметь вид x²+ y² = A².
Подставляя значения x = r cos𝜃 и y = r sin𝜃, получаем
(r cos𝜃)² + (r sin𝜃)² = A²
r²cos²θ + r²sin²θ = A²
r²(cos²θ + sin²θ) = A²
r²( 1) = A²(Поскольку cos²θ + sin²θ = 1 из тригонометрических тождеств)
r = A
, где p — радиус окружности. Таким образом, полярная форма используется для нахождения радиуса окружности из стандартной формы уравнения окружности.
Шаги по нахождению уравнения окружности
Шаг 2: С помощью уравнения формулы окружности (x -x 1 )² + (y – y 1 )² = r² выделить значения радиуса и центра окружности.
Шаг 3: После упрощения уравнения получится уравнение окружности.
Решение: Мы знаем, что уравнение окружности имеет вид
(x – x 1 )² + (y -y 1 )² = r², где x 1 и y 1 — координаты центра окружности, r — радиус.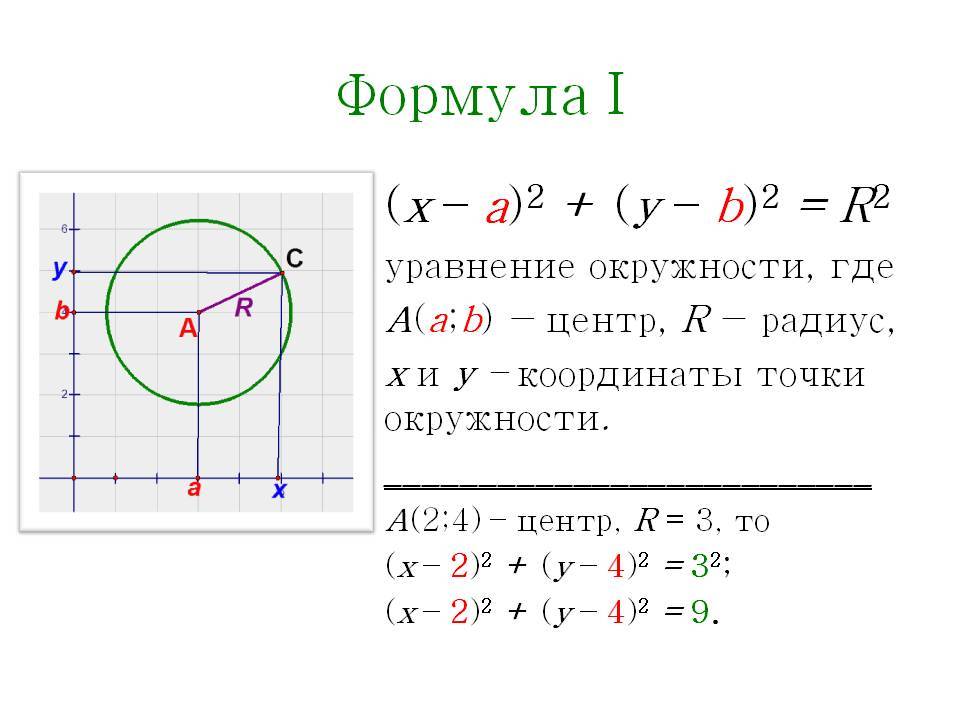
Поскольку окружность проходит через начало координат, значения x 1 и y 1 будут равны нулю.
Следовательно, стандартное уравнение окружности, проходящей через начало координат, будет x² + y² = r².
Решение: Чтобы найти решение этого вопроса, не нужно уравнение из калькулятора кругов. Мы знаем, что общее уравнение окружности имеет вид (x – x 1 )² + (y – y 1 )² = r². Поместив значение центров в x 1 и y 1 как 4 и 2, наряду с радиусом 6 единиц, уравнение окружности становится
(x – 4)² + (y – 2)² = 6²
x² + 16 – 8x + y² + 4 – 4y = 36
Упрощая приведенное выше уравнение, мы получаем окончательное уравнение окружности как,
x² + y² – 8x – 4y = 16.
Решение: Преобразование стандартного уравнения круга в полярную форму, замените значение x на r cos𝜃 и y на r sin𝜃.
Следовательно, стандартное уравнение окружности теперь принимает вид (r cos𝜃)² + (r sin𝜃)² = 25,
Решая вышеприведенное уравнение, мы получаем r² cos²𝜃 + r² sin²𝜃 = 25
r² (cos²𝜃 + sin²𝜃) = 25. Мы знаем, cos²𝜃 + sin²𝜃 = 1.
Подставляя это значение, мы получаем r² = 25. Это дает r = 5 единиц.
Следовательно, радиус окружности равен 5 единицам.
Решение: Чтобы найти значение центра окружности и радиуса, сравните данное уравнение окружности со стандартной формой, т. е. (x – x 1 )² + (у – у 1 )² = r².
При сравнении видим, что значение
Следовательно, координаты центра окружности равны (-7, 9) и радиус = 23.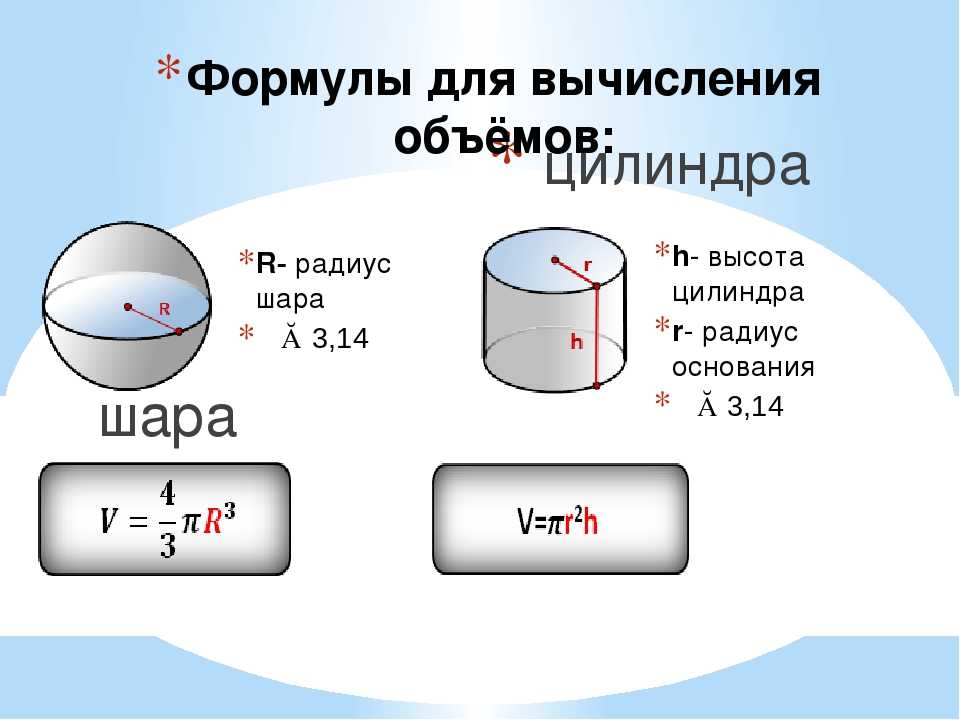
Уравнение окружности в стандартной форме, формулы, практические задачи и рисунки. Как представить окружность заданного радиуса в стандартной форме…
Практика 1
Какое уравнение окружности изображено на графике ниже? 92 = 1 $$
Практика 2
Посмотрите на график ниже, можете ли вы выразить уравнение окружности в стандартной форме?
Поскольку радиус этого круга равен 1, а его центр равен (1, 0), уравнение этого круга равно . 92 = 1
$$
92 = 1
$$
Практика 3
Посмотрите на график ниже, можете ли вы выразить уравнение окружности в стандартной форме?
Поскольку радиус этого круга равен 2, а его центр равен (3,1) , уравнение этого круга равно . 92 = 4 $$
Практика 4
Каков радиус кругов внизу?
Y 2 + X 2 = 9
$$ \sqrt{9} =3$$
Y 2 + X 2 = 16
$6 $
Д 2 + X 2 = 25
$$ \sqrt{ 25 } = 5 $$
Y 2 + X 2 = 11
$$ 7 0 9 Y 0 2 $3 9 + X 2 = а
$$ \sqrt{a}$$
Практика 5
Посмотрите на каждое уравнение стандартной формы ниже и определите центр и радиус.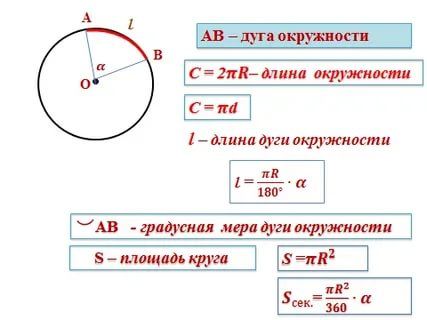
r = радиус
(у — 3) 2 + (х — 1) 2 = 9
(1, 3) r = 3
(у — 5) 2 + (х — 14) 2 = 16
3 (1, 90,00023 90,3) 5) r = 4
(у — 1) 2 + (х — 5) 2 = 25
(5, 1) r = 5
(х + 2) 2 + (у — 12) 2 = 36
(-2, 12) r = 6
(у + 7) 2 + (х + 5) 2 = 49
(-5, -7) r = 7
(х + 8) 2 + (у + 17) 2 = 49
(-8, -17) г = 7
Уравнение апплета круга
Формулы круга
Рабочие листы по кругу
Площадь кругов: формула, уравнение и диаметр
Круг — одна из самых распространенных форм. Если вы посмотрите на линии орбит планет в Солнечной системе, на простое, но эффективное функционирование колес или даже на молекулы на молекулярном уровне, круг продолжает появляться!
Окружность — это форма, в которой все точки, составляющие границу, равноудалены от одной точки, расположенной в центре.
Элементы круга
Прежде чем мы обсудим площадь кругов, давайте рассмотрим уникальные характеристики, определяющие форму круга. На рисунке ниже изображена окружность с центром О. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки О . Расстояние от центра круга до его границы называется радиусом , R .
Диаметр , D , это расстояние от одной конечной точки окружности до другой, проходящей через центр окружности . Диаметр всегда в два раза больше длины радиуса, так что если мы знаем одно из этих измерений, то мы знаем и другое! Хорда — это расстояние от одной конечной точки до другой на окружности, которое, в отличие от диаметра, составляет , а не должны проходить через центральную точку.
Иллюстрация круга, StudySmarter Original
Площадь кругов: формула / уравнение
Теперь, когда мы рассмотрели элементы круга, давайте начнем с обсуждения площади круга. Во-первых, мы начнем с определения.
Во-первых, мы начнем с определения.
Площадь круга — это пространство, занимаемое кругом на поверхности или плоскости. Измерения площади записываются в квадратных единицах, например, фут 9.0417 2 и м 2 .
Чтобы вычислить площадь круга, мы можем использовать формулу:
Для этой формулы важно знать, что равно числу пи. Что такое пи? Это константа, представленная греческой буквой, и ее значение приблизительно равно 3,14159.
Пи равно математической константе, которая определяется как отношение длины окружности к диаметру круга.
Вам не нужно запоминать число пи, потому что в большинстве калькуляторов есть клавиша для быстрого ввода, показанная как . Давайте используем формулу площади в примере, чтобы увидеть, как мы можем применить этот расчет на практике.
Радиус круга 8 м. Вычислите его площадь.
Решение:
Сначала подставим значение радиуса в формулу площади круга.
Затем мы возводим значение радиуса в квадрат и умножаем его на число пи, чтобы найти площадь в квадратных единицах. Имейте в виду, что это не равно , а скорее равно .
Расчет площади круга диаметром
Мы видели формулу площади круга, в которой используется радиус . Однако мы также можем найти площадь круга, используя его диаметр . Для этого мы делим длину диаметра на 2, что дает нам значение радиуса для ввода в нашу формулу. (Напомним, что диаметр окружности в два раза больше длины ее радиуса.) Давайте рассмотрим пример, использующий этот метод.
Круг имеет диаметр 12 метров. Найдите площадь круга.
Решение:
Начнем с формулы площади круга:
Из формулы видно, что нам нужно значение радиуса. Чтобы найти радиус круга, мы разделим диаметр на 2, например:
Теперь мы можем ввести значение радиуса 6 метров в формулу для определения площади:
Вычисление площади круги с окружностью
Помимо площади круга, другой распространенной и полезной мерой является его длина окружности.
Окружность круга — это периметр или охватывающая граница формы. Он измеряется в длине, что означает, что единицами являются метры, футы, дюймы и т. д.
Давайте посмотрим на некоторые формулы, связывающие длину окружности с радиусом и диаметром окружности:
Приведенные выше формулы показывают, что мы можем умножить на диаметр круга, чтобы вычислить его длину окружности. Поскольку диаметр в два раза больше длины радиуса, мы можем заменить его на , если нам нужно изменить уравнение окружности.
Вас могут попросить найти площадь круга, используя его длину окружности. Давайте поработаем на примере.
Длина окружности 10 м. Вычислите площадь круга.
Решение:
Сначала воспользуемся формулой длины окружности для определения радиуса круга:
Теперь, когда мы знаем радиус, мы можем использовать его для нахождения площади круга:
Итак, площадь круга с длиной окружности 10 м равна 7,95 м 2 .
Площадь полукругов и четвертей кругов с примерами
Мы также можем проанализировать форму круга с точки зрения половин или четвертей . В этом разделе мы обсудим площадь полукругов (кругов, разрезанных пополам) и четвертей кругов (кругов, разрезанных на четверти).
Площадь и длина окружности полукруга
Полукруг – это полукруг. Он образуется путем деления круга на две равные половины, разрезанные по его диаметру. Площадь полукруга можно записать как:
Где r радиус полукруга
Чтобы найти длину окружности полукруга , мы сначала разделим длину всей окружности пополам, а затем добавим дополнительную длину, равную диаметр d . Это связано с тем, что периметр или граница полукруга должны включать диаметр, чтобы замкнуть дугу. Формула длины окружности полукруга:
Вычислите площадь и длину окружности полукруга диаметром 8 см.
Решение:
Поскольку диаметр равен 8 см, радиус равен 4 см. Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:
Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:
Для длины окружности вводим значение диаметра в формулу:
Площадь и длина окружности четверти круга
Окружность можно разделить на четыре равные четверти, что дает четыре четверти круга. Чтобы вычислить площадь четверти круга, уравнение выглядит следующим образом:
Чтобы получить длину окружности четверти окружности, мы начинаем с деления длины окружности на четыре, но это дает нам только длину дуги четверти окружности. Затем нам нужно дважды добавить длину радиуса, чтобы завершить границу четверти круга. Этот расчет можно выполнить с помощью следующего уравнения:
Вычислите площадь и длину окружности четверти круга с радиусом 5 см.
Решение:
Для площади получаем:
Окружность может быть рассчитана как:
Площадь кругов — ключевые выводы
- В круге все точки, составляющие границу фигуры, равноудалены от точки, расположенной в ее центре.


 А взяв вдвое больше цифр (18) , мы могли бы вычислить длину окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0003 мм (волос в 100 раз толще этой возможной ошибки!)
А взяв вдвое больше цифр (18) , мы могли бы вычислить длину окружности, имеющей радиусом расстояние от Земли до Солнца, с погрешностью не свыше 0,0003 мм (волос в 100 раз толще этой возможной ошибки!)
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
 Позвольте нам помочь вам достичь мастерства в геометрии GMAT. Начните с регистрации на бесплатную пробную версию и учитесь у лучших в отрасли. В конце концов, мы самая популярная компания на gmatclub.
Позвольте нам помочь вам достичь мастерства в геометрии GMAT. Начните с регистрации на бесплатную пробную версию и учитесь у лучших в отрасли. В конце концов, мы самая популярная компания на gmatclub.