Функция LOG — Служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции LOG в Microsoft Excel.
Описание
Возвращает логарифм числа по заданному основанию.
Синтаксис
LOG(число;[основание])
Аргументы функции LOG описаны ниже.
-
Число Обязательный. Положительное вещественное число, для которого вычисляется логарифм.
Основание Необязательный. Основание логарифма. Если аргумент «основание» опущен, предполагается, что он равен 10.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=LOG(10) |
Логарифм числа 10. |
1 |
|
=LOG(8; 2) |
Логарифм числа 8 по основанию 2. Результат (3) — степень, в которую необходимо возвести основание, чтобы получить число 8. |
|
|
=LOG(86; 2,7182818) |
Логарифм числа 86 по основанию e (приблизительно 2,718). Результат (4,454) — степень, в которую необходимо возвести основание, чтобы получить число 86. |
4,4543473 |
Так как второй аргумент (основание) опущен, предполагается, что он равен 10. Результат (1) — степень, в которую необходимо возвести основание, чтобы получить число 10.Подготовка школьников к ЕГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Логарифмы |
| Определение логарифма, основное логарифмическое тождество |
| Свойства логарифмов |
| Использование свойств логарифмов при решениии логарифмических уравнений и неравенств |
| Десятичные логарифмы и натуральные логарифмы |
Определение логарифма, основное логарифмическое тождество
Рассмотрим два произвольных действительных числа a и b, удовлетворяющих условиям
| (1) |
Определение.
Логарифмом числа b по основанию a называют такую степень, в которую надо возвести число a, чтобы получить число b.
Другими словами, логарифм числа b по основанию a – это такое число x, которое является решением уравнения
| a x= b . | (2) |
Доказательство того, что решение уравнения (2) существует и единственно, выходит за рамки школьной программы.
Для логарифма числа b по основанию a используется обозначение:
loga b .
Таким образом, для всех действительных чисел a и b, удовлетворяющих условиям (1), справедливо равенство
которое часто называют основным логарифмическим тождеством.
Замечание. Обратим особое внимание на то, что при решении уравнения (2) мы ищем показатель степени, а при решении уравнения
x a = b.
мы ищем основание степени, которое вычисляется по формуле
и в случае, когда a – натуральное число, является корнем натуральной степени из числа b.
Пример 1. Решить уравнение
x3 = 81 .
Решение. Воспользовавшись понятием кубического корня и свойствами степеней, получаем
Ответ: .
Пример 2. Решить уравнение
3x= 81 .
Решение. Воспользовавшись тем, что число 81 является четвертой степенью числа 3 , получаем:
Ответ: 4 .
Задача. Доказать, что число
log2 3
иррационально.
Решение. Предположим противное, т.е. предположим, что указанное число рационально. Тогда существует несократимая дробь
,
числитель и знаменатель которой являются натуральными числами и такая, что справедливо равенство:
Из определения логарифма отсюда вытекает равенство:
следствием которого является равенство:
2m= 3n .
Но последнее равенство невозможно, поскольку его левая часть четное число, а правая – нечетное. Полученное противоречие доказывает требуемое в задаче утверждение.
Свойства логарифмов
Перечисленные ниже свойства логарифмов вытекают из основного логарифмического тождества:
(основное свойство логарифмов), | |
(основное свойство логарифмов), | |
(формула перехода к новому основанию логарифмов), | |
(основное свойство логарифмов), |
(основное свойство логарифмов), |
(формула перехода к новому основанию логарифмов), |
Использование свойств логарифмов при решении логарифмических уравнений и неравенств
Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.
Например, если при решении уравнения или неравенства требуется преобразовать выражение
loga ( f (x)2 ) ,
то вместо формулы
следует применять формулу
поскольку в противном случае можно потерять корни.
По той же причине при преобразовании выражений
loga ( f (x) g (x)) и
следует использовать формулы:
и
Замечание. Желающим усовершенствовать свои знания и умения при решении уравнений и неравенств с логарифмами мы рекомендуем ознакомиться с нашими учебными пособиями «Решение логарифмических уравнений» и «Решение логарифмических неравенств».
Десятичные логарифмы и натуральные логарифмы
В математике, физике и во многих других областях естествознания и технологий важное место занимают десятичные логарифмы и натуральные логарифмы.
Десятичные логарифмы – это логарифмы с основанием 10, а основанием натуральных логарифмов является иррациональное и трансцендентное число e, которое определяется по формуле
доказательство которой выходит за рамки школьной программы.
Для десятичных и натуральных логарифмов используются соответственно обозначения:
lg b и ln b,
причем
lg e = 0,43429…,
ln 10 = 2,30259…
Графики логарифмических функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
формул журнала — что такое формулы логарифма? Примеры
Прежде чем изучать формулы логов, вспомним, что такое логи (логарифмы). Логарифм — это просто еще один способ записи показателей степени.
Когда мы не можем решить задачу с помощью показателей, мы используем логарифмы. Существуют различные формулы логарифмов, которые выводятся с использованием законов показателей. Давайте изучим их, используя несколько решенных примеров.
Что такое формулы журнала?
Прежде чем приступить к изучению формул журнала, давайте вспомним несколько вещей. Существует два типа логарифмов: десятичный логарифм (который записывается как «log» и его основание равно 10, если не указано иное) и натуральный логарифм (который записывается как «ln» и его основание всегда равно «e»). Приведенные ниже формулы логарифмов показаны для десятичных логарифмов. Однако все они применимы и для натуральных логарифмов. Вот наиболее часто используемые формулы журнала
.- журнал б 1 = 0
- журнал б б = 1
- log b (xy) = log b x + log b y
- log b (x / y) = log b x — log b y
- log b a x = x log b a
- log b a = (log c a) / (log c b)
Некоторые из этих правил имеют определенные имена, такие как журнал 9.
0014 b (xy) = log b x + log b y называется формулой произведения бревен. Точно так же все свойства вместе с их именами указаны в таблице ниже.
Вывод логарифмических формул
Вот вывод некоторых важных логарифмических формул. Мы используем законы показателей при выводе логарифмических формул.
Формула произведения логарифмов
Формула произведения бревен, log b (xy) = log б х + лог б у.
Вывод:
Предположим, что log b x = m и log b y = n. Тогда по определению логарифма
x = b m и y = b n .
Тогда xy = b m × b n = b m + n (по закону экспонент, a m × a n = a m + n 3 900 b m + n в логарифмическом виде, получаем
m + n = log b xy
Подстановка значений log b x = m и log b y = n здесь,
log b (xy) = log b x b y
Частная формула логарифмов
Частная формула логарифмов: log b (x/y) = log b x — log b y.
Вывод:
Предположим, что log b x = m и log b y = n. Тогда по определению логарифма
x = b m и y = b n .
Тогда x/y = b m / b n = b m — n (по закону экспонент, a m / a n = a m — n ) 90 x/y = b m — n в логарифмическом виде, мы получаем
m — n = log b (x/y)
Подставляя значения log b x = m и log b y = n здесь,
log b (x/y) = log b x — log b y
Формула степени логарифмов
Формула степени логарифмов говорит log b a x = x log b a.
Вывод:
Пусть log b a = m. Тогда по определению логарифма a = b m .
Возведя обе стороны на x, получим
a x = (b m ) x
a x = b m x (по закону экспонент0040 m ) n = a mn )
Преобразование обратно в логарифмическую форму здесь,
лог b a x = x log b a
Изменение базовой формулы логарифмов
Изменение базовой формулы логарифмов говорит log b a = (log c a) / (log c4 б).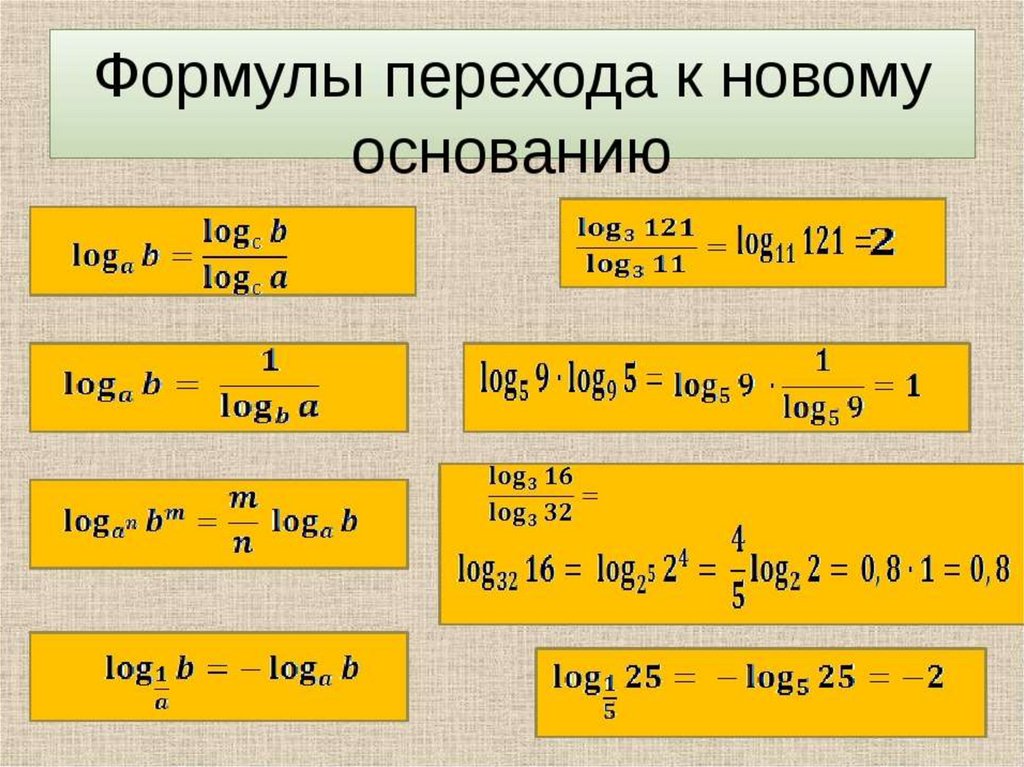
Происхождение:
Предположим, что log b a = x, log c a = y и log c b = z.
Преобразование их в экспоненциальную форму
Из (1) и (2),
b x = c y
(c z ) x = c y 9002 9 (из 0004 (3)) 0 зх = с у
Так как основания одинаковые, силы тоже должны быть одинаковыми.
zx = y (или) x = y/z.
Подставив сюда значения x, y и z,
log b a = (log c a) / (log c b).
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Примеры использования формул логарифмов
Пример 1: Преобразуйте следующее из экспоненциальной формы в логарифмическую, используя логарифмические формулы.
а) 5 3 = 125 б) 3 -3 = 1/27.
Решение:
Используя определение логарифма, = x
Используя это,
a) 5 3 = 125 ⇒ log 5 125 = 3
b) 3 -3 = 1 / 27 ⇒ log
Ответ : а) log 5 125 = 3; б) лог 3 1/27 = -3.
Пример 2: Сожмите следующее выражение в виде единичного логарифма, используя логарифмические формулы. 5 лог х + лог у — 8 лог z.
Решение:
Найти: Сжатую форму данного выражения в виде единичного логарифма с использованием формул логарифмирования.
5 log x + log y — 8 log z
= (5 log x — 8 log z) + log y (термины перегруппированы)
= (log x 5 — log z 8 ) + log y (∵ a log x = log x a )
= log (x 5 /z 8 ) + log y (∵ log x — log y = log (x/y) )
= log (x 5 y/z 8 ) (∵ log x + log y = log (xy))
Ответ : 5 log x + log y — 8 log z = log (x 5 y/z 8 ).
Пример 3: Найдите целочисленное значение log 3 (1/9), используя логарифмические формулы.
Решение:
log 3 (1/9) = log 3 1 — log 3 9 (∵ log b (x / y) = log b x 4 b — log 900 )
= 0 — log 3 3 2 (∵ log b 1 = 0)
= — 2 log 3 3 (∵ log b 9 x a ) 014 б а)
= -2 (1) (∵ log b b = 1)
= -2
Ответ: log 3 (1/9) = -2.
Часто задаваемые вопросы о формулах логарифма
Что такое формулы логарифмирования?
Формулы логарифмов связаны с логарифмами и очень полезны при решении задач на логарифмы. Некоторые важные формулы журнала:
- log b (xy) = log b
- log b (x / y) = log b x — log b y
- log b a x = x log b и
- log b a = (log c a) / (log c b)
Как вывести формулы журнала?
Законы экспонент используются для получения логарифмических формул.
Мы также используем определение логарифма при выводе логарифмических формул. т. е. мы преобразуем логарифмическую форму в экспоненциальную форму и наоборот при выводе. Подробный вывод формул журнала можно найти в разделе «Что такое формулы журнала?» раздел этой страницы.
Каковы применения формул журнала?
Проблемы, которые нельзя решить с помощью свойств показателей, можно решить с помощью журналов. Формулы журнала используются либо для сжатия группы логарифмов в один логарифм, либо наоборот.
Какая формула логарифма используется для изменения основания логарифма?
Формула изменения базы (которая является одной из формул журнала) используется для изменения базы. Используя эту формулу, log b a = (log c а) / (лог в б). Мы видим, что основание в левой части равно «b», а основания логарифмов в правой части равны «c».
Какая польза от формулы изменения основания (одна из логарифмических формул)?
Вот важное использование формулы замены основания.
Обычно в калькуляторах есть опции для вычисления логарифмов чисел с основанием 10 и с основанием «e». Чтобы найти логарифмы чисел с другим основанием, кроме 10 и «е», мы используем формулу замены основания. Например лог 2 3 = (лог. 3) / (лог. 2).
Что такое натуральные логарифмические формулы?
Формулы натуральных логарифмов такие же, как и формулы логарифмов, за исключением того, что «логарифм с некоторым основанием» заменен на «ln». Вот наиболее важные формулы натурального логарифма.
- пер (ху) = пер х + пер у
- пер (х/у) = пер х — пер у
- In a x = x In a
Формула логарифмирования — объяснение, формула, примеры решений и важные часто задаваемые вопросы
Логарифм — это показатель степени или степень, в которую нужно возвести основание, чтобы получить заданное число. Математически логарифмы выражаются следующим образом: m — это логарифм n по основанию b, если bm = n, что также можно записать как m = logb n.
Например, 43 = 64; следовательно, 3 — это логарифм 64 по основанию 4, или 3 = log464. Точно так же мы знаем, что 103 = 1000, тогда 3 = log101000. Логарифмы с основанием 10 обычно известны как обычные или бриггсовские логарифмы и просто записываются как log n. В этой статье мы обсудим, что такое логарифм, формулы логарифмов, основные формулы логарифмов, правило изменения основания, правила и формулы логарифмов, для чего используется логарифм и т. д.
Правила логарифмирования
Существует 7 правил логарифмирования, которые полезны при расширении логарифмов, сокращении логарифмов и решении логарифмических уравнений. Семь правил логарифмов обсуждаются ниже:
1. Правило произведения
\[\log_{b}{(P \times Q)} = \log_{b}{P} + \log_{b}{Q} \]
Логарифм произведения равен сумме логарифмов факторов.
2. Частное правило
\[\log_{b}{(\frac{P}{Q})} = \log_{b}{P} — \log_{b}{Q}\] 9{y}} = y \]
Правило логарифмирования основания в степени гласит, что логарифм b с рациональным показателем равен показателю, умноженному на его логарифм.
6. Основание степени логарифма Правило
b log y = y
Приведенное выше правило гласит, что возведение логарифма числа в основание логарифма равно числу.
7. Правило идентификации
\[\log_{y}{y} = 1 \]
Аргумент логарифма (в скобках) аналогичен основанию. Поскольку основание равно аргументу, y может быть больше 0, но не может быть равен 0.
Формулы логарифмирования
Ниже приведены некоторые из различных формул логарифмирования, которые помогают решать уравнения логарифмирования.
Основная формула логарифма
Некоторые из различных основных формул логарифма приведены ниже:
\[\log_{b}{(m \times n)} = \log_{b}{m} + \ log_{b}{м}\] 9{n})} \]
Сложение и вычитание
Изменение базовой формулы
.
\[\log_{n}{m} = \frac{\log_{d}{m}}{\log_{d}{n}}\]
Решенные примеры
1. Решить Следующее: 2 log429
Решение:
Дано,
\[2 \log_{4}{29} \]
С помощью замены формулы основания n получаем 9{2}\] \]
\[75x = 90\]
\[X = \frac {90}{75}\]
\[X = \frac {6}{5}\]
В математике характеристики логарифма используются для решения задач логарифмирования. Многим алгебраическим характеристикам, таким как коммутативные, ассоциативные и дистрибутивные, нас учили в начальной школе. Есть пять основных особенностей логарифмических функций.
Логарифмическое число связано с показателем степени и степенью, таким образом, если xn = m, то logxm = n. В результате мы также должны понимать экспоненциальный закон. Например, логарифм 10000 по основанию 10 равен 4, потому что 4 — это степень, в которую нужно возвести десять, чтобы получить 10000 : 104 = 10000, поэтому log1010000 = 4,9.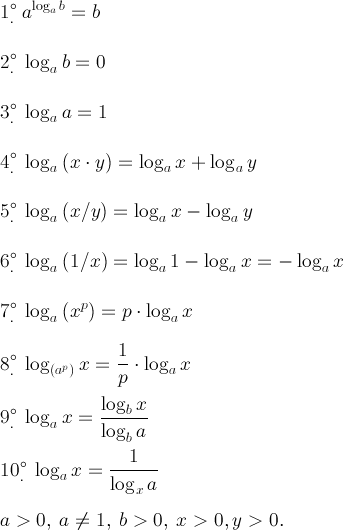
0003
Мы можем представить логарифм произведения как сумму логарифмов, логарифм частного как разность логарифмов и логарифм мощности как произведение, используя эти функции.
Вещественное число Логарифмы видны только в положительных действительных числах; отрицательные и комплексные числа имеют комплексные логарифмы.
Применение логарифмов
Логарифмы имеют широкий спектр применений как в математике, так и за ее пределами. Давайте рассмотрим несколько примеров того, как логарифмы используются в повседневной жизни:
Они используются для расчета магнитуды землетрясения.
Логарифмы используются для расчета уровня шума в децибелах, например звука колокола.
Логарифмы используются в химии для определения кислотности или уровня pH.
Они используются для расчета прироста денег при заданной процентной ставке.
Логарифмы обычно используются для расчета времени, необходимого для распада или экспоненциального развития чего-либо, например роста бактерий или радиоактивного распада.
Их также можно использовать в вычислениях, требующих преобразования умножения в сложение или наоборот.
Вместо простого вычисления мы можем использовать таблицу логарифмов, чтобы получить логарифм целого числа. Прежде чем вычислять логарифм числа, мы должны сначала понять его характеристическую и мантиссу части.
Характеристическая часть — Характеристический компонент — это целая часть числа. Любое число больше единицы имеет положительную характеристику, а если оно на единицу меньше, чем количество цифр слева от десятичной точки в данном целом числе, оно имеет отрицательную характеристику.
Если число меньше единицы, характеристика отрицательна, и число на единицу больше числа нулей справа от запятой.
Часть мантиссы. Часть мантиссы представляет собой десятичную часть логарифмического числа, которая всегда должна быть положительной. Если часть мантиссы имеет отрицательное значение, превратите ее в положительное значение.
Как вы используете таблицу журнала?
Процесс определения значения журнала числа с использованием таблицы журнала показан ниже. Во-первых, вы должны понять, как использовать таблицу журнала. Таблица журнала предоставляется как ресурс для определения значений.
Шаг 1. Понимание идеи логарифма. Каждая таблица журнала может использоваться только на определенной основе. Логарифмическая база 10 — наиболее часто используемая форма таблицы логарифмов.
Шаг 2: Определить характеристику числа и часть мантиссы.
Например, чтобы получить значение log1015,27, сначала разделите характеристику и часть мантиссы.
Часть характеристики = 15
Часть мантиссы = 27
Шаг 3. Используйте общую таблицу журнала. Теперь используйте строку 15, чтобы проверить столбец 2 и записать соответствующее значение. В итоге получается 1818.
Шаг 4. Вычислите среднюю разницу, используя таблицу логарифмов. Проведите пальцем по столбцу средней разницы 7 и строке 15 и запишите соответствующее значение как 20.
Шаг 5. Объедините значения, полученные на шагах 3 и 4. Это равно 1818 + 20 = 1838. В результате значение 1838 представляет часть мантиссы.
Шаг 6. Найдите отличительный признак. Поскольку число находится в диапазоне от 10 до 100 (от 101 до 102), отличительным признаком должен быть 1.
Шаг 7: Наконец, объедините часть характеристики и мантиссы, чтобы получить 1,1838.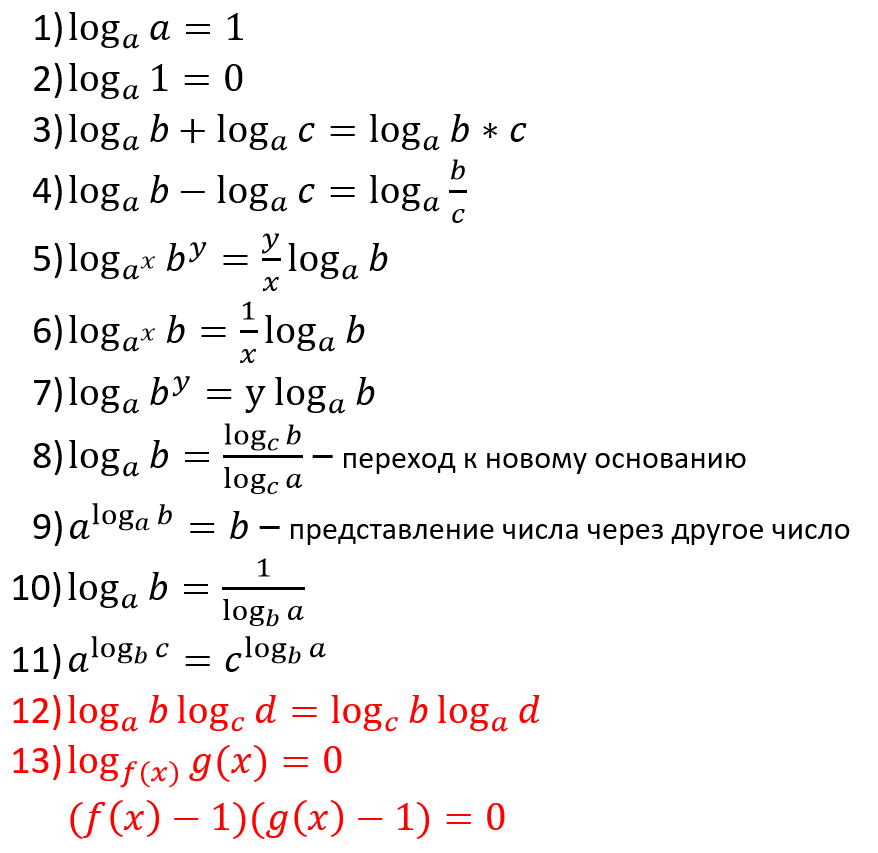
Пример
Вот пример использования таблицы логарифмов для получения значения логарифмической функции.
Определите значение log102,872.
Решение:
Шаг 1. Компонент характеристики равен 2, а часть мантиссы равна 872.
Шаг 2. Изучите строки 28 и 7 таблицы. В итоге получается значение 4579.
Шаг 3. Изучите значение средней разницы для строки 28 и среднюю разницу в столбце 2. Значение, связанное со строкой и столбцом, равно 3. получаем 4582. Это сечение мантиссы.
Шаг 5: Поскольку количество цифр слева от десятичной части равно единице, характеристическая часть меньше единицы. В результате характеристическая часть равна 0
Шаг 6: Наконец, соедините характеристики и части мантиссы. В результате получается 0,4582.