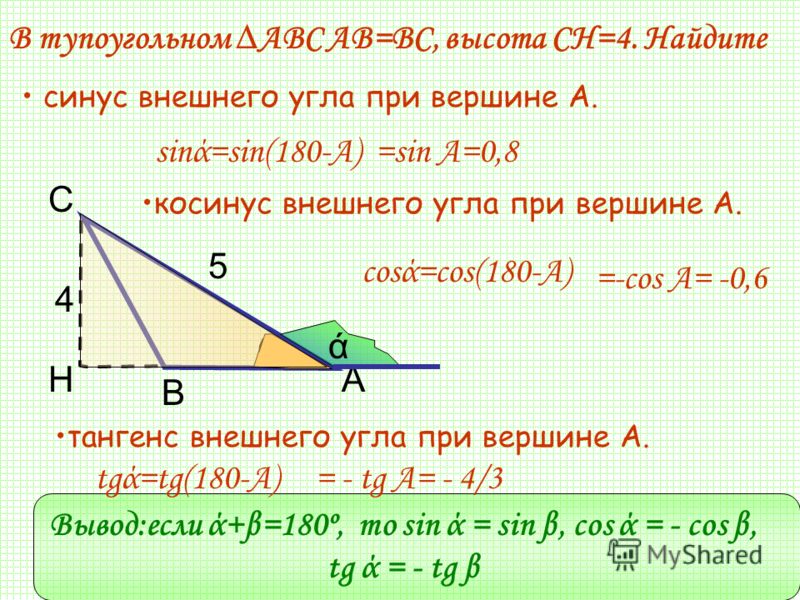
Алгоритм нахождения синуса любого угла? — Хабр Q&A
Смотря какая точность нужна. Есть формула Бхаскара, работающая на диапазоне от 0° до 180° (0-π):
sin(x°) = 4·x·(180−x)/(40500−x·(180−x))
sin(x) = 16·x·(π−x)/(5·π2−4·x·(π−x))
На большей части диапазона она даёт точность в пределах 0.2%, на краях точность падает до 2%.
Значения для углов вне этого диапазона можно получить из тождества:
sin(2·π+x) = sin(x)
sin(π+x) = -sin(x)
Ответ написан
Иногда для скорости используют(вали) табличный метод.
Т.е. создают таблицу в памяти с вычисленными значениями функции(с нужной точностью)
для какого-то фиксированного шага по углу.
Если попадаем между узлами сетки таблицы углов, то используем интерполяцию.
Ответ написан
Комментировать
1) в арифметическом сопроцессоре длина дробных чисел 10 байт, а не 8(double), так что точность повыше.
2) ряды Фурье применять тяжело, т.к. факториал (в знаменателе каждой дроби) быстро растёт.
3) есть метод CORDIC, который по небольшой таблице может рассчитать любую точность.
4) слышал на видеосеминаре, что скорее всего используются многочлены Чебышёва (знай наших!)
Ответ написан
Комментировать
Гуглите — приближенное вычисление синуса (подставьте нужную).
Ответ написан
Самым быстрым и точным, но не экономичным, считается метод интерполяции в таблице. Однако существуют более экономичные и почти столь же быстрые (а, возможно, и более быстрые) методы вычисления трансцендентных функций — это аппроксимации по методу Чебышёва и Паде-Чебышёва. Производительность соответствующих алгоритмов будет зависеть от требуемой точности. Например, для аппроксимации тригонометрических функций с одинарной точностью (7-8 значащих десятичных цифр) по методу Чебышёва, как правило, достаточно использовать многочлен с 5-ю слагаемыми. Его вычисление настолько быстрое, что может превосходить по скорости табличный метод. Для вычисления функций с двойной и более высокой точностью лучшие результаты достигаются по методу Паде-Чебышёва (аппроксимация дробно-рациональной функцией).
Дополнительным достоинством данных методов в том, что с помощью векторных команд несложно сделать, например, параллельное вычисление синуса и косинуса одного аргумента. В методе Паде-Чебышёва с помощью векторных команд возможно параллельное вычисление числителя и знаменателя функции, что почти вдвое повышает производительность. Я проверял производительность функции вычисления натурального логарифма с двойной точностью, написанной по методу Паде-Чебышёва, она превосходила стандартную библиотечную функцию. С одинарной точностью — ещё быстрее.
В качестве примера вот ссылка на быструю функцию вычисления тангенса в градусах с одинарной точностью по методу Чебышёва (сообщение от 2021-09-20 13:12:22):
Ответ написан
Комментировать
6.
 5 Соотношения синуса, косинуса и тангенса и приложения тригонометрии – Fanshawe Pre-Health Sciences Mathematics 1
5 Соотношения синуса, косинуса и тангенса и приложения тригонометрии – Fanshawe Pre-Health Sciences Mathematics 1Перейти к содержимому
Ожидается, что к концу этого раздела вы сможете
- Находить недостающую сторону прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Найдите недостающий угол прямоугольного треугольника, используя отношения синуса, косинуса или тангенса
- Решение приложений с помощью тригонометрии прямого угла
Теперь, когда мы знаем основы алгебры и геометрии, связанные с прямоугольным треугольником, мы можем приступить к изучению тригонометрии. Многие реальные жизненные задачи можно представить и решить с помощью прямоугольной тригонометрии.
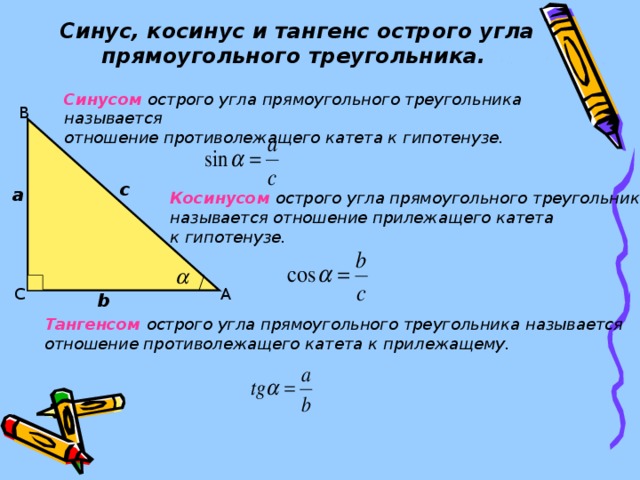
Мы знаем, что любой прямоугольный треугольник имеет три стороны и прямой угол. Сторона, противолежащая прямому углу, называется гипотенузой. Два других угла прямоугольного треугольника — острые углы (с мерой меньше [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления.
Два других угла прямоугольного треугольника — острые углы (с мерой меньше [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления.
Гипотенуза всегда является наибольшей стороной прямоугольного треугольника. Две другие стороны называются противоположной стороной и смежной стороной. Названия этих сторон зависят от того, какой из двух острых углов используется в качестве опорного угла.
Рисунок 6.5.1 В прямоугольном треугольнике каждая сторона помечена строчной буквой, соответствующей прописной букве противоположной вершины.Назовите стороны треугольника и найдите гипотенузу, противоположную и прилежащую.
Рисунок 6.5.2 РешениеМы пометили стороны строчными буквами, чтобы они совпадали с прописными буквами противоположной вершины.
[латекс]с[/латекс] является гипотенузой
[латекс]а[/латекс] противоположно
[латекс]b[/латекс] примыкает к
 5.3
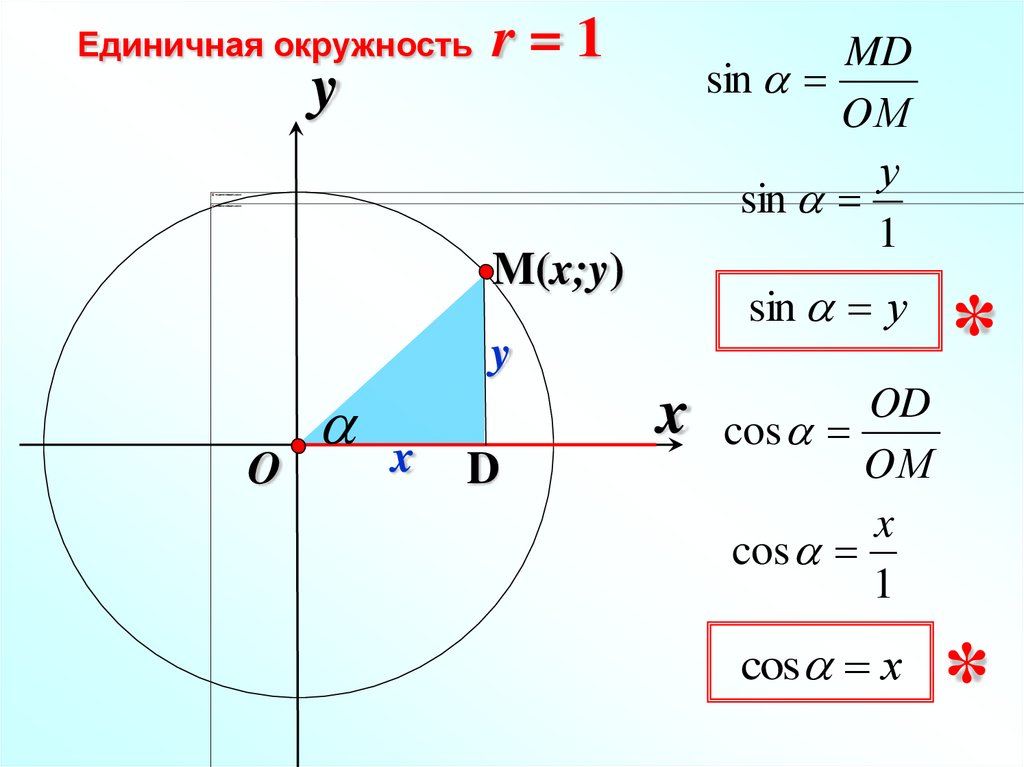
5.31) Обозначьте стороны треугольника и найдите гипотенузу, противолежащую и прилежащую.
Рисунок 6.5.4 Решение [латекс]y[/латекс] гипотенуза
[латекс]z[/латекс] напротив
[латекс]х[/латекс] примыкает
Тригонометрические отношения — это отношения сторон прямоугольного треугольника. Для любого прямоугольного треугольника мы можем определить три основных тригонометрических соотношения: синус, косинус и тангенс.
Давайте обратимся к рисунку 6.5.1 и определим три основных тригонометрических отношения как:
Три основных тригонометрических отношения- [латекс] синус (\ тета) = \ гидроразрыва {\ текст {длина противоположной стороны}} {\ текст {длина стороны гипотенузы}} [/латекс]
- [латекс] косинус (\ тета) = \ гидроразрыва {\ текст {длина прилегающей стороны}} {\ текст {длина стороны гипотенузы}} [/латекс]
- [латекс]тангенс(\тета) = \frac{\text{длина противоположной стороны}}{\text{длина соседней стороны}}[/latex]
Где [латекс]θ[/латекс] — мера опорного угла, измеренная в градусах.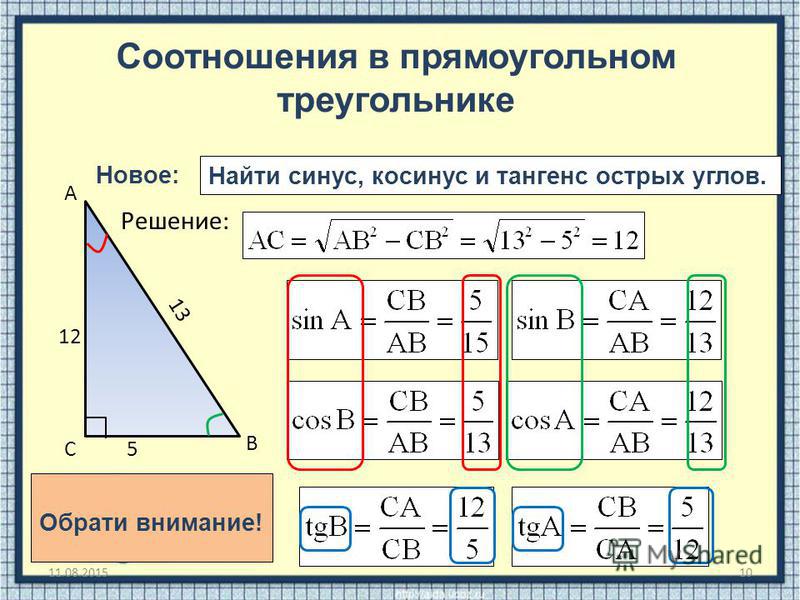
Очень часто мы используем сокращения для синуса, косинуса и тангенса.
- [латекс] грех (\ тета) = \ гидроразрыва {опп} {hyp} [/латекс]
- [латекс] соз (\ тета) = \ гидроразрыва {прил. {hyp} [/латекс]
- [латекс] загар (\ тета) = \ гидроразрыв {опп} {прил} [/латекс]
Некоторые люди помнят определение тригонометрических соотношений как SOH CAH TOA.
Давайте воспользуемся [латекс]\Delta DEF[/латекс] из примера 6.5.2, чтобы найти три отношения.
Для данного треугольника найти отношение синуса, косинуса и тангенса.
Рисунок 6.5.5 Решение[латекс]\begin{align*}sin(\theta) &= \frac{f}{d}\\[2ex]cos(\theta)&= \frac{e} {d}\\[2ex]tan(\theta)&= \frac{f}{e}\end{align*}[/latex]
2) Для данного треугольника найти отношение синуса косинуса и тангенса.
Рисунок 6.5.6 Решение[латекс]\begin{align*}sin(\theta)&= \frac{z}{y}\\[2ex]cos(\theta)&= \frac{x} {y}\\[2ex]tan(\theta)&= \frac{z}{x}\end{align*}[/latex]
В примере 6. 5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс].
5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс].
При расчетах мы обычно округляем отношения до четырех знаков после запятой, а в конце наш окончательный ответ — до одного знака после запятой, если не указано иное.
Для данного треугольника найти отношения синуса, косинуса и тангенса. При необходимости округлить до четырех знаков после запятой.
Рисунок 6.5.7 РешениеУ нас есть два возможных опорных угла: [латекс]R[/латекс] и [латекс]S[/латекс].
Используя определения, тригонометрические соотношения для угла [латекс]R[/латекс] составляют:
- [латекс]sin(R)= \frac{4}{5} = 0,8[/латекс]
- [латекс] cos(R)= \frac{3}{5} = 0,6[/латекс]
- [латекс]загар(R)=\фракция{4}{3} = 1,3333…[/латекс]
Используя определения, тригонометрические соотношения для угла [латекс]S[/латекс]:
- [латекс]sin(S)= \frac{3}{5} = 0,6[/латекс]
- [латекс] cos(S)= \frac{4}{5} = 0,8[/латекс]
- [латекс]загар(S)= \фракция{3}{4} = 0,75[/латекс]
3) Для данного треугольника найти отношения синуса, косинуса и тангенса.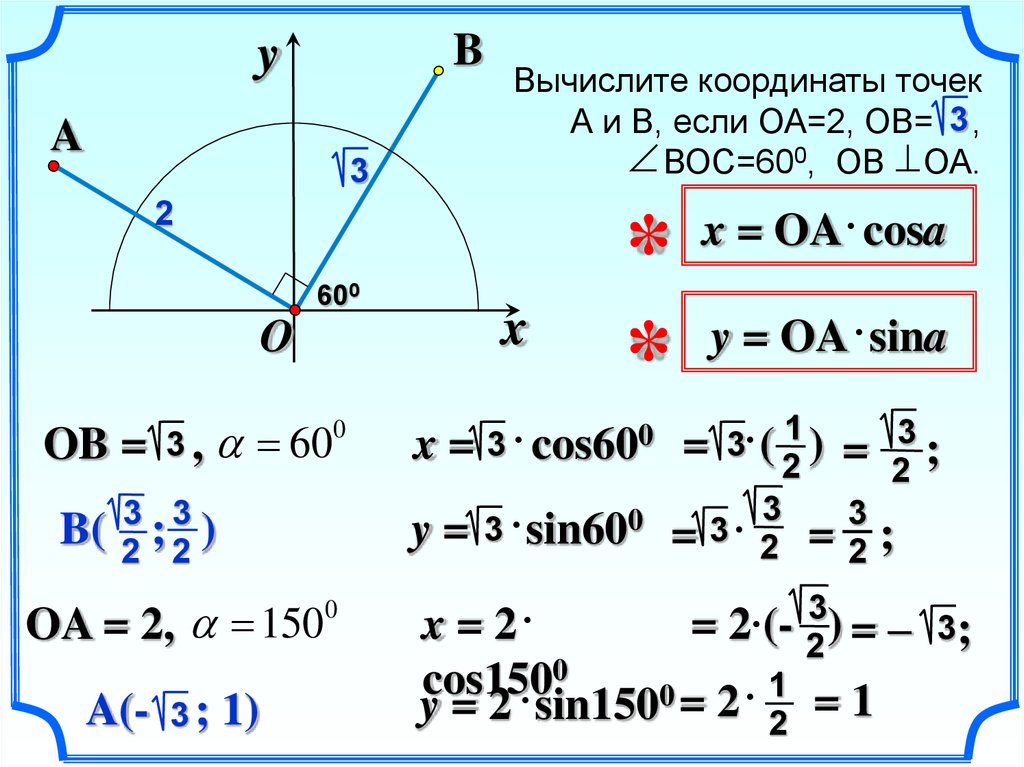 При необходимости округлить до четырех знаков после запятой.
При необходимости округлить до четырех знаков после запятой.
- [латекс]sin(F)= \frac{8}{10} = 0,8[/латекс]
- [латекс] cos(F)= \frac{6}{10} =0,6[/латекс]
- [латекс]tan(F)= \frac{8}{6} = 1,3333…[/latex]
- [латекс]sin(D)= \frac{6}{10} = 0,6[/латекс]
- [латекс] cos(D)= \frac{8}{10} = 0,8[/латекс]
- [латекс]тангенс(D)= \фракция{6}{8} = 0,75[/латекс]
Теперь воспользуемся научным калькулятором, чтобы найти тригонометрические соотношения. Сможете ли вы найти кнопки sin, cos и tan на своем калькуляторе? Чтобы найти тригонометрические соотношения, убедитесь, что ваш калькулятор находится в режиме градусов.
С помощью калькулятора найдите тригонометрические соотношения. При необходимости округлить до 4 знаков после запятой. 9\circ)=1[/латекс]
Нахождение недостающих сторон прямоугольного треугольника В этом разделе вы будете использовать тригонометрические отношения для решения задач прямоугольного треугольника. Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
Решить тригонометрические задачи
- Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
- Определите, что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое соотношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в соотношение на шаге 4 и убедившись, что он имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением
В следующих нескольких примерах, зная меру одного острого угла и длину одной стороны прямоугольного треугольника, мы решим прямоугольный треугольник относительно недостающих сторон.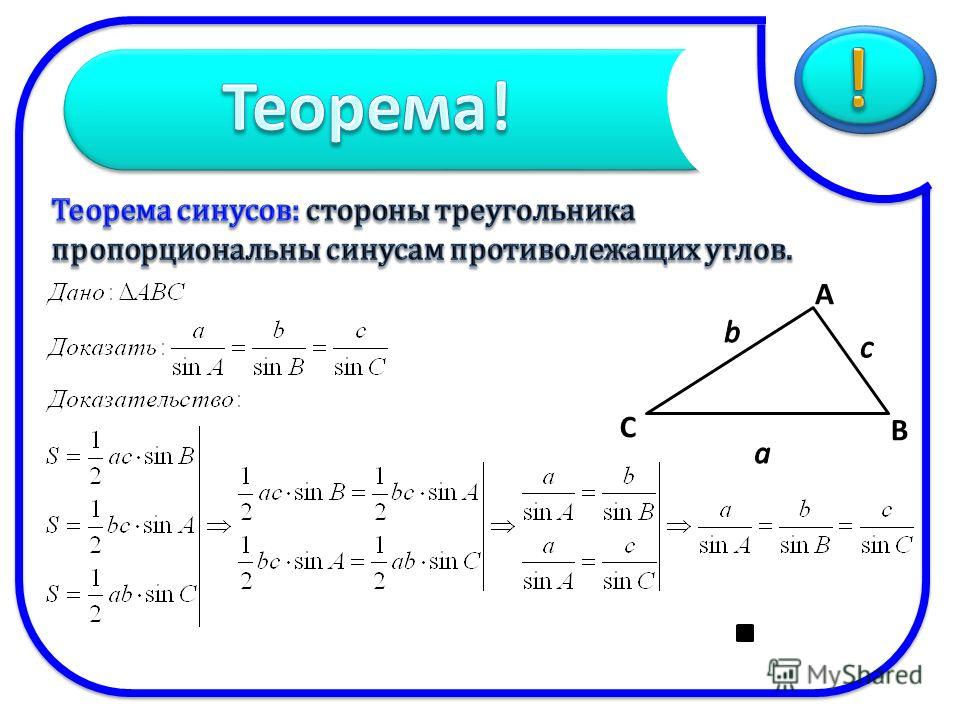
Найти недостающие стороны. Округлите окончательный ответ до двух знаков после запятой
Рисунок 6.5.9 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]Y[/латекс] — это наш опорный угол, [латекс]у[/латекс] — противоположная сторона, [латекс]z[/латекс] — смежная сторона, а [латекс]х=14[/латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
а. Противоположная сторона.
б. Соседняя сторона.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}y&=&?\\z&=&?\end{eqnarray*}[/latex] 9\circ)&=&z\\11.47&=&z\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{align*}\text{a. }\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
}\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
Шаг 7: Ответьте на вопрос полным предложением.
а. Противоположная сторона — [латекс]8.03[/латекс].
б. Соседняя сторона — [латекс]11,47[/латекс].
5) Найдите недостающие стороны. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.10 Решение[латекс]\begin{align*}a &= 20.2\\b &= 16.4\end{align*}[/latex]
Найдите гипотенузу. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.11 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]S[/латекс] – это наш опорный угол, [латекс]R[/латекс] – противоположная сторона, [латекс]r = 4[/латекс] – прилежащая сторона, а [латекс]Р[/латекс] это гипотенуза.
Шаг 2: Определите, что вы ищете.
Гипотенуза.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}p&=&?\end{eqnarray*}[/latex] 9\circ)&=&\frac{4}{p}\end{eqnarray*}[/latex]
Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}0.8480&=&\frac{4}{p}\\p&=&4.7170\;\;\text{Округление до 4 знаков после запятой}\end{eqnarray*} [/латекс]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{eqnarray*}0.8480&\overset?=&\frac{4}{4.7170}\\0.8480&=&0.8480\checkmark\end{eqnarray*}[/latex]
Шаг 7: Ответьте на вопрос полным предложением.
Гипотенуза равна [латекс]4,7[/латекс]. Окончательный ответ округлить до одного знака после запятой.
6) Найдите гипотенузу. {-1}[/latex] находятся на вашем научном калькуляторе. . 9\circ[/латекс]
{-1}[/latex] находятся на вашем научном калькуляторе. . 9\circ[/латекс]
В приведенном ниже примере у нас есть прямоугольный треугольник с двумя заданными сторонами. У нас отсутствуют острые углы. Давайте посмотрим, каковы шаги, чтобы найти недостающие углы.
Найдите недостающий [латекс]\угол Т[/латекс] . Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.13 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]T[/латекс] — это наш базовый угол, [латекс]t = 7[/латекс] — противолежащая сторона, [латекс]s[/латекс] — прилежащая сторона, а [латекс]r = 11[/ латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]T[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle T&=&?\end{eqnarray*}[/latex] 9\circ[/латекс]
Найдите недостающий угол [латекс]А[/латекс]. Округлите окончательный ответ до одного знака после запятой.
Рисунок 6.5.15 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Дается чертеж. Угол [латекс]А[/латекс] — это наш опорный угол, [латекс]а = 9[/латекс] — противолежащая сторона, [латекс]с = 5[/латекс] — прилежащая сторона, а [латекс]b[ /латекс] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]А[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle A&=&?\end{eqnarray*}[/latex]
Шаг 4: Найдите требуемое тригонометрическое соотношение.
[латекс]\begin{eqnarray*}tan A&=&\frac{9}{5}\end{eqnarray*}[/latex] 9\circ\end{align*}[/latex]
Шаг 1: Прочтите задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Дается чертеж. Угол [латекс]А[/латекс] — это наш исходный угол, [латекс]а = 8[/латекс] — противоположная сторона, [латекс]b[/латекс] — прилежащая сторона, а [латекс]с[/латекс] ] — гипотенуза.
Шаг 2: Определите, что вы ищете.
9\circ)&=&\frac{8}{c}\end{eqnarray*}[/latex]Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}\text{a.}\;0.9004&=&\frac{8}{b}\\0.9004 b&=&8\\b&=&8.8849\\[3ex]\text {b.}\;0,6691&=&\frac{8}{c}\\0,6691 c&=&8\\c&=&11,9563\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.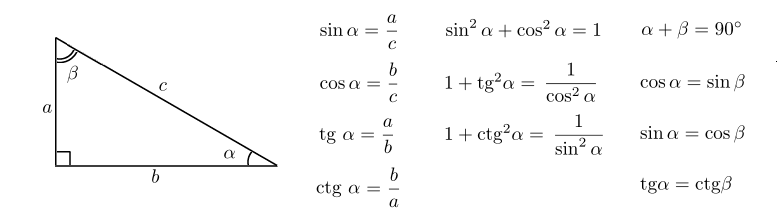
9\circ\end{align*}[/latex]
[latex]\begin{align*}a &= 6\\b &= 15.6\\c &= 16.7\end{align*}[/ латекс]
Решите прямоугольный треугольник. Округлить до двух знаков после запятой.
Рисунок 6.5.19 Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Дается чертеж. Пусть угол [латекс]D[/латекс] будет нашим опорным углом, [латекс]d = 4[/латекс] — противолежащая сторона, [латекс]f[/латекс] — прилежащая сторона, а [латекс]е = 9[/latex] — это гипотенуза.
Шаг 2: Определите, что вы ищете.
а. Угол Д.
б. Соседний.
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\text{a.}\;\angle D&=&?\\[2ex] \text{b.}\;f&=&?\end{eqnarray*}[/latex ]
Шаг 4: Найдите требуемое тригонометрическое соотношение.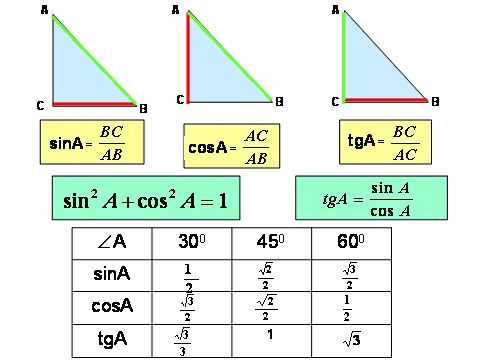
9\circ\end{align*}[/latex]
[latex]\begin{align*}d &= 29,4\\e &= 18,4\\f &= 60,6\end{align*}[/ латекс]
Решение приложений с использованием тригонометрических соотношенийВ предыдущих примерах мы смогли найти недостающие стороны и недостающие углы прямоугольного треугольника. Теперь давайте воспользуемся тригонометрическими отношениями для решения реальных задач.
Многие применения тригонометрических соотношений связаны с пониманием угла подъема или угла наклона. 9\circ[/latex] угол. Какова высота Harbour Centre?
РешениеШаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.
Рисунок 6.5.23
Угол [латекс]X[/латекс] — это наш исходный угол, [латекс]х[/латекс] — противоположная сторона, [латекс]у = 31[/латекс]м — прилежащая сторона, а [latex]z[/latex] — гипотенуза.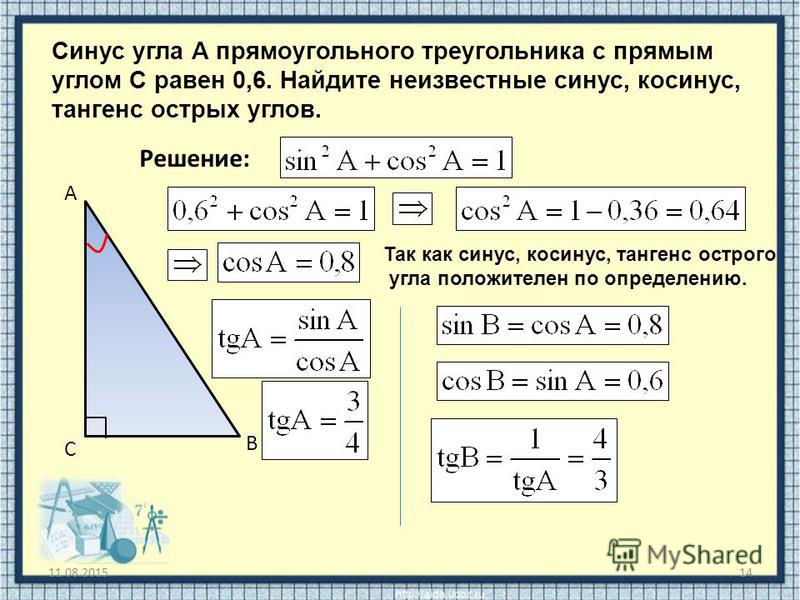
Шаг 2: Определите, что вы ищете. 9\circ)&=&\frac{x}{31}\end{eqnarray*}[/latex]
Шаг 5: Решите отношение, используя хорошие методы алгебры.
[латекс]\begin{eqnarray*}4.7046&=&\frac{x}{31}\\x&=&145.8426\end{eqnarray*}[/latex]
Шаг 6: Проверьте ответ в задаче и убедитесь, что он имеет смысл.
[латекс]\begin{eqnarray*}4.7046&\overset?=&\frac{145.8426}{31}\\4.7046&=&4.7046 \checkmark\end{eqnarray*}[/latex] 9\circ[/latex] угол. Насколько высокое здание?
Раствор[латекс]43,3[/латекс] метра
Томас стоит на вершине здания высотой [latex]45[/latex] метров и смотрит на свою подругу, которая стоит на земле в [latex]22[/latex] метрах от основания здания. Что такое угол депрессии?
Решение Шаг 1: Прочитайте задачу и убедитесь, что все слова и идеи понятны. Нарисуйте прямоугольный треугольник и обозначьте данные части.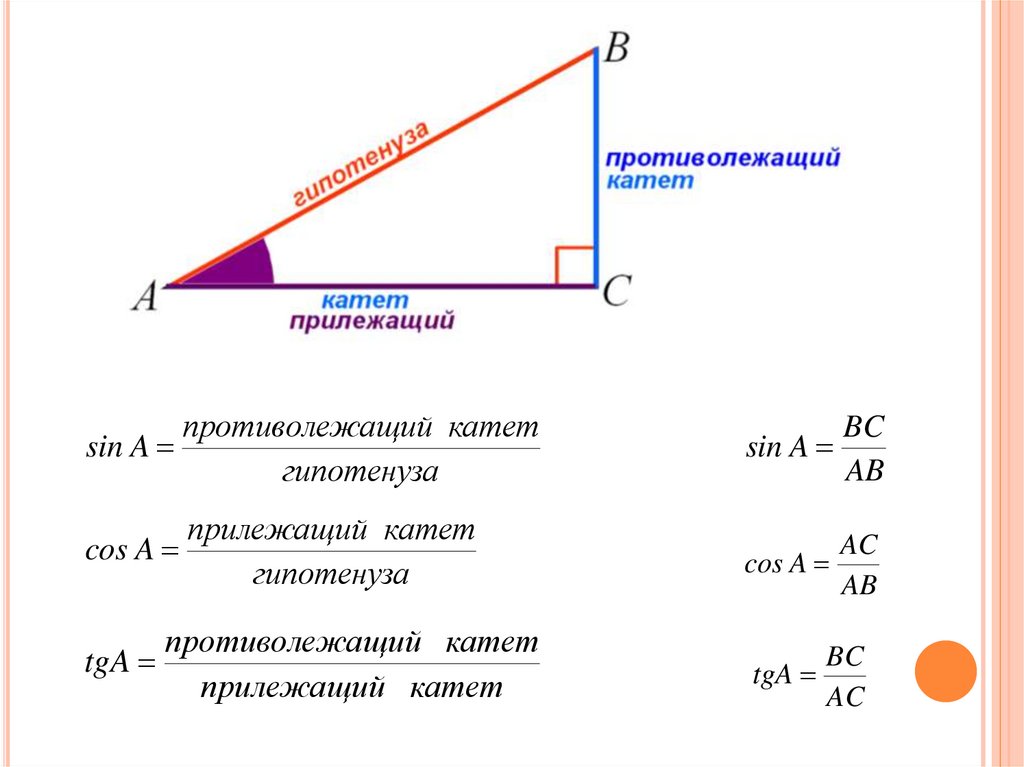
Угол [латекс]Y[/латекс] — это наш исходный угол, [латекс]у = 45[/латекс]м — противоположная сторона, [латекс]z = 22[/латекс]м — прилежащая сторона , а [latex]x[/latex] — гипотенуза.
Шаг 2: Определите, что вы ищете.
Угол [латекс]Y[/латекс].
Шаг 3: Пометьте то, что мы ищем, выбрав переменную для ее представления.
[латекс]\begin{eqnarray*}\angle Y&=&?\end{eqnarray*}[/latex] 9\circ[/латекс]
- Три основных тригонометрических соотношения: (Где [латекс]θ[/латекс] — мера опорного угла, измеренная в градусах).
- [латекс] синус\;\тета = \фракция{\текст{длина противоположной стороны}}{\текст{длина стороны гипотенузы}}[/латекс]
- [латекс]косинус\;\тета = \фракция{\текст{длина прилежащей стороны}}{\текст{длина гипотенузы}}[/латекс]
- [латекс]тангенс\;\тета = \фракция{\текст{длина противоположной стороны}}{\текст{длина соседней стороны}}[/латекс]
- Стратегия решения проблем для приложений тригонометрии
- Прочитайте задачу и убедитесь, что все слова и идеи понятны.
 Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Нарисуйте прямоугольный треугольник и обозначьте указанные части. - Определите, что мы ищем.
- Пометьте то, что мы ищем, выбрав переменную для ее представления.
- Найдите требуемое тригонометрическое соотношение.
- Решите отношение, используя хорошие методы алгебры.
- Проверьте ответ, подставив его обратно в отношение, найденное на шаге 5, и убедившись, что оно имеет смысл в контексте задачи.
- Ответьте на вопрос полным предложением.
- Прочитайте задачу и убедитесь, что все слова и идеи понятны.
а. После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
б. В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующему разделу? Почему или почему нет?
License
Fanshawe Pre-Health Sciences Mathematics 1 by Sav Spilotro, MSc распространяется под лицензией Creative Commons Attribution-ShareAlike 4. 0 International License, если не указано иное.
0 International License, если не указано иное.
Поделиться этой книгой
Поделиться в Твиттере
Использование функции косинуса для нахождения гипотенузы (Ключевой этап 3)
Урок
Функция косинуса связывает заданный угол с прилежащей стороной и гипотенузой прямоугольного треугольника. Длина гипотенузы находится по следующей формуле:
В этой формуле θ — это угол прямоугольного треугольника, прилежащая — это длина стороны, следующей за углом, а гипотенуза — это длина наибольшей стороны. На изображении ниже показано, что мы имеем в виду:
Как использовать функцию косинуса для нахождения гипотенузы прямоугольного треугольника
Найти гипотенузу прямоугольного треугольника легко, если известны угол и прилежащие к нему.
Какова длина гипотенузы изображенного ниже прямоугольного треугольника?
Пошаговая инструкция:
Начните с формулы:
Гипотенуза = смежная / cos θ
Не забудьте: / означает ÷
Подставляем в формулу угол θ и длину прилежащего. В нашем примере θ = 60°, а прилежащее равно 4 см.
В нашем примере θ = 60°, а прилежащее равно 4 см.
Гипотенуза = 4 / cos (60°) Гипотенуза = 4 ÷ cos (60°) Гипотенуза = 4 ÷ 0,5 Гипотенуза = 8 см
Ответ:
Длина гипотенузы прямоугольного треугольника с углом 30° и прилежащим 4 см равна 8 см.
Вспоминая формулу
Часто самая сложная часть поиска неизвестного угла — это вспомнить, какую формулу использовать. Всякий раз, когда у вас есть прямоугольный треугольник, в котором вы знаете одну сторону и один угол и должны найти неизвестную сторону… ……подумайте о тригонометрии… ……………подумайте о синусе, косинусе или тангенсе… …………………………..думаю СОХ КАН ТОА .
Глядя на приведенный выше пример, мы пытаемся найти H ypotenuse, и мы знаем A djacent.
Две буквы, которые мы ищем, это AH , которые входят в CAH в SOH CAH TOA. Это напоминает нам уравнение:
Это напоминает нам уравнение:
C os θ = A djacent / H ypotenuse
Это изменено, чтобы получить формулу в верхней части страницы (см. Примечание ).
H ypotenuse = A djacent / C os θ
Слайды урока
Ползунок ниже дает еще один пример нахождения гипотенузы прямоугольного треугольника (поскольку угол и прилежащее к нему известны). Откройте слайдер в новой вкладкеИнтерактивный виджет
Вот интерактивный виджет, который поможет вам узнать о функции косинуса прямоугольного треугольника.
Что такое функция косинуса?
Функция косинуса является тригонометрической функцией. Косинусом данного угла в прямоугольном треугольнике называется отношение длины прилежащего катета к длине гипотенузы.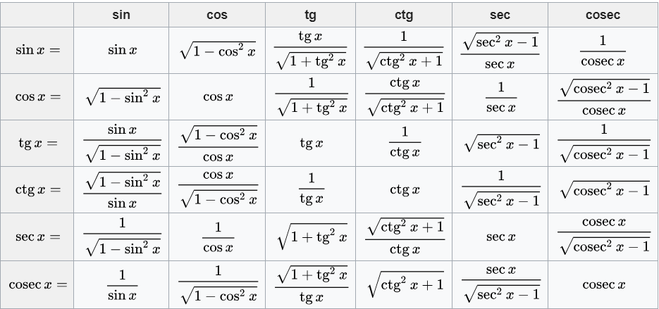

 Нарисуйте прямоугольный треугольник и обозначьте указанные части.
Нарисуйте прямоугольный треугольник и обозначьте указанные части.