Формула логарифма от логарифма: Формулы и свойства логарифмов, основные формулы логарифмов с примерами

Содержание

Свойства логарифма формулы. Основные свойства логарифмов. Свойства логарифмов алгебра.

Альфашкола
Статьи
Свойства логарифма

Свойства логарифмов

Напомним логарифм числа — это показатель степени \(log_28=3\) показывает в какую степень надо возвести число, которое стоит в основании, чтобы получить число в выражении логарифма. Если вы забыли, что такое логарифм повторите что такое логарифм.

где 2 — основание, 8 — аргумент логарифма, 3 степень основания.

Многие логарифмические выражения можно расписать или сжать, используя свойства логарифмов.

Основное свойство логарифма — переход к другому основанию: \(log_ax=\frac{log_bx}{log_ba}\) пример: \(log_28=\frac{log_88}{log_82}=\frac{1}{\frac{1}{3}}=3\)

\(log_a1=0\) если аргумент равен 1, то логарифм равен 0, так как \(a^0=1\). n u = 1/n* log_a u\) основание \(a\) в степени \(n\).
\( loga (uv) = log_a u + log_a v\) \(ln (uv) = lnu + ln v\) произведение логарифмов можно разложить на сумму этих логарифмов.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Надежда Ивановна Пехтерева

Репетитор по математике

Стаж (лет)

Образование:

Ставропольский ордена Дружбы народов государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Елена Ивановна Качанова

Репетитор по математике

Стаж (лет)

Образование:

Витебский государственный педагогический институт им. С.М. Кирова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Мария Евгеньевна Эминова

Репетитор по математике

Стаж (лет)

Образование:

Удмуртский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

Математика

Репетитор по физике
Репетитор по химии
Репетитор по русскому языку
Репетитор по английскому языку
Репетитор по обществознанию
Репетитор по истории России
Репетитор по биологии
Репетитор по географии
Репетитор по информатике

Специализации

Подготовка к ЕГЭ по математике (профильный уровень)

Репетитор по химии для подготовки к ЕГЭ
Репетитор по химии для подготовки к ОГЭ
Подготовка к олимпиадам по химии
Репетитор для подготовки к ОГЭ по физике
Подготовка к олимпиадам по физике
Репетитор по русскому языку для подготовки к ЕГЭ
ВПР по физике
Репетитор по информатике для подготовки к ОГЭ
Подготовка к ОГЭ по литературе

Свойства логарифмов, переход к новому основанию, решение более сложных задач 11 класс онлайн-подготовка на Ростелеком

Формула перехода к новому основанию

Теорема

Если , , – положительные числа, причем a и c отличны от 1, то имеет место равенство: – формула перехода к новому основанию

Доказательство

Преобразуем данное равенство, домножив левую и правую часть на знаменатель правой части:

Далее возведем в степень левой и правой части:

Преобразуем левую часть, применив свойство степеней:

Согласно основному логарифмическому тождеству:

Таким образом:

Согласно основному логарифмическому тождеству:

Следовательно:

Мы получили равенство, которое верно по основному логарифмическому тождеству. То есть:

Что и требовалось доказать.

Следствия из формулы перехода к новому основанию

1. Первое следствие мы вывели попутно, доказывая формулу перехода:

2. Подставим в предыдущую формулу :

Доказательство

Докажем третье следствие из формулы перехода к новому основанию

, при ;

Доказательство

Прологарифмируем данное равенство по основанию :

В правой и левой части вынесем степень за знак логарифма:

Так как , то:

Согласно второму следствию из формулы перехода к новому основанию , следовательно:

Домножим левую и правую часть на знаменатель правой части:

Равенство верное, следовательно:

Что и требовалось доказать.

Пример 1

Вычислите:

Решение

Разность логарифмов с одинаковым основанием – это логарифм частного, а сумма логарифмов с одинаковым основанием – логарифм произведения. А у нас в числителях и знаменателях стоят логарифмы с одинаковыми основаниями.

Применяя эти свойства, получаем:

Согласно формуле перехода к новому основанию :

Следовательно:

Из основания логарифма показатель степени выносится за знак логарифма как , а из подлогарифмического выражения – как , то есть:

Следовательно:

Ответ: .

Пример 2

Вычислите:

Решение

Нам известно следствие из формулы перехода к новому основанию:

С помощью этой формулы преобразуем показатель степени в данном выражении:

Таким образом:

Ответ: .

Пример 3

Вычислите:

Решение

Преобразуем показатель степени, избавившись от минус первой степени:

Приведем всё к одному основанию (в данном случае к 5), воспользовавшись следствием из формулы перехода к новому основанию

Домножим числитель и знаменатель на :

Следовательно:

Применим основное логарифмическое тождество:

Ответ: 5.

Пример 4

Известно, что , ; . Вычислить:

Решение

Существует два способа решения этой задачи.

1. Перейдем в логарифмах (в выражении, которое нам необходимо вычислить) к одному основанию – . Для этого воспользуемся формулой перехода к новому основанию:

а)

Так как:

– по условию, то:

б)

в) Таким образом:

2. Второе решение состоит в том, что если , то . Подставив это в наше выражение, мы получим выражение с одной переменной , вычислить его будет несложно, главное не запутаться в степенях.

Ответ: .

Пример 5

Дано: . Найти:

Решение

Заметим, что все числа в условии – это комбинации двоек и троек: ; ; ; . Перейдем в данных логарифмах к основанию 2 или 3. Например, к трем:

Таким образом:

Выразим из этого выражения :

Домножаем это выражение на 3:

Вычтем из левой и правой части выражения 1 и разделим эти части на 2:

3. Так как , то:

Домножим числитель и знаменатель на :

Ответ: .

Пример

Упростите выражение:

Решение

Согласно основному логарифмическому тождеству представим 2 в виде:

Тогда:

Следовательно:

В данном примере мы попутно доказали полезное свойство:

Ответ: 0.

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа 10-11 кл. – М.: Мнемозина, 2001.

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа 10-11 кл. – М.: Просвещение, 1990.

4. Мордкович А.Г., Денищева Л.О., Корешкова Т.А., Мишустина Т.Н., Тульчинская Е.Е. Алгебра и начала анализа 10-11 кл.: Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2001.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт youtube.com (Источник)

2. Интернет-сайт «Гипермаркет Знаний» (Источник)

3. Интернет-портал «ЯКласс» (Источник)

4. Интернет-сайт «Уроки математики» (Источник)

Домашнее задание

1. Задания 1596, 1602, 1612 (стр. 237–239) – Мордкович А.Г., Денищева Л.О., Корешкова Т.А., Мишустина Т.Н., Тульчинская Е.Е. Алгебра и начала анализа 10-11 кл.: Задачник (Источник)

2. Докажите тождество: .

3. Докажите тождество: .

Формула логарифма — определение, типы, правила и свойства

Математические сомнения

В математике логарифмы — это еще один способ записи показателей степени. Логарифм числа по основанию равен другим числам. Логарифм — это просто функция, обратная возведению в степень. Например, если 10 ² = 100, то log ₁₀ 100 = 2.

Лог _b x = n или b ⁿ = x

Где b = основание логарифмической функции.

Это можно заметить как «Логарифм x по основанию b равен n». В этой короткой статье мы узнаем определение логарифмов, два типа логарифмов, таких как десятичный логарифм и натуральный логарифм, а также различные свойства логарифмов со многими примерами.

Содержание

Что такое логарифм?
История
Типы логарифмов
Правила и свойства логарифмов
Другое имущество
Формулы основных логарифмов
Решенные примеры
Часто задаваемые вопросы (FAQ)

Логарифм — это степень, в которую нужно возвести число, чтобы получить дополнительные значения. Это наиболее удобный способ выражения больших чисел. Логарифм обладает различными важными свойствами, которые доказывают, что умножение и деление логарифмов также можно записать в логарифмической форме вычитания и сложения.

Логарифм положительного действительного числа «a» по основанию b, положительное действительное число не равно 1 [^{nb 1}], является показателем степени, на которую нужно возвести b, чтобы получить a.

т. е. b ^y = a ⇔ log _b a=y

Где

a и b = два положительных действительных числа
у = реальное число
a = аргумент, который находится внутри лога
б = база, которая внизу бревна

Ниже приведены некоторые примеры преобразования экспоненциальных форм в логарифмы.

Экспоненты	Логарифмы
6 ² = 36	Журнал ₆ 36 = 2
10 ² = 100	Журнал ₁₀ 100 = 2
3 ³ = 27	Журнал ₃ 27 = 3

История

Джон Нейпир ввел понятие логарифмов в 17 веке. Позже он использовался многими учеными, мореплавателями, инженерами и т. д. для выполнения различных расчетов, что упростило его. Проще говоря, это обратный процесс возведения в степень. В этой статье мы подробно рассмотрим определение, свойства и образцы логарифма.

Типы логарифмов

Он бывает двух типов, которые указаны ниже:

Десятичный логарифм
Натуральный логарифм

десятичный логарифм

Десятичный логарифм также известен как логарифм по основанию 10. Он представляется как log10 или просто log. Например, десятичный логарифм 1000 записывается в виде логарифма (1000). Десятичный логарифм определяет, сколько раз мы должны умножить число 10, чтобы получить требуемый результат.

Например, log ₁₀ (100) = 2

. Если мы дважды умножим число 10, то получим 100.

Натуральный логарифм

Натуральный логарифм называется логарифмом по основанию e.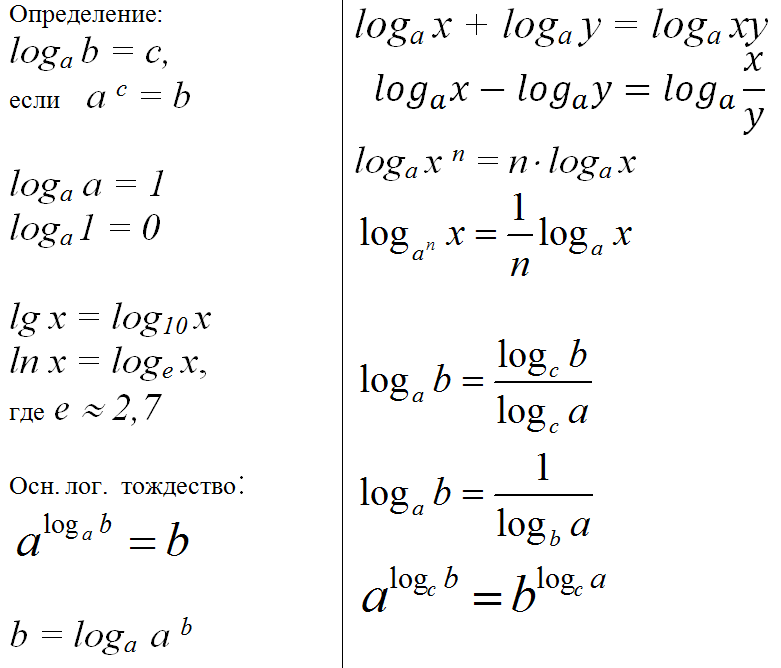 Натуральный логарифм представляется как ln или loge. Здесь «е» представляет постоянную Эйлера, которая приблизительно равна 2,71828. Например, натуральный логарифм числа 78 записывается как ln 78. Натуральный логарифм определяет, на сколько мы должны умножить «е», чтобы получить требуемый результат.

Например, ln(78) = 4,357

Таким образом, логарифм по основанию e числа 78 равен 4,357.

Логарифмы Правила и свойства

Ниже приведены определенные правила, на основании которых могут выполняться логарифмические операции:

Правило продукта

Лог _б (мн)= бревно _б м + бревно _б н

Например: журнал ₃ ( 4y ) = журнал ₃ (4) + журнал ₃ (у)

Раздел Правило

Лог _б (м/н)= лог _б м – лог _б н

Например, log ₃ ( 5/г ) = log ₃ (5) -log ₃ (г)

Экспоненциальное правило

Лог _b (m ⁿ ) = n log _b m

Пример: журнал _b (4 ³ ) = 3 log _b 4

Изменение основного правила

Бревно _б м = бревно _а м/ бревно _а б

Пример: log _b 3 = log _a 3/log _a b

Базовое правило переключения

log _b (а) = 1 / log _a (б)

Пример: log _b 7 = 1/log ₇ б

Производное бревна

Если f (x) = log _b (x), то производная от f (x) определяется выражением;

f'(x) = 1/(x ln(b))

Пример: Дано, f (x) = log ₈ (x)

Тогда f'(x) = 1/(x ln(8))

Интеграл журнала

∫log _b (x)dx = x( log _b (x) – 1/ln(b)) + C

Пример: ∫ log ₈ (x) dx = x ∙ ( log ₈ (x) – 1 / ln(8) ) + C

Другое имущество

Некоторые связанные свойства логарифмических функций:

Журнал _б б = 1
Журнал _б 1 = 0
Журнал _b 0 = не определено

Основные формулы логарифмов

логарифм _б (мин) = логарифм _б (м) + лог _б (н)
log _b (м/н) = log _b (м) – log _b (н)
Журнал _b (xy) = y log _b (x)
Log _b м√n = log _b н/м
m log _b (x) + n log _b (y) = log _b (x ^m y ⁿ )
log _b (m+n) = log _b m + log _б (1+нм)
log _b (m – n) = log _b m + log _b (1-n/m)

Решенные примеры

Q1. Журнал решения ₂ (32) = ?

Ответ. Так как 2 ⁶ = 2 × 2 × 2 × 2 × 2 = 32, 5 — показатель степени, а log ₂ (32) = 5.

Q2. Каково значение журнала ₁₀ (100)?

Ответ. журнал ₁₀ (100)= 2

Q3. Использование свойства логарифмов, найти значение x для log ₃ x= log ₃ 5+ log ₃ 4

Ответ. По правилу сложения log ₃ 5+ log ₃ 4= log ₃ (5 * 4 )

Журнал ₃ ( 20 ). Таким образом, х= 20,

Q4. S olve для x в журнале ₂ х = 4

Ответ. Эта логарифмическая функция может быть записана в экспоненциальной форме как 2 ⁴ = x

Следовательно, 2 ⁴ = 2 × 2 × 2 × 2 = 16, X = 16.

Часто задаваемые вопросы (FAQ)

Q1. Каковы три свойства логарифмов?

Ответ. Три свойства логарифма:

Правило продукта: am. ан=а. м+п
Частное правило: am/an = a. м-н
Степенное правило: (am)n = a. мн

Q2. Что такое домен журнала?

Ответ. Область определения логарифмической функции y = log x равна x > 0 или (0, ∞). Диапазон любой логарифмической функции задается всеми действительными числами (R)

Q3. Каков натуральный логарифм 0?

Ответ. Не определено

Q4. Что противоположно журналу?

Ответ. Поскольку мы знаем, что функция, обратная логарифмической, является экспоненциальной. Итак, мы знаем, что функция, обратная f(x) = log subb(x), равна f ^-1 (y) = b ^y .

В5. Как вы будете писать 1 в виде журнала?

Ответ. Логарифм x = 1 — это число y, которое мы должны возвести по основанию b, чтобы получить значение 1. Таким образом, логарифм по основанию 1 равен 0.

Формула логарифма — GeeksforGeeks шотландским математиком

Джон Нейпир (1550-1617). Логарифм Нейпира был первым, опубликованным в 1614 году. Генри Бриггс ввел десятичный логарифм. Целью Джона Нэпьера было помочь в умножении величин, которые назывались синусами.

Формулы логарифмов

Логарифм определяется как степень, в которую возводится число для получения других значений. Логарифмы обратны показателям степени. Существует уникальный способ чтения выражения логарифма. Например, б ^x = n называется потому, что x — это логарифм n по основанию b. Есть две части логарифма: Характеристика и Мантисса. Целая часть логарифма называется «Характеристика», а неотрицательная десятичная часть называется «Мантисса». Характеристика может быть отрицательной, а мантисса — нет. Например: log ₁₀ ⁽¹²⁰⁾ = 2,078 (2 — характеристика, 0,078 — мантисса).

Свойства логарифма

log _A ^MN = LOG _A ^M +LOG _A ^N (свойство продукта)
Log _A ^M/N = LOG _A ^M -LOG _{A = LOG} ^M -LOG _{A 7 A} ^M -LOG _{A ⁿ (свойство «Оценное свойство»)}
log _A M ^N = NLOG _A ^M (Power Property)
LOG _B ^A = (LOG _C ^A)/( log _c ^b ) (свойство изменения базы)
Log _B ^A√n = 1/A log _B ^N
Log 1 = LOG _A R ¹ = 0
Log _A ^A = 1 ( Правило идентификации)
Log _B ^A = LOG _B ^C => A = C (Правило равенства)
A ^Log _^A ^x = X (Rad To Log)

Натуральный логарифм

Натуральный логарифм числа — это его логарифм по основанию «е». «е» — трансцендентное и иррациональное число, значение которого примерно равно 2,71828182. Записывается как lnx. х = журнал _е х . Это особый тип логарифма, используемый для решения задач времени и роста. Он также используется для решения уравнения, в котором неизвестное выступает как показатель степени какой-либо другой величины.

Свойства натурального бревна

ln(xy) = ln(x) + ln(y) (правило произведения)
ln(x/y) = ln(x) – ln(y) (правило частного )
ln(x ^y ) = y ln(x) (логарифм мощности)
ln (e) = 1 (логарифм e)
ln (1) = 0 (логарифм 1)
ln(1/x) = -ln(x) (правило взаимности)

Применение логарифма

Логарифм используется для выражения большего значения.
Логарифм Используется для измерения интенсивности землетрясений.
Логарифм используется для измерения значения pH.
Логарифм используется для моделирования бизнес-приложений
Логарифм используется учеными для определения скорости радиоактивного распада
Логарифм используется экономистами для построения графиков.

Проблемы выборки

Вопрос 1: Решение log ₂ (x) = 4

Решение:

₂ (x) = 4
2 ⁴ = x
999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997 x = 16
значение x будет 16.

Вопрос 2: Решите log ₂ (8) = x.

Решение:

log ₂ (8) = x
2 ^x = 8
2 ^x = 2 ³
x = 3 (применяя правило равенства)
Таким образом, значение x будет равно 3.

Вопрос 3: Найдите значение x, если log 60 7 9000 x — 3) = 1.

Решение:

log ₆ (x — 3) = 1
6 ¹ = (x — 3)
x — 3 = 6
x = 9
Таким образом, значение x будет равно 9.

Вопрос 4. Найдите x, если log(x – 2) + log(x + 2) = log ₂ 1

Решение. [log1 = 0]

log[(x – 2)(x + 2)] = 0 [правило произведения]

(x – 2)(x + 2) = 1 [анти log0 = 1]

x ² – 4 = 1

x ² = 5

x = ±√5

Поскольку логарифм отрицательного числа не определен.

Таким образом, значение x будет равно √5.

Вопрос 5: Найдите значение журнала ₉ (59049).

Решение:

log ₉ (59049) [9 ⁵ =59049]
log _{0 0 9} 0 9 90 90
5log ₉ 9 (Правило идентификации, то есть log _A A]
5.

Вопрос 6: Express Log ₁₀ (5) + 1 в форме Log _{10 0008 x.}

Решение:

Log ₁₀ (5) + 1
Log ₁₀ (5) + log ₁₀ 10 [Правило идентификации]
Log ₁₀ (5 × 10) [Правило продукта]
Log _.
No related posts.

Свойства логарифма формулы. Основные свойства логарифмов. Свойства логарифмов алгебра.

Свойства логарифмов, переход к новому основанию, решение более сложных задач 11 класс онлайн-подготовка на Ростелеком

Формула перехода к новому основанию

Следствия из формулы перехода к новому основанию

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Формула логарифма — определение, типы, правила и свойства

Математические сомнения

История

Типы логарифмов

Логарифмы Правила и свойства

Другое имущество

Основные формулы логарифмов

Решенные примеры

Часто задаваемые вопросы (FAQ)

Формула логарифма — GeeksforGeeks шотландским математиком

Проблемы выборки

Добавить комментарий Отменить ответ