Формула нахождения вероятности: Классическое определение вероятности — урок. Алгебра, 9 класс.

Содержание

01Математика — Теория вероятностей — Формула полной вероятности и рекурсия

Пусть событие \(\displaystyle A\) – сумма выпавших очков превысила число \(\displaystyle 3\) ровно за два броска.

Начнём строить граф возможных исходов, учитывая результаты первого броска кости.

Обозначим зелёным цветом исходы, для которых наступление события \(\displaystyle A\) возможно, красным – невозможно.

Получаем:

Введем события:

\(\displaystyle B_{1}\) – при первом броске выпало \(\displaystyle 1{\small , }\)
\(\displaystyle B_{2}\) – при первом броске выпало \(\displaystyle 2{\small , }\)
\(\displaystyle B_{3}\) – при первом броске выпало \(\displaystyle 3\) очка.

Тогда вероятность наступления каждого из событий \(\displaystyle B_{1}{ \small ,}\,B_2\) и \(\displaystyle B_{3}\) равна

\(\displaystyle P(B_{1})=P(B_{2})=P(B_{3})=\frac{1}{6}{\small . }\)

Обозначим на рисунке эти вероятности:

Продолжим строить граф возможных исходов.

Будем его достраивать по результатам второго броска кости.

Опять обозначим зелёным цветом исходы, для которых событие \(\displaystyle A\) наступает, красным – не наступает.

Получаем:

Найдем условную вероятность \(\displaystyle P_{B_{1}}(A)\) – вероятность наступления события \(\displaystyle A\) при условии, что событие \(\displaystyle B_{1}\) произошло.

\(\displaystyle B_{1}\) – это выпадение в первом броске \(\displaystyle 1\) очка. Значит, для наступления \(\displaystyle A\) во втором броске должно выпасть \(\displaystyle 3\), \(\displaystyle 4\), \(\displaystyle 5\) или \(\displaystyle 6{\small . }\)

Тогда

\(\displaystyle P_{B_{1}}(A)=\frac{4}{6}{\small . }\)

Аналогично,

\(\displaystyle P_{B_{2}}(A)=\frac{5}{6}\) и \(\displaystyle P_{B_{3}}(A)=\frac{6}{6}{\small . }\)

Подсчитаем вероятность одновременного наступления событий \(\displaystyle A\) и \(\displaystyle B_1{\small . }\)

На рисунке это выглядит как подсчет вероятности для первой ветки графа:

Тогда

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 1\) очко и сумма больше \(\displaystyle 3)=P(B_{1}) \cdot P_{B_{1}}(A)=\frac{1}{6}\cdot\frac{4}{6}=\frac{4}{36}{\small . }\)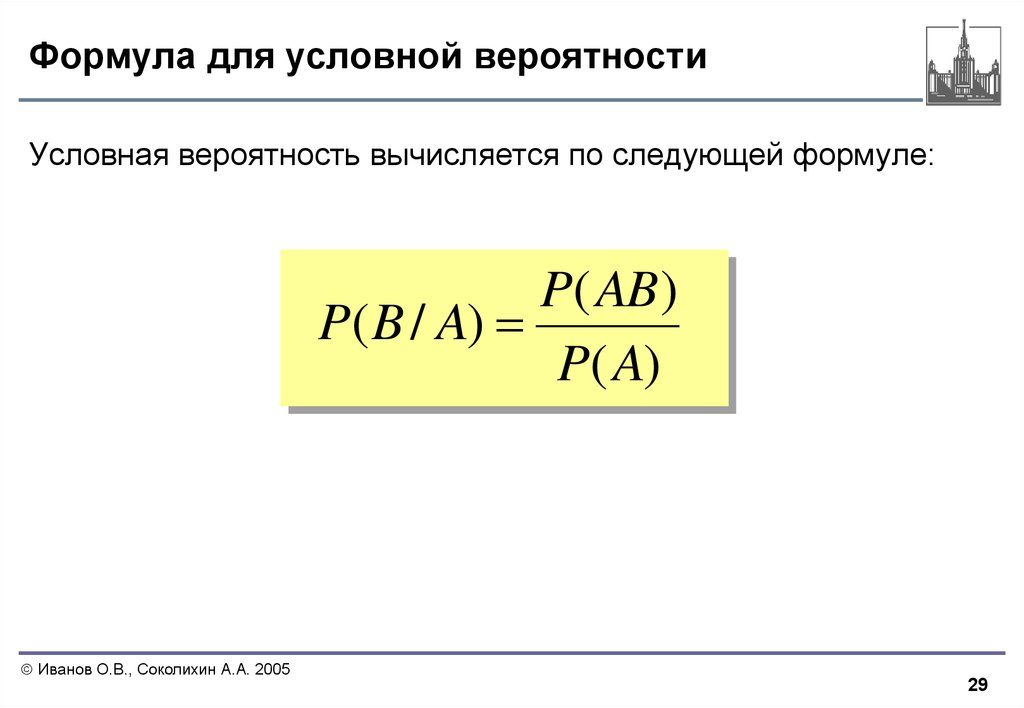

Аналогично получаем:

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 2\) очка и сумма больше \(\displaystyle 3)=P(B_{2}) \cdot P_{B_{2}}(A)=\frac{1}{6}\cdot\frac{5}{6}=\frac{5}{36}{\small . }\)

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 3\) очка и сумма больше \(\displaystyle 3)=P(B_{3}) \cdot P_{B_{3}}(A)=\frac{1}{6}\cdot\frac{6}{6}=\frac{6}{36}{\small . }\)

Осталось найти полную вероятность наступления события \(\displaystyle А{\small . }\)

Для этого необходимо просуммировать вероятности, полученные для каждой ветки нашего графа.

Тогда

\(\displaystyle P(A)=\frac{4}{36}+\frac{5}{36}+\frac{6}{36}=\frac{15}{36}\approx0{,}42{\small . }\)

Ответ: \(\displaystyle 0{,}42{\small .}\)

1.8. Формула полной вероятности

Пусть (Ω, F, Р) – вероятностное пространство и события образуют в нем полную группу событий. Это значит: 1) i≠j; 2) . События H_k часто при этом называют гипотезами. Ставится задача отыскать вероятность события А F, если известны вероятности

Событие А может быть представлено в виде А=АΩ=А(H₁+H₂+…+H_n) = AH₁+AH₂+…+AH_n, поскольку из несовместности событий следует несовместность событий , т.е. условия , имеют место для всех . Тогда | использовали свойство Р7 вероятностей, далее используем равенство (1.6)|=

= .

Итак,

Р(А)= (1.12)

Формула (1.12) носит название формулы полной вероятности.

Замечание. Формула справедлива для счетного набора гипотез , если они удовлетворяют условиям 1)– 2).

Пример 32. Среди N экзаменационных билетов «хороших» n. У кого из двух студентов вероятность взять хороший билет больше: у того, кто берет билет первым, или у того, кто берет вторым?

Решение. Для первого студента вероятность взять хороший билет равна . Для второго она зависит от предположений: Н – первый студент взял хороший билет и Н – первый студент не взял хороший билет. Вероятность гипотез Р(Н )= , Р(Н ) = . Вычислим условные вероятности: Р{второй студент взял хороший билет | первый студент взял хороший билет}= ; Р{второй студент взял хороший билет | первый студент не взял хороший билет} = . Вычислим теперь вероятность Р{второй студент взял хороший билет}:

Р{второй студент взял хороший билет}= =

Изменится ли вероятность, если билет брать не первым, не вторым, а третьим, четвертым, …, последним?

1.9. ФОРМУЛА БАЙЕСА

Любой результат сл. эксперимента несет информацию, меняющую наше представление либо о событиях сл. эксперимента, либо об условиях эксперимента. Во многих приложениях ТВ встречается задача: до опыта имеются гипотезы H₁,…, H_n с известными вероятностями Проводится опыт, в результате которого произошло событие А. Тогда вероятности всех гипотез подвергаются переоценке, могут быть найдены новые вероятности , вероятности тех же гипотез после того, как произошло событие A.

Говорят в этой ситуации, что Р (H_k), k=1,…,n, – априорные вероятности гипотез, а , k=1,…,n, –

апостериорные

Знаем, что – использовали формулы (1.5) и (1.6), k=1,…, n. С использованием формулы полной вероятности (1.12) получаем:

(1.13)

Полученная формула носит название формулы Байеса.

Пример 33. На 4 карточках написаны буквы в, к, л, о. Карточки перемешиваются и выкладываются в ряд. Какова вероятность, что получится слово «волк » – событие А.

Решение.

Решение может быть получено таким же способом, что и в примере 28, т.е. по формуле умножения вероятностей:

Пример 34. Из колоды в 36 карт наудачу вынимается 6 карт. Какова вероятность, что:

1) все они будут одной масти;

2) среди них окажется туз пик;

3) среди них окажется ровно один туз;

4) среди них окажутся ровно две бубновые карты;

5) среди них окажется хотя бы одна бубновая карта.

Решение. 1) Имеем дело с неупорядоченной выборкой без возвращения. Поскольку нас интересует состав выборки и совсем не интересует порядок выбранных карт, то Найдем число эл. событий, благоприятствующих событию A (составляющих событие А). Зафиксируем определенную масть. Чтобы имело место событие A, в выборку должны попасть любые 6 карт этой масти. Опять имеем дело с неупорядоченной выборкой по 6 элементов из 9, выборка без возвращения, следовательно, число способов выбрать 6 элементов из 9 равно C (в колоде карт одной масти 9 штук). В задаче речь идет не об определенной масти, а о любой из 4-х мастей, следовательно, . Таким образом,

2) Наряду с тузом пик в выборке присутствуют еще 5 карт, самых различных, в том числе среди них могут быть и еще тузы, число способов выбрать 5 таких карт равно , поэтому

3) В отличие от предыдущего случая, когда масть туза была известна, теперь мы ее не знаем и выбираем одного из тузов способами, остальные пять карт выбираем способами, по основному правилу комбинаторики и

4) Ясно из предыдущих рассуждений, что и

5) В этом случае удобно с вычислительной точки зрения перейти к противоположному событию, вероятность которого вычисляется много проще, событию {в выборке не окажется ни одной бубновой карты}. Вероятность этого события равна тогда

Пример 35. Какова вероятность герою «Пиковой дамы» выиграть?

Решение. В колоде, видимо, 56 карт. Германн выигрывает, если в первый вечер из колоды вынимает тройку, во второй – семерку и в третий – туза. Масть роли не играет. Следовательно, – этот результат получен по формуле умножения вероятностей. Если свести вычисления к схеме урн, то имеем урну с 56 различными шарами; опыт состоит в вынимании наудачу 3-х шаров из урны. Выборка упорядоченная, с возвращением, следовательно, согласно табл. 1 общее число эл. событий равно . Число элементарных событий, благоприятствующих событию A, находим по такой схеме: число троек, семерок, тузов в колоде поровну – 4. Поскольку масть карт роли не играет, мы можем считать число равным n =С С С . Следовательно, .

Пример 36. В лифт восьмиэтажного дома на первом этаже входят 5 человек. Независимо от других каждый может выйти с одинаковой вероятностью на любом из 7 этажей, начиная со второго. Какова вероятность, что 1) все выйдут на пятом этаже; 2) все пятеро выйдут на одном и том же этаже; 3) все пятеро выйдут на разных этажах; 4) все выйдут группами по 2, 2 и 1 человек на разных этажах?

Решение. По условию задачи общее число элементарных исходов равно, согласно табл.1, В случае 1) число элементарных событий , благоприятствующих событию A, равно 1, потому 2) Во втором случае, в отличие от первого, этаж, где все выйдут, не указан, это может быть любой из 7 этажей, потому =7, а 3) Разместить 5 различных человек по 7 этажам можно способами, следовательно 4) В последнем случае для вычисления числа эл. событий, благоприятных событию A, следует учесть число способов распределения 5 человек по трем группам – это можно сделать способами; далее, следует учесть распределение 3 групп по 7 этажам – это можно сделать способами. По основному правилу комбинаторики получаем и

Пример 37. Предположим, что n неразличимых частиц распределяются по m ячейкам. Ограничений на число частиц в ячейке нет. Событие А – в фиксированную ячейку попало ровно k частиц. Вычислить P(A).

Решение. Термин «неразличимые частицы» предполагает, что различными будут такие распределения частиц по ячейкам, которые отличаются только числом частиц в ячейках. Здесь также можно применить схему урн, но с шарами двух различных видов в ней. Пусть частицы – это белые шары, перегородки между ячейками – черные шары. Эксперимент состоит в том, что из урны последовательно вынимаются все шары. Рассматриваем, как в последовательности шаров размещены черные шары: последовательность вынутых шаров может иметь, например, вид бчбббччббббчч…б. Следовательно, в первую ячейку попала 1 частица, во вторую – 3 частицы, в третью – ни одной, в четвертую – 4 и т. д. Число всех эл. исходов совпадет с числом всевозможных размещений (m–1) черных шаров среди n+m–1 шаров обоих цветов, это число равно = . Если в фиксированную ячейку попадает k частиц, то оставшиеся n–k частиц размещаются по m–1 ячейкам произвольным образом, число таких размещений равно .

Такое размещение частиц по ячейкам носит в физике название статистики Бозе — Эйнштейна. Ей подчиняются фотоны, атомные ядра, атомы с четным числом частиц.

Пример 38. Рассмотрим ту же ситуацию, что и в примере 37, только на число частиц в ячейке имеется ограничение – в каждой ячейке может находиться не более одной частицы. Здесь предполагается m n. Событие A – занято k фиксированных ячеек. Вычислить P(A).

Решение. Эта схема размещения ассоциируется со схемой выборки из урны с m неразличимыми шарами n шаров. Выборка без возвращения, неупорядоченная. Тогда согласно табл. 1 .

На самом деле, исходами опыта могут быть такие последовательности: первые n ячеек заняты частицами, остальные свободны;

первые (n–1) ячеек заняты частицами, n-ая ячейка свободна, (n+1) ячейка занята и т. д. Число таких последовательностей совпадает с числом размещений из m элементов по n.

Такое распределение частиц по ячейкам носит название статистики Ферми — Дирака, ей подчиняются электроны, протоны, нейтроны.

Пример 39. Условия задачи, как и в примере 37, но частицы различные. На число частиц в ячейке ограничений нет. Каждая из n различных частиц может попасть в каждую из m различных ячеек. Событие A: в первую ячейку попало n₁ частиц, во вторую ячейку попало n₂ частиц, …, в m-ю ячейку попало n_m частиц, n₁+n₂+…+n_m=n. Вычислить P(A).

Решение. Условие размещения частиц предполагает, что если обратиться к схеме урн, то каждый из n различных шаров может попасть в выборку на любое место в ней. Следовательно, имеем дело с выборкой с возвращением. Размещение по ячейкам отличается одно от другого не только тем, сколько частиц в ячейке, но и какие частицы в ячейке (об этом говорит условие, что частицы различные), следовательно, выборка упорядоченная. Тогда . Число элементарных событий, благоприятствующих событию A, равно . Это значит, в первую ячейку попали любые n₁частиц из n, при этом порядок выбора частиц несущественен. Как только ячейка заполнена, остается n–n₁частиц, из которых во вторую ячейку могут попасть любые n₂ частиц и т.д. Преобразуем выражение : = =

= . Тогда .

Такое распределение частиц носит название статистики Максвелла — Больцмана, ей подчиняется идеальный газ.

Пример 40. Пусть имеется n частиц, из которых n₁ – одного типа, n₂– второго,…, n_k– k-ого типа, n=n₁+n₂+…+n_k. Случайным образом из них выбирается m частиц, m ≤ n. Событие A={в выборку попало m₁частиц первого типа,m₂ частиц – второго типа, …, m_k частиц k-ого типа}, m=m₁+m₂+…+m_k. Вычислить P(A).

Решение. Выборка без возвращения, неупорядоченная, следовательно, ; вычислим число благоприятных событию A эл. исходов: m₁частиц из n₁ мы можем выбрать способами, …, m_k частиц из n_k –способами. При этом любой способ выбора частиц одного типа комбинирует с любыми способами выбора частиц остальных типов, т.е. . Тогда

. Если число P(A) обозначить как – тем самым мы указываем на зависимость события A от чисел , , – и просчитать вероятности всех таких событий, то получим множество вероятностей , которое носит название гипергеометрического распределения. Частный случай этого распределения при к=2 рассмотрен в примере 17.

Пример 41. В спортлото «6 из 49» угадано k номеров, , – событие А_k. Найти вероятности событий А_k.

Решение. Имеем дело с гипергеометрическим распределением, в котором , тогда вероятности событий образуют множества чисел устанавливающих зависимость вероятности события A_k от числа k. Так, , если k=4; если же k=6 .

Пример 42. Одновременно бросаются две игральные кости. Событие A={на 1-ой кости выпало более 2-х очков}, событие В ={в сумме выпало четное число очков}, событие С ={в сумме выпало менее 10 очков}. Какие из событий являются независимыми?

Решение. По классическому определению вероятности событий имеем . Далее

Проверяя условия

, получаем результат: события A и В независимы, остальные события – зависимы.

Пример 43. Обнаружение воздушной цели проводится независимо двумя радиолокационными станциями. Вероятность обнаружения цели первой станцией равна 0.7, второй – 0.8. Какова вероятность, что цель будет обнаружена хотя бы одной станцией – событие A?

Решение. Введем события – цель обнаружена i-й станцией, i=1,2. Тогда событие В силу теоремы сложения вероятностей , причем по условию . Тогда

Задачу можно решить иначе:

Пример 44. В поступивших на склад трех партиях деталей годные составляют 89%, 92% и 97% соответственно, а количества деталей в партиях относятся как 1:2:3. Чему равна вероятность, что случайно выбранная деталь окажется негодной? Какова вероятность, что при этом она принадлежит первой партии?

Решение. Обозначим за события, состоящие в том, что деталь принадлежит 1-й, 2-й и 3-й партии соответственно. Эти события попарно несовместны и образуют полную группу событий. Из соотношений количеств деталей в партиях получаем . Событие А={выбрана бракованная деталь}. Тогда . По формуле полной вероятности (1.12) найдем вероятность события А: =0.06. Используем формулу Байеса (1.13) для нахождения вероятности : = .

Вероятностные правила с примерами — Cuemath

Вы, должно быть, играли в карты и получали от этого удовольствие.

Во время игры в карты вы когда-нибудь предсказывали, что следующей картой будет король, дама или туз, которые могут помочь вам выиграть игру?

Или, может быть, вы хотели, чтобы следующая карта выпала вам на пользу!

Вы когда-нибудь думали, что используете понятие вероятности в своей повседневной жизни, будь то игра в карты или что-то еще?

Существуют условия или возможности событий, происходящих одновременно, или вы случайно наткнетесь на события, происходящие последовательно, так как же узнать вероятность этих событий?

Хорошо! Существуют правила вероятности, которым вы можете следовать!

Давайте изучим приведенную ниже симуляцию, чтобы получить представление о вероятности! Введите значения для расчета вероятности чисел.

Этот мини-урок расскажет вам о вероятностных правилах, правиле дополнения и фундаментальном принципе счета.

Ознакомьтесь с интересными примерами и несколькими интерактивными вопросами в конце страницы.

План урока

1.	Что такое вероятность?
2.	Нестандартное мышление!
3.	Важные примечания к правилам вероятности
4.	Решенные примеры по вероятностным правилам
5.	Интерактивные вопросы по вероятностным правилам

Что такое вероятность?

Вероятность – это мера вероятности наступления события. Многие события невозможно предсказать с полной уверенностью.

Используя вероятность, можно предсказать только вероятность того, что событие произойдет, т. е. насколько вероятно, что оно произойдет.

Например, при подбрасывании монеты есть вероятность выпадения орла или решки.

Свойства:

Вероятность невозможного события равна фи или равна нулю.
Максимальная вероятность события — это его выборочное пространство (выборочное пространство — это общее количество возможных исходов)
Вероятность любого события находится в диапазоне от 0 до 1 (0 также может быть вероятностью).
Не может быть отрицательной вероятности события.
Если A и B являются двумя взаимоисключающими исходами (два события, которые не могут произойти одновременно), то вероятность возникновения A или B равна вероятности A плюс вероятность B.

Формула вероятности – это отношение вероятности появления исхода к общему количеству исходов.

Вероятность наступления события P(E) = количество благоприятных исходов/общее количество исходов.

Каковы правила вероятности в математике?

1. Правило сложения. -Р(А\шапка Б)\) 9{\prime}\right)=1\)

3. Условное правило

Когда уже известно, что событие A произошло, и требуется вероятность события B, тогда P(B, учитывая A)=P(A и B)P(A, учитывая B). В случае события B может быть наоборот.
\( \mathrm{P}(\mathrm{B} \mid \mathrm{A})=\mathrm{P}(\mathrm{A} \cap \mathrm{B}) \mathrm{P}(\mathrm{ A})\)

4. Правило умножения

Всякий раз, когда событие является пересечением двух других событий, то есть события A и B должны произойти одновременно. Тогда P(A и B)=P(A)⋅P(B).

\(\mathrm{P}(\mathrm{A} \cap \mathrm{B})=\mathrm{P}(\mathrm{A}) \cdot \mathrm{P}(\mathrm{B} \ mid \mathrm{A})\)

Think Tank

Случайное число выбирается от \(1\) до \(100\). Какова вероятность того, что оно кратно \(11\)?
Тим бросает верный кубик. Какова вероятность умереть, не приземлившись на \(4\)?

Что такое основной принцип счета?
Фундаментальный принцип подсчета — это правило, которое подсчитывает все возможные варианты возникновения события или общее количество возможных исходов в ситуации.
В нем говорится, что если есть \( n \) способов сделать одно и \( m \) способов сделать другое, то количество способов сделать оба действия можно получить, взяв их произведение. Это выражается как \(n \times m \).
Пример:
Продавец мороженого продает 3 вида мороженого: ванильное, шоколадное и клубничное, предлагая своим покупателям 6 разных рожков на выбор.
Сколько вариантов мороженого будет у Венди, если она пойдет к этому продавцу мороженого?
Решение
У Венди есть 3 варианта вкуса мороженого и 6 вариантов рожков мороженого.
Следовательно, по фундаментальному принципу подсчета, количество вариантов выбора, которое есть у Венди, может быть представлено как \( 3 х 6 = 18 \)

Важные примечания
Вероятность наступления события P(E) = количество благоприятных исходов/общее количество исходов.
Максимальная вероятность события равна его выборочному пространству. Вероятность любого события находится между \(0\) и \(1\).
В независимых событиях исход одного события не влияет на исход других событий, тогда как в зависимых событиях исход одного события влияет на исход другого события.
Решенные примеры
Пример 1

Бен любит читать книги.
Он часто ходит в библиотеку.
Вероятность того, что он выпишет:
(a) художественное произведение равно \(0,40\),
(b) документальное произведение равно \(0,30\),
(c) как художественная, так и научно-популярная литература равна \(0,20\)
Какова вероятность того, что он просматривает как художественную, так и документальную литературу?
Раствор
Пусть F будет событием, когда Бен проверяет художественную литературу.
Пусть N будет событием, когда Бен проверяет документальную литературу.
Тогда по правилу сложения:
\(P(F \cup N)=P(F)+P(N)-P(F \cap N)\)
\(\mathrm{P}(\mathrm{F} \cup \mathrm{N})=0,40+0,30-0,20=0,50\)
\(\следовательно\) Вероятность того, что он проверит оба, равна \ (0,5\)
Пример 2

В банке 4 зеленых и 6 желтых шариков.
Два шарика вытащили из банки.
Второй шарик вытащен без замены.
Какова вероятность того, что оба вытащенных шарика будут желтыми?
Решение
Пусть A = событие, когда первый шарик желтый; и пусть B = событие, когда второй шарик желтый. Мы знаем следующее: 9{*}(5 / 9)=30 / 90=1 / 3=0,33\)
\(\следовательно\) Вероятность того, что оба шарика желтые = \(0,33\)
Пример 3

Из колоды \(52\) карт Катя должна вытащить две карты подряд, без замены.
Она попросила Джейн посчитать вероятность последовательного вытягивания короля и ферзя.
Давайте поможем Джейн рассчитать вероятность.
Решение
Общее количество событий = общее количество карт = \(52\)
Вероятность вытянуть даму = 4/52 = 1/13
Теперь общее количество карт = \(51 \)
Вероятность вытянуть короля = 4/51
Значит, вероятность вытянуть короля и ферзя последовательно, без замены = 1/13 * 4/51 = 4/ 663
\(\ следовательно\) Вероятность 4/663
Пример 4

В классе \(6\) детей и \(6\) скамеек, на которых они могут сидеть.
Их учитель каждый месяц заставляет их сидеть на разных местах. Сколькими способами она может заставить их сидеть в классе?
Решение
Есть \(6\) детей и \(6\) скамеек для них.
Следовательно, их учитель применит фундаментальный принцип подсчета, чтобы найти количество способов, которыми она может заставить их сесть.
Количество способов, которыми она может заставить детей сидеть в классе: \( 6 \умножить на 6 = 36 \)
\(\следовательно\) Есть \(36\) способов.
Пример 5

Просматривая записи класса, учитель получил следующую информацию:
40 % учеников изучают математику и естественные науки.
60 % студентов изучают естественные науки.
Какова вероятность того, что учащиеся будут изучать математику, учитывая, что учащийся уже изучает естественные науки?
Решение
Вероятность того, что студенты изучают математику и естественные науки = P(M&S) = \(0,40\)
Вероятность того, что студенты изучают математику = P(S) = \(0,60\)
Вероятность того, что студенты изучают математику , учитывая, что он/она уже изучает науку = \(\mathrm{P}(\mathrm{S} \mid \mathrm{M}) / \mathrm{P}(\mathrm{S})\)
=\(0,40/0,60\) =\( 2/3\) = \(0,67\)
\(\следовательно\) Вероятность \(0,67\)
I интерактивные вопросы
Вот несколько заданий для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Подведем итоги
Мини-урок был посвящен увлекательной концепции правил вероятности. Математическое путешествие по правилам вероятности начинается с того, что учащийся уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
О Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению. , Что такое и/или правило в вероятности?
Когда события взаимоисключающие и мы хотим узнать вероятность получения одного события ИЛИ другого, тогда мы можем использовать правило ИЛИ, то есть P(A или B) = P(A) + P(B). Когда события независимы и мы хотим знать вероятность того, что оба события произойдут одновременно, тогда мы можем использовать правило И, P(A и B)=P(A)⋅P(B).
2. Что такое формула вероятности?
Вероятность наступления события P(E) = количество благоприятных исходов/общее количество исходов.
Вероятность и статистика — Cuemath
Рози и ее семья смотрели футбольный матч. Ей было любопытно узнать о победителе матча. Она спросила своего отца, и он сказал ей, что есть вероятность, что команда А выиграет. Рози хотела узнать, что означает слово «вероятность».
Ее папа объяснил, что у любого события есть исход. Эти результаты известны как вероятность.
Затем Рози захотела узнать, сколько матчей уже выиграла команда А и какое максимальное количество забитых ею голов. Ее отец сказал ей, что им нужно проверить статистический отчет команды А. Далее он добавил, что статистика — это раздел математики, который занимается сбором, анализом, интерпретацией и представлением данных.

План урока
1. Что такое вероятность и статистика?
2. Важные примечания о вероятности и статистике
3. Решенные примеры по теории вероятности и статистике
4. Нестандартное мышление!
5. Интерактивные вопросы по вероятности и статистике
Что такое вероятность и статистика?
Вероятность — это понятие, используемое в математике и естественных науках для определения вероятности или наступления события. Например, при подбрасывании монеты есть вероятность выпадения орла или решки.
Статистика имеет дело с набором данных. Иногда нам может быть интересно найти самый любимый или часто используемый элемент из набора данных.
В таких случаях мы можем работать с набором данных, чтобы сделать анализ и сделать вывод.
Эта концепция, которая имеет дело с анализом данных, интерпретацией и представлением данных в более осмысленном виде, называется статистикой.
Мы обсудим формулу вероятности и статистики в разделах ниже, чтобы узнать значения для различных реальных ситуаций.
Какие существуют три типа вероятности?
Теоретическая или классическая вероятность
Экспериментальная вероятность
Аксиоматическая вероятность
Теоретическая или классическая вероятность
Теоретическая вероятность измеряет благоприятный исход события.
\(\begin{align}P(Event)\: =\: \frac{Всего \:число\: из \:благоприятных\: результатов\: из\: и\: событий\:}{Всего\: число\: из\: исходы} \end{выравнивание}\)
Например, когда мы подбрасываем монету, выпадает орёл или решка.
\(\begin{align}P(Head)\: =\: \frac{1}{2} \end{align}\)
\(\begin{align}P(Tail)\: =\ : \frac{1}{2} \end{align}\)
Экспериментальная вероятность
Экспериментальная вероятность измеряет общее количество благоприятных исходов для количества повторений эксперимента.
\(\begin{align}P(Event)\: =\: \frac{Всего \:число\: из \:благоприятных\: исходов\: из\: и\: событий}{Всего\: число\ : of\: times\: the\: Experiment\: is\: made} \end{align}\)
Например, если монета подбрасывается 8 раз, а орёл выпадает 3 раза, тогда
\( \begin{align}P(Head)\: =\: \frac{3}{8} \end{align}\)
\(\begin{align}P(Tail)\: =\: \frac{ 5}{8} \end{align}\)
Аксиоматическая вероятность
Аксиоматическая вероятность — это еще один способ описания результатов события.
Существуют три правила или аксиомы, применимые ко всем типам вероятностей.
Эти правила были определены Колмогоровым и называются аксиомами Колмогорова.
Три аксиомы таковы:
Вероятность любого события больше или равна 0.
Пример пространства определяет множество всех возможных исходов события.
Если A и B являются двумя взаимоисключающими исходами (два события, которые не могут произойти одновременно), то вероятность наступления A или B равна вероятности A плюс вероятность B.
Каковы пять правил вероятности?
Вероятность невозможного события равна фи или равна нулю.
Максимальная вероятность события — это его выборочное пространство (выборочное пространство — это общее количество возможных исходов).
Вероятность любого события находится в диапазоне от 0 до 1. 0 также может быть вероятностью.
Не может быть отрицательной вероятности события.
Если A и B являются двумя взаимоисключающими исходами (два события, которые не могут произойти одновременно), то вероятность наступления A или B равна вероятности A плюс вероятность B.
Прокрутите вниз, чтобы найти некоторые формулы вероятности и статистики.
Какая формула для расчета вероятности?
У любого события есть результат. Исходов события может быть очень много.
Формула для расчета вероятности выглядит следующим образом.
Пусть P(X) обозначает вероятность события ‘X’.
\(\begin{align}P(Event)\: =\: \frac{Всего \:число\: из \:благоприятных\: исходов\: из\: и\: событий}{Всего\: число\ : of\: results} \end{align}\)(или)
\(\begin{align}P(Event)\: =\: \frac{n(X)}{n(S)} \end{align}\)
Где \(\begin{align}n (X) = the\: result\: of\: an\: event\end{align}\)
\(\begin{align}n(S) = the\: total\: number\: of\: события\: in\: the\: sample\: space\end{align}\)
Что такое формула для статистики?
В статистике используются пять важных формул. Они следующие.
Среднее =\(\begin{align}\overline{x} = \dfrac{\sum x_i}{N}\end{align}\) 92}{N}}\end{align}\)
Показатели центральной ценности
Иногда, когда мы работаем с большими объемами данных, нам нужно одно единственное значение для представления всего набора. В математике есть три меры для нахождения центрального значения заданного набора данных.
Они равны
Среднее
Медиана
Режим
Среднее
Среднее представляет собой среднее значение заданного набора чисел.
Например, в заданном наборе данных
\(\begin{align}3, 5, 7, 9 \end{align}\)
Среднее значение получается путем сложения всех чисел и деления суммы на общее количество чисел.
\(\begin{align}Среднее\: = \: \dfrac{3+5+7+9}{4} \end{align}\)
\(\begin{align} =6\end{ align}\)
Медиана
Медиана представляет центральное или среднее значение набора данных.
Например, в данном наборе данных
\(\begin{align} 2, 4, 6, 8, 9, 10, 11, 13, 15, 17, 18 \end{align}\)
Медиана получается путем выбора среднего значения, равного \ (\begin{align} 10 \end{align}\).
Режим
Режим — наиболее часто встречающийся элемент данных.
Например, в заданном наборе данных
\(\begin{align} 30,30,31,31,31,32,32,33,33,33,33,34,35,36 \end{align }\)
Режим получается путем выбора наиболее часто встречающегося элемента в наборе данных.
Здесь режим \(\begin{align} 33\end{align}\).
Показатели распространения
При измерении центрального значения нам предоставляется набор данных. Чтобы узнать, насколько широк набор данных, мы используем показатели разброса.
Они также дают нам лучшую картину, если рассчитанное центральное значение (среднее, медиана или мода) правильно отображает набор значений.
Например,
Здесь мы имеем оценки, полученные студентами на тесте
\(\begin{align} 25,40,55,60,70,86,90,100\end{align}\)
При подсчете средних оценок, полученных учащимися в 100-балльном тесте, вычисляя среднее значение, мы можем найти только средние оценки, полученные учащимися, но мы не знаем, как распределяются оценки находятся в диапазоне от 0 до 100.
При подсчете средних оценок, полученных учащимися в тесте  \(\begin{align} 100\end{align}\), средний балл не может быть больше, чем Здесь режим \( \begin{align} 100\end{align}\).
В таких случаях полезны показатели распространения.
Наиболее часто используемыми показателями распространения являются
Диапазон
Квартили и межквартильный диапазон
Стандартное отклонение
Дисперсия
Диапазон
Диапазон представляет собой разницу между минимальным и максимальным значениями в наборе данных.

Минимальное значение: \(\begin{align} 3\end{align}\).
Максимальное значение: \(\begin{align} 13\end{align}\).
\(\begin{align} Диапазон\: =\: 13 — 3 = 10\end{align}\)
Диапазон = максимальное значение — минимальное значение
Квартиль
Как следует из названия, квартиль — это мера разброса, которая группирует заданный набор значений по четвертям.
Чтобы использовать эту меру,
Сначала мы расположим значения в порядке возрастания.
Сделайте четыре равные группы значений.
\(\begin{align} Первый \:Квартиль \:(Q1) \:= \:\dfrac{(Число\: из\: значений\: в\: в\: список\: +\: 1) \раз 1}{4} \конец{выравнивание}\)
\(\begin{align} Секунда \:Квартиль \:(Q2) \:= \:\dfrac{(Число\: из\: значений\: в\: в\: список\: +\: 1) \раз 2}{4} \конец{выравнивание}\)
\(\begin{align} Третий \:Квартиль \:(Q3) \:= \:\dfrac{(Число\: из\: значений\: в\: в\: список\: +\: 1) \times 3}{4} \end{align}\)
Например, в наборе данных, показанном ниже,
Количество значений = \(\begin{align} 7 \end{align}\)
\(\begin{align}Q1 = \frac {(7+1)}{4} \times1 = 2 \end{align}\)
\(\begin{align}Q2 = \frac {(7+1)}{4} \times2 = 4 \end {align}\)
\(\begin{align}Q2 = \frac {(7+1)}{4} \times3 = 6 \end{align}\)
Межквартильный
Межквартильный диапазон получается путем вычитания третьего квартиля (Q3) и первого квартиля (Q1). Это место, где большинство значений лежат в наборе данных, или мы можем сказать, что иногда межквартильный диапазон и среднее значение совпадают.
Например,
\(\begin{align} Q3\:=\:6\end{align}\)
\(\begin{align} Q1\:=\:2\end{align }\)
Межквартильный диапазон \(\begin{align}= Q3 — Q1 \end{align}\)
Межквартильный размах \(\begin{align}= Q3 — Q1 = 6 — 2 = 4 \end{align}\)
Дисперсия
Дисперсия — это мера, которая дает нам приблизительное представление о распространение данных. Это не очень точно.
Значение дисперсии используется для вычисления стандартного отклонения набора данных.
Стандартное отклонение
Стандартное отклонение — это мера, которая показывает, насколько далеко значение данных от среднего значения.
Получается путем извлечения квадратного корня из дисперсии.
Например,
Допустим, средний балл для прохождения теста равен \(\begin{align} 60\end{align}\). Оценка, полученная учащимся, равна \(\begin{align} 75\end{align}\). Это означает, что у студента значительно выше среднего балла.
Сравнение данных
В статистике для сравнения данных используются следующие понятия
Одномерные и двумерные данные
Разброс
Выбросы
Корреляция
Одномерные данные
Одномерные данные включают сравнение данных одного типа.
Например, мы можем сравнить рост студентов
Рост в футах и дюймах: 5 футов 9дюймов, 5 футов 7 дюймов, 5 футов 5 дюймов, 5 футов 10 дюймов.
Двумерные данные
Двумерные данные включают сравнение двух типов данных.
Например, количество рубашек, проданных за все дни недели. Здесь продажи и дни недели — это два типа данных.
Количество проданных футболок День недели
\(\begin{align} 5\end{align}\) Понедельник
\(\begin{align} 10\end{align}\) вторник
\(\begin{align} 12\end{align}\) Среда
\(\begin{align} 17\end{align}\) Четверг
\(\begin{align} 16\end{align}\) Пятница
\(\begin{align} 20\end{align}\) Суббота
\(\begin{align} 22\end{align}\) Воскресенье
Диаграммы рассеяния
Диаграммы рассеивания используются, чтобы узнать, как одни данные соотносятся с другими.
Ряд точек представляет собой точечную диаграмму.
Например, приведен график, отображающий возраст и вес человека в фунтах.
Мы можем измерить, как увеличивается вес с возрастом.
Выброс
Значение, выходящее за пределы заданного набора данных, называется выбросом. Другими словами, это наименьшее и наибольшее экстремальные значения.
Например,
Здесь \(\begin{align} 1\end{align}\) и \(\begin{align} 650\end{align}\) являются крайними значениями, которые не относятся к другие значения в списке.
Корреляция
Когда два набора значений данных увеличиваются или уменьшаются вместе, мы говорим, что они коррелированы.
Корреляция положительна, если два набора данных увеличиваются вместе.
Например,
Потребление электроэнергии увеличивается по мере увеличения количества людей.
Корреляция отрицательна, если одно значение уменьшается при увеличении другого значения.
Например,
Расстояние, которое нужно преодолеть, уменьшается по мере увеличения времени ходьбы.

Важные примечания
Исход — это результат события. Выборочное пространство — это общее количество возможных исходов события.
Значение вероятности всегда находится между 0 и 1.
Центральное значение набора данных можно измерить с помощью среднего значения, медианы или режима.
Теперь давайте обсудим некоторые примеры вероятности и статистики.
Решенные примеры
Пример 1

Алан бросил кости. Какова вероятность получить число \(\begin{align} 3\end{align}\)?
Решение
\(\begin{align}P(Event) = \dfrac{Число\:из \:благоприятных\:результатов}{Всего\:количество\:из \:возможных\:результатов} \end{align}\)
Число благоприятных исходов = \(\begin{align} 1\end{align}\) (Мы можем получить \(\begin{align} 3\end{align}\), когда мы бросить кубик)
\(\begin{align}P(3) = \dfrac{1}{6}\end{align}\)
Вероятность выпадения 3 при броске кубика  \(\ begin{align}P(3) = \dfrac{1}{6}\end{align}\)
Пример 2

Найдите среднее значение, медиану и моду следующих данных.
\(\begin{align}7,10,9,10,10,8,12,13,16\end{align}\)
Решение
Расположим числа в порядке возрастания.
\(\begin{align}7,8,9,10,10,10,12,13,16\end{align}\)
\(\begin{align}Среднее\:=\: \dfrac {Сумма\:из\:все\:наблюдения}{Всего\:число\:из\:наблюдений}\конец{выравнивание}\)
\(\begin{align}Среднее\:=\:\dfrac{7+8+9+10+10+10+12+13+16}{9}\end{align}\)
\( \begin{align}Среднее\:=\:\dfrac{95}{9}\end{align}\)
\(\begin{align}Среднее\:=\:10.5\end{align}\)
\(\begin{align}Медиана\:=\:\dfrac{Число\: из\: наблюдений \:+\: 1 }{2}\end{align}\)
\(\begin{align} \:=\:\dfrac{9\:+\: 1 }{2}\end{align}\)
\(\begin{align}\:=\:\dfrac{10 }{2}\end {align}\)
\(\begin{align}Median\:=\:5\end{align}\)
\(\begin{align}Mode\:is\:the\:наиболее\:часто \:происходит\:элемент\конец{выравнивание}\)
\(\begin{align}Mode\:=\:10\end{align}\)
\(\begin{align}Среднее\:=\:10,5\end{align}\)
\(\begin{align}Median\:=\:5\end{align}\)
\(\begin{align}Mode\:=\:10\end{align}\)
Пример 3

Найдите диапазон, квартиль для следующего набора чисел.
10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60
Решение
Диапазон:
\(\begin{align}Диапазон:\\:=\: Верхний limit\:-\:Lower\: limit\end{align}\)
\(\begin{align}Upper\:limit\: =\: 60\end{align}\)
\(\begin{ align}Lower\:limit\: =\: 10\end{align}\)
\(\begin{align}Range\: =\: 60\:-\:10\end{align}\)
\(\begin{align}Диапазон\: =\: 50\end{align}\)
Квартиль:
\(\begin{align}Первый\: Квартиль (Q1) = \dfrac{(Число\: из \: значения\: в\: в\: список\: +\: 1) \times 1}{4} \end{align}\)
\(\begin{align}Секунда\: Квартиль (Q2) = \dfrac{(Число\: из\: значений\: в\: в\: список\: +\: 1) \times 2}{4 } \end{align}\)
\(\begin{align}Третий\: Квартиль (Q1) = \dfrac{(Число\: of\: values\: in\: the\: list\: +\: 1) \times 3}{4} \end{align}\)
Количество значений в списке = 11
\(\begin{align}Первый\: Квартиль (Q1) = \dfrac{(11\: +\: 1) \times 1}{4} \end{align}\)
\(\begin{align}    = \dfrac{(12) \times 1}{4} \end{align}\)
\(\begin{align} = 3 \end{align}\)
\(\begin{align}Секунды\: Квартиль (Q2) = \dfrac{(11\:+\: 1) \times 2 {4} \end{align}\)
\(\begin{align} = \dfrac{(12) \times 2}{4} \end{align}\)
\(\begin{align} = 6 \end{align}\)
\(\begin{align}Третий\: квартиль (Q3) = \dfrac{(11\:+\: 1) \times 3}{4} \end{align} \)
\(\begin{align} = \dfrac{(12) \times 3}{4} \end{align}\)
\(\begin{align} = 9 \end{align}\)
\(\begin{align}Диапазон\: =\: 50\end{align}\)
\(\begin{align}Первый\: Квартиль\: (Q1) = 3 \end{align}\)
\(\begin{align}Секунда\: Квартиль\: (Q2) = 6 \end{align}\)
\(\begin{align}Третий\: Квартиль\: (Q3) = 9 \end{align}\)

Интерактивные вопросы
Вот несколько заданий для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Аналогичный центр
Выбирается случайное число от 1 до 100. Какова вероятность того, что это множество 8
Среднее значение квадратов чисел 1, 2, 3, 4, 5 и а равно 17,33. Найдите значение «а».
Подведем итоги
Мини-урок был посвящен увлекательной концепции вероятности и статистики. Математическое путешествие вокруг вероятностей и статистических чисел начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в умах молодых. Пример с вероятностью и статистикой обогатит ваши знания по этому вопросу. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
О Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.
Часто задаваемые вопросы о вероятности и статистике
1. Что такое случайные величины?
Возможные результаты случайного события называются случайными величинами.
2. Объясните биномиальное распределение.
Вероятность успеха или неудачи события определяется биномиальным распределением. Например, в тесте есть вероятность прохождения или провала.
3. Объясните нормальное распределение.
При наличии различных наборов данных (высоких, низких или смешанных) нам необходимо приблизительное значение заданного распределения вероятностей. В этом случае мы используем нормальное распределение. Он представлен с помощью кривой нормального распределения.
4. Что такое демонстрационное пространство?
Набор всех возможных исходов или результатов конкретного эксперимента или события называется выборочным пространством.
No related posts.